Мощность, формула
Мощностью P называется отношение произвольной работы W к времени t, в течение которого совершается работа.
[
textit{Мощность} = frac{textit{Работа}}{textit{Время}}
]
Единица СИ мощности
[
[P] = text{Ватт} enspace text{(Вт)} = frac{text{Джоуль}}{text{секунда}} = text{кг} frac{м^2}{с^3}
]
Средняя мощность, формула
Если:
P — Средняя мощность (Ватт),
W — Работа (Джоуль),
t — Время затраченное на совершение работы (секунд),
то
[
average{P} = frac{W}{t}
]
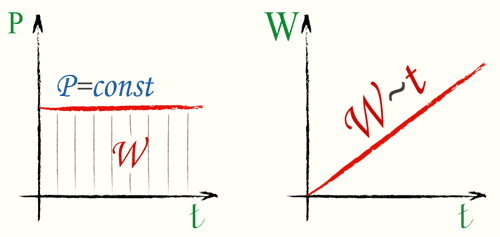
Вычислить, найти среднюю мощность по формуле (3)
Мгновенная мощность, формула
В большинстве случаев мощность зависит от времени, P=P(t).
Мгновенная мощность есть производная работы по времени:
[
P = frac{dW}{dt} = dot{W}
]
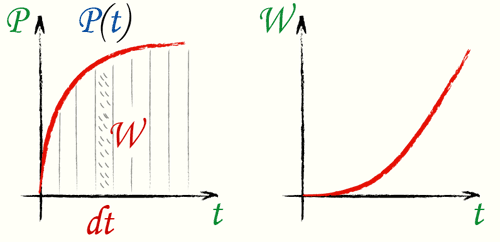
Поскольку см. (Работа)
[
dW = Fds
]
то отсюда следует см. (Мгновенная скорость)
[
P = F frac{ds}{dt} = Fu
]
Здесь:
F — Мгновенная сила (Ньютон),
u — мгновенная скорость (метр/секунда),
Мгновенная мощность равна произведению мгновенной силы на мгновенную скорость
При равномерно ускоренном движении F=const
[
P_{max} = F u_{max} ; average{P} = F average{u}
]
Вычислить, найти мгновенную мощность, по формуле (6)
Мощность |
стр. 471 |
|---|
Single Phase System
Instantaneous Power
The instantaneous power in an AC circuit is defined as the product of instantaneous voltage (v) across the element and instantaneous current (i) through the element and is denoted by lower case letter p.
Instantaneous Power, $mathrm{p=vtimes:i}$
Since, the values of instantaneous voltage and instantaneous current changes from instant to instant, thus the instantaneous power changes with time. The instantaneous power (p) is measured in watts. The instantaneous power may be positive or negative. A positive instantaneous power means power flows from source to load whereas negative instantaneous power means power flows from load to source.
Instantaneous Power Formula
Case 1 – Pure Resistive Circuit
In case of pure resistive circuit, the instantaneous value current and voltage being,
$$mathrm{v=V_{m}sinomega:t}$$
$$mathrm{i=I_{m}sinomega:t}$$
Therefore, the instantaneous power will be,
$$mathrm{p=vtimes:i=(v_{m}sinomega:t)times:(I_{m}sinomega:t)}$$
$$mathrm{Rightarrow:p=frac{V_{m}I_{m}}{2}-frac{V_{m}I_{m}}{2}cos2omega:t:::…(1)}$$
Case 2 – Pure Inductive Circuit
For pure inductive circuit, the equation of instantaneous voltage and current is given by,
$$mathrm{v=V_{m}sinomega:t}$$
$$mathrm{i=I_{m}sin(omega:t-90)}$$
Hence, the instantaneous power will be,
$$mathrm{p=vtimes:i=(V_{m}sinomega:t)times:(I_{m}sin(omega:t-90))}$$
$$mathrm{Rightarrow:p=-frac{V_{m}I_{m}}{2}sin2omega:t:::…(2)}$$
Case 3 – Pure Capacitive Circuit
The equation of instantaneous voltage and current for a pure capacitive circuit is given by,
$$mathrm{v=V_{m}sinomega:t}$$
$$mathrm{i=I_{m}sin(omega:t+90)}$$
Therefore, the instantaneous power will be,
$$mathrm{p=vtimes:i=(V_{m}sinomega:t)times:(I_{m}sin(omega:t+90))}$$
$$mathrm{Rightarrow:p=frac{V_{m}I_{m}}{2}sin2omega:t:::…(3)}$$
From the equations (1), (2) and (3) it can be noted that the instantaneous power in a single phase system varies from zero to maximum values at twice the supply frequency and also it may be positive or negative.
Average Power
The average power is defined as the average of instantaneous power over one cycle and is denoted by upper case letter P. It is also measured in watts.
Avergae Power, p = Avg. of p over one cycle
$$mathrm{p=frac{1}{2pi}int_{0}^{2pi}p:domega:t::::…(4)}$$
Average Power Formula
Case 1 – Pure Resistive Circuit
$$mathrm{mathrm{p=frac{1}{2pi}int_{0}^{2pi}p:domega:t=frac{1}{2pi}int_{0}^{2pi}frac{V_{m}I_{m}}{2}-frac{V_{m}I_{m}}{2}cos2omega:t:domega:t}}$$
$$mathrm{Rightarrow:p=frac{V_{m}I_{m}}{2}=frac{V_{m}}{sqrt{2}}times:frac{I_{m}}{sqrt{2}}=VI:::…(5)}$$
Where, V and I are the RMS values of voltage and current respectively.
Case 2 – Pure Inductive Circuit
$$mathrm{p=frac{1}{2pi}int_{0}^{2pi}p:domega:t=frac{1}{2pi}int_{0}^{2pi}-frac{V_{m}I_{m}}{2}cos2omega:t:domega:t=0:::…(6)}$$
Hence, average power absorbed by a pure inductor is zero.
Case 3 – Pure Capacitive Circuit
$$mathrm{p=frac{1}{2pi}int_{0}^{2pi}p:domega:t=frac{1}{2pi}int_{0}^{2pi}frac{V_{m}I_{m}}{2}cos2omega:t:domega:t=0:::…(7)}$$
Hence, average power absorbed by a pure capacitor is also zero.
Three Phase System
Instantaneous Power
As we know, the single phase instantaneous power (for lagging power factor load) is given by,
$$mathrm{p=frac{V_{m}I_{m}}{2}cosvarphi-frac{V_{m}I_{m}}{2}cos(2omega:t-varphi)}$$
In terms of RMS values, it becomes,
$$mathrm{p=VIcosvarphi-VIcos(2omega:t-varphi)}$$
Now, the instantaneous power in three phases (RYB –phase sequence) can be written as,
$$mathrm{p_{R}=V_{ph}I_{ph}cosvarphi-V_{ph}I_{ph}cos(2omega:t-varphi)}$$
$$mathrm{p_{Y}=V_{ph}I_{ph}cosvarphi-V_{ph}I_{ph}cos(2omega:t-varphi-120^{circ})}$$
$$mathrm{p_{H}=V_{ph}I_{ph}cosvarphi-V_{ph}I_{ph}cos(2omega:t-varphi+120^{circ})}$$
Therefore, total instantaneous power in three phase system is given by,
$$mathrm{p=P_{R}+P_{Y}+P_{H}}$$
$$mathrm{p=3V_{ph}I_{ph}cosvarphi-V_{ph}I_{ph}begin{bmatrix}cos(2omega:t-varphi)+cos(2omega:t-varphi-120^{circ}) +cos(2omega:t-varphi+120^{circ})end{bmatrix}}$$
$$mathrm{becausebegin{bmatrix}cos(2omega:t-varphi)+cos(2omega:t-varphi-120^{circ}) +cos(2omega:t-varphi+120^{circ})end{bmatrix}=0}$$
Thus,
$$mathrm{p=3V_{ph}I_{ph}cosvarphi:::…(8)}$$
$$mathrm{Rightarrow:p=sqrt{3}V_{L}I_{L}cosvarphi:::…(9)}$$
The eqns. (8) & (9) shows that the 3 phase instantaneous power is constant and is not the function of supply frequency.
Average Power
By the definition of average power, we obtain,
$$mathrm{P=frac{1}{2pi}int_{0}^{2pi}3V_{ph}I_{ph}cosvarphi:domega=3V_{ph}I_{ph}cosvarphi}$$
$$mathrm{Rightarrow:P=3V_{ph}I_{ph}cosvarphi=sqrt{3}V_{L}I_{L}cosvarphi:::…(10)}$$
Therefore, in case of a three system, the average power and instantaneous power are same.
Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Под мощностью подразумевают работу, выполненную за единицу времени, однако этот подход в большинстве случаев требует уточнений, поскольку интенсивность выполнения работы может многократно измениться за рассматриваемое время. Например, при движении автомобиля водитель увеличивает и уменьшает поступление топливно-воздушной смеси в зону сгорания, переключает передачи трансмиссии, притормаживает. Всё это влияет на текущую мощность двигателя. Поэтому в физике различают мгновенную мощность – мощность, измеренную за промежуток времени достаточно малый, чтобы считать ее величину постоянной:
$P = limlimits_{t to 0}frac{Delta A}{Delta t}$,
где $Delta t$ – промежуток времени, $Delta A$ – проделанная за это время работа.
Поскольку мгновенные величины мощности могут меняться без какой-либо четко выраженной закономерности, подсчитать их среднее значение бывает затруднительно. Поэтому среднюю мощность находят просто как
${langle}Prangle = frac{Delta A}{Delta t}$.
Следует различать мощность, связанную с общими затратами на движение и ту, что развивается для выполнения полезной работы. Так, один и тот же груз с одной и той же скоростью на одно и то же расстояние можно перевезти разными способами, например, на старинном паровозе и современном электровозе. Полезная работа будет выполнена одинаковая, но интенсивность затрат энергии – различная. Поэтому существует понятие средней полезной мощности, расчет которой зависит от многих факторов, связанных с особенностями движителей и сред, в которых выполняется работа.
Пример 1
Автомобиль массой 2 т поднимается в гору с постоянным ускорением по участку дороги с уклоном 30°. Движение длится 10 с. Скорость транспортного средства в начале подъема 20 км/ч, в конце 40 км/ч. Общая сила сопротивления (трение, вязкость воздуха и т.д.), постоянна и равна 600 Н. Определить среднюю полезную мощность двигателя.
Двигатель должен развить следующие силы:
- преодолевающую силу сопротивления;
- преодолевающую гравитацию, поскольку транспорт движется в гору;
- обеспечивающую ускорение.
Найдем их последовательно.
На преодоление силы сопротивления необходимо развить те же 600 ньютонов, но в направлении, совпадающем с вектором скорости.
Сила, преодолевающая силу тяжести, поскольку ее вектор находится под углом к вектору скорости, будет исчисляться по формуле:
$F_g = m cdot g cdot sin(alpha)$,
где $g$ – ускорение свободного падения, $m$ – масса. $alpha$ – угол наклона.
Приращение скорости:
$Delta v = v_1 – v_0 = frac{40000 – 20000}{3600} approx 5,56 frac{м}{с}$
Ускорение:
$a = frac{Delta v}{t} approx 0,556 frac{м}{с^2}$.
Просуммируем силы:
$F = 600 + 2000 cdot 9,8 cdot 0,5 + 2000 cdot 0.556 approx 600 + 9800 + 1112 = 11512 Н$
Работа равна произведению силы и пути, который можно выразить через время, начальную скорость и ускорение:
$A = F cdot (v_0 cdot t + frac{a cdot t^2}{2}) approx 11512 cdot (55,6 + 0,556 cdot 100) approx 11512 cdot 111,11 approx 1279111 Дж$
Разделив работу на время, получим среднюю полезную мощность:
$P = frac{1279111}{10} approx 127911 Вт$
Ответ: $approx 127911$ Вт. Примечание: полную мощность двигателя можно найти разделив это значение на КПД.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание
- 1 Как найти мощность формула?
- 2 Чему равно мощность?
- 3 Как найти среднюю мощность в физике?
- 4 Как найти мощность двигателя?
- 5 Как найти полную мощность?
- 6 Как рассчитать мощность источника?
- 7 Как найти мощность в цепи?
- 8 Как рассчитать мощность по току?
- 9 Как рассчитать сопротивление зная мощность и напряжение?
- 10 Как определить среднюю мощность?
- 11 Чему равен 1 ватт?
- 12 Что такое Mgh?
- 13 Как определить номинальную мощность двигателя?
Как найти мощность формула?
Определите мощность источника питания.
Напряжение – это величина, характеризующая электрическое поле, создаваемое током. Мощность равна произведению силы тока на напряжение, то есть 1 Вт = 1 А х 1 В. Формула: Р = I х V. Например, если сила тока равна 3 А, а напряжение равно 110 В, то мощность равна: 3 х 110 = 330 Вт.
Чему равно мощность?
Мо́щность — скалярная физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Как найти среднюю мощность в физике?
Средняя мощность силы — скалярная физическая величина Ν, равная отношению работы А, совершаемой силой, к промежутку времени Δt, в течение которого она совершается: N=AΔt.
Как найти мощность двигателя?
Если при работающем двигателе счетчик делает 20 оборотов в минуту, умножьте эту цифру на 60 (количество минут в часу). Получается 1200 оборотов в час. Разделите 1600 на 1200 (1.3) – это и есть мощность двигателя.
Как найти полную мощность?
Полная мощность (S)
Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью. Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А.
Как рассчитать мощность источника?
Полная мощность источника тока: P полн = P полезн + P потерь, где P полезн — полезная мощность, P полезн = I 2R; P потерь — мощность потерь, P потерь = I 2r; I — сила тока в цепи; R — сопротивление нагрузки (внешней цепи); r — внутреннее сопротивление источника тока.
Как найти мощность в цепи?
Мощность электрического тока
- Мощность электрического тока это количество работы, совершаемой за одну секунду времени, или скорость совершения работы.
- P = I*U. ( …
- U=IR.
- P = I*U =I*IR.
- Р = I2*R. ( …
- Р = I*U=U2/R (3)
- P = A/t.
Как рассчитать мощность по току?
Формула расчета мощности электрического тока
Согласно закону Ома, сила тока(I) пропорциональна напряжению(U) и обратно пропорциональна сопротивлению(R), а мощность(P) рассчитывается как произведение напряжения и силы тока. Исходя из этого, ток в участке сети рассчитывается: I = P/U.
Как рассчитать сопротивление зная мощность и напряжение?
Узнать мощность, если известны напряжение и сопротивление. W = 220 в * 220 в / 500 ом = 96.8 вт.
Как определить среднюю мощность?
Среднюю мощность развиваемую двигателем определим по формуле: P=frac{A}{t}(1). Где: А – работа совершенная двигателем, t – время движения.
Чему равен 1 ватт?
В Международной системе единиц (СИ) единицей измерения мощности является ватт [Вт],[W], равный одному джоулю [Дж],[J], делённому на секунду. 1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль. … Вт = H·м/с Вт = В·А
Что такое Mgh?
Механическая энергия равна сумме кинетической и потенциальной энергий тела. Работу по подъёму тела с постоянной скоростью можно найти по формуле: A = mgh, где h – высота, на которую поднимается центр тяжести тела.
Как определить номинальную мощность двигателя?
Pном = Мвр ∙ ωном, где Мвр – значение вращающего момента, ωном – номинальная угловая скорость двигателя.
Средняя мощность, как посчитать?
rrerwe rwerw
Ученик
(177),
закрыт
2 года назад
Мгновенная мощность в электрической цепи изменяется по закону 12 Вт, тогда за промежуток времени от 0 до 10с в цепи будет выделена средняя мощность? В ответе 12 Вт, но разве будет не 12*t (подставить 10 и 0) => 12*10-12*0=120 Вт. Или я не так считаю?
Николай Матвейчук
Просветленный
(42439)
2 года назад
Мощность это работа выполняемая за секунду.
Если каждую секунду на протяжении 10 секунд выполнялась работа в 12 джоуль, то какая в среднем выполнялась работа за одну секунду?
очевидно, что 12 джоуль, потому что каждую секунду именно столько и было. То есть очевидно, что средняя мощность 12 Ватт, если она была 12 Ватт постоянно, хоть целый год
Хьюберт Фарнсворт
Искусственный Интеллект
(109608)
2 года назад
Что за “закон 12 Вт”, по которому изменяется мощность в цепи? Не, может, я просто уже из ума выжил, но не припомню никакого 12 Вт, который открыл бы какие-то математические или физические законы. Да что там, я вообще никого по фамилии 12 Вт не помню.
hg nbУченик (111)
2 года назад
Это Xll закон Ватта, или Закон Ватта Xll, применим к нагрузкам по 12 ватт.
Анна Бородина
Оракул
(54259)
2 года назад
если есть мощность 2 ватт в первый момент и 4 во второй, то среднее будет , (2+4)/2=3.
Куклин АндрейВысший разум (189081)
2 года назад
Такого, увы, в условии нет. Там: “Мгновенная мощность в электрической цепи изменяется по закону 12 Вт”. Вот и мне интересно, как это?
rrerwe rwerw
Ученик
(177)
Куклин Андрей, А может задача специально так сформулирована. Мощность постоянная, а значит получается тогда и средняя она 12 Вт)
