Пример решения задачи по определению в заданный момент времени при сложном движении, абсолютной скорости и абсолютного ускорения точки, которая движется по ободу диска вращающегося вокруг оси.
Задача
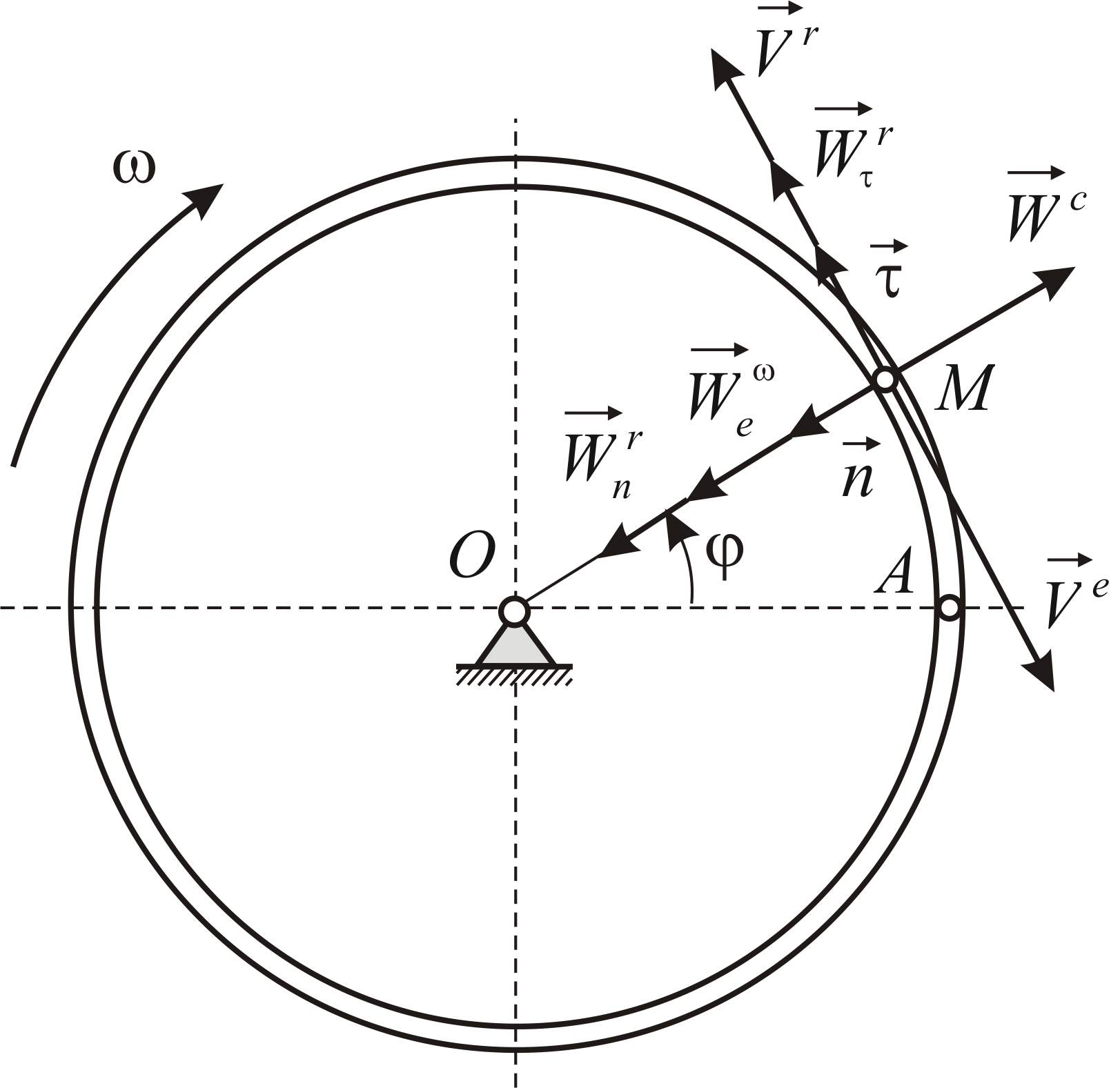
Диск радиуса R=0,5 м вращается вокруг оси, лежащей в его плоскости и касающейся диска, с угловой скоростью ω=πt2 c-1 (рисунок 3.5). По ободу диска движется точка M по закону: ∪OM=πRt2/6 м.
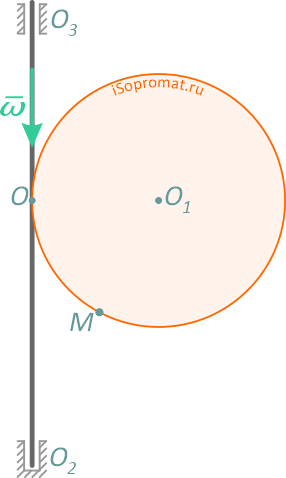
Рисунок 3.5
Требуется, в момент времени t=2c определить абсолютные скорость и ускорение точки M.
Другие примеры решений >
Помощь с решением задач >
Решение
Точка M в данном примере совершает сложное движение, которое может быть разложено на два движения: относительное движение — движение точки M по движущемуся диску (именно с ним может быть скреплена подвижная система отсчета) и переносное движение — вращение диска вместе с находящейся на нем точкой.
Поскольку переносное движение по определению это движение той точки диска, в которой находится в данный момент точка M, то сначала необходимо определить положение точки M на диске в момент времени t=2 c:
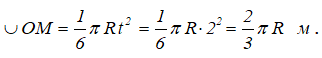
Центральный угол составит
![]()
Расчет скорости
В относительном движении закон движения задан естественным способом, поэтому скорость определяется как производная его дуговой координаты и направлена по касательной к траектории относительного движения в плоскости диска:
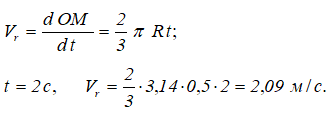
Переносное движение в данном случае — вращение вокруг неподвижной оси O2O3, расстояние до которой от точки M равно KM.
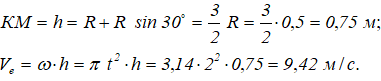
По направлению вектора угловой скорости ω определяем, что при вращении вокруг оси O2O3 точка M движется к нам, то есть вектор Ve перпендикулярен плоскости диска и для выбранной системы отсчета Mxyz, скрепленной с диском, направлен по оси Mx.
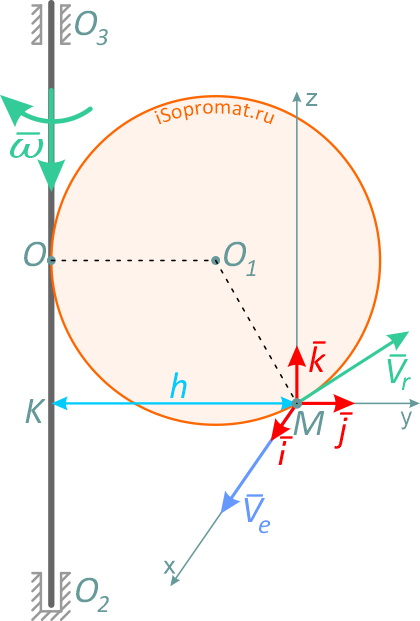
Рисунок 3.6
Абсолютная скорость точки в нашем примере определяется как геометрическая сумма векторов:
![]()
численная величина:
![]()
Спроецировав векторную сумму на выбранные оси координат, получим проекции абсолютной скорости на эти оси:
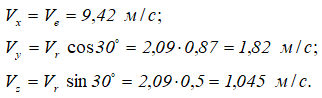
Направление вектора скорости определяют направляющие косинусы, то есть углы, которые вектор скорости составляет с выбранными осями:
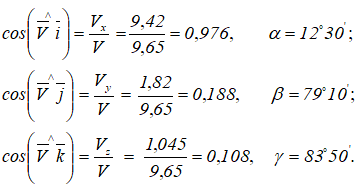
Расчет ускорения
В данном примере и переносные и относительные движения точки M — криволинейные, поэтому абсолютное ускорение определяется по формуле:
![]()
Составляющие ускорения определяются независимо друг от друга. В переносном движении точка M вращается вокруг оси O2O3 и движется по окружности радиуса h (рисунок 3.7).
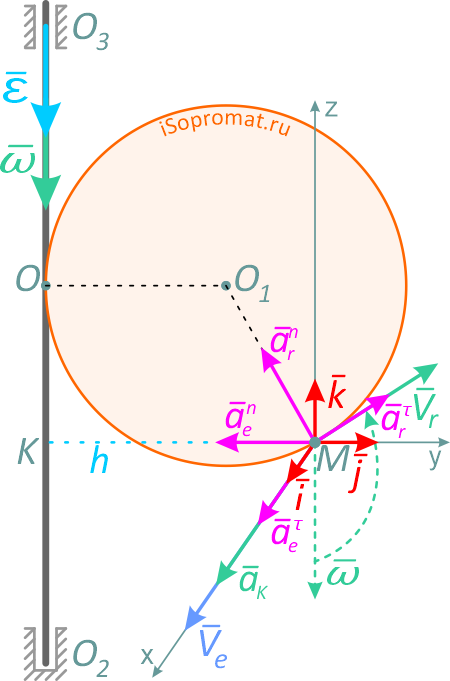
Рисунок 3.7
Нормальное ускорение в этом движении:
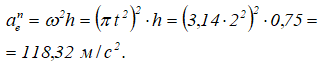
Этот вектор направлен от точки M к точке K (к оси вращения).
Касательное ускорение в переносном движении определится по формуле
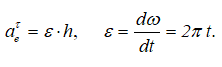
Знак производной положителен, то есть вращение ускоренное и направления векторов Ve и aeτ совпадают:
![]()
В относительном движении точка M движется по окружности радиуса R. Нормальное ускорение:
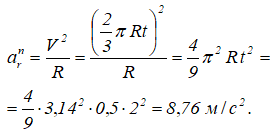
Этот вектор направлен от точки M к центру окружности — точке O1.
Касательное ускорение в относительном движении:
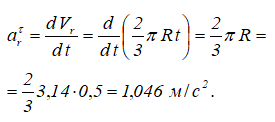
Производная от относительной скорости получена со знаком плюс, поэтому aeτ совпадает по направлению с Vr.
Кориолисово ускорение определяется по формуле
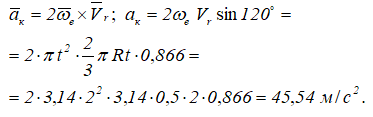
Вектор кориолисова ускорения должен быть перпендикулярен векторам ωe и Vr (в нашем случае перпендикулярен плоскости чертежа). Если смотреть навстречу вектору ak, то мы должны видеть поворот вектора ωe (мысленно перенесенного в точку) на кратчайший угол до совмещения с вектором Vr, происходящий против хода часовой стрелки. То есть в этом примере вектор ak направлен по оси Mx к нам.
Направление кориолисова ускорения может быть определено и по правилу Жуковского. Проецируем вектор V на плоскость, перпендикулярную вектору ωe (на плоскость Mxy; в данном примере эта проекция совпадает с осью My), и поворачиваем проекцию Vr на 90o в сторону вращения, то есть вектор ak направлен к нам по оси Mx.
Для определения абсолютного ускорения проецируем векторное равенство (3.6) на оси координат:
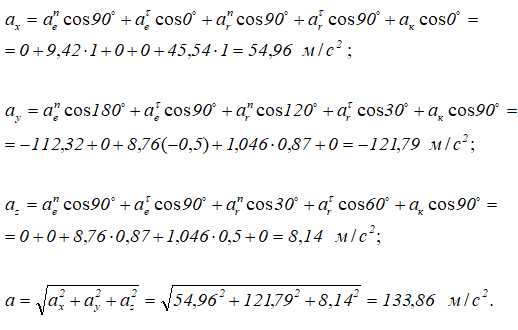
Направление вектора ускорения определяется с помощью направляющих косинусов (см. формулы (3.7)):
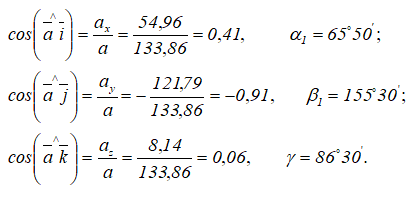
Другие примеры решения задач >
Напомним теорему сложения скоростей
при сложном движении точки:
абсолютная скорость точки равна
геометрической сумме относительной и
переносной скоростей:
![]()
Теорема сложения ускорений при сложном
движении точки имеет вид:
![]() ,
,
где вектор
![]()
называется ускорением Кориолиса.
Таким образом,
абсолютное ускорение точки равно
геометрической сумме относительного,
переносного и кориолисова ускорений.
Пример 3.3
Круглая трубка радиуса
![]() вращается вокруг горизонтальной оси
вращается вокруг горизонтальной оси![]() по часовой стрелке с постоянной угловой
по часовой стрелке с постоянной угловой
скоростью![]() .
.
Внутри трубки около ее точки![]() колеблется шарик
колеблется шарик![]() ,
,
причем так, что![]() (Рис. 3.5). Определить скорость, касательное
(Рис. 3.5). Определить скорость, касательное
и нормальное ускорения в абсолютном
движении шарика в любой момент времени.
|
|
|
Рис.3.5 |
Относительное движение шарика
представляет собой движение по окружности
радиуса![]() с центром в точке
с центром в точке![]() по закону
по закону![]() .
.
Определим закон изменения дуговой
координаты шарика в относительном
движении:
![]()
Вычислим относительную скорость и
относительное ускорение шарика:
![]()
![]()
![]()
Трубка сообщает шарику переносную
скорость
![]()
и переносное ускорение
![]()
Угол между осью вращения трубки,
вдоль которой направлен вектор ее
угловой скорости, и вектором относительной
скорости шарика равен
![]() ,
,
так что
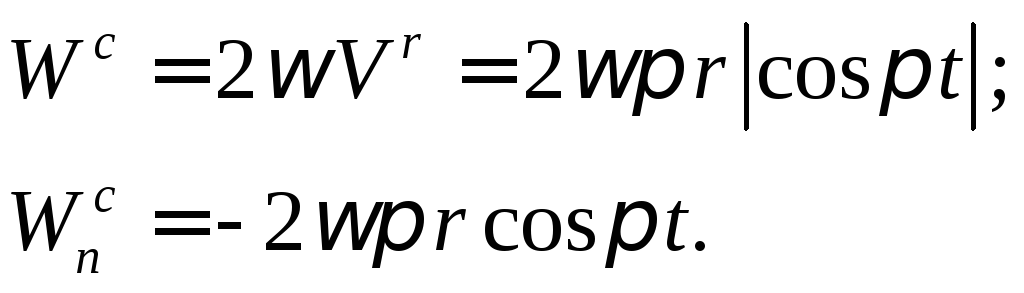
Для определения направления ускорения
Кориолиса удобнее всего воспользоваться
правилом Жуковского.
Абсолютная траектория шарика в
данном случае очевидна – это все та же
окружность с центром
![]() радиуса
радиуса![]() .
.
Используя теорему сложения скоростей,
получаем:
![]()
Используя теорему Кориолиса (3.12),
получаем:
![]()
![]()
Направления векторов указаны на Рис.
3.5. Ускорение Кориолиса и относительная
скорость представлены на рисунке для
случая
![]()
Пример 3.4
Лопатка
![]() рабочего колеса турбины, вращающегося
рабочего колеса турбины, вращающегося
против хода часовой стрелки замедленно
с угловым ускорением![]() ,
,
имеет радиус кривизны 0.2 м и центр
кривизны в точке![]() ,
,
причем![]() м. Частица воды
м. Частица воды![]() ,
,
отстоящая от оси![]() турбины на расстоянии 0.2 м, движется по
турбины на расстоянии 0.2 м, движется по
лопатке наружу и имеет скорость 0.25 м/с
и касательное ускорение 0.5 м![]() по отношению к лопатке. Определить
по отношению к лопатке. Определить
абсолютное ускорение частицы![]() в тот момент времени, когда угловая
в тот момент времени, когда угловая
скорость турбины равна 2 рад/с.
Подвижную систему координат свяжем
с рабочим колесом турбины (Рис. 3.6).
Относительной траекторией частицы воды
является кривая
![]() – лопатка турбины. Определим нормальное
– лопатка турбины. Определим нормальное
ускорение точки![]() в относительном движении
в относительном движении
![]()
Точка
![]() турбины описывает окружность с центром
турбины описывает окружность с центром![]() радиуса
радиуса![]() .
.
Определим переносное ускорение точки:
![]()
Направление ускорения Кориолиса
определяем по правилу Жуковского. Модуль
ускорения Кориолиса равен
![]()
Используя теорему Кориолиса, найдем
проекции абсолютного ускорения частицы
![]() на оси подвижной системы координат
на оси подвижной системы координат
(Рис. 3.6):
![]()
![]()
|
|
|
|
|
Рис. 3.6 |
Рис. 3.7 |
Остается определить
![]() и
и![]() .
.
Для этого используем теорему косинусов
(Рис. 3.7):
![]()
Отсюда
![]()
Таким образом,
![]()
Окончательно получаем:
![]()
Пример 3.5
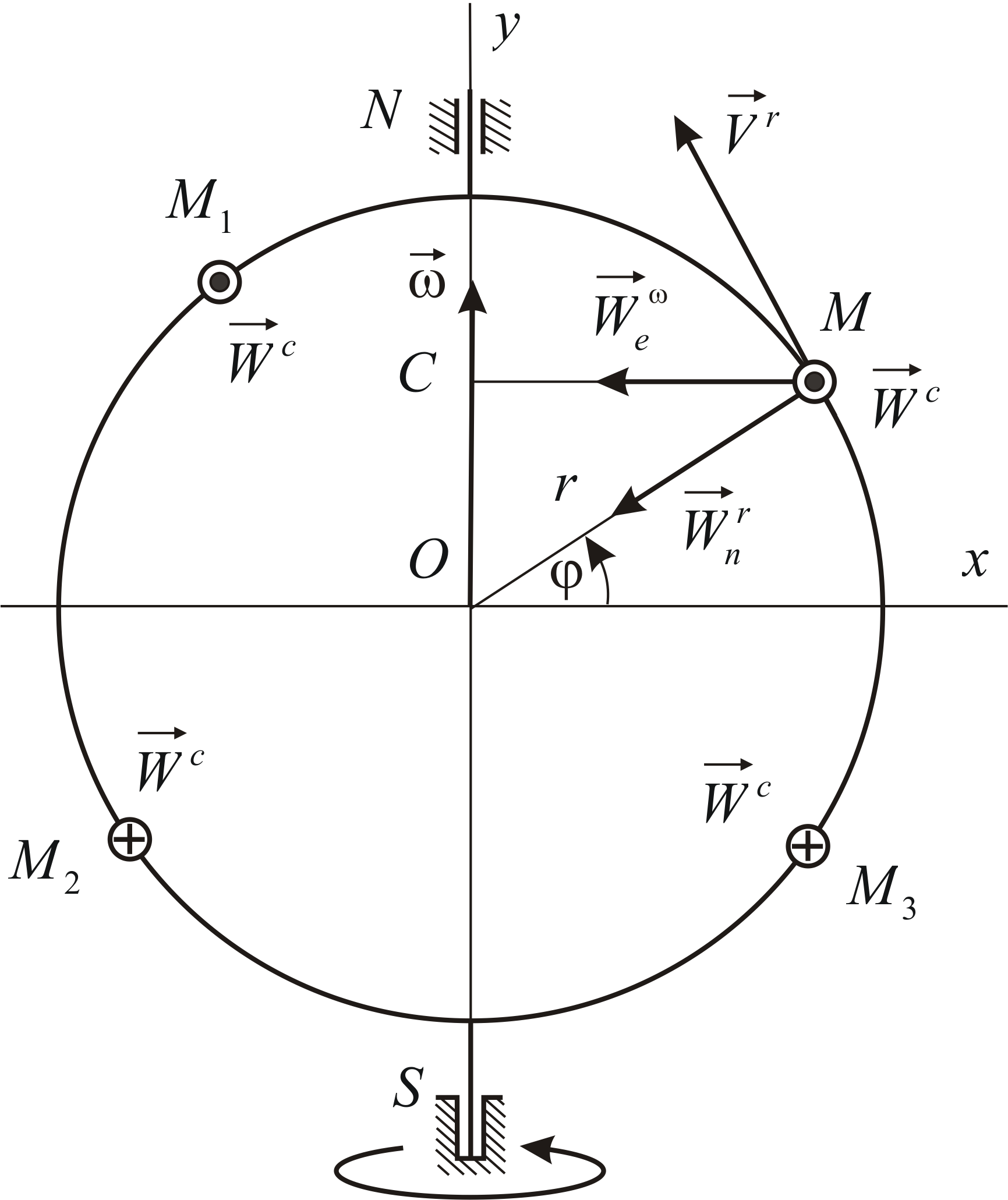
Диск радиуса
![]() вращается вокруг неподвижной оси
вращается вокруг неподвижной оси![]() с постоянной угловой скоростью
с постоянной угловой скоростью![]() .
.
По ободу диска движется точка![]() ,
,
имея относительно диска постоянную по
модулю скорость![]() .
.
Определить абсолютную скорость и
абсолютное ускорение точки![]() .
.
Подвижную систему отсчета связываем
с диском (Рис. 3.8). По отношению к диску,
т.е. в относительном движении, точка
![]() движется равномерно со скоростью
движется равномерно со скоростью![]() ,
,
описывая окружность радиуса![]() с центром в точке
с центром в точке![]() .
.
Определяем относительное ускорение
точки:
![]()
Рассмотрим переносное движение –
его совершает диск. Точка
![]() диска описывает окружность с центром
диска описывает окружность с центром![]() ,
,
плоскость которой параллельна координатной
плоскости![]() .
.
Переносная скорость
![]()
направлена по касательной к этой
окружности в сторону вращения диска,
т.е. перпендикулярно плоскости диска в
отрицательном направлении координатной
оси
![]() .
.
Поскольку вращение диска по условию
равномерное, отличным от нуля оказывается
только осестремительное ускорение:
![]()
Вектор ускорения Кориолиса точки
![]() направлен перпендикулярно плоскости
направлен перпендикулярно плоскости
чертежа, в которой расположены векторы![]() и
и![]() ,
,
причем, в ту сторону, откуда кратчайшее
совмещение направления вектора![]() с направлением вектора
с направлением вектора![]() видно против хода часовой стрелки. В
видно против хода часовой стрелки. В
указанном на Рис. 3.9 положении точки![]() вектор ускорения Кориолиса направлен
вектор ускорения Кориолиса направлен
на нас, т.е. параллелен координатной
оси![]() в положительную сторону этой оси. На
в положительную сторону этой оси. На
Рис. 3.9 это направление условно обозначено
острием стрелки, заключенным в кружок.
Модуль ускорения Кориолиса вычисляется
по формуле:
![]() .
.
|
|
|
|
|
Рис.3.8 |
Рис.3.9 |
При перемещении точки
![]() по диску направление ускорения Кориолиса
по диску направление ускорения Кориолиса
не будет изменяться до тех пор, пока![]() ,
,
т.е. пока![]() (точка
(точка![]() ).
).
При пересечении точкой![]() координатной оси
координатной оси![]() ускорение Кориолиса обращается в нуль.
ускорение Кориолиса обращается в нуль.
При движении точки в нижней части диска,
т.е. при![]() ,
,
проекция ускорения Кориолиса на
направление оси![]() становится отрицательной и вектор
становится отрицательной и вектор![]() направлен от нас (точки
направлен от нас (точки![]() и
и![]() ).
).
Таким образом,
![]()
Используя теорему сложения скоростей
![]()
находим проекции вектора абсолютной
скорости на оси подвижной системы
координат:
![]()
![]()
![]()
Используя теорему Кориолиса
![]()
находим проекции абсолютного ускорения
точки на оси подвижной системы координат:
![]()
![]()
![]()
![]()
Примечание.
Последняя задача позволяет
проиллюстрировать некоторые явления,
связанные с вращением Земли, в частности,
размыв берегов рек. Как видно, вращение
Земли приводит к возникновению у частиц
воды кориолисова ускорения, направленного
перпендикулярно линии берегов. Наличие
такого ускорения приводит к тому, что
в северном полушарии дополнительно
подмывается правый берег, который на
прямолинейных участках рек заметно
выше левого берега. В южном полушарии
более высокий левый берег. Это явление
в географии отражено в законе Бэра.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 22.10;
22.14; 22.17; 22.26; 23.1; 23.9; 23.13; 23.18; 23.19;
23.27; 23.29; 23.34; 23.47; 23.48; 23.49; 23.56.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-23;
СР-24; СР-25.
КОНТРОЛЬНЫЕ
МЕРОПРИЯТИЯ:
-
После
практического занятия №7(15) проводится
тест «МОДУЛЬ КБ».
ЛИТЕРАТУРА:
-
Антонов В.И., Белов В.А., Егорычев О.О.,
Степанов Р.Н.//Курс теоретической
механики (теория и практика) – М.:
Архитектура – С, 2011 г. -
Мещерский И.В.//Сборник задач по
теоретической механике. – Спб.: Лань,
2010 г.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2015560.03 Кб15PSY – recommendation.pdf
- #
- #
Для школьников.
Повторяем кинематику (относительность движения тел).
Имеет смысл говорить о скорости тела (материальной точки) относительно некоторого другого тела (системы отсчёта, связанной с этим другим телом).
Понятия материальной точки и системы отсчёта даны в Занятии 1.
Наиболее простым понятным примером является случай, когда лодка переплывает реку под прямым углом к берегу.
Скорость лодки в системе отсчёта, связанной с Землёй (неподвижной системе отсчёта), называют абсолютной скоростью.
Скорость лодки в системе отсчёта движущейся относительно Земли (движущейся системе отсчёта) называют относительной скоростью.
Вводится ещё понятие переносной скорости. Переносная скорость – это скорость движущейся системы отсчёта относительно неподвижной системы отсчёта (при поступательном движении). В рассматриваемом случае переносная скорость – это скорость течения реки относительно берега.
Тогда скорость лодки относительно берега (абсолютная скорость) выразится как векторная сумма относительной и переносной скоростей:
Второе и третье уравнения позволяют найти относительную скорость материальной точки (они вытекают из первого уравнения).
Примеры и решённые задачи на эти уравнения даны в Занятии 12 и в задачах 4 – 7, 8 – 9, 10 – 11, в задаче для студентов.
Сейчас же рассмотрим решение следующей задачи.
ЗАДАЧА.
Тело (материальная точка М) перемещается вдоль радиуса диска (относительно диска) со скоростью 30 см/с. Диск вращается с угловой скоростью 4 рад/с. Найти абсолютную скорость точки М в момент времени, когда она находится на расстоянии 10 см от центра диска (когда расстояние ОМ равно 10 см).
Решение.
Так как диск вращается (его движение не поступательное), то переносная скорость есть скорость того “места” в движущейся системе, где в данный момент времени находится материальная точка М.
Известная нам скорость 30 см/с является относительной скоростью.
Переносная скорость точки М в рассматриваемый момент времени найдётся через произведение угловой скорости вращения диска на радиус ОМ. Она равна 40 см/с.
Абсолютную скорость точки М найдём по теореме Пифагора:
Ответ: абсолютная скорость точки М в момент её нахождения на расстоянии ОМ, равном 10 см, равна 50 см/с.
Теперь посмотрим, как находится скорость одного движущегося тела относительно другого движущегося тела на примере следующей задачи.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Ссылки на занятия по механике даны в конце Занятия 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
iSopromat.ru
Пример решения задачи по определению в заданный момент времени абсолютной скорости и абсолютного ускорения точки, которая движется по ободу диска вращающегося вокруг оси.
Задача
Диск радиуса R=0,5 м вращается вокруг оси, лежащей в его плоскости и касающейся диска, с угловой скоростью ω=πt 2 c -1 (рисунок 3.5). По ободу диска движется точка M по закону: ∪OM=πRt 2 /6 м. В момент времени t=2 c определить абсолютные скорость и ускорение точки M.
Решение
Точка M в данном примере совершает сложное движение, которое может быть разложено на два движения: относительное движение — движение точки M по движущемуся диску (именно с ним может быть скреплена подвижная система отсчета) и переносное движение — вращение диска вместе с находящейся на нем точкой.
Поскольку переносное движение по определению это движение той точки диска, в которой находится в данный момент точка M, то сначала необходимо определить положение точки M на диске в момент времени t=2 c:
Расчет скорости
В относительном движении закон движения задан естественным способом, поэтому скорость определяется как производная его дуговой координаты и направлена по касательной к траектории относительного движения в плоскости диска:
Переносное движение в данном случае — вращение вокруг неподвижной оси O2O3, расстояние до которой от точки M равно KM.
По направлению вектора угловой скорости ω определяем, что при вращении вокруг оси O2O3 точка M движется к нам, то есть вектор Ve перпендикулярен плоскости диска и для выбранной системы отсчета Mxyz, скрепленной с диском, направлен по оси Mx.
Абсолютная скорость точки в нашем примере определяется как геометрическая сумма векторов Ve и Vr:
Спроецировав векторную сумму на выбранные оси координат, получим проекции абсолютной скорости на эти оси:
Направление вектора скорости определяют направляющие косинусы, то есть углы, которые вектор скорости составляет с выбранными осями:
Расчет ускорения
В данном примере и переносные и относительные движения точки M — криволинейные, поэтому абсолютное ускорение определяется по формуле:
Составляющие ускорения определяются независимо друг от друга. В переносном движении точка M вращается вокруг оси O2O3 и движется по окружности радиуса h (рисунок 3.7). Нормальное ускорение в этом движении:
Этот вектор направлен от точки M к точке K (к оси вращения).
Касательное ускорение в переносном движении определится по формуле
Знак производной положителен, то есть вращение ускоренное и направления векторов Ve и ae τ совпадают:
В относительном движении точка M движется по окружности радиуса R. Нормальное ускорение:
Этот вектор направлен от точки M к центру окружности — точке O1.
Касательное ускорение в относительном движении:
Производная от относительной скорости получена со знаком плюс, поэтому ae τ совпадает по направлению с Vr.
Вектор кориолисова ускорения должен быть перпендикулярен векторам ωe и Vr (в нашем случае перпендикулярен плоскости чертежа). Если смотреть навстречу вектору ak, то мы должны видеть поворот вектора ωe (мысленно перенесенного в точку) на кратчайший угол до совмещения с вектором Vr, происходящий против хода часовой стрелки. То есть в этом примере вектор ak направлен по оси Mx к нам.
Направление кориолисова ускорения может быть определено и по правилу Жуковского. Проецируем вектор V на плоскость, перпендикулярную вектору ωe (на плоскость Mxy; в данном примере эта проекция совпадает с осью My), и поворачиваем проекцию Vr на 90 o в сторону вращения, то есть вектор ak направлен к нам по оси Mx.
Для определения абсолютного ускорения проецируем векторное равенство (3.6) на оси координат:
Направление вектора ускорения определяется с помощью направляющих косинусов (см. формулы (3.7)):
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.
Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).
t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.
N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:
Количество оборотов выражается следующей формулой:
Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.
Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.
l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:
R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:
Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:
Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).
ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.
За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:
Выражая угловую скорость через частоту, получим:
Выразив частоту через количество оборотов, формула угловой скорости примет вид:
Сравним две формулы:
Преобразуем формулу линейной скорости и получим:
Отсюда получаем взаимосвязь между линейной и угловой скоростями:
Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.
За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:
Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:
Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:
Подставляем известные данные в формулу и вычисляем:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:
Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:
Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:
Произведем сокращения и получим:
Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
[spoiler title=”источники:”]
[/spoiler]
Содержание:
- Сложное движение точки
- Абсолютный, относительный и переносной движения точки
- Теорема о сложении скоростей в сложном движении точки
- Теорема о сложении ускоренного в сложном движении точки (Теорема Кориолиса *)
- Кориолисово ускорения
- Правило Жуковского
- Примеры решения задач на сложное движение точки
- Сложное движение точки и решение задач
- Порядок решения задач на сложное движение точки
- Примеры решения задач
- Задание темы К4 (сложное движение точки)
- Пример решения задания темы К4
- Сложное движение точки образцы и примеры
- Относительное, переносное и абсолютное движение точки
- Относительные, переносные и абсолютные скорости и ускорение
- Сложение скоростей и ускорений при сложном движении точки
- Примеры решения задач
- Абсолютное, относительное и переносное движение точки
- Центральная операция кинематики и динамики. Абсолютная и относительная производные по времени от вектора функции
- Теорема о сложении скоростей
- Теорема о сложении ускорений
- Вращательное и осевое ускорение в случае вращения тела вокруг неподвижной оси
- Ускорение Кориолиса
- Случаи превращения в ноль ускорения Кориолиса
- Физические причины возникновения ускорения Кориолиса
- Сложное движение материальной точки. Относительное, переносное и абсолютное движение материальной точки
- Теорема о сложении скоростей в сложном движении материальной точки
- Теорема Кориолиса
- Модуль, направление и физические причины возникновения ускорения Кориолиса
- Методика решения задач на сложное движение материальной точки
Сложное движение точки – это такое движение, при котором точка (тело) одновременно участвует в двух или нескольких движениях. Примером сложного движения могут служить: движение пассажира. перемещающегося в вагоне движущегося поезда; движение человека, перемещающегося по лестнице движущегося эскалатора.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Сложное движение точки
Сложное движение точки – это такое движение, при котором точка участвует одновременно в двух или нескольких движениях. Примеры сложного движения точки (тела): лодка, переплывающая реку; человек, идущий по движущемуся эскалатору; камень подвижной кулисы, поршень качающегося цилиндра; шары центробежного регулятора Уатта. Для описания сложного движения точки или для представления движения в виде сложного используются неподвижная система отсчета, связанная с каким-либо условно неподвижным телом, например, с Землей, и подвижная система отсчета, связанная с каким-либо движущимся телом.
Абсолютный, относительный и переносной движения точки
В разделе 2 изучалось движение точки по отношению к системе координат (системы отсчета), которую считали условно неподвижной. В то же время, рассматривая многие задачи механики, целесообразнее, а в некоторых случаях просто необходимо, проводить исследования движения точки одновременно по отношению в двух (или более) систем отсчета, из которых одна считается неподвижной, а другая (другие) движется определенным образом по отношению к ней.
Движение точки по отношению к нескольким системам отсчета называется сложным.
Например, в сложном движении находятся поршень двигателя движущегося автомобиля; груз, который поднимается краном, одновременно перемещается вдоль направляющих и поворачивается вокруг своей вертикальной оси; движение человека по вагону подвижного состава.
В этом разделе будем рассматривать движение точки относительно двух систем отсчета.
Рассмотрим движущееся тело А, которое в отдельных случаях будем называть переносной средой, в отношении которого движется точка М, которая не принадлежит телу (рис. 7.1). С телом А неизменно свяжем систему координат  которая движется относительно другой системы
которая движется относительно другой системы  которую условно считаем неподвижной.
которую условно считаем неподвижной.

Система координат  называется подвижной системой отсчета, а система
называется подвижной системой отсчета, а система  – неподвижной системе отсчета. Заметим, что неподвижную систему отсчета очень часто связывают с поверхностью Земли или неподвижными объектами на ней.
– неподвижной системе отсчета. Заметим, что неподвижную систему отсчета очень часто связывают с поверхностью Земли или неподвижными объектами на ней.
Поскольку точка М движется относительно двух систем отсчета, то ее движение, по определению, будет сложным. Введем основные понятия и обозначения в случае сложного движения точки.
Движение точки М по отношению к неподвижной системе отсчета называется абсолютным движением. Уравнения абсолютного движения точки можно записать в виде:

Траектория, скорость и ускорение точки в абсолютном движении называются абсолютной траекторией, скоростью и ускорением точки. Абсолютные скорость и ускорение будем обозначать  и
и
Движение точки М относительно подвижной системы отсчета  называется
называется
относительным движением точки, а траектория, скорость и ускорение – относительной траекторией, скоростью и ускорением. Относительные скорость и ускорение обозначают  и
и  (от латинского relativus – относительный). Уравнения относительного движения точки имеют вид:
(от латинского relativus – относительный). Уравнения относительного движения точки имеют вид:

Движение подвижной системы отсчета (а значит и тела А) относительно неподвижной
является для точки М переносным движением. Скорость и ускорение той точки тела А, с которой в данный момент времени совпадает движущаяся точка М, называется соответственно переносной скоростью и переносным ускорением точки в этот момент. Переносная скорость и ускорение обозначаются  и
и  (от латинского emporter – переносить).
(от латинского emporter – переносить).
В приведенном выше примере о человеке, что перемещается в вагоне подвижного состава, с вагоном можно связать подвижную систему координат, а с поверхностью Земли – неподвижную. Тогда движение вагона будет переносным, движение человека относительно вагона – относительным, а движение человека относительно поверхности
Земли – абсолютным. Переносной скоростью и переносным ускорением человека будет скорость и ускорение той точки вагона, в которой в заданный момент находится человек.
Основная задача кинематики сложного движения точки заключается в том, чтобы, зная кинематические характеристики относительного и переносного движений, найти соответствующие им характеристики абсолютного движения.
Теорема о сложении скоростей в сложном движении точки
Теорема. В сложном движении точки ее абсолютная скорость равна векторной сумме относительной и переносной скоростей.
Доказательство. Для доказательства рассмотрим движение точки М (рис. 7.1) относительно подвижной системы отсчета  связанной с телом А. Для общего случая, движение тела А рассмотрим как движение свободного твердого тела. Следовательно, точка М находится одновременно в двух движениях: относительном – относительно тела А и переносном – вместе с телом. Абсолютным движением точки М будет ее движение относительно неподвижной системы отсчета
связанной с телом А. Для общего случая, движение тела А рассмотрим как движение свободного твердого тела. Следовательно, точка М находится одновременно в двух движениях: относительном – относительно тела А и переносном – вместе с телом. Абсолютным движением точки М будет ее движение относительно неподвижной системы отсчета  Напомним, что поскольку переносным движением является свободное движение твердого тела, то его можно рассматривать, согласно § 6.1 раздела 6, как совокупность поступательного движения вместе с полюсом (Точка
Напомним, что поскольку переносным движением является свободное движение твердого тела, то его можно рассматривать, согласно § 6.1 раздела 6, как совокупность поступательного движения вместе с полюсом (Точка  ) и сферического вокруг полюса. Сферическую составляющую в каждый момент времени можно заменить (§ 5.1) вращением тела, а значит и подвижной системы координат
) и сферического вокруг полюса. Сферическую составляющую в каждый момент времени можно заменить (§ 5.1) вращением тела, а значит и подвижной системы координат  вокруг мгновенной оси
вокруг мгновенной оси  проходящей через
проходящей через
точку  с угловой скоростью переносного движения
с угловой скоростью переносного движения 
Положение точки М в подвижной системе координат  определяется радиусом-вектором
определяется радиусом-вектором  в неподвижной – радиусом-вектором
в неподвижной – радиусом-вектором  а положение начала подвижной системы координат (точка
а положение начала подвижной системы координат (точка  ) относительно начала О неподвижной – радиусом-вектором
) относительно начала О неподвижной – радиусом-вектором  Во время движения точки М между радиусами-векторами
Во время движения точки М между радиусами-векторами  и
и  согласно рис. 7.1 справедлива зависимость
согласно рис. 7.1 справедлива зависимость

Если координаты точки М в подвижной системе отсчета обозначить через  а орты осей этой системы –
а орты осей этой системы –  то
то

и тогда

Абсолютная скорость точки М равна производной по времени от радиусавектора что определяет ее положение в абсолютном движении. дифференцируя зависимость (7.5) и учитывая, что орты
что определяет ее положение в абсолютном движении. дифференцируя зависимость (7.5) и учитывая, что орты меняют свое направление в пространстве, получим
меняют свое направление в пространстве, получим

Изменение направлений ортов  происходит от вращения осей подвижной системы отсчета вокруг мгновенной оси
происходит от вращения осей подвижной системы отсчета вокруг мгновенной оси  с угловой скоростью
с угловой скоростью  Поэтому производные по времени от единичных ортов можно рассматривать как скорости концов этих ортов от этого вращения. Согласно формуле (3.17) раздела 3 запишем
Поэтому производные по времени от единичных ортов можно рассматривать как скорости концов этих ортов от этого вращения. Согласно формуле (3.17) раздела 3 запишем

После подстановки (7,7) в (7.6) и преобразований с учетом зависимости (7.7), получим
где скорость точки
скорость точки  начала подвижной системы координат.
начала подвижной системы координат.
Зависимость (7.8) определяет вектор абсолютной скорости точки М. Проведем ее анализ.
Поскольку в последних трех слагаемых зависимости (7.8) являются производные по времени от соответствующих уравнений относительного движения точки М (7.2), то согласно с (2.18) они являются проекциями вектора относительной скорости точки на оси
подвижной системы координат
 а сумма трех слагаемых выражает вектор относительной скорости точки М
а сумма трех слагаемых выражает вектор относительной скорости точки М

Покажем, что первые две слагаемых зависимости (7.8) определяют вектор переносной скорости точки М. Действительно, переносная скорость точки, по определению, это скорость точки, неизменно связанной с подвижной системой отсчета, с которой в данный момент времени совпадает движущаяся точка М. Такой точкой в нашем случае является точка М тела А, находящегося в свободном движении. А по формуле (6.3) скорость этой точки равна сумме скорости полюса  и вращательной скорости вокруг мгновенной
и вращательной скорости вокруг мгновенной
оси  то есть
то есть

Учитывая (7.9) и (7.10), зависимость (7.8) перепишем в виде

то есть абсолютная скорость точки равна векторной сумме переносной и относительной скоростей. Теорема доказана.
Следует заметить, что в случае, когда переносным движением является движение свободного твердого тела, то переносная скорость сама определяется диагональю
параллелограмма, построенного на векторах скорости полюса и скорости точки от вращения вокруг него
и скорости точки от вращения вокруг него  Если же переносное движение поступательное, то зависимость (7.10) принимает вид
Если же переносное движение поступательное, то зависимость (7.10) принимает вид

В случае вращательного переносного движения  где
где  – вектор, проведенный из любой точки на оси вращения к точке М.
– вектор, проведенный из любой точки на оси вращения к точке М.
Исходя из того, что в общем случае абсолютная скорость точки М определяется диагональю параллелограмма, построенного на векторах  и
и  модуль абсолютной скорости точки можно получить по формуле
модуль абсолютной скорости точки можно получить по формуле

Замечания. Если точка М находится в n движениях, то абсолютная скорость точки М равна векторной сумме векторов скоростей составляющих движений
Теорема о сложении ускоренного в сложном движении точки (Теорема Кориолиса *)
Теорема. В сложном движении точки ее абсолютное ускорение равно векторной сумме переносного, относительного и кориолисового ускоренний.
Доказательство. Вектор абсолютного ускорения точки М равна

и для его определения продифференцируем зависимость (7.6) по времени.
После возведения соответствующих членов, получим
Учитывая формулы (7.7),
Превратим зависимость (7.14), используя зависимости (7.5), (7.7), (7.9) и (7.15). Получим формулу, выражающую вектор абсолютного ускорения точки М
где  ускорения начала подвижной системы координат.
ускорения начала подвижной системы координат.
Проведем анализ зависимости (7.16).
Учитывая, что переносным движением в нашем случае является движение свободного твердого тела, то соответственно формуле (6.10) первые три слагаемых формулы (7.16) является вектором переносного ускорения точки

Поскольку в выражении есть вторые производные по времени от соответствующих уравнений относительного движения (7.2), то согласно (2.34) это выражение является вектором относительного ускорения точки
есть вторые производные по времени от соответствующих уравнений относительного движения (7.2), то согласно (2.34) это выражение является вектором относительного ускорения точки
Итак, мы установили механический смысл первых шести слагаемых зависимостях (7.16). Но, как видим, в формулу для вектора абсолютного ускорения точки М входит еще одно слагаемое.
Выражение 
называется вектором кориолисового или поворотного ускорения точки М.
Подставляя формулы (7.17), (7.18) и (7.19) в (7.16), получим

Теорема доказана.
В случае поступательного переносного движения а потому переносное ускорение точки М равна ускорению начала подвижной системы отсчета, то есть
а потому переносное ускорение точки М равна ускорению начала подвижной системы отсчета, то есть 
И одинаковое для всех точек переносного среды. Кроме этого, кориолисово ускорения в этом
случае также равна нулю и зависимость (7.20) принимает вид
и зависимость (7.20) принимает вид

Замечания. Относительные скорость и ускорение определяются в относительной системе отсчета по правилам кинематики точки: по координатного способа – через проекции на оси декартовой системы координат, как вторые производные от уравнений относительного движения точки (7.2) при натуральном способа – через проекции на оси натурального трехгранника относительной траектории.
Переносная скорость и ускорение определяются методами кинематики твердого тела. Если система  движется поступательно или вращается вокруг неподвижной оси, то используются методы раздела 3. В случае плоского движения переносного среды следует применить правила раздела 4, а для более сложных движений (сферический движение, движение свободного твердого тела) необходимо использовать методы, изложенные в
движется поступательно или вращается вокруг неподвижной оси, то используются методы раздела 3. В случае плоского движения переносного среды следует применить правила раздела 4, а для более сложных движений (сферический движение, движение свободного твердого тела) необходимо использовать методы, изложенные в
разделах 5 и 6. Методы определения кориолисового ускорения рассмотрены ниже.
Кориолисово ускорения
Кориолисовым ускорением называется составляющая абсолютного ускорения точки в ее сложном движении, равна удвоенному векторном произведения вектора переносной угловой скорости на вектор относительной скорости этой точки.
В начале выясним физические причины появления кориолисового ускорения. Как известно, вектор ускорения характеризует изменение вектора скорости как по величине, так и по направлению. Так, переносное ускорение характеризует изменение переносной скорости, а относительное -относительной скорости в соответствующих движениях точки М. Какие же изменения и которых кинематических характеристик движения точки, при ее сложном движении, характеризует кориолисово ускорения? Для ответа на этот вопрос рассмотрим движение точки М, равномерно перемещается вдоль радиуса платформы, которая равномерно вращается вокруг оси, перпендикулярной к плоскости платформы (рис. 7.2).
В этом случае переносным движением будет вращения платформы с 

относительным движением – прямолинейное движение точки вдоль радиуса
с 

Пусть в момент времени  точка занимала положение М, для которого векторы
точка занимала положение М, для которого векторы
переносной и относительной скоростей  и
и  За промежуток времени
За промежуток времени  платформа вернулась на некоторый угол
платформа вернулась на некоторый угол а точка переместилась из положения
а точка переместилась из положения и в
и в
момент времени векторы переносной и относительной скоростей будут соответственно
векторы переносной и относительной скоростей будут соответственно 
Поскольку относительное движение равномерное прямолинейный, то относительное ускорение  то есть за промежуток времени
то есть за промежуток времени  вектор
вектор  должен не измениться, а быть постоянным. Однако, как видно из рисунка, за время
должен не измениться, а быть постоянным. Однако, как видно из рисунка, за время  вектор относительной
вектор относительной
скорости  изменил свое направление от
изменил свое направление от  Это изменение вектора относительной
Это изменение вектора относительной
скорости состоялась за счет переносного движения.
Учитывая, что переносное движение – равномерное вращение и
и  то за промежуток времени
то за промежуток времени  не должна состояться изменение величины переносной скорости (это изменение характеризует вращательное ускорение, которое в нашем случае равна нулю 0).
не должна состояться изменение величины переносной скорости (это изменение характеризует вращательное ускорение, которое в нашем случае равна нулю 0).  Но, как видно из рис. 7.2, величина переносной скорости меняется от
Но, как видно из рис. 7.2, величина переносной скорости меняется от 
 Очевидно, что изменение вызвано перемещением точки с положения
Очевидно, что изменение вызвано перемещением точки с положения  которое произошло за счет относительного движения точки.
которое произошло за счет относительного движения точки.
Итак, появление кориолисового ускорения обусловлена взаимным влиянием переносного и относительных движений.
Ускорение Кориолиса характеризует изменение направления относительной скорости, обусловленной переносным движением, и величины переносной скорости за счет относительного движения.
Модуль кориолисового ускорения, исходя из (7.19), равна

Рассмотрим случаи отсутствия кориолисового ускорения точки.
Из формулы (7.22) следует, что  если:
если:
1)  то есть, когда переносное движение поступательное или угловая скорость переносного вращения равна нулю (в моменты, когда направление вращательного движения меняется на противоположный)
то есть, когда переносное движение поступательное или угловая скорость переносного вращения равна нулю (в моменты, когда направление вращательного движения меняется на противоположный)
2)  то есть в те моменты времени, когда относительная скорость равна нулю (например, в моменты времени, когда вектор
то есть в те моменты времени, когда относительная скорость равна нулю (например, в моменты времени, когда вектор  меняет свое направление на противоположный).
меняет свое направление на противоположный).
3) есть, когда векторы
есть, когда векторы  и
и  коллинеарны (параллельные).
коллинеарны (параллельные).
Направление вектора кориолисового ускорения определяется согласно правилу векторного произведения двух векторов  Во время практического решения задач целесообразно применять правило Жуковского.
Во время практического решения задач целесообразно применять правило Жуковского.
Правило Жуковского
Чтобы найти направление кориолисового ускорения, необходимо спроектировать вектор относительной скорости  на плоскость П, перпендикулярную оси переносного вращения, и вернуть эту проекцию
на плоскость П, перпендикулярную оси переносного вращения, и вернуть эту проекцию  на угол
на угол  в сторону переносного вращения (рис. 7.3).
в сторону переносного вращения (рис. 7.3).
Наличием кориолисового ускорения объясняются различные явления, которые происходят на поверхности Земли вследствие ее вращения. так замечено, что для рек, текущих в
северном полушарии, даже на прямолинейных участках, подмываются больше правы, чем левые берега; при аналогичных условиях на железнодорожных дорогах происходит интенсивнее износ правых рельсов колеи по сравнению с левыми. Все эти явления объясняются появлением кориолисова силы инерции, направленной в сторону, противоположную кориолисового ускорению, о чем пойдет речь в части «Динамика».

Примеры решения задач на сложное движение точки
Задача 1. Тележка А мостового крана, перемещает груз С в горизонтальной плоскости, движется по закону  в метрах,
в метрах,  -в секундах). Груз С при этом колеблется на подвесе
-в секундах). Груз С при этом колеблется на подвесе  длиной
длиной  по закону
по закону 
 – в радианах,
– в радианах,  – в секундах). Найти абсолютные скорость и ускорение груза С в момент времени
– в секундах). Найти абсолютные скорость и ускорение груза С в момент времени


Решение. Рассмотрим движение груза С, как материальной точки, находится в сложном движении. выберем неподвижную  и подвижную
и подвижную  системы координат, причем последнюю свяжем с подвижным тележкой (рис. 7.5). Тогда абсолютным движением груза С будет его движение относительно системы
системы координат, причем последнюю свяжем с подвижным тележкой (рис. 7.5). Тогда абсолютным движением груза С будет его движение относительно системы  переносным – движение подвижной системы
переносным – движение подвижной системы  относительно неподвижной
относительно неподвижной  или, что одно и тоже, поступательное движение тележки, а относительным движением – колебания груза на подвесе (криволинейное движение
или, что одно и тоже, поступательное движение тележки, а относительным движением – колебания груза на подвесе (криволинейное движение
точки С по кругу).

Для определения абсолютной скорости груза используем зависимость (7.11)

Чтобы определить переносную скорость, условно остановим относительное движение груза.
Тогда движение системы тележка-груз на подвесе рассматриваем как поступательное движение одного тела, происходит по закону 
Переносная скорость определится

Если  Вектор
Вектор направленный параллельно оси
направленный параллельно оси 
Чтобы найти относительную скорость груза, условно остановим переносное движение и тогда относительную скорость подсчитаем как скорость точки С при вращении вокруг точки  (криволинейное движение точки по окружности).
(криволинейное движение точки по окружности).

где  – относительная угловая скорость, в нашем случае
– относительная угловая скорость, в нашем случае

При 
Знак минус показывает, что вращение в данный момент времени происходит против положительного направления отсчета угла φ, то есть по часовой стрелки.
Итак,
Вектор  напрямлений перпендикулярно до
напрямлений перпендикулярно до  в сторону напрямку кутової швидкості.
в сторону напрямку кутової швидкості.
Модуль абсолютной скорости груза С определим по зависимости (7.12)
где α – угол между векторами и
и 
При 

Тогда 
Для определения абсолютного ускорения груза С используем зависимость (7.20)

Определим составляющие абсолютного ускорения груза. Методика определение переносного и относительного ускоренного аналогична определения переносной и относительной скоростей. переносное ускорение

Знаки  и
и  одинаковые, поэтому вектор
одинаковые, поэтому вектор  совпадает по направлению с
совпадает по направлению с 
Относительное ускорение точки, при ее движении по кругу, равна

Касательное ускорение

где  относительное угловое ускорение.
относительное угловое ускорение.
При 
Поскольку знаки  и
и одинаковые, то вращение ускоренное, и
одинаковые, то вращение ускоренное, и
совпадает по направлению с 
Тогда

Вектор  совпадает по направлению с вектором
совпадает по направлению с вектором 
Нормальное ускорение точки в относительном движении определится зависимостью

и при 
Вектор  направленный по
направленный по  от точки С до точки
от точки С до точки 
В этой задаче переносное движение является поступательным, так кориолисово ускорения равна нулю  Величину абсолютного ускорения груза найдем по его проекциями на оси неподвижной системы координат, учитывая, что при
Величину абсолютного ускорения груза найдем по его проекциями на оси неподвижной системы координат, учитывая, что при

Проекции абсолютного ускорения груза будут такими

Тогда модуль абсолютного ускорения груза С будет равняться

Задача 2. Прямоугольный треугольник АВС вращается вокруг своего катета АС ривносповильнено с угловым ускорением  при начальной угловой скорости
при начальной угловой скорости  По гипотенузе АВ движется точка М по закону
По гипотенузе АВ движется точка М по закону  в сантиметрах, t – в секундах). Найти абсолютную скорость и абсолютное ускорение точки М в момент времени
в сантиметрах, t – в секундах). Найти абсолютную скорость и абсолютное ускорение точки М в момент времени  (рис. 7.6).
(рис. 7.6).


Решение. Поскольку точка М одновременно находится в двух движениях, то
ее движение рассматриваем как сложный.
Выберем неподвижную  и подвижную
и подвижную системы координат (рис. 7.7).
системы координат (рис. 7.7).
Подвижная система связана с треугольником, вращающийся (на рис. 7.7 показана только ось  тогда переносним рухом буде обертання трикутника навколо катета АС, відносним — прямолінійний рух точки вздовж катета АВ за законом
тогда переносним рухом буде обертання трикутника навколо катета АС, відносним — прямолінійний рух точки вздовж катета АВ за законом

Абсолютная скорость точки М определится согласно (7.11)

Переносную скорость точки М определим как скорость той точки гипотенузы АВ треугольника, вращающийся с которой в данный момент времени совпадает подвижная точка М. Определим положение точки М на гипотенузе АВ при 

Переносная скорость равна

где DM – короткая расстояние от точки М до оси вращения АС;  угловая скорость вращения треугольника АВС.
угловая скорость вращения треугольника АВС.

Тогда 
Поскольку траектории переносного движения точки М в данный момент времени
является окружность радиуса DM, то вектор  будет направлен по касательной к
будет направлен по касательной к
круга в сторону вращения. Если плоскость треугольника АВС при совместить с плоскостью
совместить с плоскостью то вектор
то вектор  Относительная скорость точки М определится методами кинематики точки и будет равняться
Относительная скорость точки М определится методами кинематики точки и будет равняться

и при 
Вектор направлен по гипотенузе АВ в сторону увеличения S.
направлен по гипотенузе АВ в сторону увеличения S.
Поскольку угол между векторами  и
и  равна
равна  То модуль абсолютной
То модуль абсолютной
скорости будет равняться

В случае непоступального переносного движения абсолютное ускорение точки М в сложном движении по формуле (7.20) будет равняться

Переносное движение является вращательным, так переносное ускорение точки М в соответствии с (3.15) определится по формуле
Вектор  направлен к оси вращения треугольника вдоль радиуса MD, а вектор
направлен к оси вращения треугольника вдоль радиуса MD, а вектор  – перпендикулярно к
– перпендикулярно к  в сторону дуговой стрелки углового ускорения
в сторону дуговой стрелки углового ускорения  которое противоположное
которое противоположное  поскольку вращение замедлено.
поскольку вращение замедлено.
При прямолинейном относительном движении относительно ускорения точки М имеет только касательную составляющую, равную


векторы и
и  при
при совпадают по направлению.
совпадают по направлению.
Модуль кориолисового ускорения определится по зависимости (7.23)

Согласно принятому направлением вращения вектор  будет направлен по оси вращения в сторону положительного направления оси
будет направлен по оси вращения в сторону положительного направления оси  Поэтому угол между
Поэтому угол между  и
и  равна
равна и при
и при  кориолисово ускорения будет равняться
кориолисово ускорения будет равняться

Вектор  согласно правилу Жуковского, совпадает по направлению с вектором
согласно правилу Жуковского, совпадает по направлению с вектором 
Для нахождения модуля абсолютного ускорения точки М воспользуемся методом проекций. Для этого введем вспомогательную систему координат  оси которой направлены соответственно по касательной к переносной траектории, по радиусу MD и параллельно оси вращения (Рис. 7.7).
оси которой направлены соответственно по касательной к переносной траектории, по радиусу MD и параллельно оси вращения (Рис. 7.7).
тогда:

Модуль абсолютного ускорения точки М

Сложное движение точки и решение задач
Краткие сведения по теории:
Характер движения существенно зависит от того, в какой системе отсчета (подвижной или неподвижной) рассматривается это движение.
Движение точки относительно неподвижной системы отсчета называется абсолютным.
Движение точки по отношению к подвижной системе отсчета называется относительным.
Движение, которое имеет подвижная система отсчета со всеми неизменно связанными с ней точками пространства по отношению к условно неподвижной системы отсчета,
называется переносным.
Каждое из этих движений характеризуется своими скоростями и ускорениями.
В соответствии с законами сложения скоростей:

и ускорений:

где  абсолютные скорость и ускорение подвижной точки;
абсолютные скорость и ускорение подвижной точки;
 переносные скорость и ускорение подвижной точки;
переносные скорость и ускорение подвижной точки;
 относительные скорость и ускорение подвижной точки;
относительные скорость и ускорение подвижной точки;
 Кориолисовое ускорение.
Кориолисовое ускорение.
Величина Корриолисового ускорения определяется по формуле:

где  угловая скорость переносного движения;
угловая скорость переносного движения;
 угол между векторами
угол между векторами  и
и 
Вектор Корриолисового ускорения  направлен перпендикулярно к плоскости, в которой лежат векторы угловой скорости
направлен перпендикулярно к плоскости, в которой лежат векторы угловой скорости  и относительной скорости
и относительной скорости  в ту сторону, откуда наблюдатель видит наименьший поворот вектора
в ту сторону, откуда наблюдатель видит наименьший поворот вектора  к вектору
к вектору  против движения часовой стрелки.
против движения часовой стрелки.
Поскольку в случае плоского движения тела угол между векторами  и
и  равняется
равняется  то:
то:

При плоском движении направление  можно определить по правилу Жуковского Н.Е.: на направление Кориолисового ускорения укажет вектор относительной скорости
можно определить по правилу Жуковского Н.Е.: на направление Кориолисового ускорения укажет вектор относительной скорости  если его повернуть в плоскости расположения на
если его повернуть в плоскости расположения на  в сторону переносной угловой скорости
в сторону переносной угловой скорости 
В случае, если переносное движение является поступательным 
Если переносные и относительные движения являются криволинейными, переносными и относительными ускорениями можно изобразить в виде геометрических сумм соответствующих нормальных и касательных ускорений:

Порядок решения задач на сложное движение точки
При решении задач на сложное движение точки рекомендуется придерживаться такой последовательности:
1. Разложить движение точки на составляющие, определить абсолютное, относительное и переносное движения.
2. Выбрать две системы координат: абсолютную (неподвижную) и относительную (подвижную).
3. Мысленно остановить переносное движение, определить скорость и ускорение точки в относительном движении.
4. Мысленно остановить относительное движение, определить угловую скорость переносного движения, скорость и ускорение точки в переносном движении.
5. По известным угловым скоростям переносного движения и скоростью точки в относительном движении найти величину и направление кориолисового ускорения точки.
6. Используя метод проекций, определить проекции абсолютного ускорения и абсолютной скорости на оси неподвижной системы координат.
7. По определенным проекциям, найти модули и направления абсолютной скорости и абсолютного ускорения.
Примеры решения задач
Задача 1
Диск вращается вокруг оси, перпендикулярной к его плоскости, против хода часовой стрелки с угловой скоростью  в/c. По хорде диска от точки K к L движется точка M.
в/c. По хорде диска от точки K к L движется точка M.
Определить модуль и направление корриолисового ускорения точки M в изображенном на рис. 1 положении, если относительная скорость 

Решение. Точка M движется в плоскости диска которая перпендикулярна к оси вращения, то есть угол между векторами  и
и  составляет
составляет 
Учитывая  модуль ускорения Кориолиса равняется:
модуль ускорения Кориолиса равняется:

Поскольку вектор относительной скорости находится в плоскости перпендикулярной к оси вращения, то для определения направления ускорения Кориолиса согласно правилу
Жуковского надо повернуть вектор  по направлению угловой скорости
по направлению угловой скорости  переносного движения на угол
переносного движения на угол  (Рисс.1).
(Рисс.1).
Задача 2
Определить модуль и направление корриолисового ускорения точки M, которая движется по производной ВN кругового конуса от вершины В к точке N. Конус вращается вокруг своей оси с угловой скоростью  в/с. в направлении. показанном на рисунке, угол наклона производной к оси конуса
в/с. в направлении. показанном на рисунке, угол наклона производной к оси конуса  относительная скорость точки
относительная скорость точки 

Решение. Отложим вектор угловой скорости  переносного вращательного движения по оси вращения в сторону, с которой вращение видно против хода часовой стрелки. Относительную скорость
переносного вращательного движения по оси вращения в сторону, с которой вращение видно против хода часовой стрелки. Относительную скорость  направим от точки M до точки N. Тогда угол между
направим от точки M до точки N. Тогда угол между
векторами  и
и  (Рис.1) составит:
(Рис.1) составит:

Модуль ускорения Кориолиса точки M равен:


Чтобы найти направление ускорения Кориолиса (рис.1), спроектируем вектор относительной скорости  на плоскость S, перпендикулярную оси вращения конуса.
на плоскость S, перпендикулярную оси вращения конуса.
Проекция относительной скорости  направленная по прямой МК, которая является продолжением радиуса СМ.
направленная по прямой МК, которая является продолжением радиуса СМ.
Повернув проекцию  в направлении вращения конуса на угол
в направлении вращения конуса на угол  устанавливаем, что вектор
устанавливаем, что вектор  кориолисового ускорения направлен по касательной к кругу радиусом СМ в сторону вращения конуса.
кориолисового ускорения направлен по касательной к кругу радиусом СМ в сторону вращения конуса.
Задача 3
По хорде АВ диска, что вращается от точки А до точки В (рис.1) движется точка М, согласно уравнению  угол поворота диска изменяется по закону
угол поворота диска изменяется по закону 
Определить абсолютные скорости и ускорение точки М в момент времени, когда она находится на расстоянии  от оси вращения диска (рис.1).
от оси вращения диска (рис.1).

Решение. В данной задачи переносным движением будет вращение диска по закону
 и относительным – движение точки по хорде АВ по закону
и относительным – движение точки по хорде АВ по закону 
Запишем уравнение для определения абсолютной скорости точки М:

Для определения относительной скорости остановим переносное вращение диска и будем рассматривать движение точки по отношению к неподвижному диску.
Поскольку закон относительного движения  величина относительной скорости определяется как первая производная от пути по времени:
величина относительной скорости определяется как первая производная от пути по времени:

Вектор  относительной скорости направлен по хорде АВ (рис. 1) от точки А до точки В.
относительной скорости направлен по хорде АВ (рис. 1) от точки А до точки В.
Переносной скоростью  точки М будет скорость той точки диска, с которой в данный момент совпадает точка М.
точки М будет скорость той точки диска, с которой в данный момент совпадает точка М.
Из условия задачи следует, что точка М в данный момент времени находится посередине хорды АВ на расстоянии  от оси вращения диска.
от оси вращения диска.
Переносная скорость вращающегося движения определяется по формуле:

где  – угловая скорость переносного вращательного движения.
– угловая скорость переносного вращательного движения.
Угловую скорость переносного вращательного движения найдем как первую производную от угла поворота  по времени:
по времени:
 в/с.
в/с.
Таким образом, переносная скорость вращательного движения равна:

Вектор переносной скорости направлен перпендикулярно радиусу OM в сторону вращения диска.
Поскольку векторы  и
и  направленны вдоль одной прямой в разные стороны (рис. 1), то для определения абсолютной скорости от операции векторного сложения скоростей можно перейти к их алгебраическому сложению.
направленны вдоль одной прямой в разные стороны (рис. 1), то для определения абсолютной скорости от операции векторного сложения скоростей можно перейти к их алгебраическому сложению.
Тогда:

В зависимости от абсолютных значений скоростей  и
и  вектор
вектор  будет направлен или в сторону
будет направлен или в сторону  или в сторона
или в сторона 
Определить абсолютное ускорение точки M. Поскольку переносное движение является вращательным, то абсолютное ускорение точки равно:

Модуль относительного ускорения определим как производную от относительной скорости по времени:

Направленный вектор  вдоль хорды AB от точки A до точки B (рис.2).
вдоль хорды AB от точки A до точки B (рис.2).
Переносное ускорение  точки диска, которая совпадает с точкой M, учитывая, что она движется по кругу радиусом h, состоит из переносного тангенциального (касательного) ускорения
точки диска, которая совпадает с точкой M, учитывая, что она движется по кругу радиусом h, состоит из переносного тангенциального (касательного) ускорения  и переносного нормального ускорения
и переносного нормального ускорения 

Вычислим модули нормального  и тангенциального
и тангенциального  ускорений:
ускорений:

где  угловое ускорение переносного вращательного движения.
угловое ускорение переносного вращательного движения.
Переносное нормальное ускорение направлено вдоль радиуса к центру вращения O (рис.2).

Поскольку движение точки M происходит в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется из формулы:

Для определения направления ускорения Кориолиса (рис.2) необходимо вектор относительной скорости  повернуть на
повернуть на  в сторону угловой скорости
в сторону угловой скорости 
переносного вращательного движения, то есть против хода часовой стрелки.
Для определения величины и направления абсолютного ускорения  сначала добавим векторы
сначала добавим векторы  и
и  которые направлены вдоль одной прямой в противоположные стороны.
которые направлены вдоль одной прямой в противоположные стороны.
Найдена векторная сумма  направлена перпендикулярно к вектору
направлена перпендикулярно к вектору  и по модулю равняется
и по модулю равняется

Таким образом, абсолютное ускорение точки M равняется сумме векторов:

Поскольку вектор  перпендикулярный к вектору
перпендикулярный к вектору  вектор
вектор  будет изображаться диагональю прямоугольника со сторонами
будет изображаться диагональю прямоугольника со сторонами  и
и  (рис.2).
(рис.2).
Модуль абсолютного ускорения равняется:

Ответ: 
Задание темы К4 (сложное движение точки)
Вдоль стороны AB (см. задачу К3 и рис. К4.1) движется ползун 2, шарнирно
соединённый со стержнем EK, который движется в неподвижных направляющих параллельно оси  Точка E разделяет сторону AB в пропорции, которую указано в таблице К5 коэффициентом пропорциональности
Точка E разделяет сторону AB в пропорции, которую указано в таблице К5 коэффициентом пропорциональности 
Определить путем построения планов скоростей и ускорений по известным из задачи К3 кинематическим характеристикам движения фигуры АВС абсолютные скорости и
ускорение точек Е и К.


Пример решения задания темы К4
Изобразим на стороне AB тела 1 (рис.К4.2, а) ползун 2, который соединен шарниром Е со стержнем 3. Ползун 2 может двигаться поступательно по стороне AB, а стержень
3 – поступательно в вертикальных направляющих. Положение шарнира Е на стороне AB определяем по заданному коэффициенту пропорциональности 

1. Анализ движения стержня ЕК
Рассмотрим точку  принадлежащую одновременно ползуну 2 и стержню 3. Эта точка осуществляет сложное движение, двигаясь как по направляющей AB, так и вместе с фигурой ABC .
принадлежащую одновременно ползуну 2 и стержню 3. Эта точка осуществляет сложное движение, двигаясь как по направляющей AB, так и вместе с фигурой ABC .
Очевидно, скорость и ускорение точки  в ее поступательном движении вместе со стержнем ЕК относительно неподвижной опоры (которое видит неподвижный наблюдатель) следует считать абсолютным. Обозначим их соответственно
в ее поступательном движении вместе со стержнем ЕК относительно неподвижной опоры (которое видит неподвижный наблюдатель) следует считать абсолютным. Обозначим их соответственно  и
и 
Тогда движение точки  ползуна 2 вдоль направляющей AB будет относительным. Скорость
ползуна 2 вдоль направляющей AB будет относительным. Скорость  и ускорение
и ускорение  точки
точки  в относительном движении направлены вдоль стороны AB, поскольку ползун движется относительно стержня поступательно.
в относительном движении направлены вдоль стороны AB, поскольку ползун движется относительно стержня поступательно.
Одновременно ползун 2 движется вместе с фигурой ABC . Это движение для точки 
является переносным. Переносные скорость и ускорение  следует определить как скорость и ускорение той точки
следует определить как скорость и ускорение той точки  фигуры ABC, с которой в данный момент времени совпадает точка
фигуры ABC, с которой в данный момент времени совпадает точка  ползуна 2.
ползуна 2.
2. Определение переносной, абсолютной и относительной скорости точки Е2
Приняв точку A тела 1, осуществляющую плоское движение, за полюс (рис. К4.2, б), определим скорость точки  стороны AB используя свойство сходства фигур
стороны AB используя свойство сходства фигур
ABС тела 1 и abc плана скоростей, в соответствии с какой:

Из этой пропорции определим отрезок 

Отрезок откладываем на стороне ab фигуры abc плана скоростей (рис.К4.2, б) в направлении от точки “a” до точки “b”. Величине переносной скорости ползуна 2 на
плане будет соответствовать отрезок 

Запишем уравнение для абсолютной скорости точки  ползуна 2:
ползуна 2:

В этом уравнении нам известны:
- величина и направление переносной скорости
 (из плана скоростей);
(из плана скоростей); - направление относительной скорости
 (вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно;
(вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно; - направление абсолютной скорости
 (вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
(вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
Для решения уравнения (2) воспользуемся планом скоростей (рис.К4.2, б). Поскольку согласно уравнению до вектора  необходимо добавить вектор
необходимо добавить вектор  то с точки
то с точки 
проведем прямую  параллельную к AB, а с полюса
параллельную к AB, а с полюса  проведем направление абсолютной скорости
проведем направление абсолютной скорости  вертикальную прямую. Точка пересечения этих прямых “к” и будет решением уравнения (2), а отрезок
вертикальную прямую. Точка пересечения этих прямых “к” и будет решением уравнения (2), а отрезок  будет изображать
будет изображать
в масштабе  абсолютную скорость точек
абсолютную скорость точек  и К:
и К:

3. Определение переносного и абсолютного ускорения точки Е2
Определить переносное ускорение точки  ползуна 2.
ползуна 2.
Из условия сходства фигур ABС тела 1 и abc плана ускорений (рис.К4.2,в) следует, что точка  (конец вектора ускорения
(конец вектора ускорения  ) на плане ускорений будет лежать на отрезке ab. При этом расстояние
) на плане ускорений будет лежать на отрезке ab. При этом расстояние  может быть найдено из пропорции (1). Поскольку на плане
может быть найдено из пропорции (1). Поскольку на плане
ускорений  то:
то:


Тогда отрезок  будет изображать переносное ускорение точки
будет изображать переносное ускорение точки 
в масштабе плана ускорений 

Запишем векторное уравнение для абсолютного ускорения для точки  ползуна 2:
ползуна 2:

Определим сначала величину и направление Кориолисового ускорения.
Поскольку движение происходит в плоскости  то есть угол между векторами относительной скорости
то есть угол между векторами относительной скорости  и угол переносной скорости
и угол переносной скорости  равняется
равняется  то для определения величины
то для определения величины  воспользуемся формулой (4.4):
воспользуемся формулой (4.4):

Угловая переносная скорость  равняется угловой скорости тела 1, то есть
равняется угловой скорости тела 1, то есть 
Величину относительной скорости  определим из плана скоростей. (рис. К4.2, б). Измерение отрезка
определим из плана скоростей. (рис. К4.2, б). Измерение отрезка  который на плане скоростей в масштабе
который на плане скоростей в масштабе 
изображает  находим:
находим:

Тогда:

Направление Кориолисового ускорения определим по правилу Жуковского Н.Е., для этого вектор относительной скорости  что на плане скоростей (рис. К4.2, б) изображается вектором
что на плане скоростей (рис. К4.2, б) изображается вектором  повернем в сторону угловой переносной скорости
повернем в сторону угловой переносной скорости  направление которой показано на рис. К4.2,а, на
направление которой показано на рис. К4.2,а, на  (рис. К4.2, г).
(рис. К4.2, г).
Таким образом, в уравнении (3) нам известны:
- величина и направление переносного ускорения

- величина и направление Корриолисового ускорения

- направление относительного ускорения
 (вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно;
(вдоль AB), поскольку ползун 2 движется относительно стержня AB поступательно; - направление абсолютного ускорения
 (вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
(вдоль EК), поскольку ползун 3 движется поступательно в вертикальных направляющих.
Все это позволяет нам построить многоугольник ускорений в соответствии с уравнением (3) на плане ускорений, или отдельным чертежом. Учитывая, что величины отрезков, которые будут изображать некоторые ускорения, слишком большие и выходят за пределы чертежа, для нахождения абсолютного ускорения точки  построим отдельный план ускорений с масштабным коэффициентом:
построим отдельный план ускорений с масштабным коэффициентом:

Сначала из произвольной точки  (рис. К4.2, д) за направлением
(рис. К4.2, д) за направлением  (рис. К4.2, в) отложим вектор
(рис. К4.2, в) отложим вектор  который в масштабе
который в масштабе  будет изображать
будет изображать 

До этого вектора в направлении Кориолисового ускорения (рис. К4.2, г) добавим вектор  который в масштабе
который в масштабе  будет изображать
будет изображать 

Через конец вектора  параллельно AB проведем направление относительного ускорения
параллельно AB проведем направление относительного ускорения  (перпендикулярно
(перпендикулярно  или параллельно AB), а через полюс
или параллельно AB), а через полюс  направление абсолютного ускорения
направление абсолютного ускорения  (параллельно ЕК). Точка пересечения “к” этих двух направлений и будет решением уравнения (3), а вектор
(параллельно ЕК). Точка пересечения “к” этих двух направлений и будет решением уравнения (3), а вектор  в масштабе
в масштабе 
будет изображать абсолютное ускорение точек К и 
Замерив отрезок  получим:
получим:

Примечание. Поскольку все построения расчетные графических работ по кинематике К1, К3 и К4 рекомендуется выполнять на бумаге форматом А3, то после выполнения данной курсовой работы ее графическая часть будет иметь вид подобный изображенному на с. 188.

Сложное движение точки образцы и примеры
Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.
Относительное, переносное и абсолютное движение точки
При исследовании движения точки выбирают некоторую систему отсчета (темы 1 и 2), относительно которой рассматривают движение точки.
В некоторых случаях приходится рассматривать движение точки относительно двух различных систем отсчета. Например, движение пассажира в поезде можно рассматривать как по отношению к поезду, так и по отношению к Земле.
При этом движение одной и той же точки относительно двух различных систем отсчета будет разным. Например, точка обода колеса движущегося железнодорожного вагона относительно Земли пишет циклоиду, а относительно вагона – окружение.
При рассмотрении движения точки по отношению к двум системам отсчета и система, которая в данной задаче условно принята за неподвижную, называется основной системой отсчета (неподвижной), а система, которая движется относительно основной, называется подвижной системой отсчета.
Движение точки относительно основной системы отсчета называется абсолютным движением, а ее движение относительно подвижной системы отсчета – относительным движением.
Пусть есть две системы координат  и
и  и некоторая подвижная точка
и некоторая подвижная точка  (рис.3.1).
(рис.3.1).

Выберем систему координат  за основную. Тогда движение системы
за основную. Тогда движение системы  относительно системы
относительно системы  будет переносным. Движение точки
будет переносным. Движение точки  относительно системы
относительно системы  будет относительным, а движение точки
будет относительным, а движение точки  относительно системы
относительно системы  будет абсолютным.
будет абсолютным.
Надо заметить, что переносным движением является движение не самой точки  , а того тела, с которым связана подвижная система координат
, а того тела, с которым связана подвижная система координат  , тогда как относительное и абсолютное движение является движением самой точки
, тогда как относительное и абсолютное движение является движением самой точки  , которое рассматривается соответственно относительно подвижной и основной систем отсчета. В переносном движении подвижная система координат может иметь любой вид движения.
, которое рассматривается соответственно относительно подвижной и основной систем отсчета. В переносном движении подвижная система координат может иметь любой вид движения.
Основная задача этого раздела состоит в том, чтобы по известным относительным и переносным движениям определить абсолютное движение точки (движение точки  относительно системы отсчета
относительно системы отсчета  ).
).
Выбор основной и подвижной систем отсчета, а соответственно, и разделение движения точки на абсолютное и относительное зависит от постановки конкретной задачи. В большинстве случаев за основную систему отсчета принимают систему, которую связано с Землей.
Относительные, переносные и абсолютные скорости и ускорение
Относительной скоростью  точки называется ее скорость в относительном движении, то есть по отношению к подвижной системе отсчета.
точки называется ее скорость в относительном движении, то есть по отношению к подвижной системе отсчета.
Абсолютной скоростью  точки называется ее скорость в абсолютном движении, то есть по отношению к основной системе отсчета.
точки называется ее скорость в абсолютном движении, то есть по отношению к основной системе отсчета.
Переносной скоростью  называется скорость относительно основной системы отсчета той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
называется скорость относительно основной системы отсчета той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
Аналогично введем понятие относительного, абсолютного и переносного ускорения точки.
Относительным ускорением  точки называется ее ускорение в относительном движении, то есть по отношению к подвижной системе отсчета.
точки называется ее ускорение в относительном движении, то есть по отношению к подвижной системе отсчета.
Абсолютным ускорением  точки называется ее ускорение в абсолютном движении, то есть по отношению к основной системе отсчета.
точки называется ее ускорение в абсолютном движении, то есть по отношению к основной системе отсчета.
Переносным ускорением  называется ускорение относительно основной системы отсчета той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
называется ускорение относительно основной системы отсчета той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
Обратим внимание на то, что переносное движение – это движение всей подвижной системы отсчета, то есть некоторого тела, с которым связана подвижная система координат, а переносная скорость и переносное ускорение – это скорость и ускорение конкретной точки этого тела.
Сложение скоростей и ускорений при сложном движении точки
Зависимость между абсолютной, переносной и относительной скоростями точки определяется теоремой сложения скоростей, согласно которой абсолютная скорость точки равна векторной сумме переносной и относительной скоростей:
 (3.1)
(3.1)
где  – абсолютная скорость точки;
– абсолютная скорость точки;
 – относительная скорость точки;
– относительная скорость точки;
 – переносная скорость.
– переносная скорость.
Для определения относительной скорости точки достаточно мысленно остановить переносное движение и найти по правилам кинематики скорость точки относительно системы отсчета, которая была подвижной.
Для определения переносной скорости – достаточно мысленно остановить относительное движение и найти переносную скорость как скорость той точки подвижной системы отсчета, с которой в данный момент времени совпадает движущаяся точка.
Зависимость между абсолютным, относительным и переносным ускорением точки при поступательном движении подвижной системы отсчета выражается векторным уравнением:
 (3.2)
(3.2)
где  – абсолютное ускорение точки;
– абсолютное ускорение точки;
 – относительное ускорение точки;
– относительное ускорение точки;
 – переносное ускорение точки.
– переносное ускорение точки.
Если переносным движением является вращательный, или сложный, то теорема о сложении ускорений приобретает вид:
 , (3.3)
, (3.3)
где  – ускорение Кориолиса (поворотное ускорение точки).
– ускорение Кориолиса (поворотное ускорение точки).
3.4. Ускорение Кориолиса
 .
.
Модуль ускорения Кориолиса равен:

где  – угол между векторами
– угол между векторами  и
и  .
.
Ускорение Кориолиса характеризует:
- изменение модуля и направления переносной скорости точки вследствие ее относительного движения;
- изменение направления относительной скорости точки вследствие вращательного переносного движения.
Ускорение Кориолиса равно нулю в трех случаях:
Направление ускорения Кориолиса определяется как направление вектора векторного произведения 

 .
.
Пусть точка  (рис.3.2) движется со скоростью
(рис.3.2) движется со скоростью  относительно тела, которое вращается вокруг оси
относительно тела, которое вращается вокруг оси  с угловой скоростью
с угловой скоростью  . Если построить в точке
. Если построить в точке  кроме
кроме  вектор
вектор  , то вектор векторного произведения
, то вектор векторного произведения 

 , то есть вектор ускорения Кориолиса
, то есть вектор ускорения Кориолиса  , будет направлен перпендикулярно плоскости, в которой лежат векторы
, будет направлен перпендикулярно плоскости, в которой лежат векторы  и
и  в ту сторону, откуда поворот вектора
в ту сторону, откуда поворот вектора  к вектору относительной скорости
к вектору относительной скорости  на наименьший угол виден против хода часовой стрелки.
на наименьший угол виден против хода часовой стрелки.

Для определения направления ускорения Кориолиса удобно пользоваться правилом Жуковского: чтобы найти направление ускорения Кориолиса надо спроектировать относительную скорость точки  на плоскость, перпендикулярную оси переносного вращения, и вернуть в этой плоскости полученную проекцию на
на плоскость, перпендикулярную оси переносного вращения, и вернуть в этой плоскости полученную проекцию на  в сторону переносного вращения (рис.3.3).
в сторону переносного вращения (рис.3.3).

Действительно, полученное направление  (рис.3.3) перпендикулярное плоскости треугольника, который образован относительной скоростью
(рис.3.3) перпендикулярное плоскости треугольника, который образован относительной скоростью  и ее проекцией
и ее проекцией  ‘отн, а эта плоскость совпадает с плоскостью векторов
‘отн, а эта плоскость совпадает с плоскостью векторов  и
и  , которой должен быть перпендикулярным вектор ускорения Кориолиса.
, которой должен быть перпендикулярным вектор ускорения Кориолиса.
Если вектор  перпендикулярен
перпендикулярен  , то есть
, то есть 

 и соответственно
и соответственно



 , то величина ускорения Кориолиса будет равна:
, то величина ускорения Кориолиса будет равна:

 . (3.5)
. (3.5)
Такой случай возможен, если относительное движение точки происходит в плоскости перпендикулярной оси переносного вращения. В этом случае векторы  ,
,  и
и  взаимно перпендикулярны (рис. 3.4).
взаимно перпендикулярны (рис. 3.4).

Рассмотрим два примера определения модуля и направления ускорения Кориолиса .
Пример 1. Диск вращается вокруг оси, которая перпендикулярна его плоскости, против хода часовой стрелки с угловой скоростью  . По хорде диска от точки
. По хорде диска от точки  к
к  движется точка
движется точка  .
.
Определить модуль и направление ускорения Кориолиса точки  в изображенном на рис. 3.5 положении, если относительная скорость
в изображенном на рис. 3.5 положении, если относительная скорость 
 .
.
Точка  движется в плоскости диска которая перпендикулярна оси вращения, то есть угол между векторами
движется в плоскости диска которая перпендикулярна оси вращения, то есть угол между векторами  и
и  составляет
составляет  . Учитывая, что
. Учитывая, что 


 , модуль ускорения Кориолиса равен:
, модуль ускорения Кориолиса равен:



Поскольку вектор относительной скорости лежит в плоскости перпендикулярной оси вращения, то для определения направления ускорение Кориолиса согласно правилу Жуковского надо повернуть вектор  по направлению угловой скорости
по направлению угловой скорости  переносного движения на угол
переносного движения на угол  (рис.3.5).
(рис.3.5).

Пример 2. Определить модуль и направление ускорение Кориолиса точки  , которая движется по образующей
, которая движется по образующей  кругового конуса от вершины
кругового конуса от вершины  к точке
к точке  . Конус вращается вокруг своей оси с угловой скоростью
. Конус вращается вокруг своей оси с угловой скоростью  в направлении, показанном на рис.3.6, угол наклона образующей к оси конуса
в направлении, показанном на рис.3.6, угол наклона образующей к оси конуса  , относительная скорость точки
, относительная скорость точки 
 .
.
Отложим вектор угловой скорости  переносного вращательного движения по оси вращения в сторону, из которой вращения видно против хода часовой стрелки. Относительную скорость
переносного вращательного движения по оси вращения в сторону, из которой вращения видно против хода часовой стрелки. Относительную скорость  направим от точки
направим от точки  к точке
к точке  . Тогда угол между векторами
. Тогда угол между векторами  и
и  (рис 3.6) составит:
(рис 3.6) составит:





Модуль ускорения Кориолиса точки  равен:
равен:














Чтобы найти направление ускорения Кориолиса (рис.3.6), спроектируем вектор относительной скорости  на плоскость
на плоскость  , которая перпендикулярна оси вращения конуса.
, которая перпендикулярна оси вращения конуса.

Проекция относительной скорости 

 направлена по прямой
направлена по прямой  , которая является продолжением радиуса
, которая является продолжением радиуса  .
.
Если повернуть проекцию 

 в направлении вращения конуса на угол
в направлении вращения конуса на угол  , устанавливаем, что вектор
, устанавливаем, что вектор  ускорения Кориолиса направлен по касательной к окружности радиусом
ускорения Кориолиса направлен по касательной к окружности радиусом  в сторону вращения конуса.
в сторону вращения конуса.
Примеры решения задач
Задача №1
Клин  (рис.3.7) с углом наклона рабочей поверхности
(рис.3.7) с углом наклона рабочей поверхности  , который движется поступательно по горизонтальной поверхности со скоростью
, который движется поступательно по горизонтальной поверхности со скоростью  , поднимает стержень
, поднимает стержень  , который движется в вертикальном направлении.
, который движется в вертикальном направлении.

Найти абсолютную скорость стержня  .
.
Решение. Учитывая, что стержень  в вертикальном направлении будет двигаться прямолинейно поступательно, то достаточно определить скорость любой его точки.
в вертикальном направлении будет двигаться прямолинейно поступательно, то достаточно определить скорость любой его точки.
Рассмотрим движение точки  стержня.
стержня.
Поскольку точка  стержня должна все время касаться клина
стержня должна все время касаться клина  , то рассмотрим ее движение как сложное – относительным будет движение точки
, то рассмотрим ее движение как сложное – относительным будет движение точки  по отношению к клину, а переносным – движение точки
по отношению к клину, а переносным – движение точки  вместе с клином.
вместе с клином.
По отношению к клину точка  стержня может двигаться только вдоль рабочей поверхности
стержня может двигаться только вдоль рабочей поверхности  . Таким образом, относительная скорость
. Таким образом, относительная скорость  будет направлена вдоль
будет направлена вдоль  .
.
Клин  движется поступательно горизонтальной поверхностью, то есть скорости всех его точек одинаковы. Таким образом, переносная скорость
движется поступательно горизонтальной поверхностью, то есть скорости всех его точек одинаковы. Таким образом, переносная скорость  точки
точки  стержня, которая совпадает с точкой
стержня, которая совпадает с точкой  клина будет равна
клина будет равна  .
.
Абсолютную скорость точки  стержня определим из векторного уравнения:
стержня определим из векторного уравнения:


 (1)
(1)
Для решения векторного уравнения (1) построим параллелограмм на векторах  и
и  (рис.3.7). При построении надо учесть, что
(рис.3.7). При построении надо учесть, что  , как диагональ параллелограмма, должна быть направлена вертикально.
, как диагональ параллелограмма, должна быть направлена вертикально.
Поскольку угол между векторами  и
и  прямой, то получим:
прямой, то получим:

Ответ: 
Задача № 2
Круг радиусом  (рис.3.8) равномерно вращается в своей плоскости вокруг центра
(рис.3.8) равномерно вращается в своей плоскости вокруг центра  по ходу часовой стрелки и делает
по ходу часовой стрелки и делает  оборотов в минуту. По кругу равномерно в противоположном направлении движется точка
оборотов в минуту. По кругу равномерно в противоположном направлении движется точка  и делает
и делает  оборотов в минуту.
оборотов в минуту.

Найти абсолютное ускорение точки  .
.
Решение. Движение точки  рассмотрим как сложное. Переносным движением будет вращение круга вместе с точкой
рассмотрим как сложное. Переносным движением будет вращение круга вместе с точкой  вокруг центра
вокруг центра  , а относительным – движение точки
, а относительным – движение точки  по кругу.
по кругу.
Абсолютное ускорение точки  , учитывая, что переносным будет вращательное движение, равно:
, учитывая, что переносным будет вращательное движение, равно:



Поскольку переносное движение вращательное, то переносное ускорение точки круга с которой совпадает точка  , будет иметь нормальную
, будет иметь нормальную  и тангенциальную
и тангенциальную  составляющую.
составляющую.
Учитывая, что при равномерном вращении угловое ускорение  , тангенциальная составляющая переносного ускорения
, тангенциальная составляющая переносного ускорения

Величина переносного нормального ускорения  определим из формулы:
определим из формулы:

где  – угловая скорость круга.
– угловая скорость круга.
Направлено это ускорение вдоль радиуса от точки  к точке
к точке  (рис.3.8).
(рис.3.8).
Учитывая то, что точка  по кругу радиуса
по кругу радиуса  движется равномерно, модуль относительного ускорения будет иметь тоже только одну нормальную составляющую
движется равномерно, модуль относительного ускорения будет иметь тоже только одну нормальную составляющую 

 :
:




где  – угловая скорость вращения точки
– угловая скорость вращения точки  по кругу.
по кругу.
Направлено это ускорение от точки  к точке
к точке  (рис.3.8).
(рис.3.8).
Поскольку точка  движется в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется по формуле:
движется в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется по формуле:

 .
.
Учитывая, что 
 , достанем:
, достанем:

Для определения направления ускорения Кориолиса повернем вектор относительной скорости  , который направлен по касательной к кругу, в направлении переносной угловой
, который направлен по касательной к кругу, в направлении переносной угловой  на
на  (рис.3.8). Таким образом, это ускорение направлено вдоль радиуса от центра вращения
(рис.3.8). Таким образом, это ускорение направлено вдоль радиуса от центра вращения  .
.
Поскольку все ускорения направлены вдоль одной прямой, то их можно сложить алгебраически:




 ,
,
или с учетом выражений для  ,
, 

 и
и  :
:

Подставив зависимости для угловых скоростей  и
и  , получим:
, получим:

Ответ: 
Задача №3
По хорде  вращающегося диска от точки
вращающегося диска от точки  к точке
к точке  движется точка
движется точка  согласно уравнению
согласно уравнению  , угол поворота диска изменяется по закону
, угол поворота диска изменяется по закону  .
.
Определить абсолютные скорости и ускорения точки  в момент времени, когда она находится на расстоянии
в момент времени, когда она находится на расстоянии  от оси вращения диска (рис.3.9).
от оси вращения диска (рис.3.9).
Решение. В данной задаче переносным движением будет вращение диска по закону  , а относительным – движение точки по хорде
, а относительным – движение точки по хорде  по закону
по закону  .
.
Запишем уравнение для определения абсолютной скорости точки  :
:



Для определения относительной скорости остановим переносное вращение диска и будем рассматривать движение точки по отношению к неподвижному диску. Поскольку закон относительного движения  , то величина относительной скорости определяется как первая производная от пути по времени:
, то величина относительной скорости определяется как первая производная от пути по времени:


Вектор относительной скорости направлен по хорде  (рис. 3.9) от точки
(рис. 3.9) от точки  к точке
к точке  .
.

Переносной скоростью  точки
точки  будет скорость той точки диска, с которой в данный момент совпадает точка
будет скорость той точки диска, с которой в данный момент совпадает точка  .
.
Из условия задачи вытекает, что точка  в данный момент времени находится посередине хорды
в данный момент времени находится посередине хорды  на расстоянии
на расстоянии  от оси вращения диска.
от оси вращения диска.
Переносная скорость вращательного движения определяется по формулой:

где  – угловая скорость переносного вращательного движения.
– угловая скорость переносного вращательного движения.
Угловую скорость переносного вращательного движения найдем как первую производную от угла поворота  по времени:
по времени:

Таким образом, переносная скорость вращательного движения равна:

Вектор переносной скорости направлен перпендикулярно радиусу  в сторону вращения диска.
в сторону вращения диска.
Поскольку векторы  и
и  направлены вдоль одной прямой в разные стороны (рис. 3.9), то для определения абсолютной скорости от операции векторного сложения скоростей можно перейти к их алгебраическому сложению.
направлены вдоль одной прямой в разные стороны (рис. 3.9), то для определения абсолютной скорости от операции векторного сложения скоростей можно перейти к их алгебраическому сложению.
Тогда:



В зависимости от абсолютных значений скоростей  и
и  , вектор
, вектор  будет направлен либо в сторону
будет направлен либо в сторону  , либо в сторону
, либо в сторону  .
.
Определим абсолютное ускорение точки  . Поскольку переносное движение является вращательным, то абсолютное ускорение точки равно:
. Поскольку переносное движение является вращательным, то абсолютное ускорение точки равно:



Модуль относительного ускорения определим как производную от относительной скорости по времени:


Направлен вектор  вдоль хорды
вдоль хорды  от точки
от точки  к точке
к точке  (рис.3.10).
(рис.3.10).

Переносное ускорение  точки диска, которая совпадает с точкой
точки диска, которая совпадает с точкой  , учитывая, что она движется по окружности радиусом
, учитывая, что она движется по окружности радиусом  , состоит из переносного тангенциального (касательного) ускорения
, состоит из переносного тангенциального (касательного) ускорения  и переносного нормального ускорения
и переносного нормального ускорения  :
:

Вычислим модули нормального  и тангенциального
и тангенциального  ускорений:
ускорений:

где  – угловое ускорение переносного вращательного движения.
– угловое ускорение переносного вращательного движения.
Переносное нормальное ускорение направлено вдоль радиуса к центру вращения  (рис.3.10).
(рис.3.10).
Поскольку движение точки  происходит в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется из формулы:
происходит в плоскости, перпендикулярной оси вращения, то ускорение Кориолиса определяется из формулы:



Для определения направления ускорения Кориолиса (рис.3.10) необходимо вектор относительной скорости  повернуть на
повернуть на  в бок угловой скорости
в бок угловой скорости  переносного вращательного движения, то есть против хода часовой стрелки.
переносного вращательного движения, то есть против хода часовой стрелки.
Для определения величины и направления абсолютного ускорения  сначала сложим векторы
сначала сложим векторы  и
и  , которые направлены вдоль одной прямой в противоположные стороны. Найденная векторная сумма
, которые направлены вдоль одной прямой в противоположные стороны. Найденная векторная сумма  направлена перпендикулярно вектору
направлена перпендикулярно вектору  и по модулю равнa
и по модулю равнa 
Таким образом, абсолютное ускорение точки  равно сумме векторов:
равно сумме векторов:

 .
.
Поскольку вектор от  перпендикулярен вектору
перпендикулярен вектору  , то вектор
, то вектор  будет изображаться диагональю прямоугольника со сторонами
будет изображаться диагональю прямоугольника со сторонами  и
и  (рис.3.10).
(рис.3.10).
Модуль абсолютного ускорения будет равен:

Ответ: 
Задача №4
В состав механизма Витворта (рис.3.11) входит: кривошип 1, ползун 2 и кулиса 3. Кривошип  механизма вращается с постоянной угловой скоростью
механизма вращается с постоянной угловой скоростью 

Определить скорость и ускорение точки  и угловую скорость и угловое ускорение кулисы 3 механизма в положении,
и угловую скорость и угловое ускорение кулисы 3 механизма в положении,
когда: 
Решение. Особенность этого механизма заключается в том, что в точке  между собой соединяются кривошип 1, ползун 2 и кулиса 3 (рис.3.12).
между собой соединяются кривошип 1, ползун 2 и кулиса 3 (рис.3.12).
Пересечение 

Кривошип 1 и ползун 2 между собой соединены цилиндрическим шарниром, что позволяет ползуну относительно кривошипа возвращаться, а на кулисе 3 параллельно ее оси сделаны направляющие, по которым ползун 2 может двигаться поступательно.
При повороте кривошипа 1 ползун 2 скользит по кулисе 3 и заставляет ее поворачиваться вокруг точки  . Расстояние от точки
. Расстояние от точки  к точке
к точке  на кулисе 3 с поворотом кривошипа 1 меняется.
на кулисе 3 с поворотом кривошипа 1 меняется.
Такой механизм позволяет преобразовать вращательное движение кривошипа в колебательное движение кулисы, если  , или в вращательное, с другим законом изменения угловой скорости чем у кривошипа, движение кулисы, если
, или в вращательное, с другим законом изменения угловой скорости чем у кривошипа, движение кулисы, если  .
.
Таким образом, в точке  механизма (рис.3.12) будем рассматривать три разные точки:
механизма (рис.3.12) будем рассматривать три разные точки:  , принадлежащая кривошипу 1;
, принадлежащая кривошипу 1;  – ползуну 2 и
– ползуну 2 и  – кулисе 3. Все эти точки лежат одна под второй на рис.3.11.
– кулисе 3. Все эти точки лежат одна под второй на рис.3.11.
Перед решением задачи в произвольном масштабе построим схему механизма (рис.3.13,а) для заданного положения кривошипа.
Первой определим скорость точки  , принадлежащей кривошипу 1, который вращается вокруг точки
, принадлежащей кривошипу 1, который вращается вокруг точки  с угловой скоростью
с угловой скоростью  :
:

Направлена скорость  перпендикулярно
перпендикулярно  в сторону вращения кривошипа 1 (рис.3.13, а).
в сторону вращения кривошипа 1 (рис.3.13, а).
Скорость точки  , принадлежащей ползуну 2, который соединен с кривошипом 1 шарниром, равна скорости точки
, принадлежащей ползуну 2, который соединен с кривошипом 1 шарниром, равна скорости точки  :
:

Для определения скорости точки  кулисы 3, примем движение ползуна 2 за переносное. Тогда кулиса 3 относительно ползуна 2 может двигаться поступательно и скорость точки
кулисы 3, примем движение ползуна 2 за переносное. Тогда кулиса 3 относительно ползуна 2 может двигаться поступательно и скорость точки  кулисы 3 относительно точки
кулисы 3 относительно точки  ползуна 2 будет направлена вдоль направляющих, то есть вдоль
ползуна 2 будет направлена вдоль направляющих, то есть вдоль  .
.

Запишем уравнение для скоростей при сложном движении точки  относительно
относительно  :
:

где  – переносная скорость точки
– переносная скорость точки  ползуна, которая в настоящий момент времени совпадает с точкой
ползуна, которая в настоящий момент времени совпадает с точкой  кулисы. Эта скорость уже определена;
кулисы. Эта скорость уже определена;
 – относительная скорость точки
– относительная скорость точки  относительно
относительно  . Направлена эта скорость вдоль
. Направлена эта скорость вдоль  ;
;
 – абсолютная скорость точки
– абсолютная скорость точки  кулисы 3. Учитывая, что кулиса 3 вращается вокруг неподвижной точки
кулисы 3. Учитывая, что кулиса 3 вращается вокруг неподвижной точки  , то эта скорость будет направлена перпендикулярно
, то эта скорость будет направлена перпендикулярно  .
.
Векторное уравнение (1) решим путем построения плана скоростей.
Поскольку направления скорости в правой и в левой части уравнения (1) известны, то из полюса плана скоростей сначала построим правую часть уравнения, а затем левую.
Согласно правой части уравнения (1) с полюса  (рис.3.13,б) откладываем вектор
(рис.3.13,б) откладываем вектор  по направлению
по направлению  (рис.3.13, а), который в масштабе будет изображать эту скорость. (Поскольку
(рис.3.13, а), который в масштабе будет изображать эту скорость. (Поскольку  , то скорости этих точек на плане будут изображаться одним вектором, то есть на плане скоростей точки
, то скорости этих точек на плане будут изображаться одним вектором, то есть на плане скоростей точки  и
и  совпадают). Через точку
совпадают). Через точку  проведем линию
проведем линию  параллельно
параллельно  , вдоль которой от точки
, вдоль которой от точки  будет направлен вектор, что будет изображать относительную скорость
будет направлен вектор, что будет изображать относительную скорость  (величина и направление этой скорости неизвестны).
(величина и направление этой скорости неизвестны).
Теперь построим левую часть уравнения (1). Поскольку абсолютная скорость  направлена перпендикулярно
направлена перпендикулярно  , то с полюса
, то с полюса  по этому направлению проводим линию к пересечению в точке
по этому направлению проводим линию к пересечению в точке  с линией
с линией  . Точка пересечения
. Точка пересечения  будет решением векторного уравнения (1).
будет решением векторного уравнения (1).
Вектор  на плане скоростей в масштабе изображает абсолютную скорость
на плане скоростей в масштабе изображает абсолютную скорость  , а вектор
, а вектор  – относительную скорость
– относительную скорость  .
.
Поскольку на плане скоростей вектор  перпендикулярен
перпендикулярен  , а
, а  перпендикулярен
перпендикулярен  , то угол между этими векторами равен углу между
, то угол между этими векторами равен углу между  и
и  на схеме механизма, то есть
на схеме механизма, то есть  .
.
Угол при вершине  плана скоростей будет прямым, поскольку линия
плана скоростей будет прямым, поскольку линия  перпендикулярна
перпендикулярна  , а линия
, а линия  параллельна
параллельна  .
.
Таким образом треугольник  на плане скоростей прямоугольный, с углами при вершинах:
на плане скоростей прямоугольный, с углами при вершинах:  и
и  .
.
Из плана скоростей определяем:
 или
или 
 или
или 
Учитывая, что кулиса 3 вращается вокруг точки  , то для угловой скорости кулисы
, то для угловой скорости кулисы  получим:
получим:

где  – длина кулисы для этого положения механизма. С
– длина кулисы для этого положения механизма. С  (рис.13.3,а):
(рис.13.3,а): 
Поскольку ползун 2 относительно кулисы 3 движется поступательно, то  .
.
Для определения направления угловой скорости  предварительно перенесем вектор
предварительно перенесем вектор  в точку
в точку  механизма (рис.3.13, а). Угловая скорость
механизма (рис.3.13, а). Угловая скорость  направлена против хода часовой стрелки.
направлена против хода часовой стрелки.
Определим ускорение точек механизма.
Поскольку кривошип 1 вращается вокруг центра  с постоянной угловой скоростью
с постоянной угловой скоростью  , то ускорение точки
, то ускорение точки  имеет только нормальную составляющую:
имеет только нормальную составляющую:

Направлено ускорение точки  вдоль кривошипа к центру вращения
вдоль кривошипа к центру вращения  (рис.3.14, а).
(рис.3.14, а).
Ускорение точки  ползуна 2, учитывая, что кривошип и ползун соединены шарниром, равно ускорению точки
ползуна 2, учитывая, что кривошип и ползун соединены шарниром, равно ускорению точки  :
:


Для ускорения точки  кулисы 3 запишем векторное уравнение для сложного движения точки, учтя при этом, что движение ползуна 2 принято за переносное
кулисы 3 запишем векторное уравнение для сложного движения точки, учтя при этом, что движение ползуна 2 принято за переносное

где  – абсолютное ускорение точки
– абсолютное ускорение точки  ;
;
 – переносное ускорение точки
– переносное ускорение точки  ползуна, которая в настоящий момент времени совпадает с точкой
ползуна, которая в настоящий момент времени совпадает с точкой  кулисы;
кулисы;
 – ускорение точки
– ускорение точки  относительно
относительно  , направлено по оси кулисы
, направлено по оси кулисы  ;
;
 – ускорение Кориолиса точки
– ускорение Кориолиса точки  .
.
Поскольку относительное движение происходит в плоскости, перпендикулярной оси вращения ползуна 2, то ускорения Кориолиса определим из формулы:

где  – угловая скорость вращательного переносного движения ползуна 2,
– угловая скорость вращательного переносного движения ползуна 2, 
 – относительная скорость точки
– относительная скорость точки  относительно
относительно  ,
,

Для определения направления ускорения Кориолиса необходимо вектор относительной скорости  вернуть на
вернуть на  в сторону переносного вращательного движения, то есть в направлении угловой скорости
в сторону переносного вращательного движения, то есть в направлении угловой скорости  . Направление повернутого вектора (рис.3.13,в), который будет перпендикулярен оси кулисы
. Направление повернутого вектора (рис.3.13,в), который будет перпендикулярен оси кулисы  , соответствует направлению ускорения Кориолиса.
, соответствует направлению ускорения Кориолиса.
С другой стороны, точка  принадлежит кулисе 3, которая вращается вокруг центра
принадлежит кулисе 3, которая вращается вокруг центра  . Таким образом, ускорение
. Таким образом, ускорение  будет иметь две составляющие:
будет иметь две составляющие:

где  – нормальное ускорение точки
– нормальное ускорение точки  при ее вращении вокруг точки
при ее вращении вокруг точки  направлено по оси кулисы от точки
направлено по оси кулисы от точки  к точке
к точке  (рис.3.14,а) и по модулю равно:
(рис.3.14,а) и по модулю равно: 
 – тангенциальное ускорение точки
– тангенциальное ускорение точки  при ее вращении вокруг точки
при ее вращении вокруг точки  , направлено перпендикулярно оси кулисы
, направлено перпендикулярно оси кулисы  и по модулю равно:
и по модулю равно:  .
.
Решим систему векторных уравнений (2, 3) графически, путем построения плана ускорений.
Первым построим векторное уравнение (2). Из произвольного полюса  (рис.3.14,б) отложим направленный отрезок
(рис.3.14,б) отложим направленный отрезок  , изображающий ускорение
, изображающий ускорение  и направлен параллельно линии
и направлен параллельно линии  от точки
от точки  к точке
к точке  .
.
Длину отрезка  выберем
выберем  . Тогда масштабный коэффициент плана ускорений будет равен:
. Тогда масштабный коэффициент плана ускорений будет равен:

От точки  отложим вектор
отложим вектор  , который изображает ускорение Кориолиса
, который изображает ускорение Кориолиса  . Направлен этот вектор перпендикулярно оси кулисы
. Направлен этот вектор перпендикулярно оси кулисы  по определенному ранее направлению (рис.3.13, в).
по определенному ранее направлению (рис.3.13, в).
Длина вектора  равна:
равна:

Через конец вектора  проводим линию
проводим линию  , вдоль которой будет направлен вектор
, вдоль которой будет направлен вектор  , который будет изображать относительное ускорение
, который будет изображать относительное ускорение  . Направление и длина этого вектора неизвестны.
. Направление и длина этого вектора неизвестны.
Следующим построим векторное уравнение (3). С полюса  отложим вектор
отложим вектор  , изображающий нормальное ускорение
, изображающий нормальное ускорение  . Направлен этот вектор параллельно оси кулисы
. Направлен этот вектор параллельно оси кулисы  от точки
от точки  к точке
к точке  и имеет длину:
и имеет длину:

Через конец вектора  проводим линию
проводим линию  , вдоль которой будет направлен вектор
, вдоль которой будет направлен вектор  , который будет изображать тангенциальное ускорение
, который будет изображать тангенциальное ускорение  .
.
Решением системы (2, 3) будет точка пересечения линий  и
и  , а вектор
, а вектор  будет изображать ускорение
будет изображать ускорение  .
.
Из плана ускорений определяем:

Угловое ускорение кулисы 3 и ползуна 2 определим через известное тангенциальное ускорение  :
:

Для определения направления углового ускорения  надо перенести в точку
надо перенести в точку  механизма тангенциальное ускорение
механизма тангенциальное ускорение  (рис.3.14, а). Угловое ускорение
(рис.3.14, а). Угловое ускорение  направлено против хода часовой стрелки.
направлено против хода часовой стрелки.
Ответ: 

Абсолютное, относительное и переносное движение точки
В кинематике точки, рассматривается движение точки относительно неподвижной системы координат (прямоугольной декартовой или относительно осей натурального трехгранника). Однако часто приходится исследовать движение точки в отношении двух и более систем координат (тел отсчета), из которых одна система координат осуществляет движение относительно другой, условно берется за неподвижную. Например, при изучении роботов-манипуляторов следует вводить несколько систем координат. Итак, предположим, что система координат  , неизменно связана с некоторым телом, движется относительно другой системы координат
, неизменно связана с некоторым телом, движется относительно другой системы координат  , которая условно взята за неподвижную (рис. 9.1).
, которая условно взята за неподвижную (рис. 9.1).
Движение точки М относительно неподвижной системы координат называется абсолютным, а относительно подвижной системы координат – относительным. Скорости и ускорения точки, рассматриваемые в отношении данных систем, соответственно называются абсолютными и относительными.
Движение подвижной системы координат  (или неизменно связанного с ней тела G) относительно неподвижной системы отсчета
(или неизменно связанного с ней тела G) относительно неподвижной системы отсчета  , является для подвижной точки переносным движением, то есть это движение той точки подвижной системы координат, с которой в данный момент времени совпадает подвижная точка М. Соответственно скорости и ускорения точки, неизменно связанной с подвижной системой координат, в которой в данный момент времени находится подвижная точка, называются переносными.
, является для подвижной точки переносным движением, то есть это движение той точки подвижной системы координат, с которой в данный момент времени совпадает подвижная точка М. Соответственно скорости и ускорения точки, неизменно связанной с подвижной системой координат, в которой в данный момент времени находится подвижная точка, называются переносными.
Основной задачей сложного движения точки является установление зависимости между кинематическими характеристиками абсолютного, переносного и относительного движений. Уравнениями абсолютного движения точки есть, например, зависимости координат точки М, заданных в неподвижной системе координат, как функции времени:
 (9.1)
(9.1)
Аналогично для уравнения относительного движения:
 (9.2)
(9.2)
Уравнения (9.1) и (9.2) определяют в параметрической форме в соответствии абсолютную и
относительную траектории. Если уравнение (9.1) и (9.2) известны, то проекции абсолютной и относительной скоростей определяются соответственно как первые производные по времени приведенных функций; тогда вторые производные по времени от этих функций
определяют проекции абсолютного и относительного ускорений. В дальнейшем введем такие обозначения:  – абсолютная, относительная и переносная скорости,
– абсолютная, относительная и переносная скорости,  – абсолютное, относительное и переносное ускорение.
– абсолютное, относительное и переносное ускорение.


Пример 1. Пусть стержень ОА вращается вокруг неподвижной оси  , (рис. 9.2). Вдоль
, (рис. 9.2). Вдоль
стержня движется гладкое кольцо, рассматриваемое как материальная точка М. Выясните характер относительного и переносного движений.
Решение. Выберем в точке О начало неподвижной системы координат  . Движение точки М в этой системе координат называется абсолютным. Подвижная система координат Oxyz, связана со стержнем, приведена на рис. 9.2. Абсолютное движение точки М происходит в плоскости
. Движение точки М в этой системе координат называется абсолютным. Подвижная система координат Oxyz, связана со стержнем, приведена на рис. 9.2. Абсолютное движение точки М происходит в плоскости  а относительное вдоль подвижной оси
а относительное вдоль подвижной оси  . Для установления характера переносного движения выясним, какое движение, подвижная система координат Oxyz осуществляет по отношению к неподвижной. Согласно условию задачи, ось
. Для установления характера переносного движения выясним, какое движение, подвижная система координат Oxyz осуществляет по отношению к неподвижной. Согласно условию задачи, ось  вращается вокруг оси
вращается вокруг оси  . Итак, переносным движением здесь является вращательное движение стержня вокруг оси
. Итак, переносным движением здесь является вращательное движение стержня вокруг оси  .
.
Итак, сложное движение точки М (кольца) можно рассматривать как совокупность прямолинейного относительного (вдоль стержня ОА) и вращательного переносного вокруг неподвижной оси Oz вместе со стержнем. Установив характер абсолютного, относительного и переносного движений, можно решать, например, такие задачи:
а) по заданным относительным и переносным движениями определять сложное (абсолютное) движение точки;
б) по заданным сложным движениям точки определить составляющие простых движений.
Центральная операция кинематики и динамики. Абсолютная и относительная
производные по времени от вектора функции
Пусть  – система координат, взятая
– система координат, взятая
за неподвижную, a  – подвижная система координат, орты которой
– подвижная система координат, орты которой  (рис. 9.3, а).
(рис. 9.3, а).
Рассмотрим произвольную точку М, которая движется относительно как подвижной, так и неподвижной систем координат. Пусть положение этой точки в подвижной системе координат определяется радиусом-вектором  в виде:
в виде:
 (9.3)
(9.3)
Установим связь между производными от функции, вычисленными в подвижной и неподвижной системах координат. Для этого сначала найдем производную по времени от вектора  в неподвижной системе, которая называется абсолютной производной от вектора
в неподвижной системе, которая называется абсолютной производной от вектора  . по времени и:
. по времени и:

 (9.4)
(9.4)
Первые три члена этого выражения представляют собой производную от вектора  , вычисленную по предположениям, что орты подвижной системы координат по направлению не меняются, что соответствует вычислению производной в подвижной системе координат. Это выражение называется локальной (относительной) производной и обозначается
, вычисленную по предположениям, что орты подвижной системы координат по направлению не меняются, что соответствует вычислению производной в подвижной системе координат. Это выражение называется локальной (относительной) производной и обозначается 
 (9.5)
(9.5)
Рассмотрим теперь последние три слагаемых в (9.4), которые обозначим через:
 (9.6)
(9.6)

Умножив обе части (9.6) скалярно на  получим:
получим:
 (9.7)
(9.7)
Правые части этих выражений являются проекциями вектора  на оси подвижной системы координат. Обозначим их через
на оси подвижной системы координат. Обозначим их через  Воспользуемся очевидными соотношениями (рис. 9.3, б):
Воспользуемся очевидными соотношениями (рис. 9.3, б):
 (9.8)
(9.8)
Продифференцировав их по времени, получим:
 (9.9)
(9.9)
Введем обозначения:
 (9.10)
(9.10)
Тогда выражения (9.7) с учетом соотношений (9.8)-(9.10) можно записать в форме:
 (9.11)
(9.11)
Если ввести на рассмотрение вектор:
 (9.12)
(9.12)
то выражение (9.6) можно подать в виде:
 (9.13)
(9.13)
Подставив (9.13) и (9.5) в выражение (9.4) получим формулу, которая устанавливает связь между производной не только вектора  но и произвольного вектора
но и произвольного вектора  по времени, вычисленного в неподвижной и подвижной системах координат:
по времени, вычисленного в неподвижной и подвижной системах координат:
 (9.14)
(9.14)
Отметим, что во второй формуле (9.14) указана система координат, в которой вычисляется соответствующая производная.
Здесь вектор to можно рассматривать как угловую скорость вращения подвижной системы координат Oxyz относительно неподвижной  Формулу (9.14) называют формулой
Формулу (9.14) называют формулой
Бура. Она имеет следующее содержание: абсолютная производная произвольного вектора  по времени:
по времени:
 равна сумме локальной производной и
равна сумме локальной производной и векторному произведению вектора
векторному произведению вектора  вращения подвижной системы координат на дифференцируемый вектор
вращения подвижной системы координат на дифференцируемый вектор 
Поскольку формула (9.14) может быть распространена на любой вектор, то в дальнейшем будем широко пользоваться ею не только в кинематике, но и в динамике.
Рассмотрим теперь частные случаи.
1. Если система Oxyz неподвижная, то  следовательно,
следовательно,  то есть
то есть
 (9.15)
(9.15)
2. Если вектор  неподвижный относительно неподвижных осей координат
неподвижный относительно неподвижных осей координат  то
то
 (9.16)
(9.16)
3. Если вектор  неизменно связанный с системой координат
неизменно связанный с системой координат  то
то
 (9.17)
(9.17)
Отметим, что в формуле (9.14) не раскрыто пока физического смысла вектора 
Полностью он будет установлен в кинематике в разделе “Движение свободного твердого тела”. Сейчас ограничимся рассмотрением некоторых случаев, которые частично отвечают на этот вопрос.
4. Рассмотрим движение подвижной системы координат, считая, что последняя неизменно связана с телом, которое вращается вокруг неподвижной оси, например  Тогда
Тогда  и
и 
являются скоростями точек, которые совпадают с концами векторов  и
и  и вычисленные относительно неподвижной системы координат, то есть являются скоростями точек неизменной системы, которой является система координат Oxyz. Причем эти скорости имеют направления в соответствии ортов
и вычисленные относительно неподвижной системы координат, то есть являются скоростями точек неизменной системы, которой является система координат Oxyz. Причем эти скорости имеют направления в соответствии ортов и
и  (рис. 9.3, б). Итак, выражение для скоростей
(рис. 9.3, б). Итак, выражение для скоростей
точек, которые совпадают с концами единичных векторов  и
и  , можно записать в виде:
, можно записать в виде:
 (9.18)
(9.18)
Сравнив эти выражения полученной ранее формуле Эйлера, делаем вывод, что вектор  имеет реальный физический смысл.
имеет реальный физический смысл.
А именно – это вектор угловой скорости тела, которое вращается вокруг неподвижной оси.
Этот вывод легко обобщается на случай произвольной точки М, положение которой
в подвижной системе координат определяется радиусом-вектором  Тогда вектор
Тогда вектор  в выражении (9.14) имеет смысл скорости точки, неизменно связанной с телом, которое вращается в неподвижной системе координат, то есть:
в выражении (9.14) имеет смысл скорости точки, неизменно связанной с телом, которое вращается в неподвижной системе координат, то есть:
 (9.19)
(9.19)
что соответствует формуле (8.23)
5. Если скалярно умножить обе части выражения (9.18) соответственно на  и
и  , то
, то
получим:
 (9.20)
(9.20)
Левые части этих выражений являются соответственно проекциями вектора  на орт
на орт и
и  на орт
на орт  , а правые части имеют значения соответственно
, а правые части имеют значения соответственно  и
и  , поскольку
, поскольку 
 . Итак, проекциями скоростей единичных векторов
. Итак, проекциями скоростей единичных векторов  и
и  являются
являются  и
и 
(рис. 9.3, б).
6. Рассмотрим подвижную систему координат и предположим, что она совершает вращательное движение как твердое тело вокруг неподвижной оси  , которое определяется углом поворота
, которое определяется углом поворота  , который задается относительно положения
, который задается относительно положения 
(Рис. 9.4). тогда:
 (9.21)
(9.21)
где  – орты осей
– орты осей 
Отсюда получим соотношение, с которыми уже встречались в полярной системе
координат:
 (9.22)
(9.22)
Умножив теперь скалярно обе части полученных выражений соответственно на j и
и, будем иметь:
 (9.23)
(9.23)
Как видим, производная от угла поворота является ничем иным, как угловой скоростью вращения подвижной системы координат. Таким образом, для одной из компонентов в (9.10) также установлено физический смысл.
7. Пусть подвижная система отсчета осуществляет поступательное движение. Тогда:

Следовательно,  и формула (9.14) имеет такую физическую интерпретацию: все точки тела движутся с равными по величине и направлением скоростями, что было установлено нами ранее при изучении поступательного движения тела. Таким образом, для отдельных случаев движения подвижной системы координат Oxyz установлен физический смысл вектора
и формула (9.14) имеет такую физическую интерпретацию: все точки тела движутся с равными по величине и направлением скоростями, что было установлено нами ранее при изучении поступательного движения тела. Таким образом, для отдельных случаев движения подвижной системы координат Oxyz установлен физический смысл вектора  – это вектор угловой скорости тела, или подвижной системы координат Oxyz. Далее будут приведены соответствующее обоснования и для общего случая движений подвижной системы отсчета, неизменно связанной с движением твердого тела.
– это вектор угловой скорости тела, или подвижной системы координат Oxyz. Далее будут приведены соответствующее обоснования и для общего случая движений подвижной системы отсчета, неизменно связанной с движением твердого тела.
Теорема о сложении скоростей
Теорема. Абсолютная скорость точки при сложном движении равна векторной сумме относительной
точки при сложном движении равна векторной сумме относительной  и переносной
и переносной  скоростей.
скоростей.
Доказательство. Рассмотрим движение точки М относительно некоторого тела G (рис. 9.1), с которым неизменно связана подвижная система координат Oxyz, которая, в свою очередь, движется относительно условно неподвижной системы координат. Пусть положение точки М в подвижной системе координат определяется радиусом-вектором  , в неподвижной – радиусом-вектором
, в неподвижной – радиусом-вектором  , а положение начала О подвижной системы координат относительно неподвижной
, а положение начала О подвижной системы координат относительно неподвижной  , – радиусом-вектором
, – радиусом-вектором  . Тогда:
. Тогда:
 (9.24)
(9.24)
Продифференцировав это выражение в соответствии формуле (9.14):
 (9.25)
(9.25)
Здесь индекс  отражает то, что вектор
отражает то, что вектор  характеризует переносное движение. На основании определения абсолютной, относительной и переносной скоростей получим:
характеризует переносное движение. На основании определения абсолютной, относительной и переносной скоростей получим:
 (9.26)
(9.26)
С учетом этих обозначений, выражение (9.25) будет иметь следующий вид:
 (9.27)
(9.27)
который отражает теорему о распределении скоростей точек при сложном движении. Очевидно, что формула (9.27) отражает правило параллелограмма для сложения скоростей.
Модуль абсолютной скорости  на основании теоремы косинусов определяется в виде:
на основании теоремы косинусов определяется в виде:
 (9.28)
(9.28)
Пример 2. Вдоль хорды АВ (рис. 95) вращающегося диска движется точка М от точки
А к точке В в соответствии с уравнением  . Закон вращения диска
. Закон вращения диска  . Определить абсолютную скорость точки в момент, когда она находится от оси вращения диска на расстоянии
. Определить абсолютную скорость точки в момент, когда она находится от оси вращения диска на расстоянии 

Решение. Движение точки М вдоль хорды подвижного диска относительно. Поэтому относительная скорость и направлена по хорде АВ

Диск вращается вокруг оси, перпендикулярной к его плоскости. Итак, переносное движение диска будет вращательным, поэтому переносная скорость точки М направлена перпендикулярно к ОМ в сторону вращения диска. По теореме о сложении скоростей абсолютная скорость  Поскольку
Поскольку 

В некоторых задачах кинематики сложного движения точки нужно определить относительную скорость  . С формулы (9.27) видно, что:
. С формулы (9.27) видно, что:

Итак, чтобы построить вектор относительной скорости, следует добавить вектор абсолютная скорости к вектору, направленному противоположно переносной скорости.
Теорема о сложении ускорений
Теорема Кориолиса. Абсолютное ускорение точки при сложном движении равно
векторной сумме относительного, переносного ускорений и ускорения Кориолиса.
Доказательство. По определению ускорения точки, с учетом (9.27), имеем:
 (9.29)
(9.29)
где
 (9.30)
(9.30)
С помощью формулы (9.14) для абсолютной производной, определим каждое слагаемое ускорения отдельно, учитывая, что векторы  и
и  заданные в подвижной системе
заданные в подвижной системе
координат Oxyz и поэтому именно на них распространяются формулы (9.14):
 (9.31)
(9.31)


 )9.32)
)9.32)
Введем обозначения:
 (9.33)
(9.33)
Тогда (9.32) перепишем в виде:

 (9.34)
(9.34)
где 
Введем обозначения в соответствии с определениями абсолютного, относительного и переносного ускорений:
 (9.35)
(9.35)
Подставив (9.31) и (9.34) в выражение (9.29), с учетом (9.35), получим:
 (9.36)
(9.36)
Последнее слагаемое в этой формуле, который не входит ни в относительное, ни в переносное ускорения, называется поворотным или кориолисовым ускорением  :
:
 (9.37)
(9.37)
Окончательно получим:
 (9.38)
(9.38)
Теорема доказана.
Заметим, что в ряде случаев может стать полезной формула для определения ускорения, которая непосредственно следует из (9.14):
 (9.39)
(9.39)
Отметим, что когда переносное движение подвижной системы координат Oxyz является поступательным  , ускорение Кориолиса обращается в ноль. Тогда формула (9.38)
, ускорение Кориолиса обращается в ноль. Тогда формула (9.38)
принимает вид:
 (9.40)
(9.40)
то есть при поступательном движении абсолютное ускорение точки равно геометрической
сумме относительного и переносного ускорений.
Следовательно, эта формула отражает правило параллелограмма для сложения ускорений в данном случае. В следующих разделах проанализируем выражения для каждой составляющей ускорения более детально.
Вращательное и осевое ускорение в случае вращения тела вокруг неподвижной оси
Проанализируем две составляющие переносного ускорение точки в выражении (9.35)  и
и  , обусловленные движением тела относительно полюса О.
, обусловленные движением тела относительно полюса О.

Поскольку кинематическое содержание векторов  и
и  в общем случае движения тела, а следовательно, подвижной системы координат еще до конца не раскрыто , пока ограничимся рассмотрением только частного случая вращения тела вокруг неподвижной оси
в общем случае движения тела, а следовательно, подвижной системы координат еще до конца не раскрыто , пока ограничимся рассмотрением только частного случая вращения тела вокруг неподвижной оси  (рис. 9.6), для которого физический смысл векторов
(рис. 9.6), для которого физический смысл векторов  и
и  полностью определен.
полностью определен.
Введем следующие обозначения:
 (9.41)
(9.41)
и будем называть ускорение  вращательным, а
вращательным, а  осевым.
осевым.
Рассмотрим ускорения произвольной точки М, неизменно связанной с телом, вращения вокруг неподвижной оси (рис. 9.6).
В этом случае 
 поэтому ускорения точки М согласно
поэтому ускорения точки М согласно
(9.38), запишем в виде, опустив индекс  при
при  и
и  :
:

 (9.42)
(9.42)
Кроме того, ускорение этой же точки, согласно п. 8.3, можно представить в виде векторной суммы нормального и тангенциально ускорений:
 (9.43)
(9.43)
Установим связь между составляющими ускорения точки М которые есть в выражениях (9.42) и (9.43). Прежде всего покажем, что составляющая ускорения точки  направлена вдоль перпендикуляра MN, который опущен с точки М на ось вращения
направлена вдоль перпендикуляра MN, который опущен с точки М на ось вращения  . Для того чтоб
. Для того чтоб
подчеркнуть это обстоятельство, его называют осевым ускорением. Действительно, если  (рис. 9.6) – это радиус-вектор точки М то вектор ее скорости
(рис. 9.6) – это радиус-вектор точки М то вектор ее скорости  направленный по касательной к траектории (круга) точки, перпендикулярно к плоскости треугольника OMN. Тогда вектор осевого ускорения
направленный по касательной к траектории (круга) точки, перпендикулярно к плоскости треугольника OMN. Тогда вектор осевого ускорения
 (9.44)
(9.44)
будет направлен перпендикулярно к плоскости KLM, которая содержит прямую МК, параллельную оси вращения  (рис. 9.6). Итак, вектор
(рис. 9.6). Итак, вектор  направленный вдоль MN. Учитывая, что
направленный вдоль MN. Учитывая, что

 (9.45)
(9.45)
получим:
 (9.46)
(9.46)
Сравнив последнее выражение с соответствующим выражением (8.27) для нормального ускорения точки, которое всегда направлено по главной нормали к абсолютной траектории с центром кривизны в точке N, которая лежит на оси вращения, получим:
 (9.47)
(9.47)
Рассмотрим теперь вторую составляющую ускорения  , которую называют вращательным ускорением. Поскольку выполняется равенство (9.47), то с учетом (9.42) и (9.43), получим:
, которую называют вращательным ускорением. Поскольку выполняется равенство (9.47), то с учетом (9.42) и (9.43), получим:
 (9.48)
(9.48)
Далее будет показано, что в общем случае движение твердого тела 
 Если учесть, что при вращении тела вокруг неподвижной оси направления векторов
Если учесть, что при вращении тела вокруг неподвижной оси направления векторов  и
и  всегда совпадают (и совпадают с осью вращения), то в каждой точке вектора скорости и касательного ускорения направлены вдоль одной прямой – касательной к траектории. Модуль вращательного ускорения запишем в виде:
всегда совпадают (и совпадают с осью вращения), то в каждой точке вектора скорости и касательного ускорения направлены вдоль одной прямой – касательной к траектории. Модуль вращательного ускорения запишем в виде:

 (9.49)
(9.49)
Ускорение Кориолиса
По формуле (9.37) ускорение Кориолиса появляется тогда, когда переносное движение является вращательным:
 (9.50)
(9.50)
Как видно из приведенной формулы, ускорение Кориолиса равно удвоенному векторному произведению вектора  на относительную скорость точки
на относительную скорость точки  Направление ускорения Кориолиса определяется по правилу векторного произведения. Оно направлено вдоль
Направление ускорения Кориолиса определяется по правилу векторного произведения. Оно направлено вдоль
нормали к плоскости, в которой расположены векторы  и
и  , в той части пространства, с
, в той части пространства, с
которой, если смотреть с конца вектора  , видно поворот на наименьший угол от вектора
, видно поворот на наименьший угол от вектора  к вектору
к вектору  против хода часовой стрелки (в правой системе координат).
против хода часовой стрелки (в правой системе координат).
Модуль ускорения Кориолиса находим по формуле:
 (9.51)
(9.51)
Спроектировав обе части равенства (9.50) на подвижные оси координат, получим такие выражения для проекций ускорения Кориолиса :
 (9.52)
(9.52)
где  – проекции угловой скорости на оси подвижной системы координат
– проекции угловой скорости на оси подвижной системы координат 
 – проекции относительной скорости на эти самые оси.
– проекции относительной скорости на эти самые оси.
Тогда модуль ускорения Кориолиса :
 (9.53)
(9.53)
Направление  определяется направляющими косинусами углов, которые вектор
определяется направляющими косинусами углов, которые вектор  образует соответственно с ортами
образует соответственно с ортами  подвижных осей:
подвижных осей:
 (9.54)
(9.54)
Случаи превращения в ноль ускорения Кориолиса
Как следует из (9.51), ускорение Кориолиса равно нулю в те моменты (или на тех промежутках времени), когда:
1) вектор  равен нулю, то есть переносное движение является поступательным;
равен нулю, то есть переносное движение является поступательным;
2) относительная скорость  равна нулю, то есть нет относительного движения;
равна нулю, то есть нет относительного движения;
3)  то есть вектор
то есть вектор  и
и  – коллинеарные.
– коллинеарные.
Следует отметить, что в те моменты времени, когда ускорения Кориолиса превращается в ноль, абсолютное ускорение точки определяется по правилу параллелограмма.
тогда:
 (9.55)
(9.55)
а модуль этого ускорения определяется по теореме косинусов:
 (9.56)
(9.56)
Физические причины возникновения ускорения Кориолиса
Покажем, что ускорение Кориолиса возникает вследствие таких двух причин:
1. Представим себе два прямолинейных отрезка  , и
, и  , по которым движутся
, по которым движутся
точки  и
и  (рис. 9.7). Отрезок
(рис. 9.7). Отрезок  движется поступательно, а отрезок
движется поступательно, а отрезок  вращается вокруг точки
вращается вокруг точки  Обозначим через
Обозначим через  и
и  соответственно относительную и переносную скорости точки М. Переносным движением точки (рис. 9.7, а) является поступательное движение, обусловленное движением отрезка
соответственно относительную и переносную скорости точки М. Переносным движением точки (рис. 9.7, а) является поступательное движение, обусловленное движением отрезка  . Через элементарный промежуток времени отрезок
. Через элементарный промежуток времени отрезок 

займет положение  Поскольку переносное движение – поступательное, то переносные
Поскольку переносное движение – поступательное, то переносные
скорости точки  и
и  одинаковы.
одинаковы.
Переносным движением точки  (рис. 9.7, б) является вращательное движение, вызванное вращением отрезка
(рис. 9.7, б) является вращательное движение, вызванное вращением отрезка  вокруг точки
вокруг точки  . Поэтому переносные скорости точки М2 на отрезке
. Поэтому переносные скорости точки М2 на отрезке  и
и  разные:
разные: 

Итак, переносная скорость точки  меняется в зависимости от ее относительного движения вдоль отрезка
меняется в зависимости от ее относительного движения вдоль отрезка  . При этом скорость изменения переносной скорости
. При этом скорость изменения переносной скорости  точки
точки  во времени, которая создает дополнительное ускорение, пропорциональна относительной скорости
во времени, которая создает дополнительное ускорение, пропорциональна относительной скорости  и угловой скорости переносного движения
и угловой скорости переносного движения  В этом суть первой физической причины возникновения ускорения Кориолиса.
В этом суть первой физической причины возникновения ускорения Кориолиса.
2. Вторая физическая причина возникновения ускорения Кориолиса такова:
относительная скорость точки  , то есть
, то есть  , зависит от переносного вращательного движения, поскольку при вращении отрезка
, зависит от переносного вращательного движения, поскольку при вращении отрезка  меняется направление относительной скорости
меняется направление относительной скорости  (Рис. 9.7, б).
(Рис. 9.7, б).
Следовательно, скорость изменение во времени относительной скорости точки (т.е. ускорение точки, которое зависит от приведенной выше причины) также будет пропорционально относительной скорости  и угловой скорости
и угловой скорости  переносного движения.
переносного движения.
А. И. Сомов обратил внимание на то, что ускорения Кориолиса как будто вращает вектор относительной скорости в направлении переносного вращательного движения, из-за чего назвал ускорение Кориолиса поворотным.
Подводя итог изложенного и обращаясь к формуле (9.34), видим, что изменение во времени переносной скорости при условии, что переносное движение является непоступательным, вызывается не только переносным, но и относительным движением точки. Дополнительное ускорение равно векторному произведению  . Так же из формулы (9.31) следует, что изменение относительной скорости во времени вызвано не только относительным, но и переносным движением точки. Дополнительное ускорение и в этом случае равна
. Так же из формулы (9.31) следует, что изменение относительной скорости во времени вызвано не только относительным, но и переносным движением точки. Дополнительное ускорение и в этом случае равна 
Ускорение Кориолиса  , таким образом, равно удвоенному векторному произведению
, таким образом, равно удвоенному векторному произведению
векторов  и
и  , то есть
, то есть  и характеризует изменение во времени относительной скорости через переносное непоступательное движение и переносной скорости – через относительное движение точки.
и характеризует изменение во времени относительной скорости через переносное непоступательное движение и переносной скорости – через относительное движение точки.
Пример 3. Определить абсолютное ускорение точки в примере 2, приведенном в п. 9.3.
Решение. Поскольку переносное движение является вращательным, то абсолютное ускорение точки М (Рис. 9.5) определим по теореме Кориолиса:

Поскольку  и переносная угловая скорость- постоянная
и переносная угловая скорость- постоянная  то
то  и
и  Следовательно,
Следовательно,



Относительное движение точки М происходит вдоль прямой АВ, поэтому относительное ускорение  направлено вдоль АВ, ускорение
направлено вдоль АВ, ускорение  – вдоль ОМ к центру вращения. Направление ускорения Кориолиса определяем по правилу векторного произведения
– вдоль ОМ к центру вращения. Направление ускорения Кориолиса определяем по правилу векторного произведения  . Вектор
. Вектор  направленный перпендикулярно к диску , а
направленный перпендикулярно к диску , а  -вдоль хорды. Итак, ускорения Кориолиса
-вдоль хорды. Итак, ускорения Кориолиса  также направлено по ОМ от центра О вращения диска. Вектор абсолютного ускорения направлен по диагонали прямоугольника со сторонами
также направлено по ОМ от центра О вращения диска. Вектор абсолютного ускорения направлен по диагонали прямоугольника со сторонами  (рис. 9.8), и
(рис. 9.8), и


Пример 4. На подвижных объектах (самолетах, кораблях и т.д.) используются гироскопические приборы маятникового типа для определения отклонения объектов от горизонтали. При движении относительно Земли в этих приборах возникают так называемые скоростные и баллистические девиации (погрешности), обусловленные тем, что эти объекты, двигаясь горизонтально по поверхности Земли (или по сфере радиусом  , где h – высота полета), на самом деле вращаются в инерциальном пространстве и поэтому они движутся с ускорением в инерциальной системе координат, если даже их скорость относительно Земли является постоянной. Поэтому необходимо найти
, где h – высота полета), на самом деле вращаются в инерциальном пространстве и поэтому они движутся с ускорением в инерциальной системе координат, если даже их скорость относительно Земли является постоянной. Поэтому необходимо найти
угловую скорость вращения подвижного объекта и его ускорение в географической системе координат, если составляющая относительной скорости объекта к северу  , на восток –
, на восток –  (рис. 9.9), а угловая скорость суточного вращения Земли –
(рис. 9.9), а угловая скорость суточного вращения Земли –  .
.
Решение. Движение объекта (точку О) задано в сферической системе координат:  – географическая долгота, что отсчитывается от меридиана Гринвича;
– географическая долгота, что отсчитывается от меридиана Гринвича;  – географическая широта, что отсчитывается от экватора;
– географическая широта, что отсчитывается от экватора;  – радиус сферы, по которой движется объект:
– радиус сферы, по которой движется объект:  где
где  – средний радиус Земли. Отметим, что линейная скорость точки на земной поверхности, расположенной на экваторе равна 1852 км/ч относительно неподвижной системы координат.
– средний радиус Земли. Отметим, что линейная скорость точки на земной поверхности, расположенной на экваторе равна 1852 км/ч относительно неподвижной системы координат.
Ось  направлена на север (N) по касательной к меридиану,
направлена на север (N) по касательной к меридиану,  – на восток (£) по касательной к параллели, а
– на восток (£) по касательной к параллели, а  – по вертикали вверх.
– по вертикали вверх.
Очевидно, что движение объекта с составляющей скорости  вызванной изменением угла
вызванной изменением угла  – географической широты, а движение по составляющей скорости на восток
– географической широты, а движение по составляющей скорости на восток  – географической долготы
– географической долготы  . Итак, угловая скорость
. Итак, угловая скорость  направлена перпендикулярно к плоскости параллели и параллельная угловой скорости вращения Земли
направлена перпендикулярно к плоскости параллели и параллельная угловой скорости вращения Земли  , а угловая скорость
, а угловая скорость  направлена в сторону, противоположную направлению оси
направлена в сторону, противоположную направлению оси  .
.
С учетом этого, очевидно, что:
 (1)
(1)
Если теперь учесть и угловую скорость вращения Земли  , то проекции угловой скорости на оси географической системы координат будут:
, то проекции угловой скорости на оси географической системы координат будут:



 (2)
(2)

В данном случае вращательное движение Земли является переносным, а движение объекта по поверхности относительным. С учетом этого и формул (2) приведем формулы для абсолютной скорости объекта в проекциях на оси географической системы координат:
 (3)
(3)
Используя уравнение (3) выражение (2) можно переписать в форме:


 (4)
(4)

Найдем теперь абсолютное ускорение подвижного объекта, воспользовавшись формулой
(9.39):
 (5)
(5)
тут  – угловая скорость вращения системы координат
– угловая скорость вращения системы координат  относительно неподвижной системы координат, которая определяется выражениями (2) или (4)
относительно неподвижной системы координат, которая определяется выражениями (2) или (4)

Проектируя (5) на оси  будем иметь:
будем иметь:
 (6)
(6)
Подставив в (6) выражения (3) и (4), получим:
 (7)
(7)
При горизонтальном движении объекта  то есть
то есть  поэтому формулы (7) немного упрощаются:
поэтому формулы (7) немного упрощаются:

 (8)
(8)


В выражениях (8) не видно явно ускорения Кориолиса, хотя понятно, что оно должно было иметь место, потому что переносное движение Земли является вращательным.
Для того, чтобы выделить явно ускорение Кориолиса, осевое ускорение, вращательное и относительное, нужно формулы (8) записать в развернутом виде:



 (9)
(9)


Перепишем в конечном итоге формулы (9) так, чтобы на первом месте было переносное, дальше относительное и в конце ускорения Кориолиса (таблица).
Таким образом, задача решена.
Пример 5. Точка М неравномерно движется по ободу колеса радиусом R с относительной
скоростью вращается с переменной угловой скоростью  Найти двумя методами ускорения точки:
Найти двумя методами ускорения точки:
1) задавая движение точки в натуральной системе координат;
2) используя понятие сложного движения точки.
Решение. 1. При заданном движения точки в натуральной системе координат нужно учесть, что ускорение в данном случае имеет две составляющие – тангенциальное и нормальное
и нормальное  ускорения:
ускорения:
 (1)
(1)
Следовательно, для определения ускорений по формулам (1) нужно найти  .
.
Очевидно, что  – это по сути абсолютная скорость точки, поэтому:
– это по сути абсолютная скорость точки, поэтому:
 (2)
(2)
Подставив (2) в (1), получим:
 (3)
(3)
Если спроектировать эти ускорения на оси ортогональной системы координат  то получим:
то получим:
 (4)
(4)
При  и
и  соответственно получим:
соответственно получим:
 (5)
(5)

2. Использование понятия сложного движения точки. В этом случае (рис. 9.10,б)
 (6)
(6)
Переносное ускорение имеет две составляющие  и
и  Вращающаяся составляющая ускорения
Вращающаяся составляющая ускорения  направленная в данном случае по оси
направленная в данном случае по оси  и равна:
и равна:

 (7)
(7)
Осевое ускорения будет направлено к оси вращения, проходящей через точку О (рис. 9.10, б) и равно:
 (8)
(8)
Ускорение Кориолиса в этом случае направлено по оси Оу и равно:
 (9)
(9)
Относительное ускорение в этом случае определяется по формуле (9.31), в которой нужно учесть только ту составляющую угловой скорости  , которая обусловлена только относительным движением, потому что взаимодействие вращательного переносного движения и относительной скорости учтено в ускорении Кориолиса:
, которая обусловлена только относительным движением, потому что взаимодействие вращательного переносного движения и относительной скорости учтено в ускорении Кориолиса:
 (10)
(10)
Очевидно, что
 (11)
(11)
Спроектировав выражение (10) на оси  и
и  и учитывая (11), получим:
и учитывая (11), получим:
 (12)
(12)
Найдем теперь проекции абсолютных ускорений на осях  и
и 
 (13)
(13)
Сравнивая выражения (3), (4) и (13), видим, что проекции ускорения на оси  и
и  совпадают. Причем в этом случае при любой
совпадают. Причем в этом случае при любой 
 (14)
(14)
Для сравнения найдем ускорение по формуле (9.39)
 (15)
(15)
Отметим, что в данном случае в формуле (15) нужно задать полную угловую скорость
вращения подвижной системы координат:
 (16)
(16)
В нашем случае  определяется по формуле (6),
определяется по формуле (6),  Из формулы (15) с учетом (6) и (16), получим:
Из формулы (15) с учетом (6) и (16), получим:
 (17)
(17)
или
 (18)
(18)
Нетрудно заметить, что выражения (3), (13) и (18) одинаковые, то есть приведенный способ решения задачи оказался достаточно эффективным. Задача решена.
Сложное движение материальной точки. Относительное, переносное и абсолютное движение материальной точки
Сложное движение материальной точки — это такое движение, при котором точка может одновременно участвовать в двух и более движениях.
Для представления о сложном движение приведем такой пример. Если человека принять за материальную точку, то ее движение по палубе корабля будет сложным, когда это движение рассматривать относительно палубы и относительно берега (поверхности Земли). Движение человека относительно палубы является относительным, вместе с кораблем — переносным, а относительно поверхности Земли — абсолютным.
При сложном движении можно рассматривать точку, тело переноса или подвижное переносное пространство, с которым связана подвижная система координат, и неподвижную систему координат, которая скреплена с поверхностью Земли.
Движение точки относительно тела переноса или подвижной системы отсчета называется относительным, а скорость и ускорение точки в этом движении — относительными скоростью и ускорением, они обозначаются  ,
,  (relative — относительный).
(relative — относительный).
Движение точки вместе с подвижным пространством, а точнее вместе с той точкой подвижного пространства, с которой в данный момент совпадает заданная точка, называется переносным движением, а скорость и ускорение точки в этом движении — переносными скоростью и ускорением, они обозначаются  ,
,  (exporter — захватить).
(exporter — захватить).
Движение материальной точки относительно неподвижной системы координат называется абсолютным, а скорость и ускорение — абсолютными, они обозначаются  ,
,  .
.
Теорема о сложении скоростей в сложном движении материальной точки
Сформулируем эту теорему.
Абсолютная скорость материальной точки при сложном ее движении равна геометрической сумме ее переносной и относительной скоростей:
 .
.
Докажем это. Выберем материальную точку М (рис. 2.45), что движется независимо по своему закону относительно подвижной системы отсчета Oxyz, которая жестко связана с телом S, и вместе с ним перемещается относительно неподвижной системы координат  . Начало подвижной системы координат Oxyz (центр O) выбрано в теле S произвольно, на соответствующих осях координат показаны единичные векторы (орты)
. Начало подвижной системы координат Oxyz (центр O) выбрано в теле S произвольно, на соответствующих осях координат показаны единичные векторы (орты)  ,
,  и
и  .
.
Определим положение материальной точки М относительно выбранных осей координат. Так, относительно подвижной системы координат Oxyz ее положение определяется радиус-вектором  . Положение точки М относительно неподвижной системы координат
. Положение точки М относительно неподвижной системы координат  определяется радиус-вектором
определяется радиус-вектором  .
.
Положение начала (центр O) подвижной системы координат Oxyz относительно неподвижной системы координат  будет определяться радиус-вектором
будет определяться радиус-вектором  .
.
Как видно из образованного на рис. 2.46 векторного треугольника  , всегда сохраняется векторное соотношение:
, всегда сохраняется векторное соотношение:
 ,
,
или, если представить радиус-вектор  в проекциях на оси координат Oxyz с учетом единичных векторов
в проекциях на оси координат Oxyz с учетом единичных векторов  ,
,  и
и  :
:
 .
.

Используя выражение определим абсолютную скорость  материальной точки М.
материальной точки М.
При произвольном переносном движении тела орты  ,
,  и
и  меняют свое направление и поэтому являются переменными векторами. Тогда все члены, входящие в выражение выше, считаются переменными величинами. На основании формулы искомая скорость будет равна:
меняют свое направление и поэтому являются переменными векторами. Тогда все члены, входящие в выражение выше, считаются переменными величинами. На основании формулы искомая скорость будет равна:
 .
.
Перегруппируем правую часть выражения и перепишем его:

Рассмотрим подробно выражение. Так, в последней скобке в этом выражении можно сделать следующие обозначения:
 ,
,
 ,
,
 .
.
Тогда она представляет собой
 — относительную скорость точки.
— относительную скорость точки.
Рассмотрим далее первую скобку в выражении, где
 — скорость начала подвижной системы координат Oxyz или скорость полюса O.
— скорость начала подвижной системы координат Oxyz или скорость полюса O.
По формулам Пуассона другие составляющие первой скобки выражения можно представить так:
 ,
,
 ,
,
 ,
,
где  — угловая скорость переносного движения, или скорость вращения подвижных осей координат и неизменно связанных с ними ортов
— угловая скорость переносного движения, или скорость вращения подвижных осей координат и неизменно связанных с ними ортов  ,
,  и
и  .
.
Подставим в первую скобку выражения:

 .
.
Тогда выражение окончательно будет иметь следующий вид:
 .
.
Сумма  является скоростью переносного движения, где
является скоростью переносного движения, где  0 — скорость полюса или начала отсчета подвижной системы координат.
0 — скорость полюса или начала отсчета подвижной системы координат.
Поскольку переносное движение в общем случае является сложным, то он разделяется на поступательное вместе с полюсом (точкой О) и вращательное вокруг полюса
Окончательно имеем:
 .
.
Что и необходимо было доказать.
Выражение называют параллелограммом скоростей.
Когда угол  , тогда модуль абсолютной скорости равен:
, тогда модуль абсолютной скорости равен:
 ,
,
Если  , так модуль абсолютной скорости
, так модуль абсолютной скорости  движения материальной точки определяется по теореме косинусов:
движения материальной точки определяется по теореме косинусов:
 .
.
Теорема Кориолиса
Сформулируем эту теорему.
Абсолютное ускорение материальной точки при произвольном переносном движении равно геометрической сумме трех ускорений: переносного, относительного и дополнительного ускорения, которое называется поворотным ускорением или ускорением Кориолиса.
Итак:
 ,
,
где  — абсолютное ускорение материальной точки;
— абсолютное ускорение материальной точки;  — переносное ускорение;
— переносное ускорение;  — относительное ускорение;
— относительное ускорение;  — ускорение Кориолиса.
— ускорение Кориолиса.
Предположим, что материальная точка М имеет сложное движение. Считаем, что она движется относительно подвижной системы координат Oxyz, которая сама произвольным образом перемещается относительно другой — неподвижной системы  (рис. 2.46). Покажем
(рис. 2.46). Покажем  ,
,  ,
,  — орты подвижной системы координат Oxyz. Координаты точки M в подвижной системе отсчета — x, y, z.
— орты подвижной системы координат Oxyz. Координаты точки M в подвижной системе отсчета — x, y, z.
Как и в предыдущем случае, определим положение материальной точки М. Так, положение точки М в подвижной системе координат Oxyz определяется радиус-вектором  . Ее положения относительно неподвижной системы координат
. Ее положения относительно неподвижной системы координат  определяется радиус-вектором
определяется радиус-вектором  . Положение точки О (начала отсчета подвижной системы координат Oxyz) в неподвижной системе координат
. Положение точки О (начала отсчета подвижной системы координат Oxyz) в неподвижной системе координат  определяется радиус-вектором
определяется радиус-вектором  .
.
Абсолютное ускорение материальной точки М равна производной по времени от абсолютной скорости:

 .
.
Проведем преобразование и анализ выражения. В первой скобке составляющая
 — ускорение полюса O.
— ускорение полюса O.
Превратим дальше выражение первой скобки, пользуясь формулами Пуассона:






 — ускорение точки в переносном сферическом движении тела вокруг полюса.
— ускорение точки в переносном сферическом движении тела вокруг полюса.
Во второй скобке
 — относительное ускорение точки.
— относительное ускорение точки.
В уравнении есть еще такие два выражения, которые также надо превратить:


 — ускорение Кориолиса или поворотное ускорение.
— ускорение Кориолиса или поворотное ускорение.
Учитывая сделанные преобразования, окончательно запишем:
 .
.
Что и требовалось доказать.
 ,
,
где  — ускорение начала подвижной системы координат (полюса О) и независимого сферического движения тела вокруг полюса, что выражается составляющей ускорения
— ускорение начала подвижной системы координат (полюса О) и независимого сферического движения тела вокруг полюса, что выражается составляющей ускорения  .
.
Модуль, направление и физические причины возникновения ускорения Кориолиса
Рассмотрим подробно ускорения Кориолиса и его свойства. Оно, согласно формуле, имеет следующий вид:
 .
.
Ускорение Кориолиса равна двойному векторном произведения векторов переносной угловой скорости и относительной скорости точки.
Как известно, модуль векторного произведения равен:

Из выражения видно, что модуль ускорения Кориолиса равен нулю  в следующих случаях:
в следующих случаях:
1.  переносное движение не является вращательным, поэтому ускорение Кориолиса называют также поворотным ускорением;
переносное движение не является вращательным, поэтому ускорение Кориолиса называют также поворотным ускорением;
2.  движение точки в данный момент времени не является сложным;
движение точки в данный момент времени не является сложным;
3.  ,или
,или  — векторы переносной угловой скорости и относительной скорости параллельны.
— векторы переносной угловой скорости и относительной скорости параллельны.
Модуль ускорения Кориолиса будет максимальным, если угол между векторами  и
и  составляет 90º или 270º, в этом случае:
составляет 90º или 270º, в этом случае:

Направление ускорения Кориолиса можно найти по двум методами: математическим — по определению векторного произведения двух векторов и физическим — по способу Жуковского.
Рассмотрим первый способ.
Предположим, что тело S вращается вокруг оси z против направления хода часовой стрелки.
Это тело переноса и вектор  направлен вверх вдоль оси z (рис. 2.47). Независимо по телу S по своей траектории движется точка М со скоростью
направлен вверх вдоль оси z (рис. 2.47). Независимо по телу S по своей траектории движется точка М со скоростью  (вектор АМ). Перенесем условно вектор
(вектор АМ). Перенесем условно вектор  в точку М. Вектор ускорения Кориолиса
в точку М. Вектор ускорения Кориолиса  , как итоговый вектор векторного произведения, перпендикулярный плоскости, которую образуют эти векторы (параллелограмм МАВС). Остается определить, к нам этот вектор направлен, или от нас. В данном случае (рис. 2.47) вектор
, как итоговый вектор векторного произведения, перпендикулярный плоскости, которую образуют эти векторы (параллелограмм МАВС). Остается определить, к нам этот вектор направлен, или от нас. В данном случае (рис. 2.47) вектор  направлен к нам, потому что кратчайший переход от вектора
направлен к нам, потому что кратчайший переход от вектора  к вектору
к вектору  происходит против направления хода часовой стрелки.
происходит против направления хода часовой стрелки.

Таким образом, вектор ускорения Кориолиса перпендикулярен плоскости, которую образуют векторы переносной угловой скорости и относительной скорости, и направлен в ту сторону, откуда видим, что кратчайший переход от вектора угловой скорости к вектору относительной скорости происходит против часовой стрелки.
Переходим к рассмотрению определения направления вектора ускорения Кориолиса по методу Жуковского.
Для определения направления вектора ускорения Кориолиса этим методом необходимо вектор относительной скорости  спроецировать на плоскость π, перпендикулярной оси переносного вращения
спроецировать на плоскость π, перпендикулярной оси переносного вращения  , затем вернуть проекцию
, затем вернуть проекцию  в плоскости π на угол 90º в направлении переносного вращения (рис. 2.48).
в плоскости π на угол 90º в направлении переносного вращения (рис. 2.48).
Нетрудно понять, что в плоских механизмах, которые являются объектом курсового проекта по теории механизмов и машин, вектор  всегда будет расположен в плоскости движения механизма. Поэтому для определения направления ускорения Кориолиса достаточно повернуть вектор
всегда будет расположен в плоскости движения механизма. Поэтому для определения направления ускорения Кориолиса достаточно повернуть вектор  на 90º в направлении переносного поворота ωе.
на 90º в направлении переносного поворота ωе.

Рассмотрим далее физические причины возникновения поворотного ускорения или ускорение Кориолиса.
Пусть по пластине, расположенной в плоскости рисунка и равномерно вращается вокруг вертикальной оси с постоянной угловой скоростью  (направление вращения показано стрелкой), движется прямолинейно вдоль ее радиуса материальная точка М с постоянной относительной скоростью
(направление вращения показано стрелкой), движется прямолинейно вдоль ее радиуса материальная точка М с постоянной относительной скоростью  (рис. 2.49). Через некоторое время пластина повернется на угол 𝞿 и точка М окажется в положении M1 на большем расстоянии от оси вращения А. В результате этого вернется вектор
(рис. 2.49). Через некоторое время пластина повернется на угол 𝞿 и точка М окажется в положении M1 на большем расстоянии от оси вращения А. В результате этого вернется вектор  результате переносного вращения, увеличится по модулю и вернется вектор переносной скорости
результате переносного вращения, увеличится по модулю и вернется вектор переносной скорости  .
.

Из выше приведенного можно сформулировать две физические причины возникновения ускорения Кориолиса:
— изменение направления вектора относительной скорости материальной точки в результате переносного вращения;
— изменение модуля и направления вектора переносной скорости точки в результате ее относительного движения; это видно из следующих выражений переносной скорости движения для различных ее положений M и M1 (расстояние  ):
):
 ,
,
 .
.
Следовательно, ускорение Кориолиса — это новый кинематический эффект, который возникает в результате взаимодействия, взаимовлияния векторов относительной и переносной скоростей при вращательном переносном движении.
Влияние ускорения Кориолиса наблюдается в природе и технике.
Так, за счет сил инерции масс воды, которые формируются этим ускорением, размываются правые берега рек, текущих вдоль меридиана. Поэтому правые берега в северном полушарии всегда являются крутыми. В южном полушарии – наоборот, левые берега являются крутыми.
В технике ускорения Кориолиса возникает в так называемых кулисных механизмах (кулиса — это подвижная направляющая). Относительно кулисы движется кулисный камень, а переносным движением является поворот кулисы относительно недвижимого центра.
Методика решения задач на сложное движение материальной точки
1. Выяснить, движение точки является относительным, какое является переносным, проанализировать законы движения и условие задачи.
2. Для определения характеристик относительного движения необходимо условно остановить переносное движение. Найти положение точки в заданный момент времени на траектории относительного движения.
3. Для определения характеристик переносного движения необходимо условно остановить относительное движение и рассмотреть движение точки, принадлежащей телу переноса, которая совпадает в данный момент с этой точкой.
4. Для определения параметров абсолютного движения точки необходимо выбрать систему координат с началом в самой точке, затем методом проекций определить проекции абсолютных скорости и ускорения и, наконец, полные скорости и ускорения
Пример.
Кольцевая трубка (рис. 2.50) радиуса 16 см вращается вокруг горизонтальной диаметра ОА по закону  рад. Внутри трубки движется жидкость согласно уравнению
рад. Внутри трубки движется жидкость согласно уравнению  см. Определить абсолютную скорость и абсолютное ускорение частицы М жидкости в момент времени
см. Определить абсолютную скорость и абсолютное ускорение частицы М жидкости в момент времени , если в начальный момент частица была в точке А.
, если в начальный момент частица была в точке А.
Решение
Определяем положение точки М в момент времени t1. Положение точки M удобно определить углом α. Определим его с помощью такого выражения:
 рад,
рад,
 .
.

Точка М в заданный момент времени изображена на рис. 2.50. Выберем подвижную систему координат, жестко связанную с кольцевой трубкой.
Выделяем переносное движение точки M. Для этого скрепляем точку М с подвижной системой координат. В этом случае точка M будет описывать круг в плоскости, перпендикулярной к диаметру ОА, радиус которого будет равен:
 ,
,
Вычислим переносную скорость точки М как скорость вращения данной точки вокруг оси ОА. Она равна:

Определим угловую скорость вращения трубки.

 .
.
Вектор угловой скорости направлен вдоль оси вращения.
Переносная скорость  точки M равна:
точки M равна:
 .
.
Для момента времени  имеем такое значение переносной скорости точки M:
имеем такое значение переносной скорости точки M:
 .
.
Вектор переносной скорости направлен перпендикулярно к плоскости чертежа в направлении вращения.
Относительное движение точки М — это движение жидкости относительно трубки. В этом случае точка М будет двигаться по кругу диаметром ОА.
Вычисляем относительную скорость точки М. Она равна:
 .
.
Для момента времени  находим значение относительной скорости движения
находим значение относительной скорости движения  :
:

Направляем вектор относительной скорости  по касательной к упомянутой окружности в точке M.
по касательной к упомянутой окружности в точке M.
Векторы переносной  и относительно
и относительно  скоростей изображены на рис. 2.50.
скоростей изображены на рис. 2.50.
Учитывая, что векторы  и
и  взаимно перпендикулярны, находим абсолютную скорость точки M. Она равна:
взаимно перпендикулярны, находим абсолютную скорость точки M. Она равна:
 .
.
Абсолютное ускорение точки M будет равно:
 .
.
Находим переносное нормальное ускорение точки M:
 .
.
При  значение переносного нормального ускорения равно:
значение переносного нормального ускорения равно:
 .
.
Направленный вектор переносного нормального ускорения  по перпендикуляру к оси вращения OA.
по перпендикуляру к оси вращения OA.
Переносное касательное ускорение  точки М равно:
точки М равно:
 .
.
Определим угловое ускорение трубки. Оно будет равно:
 .
.
Угловое ускорение  положительное, следовательно, вращения трубки являются ускоренными.
положительное, следовательно, вращения трубки являются ускоренными.
Вычисляем переносное касательное ускорение  точки M. Оно будет равно:
точки M. Оно будет равно:
 .
.
Для  имеем значение этого ускорения:
имеем значение этого ускорения:
 .
.
Направленное переносное касательное ускорение  точки M так же, как и переносная скорость
точки M так же, как и переносная скорость  , перпендикулярна к плоскости трубки.
, перпендикулярна к плоскости трубки.
Находим относительное касательное ускорение  точки М. Оно равно:
точки М. Оно равно:
 .
.
Вектор относительного касательного ускорения  совпадает с направлением вектора относительной скорости
совпадает с направлением вектора относительной скорости  , потому что относительное движение ускоренно, о чем говорит положительный знак в касательном ускорении
, потому что относительное движение ускоренно, о чем говорит положительный знак в касательном ускорении  .
.
Вычислим относительное нормальное ускорение  :
:
 .
.
Для момента времени  имеем такое значение этого ускорения:
имеем такое значение этого ускорения:
 .
.
Направленный вектор нормального относительного ускорения  по радиусу к центру кольца трубки.
по радиусу к центру кольца трубки.
Находим ускорение Кориолиса  . Оно будет равно:
. Оно будет равно:
 .
.
Направлено ускорение Кориолиса перпендикулярно плоскости, в которой лежат векторы
 и
и  , таким образом, что если посмотреть с положительного конца этого вектора, то поворот от
, таким образом, что если посмотреть с положительного конца этого вектора, то поворот от  к
к  на наименьший угол происходит против направления хода часовой стрелки. Таким образом, вектор ускорения Кориолиса
на наименьший угол происходит против направления хода часовой стрелки. Таким образом, вектор ускорения Кориолиса  направлен по одной прямой с вектором переносного касательного ускорения
направлен по одной прямой с вектором переносного касательного ускорения  , но имеет направление в противоположную сторону.
, но имеет направление в противоположную сторону.
Находим относительное касательное ускорение  точки М. Оно равно:
точки М. Оно равно:
 .
.
Вектор относительного касательного ускорения  совпадает с направлением вектора относительной скорости
совпадает с направлением вектора относительной скорости  , потому что относительное движение ускоренно, о чем говорит положительный знак в касательном ускорении
, потому что относительное движение ускоренно, о чем говорит положительный знак в касательном ускорении  .
.
Вычислим относительное нормальное ускорение  :
:
 .
.
Для момента времени  имеем такое значение этого ускорения:
имеем такое значение этого ускорения:
 .
.
Направленный вектор нормального относительного ускорения  по радиусу к центру кольца трубки.
по радиусу к центру кольца трубки.
Находим ускорение Кориолиса  . Оно будет равно:
. Оно будет равно:
 .
.
Направлено ускорение Кориолиса перпендикулярно плоскости, в которой лежат векторы  и
и  , таким образом, что если посмотреть с положительного конца этого вектора, то поворот о т
, таким образом, что если посмотреть с положительного конца этого вектора, то поворот о т  к
к  на наименьший угол происходит против направления хода часовой стрелки. Таким образом, вектор ускорения Кориолиса
на наименьший угол происходит против направления хода часовой стрелки. Таким образом, вектор ускорения Кориолиса  направлен по одной прямой с вектором переносного касательного ускорения
направлен по одной прямой с вектором переносного касательного ускорения  , но имеет направление в противоположную сторону.
, но имеет направление в противоположную сторону.
Векторы относительного, переносного и ускорение Кориолиса изображены на рис. 2.51.

Для нахождения абсолютного ускорения  выберем систему координат, как показано на рис. 2.51, и спроектируем векторное равенство, которое определяет абсолютное ускорение точки М, на оси данной системы координат:
выберем систему координат, как показано на рис. 2.51, и спроектируем векторное равенство, которое определяет абсолютное ускорение точки М, на оси данной системы координат:
 /
/
 /
/
 .
.
Модуль абсолютного ускорения  равен:
равен:
 .
.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки