где
k
— постоянная
Больцмана.
Средняя кинетическая
энергия молекулы с жесткими связями,
включающая кинетическую энергию
поступательного и вращательного
движения, выражается
где
i
— число степеней
свободы молекулы (поступательных и
вращательных).
![]() .
.
Зависимость
давления газа p
от высоты
h в гравитационном
поле (барометрическое распределение)
где
po
— давление
газа на высоте, условно принятой за
начало отсчета (h=0),
mo
— масса
молекулы газа,
— молярная
масса, T
– температура газа.
где
то
—
масса одной молекулы.
![]() .
.
![]() и
и
![]() .
.
![]() .
.
![]() .
.
![]() .
.
где
Q—теплота,
сообщенная системе (газу);
U
—
изменение внутренней
энергии системы; А
— работа, совершенная
системой против внешних сил.
где
=Ср/СV—показатель
адиабаты.
Уравнения Пуассона,
связывающие параметры идеального газа
при адиабатическом процессе:
 ,
,
 ,
, .
.
где
Q1
— теплота, полученная
рабочим телом от теплоотдатчика
(нагревателя);
Q2
— теплота, переданная
рабочим телом теплоприемнику
(холодильнику),
T1
и T2—термодинамические
температуры теплоотдатчика и
теплоприемника.
Изменение энтропии
при переходе системы из состояния 1 в
состояние 2 определяется формулой
где
dQ
—
элементарное количество теплоты,
полученное или переданное системе в
каком-либо процессе, T
— температура
системы при
этом процессе.
где
<v>
—
средняя арифметическая
скорость молекул,
<z>
—
среднее число столкновений молекулы в
единицу времени, d
—
эффективный диаметр
молекулы, n
—
число молекул в единице объема
(концентрация молекул).
где
F —
сила поверхностного натяжения, действующая
на контур l,
ограничивающий поверхность жидкости;
E
— изменение свободной
энергии поверхностной пленки жидкости,
связанное с изменением площади S
поверхности этой пленки.
Формула
Лапласа, выражающая давление р,
создаваемое сферической поверхностью
жидкости,
где
R
— радиус сферической
поверхности.
где
— краевой угол
(=0
при полном смачивании стенок трубки
жидкостью;
=
при полном несмачивании),
R—радиус
канала трубки;
— плотность жидкости,
g
— ускорение
свободного падения.
Высота подъема
жидкости между двумя близкими и
параллельными друг другу плоскостями
где
d
— расстояние
между плоскостями.
Определить
количество вещества
v
и число N
молекул кислорода
массой т=0,5
кг.
Сколько
атомов содержится в ртути:
1) количеством
вещества
v=0,2
моль; 2)
массой т=1
г?
Вода
при температуре t=4°С
занимает объем V=1
см3.
Определить количество вещества
v
и число N
молекул воды.
Найти
молярную массу
и массу тo
одной молекулы поваренной соли.
Определить
массу тo
одной молекулы углекислого газа.
Определить
концентрацию п
молекул кислорода, находящегося в
сосуде вместимостью V=2
л.
Количество вещества
v
кислорода равно
0,2 моль.
Определить
количество вещества
v
водорода,
заполняющего сосуд
объемом V=3
л, если концентрация молекул газа в
сосуде n
=21018
м3.
В
баллоне вместимостью V=3
л содержится кислород
массой т=10
г. Определить концентрацию n
молекул газа.
Плотность
газа
при давлении p=96
кПа и температуре
t=0°C
равна 1,35
г/л. Найти молярную массу
газа.
Определить
количество вещества
v
и число N
молекул азота массой m=0,2
кг.
В
цилиндр длиной
l=1,6
м, заполненный
воздухом при нормальном атмосферном
давлении ро
начали медленно вдвигать поршень
площадью основания
S=200
см3.
Определить силу
F,
действующую на поршень, если его
остановить на расстоянии l1=10
см от дна цилиндра.
В
баллоне находится газ при температуре
Т1=400
К. До какой температуры Т2
надо нагреть газ, чтобы его давление
увеличилось в
1,5 раза?
Баллон
вместимостью V=20
л
заполнен азотом
при температуре T=400
К. Когда часть газа
израсходовали, давление в баллоне
понизилось на р=200
кПа. Определить
массу m
израсходованного газа. Процесс считать
изотермическим.
В
баллоне вместимостью V=15
л находится аргон
под давлением p1=600
кПа и при температуре
Т1=300
К. Когда из баллона было взято некоторое
количество газа, давление в баллоне
понизилось до p2=400
кПа, а температура
установилась Т2=260
К. Определить массу
m
аргона, взятого из баллона.
Два
сосуда одинакового объема содержат
кислород. В одном сосуде давление р1=2
МПа
и температура T1=800
K, в другом р2=2,5
МПа,
T2=200
К. Сосуды соединили трубкой и охладили
находящийся в них кислород до температуры
T=200
К. Определить
установившееся в сосудах давление р.
Вычислить
плотность
азота, находящегося в баллоне под
давлением р=2
МПа и имеющего
температуру Т=400
К.
Определить
относительную молекулярную массу
Mr
газа, если при температуре Т=154
К и давлении р=2,8
МПа он имеет плотность =6,1
кг/м3.
Найти
плотность
азота при температуре Т=400
К и давлении р=2
МПа.
В
сосуде вместимостью
V=40
л находится кислород
при температуре Т=300
К. Когда часть газа израсходовали,
давление в баллоне понизилось на р=100
кПа. Определить массу
m
израсходованного кислорода. Процесс
считать изотермическим.
Определить
плотность
водяного пара, находящегося под давлением
р=2,5
кПа и имеющего температуру Т=250
К.
Определить
внутреннюю энергию
U
водорода, а также среднюю кинетическую
энергию
молекулы этого газа при температуре
Т=300
К, если количество вещества
v
этого газа равно
0,5 моль.
Определить
суммарную кинетическую энергию Ek
поступательного движения всех молекул
газа, находящегося в сосуде вместимостью
V=3
л под давлением
р=540
кПа.
Количество
вещества гелия
v=l,5
моль, температура
Т=120
К. Определить суммарную кинетическую
энергию Ek
поступательного движения всех молекул
этого газа.
Молярная
внутренняя энергия
Um
некоторого двухатомного газа равна
6,02 кДж/моль. Определить
среднюю кинетическую энергию вр
вращательного движения одной молекулы
этого газа. Газ считать идеальным.
Определить
среднюю кинетическую энергию
одной молекулы
водяного пара при температуре
Т=500
К.
Определить
среднюю квадратичную скорость vкв
молекулы газа,
заключенного в сосуд вместимостью V=2
л под давлением р=200
кПа. Масса газа m=0,3
г.
Водород
находится при температуре Т=300
К. Найти среднюю
кинетическую энергию вр
вращательного движения одной молекулы,
а также суммарную кинетическую энергию
Ek
всех молекул этого газа; количество
водорода
v=0,5
моль.
При
какой температуре средняя кинетическая
энергия п
поступательного движения молекулы
газа равна
4,1410-21
Дж?
В
азоте взвешены мельчайшие пылинки,
которые движутся так, как если бы они
были очень крупными молекулами. Масса
каждой пылинки равна
610-10
г. Газ находится при температуре Т=400
К. Определить средние квадратичные
скорости vкв,
а также средние кинетические энергии
п
поступательного движения молекулы
азота и пылинки.
Определить
среднюю кинетическую энергию п
поступательного движения и вр
вращательного движения молекулы азота
при температуре Т=1
К.
Определить также полную кинетическую
энергию Ek
молекулы при тех же условиях.
Определить
молярную массу
двухатомного газа
и его удельные теплоемкости cp
и cV,
если известно, что разность
удельных теплоемкостей этого газа
cp—cV
равна 260
Дж/(кгК).
Найти
удельные cV
и cp,
а также молярные СV
и Сp
теплоемкости углекислого газа.
Определить
показатель адиабаты
идеального газа, который при температуре
Т=350
К и
давлении р=0,4
МПа занимает объем V=300
л и имеет теплоемкость СV=857
Дж/К.
В
сосуде вместимостью V=6
л находится при
нормальных условиях двухатомный газ.
Определить теплоемкость СV
этого газа при постоянном объеме.
Определить
относительную молекулярную массу Mr
и молярную массу
газа, если разность его удельных
теплоемкостей cp—cV=2,08
кДж/(кгК).
Определить
молярные теплоемкости газа, если его
удельные теплоемкости cV=10,4
кДж/(кгК)
и cp=14,6
кДж/(кгК).
Найти
удельные cV
и cp
и молярные CV
и Cp
теплоемкости азота
и гелия.
Вычислить
удельные теплоемкости газа, зная, что
его молярная масса
=410-3
кг/моль и отношение молярных теплоемкостей
Ср/СV=1,67.
Трехатомный
газ под давлением р=240
кПа
и температуре t=20°С
занимает объем V=10
л. Определить теплоемкость Ср
этого газа при постоянном давлении.
Одноатомный
газ при нормальных условиях занимает
объем V=5
л. Вычислить теплоемкость СV
этого газа при
постоянном объеме.
Найти
среднее число z
столкновений за время t=1
с и
длину свободного пробега
l
молекулы гелия, если газ находится под
давлением р=2
кПа при температуре
Т=200
К.
Определить
среднюю длину свободного пробега l
молекулы азота в
сосуде вместимостью V=5
л.
Масса газа т=0,5
г.
Водород
находится под давлением р=20
мкПа и имеет
температуру Т=300
К. Определить среднюю длину свободного
пробега l
молекулы такого газа.
При
нормальных условиях длина свободного
пробега l
молекулы водорода равна
0,160 мкм. Определить
диаметр d
молекулы водорода.
Какова
средняя арифметическая скорость молекул
кислорода при нормальных условиях,
если известно, что средняя длина
свободного пробега
l
молекулы кислорода при этих условиях
равна 100
нм?
Кислород
находится под давлением р=133
нПа при температуре
Т=200 К. Вычислить
среднее число z
столкновений молекулы кислорода при
этих условиях за время t=1
с.
При
каком давлении р
средняя длина свободного пробега
l
молекул азота равна
1 м, если температура
газа t=10°С?
В
сосуде вместимостью V=5
л находится водород
массой m=0,5
г. Определить среднюю длину свободного
пробега l
молекулы водорода
в этом сосуде.
Средняя
длина свободного пробега
l
молекулы водорода при некоторых условиях
равна 2
мм. Найти плотность
водорода при этих
условиях.
В
сферической колбе вместимостью V=3
л, содержащей азот,
создан вакуум с давлением р=80
мкПа. Температура газа Т=250
К. Можно ли считать вакуум в колбе
высоким? Вакуум считается высоким, если
длина свободного пробега молекул в нем
много больше линейных размеров сосуда.
Определить
количество теплоты
Q, которое надо
сообщить кислороду объемом
V=50
л и массой 1 моль при его изохорическом
нагревании, чтобы давление газа
повысилось на
p=0,5
Мпа
При
изотермическом расширении азота при
температуре Т=280
К объем его увеличился
в два раза. Определить:
1) совершенную при
расширении газа работу А,
2) изменение
U
внутренней энергии;
3) количество теплоты
Q, полученное газом.
Масса азота m=0,2
кг.
При
адиабатическом сжатии давление воздуха
было увеличено от р1=50
кПа до р2=0,5
МПа. Затем при
неизменном объеме температура воздуха
была понижена до первоначальной.
Определить давление р3
газа в конце процесса.
Кислород
массой m=200
г занимает объем
V1=100
л и находится под
давлением р1=200
кПа. При нагревании
газ расширился при постоянном давлении
до объема V2=300
л, а затем его
давление возросло до р2=500
кПа при неизменном
объеме. Найти изменение внутренней
энергии U
газа, совершенную газом работу А
и теплоту Q,
переданную газу. Построить график
процесса.
Объем
водорода при изотермическом расширении
при температуре Т=300
К
увеличился в п=3
раза. Определить работу А,
совершенную газом, и теплоту
Q,
полученную при
этом. Масса т
водорода равна
200 г.
Азот
массой m=0,1
кг был изобарически нагрет от температуры
Т1=200
К до температуры Т2=400
К. Определить работу А,
совершенную газом, полученную газом
теплоту Q
и изменение
U
внутренней энергии азота.
Во
сколько раз увеличится объем водорода,
содержащий количество вещества
v=0,4
моль при изотермическом расширении,
если при этом газ получит количество
теплоты Q=800
Дж? Температура водорода Т=300
К.
Какая
работа А
совершается при изотермическом
расширении водорода массой m=5
г, взятого при
температуре Т=290
К, если объем газа
увеличивается в три раза?
Какая
доля w1
количества теплоты
Q,
подводимого к идеальному двухатомному
газу при изобарическом процессе,
расходуется на увеличение
U
внутренней энергии газа и какая доля
w2
— на работу А
расширения? Рассмотреть три случая,
если газ: 1)
одноатомный; 2)
двухатомный;
3) трехатомный.
Определить
работу А,
которую совершит азот, если ему при
постоянном давлении сообщить количество
теплоты Q=21
кДж. Найти также изменение
U
внутренней энергии газа.
Идеальный
газ совершает цикл Карно при температурах
теплоприемника Т2=290
К и теплоотдатчика Т1=400
К. Во сколько раз увеличится коэффициент
полезного действия
цикла, если температура теплоотдатчика
возрастет до T1,1=600
К?
Идеальный
газ совершает цикл Карно. Температура
Т1
теплоотдатчика
в четыре раза (n=4)
больше температуры теплоприемника.
Какую долю w
количества теплоты, полученного за
один цикл от теплоотдатчика, газ отдаст
теплоприемнику?
Определить
работу A2
изотермического сжатия газа, совершающего
цикл Карно, КПД которого =0,4,
если работа
изотермического расширения равна A1=8
Дж.
Найти
изменение энтропии 1 кг льда находящегося
при температуре 0оС.
Найти
изменение энтропии при изобарическом
расширении 8 г
гелия от объема
V1=10
л до V2=25
л.
Найти
изменение энтропии при изотермическом
расширении 6 г
водорода
от 105
Па до 0,5105
Па.
Во
сколько раз увеличится коэффициент
полезного действия
цикла Карно при
повышении температуры теплоотдатчика
от Т1=380
К до Т1,1=560
К? Температура теплоприемника Т2=280
К.
Идеальная
тепловая машина работает по циклу
Карно. Температура теплоотдатчика
Т1=500
К, температура теплоприемника Т2=250
К. Определить термический КПД
цикла, а также работу A1
рабочего вещества при изотермическом
расширении, если при изотермическом
сжатии совершена работа A2=70
Дж.
Газ,
совершающий цикл Карно, получает теплоту
Q1=84
кДж.
Определить работу
А
газа, если температура
Т1
теплоотдатчика в три раза выше температуры
Т2
теплоприемника.
В
цикле Карно газ получил от теплоотдатчика
теплоту Q1=500
Дж
и совершил работу
А=100
Дж. Температура теплоотдатчика
Т1=400
К. Определить температуру Т2
теплоприемника.
Найти
массу m
воды, вошедшей в стеклянную трубку с
диаметром канала d=0,8
мм, опущенную в воду
на малую глубину. Считать смачивание
полным.
Какую
работу А
надо совершить при выдувании мыльного
пузыря, чтобы увеличить его объем от
V1=8
см-3
до V2=16
см-3?
Считать процесс изотермическим.
Какая
энергия Е
выделится при слиянии двух капель ртути
диаметром d1=0,8
мм и
d2=1,2
мм в одну каплю?
Определить
давление р
внутри воздушного пузырька диаметром
d=4
мм, находящегося в воде у самой ее
поверхности. Считать атмосферное
давление нормальным.
Пространство
между двумя стеклянными параллельными
пластинками с площадью поверхности
S=100
см2
каждая, расположенными
на расстоянии l=20
мкм друг от друга, заполнено водой.
Определить силу
F,
прижимающую пластинки друг к другу.
Считать мениск вогнутым с диаметром
d,
равным расстоянию между пластинками.
Глицерин
поднялся в капиллярной трубке диаметром
канала d=1
мм на высоту
h=20
мм. Определить поверхностное натяжение
глицерина. Считать смачивание полным.
В воду
опущена на очень малую глубину стеклянная
трубка с диаметром канала
d=1
мм. Определить массу т
воды, вошедшей в трубку.
На
сколько давление р
воздуха внутри мыльного пузыря больше
нормального атмосферного давления ро,
если диаметр пузыря
d=5
мм?
Воздушный
пузырек диаметром
d=2,2
мкм находится в воде у самой ее
поверхности. Определить плотность
воздуха в пузырьке, если воздух над
поверхностью воды находится при
нормальных условиях.
Две
капли ртути радиусом r=1,2
мм каждая слились
в одну большую каплю. Определить энергию
Е, которая
выделится при этом слиянии. Считать
процесс изотермическим.
Определить
давления р1
и р2
газа, содержащего N=109
молекул и имеющего объем
V=1
см-3,
при температурах T1=З
К и T2=1000
К.
При
температуре t=35°С
и давлении р=708
кПа плотность некоторого газа =12,2
кг/м3.
Определить относительную молекулярную
массу Mr
газа.
Какой
объем V
занимает смесь азота массой т1=1
кг и гелия массой т2=1
кг при нормальных условиях?
В
баллоне вместимостью V=15
л находится смесь,
содержащая
m1=10
г водорода, m2=54
г водяного пара и
m3=60
г оксида углерода. Температура смеси
t=27°С.
Определить
давление.
Найти
полную кинетическую энергию, а также
кинетическую энергию вращательного
движения одной молекулы аммиака NH3
при температуре
t=27°C.
Определить
удельные теплоемкости cV
и cp
газообразного оксида углерода СО.
Смесь
газа состоит из кислорода
О2
с массовой долей
w1=85%
и озона О3
с массовой долей
w2=15%.
Определить
удельные теплоемкости cV
и cp
этой газовой смеси.
Газовая
смесь состоит из азота массой
т1=3
кг и водяного пара
массой т2=1
кг. Принимая эти газы за идеальные,
определить удельные теплоемкости cV
и cp
газовой смеси.
Молекула
газа состоит из двух атомов; разность
удельных теплоемкостей газа при
постоянном давлении и постоянном объеме
равна 260
Дж/(кгК).
Найти молярную массу газа и его удельные
теплоемкости cV
и cp.
Найти
среднюю длину
<l>
свободного пробега молекулы водорода
при р=133
мПа и t=-173°С.
Один
киломоль двухатомного идеального газа
совершает замкнутый цикл, график
которого в координатах p,V
представляет собой
прямоугольник Координаты вершин данного
прямоугольника равны: p1=1,2
МПа, V1=2
м3
;
p2=1,6
МПа, V2=2
м3
;
p3=1,6
МПа, V3=3
м3
;
p4=1,2
МПа, V4=3
м3
.
Изобразить процесс на рисунке. Определить:
1) теплоту
Q1,
полученную от теплоотдатчика;
2) теплоту
Q2,
переданную теплоприемнику;
3) работу А,
совершаемую газом за один цикл;
4) термический КПД
цикла.
Водород
занимает объем V=10
м3
при давлении р1=0,1
МПа. Его нагрели при постоянном объеме
до давления р2=0,З
МПа. Определить изменение
U
внутренней энергии газа, работу А,
совершенную газом, и теплоту
Q, сообщенную газу.
Кислород
при неизменном давлении р=80
кПа нагревается.
Его объем увеличивается от
V1=1
м3
до V2=3
м3.
Определить изменение U
внутренней энергии кислорода, работу
А,
совершенную им при расширении, а также
теплоту Q,
сообщенную газу.
В
цилиндре под поршнем находится азот,
имеющий массу
m=0,6
кг и занимающий объем
V1=1,2
м3,
при температуре
T1=560
К. В результате нагревания газ расширился
и занял объем
V2=4,2
м3,
причем температура осталась неизменной.
Найти изменение
U
внутренней энергии газа, совершенную
им работу А
и теплоту Q,
сообщенную газу.
В
бензиновом автомобильном двигателе
степень сжатия горючей смеси равна
6,2. Смесь засасывается
в цилиндр при температуре t1=15°С.
Найти температуру t2
горючей смеси в конце такта сжатия.
Горючую смесь рассматривать как
двухатомный идеальный газ, процесс
считать адиабатическим.
Найти
изменение энтропии при превращении 10
г льда находящегося при температуре
-20оС
в пар при 100оС.
Какую
энергию надо затратить, чтобы выдуть
мыльный пузырь
диаметром
d=12
см? Каково будет добавочное давление
внутри этого пузыря?
На
нижнем конце трубки диаметром d=0,2
см повисла шарообразная
капля воды. Найти диаметр этой капли.
В
сосуд с ртутью частично погружены две
вертикально расположенные и параллельные
друг другу стеклянные пластинки.
Расстояние между пластинками d=1
мм. Определить разность h
уровней ртути в сосуде и между пластинками,
краевой угол принять равным 138°.
Вычислить энергию поступательного движения одной молекулы и суммарную энергию всех молекул. Напишите формулы пожалуйста
Ученик
(99),
закрыт
13 лет назад
Леонид Фурсов
Высший разум
(788035)
13 лет назад
Кинетическая энергия поступательного движения зависит от количества атомов в молекуле. Кинетическая энергия поступательного движения одноатомной молекулы определяется по формуле: Ek=(3/2)*k*T, где к-постоянная Больцмана, Т-абсолютная температура. На одну степень свободы приходится энергия (1/2)*k*T.
Источник: физика.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,944 -
разное
16,904
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Представляем формулу основного уравнения молекулярно-кинетической теории (МКТ) газов:
(где n=NV – это концентрация частиц в газе, N – это число частиц, V – это объем газа, 〈E〉 – это средняя кинетическая энергия поступательного движения молекул газа, υkv – это средняя квадратичная скорость, m0 – это масса молекулы) связывает давление – макропараметр, достаточно просто измеряющийся с такими микропараметрами, как средняя энергия движения отдельной молекулы (или в другом выражении), как масса частицы и ее скорость. Но находя только лишь давление, нельзя установить кинетические энергии частиц отдельно от концентрации. Поэтому для нахождения в полном объеме микропараметров нужно знать еще какую-то физическую величину, связанную с кинетической энергией частиц, составляющих газ. За данную величину можно взять термодинамическую температуру.
Газовая температура
Для определения газовой температуры нужно вспомнить важное свойство, которое сообщает о том, что в условиях равновесия средняя кинетическая энергия молекул в смеси газов одинаковая для различных компонентов данной смеси. Из данного свойства следует то, что если 2 газа в различных сосудах находятся в тепловом равновесии, тогда средние кинетические энергии молекул данных газов одинаковые. Это свойство мы и будем использовать. К тому же в ходе экспериментов доказано, что для любых газов (при неограниченном числе), которые находятся в состоянии теплового равновесия, справедливо следующее выражение:
С учетом вышесказанного, используем (1) и (2) и получаем:
Из уравнения (3) следует, что величина θ, которой мы обозначили температуру, вычисляется в Дж, в чем измеряется также и кинетическая энергия. В лабораторных работах температура в системе измерения вычисляется в кельвинах. Поэтому введем коэффициент, который уберет данное противоречие. Он обозначается k, измеряется в ДжК и равняется 1,38·10-23. Данный коэффициент называется постоянной Больцмана. Таким образом:
θ=kT (4), где T – это термодинамическая температура в кельвинах.
Связь термодинамической температуры и средней кинетической энергией теплового движения молекул газа выражается формулой:
E=32kT (5).
Из уравнения (5) видно, что средняя кинетическая энергия теплового движения молекул прямо пропорциональна температуре газа. Температура является абсолютной величиной. Физический смысл температуры заключается в том, что она, с одной стороны, определяется средней кинетической энергией, которая приходится на 1 молекулу. А с другой стороны, температура – это характеристика системы в целом. Таким образом, уравнение (5) показывает связь параметров макромира с параметрами микромира.
Известно, что температура – это мера средней кинетической энергии молекул.
Можно установить температуру системы, а затем рассчитать энергию молекул.
Абсолютный ноль температур
В условиях термодинамического равновесия все составляющие системы характеризуются одинаковой температурой.
Температура, при которой средняя кинетическая энергия молекул равняется 0, давление идеального газа равняется 0, называется абсолютным нулем температур. Абсолютная температура никогда не является отрицательной.
Необходимо найти среднюю кинетическую энергию поступательного движения молекулы кислорода, если температура T=290 K. А также найти среднюю квадратичную скорость капельки воды диаметра d=10-7 м, взвешенной в воздухе.
Решение
Найдем среднюю кинетическую энергию движения молекулы кислорода по уравнению, связывающему энергию и температуру:
E=32kT (1.1).
Поскольку все величины заданы в системе измерения, проведем вычисления:
E=32·1,38·10-23·10-7=6·10-21 Дж.
Перейдем ко второй части задания. Положим, что капелька, взвешенная в воздухе, – это шар (рисунок 1). Значит, массу капельки можно рассчитать как:
m=ρ·V=ρ·πd36.

Рисунок 1
Найдем массу капельки воды. Согласно справочных материалов, плотность воды в нормальных условиях равняется ρ=1000 кгм3, тогда:
m=1000·3,14610-73=5,2·10-19 (кг).
Масса капельки чрезмерно маленькая, поэтому, сама капелька сравнима с молекулой газа, и тогда можно использовать при расчетах формулу средней квадратичной скорости капли:
E=mυkυ22 (1.2),
где 〈E〉 мы уже установили, а из (1.1) понятно, что энергия не зависит от разновидности газа, а зависит только лишь от температуры. Значит, мы можем применить полученную величину энергии. Найдем из (1.2) скорость:
υkυ=2Em=6·2Eπρd3=32kTπρd3 (1.3).
Рассчитаем:
υkυ=2·6·10-215,2·10-19=0,15 мс
Ответ: Средняя кинетическая энергия поступательного движения молекулы кислорода при заданной температуре равняется 6·10-21 Дж. Средняя квадратичная скорость капельки воды при заданных условиях равняется 0,15 м/с.
Средняя энергия поступательного движения молекул идеального газа равняется 〈E〉, а давление газа p. Необходимо найти концентрацию частиц газа.
Решение
В основу решения задачи положим уравнение состояния идеального газа:
p=nkT (2.1).
Прибавим к уравнению (2.1) уравнение связи средней энергии поступательного движения молекул и температуры системы:
E=32kT (2.2).
Из (2.1) выражаем необходимую концентрацию:
n=pkT 2.3.
Из (2.2) выражаем kT:
kT=23E (2.4).
Подставляем (2.4) в (2.3) и получаем:
n=3p2E
Ответ: Концентрацию частиц можно найти по формуле n=3p2E.
Повседневный опыт показывает, что недвижимые тела можно привести в движение, а движимые остановить. Мы с вами постоянно что-то делаем, мир вокруг суетится, светит солнце… Но откуда у человека, животных, да и у природы в целом берутся силы для выполнения этой работы? Исчезает ли механическое движение бесследно? Начнет ли двигаться одно тело без изменения движения другого? Обо всем этом мы расскажем в нашей статье.
Понятие энергии
Для работы двигателей, которые придают движение автомобилям, тракторам, тепловозам, самолетам, нужно топливо, которое является источником энергии. Электродвигатели придают движение станкам при помощи электроэнергии. За счет энергии воды, падающей с высоты, оборачиваются гидротурбины, соединенные с электрическими машинами, производящими электрический ток. Человеку для того, чтобы существовать и работать, также нужна энергия. Говорят, что для того, дабы выполнять какую-нибудь работу, необходима энергия. Что же такое энергия?
- Наблюдение 1. Поднимем над землей мяч. Пока он пребывает в состоянии спокойствия, механическая работа не выполняется. Отпустим его. Под действием силы тяжести мяч падает на землю с определенной высоты. Во время падения мяча выполняется механическая работа.
- Наблюдение 2. Сомкнем пружину, зафиксируем ее нитью и поставим на пружину гирьку. Подожжем нить, пружина распрямится и поднимет гирьку на некую высоту. Пружина выполнила механическую работу.
- Наблюдение 3. На тележку закрепим стержень с блоком в конце. Через блок перекинем нить, один конец которой намотан на ось тележки, а на другом висит грузик. Отпустим грузик. Под действием силы тяжести он будет опускаться книзу и придаст тележке движение. Грузик выполнил механическую работу.

После анализа всех вышеперечисленных наблюдений можно сделать вывод, что если тело или несколько тел во время взаимодействия выполняют механическую работу, то говорят, что они имеют механическую энергию, либо энергию.
Понятие энергии
Энергия (от греч. слова энергия – деятельность) – это физическая величина, которая характеризирует способность тел выполнять работу. Единицей энергии, а также и работы в системе СИ является один Джоуль (1 Дж). На письме энергия обозначается буквой Е. Из вышеуказанных экспериментов видно, что тело выполняет работу тогда, когда переходит из одного состояния в другое. Энергия тела при этом меняется (уменьшается), а выполненная телом механическая работа равна результату изменения ее механической энергии.
Виды механической энергии. Понятие потенциальной энергии

Различают 2 вида механической энергии: потенциальную и кинетическую. Сейчас подробнее рассмотрим потенциальную энергию.
Потенциальная энергия (ПЭ) – это энергия, определяющаяся взаимным положением тел, которые взаимодействуют, либо частями того самого тела. Поскольку любое тело и земля притягивают друг друга, то есть взаимодействуют, ПЭ тела, поднятого над землей, будет зависеть от высоты поднятия h. Чем выше поднято тело, тем больше его ПЭ. Экспериментально установлено, что ПЭ зависит не только от высоты, на которую оно поднято, но и от массы тела. Если тела были подняты на одинаковую высоту, то тело, имеющее большую массу, будет иметь и большую ПЭ. Формула данной энергии выглядит следующим образом: Eп = mgh, где Eп – это потенциальна энергия, m – масса тела, g = 9,81 Н/кг, h – высота.
Потенциальная энергия пружины
Потенциальной энергией упруго деформированного тела называют физическую величину Eп, которая при изменении скорости поступательного движения под действием сил упругости уменьшается ровно на столько, на сколько растет кинетическая энергия. Пружины (как и другие упруго деформированные тела) имеют такую ПЭ, которая равна половине произведения их жесткости k на квадрат деформации: x = kx2: 2.
Энергия кинетическая: формула и определение
Иногда значение механической работы можно рассматривать без употребления понятий силы и перемещения, акцентировав внимание на том, что работа характеризует изменение энергии тела. Все, что нам может потребоваться, – это масса некоего тела и его начальная и конечная скорости, что приведет нас к кинетической энергии. Кинетическая энергия (КЭ) – это энергия, принадлежащая телу вследствие собственного движения.

Кинетическую энергию имеет ветер, ее используют для придания движения ветряным двигателям. Движимые массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их оборачиваться. Вращательное движение при помощи систем передач передается механизмам, выполняющим определенную работу. Движимая вода, оборачивающая турбины электростанции, теряет часть своей КЭ, выполняя работу. Летящий высоко в небе самолет, помимо ПЭ, имеет КЭ. Если тело пребывает в состоянии покоя, то есть его скорость относительно Земли равна нулю, то и его КЭ относительно Земли равна нулю. Экспериментально установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его КЭ. Формула кинетической энергии поступательного движения в математическом выражении следующая:

Где К – кинетическая энергия, m – масса тела, v – скорость.
Изменение кинетической энергии
Поскольку скорость движения тела является величиной, зависящей от выбора системы отсчета, значение КЭ тела также зависит от ее выбора. Изменение кинетической энергии (ИКЭ) тела происходит вследствие действия на тело внешней силы F. Физическую величину А, которая равна ИКЭ ΔЕк тела вследствие действия на него силы F, называют работой: А = ΔЕк. Если на тело, которое движется со скоростью v1, действует сила F, совпадающая с направлением, то скорость движения тела вырастет за промежуток времени t к некоторому значению v2. При этом ИКЭ равно:
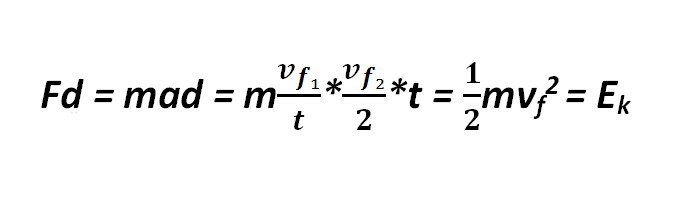
Где m – масса тела; d – пройденный путь тела; Vf1 = (V2 – V1); Vf2 = (V2 + V1); a = F : m. Именно по этой формуле высчитывается, на сколько изменяется энергия кинетическая. Формула также может иметь следующую интерпретацию: ΔЕк = Flcosά, где cosά является углом между векторами силы F и скорости V.
Средняя кинетическая энергия
Кинетическая энергия представляет собой энергию, определяемую скоростью движения разных точек, которые принадлежат этой системе. Однако следует помнить, что необходимо различать 2 энергии, характеризующие разные виды движения: поступательное и вращательное. Средняя кинетическая энергия (СКЭ) при этом является средней разностью между совокупностью энергий всей системы и ее энергией спокойствия, то есть, по сути, ее величина – это средняя величина потенциальной энергии. Формула средней кинетической энергии следующая:

где k – это константа Больцмана; Т – температура. Именно это уравнение является основой молекулярно-кинетической теории.
Средняя кинетическая энергия молекул газа
Многочисленными опытами было установлено, что средняя кинетическая энергия молекул газа в поступательном движении при заданной температуре одна и та же, и не зависит от рода газа. Кроме того, было установлено также, что при нагревании газа на 1 оС СКЭ увеличивается на одно и то же самое значение. Сказать точнее, это значение равно: ΔЕк = 2,07 х 10-23Дж/оС. Для того чтобы вычислить, чему равна средняя кинетическая энергия молекул газа в поступательном движении, необходимо, помимо этой относительной величины, знать еще хотя бы одно абсолютное значение энергии поступательного движения. В физике достаточно точно определены эти значения для широкого спектра температур. К примеру, при температуре t = 500 оС кинетическая энергия поступательного движения молекулы Ек = 1600 х 10-23Дж. Зная 2 величины (ΔЕк и Ек), мы можем как вычислить энергию поступательного движения молекул при заданной температуре, так и решить обратную задачу – определить температуру по заданным значениям энергии.
Напоследок можно сделать вывод, что средняя кинетическая энергия молекул, формула которой приведена выше, зависит только от абсолютной температуры (причем для любого агрегатного состояния веществ).
Закон сохранения полной механической энергии
Изучение движения тел под действием силы тяжести и сил упругости показало, что существует некая физическая величина, которую называют потенциальной энергией Еп; она зависит от координат тела, а ее изменение приравнивается ИКЭ, которая взята с противоположным знаком: ΔЕп = –ΔЕк. Итак, сумма изменений КЭ и ПЭ тела, которые взаимодействуют с гравитационными силами и силами упругости, равна 0: ΔЕп + ΔЕк = 0. Силы, которые зависят только от координат тела, называют консервативными. Силы притяжения и упругости являются консервативными силами. Сумма кинетической и потенциальной энергий тела является полной механической энергией: Еп + Ек = Е.

Этот факт, который был доказан наиболее точными экспериментами,
называют законом сохранения механической энергии. Если тела взаимодействуют силами, которые зависят от скорости относительного движения, механическая энергия в системе взаимодействующих тел не сохраняется. Примером сил такого типа, которые называются неконсервативными, являются силы трения. Если на тело действуют силы трения, то для их преодоления необходимо затратить энергию, то есть ее часть используется на выполнение работы против сил трения. Однако нарушение закона сохранения энергии здесь только мнимое, потому что он является отдельным случаем общего закона сохранения и преобразования энергии. Энергия тел никогда не исчезает и не появляется вновь: она лишь преобразуется из одного вида в другой. Этот закон природы очень важен, он выполняется повсюду. Его еще иногда называют общим законом сохранения и преобразования энергии.
Связь между внутренней энергией тела, кинетической и потенциальной энергиями
Внутренняя энергия (U) тела – это его полная энергия тела за вычетом КЭ тела как целого и его ПЭ во внешнем поле сил. Из этого можно сделать вывод, что внутренняя энергия состоит из КЭ хаотического движения молекул, ПЭ взаимодействия между ними и внутремолекулярной энергии. Внутренняя энергия – это однозначная функция состояния системы, что говорит о следующем: если система находится в данном состоянии, ее внутренняя энергия принимает присущие ему значения, независимо от того, что происходило ранее.
Релятивизм
Когда скорость тела близка к скорости света, кинетическую энергию находят по следующей формуле:

Кинетическая энергия тела, формула которой была написана выше, может также рассчитываться по такому принципу:

Примеры задач по нахождению кинетической энергии
1. Сравните кинетическую энергию шарика массой 9 г, летящего со скоростью 300 м/с, и человека массой 60 кг, бегущего со скоростью 18 км/час.
Итак, что нам дано: m1 = 0,009 кг; V1 = 300 м/с; m2 = 60 кг, V2 = 5 м/с.
Решение:
- Энергия кинетическая (формула): Ек = mv2 : 2.
- Имеем все данные для расчета, а поэтому найдем Ек и для человека, и для шарика.
- Ек1 = (0,009 кг х (300 м/с)2) : 2 = 405 Дж;
- Ек2 = (60 кг х (5 м/с)2) : 2= 750 Дж.
- Ек1 < Ек2.
Ответ: кинетическая энергия шарика меньше, чем человека.
2. Тело с массой 10 кг было поднято на высоту 10 м, после чего его отпустили. Какую КЭ оно будет иметь на высоте 5 м? Сопротивлением воздуха разрешается пренебречь.
Итак, что нам дано: m = 10 кг; h = 10 м; h1 = 5 м; g = 9,81 Н/кг. Ек1 – ?
Решение:
- Тело определенной массы, поднятое на некую высоту, имеет потенциальную энергию: Eп = mgh. Если тело падает, то оно на некоторой высоте h1 будет иметь пот. энергию Eп = mgh1 и кин. энергию Ек1. Чтобы была правильно найдена энергия кинетическая, формула, которая была приведена выше, не поможет, а поэтому решим задачу по нижеследующему алгоритму.
- В этом шаге используем закон сохранения энергии и запишем: Еп1 + Ек1 = Еп.
- Тогда Ек1 = Еп – Еп1 = mgh – mgh1 = mg(h-h1).
- Подставив наши значения в формулу, получим: Ек1 = 10 х 9,81(10-5) = 490,5 Дж.
Ответ: Ек1 = 490,5 Дж.
3. Маховик, имеющий массу m и радиус R, оборачивается вокруг оси, проходящей через его центр. Угловая скорость оборачивания маховика – ω. Дабы остановить маховик, к его ободу прижимают тормозную колодку, действующей на него с силой Fтрения. Сколько оборотов сделает маховик до полной остановки? Учесть, что масса маховика сосредоточена по ободу.
Итак, что нам дано: m; R; ω; Fтрения. N – ?
Решение:
- При решении задачи будем считать обороты маховика подобными оборотам тонкого однородного обруча с радиусом R и массой m, который оборачивается с угловой скоростью ω.
- Кинетическая энергия такого тела равна: Ек = (Jω2) : 2, где J = mR2.
- Маховик остановится при условии, что вся его КЭ истратится на работу по преодолению силы трения Fтрения, возникающей между тормозной колодкой и ободом: Ек = Fтрения*s, где s – это тормозной путь, который равен 2πRN.
- Следовательно, Fтрения*2πRN = (mR2ω2) : 2, откуда N = (mω2R) : (4πFтр).
Ответ: N = (mω2R) : (4πFтр).
В заключение
Энергия – это важнейшая составляющая во всех аспектах жизни, ведь без нее никакие тела не смогли бы выполнять работу, в том числе и человек. Думаем, статья вам внятно дала понять, что собой представляет энергия, а развернутое изложение всех аспектов одной из ее составляющих – кинетической энергии – поможет вам осознать многие процессы, происходящих на нашей планете. А уж о том, как найти кинетическую энергию, вы можете узнать из приведенных выше формул и примеров решения задач.
