Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.

Функция
Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Если a > 0 , прямая будет проходить через I и III координатные четверти.
b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.
b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Парабола
Графиком функции y = a x 2 + b x + c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a , b , c :
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a > 0 , ветки параболы направлены вверх.
- Если a < 0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти x в – координату вершины параболы.
x в = − b 2 a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D > 0 – две точки пересечения.
- Если D = 0 – одна точка пересечения.
- Если D < 0 – нет точек пересечения.




Гипербола
Графиком функции y = k x является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k < 0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .


Квадратный корень
Функция y = x имеет следующий график:

Возрастающие/убывающие функции
Функция y = f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:

Функция y = f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Скачать домашнее задание к уроку 5.
Исследование функции и построение графика
На этой странице мы постарались собрать для вас наиболее полную информацию об исследовании функции. Больше не надо гуглить! Просто читайте, изучайте, скачивайте, переходите по отобранным ссылкам.
Что будет дальше?
Исследование функции и построение графика
Общая схема исследования
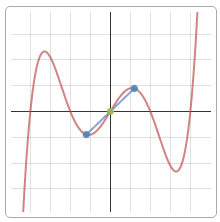
Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят график онлайн для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены “горбы” выпуклости, где не определены значения и т.п.
А уже на основании этих “особенностей” и строится макет графика – картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).
Начнем, конечно же, с плана. Исследование функции – объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.
Алгоритм
- Найти область определения. Выделить особые точки (точки разрыва).
- Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
- Найти точки пересечения с осями координат.
- Установить, является ли функция чётной или нечётной.
- Определить, является ли функция периодической или нет (только для тригонометрических функций).
- Найти точки экстремума и интервалы монотонности.
- Найти точки перегиба и интервалы выпуклости-вогнутости.
- Найти наклонные асимптоты. Исследовать поведение на бесконечности.
- Выбрать дополнительные точки и вычислить их координаты.
- Построить график и асимптоты.
В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.
Схема исследования в формате pdf: скачать.
Полный пример решения онлайн
Полезная страница? Сохрани или расскажи друзьям
Провести полное исследование и построить график функции
$$
y(x)=frac{x^2+8}{1-x}.
$$
1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, quad Rightarrow quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-infty; 1) cup (1;+infty).
$$
2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:
![]()
Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ – вертикальная асимптота.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:
![]()
Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.
Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:
![]()
Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.
Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x in (-infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x in (1; +infty)$ функция $ylt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).
4) Функция не является ни четной, ни нечетной, так как:
![]()
5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.
6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:
![]()
![]()
Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):
![]()
Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:
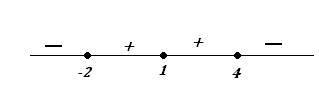
При $x in (-infty; -2), (4;+infty)$ производная $y’ lt 0$, поэтому функция убывает на данных промежутках.
При $x in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.
При этом $x=-2$ – точка локального минимума (функция убывает, а потом возрастает), $x=4$ – точка локального максимума (функция возрастает, а потом убывает).
Найдем значения функции в этих точках:
![]()
![]()
Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.
7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:
![]()
![]()
![]()
Приравняем вторую производную к нулю:
![]()
Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x in (-infty; 1)$ выполняется $y” gt 0$, то есть функция вогнутая, когда $x in (1;+infty)$ выполняется $y” lt 0$, то есть функция выпуклая.
8) Исследуем поведение функции на бесконечности, то есть при ![]() .
.
![]()
Так как пределы бесконечны, горизонтальных асимптот нет.
Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:
![]()
![]()
Получили, у что функции есть одна наклонная асимптота $y=-x-1$.
9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
$$
y(-5)=5.5; quad y(2)=-12; quad y(7)=-9.5.
$$
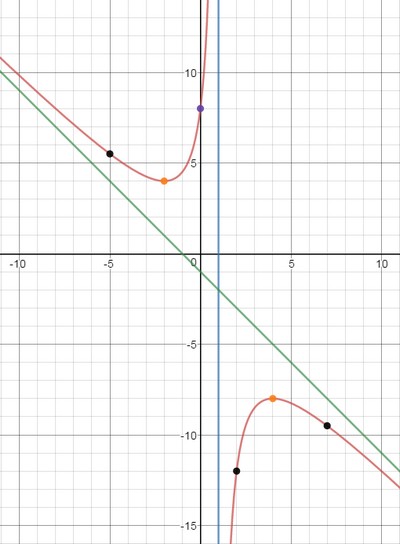
10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):
Примеры решений по исследованию функции
Разные функции (многочлены, логарифмы, дроби) имеют свои особенности при исследовании (разрывы, асимптоты, количество экстремумов, ограниченная область определения), поэтому здесь мы пострались собрать примеры из контрольных на исследование функций наиболее часто встречающихся типов. Удачи в изучении!
Задача 1. Исследовать функцию методами дифференциального исчисления и построить график.
$$y=frac{e^x}{x}.$$
Задача 2. Исследовать функцию и построить ее график.
$$y=-frac{1}{4}(x^3-3x^2+4).$$
Задача 3. Исследовать функцию с помощью производной и построить график.
$$y=ln frac{x+1}{x+2}.$$
Задача 4. Провести полное исследование функции и построить график.
$$y=frac{x}{sqrt{x^2+x}}.$$
Задача 5. Исследовать функцию методом дифференциального исчисления и построить график.
$$y=frac{x^3-1}{4x^2}.$$
Задача 6. Исследовать функцию на экстремумы, монотонность, выпуклость и построить график.
$$y=frac{x^3}{x^2-1}.$$
Поможем с исследованием функции: быстро, подробно
Задача 7. Проведите исследование функции с построением графика.
$$y=frac{x^3}{2(x+5)^2}.$$
Задача 8. Построить график функции $y=y(x)$, заданной параметрически
$$x=frac{t^2}{t+1}, y=frac{1}{t}-frac{t^3}{3}.$$
Задача 9. Исследовать функцию и построить ее график $r=1+tg phi$.
Задача 10. Исследовать функцию и построить ее график $(x^2+y^2)^3=4x^2y^2$.
Задача 11. Провести полное исследование периодической функции
$y = cos 3x – 2 sin 6x$ и построить её график.
Задача 12. Провести полное исследование и построить график функции $y=f(x)$ с помощью Excel. Найти наибольшее и наименьшее значения функции на отрезке $[-3; -1]$.
$$y=frac{4-x^3}{x^2}.$$
Задача 13. Провести полное исследование и построить график функции.
$$f(x)=frac{x}{2}-arccosfrac{2x}{1+x^2}.$$
Еще примеры исследования функции (контрольные работы)
Как построить график онлайн?
Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).
Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?
Графический калькулятор Desmos
Desmos.com
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:
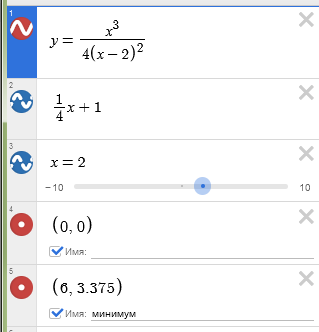
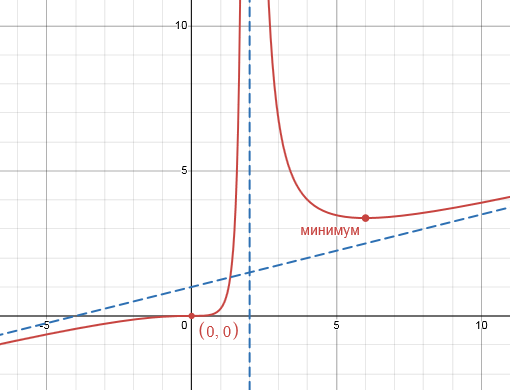
При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.
Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!
Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):
Сайт для построения графиков y(x).ru
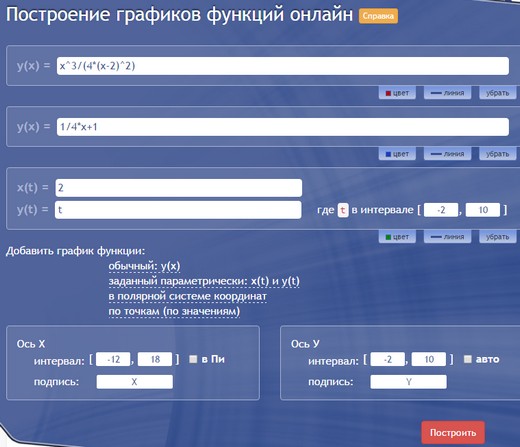
y(x).ru
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:
И такой график получается в итоге:
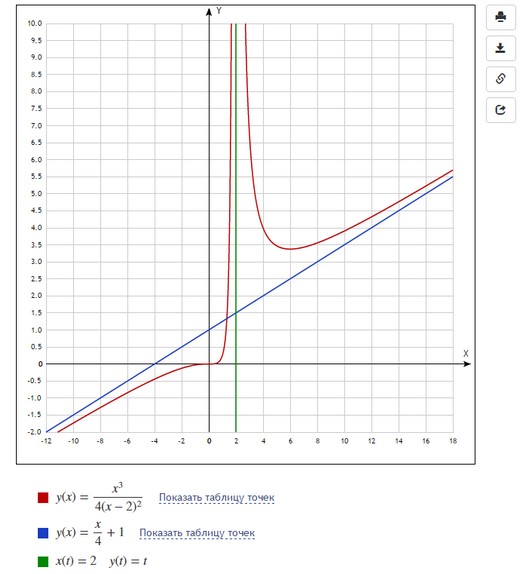
Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).
Другие сайты
Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:
- ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
- mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
- easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
- grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет
Больше знаний: теория и практика
Еще немного ссылок для тех, кто хочет углубиться в тему. Первая ссылка на теоретический материал, где вы найдете и подробные примеры, и отсылки к предыдущим разделам теории (а исследовать функцию не зная пределов, производных, понятия непрерывности и т.п. нельзя) с не менее подробным объяснением. Все это сдобрено порцией юмора, отчего очень “съедобно” даже для полного чайника в математике: Исследование функций от Александра Емелина.
Вторая ссылка практическая, для тех, кто хочет научиться строить красивые графики в Desmos.com (см. выше описание): Полная инструкция по работе с Desmos. Эта инструкция довольно старая, с тех пор интерфейс сайта поменялся в лучшую сторону, но основы остались неизменными и помогут быстро разобраться с важными функциями сервиса.
Официальные инструкции, примеры и видео-инструкции на английском можно найти тут: Learn Desmos.
Решебник
Срочно нужна готовая задача? Более сотни разных функций с полным исследованием уже ждут вас. Подробное решение, быстрая оплата по SMS и низкая цена – около 50 рублей. Может, и ваша задача уже готова? Проверьте!
Полезные видео-ролики
Вебинар по работе с Desmos.com. Это уже полноценный обзор функций сайта, на целых 36 минут. К сожалению, он на английском языке, но базовых знаний языка и внимательности достаточно, чтобы понять большую часть.
Классный старый научно-популярный фильм “Математика. Функции и графики”. Объяснения на пальцах в прямом смысле слова самых основ.
Закажите полное исследование функции в МатБюро
Понравилось? Добавьте в закладки
Для многих учащихся, тема “Графики” и все что с ними связано, очень сложна и почти все как один говорит, что не понимает их. А на самом деле, все легко. Достаточно уметь выполнять простые арифметические действия. Если сравнивать задания из второй части ОГЭ по математике, то решить текстовую задачу, чаще бывает сложнее, чем построить график и ответить на вопрос. Сложность заключается в том, что задача требует размышления, правильного прочтения текста, и составление математической модели. При выполнения заданий на построение графиков, нужно всего лишь следовать алгоритму построения. Что можно описать конкретными шагами, то всегда легко.
Разберем построение следующего графика функции и определим шаги для выполнения таких заданий.
Напишем алгоритм построения:
1) Находим ОДЗ функции, т.е. находим такие значения, при которых знаменатель дроби может превратится в ноль.
Как видим, функция не может принимать значения при х=0, х=2/9 и х=-2/9.
2) Упрощаем дробное выражение:
В итоге мы получаем простую функцию, которая называется – обратная пропорциональная зависимость (гипербола).
3) Применяем свойство модуля.
Когда мы выполнили раскрытие модуля, содержащего в функции, и нашли координаты точек для построения графика, можем уже построить график на координатной плоскости.
4) Строим график функции
Если на графике не будут указаны выколотые точки (черные пустые точки на графике), то график будет считаться не верным
5) Отвечаем на вопрос задания, находим параметр по графику. В данном задании нужно было ответить на следующий вопрос:
Поскольку график функции y=kx, это график прямой пропорциональности, то он проходит через координату (0;0). Что бы прямая y=kx не имела с нашим графиком общих точек, то она должна проходить через выколотые точки, как это показано на рисунке красными линиями
Осталось найти значения параметра K. Для этого, в прямую y=kx подставим координаты выколотых точек (2/9; -9/2) и (-2/9; -9/2).
В ответе получаем три значения параметра К. Третье значение К=0 соответствует прямой которая совпадает с осью Ох.
Итак, в алгоритме у нас получилось 5 шагов:
1) Находим ОДЗ функции.
2) Упрощаем дробное выражение функции
3)Раскрываем модуль по его свойству и находи точки для построения графика.
4) Строим график по точкам, которые нашли в пункте 3.
5) Находим параметр.
Так же разбор этого задания, вы можете посмотреть ниже:
Спасибо, что прочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Download Article
Download Article
A graph of a function is a visual representation of a function’s behavior on an x-y plane. Graphs help us understand different aspects of the function, which would be difficult to understand by just looking at the function itself. You can graph thousands of equations, and there are different formulas for each one. That said, there are always ways to graph a function if you forget the exact steps for the specific type of function.
-

1
-

2
Use the constant to mark your y-intercept. The y-intercept is where the function crosses the y-axis on your graph. In other words, it is the point where
. So, to find it, you simply set x to zero, leaving the constant in the equation alone. For the earlier example,
, your y-intercept is 5, or the point (0,5). On your graph, mark this spot with a dot.[2]
Advertisement
-

3
Find the slope of your line with the number right before the variable. In your example,
, the slope is “2.” That is because 2 is right before the variable in the equation, the “x.” Slope is how steep a line is, or how high the line goes before going to the right or left. Bigger slopes mean steeper lines.
-

4
Break the slope into a fraction. Slope is about steepness, and steepness is simply the difference between movement up and down and movement left and right. Slope is a fraction of rise over run. How much does the line “rise” (go up) before it “runs” (goes to the side)? For the example, the slope of “2” could be read as
.[3]
- If the slope is negative, that means the line goes down as you move to the right.
-

5
Starting at your y-intercept, follow your “rise” and “run” to graph more points. Once you know your slope, use it to plot out your linear function. Start at your y-intercept, here (0,5), and then move up 2, over 1. Mark this point (1,7) as well. Find 1-2 more points to create an outline of your line.[4]
-

6
Use a ruler to connect your dots and graph your linear function. To prevent mistakes or rough graphs, find and connect at least three separate points, though two will do in a pinch. This is the graph of your linear equation![5]
Advertisement
-

1
Determine the function. Get the function of the form like f(x), where y would represent the range, x would represent the domain, and f would represent the function. As an example, we’ll use y = x+2, where f(x) = x+2.[6]
-

2
Draw two lines in a + shape on a piece of paper. The horizontal line is your x axis. The vertical line is your y axis.
-

3
Number your graph. Mark both the x axis and the y axis with equally-spaced numbers. For the x axis, the numbers are positive on the right side and negative on the left side. For the y axis, the numbers are positive on the upper side and negative on the lower side.[7]
-

4
Calculate a y value for 2-3 x values. Take your function f(x) = x+2. Calculate a few values for y by putting the corresponding values for x visible on the axis into the function. For more complicated equations, you may want to simplify the function by getting one variable isolated first.[8]
- -1: -1 + 2 = 1
- 0: 0 +2 = 2
- 1: 1 + 2 = 3
-

5
Draw the graph point for each pair. Simply sketch imaginary lines vertically for each x axis value and horizontally for each y axis value. The point where these lines intersect is a graph point.[9]
-

6
Remove the imaginary lines. Once you have drawn all the graph points, you can erase the imaginary lines. Note: the graph of f(x) = x would be a line parallel to this one passing through the origin (0,0), but f(x) = x+2 is shifted two units up (along the y-axis) on the grid because of the +2 in the equation.[10]
Advertisement
-

1
-

2
Find any zeros first. Zeros, also called x-intercepts, are the points where the graph crosses the horizontal line on the graph. While not all graphs even have zeros, most do, and it is the first step you should take to get everything on track. To find zeros, simply the entire function to zero and solve. For example:
-

3
Find and mark any horizontal asymptotes, or places where it is impossible for the function to go, with a dotted line. This is usually points where the graph does not exist, like where you are dividing by zero. If your equation has a variable in a fraction, like
, start by setting the bottom of the fraction to zero. Any places where it equals zero can be dotted off (in this example, a dotted line at x=2 and x=-2), since you cannot ever divided by zero. Fractions, however, are not the only places you can find asymptotes. Usually, all you need is some common sense:
-

4
Plug in and graph several points. Simply pick a few values for x and solve the function. Then graph the points on your graph. The more complicated the graph, the more points you’ll need. In general, -1, 0, and 1 are the easiest points to get, though you’ll want 2-3 more on either side of zero to get a good graph.[13]
- For the equation
, you might plug in -1,0,1, -2, 2, -10, and 10. This gives you a nice range of numbers to compare.
- Be smart selecting numbers. In the example, you’ll quickly realize that having a negative sign doesn’t matter — you can stop testing -10, for example, because it will be the same as 10.
- For the equation
-

5
Map the end behavior of the function to see what happens when it is really huge. This gives you an idea of the general direction of a function, usually as a vertical asymptote. For example — you know that eventually,
gets really, really big. Just one additional “x” (one million vs. one million and one) makes y much bigger. There are a few ways to test end behavior, including:
-

6
Connect the dots, avoiding asymptotic and following the end behavior to graph an estimate of the function. Once you have 5-6 points, asymptotes, and a general idea of end behavior, plug it all in to get an estimated version of the graph.[15]
-

7
Get perfect graphs using a graphing calculator. Graphing calculators are powerful pocket computers that can give exact graphs for any equation. They allow you to search exact points, find slope lines, and visualize difficult equations with ease. Simply input the exact equation into the graphing section (usually a button labeled “F(x) = “) and hit graph to see your function at work.
Advertisement
Add New Question
-
Question
How do I sketch a graph of a square root function?

The process is the same as shown in the article above except, of course, it involves calculating (or estimating) the square roots of certain values.
-
Question
How do I graph function y = -2 sin(2/3x)?

Choose a value for x. Find 2/3 of that value. Then use a trigonometry table to find the sine of that last value. Then multiply the sine by -2. That gives you the value of y that corresponds to the chosen value of x. Do this again for other x values, and you will then have several x-y pairs to form the graph of the function.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
If you are ever completely lost with what to do, start plugging in points. You could technically graph the entire function like this if you tried infinite combinations of numbers.
-
Graphing calculators are a great way to practice. Try to graph by hand, then use the calculator to get a perfect image of the graph and see how you did.
Advertisement
References
About This Article
Article SummaryX
To graph a function, start by plugging in 0 for x and then solving the equation to find y. Then, mark that spot on the y-axis with a dot. Next, find the slope of the line, which is the number that’s right before the variable. Once you know your slope, write it as a fraction over 1 and then use the rise over run to plot the rest of the points from the spot you marked on the y-axis. Finally, use a ruler to draw a line connecting all of the points on your graph. To learn how to graph complicated functions by hand, scroll down!
Did this summary help you?
Thanks to all authors for creating a page that has been read 138,399 times.
Did this article help you?
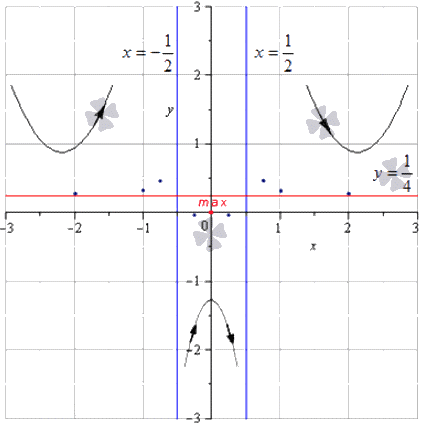
Если в задаче необходимо произвести полное исследование функции f(x)=x24x2-1 с построением его графика, тогда рассмотрим этот принцип подробно.
Для решения задачи данного типа следует использовать свойства и графики основных элементарных функций. Алгоритм исследования включает в себя шаги:
Нахождение области определения
Так как исследования проводятся на области определения функции, необходимо начинать с этого шага.
Заданный пример предполагает нахождение нулей знаменателя для того, чтобы исключить их из ОДЗ.
4×2-1=0x=±12⇒x∈-∞; -12∪-12; 12∪12; +∞
В результате можно получить корни, логарифмы, и так далее. Тогда ОДЗ можно искать для корня четной степени типа g(x)4 по неравенству g(x)≥0, для логарифма logag(x) по неравенству g(x)>0.
Исследование границ ОДЗ и нахождение вертикальных асимптот
На границах функции имеются вертикальные асимптоты, когда односторонние пределы в таких точках бесконечны.
Для примера рассмотрим приграничные точки, равные x=±12.
Тогда необходимо проводить исследование функции для нахождения одностороннего предела. Тогда получаем, что: limx→-12-0f(x)=limx→-12-0x24x2-1==limx→-12-0x2(2x-1)(2x+1)=14(-2)·-0=+∞limx→-12+0f(x)=limx→-12+0x24x-1==limx→-12+0x2(2x-1)(2x+1)=14(-2)·(+0)=-∞limx→12-0f(x)=limx→12-0x24x2-1==limx→12-0x2(2x-1)(2x+1)=14(-0)·2=-∞limx→12-0f(x)=limx→12-0x24x2-1==limx→12-0x2(2x-1)(2x+1)=14(+0)·2=+∞
Отсюда видно, что односторонние пределы являются бесконечными, значит прямые x=±12 – вертикальные асимптоты графика.
Исследование функции и на четность или нечетность
Когда выполняется условие y(-x)=y(x), функция считается четной. Это говорит о том, что график располагается симметрично относительно Оу. Когда выполняется условие y(-x)=-y(x), функция считается нечетной. Значит, что симметрия идет относительно начала координат. При невыполнении хотя бы одного неравенства, получаем функцию общего вида.
Выполнение равенства y(-x)=y(x) говорит о том, что функция четная. При построении необходимо учесть, что будет симметричность относительно Оу.
Нахождение возрастания и убывания, точек экстремума
Для решения неравенства применяются промежутки возрастания и убывания с условиями f'(x)≥0 и f'(x)≤0 соответственно.
Стационарные точки – это такие точки, которые обращают производную в ноль.
Критические точки – это внутренние точки из области определения, где производная функции равняется нулю или не существует.
При решении необходимо учитывать следующие замечания:
- при имеющихся промежутках возрастания и убывания неравенства вида f'(x)>0 критические точки в решение не включаются;
- точки, в которых функция определена без конечной производной , необходимо включать в промежутки возрастания и убывания (к примеру, y=x3, где точка х=0 делает функцию определенной, производная имеет значение бесконечности в этой точке, y’=13·x23, y'(0)=10=∞, х=0 включается в промежуток возрастания);
- во избежание разногласий рекомендовано пользоваться математической литературой, которая рекомендована министерством образования.
Включение критических точек в промежутки возрастания и убывания в том случае, если они удовлетворяют области определения функции.
Для определения промежутков возрастания и убывания функции необходимо найти:
- производную;
- критические точки;
- разбить область определения при помощи критических точек на интервалы;
- определить знак производной на каждом из промежутков, где + является возрастанием, а – является убыванием.
Найти производную на области определения f'(x)=x2′(4×2-1)-x24x2-1′(4×2-1)2=-2x(4×2-1)2.
Решение
Для решения нужно:
- найти стационарные точки, данный пример располагает х=0;
- найти нули знаменателя, пример принимает значение ноль при x=±12.
Выставляем точки на числовой оси для определения производной на каждом промежутке. Для этого достаточно взять любую точку из промежутка и произвести вычисление. При положительном результате на графике изображаем +, что означает возрастание функции, а – означает ее убывание.
Например, f'(-1)=-2·(-1)4-12-12=29>0, значит, первый интервал слева имеет знак +. Рассмотрим на числовой прямой.

Ответ:
- происходит возрастание функции на промежутке -∞; -12 и (-12; 0];
- происходит убывание на промежутке [0; 12) и 12; +∞.
На схеме при помощи + и – изображается положительность и отрицательность функции, а стрелочки – убывание и возрастание.
Точки экстремума функции – точки, где функция определена и через которые производная меняет знак.
Если рассмотреть пример, где х=0, тогда значение функции в ней равняется f(0)=024·02-1=0. При перемене знака производной с + на – и прохождении через точку х=0, тогда точка с координатами (0; 0) считается точкой максимума. При перемене знака с – на + получаем точку минимума.
Нахождение промежутков выпуклости и вогнутости функции и точек перегиба
Выпуклость и вогнутость определяется при решении неравенств вида f”(x)≥0 и f”(x)≤0. Реже используют название выпуклость вниз вместо вогнутости, а выпуклость вверх вместо выпуклости.
Для определения промежутков вогнутости и выпуклости необходимо:
- найти вторую производную;
- найти нули функции второй производной;
- разбить область определения появившимися точками на интервалы;
- определить знак промежутка.
Найти вторую производную из области определения.
Решение
f”(x)=-2x(4×2-1)2’==(-2x)'(4×2-1)2–2x4x2-12′(4×2-1)4=24×2+2(4×2-1)3
Находим нули числителя и знаменателя, где на примере нашего примера имеем, что нули знаменателя x=±12
Теперь необходимо нанести точки на числовую ось и определить знак второй производной из каждого промежутка. Получим, что

Ответ:
- функция является выпуклой из промежутка -12; 12;
- функция является вогнутой из промежутков -∞; -12 и 12; +∞.
Точка перегиба – это точка вида x0; f(x0). Когда в ней имеется касательная к графику функции, то при ее прохождении через x0 функция изменяет знак на противоположный.
Иначе говоря, это такая точка, через которую проходит вторая производная и меняет знак, а в самих точках равняется нулю или не существует. Все точки считаются областью определения функции.
В примере было видно, что точки перегиба отсутствуют, так как вторая производная изменяет знак во время прохождения через точки x=±12. Они , в свою очередь, в область определения не входят.
Нахождение горизонтальных и наклонных асимптот
При определении функции на бесконечности нужно искать горизонтальные и наклонные асимптоты.
Наклонные асимптоты изображаются при помощи прямых, заданных уравнением y=kx+b, где k=limx→∞f(x)x и b=limx→∞f(x)-kx.
При k=0 и b, не равному бесконечности, получаем, что наклонная асимптота становится горизонтальной.
Иначе говоря, асимптотами считают линии, к которым приближается график функции на бесконечности. Это способствует быстрому построению графика функции.
Если асимптоты отсутствуют, но функция определяется на обеих бесконечностях, необходимо посчитать предел функции на этих бесконечностях, чтобы понять, как себя будет вести график функции.
На примере рассмотрим, что
k=limx→∞f(x)x=limx→∞x24x2-1x=0b=limx→∞(f(x)-kx)=limx→∞x24x2-1=14⇒y=14
является горизонтальной асимптотой. После исследования функции можно приступать к ее построению.
Вычисление значения функции в промежуточных точках
Чтобы построение графика было наиболее точным, рекомендовано находить несколько значений функции в промежуточных точках.
Из рассмотренного нами примера необходимо найти значения функции в точках х=-2 , х=-1 , х=-34 ,х=-14. Так как функция четная, получим, что значения совпадут со значениями в этих точках, то есть получим х=2 , х=1 , х=34 , х=14.
Запишем и решим:
f(-2)=f(2)=224·22-1=415≈0,27f(-1)-f(1)=124·12-1=13≈0,33f-34=f34=3424342-1=920=0,45f-14=f14=1424·142-1=-112≈-0,08
Построение графика
Для определения максимумов и минимумов функции, точек перегиба, промежуточных точек необходимо строить асимптоты. Для удобного обозначения фиксируются промежутки возрастания, убывания, выпуклость, вогнутость. Рассмотрим на рисунке, изображенном ниже.
Необходимо через отмеченные точки проводить линии графика, что позволит приблизить к асимптотам, следуя стрелочкам.
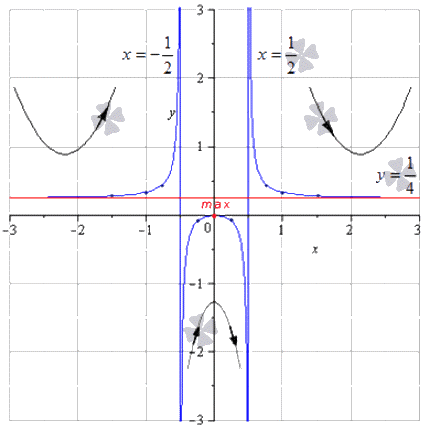
На этом заканчивается полное исследование функции. Встречаются случаи построения некоторых элементарных функций, для которых применяют геометрические преобразования.
