Как найти расстояние против течения формула

Для решения задач на движение по прямой используется одна основная формула:

где:

• Скорость (V) — расстояние, пройденное за единицу времени.
• Время (t) — время в пути.
• Расстояние (S) — пройденный путь, или расстояние.

Зная эту формулу (для расстояния), вы можете легко  вывести из неё формулу для скорости, или времени.

Если вы запомните эту формулу, то сможете решить любую задачу на движение, так как все задачи на движение по прямой — это применение данной формулы к одному или нескольким взаимосвязанным объектам.

Рассмотрим, как решать разные задачи на движение в зависимости от условий и уровня сложности.

Все задачи на движение делятся на следующие типы:

• простые задачи на скорость, время и расстояние;
• задачи на движение в разных направлениях: сближение и удаление;
• задачи на движение в одном направлении: сближение и удаление;
• решение задач на движение по реке.

Решение простых задач на движение: скорость, время и расстояние

В простых задачах на движение, как правило, есть один движущийся объект, для которого нужно найти неизвестную величину: скорость, время или расстояние. В данном случае применяется формула в ее первоначальном виде:

Задача 1. Автомобиль ехал 2ч со скоростью 85 км/ч. Определите расстояние. 
Решение: Вычислим путь по формуле: S=V × t= 2 ч * 85 км/ч = 170 км.

Задача 2. Велосипедист проехал 60 км за 5ч. Определите скорость.
Решение: Вычислим скорость велосипедиста по формуле: V = S:t = 60 км : 5 ч = 12 км/ч.

Задача 3. Мотоциклист проехал 30 км со скоростью 15км/ч. Сколько времени он затратил на этот путь? 
Решение: Вычислим время движения мотоциклиста по формуле: t = S:V = 30 км : 15 км/ч = 2 ч.

В таких задачах нужно также следить, чтобы были одинаковыми единицы измерения. Например, если расстояние измеряется в километрах, а время — в часах,  то скорость буде измеряться в км/час. Но если единицы измерения скорости — метр/час, а время дано в минутах, то в этом случае скорость и время нужно привести к одинаковым единица измерения, иначе ответ будет неверным.

Задача 4. Мотоциклист ехал 30 минут со скоростью 60 км/ч. Какое расстояние он проехал?
Решение: для того, чтобы вычислить расстояние, нужно время и скорость привести к одинаковым единицам измерения. При этом есть 2 способа:
1) Переведем время: 30 минут = 30/60 = 0,5 часа.
Найдем расстояние: 60 км/ч * 0,5 ч = 30 км.
2) Переведем скорость: 60 км/ч = 60км / 1час = 60км / 60 мин = 1км/мин.
Найдем расстояние: 1км/мин*30минут = 30 км.

Решение задач на движение в разных направлениях: сближение (встречное движение) и удаление (противоположное движение)

При встречном движении расстояние между объектами уменьшается. Объекты приближаются друг к другу со скоростью сближения.
Скорость сближения находится по формуле:

При движении в противоположных направлениях скорости объектов направлены в разные стороны. Объекты удаляются друг от друга со скоростью удаления.
Скорость удаления находится по формуле: 

При решении подобных задач лучше нарисовать схему движения, чтобы было легче решать.

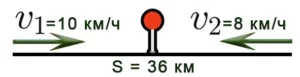
Задача 5. Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого велосипедиста 10 км/ч, второго — 8 км/ч. Через сколько часов они встретятся? 
Решение: 1) Найдем скорость сближения: V=10+8 = 18 км/ч.
2) Найдем время: t = S:V = 36 : 18 = 2 ч.

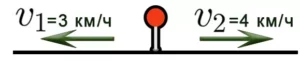
Задача 6. Два пешехода вышли одновременно из одного и того же пункта в противоположных направлениях. Скорость первого пешехода 3км/ч, второго — 4км/ч. Какое расстояние между ними будет через 30 минут?
Решение: 1) Найдем скорость удаления пешеходов: V = 3+4=7 км/час.
2) Переведем в соответствие единицы измерения: t=30 мин = 0,5 ч.
3) Найдем расстояние: S=V × t = 7 × 0,5 = 3,5 км.

Задача 7. Два автобуса выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 300 км. Через 2 часа они встретились. Найдите второго второго автобуса, если первый ехал со скоростью 70 км/ч.
Решение. 1) Нам известно расстояние и скорость, поэтому найдем скорость по формуле: V = S:t = 300:2=150км/ч. Это скорость сближения.
2) Найдем скорость второго автобуса: 150-70 = 80км/ч.

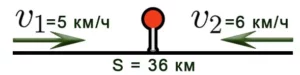
Решение задач на движение в одном направлении: сближение и удаление

Если два объекта движутся в одном направлении и один объект “догоняет” второй, то расстояние между объектами уменьшается.
Скорость сближения при таком движении определяют по формуле:

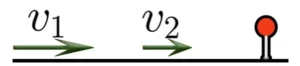
Если два объекта движутся в одном направлении и один объект “отстает” от второго, то расстояние между объектами увеличивается.
Скорость удаления при таком движении определяют по формуле:

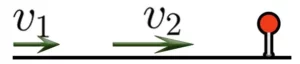
Если объект движется в стоячей воде (озере), то его скорость называют собственной скоростью объекта. То есть, скорость объекта равная собственной скорости объекта.

Заметим, что плот — это тело, у которого собственная скорость равна нулю (V=0). Значит, плот может плыть только по течению и со скоростью течения.

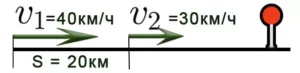
Задача 8. Расстояние между двумя автомобилями, движущимися в одном направлении, составляет 20 км. Первый автомобиль едет со скоростью 40км/ч, второй — со скоростью 30км/ч. Через сколько часов первый автомобиль догонит второй?
Решение. 1) Найдем скорость сближения автомобилей: V=40-30=10км/ч.

2) Зная расстояние (20км) и скорость сближения (10км/ч) найдем время: 20:10=2 часа.

Задача 9. Из одного населенного пункта выехали автомобиль и автобус. скорость автомобиля 70 км/ч, скорость автобуса — 50 км/ч. Какое расстояние будет между ними через 3 часа?
Решение. 1) Найдем скорость удаления : V=70-50=20км/ч.
2) Зная скорость удаления и время, найдем расстояние: S = 20*3 =60 км.

Решение задач на движение по реке

Особенностью задач на движение реке является то, что у объекта появляется дополнительная скорость — скорость течения реки. При этом возможно два варианта:

• по течению реки → скорость увеличивается;
• против течения реки → скорость уменьшается.

Таким образом, в задачах рассматривают 2 скорости: 

• Скорость собственная — Vs;
• Скорость течения реки — Vt.

Задача 9. Собственная скорость лодки составляет 12 км/ч. Скорость течения реки равна 3 км/ч. Какое расстояние проплывёт лодка через 3 часа, если она плывёт по течению реки?
Решение. 1) Найдем скорость лодки. Так как она плывет по течению реки, ее скорость увеличивается. 
V = Vs+ Vt = 12+3 =15км/ч.
2) Найдем расстояние: S=V×t = 15×3=45км.

Задача 10. Собственная скорость катера составляет 30 км/ч. Скорость течения реки равна 4 км/ч. Какое расстояние преодолеет катер через 4 часа, если он плывёт против течения реки?
Решение. 1) Найдем скорость. Так как катер плывет против течения реки, его скорость уменьшится. 
V = Vs- Vt = 30-4 =26 км/ч.
2) Найдем расстояние: S=V×t = 26 * 4 = 104 км.

Задача 10. Скорость лодки равна 10 км/ч. При этом надо успеть проплыть 25 км за 2 часа по течению реки. Какой должна быть скорость течения реки, чтобы успеть в срок? 
Решение. 1) Найдем нужную скорость: V=S:t = 25:2=12,5 км/ч.
2) Найдем скорость, которую нужно прибавить до нужно (скорость течения реки): 12,5-10=2,5км/ч.

Задача 11. Уровень ЕГЭ.
Катер прошёл по течению реки 120 км и вернулся обратно. Известно, что обратный путь занял на 1 час больше времени, а скорость катера в неподвижной воде равна 27 км/ч. Найдите скорость течения.
Решение: Пусть Vt — cкорость течения реки, тогда:
1) В одну сторону: 27+Vt  – скорость перемещения катера по течению, S=120км.
2) В обратную сторону: 27-Vt  – скорость перемещения катера против течения, S=120км.
Выразим время:
1) В одну сторону:  t=S:V = 120:(27+Vt) – время, затраченное катером на перемещение по течению,
2) В обратную сторону:  t=S:V = 120:(27-Vt) – время, затраченное катером на перемещение против течения.
Так как время перемещения против течения на час больше, чем время по течению, то:
120:(27+Vt) +1 = 120:(27-Vt).
Далее решаем уравнение и получаем ответ 3 км/ч.

Больше задач на движение Ваш ребёнок может решить, скачав программы:

Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.

Полезные советы для решения задач на движения

• В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который  будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
• Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.
• При решении задач на движение рисуйте картинки. Особенно, когда текст задачи большой и сразу в голове не укладывается. Чаще всего это нужно делать в задачах, где кто-то кого-то догоняет, встречается, или перемещается между пунктами А и В туда и обратно. На картинке сразу видно, какие отрезки пути можно просчитать. Картинка облегчает составление математической модели.

Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.

Через уравнение.

S – пройденный путь, растояние, которое прошла, например, лодка. (км)

t – время, за которое она прошла расстояние S. (часов, минут)

V – собственная её скорость (км/ч, м/ч)

Такие задачи решаются далее: если известны: (под формулы подставляем числа)

t и V, то перемножаем – t * V, получаем S.

t и S, то расстояние делим время – S : t, получаем V

S и V, также – S : V, получаем t

Также если в задаче указана V (её ищем)

по течению, то V собственная + V по течению

против течения, то V собств. – V прот. теч.

Тогда формулы звучат так: если известны:

t и V, то t * (V с. +/- V) = S

t и S, то S : t = V с. +/- V

V и S, то S : (V c. +/- V) = t

Теперь ещё раз:

V c. – собственная скорость

V c. + V – скорость + скорость по теч.

V c. – V – скорость + скорость прот. теч.

Ну так чтоли… Плохой из меня учитель(((

Решение задач с помощью уравнений.
Движение по воде.

ФОРМУЛЫ.

V
соб. – собственная скорость (скорость в стоячей
воде)

Vтеч.р.
– скорость течения реки

Vпо
теч. = V соб. + Vтеч.р.

Vпр.
теч. = V соб. – Vтеч.р.

Задача
1. Лодка
плыла 1,4
ч по течению реки и 1,7 ч против течения. Путь,
который проплыла лодка по течению, оказался на 2,2 км меньше пути, который она
проплыла против течения. Найдите скорость
течения реки, если скорость лодки в стоячей воде 28 км/ч.

	V (км/ч)	t (ч)	S (км)
По течению	28 + x	1,4	1,4(28 + x)
Против течения	28 – x	1,7	1,7(28 – x)

V соб. = 28 км/ч

Vтеч.р. = x км/ч

1)     
1,7(28 – x) – 1,4(28 + x) = 2,2

47,6 – 1,7x – 39,2  – 1,4x = 2,2

-1,7x – 1,4x= 2,2 – 47,6 +39,2

-3,1x = -6,2

x = -6,2 : (-3,1)

x = 2

2)     
2 км/ч – Vтеч.р.

Ответ. 2

Задача
2. Расстояние между двумя пунктами катер прошёл по течению реки за 7
часов, а против течения за 8 часов. Найдите расстояние
между этими пунктами, если скорость течение реки 3,5 км/ч

	V (км/ч)	t (ч)	S (км)
По течению	x + 3,5	7	7(x + 3,5)
Против течения	x – 3,5	8	8(x – 3,5)

V соб. = x км/ч

Vтеч.р. = 3,5 км/ч

1)     
7(x + 3,5) = 8(x – 3,5)

7x + 24,5 = 8x – 28

7x – 8x= -28 – 24,5

-x = -52,5

x = 52,5

2)   52,5 км/ч – V
соб.

3)   7(52,5 + 3,5) = 7 · 56 = 392 км –
расстояние

Ответ. 392

РЕШИ ЗАДАЧИ ПО ОБРАЗЦУ.

1)      Туристы на байдарке плыли
2,4 ч по течению реки и 1,8 ч против течения. Путь, который байдарка проплыла
по течению, был на 14,1 км больше, чем путь, пройденный против течения. Найдите
скорость байдарки в стоячей воде, если скорость течения 2,5 км/ч.

2)      Расстояние между двумя
пунктами катер прошел по течению реки за 5 часов, а против течения – за 6
часов. Найдите расстояние между этими пунктами, если скорость течения реки 3
км/ч.

3)      Катер
проходит по течению реки за 5 ч такое же расстояние, как за 6 ч 15 мин против
течения. Найдите скорость катера в стоячей воде, если скорость течения реки
равна 2,4 км/ч.

4)      Моторная
лодка прошла 7 ч по течению реки и 6 ч против течения. Определите скорость
течения реки, если скорость лодки в стоячей воде 10
км/ч и за все путешествие лодка прошла 132
км.

Давайте сегодня рассмотрим движение по реке и связанные с этим задачи.

Движение по реке отличается тем, что на движущийся объект воздействует еще и сила течения реки. В реальной жизни и вне реки на нас воздействует ветер, сопротивление воздуха и прочие вещи, но в математике мы этим пренебрегаем.

В задачах на движение по реке важно учитывать направление движения – по течению и против. Если объект в задаче движется по течению, то к его собственной скорости, иногда ее еще называют скоростью в стоячей воде, скоростью в пруду, добавляется скорость реки (течения). Если объект плывет против течения, то скорость реки его сносит назад, поэтому его собственная скорость уменьшается как раз на скорость течения.

Расстояние от пункта A до пункта B по реке равно 120 км. Сколько времени потратит моторная лодка на путь от пункта A до B, если её собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?

Рассмотрите два варианта: 1) лодка движется по течению реки; 2) лодка движется против течения реки.

Решение: Если моторная лодка будет двигаться по течению реки, то её скорость будет равна сумме собственной скорости со скоростью течения реки:

27 + 3 = 30 (км/ч)

Значит расстояние между пунктами лодка преодолеет за:

120 : 30 = 4 (ч)

Если лодка будет двигаться против течения реки, то её скорость будет равна разности собственной скорости и скорости течения реки:

27 – 3 = 24 (км/ч)

Значит, чтобы узнать сколько времени потратит лодка на путь от пункта A до пункта B, надо расстояние разделить на скорость:

120 : 24 = 5 (ч)

Ответ:
1) При движении по течению реки моторная лодка потратит 4 часа на путь от пункта A до пункта B.
2) При движении против течения реки моторная лодка потратит 5 часов на путь от пункта A до пункта B.