Как найти математическое ожидание?
Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание – это первый начальный момент заданной СВ.
Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины – срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).
Нужна помощь? Решаем теорию вероятностей на отлично
Полезная страница? Сохрани или расскажи друзьям
Формула среднего случайной величины
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Пример нахождения математического ожидания
Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.
Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.
Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.
Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$
Другие задачи с решениями по ТВ
Подробно решим ваши задачи по теории вероятностей
Вычисление математического ожидания онлайн
Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$.
Видео. Полезные ссылки
Видеоролики: что такое среднее (математическое ожидание)
Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Спасибо за ваши закладки и рекомендации
Полезные ссылки
А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по терверу. Для закрепления материала – еще примеры решений по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Содержание:
Системы случайных величин или случайные векторы:
При изучении случайных явлений в зависимости от их сложности приходится использовать два, три и большее число случайных величин.
Например, 1) попадание снаряда в цель определяется не одной, а двумя случайными величинами: абсциссой и ординатой точки попадания, 2) случайное отклонение точки разрыва снаряда при дистанционной стрельбе определяется комплексом трех случайных величин: тремя координатами этой точки.
Определение 57. Совместное рассмотрение двух или нескольких случайных величин приводит к системе случайных величин или к случайному вектору.
(X, Y) – двумерный случайный вектор или система двух СВ.
Изучать систему – значит изучать сами случайные величины, ее составляющие; связи и зависимости между ними.
Геометрическая интерпретация системы: 1) систему двух случайных величин (X, У) рассматривают как случайную точку на плоскости (Охх) или как случайный вектор с составляющими X, У; 2) систему трех случайных величин (X, У, Z) рассматривают как случайную точку на плоскости (Оxyz) или как случайный вектор с составляющими X, У; Z и т.д.
В зависимости от типа случайных величин, образующих систему, могут быть дискретные, непрерывные и смешанные системы.
Определение 58. Двумерный случайный вектор (X, У) называется вектором дискретного типа (СВДТ), если множество его возможных значений не более, чем счетно.
Определение 59. (первое определение) Двумерный случайный вектор (X, У) называется вектором непрерывного типа (СВНТ), если множество его возможных значений непрерывно заполняет некоторую область плоскости (Оху)-
Определение 60. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Законы распределения СВДТ и СВНТ
Таблица распределения – закон распределения СВДТ:
Рассмотрим двумерный случайный вектор (X, У), где X и У – дискретные случайные величины с возможными значениями 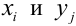

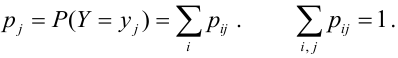
Пример:
Из цифр 1, 2, 3, 4, 6, 8, 9 наудачу отбирают две цифры. Х – число четных цифр в выборке, Y – число нечетных. Описать закон распределения.
Решение.
X (четные) – 2, 4, 6, 8; Y ( нечетные) – 1, 3, 9. Следовательно, возможные значения X 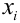 :
: 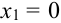 (нет четных цифр),
(нет четных цифр), 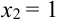 (одна цифра четная),
(одна цифра четная), 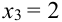 (обе цифры четные); возможные значения Y
(обе цифры четные); возможные значения Y 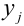 :
: 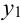
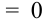 (нет нечетных цифр),
(нет нечетных цифр), 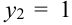 (одна цифра нечетная),
(одна цифра нечетная), 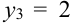 (обе цифры нечетные). Найдем вероятности.
(обе цифры нечетные). Найдем вероятности.
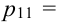 (0 четных, 0 нечетных) = 0, не выбираем ни одной цифры, а по условию выбираем две цифры. Аналогично,
(0 четных, 0 нечетных) = 0, не выбираем ни одной цифры, а по условию выбираем две цифры. Аналогично, 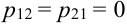 (выбираем всего одну цифру либо нечетную, либо четную),
(выбираем всего одну цифру либо нечетную, либо четную), 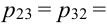
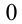 (выбираем три цифры вместо двух по условию),
(выбираем три цифры вместо двух по условию), 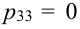 (выбираем четыре цифры вместо двух по условию).
(выбираем четыре цифры вместо двух по условию).
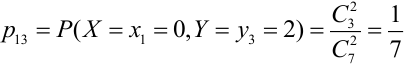 — (обе цифры нечетные),
— (обе цифры нечетные),
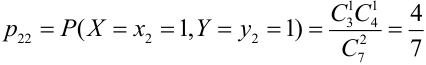 — (одна четная, одна нечетная),
— (одна четная, одна нечетная),
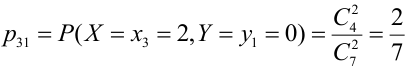 — (обе цифры четные).
— (обе цифры четные).
Таблица распределения имеет вид:

Проверка: 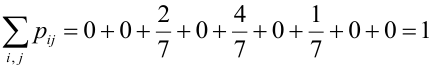
Пример:
Дана таблица распределения случайного вектора (X, Y). Получить ряды распределения для Х и Y отдельно.
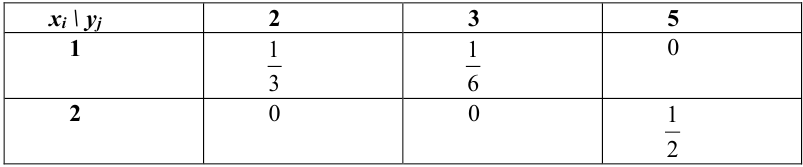
Решение.
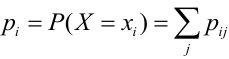 , (складываем по строкам), следовательно,
, (складываем по строкам), следовательно,
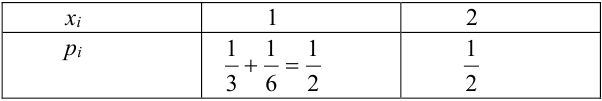
Проверка: 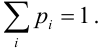
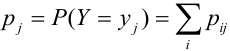 , (складываем по столбцам), следовательно,
, (складываем по столбцам), следовательно,

Проверка: 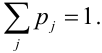
Функция распределения – закон распределения СВДТ и СВНТ
Функция распределения – универсальный закон распределения случайных векторов как дискретного, так и непрерывного типа.
Определение 61. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x,y), равная вероятности совместного выполнения двух неравенств: X < х, Y < у, т.е. 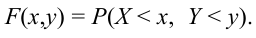
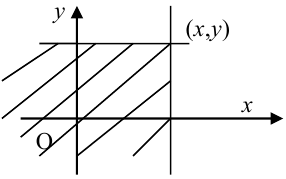
Геометрически F(x,y) представляет вероятность попадания случайной точки (X,Y) в левый нижний бесконечный квадрант плоскости с вершиной в точке (х,у).
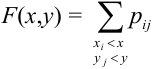 – для СВДТ
– для СВДТ
Свойства F(x;y).
1. Условие согласованности:
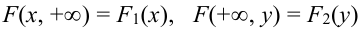
Пояснение. Отодвигая одну из границ квадранта в бесконечность, получаем полуплоскость, вероятность попадания в которую есть функция распределения одной случайной величины.
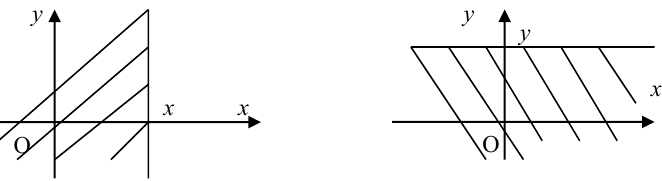
2. 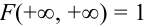
Пояснение. Квадрант обращается во всю координатную плоскость, попадание случайной точки в которую есть достоверное событие.
3. 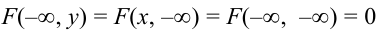
Пояснение. Отодвигая ту или иную границу квадранта в (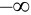 ), убеждаемся, что вероятность случайной точки попасть в квадрант равна нулю.
), убеждаемся, что вероятность случайной точки попасть в квадрант равна нулю.
4. F(x, у) – неубывающая функция по каждому аргументу.
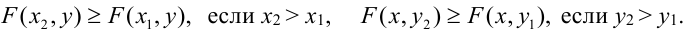
5. Вероятность попадания случайной точки (X, У) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
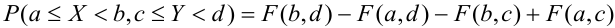
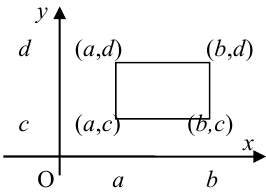
Определение 62. (второе определение) Двумерный случайный вектор называется случайным вектором непрерывного типа (СВНТ), если его функция распределения непрерывна на всей плоскости и существует неотрицательная и интегрируемая по Риману в бесконечных пределах по х, у функция 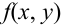 , называемая плотностью распределения СВНТ.
, называемая плотностью распределения СВНТ.
Пример №1
Найти функцию распределения, если случайный вектор задан таблицей распределения:
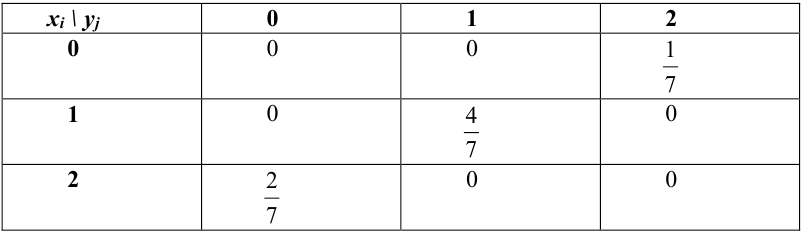
Решение.
Случайный вектор дискретного типа, следовательно, 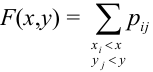
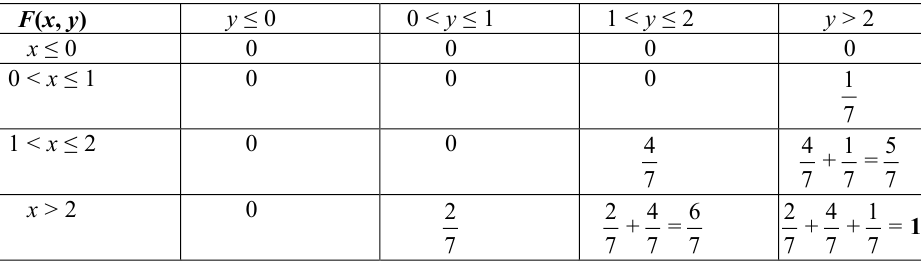
Плотность распределения (Для СВНТ)
Определение 63. (первое определение) Плотностью распределения системы двух непрерывных случайных величин называется предел отношения вероятности попадания случайной точки (X, Y) в элементарный прямоугольник к площади прямоугольника, когда оба его размера стремятся к нулю:
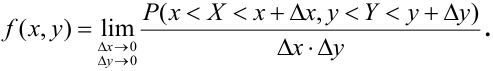
Распишем интервальную вероятность с помощью функции распределения:
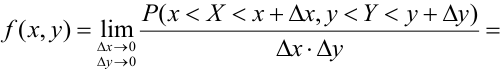
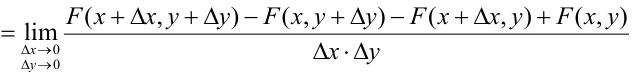
Правая часть равенства – определение смешанной производной функции двух переменных F(x, у), отсюда следует
Определение 64. (второе определение) Плотностью распределения системы двух непрерывных случайных величин называется смешанная частная производная от функции распределения системы:
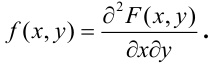
Отсюда, 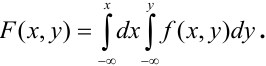
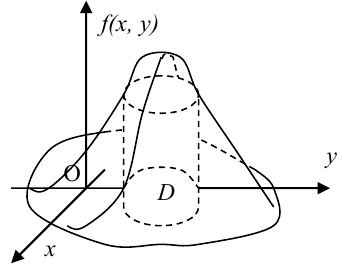
Геометрически 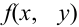 можно изобразить некоторой поверхностью, которую называют поверхностью распределения.
можно изобразить некоторой поверхностью, которую называют поверхностью распределения.
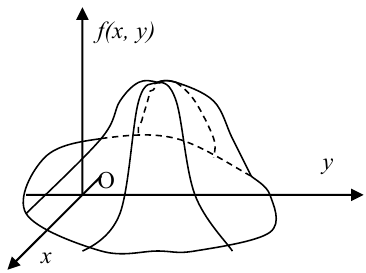
Вероятность попадания случайной точки в некоторую область D плоскости (Oxy) находится по формуле:
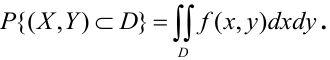
Геометрически вероятность попадания случайной точки в область D плоскости (Oxy) изображается объемом цилиндрического тела, ограниченного поверхностью распределения и опирающегося на эту область.
Свойства плотности
1. 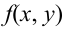 – неотрицательная функция, т.е.
– неотрицательная функция, т.е. 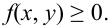
2. Условие нормировки: 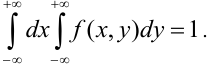
Пример №2
Дана плотность распределения непрерывного вектора 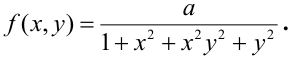
Найти: 1) коэффициент а, 2) функцию распределения F(x, у), 3) вероятность попадания случайной точки в прямоугольник с вершинами в точках O(0,0), A(0,1), 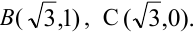
Решение.
1) Для вычисления коэффициента а применим условие нормировки:
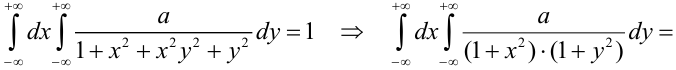
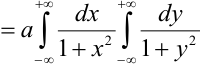
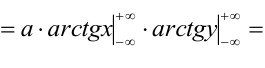
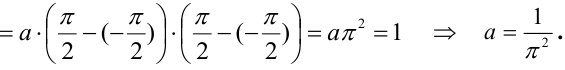
2) По определению 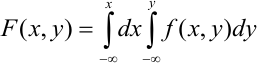
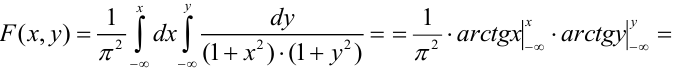
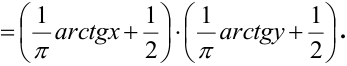
3) Вероятность попадания в прямоугольник.
1 способ:
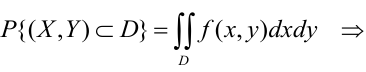
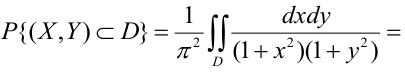
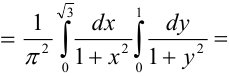
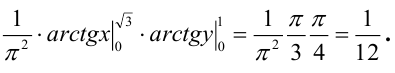
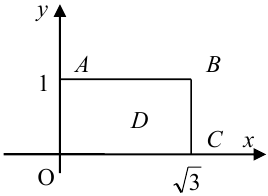
2 способ (по 5 свойству):
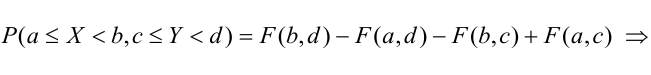
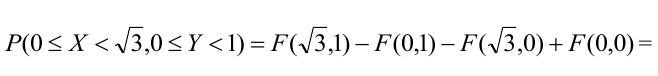
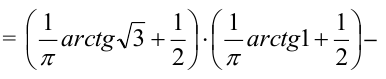
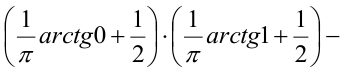
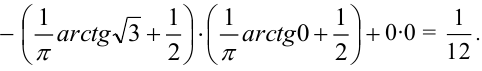
Пример №3
Дана плотность распределения непрерывного вектора 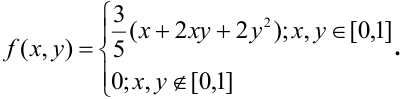 Найти вероятность того, что случайная точка принадлежит треугольнику с вершинами в точках O(0,0), A(1,2), B(0,1).
Найти вероятность того, что случайная точка принадлежит треугольнику с вершинами в точках O(0,0), A(1,2), B(0,1).
Решение.
Плотность распределения задана в квадрате. Область пересечения квадрата с заданным треугольником заштрихованный треугольник, ограниченный снизу прямой 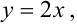 сверху – прямой
сверху – прямой 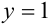 , причем,
, причем, 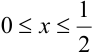 , следовательно,
, следовательно, 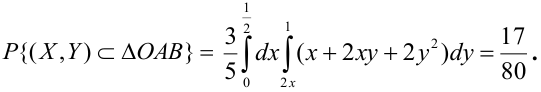
Плотности распределения отдельных величин, входящих в систему
Пусть известна плотность распределения 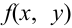 случайного вектора. Согласно свойству 1 (условие согласованности) для функции распределения
случайного вектора. Согласно свойству 1 (условие согласованности) для функции распределения 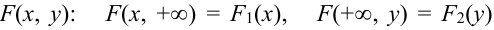 , можем записать, что,
, можем записать, что,
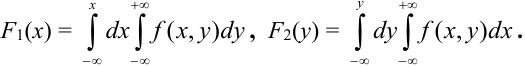
Отсюда, дифференцированием первого равенства по х, а второго по у, получим, что плотности распределения одной из величин равны интегралу от плотности распределения системы в бесконечных пределах по аргументу, соответствующему другой случайной величине:
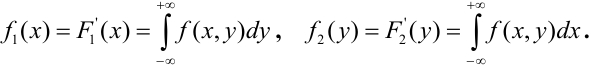
Ставится вопрос, как по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. В общем случае эта задача не разрешима, но, с другой стороны, закон распределения системы должен содержать все сведения о величинах, входящих в систему, в том числе и сведения о том, как они связаны между собой.
Определение 65. Случайные величины X и Y, входящие в систему, называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае, они называются зависимыми.
Теорема. Для того, чтобы дискретные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
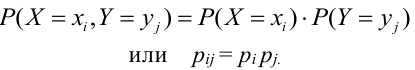
Для того, чтобы непрерывные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
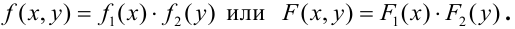
Пример №4
Дана плотность распределения непрерывного вектора: 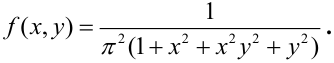
Зависимы или независимы случайные величины, входящие в систему?
Решение.
Представим плотность в виде произведения:
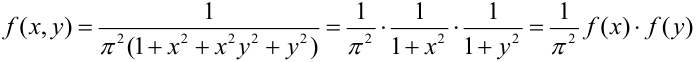 , следовательно, по теореме, X и Y – независимые величины.
, следовательно, по теореме, X и Y – независимые величины.
Пример №5
Дано распределение дискретных независимых случайных величин Х и Y:
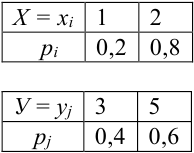
Записать закон распределения случайного вектора (Х + Y).
Решение.
Найдем возможные значения случайного вектора (Х+ Y): 1 + 3 = 4, 2 + 3 =5, 1+5 = 6, 2 + 5 = 7.
Найдем их вероятности, пользуясь условием независимости:
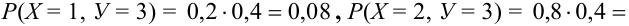
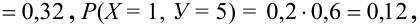
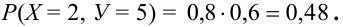
Следовательно, ряд распределения случайного вектора (Х + Y) имеет вид:

Замечание. Одним из наиболее простых распределений системы двух непрерывных величин является равномерное распределение.
Определение 66. Система двух непрерывных случайных величин имеет равномерное распределение в области D плоскости (Оху), если плотность распределения в точках области D постоянна и равна нулю в остальных точках плоскости:
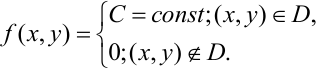
В силу свойства 2 плотности имеем, что 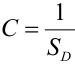 , где
, где 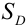 – площадь области D. Тогда вероятность попадания случайной точки в некоторую область
– площадь области D. Тогда вероятность попадания случайной точки в некоторую область 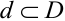 плоскости (Охy) находится по формуле:
плоскости (Охy) находится по формуле:
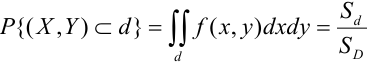
Определение 67. Пусть Х и Y независимые величины, распределенные по нормальному закону, их плотности распределения имеет вид:
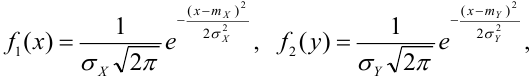
Следовательно, плотность распределения системы (Х,Y) на основании теоремы умножения плотностей распределения для случая независимых величин получим в виде
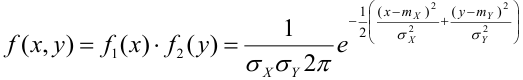
Если X и Y зависимы между собой, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему, что привело к введению условных законов распределения.
Определение 68. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.
Обозначим G (х,у) – множество возможных значений случайного вектора (X, Y).
Рассмотрим СВДТ.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у называется совокупность возможных значений 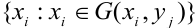 и соответствующих этим значениям условных вероятностей
и соответствующих этим значениям условных вероятностей 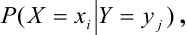 определяемых равенством:
определяемых равенством:
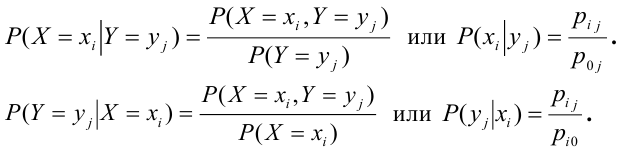
Рассмотрим CBHT.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у :
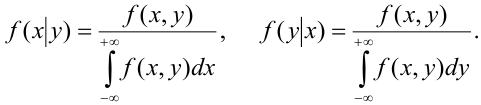
Теорема (умножения законов распределения): 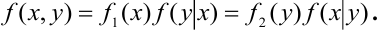
Условие нормировки: 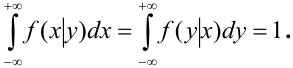
Условие независимости Х от Y: 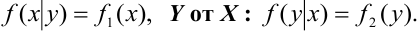
Числовые характеристики системы
Определение 69. Начальным моментом 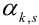 порядка
порядка 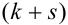 случайного вектора (X,Y) называется математическое ожидание произведения
случайного вектора (X,Y) называется математическое ожидание произведения 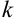 -ой степени Х на s-ую степень Y:
-ой степени Х на s-ую степень Y:
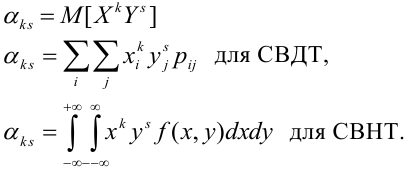
Математическое ожидание дискретных случайных величин Х и Y, входящих в систему:
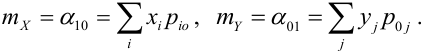
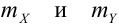 определяют координаты точки, называемой центром рассеивания системы на плоскости.
определяют координаты точки, называемой центром рассеивания системы на плоскости.
Определение 70. Центральным моментом 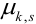 порядка
порядка 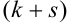 случайного вектора (Х,Y) называется математическое ожидание произведения
случайного вектора (Х,Y) называется математическое ожидание произведения 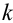 -ой и s-ой степеней соответствующих центрированных величин:
-ой и s-ой степеней соответствующих центрированных величин:
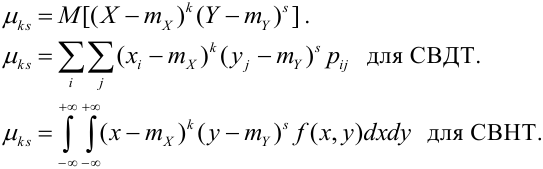
Дисперсия случайных величин X и Y, входящих в систему – характеристика рассеивания случайной точки в направлении осей (ох) и (оу):

Дисперсия дискретных случайных величин Х и Y, входящих в систему:
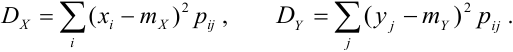
Дисперсия непрерывных случайных величин Х и Y, входящих в систему:
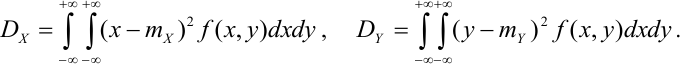
Замечание. Для краткого описания условных законов распределения используются различные характеристики, наиболее важной из которых является математическое ожидание:
Определение 71. Условным математическим ожиданием дискретной случайной величины X при условии, что Y принимает одно из своих возможных значений 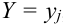 , называется сумма произведений возможных значений Х на их условные вероятности:
, называется сумма произведений возможных значений Х на их условные вероятности:
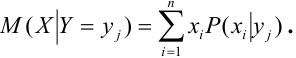
Для непрерывной случайной величины X: 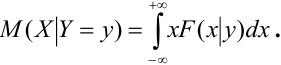
Аналогично, вводится понятие условного мат. ожидания для СВ Y.
Пример №6
По некоторой цели производится два выстрела. Вероятность попадания при одном выстреле равна р. Рассмотрим две случайные величины: X – число попаданий в цель, Y – число промахов. Составить таблицу распределения, записать функцию распределения системы F(x,y) и найти числовые характеристики 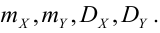
Решение.

Случайный вектор дискретного типа, следовательно, 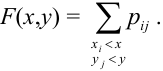


Пояснение: 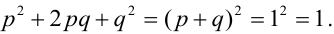
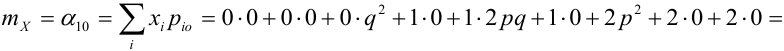
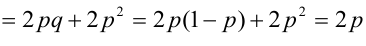
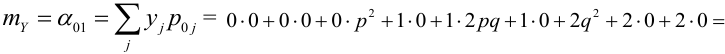
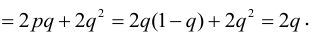
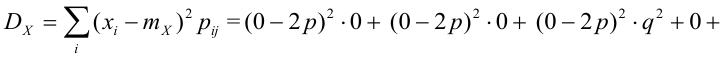
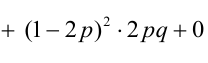
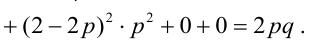
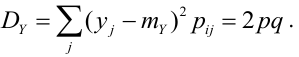
Ковариация, корреляция и линии регрессии
Особую роль при исследовании системы играет второй смешанный центральный момент.
Определение 72. Второй смешанный центральный момент 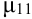 называется корреляционным или моментом связи или ковариацией:
называется корреляционным или моментом связи или ковариацией:
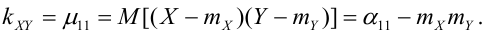
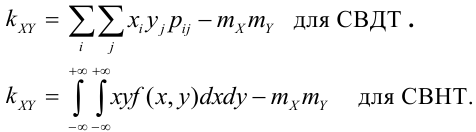
Теория корреляции решает две задачи: 1) установление формы связи между случайными величинами, 2) определение тесноты и силы этой связи.
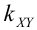 , помимо рассеивания, характеризует взаимное влияние случайных величин X и Y, входящих в систему. Для оценки степени влияния используется не сам момент, а безразмерное соотношение, которое называется нормированной ковариацией или коэффициентом корреляции:
, помимо рассеивания, характеризует взаимное влияние случайных величин X и Y, входящих в систему. Для оценки степени влияния используется не сам момент, а безразмерное соотношение, которое называется нормированной ковариацией или коэффициентом корреляции:
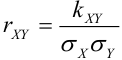 – коэффициент корреляции двух случайных компонент X и Y случайного вектора.
– коэффициент корреляции двух случайных компонент X и Y случайного вектора.
(Иногда его обозначают как 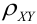 ).
).
Средние квадратические отклонения случайных величин X и Y равны 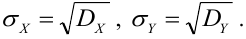
Определение 17. X и Y называются некоррелированными случайными величинами, если их коэффициент корреляции 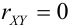 , и коррелированными, если отличен от нуля.
, и коррелированными, если отличен от нуля.
Свойства коэффициента корреляции
Свойства коэффициента корреляции 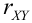 :
:
1. Если X и Y – независимые СВ, то 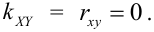 (X и Y некоррелированные случайные величины). Обратное утверждение неверно, так как X и Y могут быть зависимыми, но при этом
(X и Y некоррелированные случайные величины). Обратное утверждение неверно, так как X и Y могут быть зависимыми, но при этом 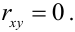
2. 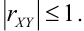
3. В случае 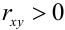 говорят о положительной корреляции X и Y , что означает: при возрастании одной из них другая тоже имеет тенденцию в среднем возрастать. Например, вес и рост человека.
говорят о положительной корреляции X и Y , что означает: при возрастании одной из них другая тоже имеет тенденцию в среднем возрастать. Например, вес и рост человека.
4. В случае 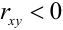 говорят об отрицательной корреляции X и Y , что означает: при возрастании одной из них другая имеет тенденцию в среднем убывать. Например, время, потраченное на подготовку прибора к работе и количество неисправностей, обнаруженных при его работе.
говорят об отрицательной корреляции X и Y , что означает: при возрастании одной из них другая имеет тенденцию в среднем убывать. Например, время, потраченное на подготовку прибора к работе и количество неисправностей, обнаруженных при его работе.
Взаимная связь двух случайных величин, помимо 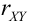 , может быть описана с помощью линий регрессии. Действительно, хотя при каждом значении Х = х величина У остается случайной величиной, допускающей рассеивание своих значений, однако зависимость Y от X сказывается часто в изменении средних размеров Y при переходе от одного значения х к другому. С изменением х будет изменяться и
, может быть описана с помощью линий регрессии. Действительно, хотя при каждом значении Х = х величина У остается случайной величиной, допускающей рассеивание своих значений, однако зависимость Y от X сказывается часто в изменении средних размеров Y при переходе от одного значения х к другому. С изменением х будет изменяться и 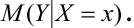 Это означает, что можно рассматривать функцию
Это означает, что можно рассматривать функцию 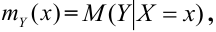 областью определения которой является множество возможных значений случайной величины X. Эта функция носит название регрессии Y и X.
областью определения которой является множество возможных значений случайной величины X. Эта функция носит название регрессии Y и X.
Аналогично, зависимость Х от Y описывает функция 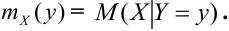
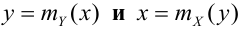 – уравнения регрессии
– уравнения регрессии
Линии, определенные этими уравнениями, называются кривыми или линиями регрессии. (Вводятся лишь для непрерывных СВ, для ДСВ линии будут состоять из точек.)
Если обе линии регрессии – прямые, то корреляционную зависимость называют линейной (линейная корреляция). Для нормально распределенного случайного вектора (X,Y) уравнения регрессии линейные:
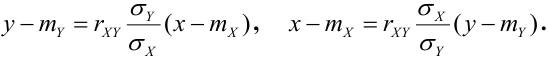
Связь коэффициента корреляции и линий регрессии
1) Если 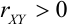 , то линии регрессии наклонены вправо.
, то линии регрессии наклонены вправо.
2) Если 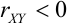 , то линии регрессии наклонены влево.
, то линии регрессии наклонены влево.
3) Если 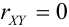 , то линии регрессии проходят параллельно осям координат.
, то линии регрессии проходят параллельно осям координат.
4) Если, 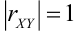 , то линии регрессии сливаются в одну линию, а случайные величины X и Y связаны между собой линейной функциональной зависимостью
, то линии регрессии сливаются в одну линию, а случайные величины X и Y связаны между собой линейной функциональной зависимостью 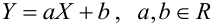 , причем знак коэффициента корреляции (
, причем знак коэффициента корреляции (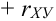 ) или (
) или (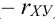 ) берется в зависимости от знака (+ или -) коэффициента а, который называется коэффициентом регрессии.
) берется в зависимости от знака (+ или -) коэффициента а, который называется коэффициентом регрессии.
Часто пишут уравнение в виде: 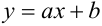 и называют его уравнением парной регрессии, где коэффициент регрессии
и называют его уравнением парной регрессии, где коэффициент регрессии 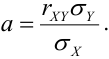
Определение 73. Ковариационной матрицей случайного вектора называется симметрическая действительная матрица, элемент которой представляет собой ковариации соответствующих пар компонент: 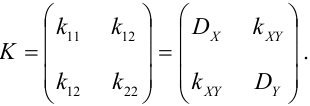
Определение 74. Корреляционной матрицей случайного вектора называется нормированная ковариационная матрица 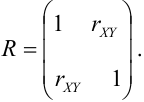
Пример №7
Дано уравнение парной регрессии 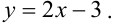 Выберите правильный коэффициент корреляции:
Выберите правильный коэффициент корреляции: 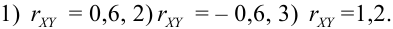
Решение.
Из рассмотрения исключаем 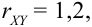 так как по 2 свойству
так как по 2 свойству 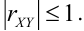 Коэффициент регрессии а = 2, т.е. со знаком «+», следовательно,
Коэффициент регрессии а = 2, т.е. со знаком «+», следовательно, 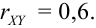
Замечание. Можно было знак 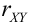 определить с помощью следующего рассуждения: возьмем два возрастающие значения х:
определить с помощью следующего рассуждения: возьмем два возрастающие значения х: 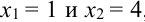 , тогда
, тогда 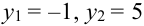 , т.е. с возрастанием х возрастает у, отсюда,
, т.е. с возрастанием х возрастает у, отсюда, 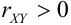 , следовательно,
, следовательно, 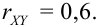
Пример №8
Дано уравнение парной регрессии  Найти
Найти 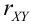 .
.
Решение.
Из формулы 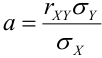 выразим
выразим 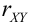 . Получим
. Получим 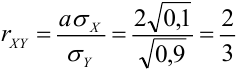 .
.
Свойства математического ожидания и дисперсии
1. X, Y как зависимые, так и независимые случайные величины, тогда 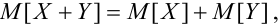
2. 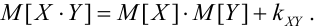
Если X, Y – некоррелированные, то 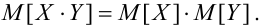
Если X, Y- независимые, то 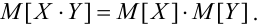
3. 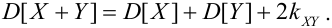
Если X, Y- некоррелированные, то 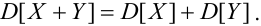
4. Если X, Y-независимые, то 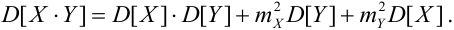
Пример №9
Даны законы распределения случайных величин X, Y:
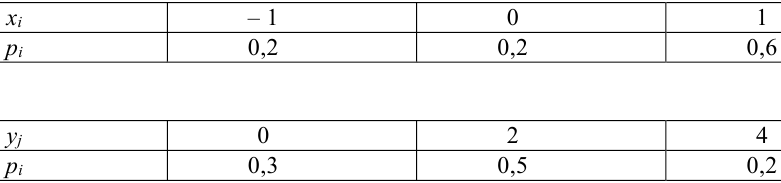
Найти 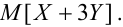
Решение.
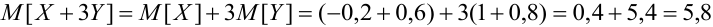 .
.
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
- Точечные оценки, свойства оценок
- Алгебра событий – определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Случайные события – определение и вычисление
Математическое ожидание — это ожидаемый результат от какого-то действия.
Например, можно рассчитать ожидаемую стоимость инвестиции в определённый момент в будущем. Рассчитывая математическое ожидание перед тем, как инвестировать, можно выбрать наилучший сценарий который, по мнению инвестора, даст наилучший результат.
Случайная величина может быть двух типов:
- Дискретной: число возможных значений X — это числимое конечное или бесконечное множество точек; пример: количество дефектных устройств в производстве фабрики.
- Непрерывной: X может принимать любое значение в заданном диапазоне; пример: концентрация углекислого газа в воде.
Математическое ожидание дискретной случайной величины рассчитывается этой формулой:

Где:
М — математическое ожидание,
X — случайная величина,
p — вероятность появления случайной величины.
Математическое ожидание дискретной случайной величины рассчитывается:
1. Сначала нужно умножить каждое из возможных результатов на свою вероятность (например: вероятность, что выпадет “1” — 1/6, “2” — 1/3, значит умножаем 1 на 1/6, 2 на 1/3, и т.д.),
2. Затем суммируем все эти значения (1 × 1/6 + 2 × 1/3 и т.д.).
Для непрерывной случайной величины используется эта формула:

Где:
М — математическое ожидание
f (x) — функция (которая будет предоставлена в условии задачи)
x — случайная величина
dx — элемент интегрирования
В этом случае рассчитывается интеграл в заданном интервале.
Примеры вычисления математического ожидания
Кратко:
- если в задаче даётся таблица с данными, то перемножаем каждое событие на его вероятность и потом всё складываем;
- если в задаче дают функцию с заданным интервалом, то вычисляем интеграл с этим интервалом.
Пример 1
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | −1 | 1 | 2 | 3 | 4 |
| pi | 0,1 | 0,2 | 0,3 | 0,1 | 0,3 |
Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = −1×0,1+ 1×0,2 + 2×0,3 + 3×0,1 + 4×0,3 = −0,1 + 0,2 + 0,6 + 0,3 + 1,2 = 2,2
Пример 2
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = 2x, при x∈(0,1) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:


Пример 3
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | 1 | 2 | 3 | 4 | 5 |
| pi | 0,3 | 0,3 | 0,1 | 0,1 | 0,2 |
Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = 1×0,3 + 2×0,3 + 3×0,1 + 4×0,1 + 5×0,2 = 0,3 + 0,6 + 0,3 + 0,4 + 1 = 2,6
Пример 4
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = (1/10).(3x²+1), при x∈(0,2) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:



Узнайте больше про Интегралы.
Основные свойства математического ожидания
- Математическое ожидание постоянной равно самой постоянной: М(c)=c.
- Математическое ожидание сложения/вычитания двух случайных величин равно сумме/вычитанию их математических ожиданий: пусть X и Y — две случайные величины, значит М (X ± Y) = М (X) ± М (Y).
- Если умножить случайную величину X на c, её среднее значение также умножается на эту константу (c): М (cX) = cМ (X).
- Если добавить или вычесть c из случайной величины X, то произойдёт та же операция (сложение или вычитание константы) с её средним значением: М (X ± c) = М (X) ± c.
- Если X и Y — две независимые случайные величины, значит: М(XY)=М(X)×М(Y).
Узнайте больше про Теорию вероятностей.
Математическое ожидание, дисперсия, среднее квадратичное отклонение
Эти величины определяют некоторое
среднее значение, вокруг которого
группируются значения случайной
величины, и степень их разбросанности
вокруг этого среднего значения.
Математическое ожидание Mдискретной случайной величины – это
среднее значение случайной величины,
равное сумме произведений всех возможных
значений случайной величины на их
вероятности.
![]()
Свойства математического ожидания:
-
Математическое ожидание постоянной
величины равно самой постоянной . -
Постоянный множитель можно выносить
за знак математического ожидания . -
Математическое ожидание произведения
двух независимых случайных величин
равно произведению их математических
ожиданий . -
Математическое ожидание суммы двух
случайных величин равно сумме
математических ожиданий слагаемых
Для описания многих практически важных
свойств случайной величины необходимо
знание не только ее математического
ожидания, но и отклонения возможных ее
значений от среднего значения.
Дисперсия случайной величины— мера разброса случайной величины,
равная математическому ожиданию квадрата
отклонения случайной величины от ее
математического ожидания.
![]() .
.
Принимая во внимание свойства
математического ожидания, легко показать
что
![]()
Казалось бы естественным рассматривать
не квадрат отклонения случайной величины
от ее математического ожидания, а просто
отклонение. Однако математическое
ожидание этого отклонения равно нулю.
Это объясняется тем, что одни возможные
отклонения положительны, другие
отрицательны, и в результате их взаимного
погашения получается ноль. Можно было
бы принять за меру рассеяния математическое
ожидание модуля отклонения случайной
величины от ее математического ожидания,
но как правило, действия связанные с
абсолютными величинами, приводят к
громоздким вычислениям.
Свойства дисперсии:
-
Дисперсия постоянной равна нулю.
-
Постоянный множитель можно выносить
за знак дисперсии, возводя его в квадрат. -
Если x и y независимые случайные величины
, то дисперсия суммы этих величин равна
сумме их дисперсий.
Средним квадратическим отклонением
случайной величины(иногда применяется
термин «стандартное отклонение случайной
величины») называется число равное![]() .
.
Среднее квадратическое отклонение,
является, как и дисперсия, мерой рассеяния
распределения, но измеряется, в отличие
от дисперсии, в тех же единицах, которые
используют для измерения значений
случайной величины.
Решение задач:
1)Дана случайная величина Х:
-
xi
-3
-2
0
1
2
pi
0,1
0,2
0,05
0,3
0,35
Найти М(х), D(X).
Решение:
![]() .
.
![]() =9
=9![]() =2,31.
=2,31.
![]() .
.
2) Известно, что М(Х)=5, М(Y)=2.
Найти математическое ожидание случайной
величиныZ=6X-2Y+9-XY.
Решение:М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.
Пример:Известно, чтоD(Х)=5,D(Y)=2. Найти
математическое ожидание случайной
величиныZ=6X-2Y+9.
Решение:D(Z)=62D(Х)-22D(Y)+0=180-8=172.
Тема 7. Непрерывные случайные величины
Задача 14
Случайная
величина, значения которой заполняют
некоторый промежуток, называется
непрерывной.
Плотностью распределениявероятностей непрерывной случайной
величины Х называется функцияf(x)– первая производная от функции
распределенияF(x).
![]()
Плотность
распределения также называют
дифференциальной
функцией.
Для описания дискретной случайной
величины плотность распределения
неприемлема.
Зная плотность распределения, можно
вычислить вероятность того, что некоторая
случайная величина Х примет значение,
принадлежащее заданному интервалу.
Вероятность того, что непрерывная
случайная величина Х примет значение,
принадлежащее интервалу (a,
b), равна определенному
интегралу от плотности распределения,
взятому в пределах от a
до b.
![]()
Функция распределения может быть легко
найдена, если известна плотность
распределения, по формуле:
![]()
Свойства плотности распределения.
1) Плотность распределения – неотрицательная
функция.
![]()
2) Несобственный интеграл
от плотности распределения в пределах
от -доравен единице.
![]()
Решение задач.
1.Случайная величина подчинена
закону распределения с плотностью:

Требуется найти коэффициент а,
определить вероятность того, что
случайная величина попадет в интервал
от 0 до![]() .
.
Решение:
Для нахождения коэффициента авоспользуемся свойством![]() .
.
![]()
![]()
![]()
2 .Задана непрерывная случайная
величинахсвоей функцией распределенияf(x).
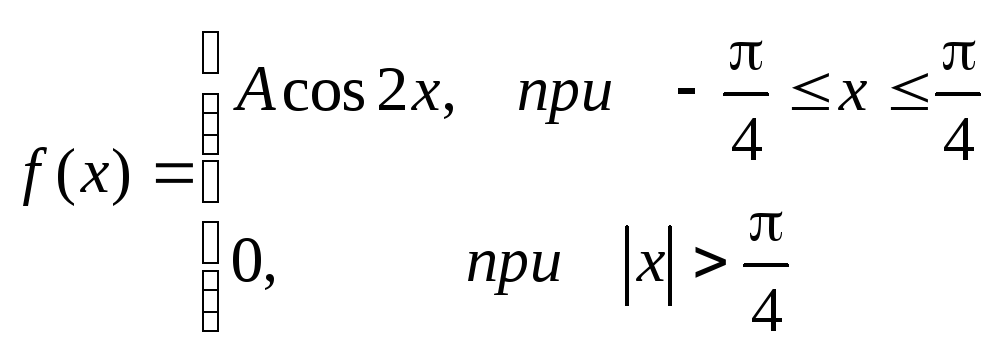
Требуется определить
коэффициент А, найти функцию распределения,
определить вероятность того, что
случайная величинахпопадет в
интервал![]() .
.
Решение:
Найдем коэффициент А.
![]()
Найдем функцию распределения:
1) На участке
![]() :
:![]()
2) На участке
![]()
![]()
3) На участке
![]()
![]()
Итого:


Найдем вероятность попадания случайной
величины в интервал
![]() .
.
![]()
Ту же самую вероятность можно искать
и другим способом:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
