§ Предисловие
Это алгоритм для шифрования сообщений. Он сложный, трудоемкий и напрямую не используется из-за своей очень невысокой скорости работы. А скорость работы у него невероятно медленная по той причине, что такой алгоритм оперирует гигантскими числами.
§ Открытый и закрытый ключи
Этот алгоритм основан на ключах, один из них открытый, другой – закрытый. Это называется пара ключей (публичный — то есть открытый, и приватный — закрытый). Ключи представляют собой просто очень большое число, то есть реально, просто число, и ничего более, кроме того, что оно гигантское. Для простоты и наглядности ключи у меня будут далее крайне простыми, не превышающие тысячи, поскольку чем больше ключ, тем сложнее его считать.
Теперь представим следующую ситуацию. Есть Алиса, и есть Боб. Они сверхсекретные агенты, и они не могут выдать то, о чем они болтают между собой, и какие сверхсекретные данные передают. Алиса сидит на телефоне, Боб сидит на другом конце телефона а посередине сидит их общий заклятый враг и внимательно слушает, о чем они говорят. Алисе надо передать Бобу очень секретное число, но просто сказать по телефону она ему не может — враг не дремлет.
- Алиса спрашивает у Боба открытый ключ, он ей говорит его по телефону. Ключ становится известен всем, в том числе не только Алисе, но и еще тому, кто сидит и слушает их
- Алиса берет это число (открытый ключ), производит определенные действия над тем числом, что хочет закодировать и отсылает Бобу. Человек посередине эту информацию тоже перехватил.
- Боб же берет закрытый ключ, который он создал вместе с открытым и производя математические действия, расшифровывает число Алисы
- Человек посередине не знает закрытого ключа Боба, а по открытому ключу он не может ничего сделать, потому что расшифровать сообщение можно только с помощью закрытого. Человек с досады кусает свои локти.
Вкратце:
- Боб создает открытый и закрытый ключи (они взаимосвязаны, как Том и Джерри)
- Алиса получает открытый ключ Боба
- Кодирует с его помощью свое число
- Отсылает число по небезопасному каналу связи
- Боб расшифровывает число с помощью закрытого ключа
Более абстрактно:
- Создать открытый и закрытый ключи
- Передать открытый ключ тому, кто будет шифровать
- Зашифровать сообщение с помощью открытого ключа
- Передать зашифрованное сообщение по каналу связи
- Расшифровать сообщение с помощью закрытого ключа
§ Открытый ключ
Задача создать открытый и закрытый ключи – очень сложна, если речь заходит о колоссальных цифрах. Сложность именно в том, как их быстро вычислить. Дело в том, что если взять два гигантских простых числа, и умножить, обратно потом найти эти простые числа уже весьма проблематично. Алгоритм RSA устройчив к взлому исключительно потому, что:
Невозможно быстро и эффективно разложить на множители огромные числа
Вот так вот. Если бы это было реально, то алгоритм RSA утратил бы свою криптостойкость и пришлось бы искать еще какой-нибудь метод. Сейчас рулят эллиптические кривые, но я без понятия как они работают, поэтому расскажу только про RSA.
Шаг 1. Взять два простых числа p и q
Кстати говоря, это далеко не так просто, как кажется. Если речь идет о небольших простых числах, не превышающих к примеру миллиарда, то их нахождение для взломщика не составляет вообще никакого труда. На любом процессоре разложить подобные числа можно за несколько миллисекунд. Однако, как только речь заходит о числах порядка аж 800-1000 десятичных знаков, то тогда никакой сверхмощной видеокарты, да и вообще вычислительной мощности всей планеты не хватит, чтобы даже за 1 год взломать такой код. Единственный, кто может справиться с этой задачей – это алгоритм Шора для квантовых компьютеров, которые сейчас находятся пока что в довольно неразвитой стадии на 2020 год.
Да, простые то числа взять можно, только вот надо чтобы они реально простые были, потому что составные числа работать не будут в RSA вообще. Они будут просто ломать всё. Это значит, что надо бы еще найти простые числа, а это сложная задача. Существуют разные тесты простоты, но в этой статье я их рассматривать не буду.
Получив простые числа p, q, надо их перемножить:
n = pq
И получим n, который будет играть важную роль дальше.
Шаг 2. Вычислить открытую экспоненту e
Перед тем, как вычислить открытую экспоненту, надо рассчитать функцию Эйлера, которая считается для двух простых чисел невероятно простым способом:
phi (n) = (p-1)(q-1)
То есть нужно лишь просто вычесть из p и q по единице и умножить их. Для чего это все? Здесь есть строгое математическое доказательство, приводить которое я тут не буду, потому что сложно и много. Просто надо поверить на слово. А если хочется проверить, то надо смотреть специальную литературу.
Теперь самый ответственный момент. Надо взять наобум число
e
такое, которое бы попало в следующий диапазон:
1 lt e lt phi(n)
И при этом его наибольший общий делитель (НОД) был равен 1, или, другими словами, чтобы ни одно целое число, кроме 1, не смогло поделить
e
и
phi (n)
, то есть, чтобы у этих двух чисел не было наибольшего общего делителя, больше чем 1.
Примеры:
- Числа 5 и 15 имеют НОД(5,15) = 5 — число 15 делится на 5, и 5 делится на 5 без остатка
- НОД(7, 14) = 7 — число 7 делится на 7, и 14 делится на 7 тоже
- НОД(12, 15) = 3 — число 12 делится на 3, число 15 делится на 3
- НОД(9, 11) = 1 — вот это в самый раз, ни одно число не делится, кроме как на 1
Шаг 3. Открытый ключ
Теперь появились все данные, чтобы найти открытый ключ, который представлен как пара {e, n}. Теперь перейду к практической части вычисления открытого ключа.
- Берется (для примера) p=47, q=31, оба числа простые
- Получается n = pq = 47*31 = 1457 — это число часть как открытого, так и закрытого ключа
- Вычисляем
phi (n) = (p-1)(q-1)= (47-1)(31-1) = 1380
- Теперь, надо взять такое
e, чтобы НОД(
e,
phi (n)) = 1, берем число e=257 (для примера), проверятся НОД(257, 1380) = 1, все верно
Открытый ключ {e, n} равен {257, 1457}.
§ Закрытый ключ
Теперь задача в том, чтобы сформировать закрытый ключ на числах p, q. Как я и говорил ранее, закрытый ключ нужен, чтобы расшифровать то сообщение, которое было зашифровано с помощью открытого ключа. Закрытый ключ базируется на тех же самых p,q, и потому у него будет точно та же компонента n, что и у открытого ключа. Закрытый же ключ будет представлен как пара {d, n}, где d – закрытая компонента, n = pq.
Существует формула для поиска закрытого ключа:
d = e^{-1} mod phi (n)
Но, ее понять сложно без подготовки. Лучше ее переписать в следующем виде:
(de) mod phi(n) = 1
И что это значит? Это значит, что надо найти
d
такое, что при умножении на
e
и потом после деления на
phi(n)
получился остаток 1.
Вот возьмем простой пример, допустим
e
= 7,
phi(n)
= 60:
7d mod 60 = 1
Теперь надо подобрать такое d, при котором остаток от деления на 60 был бы 1. Пробуем:
- d = 1 — 7*1 mod 60 = 7, не подходит
- d = 9 — 7*9 mod 60 = 63 mod 60 = 3, не подходит
- d = 23 — 23*7 mod 60 = 161 mod 60 = 41, не подходит
- d = 43 — 43*7 mod 60 = 301 mod 60 = 1, подошло
Получается, что для числа
e
= 7 число
d
= 43. Таким образом, мы смогли найти закрытый ключ {43, 77}, при этом открытый ключ был {7, 77}.
Поиск закрытого ключа происходит с помощью расширенного алгоритма Евклида, объяснение которого здесь тоже не приводится.
§ Пример шифрования и дешифрования
А теперь самое главное: как шифровать и дешифровать сообщение.
Шифрование числа происходит по следующей формуле:
b = a^e mod n
Дешифрование происходит так:
a = b^d mod n
И это весь алгоритм. Стоит только учесть, что так как числа
d
и
e
огромны, то не так просто будет возвести такие числа в такую вот степень.
Для начала, составим открытый и закрытый ключи. Генерация открытого ключа происходит по такому алгоритму:
- Возьмем p=11, q=23, n = pq = 253
- Число Эйлера
phi(n) = (11-1)(13-1) = 220 - Выберем открытую экспоненту
e= 17, ибо НОД(17, 220) = 1
Итак, открытый ключ будет равен {17, 253}. Теперь надо найти закрытый ключ, используя вот это уравнение:
17d mod 253 = 1
Пока что находим перебором, но можно искать с помощью расширенного алгоритма НОД. Но в данном случае просто перебором, про НОД позже расскажу.
Путем подбора (я просто программой перебрал числа d=1..253),
d
оказалось равным 134. Проверим, 134*17 mod 253 = 1, все подошло. Закрытый ключ равен {134, 253}.
Теперь надо попробовать что-нибудь зашифровать и расшифровать. Поскольку число n у нас 253, то зашифровать можно сообщение только от 0 до 252 включительно, ибо если попытаться использовать 253, то такое сообщение просто превратится в 0 при расшифровке. Это не проблема, но надо учитывать, что шифровать число более чем n нельзя.
Выбираем a=110, теперь шифруем с помощью открытого ключа.
b = 110^{17} mod 253 = 77
У нас получился b=77. Даже зная n=253, нельзя получить обратно 110, потому что нужен для этого закрытый ключ. Однако, если разложить 253 на простые множители p, q, то тогда можно найти и закрытый ключ d. Однако, при большом значении n это сделать невозможно. Расшифровка с помощью закрытого ключа делается так:
a = 77^{134} mod 253 = 110
Что и требовалось сделать. Все работает корректно. Процедура для быстрого возведения в степень приведена в этой статье.
§ Нахождение закрытого ключа с помощью расширенного НОД
Существуют способы, при которых можно найти d, зная e, не используя при этом перебор, и этот способ – расширенный алгоритм Евклида, о котором я уже писал ранее в другой статье. То есть как находить коэффициенты к расширенному алгоритму, об этом здесь я говорить не стану, а только опишу самую суть того, почему надо использовать именно этот НОД.
Поскольку числа
e
и
phi(n)
взаимно простые, но их НОД будет равен 1:
НОД(
e
,
phi(n)
) =
xe + yphi(n)
= 1
Здесь значения x, y получаются из решения расширенного алгоритма НОД. Теперь применим модуль к левой и правой части:
xe mod phi(n) + yphi(n) mod phi(n) = 1 mod phi(n)
Поскольку любой модуль от 1 будет 1, а модуль самого от себя,
yphi(n) mod phi(n)
будет равняться 0, то уравнение сокращается:
xe mod phi(n) = 1
Тут сразу же видно, что x – это как раз тот самый искомый d. В общем-то и всё.
§ Программный код
Получение значений расширенного НОД:
int NOD(int a, int b, int & x, int & y) { int x1, y1, d; if (a == 0) { x = 0; y = 1; return b; } d = NOD(b % a, a, x1, y1); x = y1 - (int)(b / a) * x1; y = x1; return d; }
Быстрое возведение в степень:
unsigned long fpow(unsigned long a, unsigned long b, unsigned long m) { int id; unsigned long r = 1; for (id = 31; id >= 0; id--) { if (b & (1 << id)) r = (r * a) % m; if (id) r = (r * r) % m; } return r; }
22 ноя, 2020
© 2007-2023 Все киты ништяково колючие
I have some inputs and outputs of a encryption function and i’m trying to find algorithm of it:
input:hello
output:eee5ab79be1ca8033fc790603b4d308c3c0a4e38
input:test
output:ebf3c7fb5cecf8ca04ca79dd0bbaa6e42120ffec
input:tennis
output:97e6335558d16337a5e712a3525a3766ab7a3454
input:a
output:0c57bfdc2835cdf0fab05fe08d37ffc5373f1ba8
input:b
output:67482459148ba04c2f12e83cdd18cbfe343978ee
input:c
output:380050d0dbf8293d16b7b4837d84abf4ae6b6d83
input:d
output:d0eae9775bac581b174dc4eaf0f6cc6cd284ad61
input:e
output:00626906c39804e9f441800c629900fd706002f8
input:f
output:7d6ae6cf3aa98f05bace0abc355474810f37c83d
input:0
output:324df299bcf4760d1523cb63ef5c4b2d1d4d371b
input:1
output:4a35df90d96cf1ed7aa008e99d1637b941d29605
input:2
output:2629ecf6a43d69aa06f7dfd5eabdba318d23132d
input:3
output:90225564ae81006f3747fb90d51dab4bac26fbac
input:4
output:3100cc28c4ef0f79e2d29c77a265aef1b2d0e70a
input:5
output:325fbdc73b2e874c287471e315949dc972846434
input:6
output:7d1bad0d82c2b62cfa0719f45acc50732579c206
input:7
output:89dd853798aea657f9ce236b248993b1f5c7bf55
input:8
output:83038f49e7954004aeafd2073b0c0c5a91d1ae7a
input:9
output:ab8fcf8532ed3c0367d6e5fa7230e4317296d6e4
outputs are hexadecimal and fixed length(40 characters)
inputs are unicode characters
Can anyone help me?
AlexEr81 |
|
|
Статус: Активный участник Группы: Участники Сказал(а) «Спасибо»: 9 раз |
с помощью CryptExportPublicKeyInfoEx получаю открытый ключ из контейнера. а как заранее определить какой у ключа алгоритм ? или нужно перебирать значение pszPublicKeyObjId пока CryptExportPublicKeyInfoEx не отработает успешно? |
 |
|
|
Boris@Serezhkin.com |
|
|
Статус: Активный участник Группы: Участники Сказал(а) «Спасибо»: 4 раз |
Автор: AlexEr81 получаю открытый ключ из контейнера. а как заранее определить какой у ключа алгоритм ? А какой у ключа может быть алгоритм? Танцевать надо от печки, Чей контейнер, от какого сертификата… |
|
|
|
|
AlexEr81 |
|
|
Статус: Активный участник Группы: Участники Сказал(а) «Спасибо»: 9 раз |
может неправильно вопрос написал. поясню на примере в чем дело. DH . а у ключа СД алгоритм – ГОСТ Р 34.10-2001. |
|
|
|
|
Максим Коллегин |
|
|
Статус: Сотрудник Группы: Администраторы Сказал «Спасибо»: 21 раз |
Может тогда воспользоваться CryptExportKey? |
|
Знания в базе знаний, поддержка в техподдержке |
|
|
|
WWW |
|
AlexEr81 |
|
|
Статус: Активный участник Группы: Участники Сказал(а) «Спасибо»: 9 раз |
а как для CryptExportKey получить HCRYPTKEY hKey? Отредактировано пользователем 5 октября 2015 г. 15:40:16(UTC) |
|
|
|
|
Максим Коллегин |
|
|
Статус: Сотрудник Группы: Администраторы Сказал «Спасибо»: 21 раз |
Попробуйте AT_SIGNATURE |
|
Знания в базе знаний, поддержка в техподдержке |
|
|
|
WWW |
|
|
AlexEr81
оставлено 05.10.2015(UTC) |
1 пользователь поблагодарил Максим Коллегин за этот пост.|
AlexEr81 |
|
|
Статус: Активный участник Группы: Участники Сказал(а) «Спасибо»: 9 раз |
спасибо за подсказку! CryptExportPublicKeyInfoEx сработал с параметром AT_SIGNATURE. данные получились верные |
|
|
|
| Пользователи, просматривающие эту тему |
|
Guest |
Быстрый переход
Вы не можете создавать новые темы в этом форуме.
Вы не можете отвечать в этом форуме.
Вы не можете удалять Ваши сообщения в этом форуме.
Вы не можете редактировать Ваши сообщения в этом форуме.
Вы не можете создавать опросы в этом форуме.
Вы не можете голосовать в этом форуме.
Информационные технологии становятся неотъемлемой частью жизни каждого из нас. Мы передаем информацию через интернет, храним ее на своих компьютерах, пользуемся электронной почтой, оплачиваем покупки с помощью электронных денег… Вследствие этого возникает проблема — как передать нужную информацию нужному адресату втайне от других?
На сегодняшний день защита информации с помощью криптографических методов считается одной из самых надежных, т. к. эти методы решают проблемы, возникающие не только при хранении, но и при передаче информации. Но их слабым местом всегда была проблема передачи ключей.
Решение этой проблемы было найдено в середине 70-х годов XX века. Тогда были предложены криптосистемы с открытым ключом. Концепция криптографии с открытым ключом была предложена в 1976 г. У. Диффи и М. Хеллманом в работе «Новые направления в криптографии». В криптосистеме с открытым ключом для шифрования и расшифрования используются различные ключи. Общая идея такой системы заключается в использовании при зашифровке сообщения такой функции от открытого ключа и сообщения, которую очень трудно обратить. Это обеспечивает более высокую криптостойкость системы.
Достоинства асимметричных криптосистем:
– секретный ключ известен только одной стороне;
– секретный ключ не нужно передавать;
– ключи можно долго не менять;
Недостатки асимметричных криптосистем:
– более высокие затраты времени и других ресурсов;
– более длинные ключи;
– сложнее внести изменения.
Появление асимметричной криптографии открыло сразу несколько новых прикладных направлений, в частности системы электронной цифровой подписи (ЭЦП) и электронных денег.
Итак, криптосистема с открытым ключом (или двухключевая криптосистема, асимметричная криптосистема) — система шифрования и/или электронной цифровой подписи, при которой открытый ключ передаётся по открытому (то есть незащищённому, доступному для наблюдения) каналу и используется для проверки электронной цифровой подписи и для шифрования сообщения. Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, которые обладают следующими свойствами:
– Если известно x, то f(x) вычислить относительно просто
– Если известно y=f(x), то для вычисления x нет простого (эффективного) пути.
В асимметричных криптосистемах для шифрования используется один ключ, а для расшифрования — другой. Первый ключ является открытым и может быть опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью открытого ключа невозможно. Для расшифрования данных получатель зашифрованной информации использует второй ключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа шифрования. Раскрытие секретного ключа по известному открытому ключу должно быть вычислительно неразрешимой задачей.
RSA — криптографический алгоритм с открытым ключом, основывающийся на вычислительной сложности задачи факторизации больших целых чисел. Аббревиатура RSA образована от первых букв фамилий предложивших его авторов: Ronald Rivest, Adi Shamir, Leonard Adleman. В общем случае, криптосистема RSA относится к шифрам простой замены.
Для шифрования используется операция возведения в степень по модулю большого числа. Для дешифрования за разумное время (обратной операции) необходимо уметь вычислять функцию Эйлера от данного большого числа, для чего необходимо знать разложения числа на простые множители.
В RSA каждый ключ состоит из пары целых чисел. Каждый участник создаёт свой открытый и закрытый ключ самостоятельно. Закрытый ключ каждый из них держит в секрете, а открытые ключи можно сообщать кому угодно или даже публиковать их.
Алгоритм создания ключей:
1. Выбираются два больших простых числа p и q (держатся в секрете).
2. Вычисляется модуль n=p∙q и функция Эйлера φ(n)=(p-1)(q-1).
3. Выбирается целое число e, взаимно простое со значением функции Эйлера от числа n из интервала (1; φ(n)).
4. Вычисляется d, учитывая, что e и d имеют мультипликативную обратную связь, т. е. e∙d=1(modφ(n)).
5. Пара чисел е и n публикуется как открытый ключ шифрования, а d сохраняется как закрытый (секретный) ключ.
6. Размер ключа связан с размером модуля n. Два числа p и q, произведением которых является модуль, должны иметь приблизительно одинаковую длину, поскольку в этом случае найти сомножители (факторы) сложнее, чем в случае, когда длина чисел значительно различается.
7. Если два числа чрезвычайно близки друг к другу или их разность близка к некоторому предопределенному значению, то возникает потенциальная угроза безопасности, однако такая вероятность — близость двух случайно выбранных чисел — незначительна.
Без ограничения общности положим p > q.
Возьмем Y = (p+q)/2 и X = (p-q)/2.
n = p*q = Y2 — X2.
Имеем Y = sqrt (n –X2).
Таким образом, значения p и q можно легко найти, если разность p — q достаточно мала.
Оптимальный размер модуля определяется требованиями безопасности: модуль большего размера обеспечивает большую безопасность, но и замедляет работу алгоритма RSA. Длина модуля выбирается в первую очередь на основе значимости защищаемых данных и необходимой стойкости защищенных данных и во вторую очередь — на основе оценки возможных угроз.
При шифровании сообщение разбивается на блоки длиной меньше разрядности n. Зашифрованное сообщение будет состоять из блоков той же длины.
Шифрование производится по следующей формуле:
C = E (e,n) (M) = Me (mod n), где E(e,n) — преобразование, а (e,n) — ключ зашифрования.
Для расшифрования используется то же преобразование, только с другим показателем степени:
M = D (d,n) (C) = Cd (mod n), где D(d,n) — преобразование, а (d,n) — ключ расшифрования.
Для вычисления числа d нужно использовать расширенный алгоритм Евклида, который работает только если числа e и φ(n) взаимно просты. Вычисление числа d сводится к решению уравнения φ(n)*x+e*d = 1 в натуральных числах. Число x не существенно.
Алгоритм RSA выполняет следующие задачи: обеспечения целостности и конфиденциальности информации, обеспечения аутентификации, обеспечения отказа от авторства или приписывания авторства.
Для проведения криптоанализа с помощью алгоритма RSA был зашифрован текст. Исходный текст имеет следующий вид:
Коротышки были неодинаковые: одни из них назывались малышами, а другие — малышками. Малыши всегда ходили либо в длинных брюках навыпуск, либо в коротеньких штанишках на помочах, а малышки любили носить платьица из пестренькой, яркой материи. Малыши не любили возиться со своими прическами, и поэтому волосы у них были короткие, а у малышек волосы были длинные, чуть не до пояса. Малышки очень любили делать разные красивые прически, волосы заплетали в длинные косы и в косы вплетали ленточки, а на голове носили бантики. Многие малыши очень гордились тем, что они малыши, и совсем почти не дружили с малышками. А малышки гордились тем, что они малышки, и тоже не хотели дружить с малышами. Если какая-нибудь малышка встречала на улице малыша, то, завидев его издали, сейчас же переходила на другую сторону улицы. И хорошо делала, потому что среди малышей часто попадались такие, которые не могли спокойно пройти мимо малышки, а обязательно скажут ей что-нибудь обидное, даже толкнут или, еще того хуже, за косу дернут. Конечно, не все малыши были такие, но ведь этого на лбу у них не написано, поэтому малышки считали, что лучше заранее перейти на другую сторону улицы и не попадаться навстречу. За это многие малыши называли малышек воображульками — придумают же такое слово! — а многие малышки называли малышей забияками и другими обидными прозвищами.
Длина текста 1428 знаков с пробелами. Текст состоит из букв русского алфавита верхнего и нижнего регистра и знаков препинания.
Гистограмма открытого текста представлена на Рисунке 1.
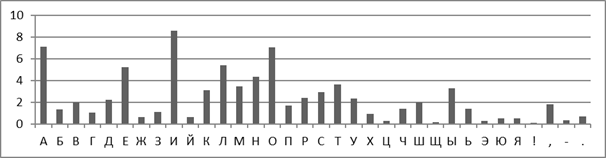
Рис. 1. Гистограмма открытого текста
Из гистограммы можно увидеть частоту встречаемости букв в данном литературном тексте.
Если разбить текст на биграммы, то их получится 570. На Рисунке 2 приведена диаграмма для полученных биграмм.
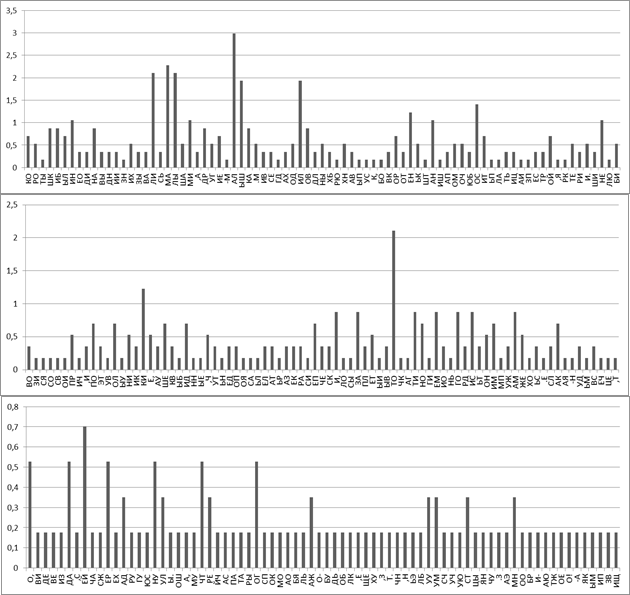
Рис. 2. Диаграмма биграмм открытого текста
Шифрование и расшифрование текста с помощью RSA производилось с использованием следующих ключей: {17053, 86041} — открытый ключ, {8977, 86041} — закрытый ключ. Длина зашифрованного текста составляет 3336 знаков с пробелами. Возьмем за шифробозначения блоки, разделенные пробелами. Всего 570 шифробозначений. Гистограмма зашифрованного текста представлена ниже на Рисунке 3.
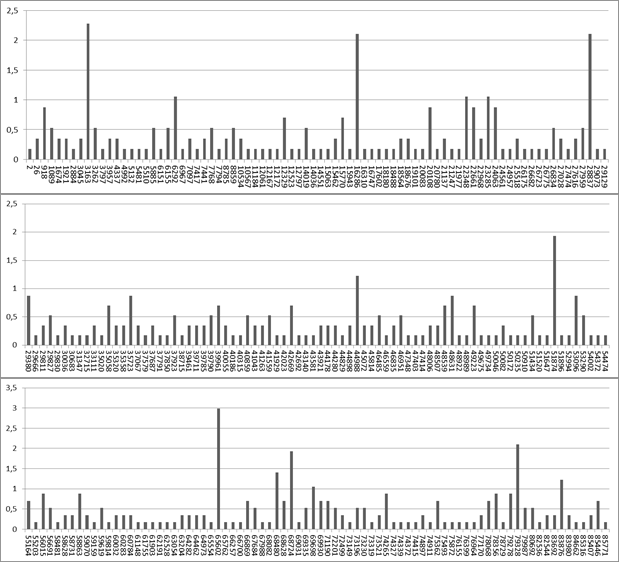
Рис. 3. Гистограмма зашифрованного текста
Разобьем текст на биграммы (всего 285 биграмм) и построим диаграмму. Т. к. повторения биграмм попадаются очень редко, укажем на ней только те, которые встречаются больше одного раза (Рис. 4).
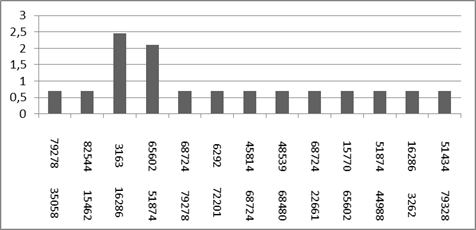
Рис. 4. Диаграмма биграмм зашифрованного текста
Криптоанализ шифртекста, полученного с помощью шифра RSA.
Существует несколько способов взлома шифра RSA:
1. Попытка найти закрытый ключ, соответствующий необходимому открытому ключу. Это позволит нападающему читать все сообщения, зашифрованные открытым ключом и подделывать подписи. Для выполнения такой задачи необходимо найти сомножители p и q, что является сложной задачей, если ключи выбраны в соответствии с требованиями.
2. Поиск метода вычисления корня степени e из mod n. Т. к. С = Me (mod n), то корнем степени e из (mod n) является сообщение M. Вычислив корень, можно вскрыть зашифрованные сообщения и подделывать подписи, даже не зная закрытый ключ. Но в настоящее время неизвестны методы, которые позволяют взломать RSA таким образом, если ключ имеет большой размер.
3. Атака по предполагаемому открытому тексту. Нападающий, имея зашифрованный текст, предполагает, что сообщение содержит какой-то определенный текст, например, «Дальнейшие инструкции завтра», затем шифрует предполагаемый текст открытым ключом получателя и сравнивает полученный текст с имеющимся зашифрованным текстом. Такую атаку можно предотвратить, добавив в конец сообщения несколько случайных битов.
4. Если кто-то посылает одно и то же сообщение M трем корреспондентам, каждый из которых использует общий показатель e = 3, нападающий может перехватить эти сообщения и расшифровать сообщение M. Такую атаку можно предотвратить, вводя в сообщение перед каждым шифрованием несколько случайных бит.
5. Также существуют несколько атак по зашифрованному тексту (или атаки отдельных сообщений с целью подделки подписи), при которых нападающий создает некоторый зашифрованный текст и получает соответствующий открытый текст, например, заставляя обманным путем зарегистрированного пользователя расшифровать поддельное сообщение.
Кроме вышеперечисленного нужно соблюдать все необходимые требования безопасности, чтобы секретные ключи оставались в секрете, т. к. злоумышленник может попробовать завладеть ими, если система должным образом не защищена.
Поиск закрытого ключа, соответствующего необходимому открытому ключу. Закрытый ключ является произведением простых чисел p и q, поэтому нам необходимо найти эти сомножители. Для этого можно воспользоваться методом факторизации Ферма.
Метод основан на поиске таких целых чисел x и y, которые удовлетворяют соотношению x2-y2=n, что ведёт к разложению n=(x-y)(x+y). Рассмотрим алгоритм поиска простых сомножителей по методу факторизации Ферма:
x2-y2=n равносильно x2-n= y2
Найдем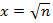 
– наименьшее число, при котором разность x2-n неотрицательна. Для этого для каждого значения k∈N, начиная с k=1, будем вычислять 
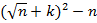до тех пор, пока значение этого выражения не будет являться точным квадратом. Таким образом, находим k, а затем вычисляем 
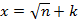и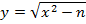 
. Полученные x и y являются искомыми простыми сомножителями.
Для обеспечения высокой надежности алгоритма RSA необходимо, чтобы используемые ключи соответствовали ряду требований:
– размеры ключей должны быть очень большими (рекомендовано 1024 бит, для особо важной информации — 2048 бит);
– числа p и q должны иметь приблизительно одинаковую длину, поскольку в этом случае найти сомножители (факторы) сложнее, чем в случае, когда длина чисел значительно различается;
– если разность p — q достаточно мала, то их очень легко найти, следовательно, их значения не должны быть близки друг к другу.
Так как компьютер, который был использован для шифрования, имеет невысокие возможности, были выбраны небольшие ключи, поэтому вскрыть текст возможно (число 17053 легко раскладывается на множители).
Итак, алгоритм RSA является достаточно криптостойким шифром. Трудоемкость криптоанализа обеспечивается сложностью нахождения простых сомножителей закрытого ключа. В зависимости от защищаемых данных определяется длина ключа для обеспечения необходимой криптостойкости.
В настоящее время криптографическая система RSA получила широкое распространение. Она была первой системой, пригодной и для шифрования, и для цифровой подписи. Сейчас она используется в большом числе криптографических приложений, также ее используют в сочетании с симметричными криптосистемами.
Наука не стоит на месте. Вычислительные машины становятся еще мощнее, с их помощью можно решать все более и более сложные задачи. Поэтому и криптография должна постоянно совершенствовать свои методы, чтобы суметь противодействовать злоумышленникам.
Литература:
1. Бутакова Н. Г., Семененко В. А., Федоров Н. В. Криптографическая защита информации: Учебное пособие. — М.:МГИУ, 2011. — 316 с.
2. Введение в криптографию / Под общей редакцией В. В. Ященко. — 3-е изд., доп. — М.: МЦНМО: «ЧеРо», 2000. — 288 с.
3. Коутинхо С.. Введение в теорию чисел. Алгоритм RSA. — М.: Постмаркет, 2001. — 328 с.
4. Словарь криптографических терминов / Под редакцией Б. А. Погорелова и В. Н. Сачкова.- М: МЦНМО, 2006.
5. Математическая криптография [Электронный ресурс].- Режим доступа: http://cryptography.ru/
Основные термины (генерируются автоматически): RSA, открытый ключ, закрытый ключ, зашифрованный текст, ключ, число, малышка, сообщение, секретный ключ, электронная цифровая подпись.
