Эквивалентное сопротивление резисторов
Расчет реальной электрической цепи в идеальном виде невозможен по причине отсутствия математических методик учета индивидуальных параметров каждого составляющего элемента. Это естественно, так как любая деталь имеет свои паразитные характеристики, которые нереально учесть при расчетах. Для устранения этой проблемы было введено понятие эквивалентной замены. При этом в расчет принимается только одна определяющая характеристика элемента. Так, например, эквивалентное сопротивление резисторов в электрической схеме, отображает только величину сопротивления без влияния на него сторонних факторов.

В электротехнике существует два основных варианта включения деталей в электрической цепи – это последовательное и параллельное соединение. Объединяющей для них является смешанная схема, которая по сути может быть разбита на участки с вышеприведенными характеристиками.
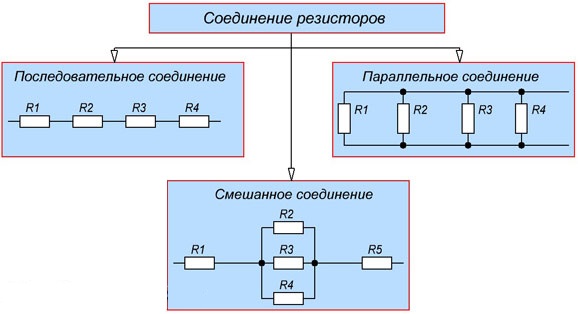
Рассмотрим эквивалентное соединение резисторов в каждом отдельном случае.
Эквивалентное сопротивление при последовательно соединенных резисторов
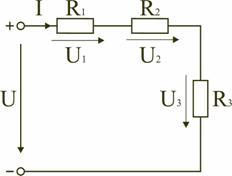
При данном типе размещения резисторов в цепи условная схема будет соответствовать рис. 1.
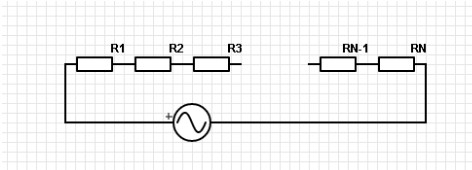
Для того чтобы определить эквивалентное сопротивление
резисторов необходимо вспомнить закон Ома. Для последовательного соединения он
гласит что общее, а в нашем случае эквивалентное сопротивление, соответствует
следующему уравнению:
Rэкв=
R1+R2+R3+RN-1+RN
Рассмотрим пример последовательного соединения трех резисторов, сопротивление которых равно 10, 20 и 30 Ом, соответственно. Согласно выше приведенной формуле общее сопротивление всех этих резисторов на данном участке цепи будет равно 60 Ом. Таким образом, при расчетах параметров электрической схемы нет надобности использовать индивидуальные характеристики отдельных элементов. Их можно просто заменить одним значением эквивалентным их сумме.
Кроме теории, данное суммирование значений сопротивлений
элементов, имеет и практическое применение – в случае необходимости всегда можно
заменить несколько резисторов одним. Также имеет место и обратное утверждение –
при отсутствии деталей с требуемой характеристикой ее можно заменить на
несколько других, эквивалентное сопротивление которых будет соответствовать
требуемому значению. Все это справедливо
и для параллельного соединения резисторов, только с некоторыми особенности.
Эквивалентное сопротивление при параллельном соединении резисторов
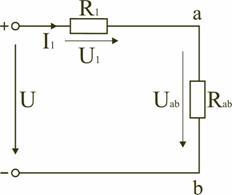
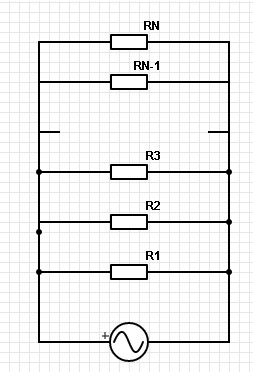
Общая схема при данном включении резисторов в цепь соответствует рис. 2.
Определить эквивалентное сопротивление параллельно
соединенных резисторов позволяет закон Ома согласно которому, в данном варианте,
справедливо равенство:
1/R экв =1/R1+1/R2+1/R3+1/R
N-1+1/RN
Возвращаясь к нашему примеру с резисторами 10, 20 и 30 Ом. Можно
определить эквивалентное сопротивление для данного случая, преобразуя уравнение
и получаем следующую формулу:
R экв = R1 х R2
х R3 / (R1 x R2) + (R1
x R3) + (R2 x R3) = 5,45
Ом
Важный момент: При параллельном включении резисторов в цепь эквивалентное сопротивление будет всегда меньше наименьшего значения отдельного элемента. При последовательном соединении R экв обязательно больше самого большого параметра.
Эквивалентное сопротивление при смешанном соединении резисторов
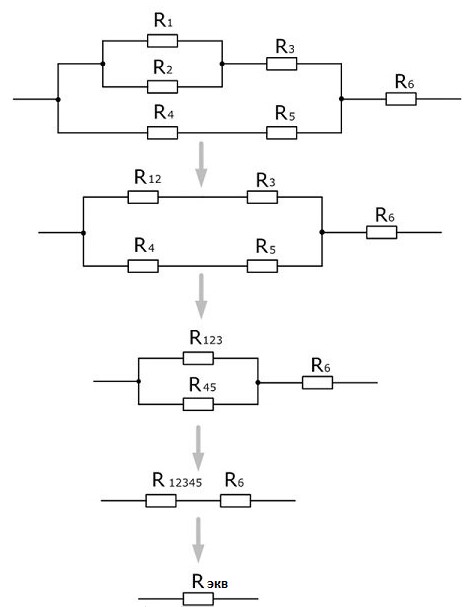
Определение эквивалентного сопротивления при смешанном соединении резисторов не представляет особых сложностей. Для этого достаточно разбить существующую цепочку на логические составляющие – блоки. Т.е. максимально упростить схему, приведя ее в соответствие с характеристиками свойственных тому или иному типу соединения. На рис. 3 приведена типичная схема упрощения, которая получила название метод свертывания цепи.
Данная схема позволяет наглядно понять, как можно определить эквивалентное сопротивление резисторов при смешанном соединении. Обращаем внимание, что начинать процесс упрощения можно в произвольном порядке. Так, например, объединение резисторов R1 и R2 не обязательно должно быть первым шагом. Можно совершенно смело на первом этапе найти R экв сумме сопротивлений последовательно включенных в цепь резисторов R4 и R5. Определение эквивалентного сопротивления для резисторов необходимо осуществлять в зависимости от типа соединения.

В заключение вернемся к самому понятию эквивалентной замены резисторов. В рассмотренных нами случаях речь шла об идеальном варианте. То есть в расчет принимается только величина сопротивления при нулевых значениях остальных характеристик. Также обращаем внимание, что при составлении эквивалентной схемы любых элементов электрической цепи, не только резисторов, можно вводить дополнительные переменные, которые будут влиять на конечные итоги.
Содержание
- 1 Параллельное соединение резисторов. Калькулятор для расчета
- 1.1 Формула параллельного соединения резисторов
- 1.2 Пример №1
- 1.3 Пример расчета №2
- 1.4 Как рассчитать сложные схемы соединения резисторов
- 1.5 Ток, протекающий в цепи параллельно соединенных резисторах
- 1.6 Параллельное соединение резисторов — онлайн калькулятор
- 1.7 Подведем итог
- 2 Эквивалентное сопротивление
- 2.1 Последовательное соединение элементов
- 2.2 Параллельное соединение
- 2.3 Расчёт при смешанном соединении устройств
- 3 Эквивалентное сопротивление резисторов
- 3.1 Эквивалентное сопротивление при последовательно соединенных резисторов
- 3.2 Эквивалентное сопротивление при параллельном соединении резисторов
- 3.3 Эквивалентное сопротивление при смешанном соединении резисторов
Параллельное соединение резисторов. Калькулятор для расчета
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Отправить сообщение об ошибке.
Источник: http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/
Эквивалентное сопротивление
> Теория > Эквивалентное сопротивление
Если электрическая цепь содержит несколько резисторов, то для подсчёта её основных параметров (силы тока, напряжения, мощности) удобно все резистивные устройства заменить на одно эквивалентное сопротивление цепи. Только для него должно выполняться следующее требование: его сопротивление должно быть равным суммарному значению сопротивлений всех элементов, то есть показания амперметра и вольтметра в обычной схеме и в преобразованной не должны измениться. Такой подход к решению задач называется методом свёртывания цепи.
Внимание! Расчёт эквивалентного (общего или суммарного) сопротивления в случае последовательного или параллельного подключения выполняется по разным формулам.
Последовательное соединение элементов
В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.
При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.
Последовательное подключение приборов
Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:
I = U/R.
Из вышестоящего выражения получаем значение R:
R = U/I (1).
Поскольку при последовательном соединении:
- I = I1 = I2 =…= IN (2),
- U = U1 + U2 +…+ UN (3),
формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:
- Rэкв = (U1 + U2 + …+ UN)/I,
- Rэкв = R1 + R2 + … + RN (4).
Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:
Rобщ = N·R (5).
Параллельное соединение
При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.
Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.
В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.
Если имеются N резистивных устройств, подключенных таким образом, то:
I = I1 + I2 + … + IN (6),
U = U1 = U2 = … = UN (7).
Из выражений (1), (6) и (7) имеем:
- Rобщ = U/(I1 + I2 + …+ IN),
- 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).
Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:
Rобщ = R · R / N·R = R / N (9).
Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.
Расчёт при смешанном соединении устройств
В случае смешанного подключения присутствуют участки с последовательным и параллельным подключениями элементов.
При решении задачи используют метод сворачивания цепи (метод эквивалентных преобразований). Его используют для вычисления параметров в том случае, если есть один источник энергии.
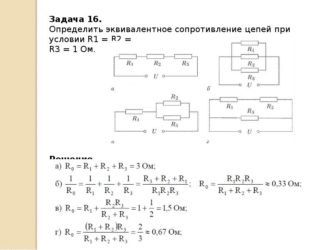
Предположим, задана следующая задача. Электрическая схема (см. рис. ниже) состоит из 7 резисторов. Рассчитайте токи на всех резисторах, если имеются следующие исходные данные:
- R1 = 1Ом,
- R2 = 2Ом,
- R3 = 3Ом,
- R4 = 6Ом,
- R5 = 9Ом,
- R6 = 18Ом,
- R7 = 2,8Ом,
- U = 32В.
Из закона Ома имеем:
I = U/R,
где R – суммарное сопротивление всех приборов.
Его будем находить, воспользовавшись методом сворачивания цепи.
Элементы R2 и R3 подключены параллельно, поэтому их можно заменить на R2,3, величину которого можно рассчитать по формуле:
R2,3= R2·R3 / (R2+R3).
R4, R5 и R6 также включены параллельно, и их можно заменить на R4,5,6, которое вычисляется следующим образом:
1/R4,5,6 = 1/R4+1/R5+1/R6.
Таким образом, схему, изображённую на картинке выше, можно заменить на эквивалентную, в которой вместо резисторов R2, R3 и R4, R5, R6 используются R2,3 и R4,5,6.
Согласно картинке выше, в результате преобразований получаем последовательное соединение резисторов R1, R2,3, R4,5,6 и R7.
Rобщ может быть найдено по формуле:
Rобщ = R1 + R2,3 + R4,5,6 + R7.
Подставляем числовые значения и рассчитываем R для определённых участков:
- R2.3 = 2Ом·3Ом / (2Ом + 3Ом) = 1,2Ом,
- 1/R4,5,6 = 1/6Ом + 1/9Ом + 1/18Ом = 1/3Ом,
- R4,5,6 = 3Ом,
- Rэкв = 1Ом + 1,2Ом + 3Ом + 2,8Ом= 8Ом.
Теперь, после того, как нашли Rэкв, можно вычислять значение I:
I = 32В / 8Ом = 4А.
После того, как мы получили величину общего тока, можно вычислить силу тока, протекающую на каждом участке.
Поскольку R1, R2,3, R4,5,6 и R7 соединены последовательно, то:
I1 = I2,3 = I4,5,6 = I7 = I = 4А.
На участке R2,3 напряжение находим по формуле:
- U2,3 = I2,3·R2,3,
- U2,3 = 4А·1,2Ом = 4,8В.
Поскольку R2 и R3 подключены параллельно, то U2,3 = U2 = U3, следовательно:
- I2 = U2 / R2,
- I2 = 4,8В / 2Ом = 2,4А,
- I3 = U3 / R3,
- I3 = 4,8В / 3Ом = 1,6А.
Проверяем правильность решения:
- I2,3 = I2 + I3,
- I2,3 = 2,4А + 1,6А = 4А.
На участке R4,5,б напряжение также находим, исходя из закона Ома:
- U4,5,6 = I4,5,6·R4,5,6,
- U4,5,6 = 4А·3Ом = 12В.
Так как R4, R5, Rб подключены параллельно друг к другу, то:
U4,5,6 = U4 = U5 = U6 = 12В.
Вычисляем I4, I5, I6:
- I4 = U4 / R4,
- I4 = 12В / 6Ом = 2А,
- I5 = U5 / R5,
- I5 = 12В / 9Ом » 1,3А,
- I6 = U6 / R6,
- I5 = 12В / 18Ом » 0,7А.
Проверяем правильность решения:
I4,5,6 = 2А + 1,3А + 0,7А = 4А.
Чтобы автоматизировать выполнение расчётов эквивалентных значений для различных участков цепи, можно воспользоваться сервисами сети Интернет, которые предлагают на их сайтах выполнить онлайн вычисления нужных электрических характеристик. Сервис обычно имеет встроенную специальную программу – калькулятор, которая помогает быстро выполнить расчет сопротивления цепи любой сложности.
https://www.youtube.com/watch?v=OP6nJnzO1Sc
Таким образом, использование метода эквивалентных преобразований при расчёте смешанных соединений различных устройств позволяет упростить и ускорить выполнение вычислений основных электрических параметров.
Источник: https://elquanta.ru/teoriya/ehkvivalentnoe-soprotivlenie.html
Эквивалентное сопротивление резисторов
Расчет реальной электрической цепи в идеальном виде невозможен по причине отсутствия математических методик учета индивидуальных параметров каждого составляющего элемента. Это естественно, так как любая деталь имеет свои паразитные характеристики, которые нереально учесть при расчетах.
Для устранения этой проблемы было введено понятие эквивалентной замены. При этом в расчет принимается только одна определяющая характеристика элемента.
Так, например, эквивалентное сопротивление резисторов в электрической схеме, отображает только величину сопротивления без влияния на него сторонних факторов.
В электротехнике существует два основных варианта включения деталей в электрической цепи – это последовательное и параллельное соединение. Объединяющей для них является смешанная схема, которая по сути может быть разбита на участки с вышеприведенными характеристиками.
Рассмотрим эквивалентное соединение резисторов в каждом отдельном случае.
Эквивалентное сопротивление при последовательно соединенных резисторов
При данном типе размещения резисторов в цепи условная схема будет соответствовать рис. 1.
Рисунок 1
Для того чтобы определить эквивалентное сопротивлениерезисторов необходимо вспомнить закон Ома. Для последовательного соединения онгласит что общее, а в нашем случае эквивалентное сопротивление, соответствуетследующему уравнению:
Rэкв=R1+R2+R3+RN-1+RN
Рассмотрим пример последовательного соединения трех резисторов, сопротивление которых равно 10, 20 и 30 Ом, соответственно. Согласно выше приведенной формуле общее сопротивление всех этих резисторов на данном участке цепи будет равно 60 Ом. Таким образом, при расчетах параметров электрической схемы нет надобности использовать индивидуальные характеристики отдельных элементов. Их можно просто заменить одним значением эквивалентным их сумме.
Кроме теории, данное суммирование значений сопротивленийэлементов, имеет и практическое применение – в случае необходимости всегда можнозаменить несколько резисторов одним. Также имеет место и обратное утверждение –при отсутствии деталей с требуемой характеристикой ее можно заменить нанесколько других, эквивалентное сопротивление которых будет соответствоватьтребуемому значению. Все это справедливои для параллельного соединения резисторов, только с некоторыми особенности.
Эквивалентное сопротивление при параллельном соединении резисторов
Общая схема при данном включении резисторов в цепь соответствует рис. 2.
Рисунок 2
Определить эквивалентное сопротивление параллельносоединенных резисторов позволяет закон Ома согласно которому, в данном варианте,справедливо равенство:
1/R экв =1/R1+1/R2+1/R3+1/RN-1+1/RN
Возвращаясь к нашему примеру с резисторами 10, 20 и 30 Ом. Можноопределить эквивалентное сопротивление для данного случая, преобразуя уравнениеи получаем следующую формулу:
R экв = R1 х R2х R3 / (R1 xR2) + (R1x R3) + (R2 xR3) = 5,45Ом
Важный момент: При параллельном включении резисторов в цепь эквивалентное сопротивление будет всегда меньше наименьшего значения отдельного элемента. При последовательном соединении R экв обязательно больше самого большого параметра.
Эквивалентное сопротивление при смешанном соединении резисторов
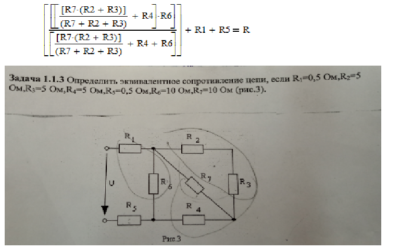
Определение эквивалентного сопротивления при смешанном соединении резисторов не представляет особых сложностей. Для этого достаточно разбить существующую цепочку на логические составляющие – блоки. Т.е. максимально упростить схему, приведя ее в соответствие с характеристиками свойственных тому или иному типу соединения. На рис. 3 приведена типичная схема упрощения, которая получила название метод свертывания цепи.
Рисунок 3
Данная схема позволяет наглядно понять, как можно определить эквивалентное сопротивление резисторов при смешанном соединении. Обращаем внимание, что начинать процесс упрощения можно в произвольном порядке.
Так, например, объединение резисторов R1 и R2 не обязательно должно быть первым шагом. Можно совершенно смело на первом этапе найти R экв сумме сопротивлений последовательно включенных в цепь резисторов R4 и R5.
Определение эквивалентного сопротивления для резисторов необходимо осуществлять в зависимости от типа соединения.
В заключение вернемся к самому понятию эквивалентной замены резисторов. В рассмотренных нами случаях речь шла об идеальном варианте. То есть в расчет принимается только величина сопротивления при нулевых значениях остальных характеристик. Также обращаем внимание, что при составлении эквивалентной схемы любых элементов электрической цепи, не только резисторов, можно вводить дополнительные переменные, которые будут влиять на конечные итоги.
Источник: http://podvi.ru/elektrokompanenty/ekvivalentnoe-soprotivlenie-rezistorov.html
Как определить эквивалентное сопротивление резисторов при последовательном и при параллельном соединении?
Мастер
(1201),
закрыт
9 лет назад
Андрей Степанов
Просветленный
(22749)
12 лет назад
1.При последовательном соединении n резисторов с сопротивлением R1, R2, ..Rn, эквивалентное сопротивление равно сумме сопротивлений этих резисторов:
Rэ = R1+R2+…+Rn
2. При параллельном соединении n резисторов с сопротивлением R1, R2, ..Rn, эквивалентное сопротивление цепи вычисляется из формулы:
1/Rэ = 1/R1 + 1/R2 +..+1/Rn
Успехов!
Виды резисторов
Внутреннее устройство детали может быть различным, но преимущественно это изолятор цилиндрической формы, с нанесённым на его внешнюю поверхность слоем либо несколькими витками тонкой проволоки, проводящими ток и рассчитанными на заданное значение сопротивления, измеряемое в омах.
Существующие разновидности резисторов:
- Постоянные. Имеют неизменное сопротивление. Применяются, когда определенный участок электроцепи требует установки заданного уровня по току или напряжению. Такие компоненты необходимо рассчитывать и подбирать по параметрам;
- Переменные. Оснащены несколькими выводными контактами. Их сопротивление поддается регулировке, которая может быть плавной и ступенчатой. Пример использования – контроль громкости в аудиоаппаратуре;
- Подстроечные – представляют собой вариант переменных. Разница в том, что регулировка подстроечных резисторов производится очень редко;
- Есть еще резисторы с нелинейными характеристиками – варисторы, терморезисторы, фоторезисторы, сопротивление которых меняется под воздействием освещения, температурных колебаний, механического давления.
Важно! Материалом для изготовления практически всех нелинейных деталей, кроме угольных варисторов, применяемых в стабилизаторах напряжения, являются полупроводники.
В чем измеряется сопротивление резистора
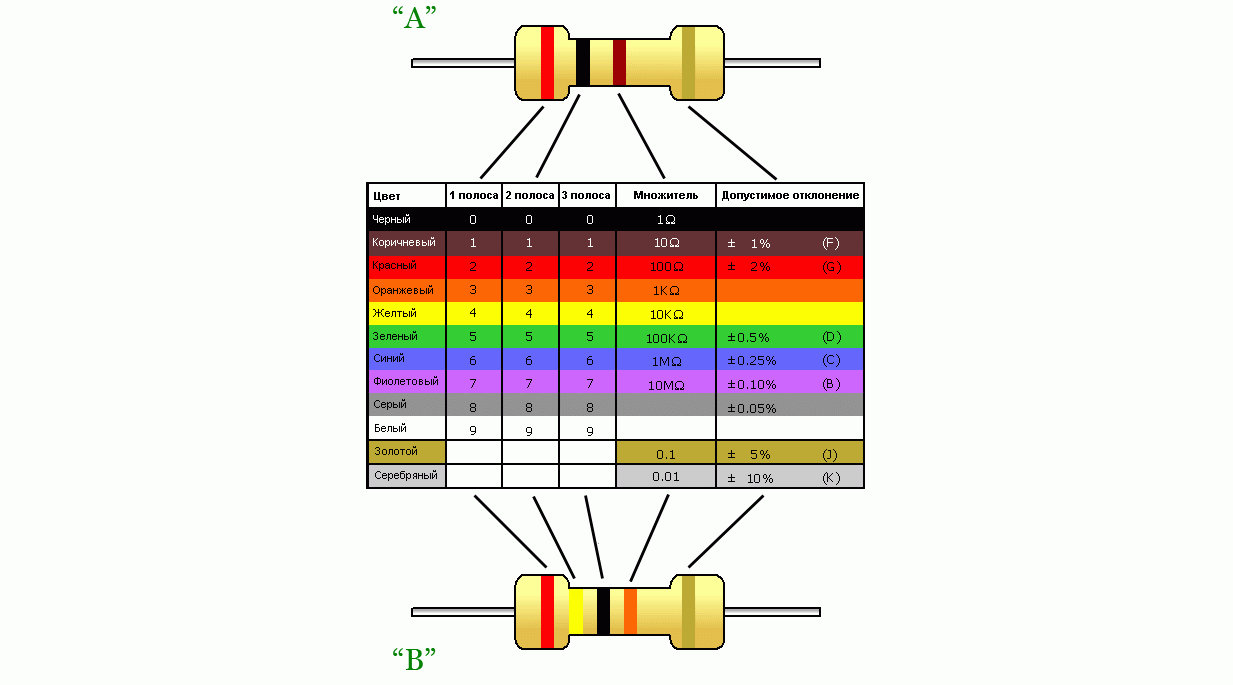
Чтобы ответить на вопрос в чем измеряется сопротивление резистора, нужно обратиться к стандартизации и наукам об измерениях. Международная и общепринятая схема цветовых кодов резисторов была разработана много лет назад как простой и быстрый способ определения омического значения резистора независимо от его размера или состояния. Он состоит из набора отдельных цветных колец или полос в спектральном порядке, представляющих каждую цифру значения резисторов. Сила сопротивления определеяет качество резистора.
Цветовая маркировка резистора всегда считывается по одной полосе за раз, начиная слева направо, с большей полосой допуска ширины, ориентированной на правую сторону, что указывает на ее допуск. Путем сопоставления цвета первой полосы с соответствующим номером в столбце цифр цветовой диаграммы под первой цифрой идентифицируется, и это представляет первую цифру значения сопротивления.
Опять же, сопоставляя цвет второй полосы с соответствующим номером в столбце цифр цветовой диаграммы, мы получаем вторую цифру значения сопротивления и так далее. Затем цветовой код резистора читается слева направо, как показано ниже:

Это система маркировки. Резисторы бывают разных размеров и значений сопротивления, а чтобы вычислить нужный, и существуют формулы расчета. Резисторы изготавливаются по определенной стандартной сетке, которая подходит для большинства целей. Чтобы не быть голословными, нужно приложить цветовую таблицу.
Вместо последовательных значений сопротивления от 1 Ом (базовая единица измерений) и выше, определенные значения резисторов существуют в определенных пределах допуска. Допуск резистора представляет собой максимальную разницу между его фактическим значением и требуемым значением и обычно выражается как зависимость положительного или отрицательного значения в процентах. Например, резистор с допуском 1 кОм ± 20% может иметь максимальное и минимальное значение сопротивления:
Максимальное значение сопротивления
- 1 кОм или 1000 Ом + 20% = 1200 Ом
Минимальное значение сопротивления
- 1 кОм или 1000 Ом – 20% = 800 Ом
Параметры резисторного элемента
- Для резисторов применяется понятие мощности. При прохождении через них электротока происходит выделение тепловой энергии, рассеиваемой в окружающее пространство. Мощность детали является параметром, который показывает, сколько энергии она может выделить в виде тепла, оставаясь работоспособной. Мощность зависит от габаритов детали, поэтому у маленьких зарубежных резисторов ее определяют на глаз, сравнивая с российскими, технические характеристики которых известны;
Ряд сопротивления резистора Е24
Важно! Импортные резисторные элементы идентичной мощности имеют несколько меньшие размеры, так как российские производятся с некоторым запасом по этому показателю.
На схеме мощность показана следующим образом.

- Второй параметр – сопротивление элемента. На российских деталях типа МЛТ и крупных импортных образцах оба параметра указываются на корпусе (мощность – Вт, сопротивление – Ом, кОм, мОм). Для визуального определения сопротивления миниатюрных импортных элементов применяется система условных обозначений с помощью цветных полосок;

- Допуски. Невозможно изготовить деталь с номинальным сопротивлением, в точности соответствующим заявленному значению. Поэтому всегда указываются границы погрешности, называемые допуском. Его величина – 0,5-20%;
- ТКС – коэффициент температуры. Показывает, как варьируется сопротивление при изменении внешней температуры на 1°С. Желательно, но не обязательно подбирать элементы с близким или идентичным значением этого показателя для одной цепи.
Как использовать на практике
Существует множество различных типов резисторов, которые можно использовать как в электрических, так и в электронных цепях для управления током или для падения напряжения различными способами. Но для того, чтобы сделать это, реальный резистор должен иметь некоторую форму «резистивного» или «резистивного» значения. Резисторы доступны в диапазоне различных значений сопротивления от долей Ом ( Ом ) до миллионов Ом.
Очевидно, что было бы нецелесообразно иметь в наличии резисторов каждого возможного значения , например, 1 Ом , 2 Ом , 3Ω , 4Ω и т.д., потому что буквально десятки сотен тысяч, если не десятки миллионов различных резисторов должны существовать , чтобы покрыть все возможные значения. Вместо этого резисторы изготавливаются в так называемых «предпочтительных значениях», а их значения сопротивления печатаются на корпусе цветными чернилами.
Значение сопротивления, допуск и номинальная мощность обычно печатаются на корпусе резистора в виде цифр или букв, когда корпус резистора достаточно большой, чтобы считывать отпечаток, например, большие силовые резисторы. Но когда резистор маленький, такой как углеродный или пленочный тип на 1/4 Вт, эти характеристики должны быть показаны другим способом, так как отпечаток будет слишком маленьким для чтения. Подача большого напряжения нагреет краску и расплавит надписи.
Таким образом, чтобы преодолеть это, маленькие резисторы используют цветные окрашенные полосы, чтобы указать как их значение сопротивления, так и их допуск с физическим размером резистора, указывающим его номинальную мощность. Эти цветные окрашенные полосы производят систему идентификации, обычно известную как цветовой код резисторов.

Расчет резисторов
Для расчета сопротивления резистора формула применяемая в первую очередь – это закон Ома:
I = U/R.
Исходя из этой формулы, можно вывести выражение для сопротивления:
R = U/I,
где U – разность потенциалов на выводных контактах резистора.
Пример. Необходимо провести зарядку аккумулятора 2,4 В зарядным током 50 мА от автомобильной 12-вольтовой батареи. Прямое соединение сделать нельзя из-за слишком высоких показателей по току и напряжению. Но возможно поставить в схему сопротивление, которое обеспечит нужные параметры.
Предварительно нужно рассчитать резистор:
- Расчет начинается с определения падения напряжения, которое должен обеспечить резисторный элемент:
U = 12-2,4 = 9,6 B
- Протекающий по детали ток – 50 мА. Следовательно, R = 9,6/0,05 = 192 Ом
Теперь можно уже подобрать нужный резистор по одному показателю.
Если рассчитанной детали не нашлось, можно применить соединение из нескольких резисторных элементов, установив их последовательно или параллельно. Расчет сопротивлений при этом имеет свои особенности.
Последовательное соединение
Последовательно соединенные сопротивления складываются:
R = R1+ R2.
Если нужно получить общий результат 200 Ом, и имеется один резистор на 120 Ом, то расчет другого:
R2 = R-R1 = 200-120 = 80 Ом.

Параллельное соединение
При параллельной схеме другая зависимость:
1/R = 1/R1 + 1/R2.
Или преобразованный вариант:
R = (R1 x R2)/ (R1 + R2).
Важно! Параллельное соединение можно использовать, когда в наличии детали с большим сопротивлением, чем требуется, последовательное наоборот.
Пример. Необходимо сопротивление 200 Ом. Имеется деталь R2 на 360 Ом. Какое сопротивление подобрать еще? R1 = R2/(R2/R-1) = 360/(360/200-1) = 450 Ом.

Смешанное соединение
В смешанных схемах присутствуют последовательно-параллельные комбинации. Расчет таких схем сводится к их упрощению путем преобразований. На рисунке ниже представлено, как упростить схему, рассчитывая общий показатель для шести резисторов с учетом их соединения.

Мощность
Определив сопротивление, еще нельзя выбрать деталь. Чтобы обеспечить надежную работу схемы, необходимо найти и другой параметр – мощность. Для этого надо знать, как рассчитать мощность резисторного элемента.
Формулы, по которым можно рассчитать мощность резистора:
- P = I² x R;
- P = U²/R.
Пример. I = 50 мА; R = 200 Ом. Тогда P = I² x R = 0,05² x 200 = 0,5 Вт.
Если не учитывать значение тока, расчет мощности резистора ведется по другой формуле.
Пример. U = 9,6 В, R = 200 Ом. P = U²/R = 9,6²/200 = 0,46 Вт. Получился тот же результат.
Теперь, зная точные параметры рассчитываемого резисторного элемента, подберем радиодеталь.
Важно! При выборе деталей возможно их заменить на резисторы с мощностью, больше рассчитанной, но обратный вариант не подходит.
Это основные формулы для расчета резисторных деталей, на основании которых производится анализ узлов схемы, где главным является определение токов и напряжений, протекающих через конкретный элемент.
От чего зависит сопротивление резистора
Температура и последовательность включения – два главных фактора, которые определяют сопротивление в цепи. Но помимо этих показателей есть и допуски. Как же измерять? В большинстве электрических или электронных цепей большой 20% -ный допуск на один и тот же резистор, как правило, не является проблемой, но если для высокоточных цепей, таких как фильтры, генераторы или усилители и т. д., требуются резисторы с малым допуском, то необходимо использовать резистор с правильным допуском. Так как резистор с допуском 20% обычно не может использоваться для замены типа допуска 2% или даже 1%.
Некоторые факты
- Каждый электропроводный материал имеет некоторое сопротивление, являющееся сопротивляемостью материала электрическому току.
- Сопротивление измеряется в Омах. Символ единицы измерения Ом — Ω.
- Разные материалы имеют разные значения сопротивления.
- Например, сопротивление меди 0.0000017 Ом/см 3
- Сопротивление керамики около 10 14 Ом/см 3
- Чем больше значение сопротивления, тем выше сопротивляемость электрическому току. Медь, которая часто используется в электрических проводах, имеет очень малое сопротивление. С другой стороны, сопротивление керамики очень велико, что делает ее прекрасным изолятором.
- Работа всей цепи зависит от того, какой тип соединения вы выберете для подключения резисторов в этой цепи.
- U=IR. Это закон Ома, установленный Георгом Омом в начале 1800х. Если вам даны любые две из этих переменных, вы легко найдете третью.
- U=IR: Напряжение (U) есть результат умножения силы тока (I) * на сопротивление (R).
- I=U/R: Сила тока есть частное от напряжение (U) ÷ сопротивление (R).
- R=U/I: Сопротивление есть частное от напряжение (U) ÷ сила тока (I).
- Запомните: при параллельном соединении существует несколько путей прохождения тока по цепи, поэтому в такой цепи общее сопротивление будет меньше сопротивления каждого отдельного резистора. При последовательном соединении ток проходит через каждый резистор в цепи, поэтому сопротивление каждого отдельного резистора добавляется к общему сопротивлению.
- Общее сопротивление в параллельной цепи всегда меньше сопротивления одного резистора с самым низким сопротивлением в этой цепи. Общее сопротивление в последовательной цепи всегда больше сопротивления одного резистора с самым высоким сопротивлением в этой цепи.
Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением R экв, и вся схема представляется в виде схемы на рис. 1.3, где R=R экв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа.
Электрическая цепь с последовательным соединением элементов
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U 1 + U 2 + U 3 или IR экв = IR 1 + IR 2 + IR 3 ,
откуда следует
R экв = R 1 + R 2 + R 3 .
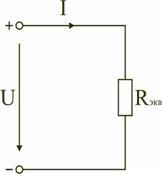
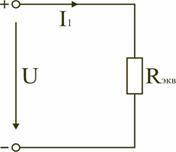
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
и по вышеприведенным формулам рассчитывают падение напряжений U 1 , U 2 , U 3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I 1 + I 2 + I 3 , т.е. ,
откуда следует, что
.
В том случае, когда параллельно включены два сопротивления R 1 и R 2 , они заменяются одним эквивалентным сопротивлением
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
g экв = g 1 + g 2 + g 3 .
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление R экв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U = IR экв = I 1 R 1 = I 2 R 2 = I 3 R 3 .
Отсюда следует, что
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R. Сопротивления R 4 и R 5 включены параллельно, тогда сопротивление участка цепи cd равно:
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
На схеме (рис. 1.8) сопротивление R 3 и R cd соединены последовательно, и тогда сопротивление участка цепи ad равно:
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
На схеме (рис. 1.9) сопротивление R 2 и R ad соединены параллельно, тогда сопротивление участка цепи аb равно
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R 1 и R ab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
.
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Соединение элементов электрической цепи по схемам «звезда» и «треугольник»
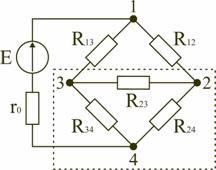
В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R 12 , R 13 , R 24 , R 34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
Резисторы применяются практически во всех электросхемах. Это наиболее простой компонент, в основном, служащий для ограничения или регулирования тока, благодаря наличию сопротивления при его протекании.
Видео
Или электрической цепи электрическому току .
Электрическое сопротивление определяется как коэффициент пропорциональности R
между напряжением
U
и силой постоянного тока
I
в законе Ома для участка цепи .
Единица сопротивления называется омом
(Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом (1 Ом) — это сопротивление такого проводника, в котором при напряжении
1В
сила тока равна
1А
.
Делитель напряжения
Наиболее применяемые готовые блоки питания рассчитаны на выходные напряжения: 9, 12 или 24 вольта. В то же время большинство электронных схем и устройств использует напряжение питания в интервале от 3 до 5 В. В этом случае возникает потребность снизить величину Uпит до необходимого значения. Сделать это можно, используя делитель напряжения, который имеет много вариантов исполнения. Самый простой – делитель на резисторах.

Мощность резистора
Подобные делители напряжения применяются исключительно в маломощных контурах. Это обусловлено их низким КПД. Часть мощности блока питания рассеивается на делителе, превращаясь в тепло. Эти потери тем больше, чем больше нужно уменьшить исходное напряжение. Подключение нагрузки параллельно одному плечу требует того, чтобы Rн было намного больше резистора, установленного в этом плече. Иначе делитель будет выдавать нестабильное питание.
При такой схеме напряжение по плечам делителя распределяется согласно полученным соотношениям между R1 и R2. Величина сопротивлений при этом роли не играет. Но следует помнить, что при низких значениях R1 и R2 увеличивается и мощность на нагрузке, и величина потерь на нагревание элементов.
Внимание! Перед тем, как вычислять точные параметры, нужно помнить, как подобрать резисторы. При их равном значении напряжение на выходе делится пополам. Если равенство не соблюдается, снимать поделенное напряжение нужно с элемента, имеющего больший номинал.

Онлайн калькулятор для расчета светодиодов
Для автоматического расчета понадобятся следующие данные:
- напряжение источника или блока питания, В;
- номинальное прямое напряжение устройства, В;
- прямой номинальный рабочий ток, мА;
- количество светодиодов в цепочке или включенных параллельно;
- схема подключения светодиода(ов).
Исходные данные можно взять из паспорта диода.
После введения их в соответствующие окна калькулятора нажмите на кнопку «Рассчитать» и получите номинальное значение резистора и его мощность.
Мощность резистора — что это такое, на что влияет
Рассеиваемая мощность резисторного элемента — это макс. ток, который может выдерживать сопротивление долгое время без ущерба для работоспособности.
То есть, этот параметр необходимо подбирать для каждой электросхемы отдельно. Мощность вычисляется с помощью следующей формулы: P = I * R.
Физически рассеиваемый параметр резисторного устройства — это то количество тепла, которое его корпус может «передать» и не сгореть. Мощность в первую очередь влияет на надёжность работы резисторного устройства.
Важно! Все резисторные компоненты, вне зависимости от установленных параметров, функционируют на основании закона Ома, это главный ключ благодаря которому определяется напряжение. Спад напряжения – это разница в показателях на входе и выходе. Внутри механизма протекающий ток меняется или ограничивается – электроны сталкиваются с неоднородной структурой материала проводниковой.
Как определить по внешнему виду
На принципиальной электросхеме выделена, необходимая мощность резисторного элемента — тут все ясно. Но как вычислить мощность по визуальному виду на плате для печати? В общем, чем огромнее корпус, тем больше он может рассеивать тепла.
На российских сопротивлениях рядом с цифрами ставят букву В и все. А в зарубежных указывают W. Но эти символы есть не всегда. В иностранных может выделяться V или SW перед цифрами. Еще в импортных может также красоваться буква B, а в российских МЛТ может быть пустота или буква W. Сложно что-то понять, конечно. Подробнее о буквенной маркировке резисторов, читайте тут.
Еще есть небольшие замкнутые резисторные устройства, на которых и номинал невозможно поместить. В зарубежных он нанесен цветовыми полосами. Как в таком случае вычислить мощность рассеивания, насколько важен цвет? В старом ГОСТе была табличка соответствий габаритов и мощностей. Отечественные резисторные элементы по-прежнему изготавливают в соответствии с ней. Импортные, кстати, тоже, но они по габаритам уступают нашим. Однако и с ними можно разобраться.
Если не можете решить, к какой группе причислить определенный экземпляр, лучше считать что он слабый в плане мощности. Тогда компонент точно не сгорит.
Важно! Есть резисторные элементы крупные с малой рассеивающей способностью и наоборот. Но в подобных случаях, обозначают этот параметр в маркировке, как и информацию о соединении.
Параллельное соединение светодиодов
Так же можно подключить светодиоды и параллельно, но это создает больше проблем, чем при последовательном соединении.

Ограничивать ток параллельно соединенных светодиодов одним общим резистором не совсем хорошая идея, поскольку в этом случае все светодиоды должны иметь строго одинаковое рабочее напряжение. Если какой-либо светодиод будет иметь меньшее напряжение, то через него потечет больший ток, что в свою очередь может повредить его.
И даже если все светодиоды будут иметь одинаковую спецификацию, они могут иметь разную вольт-амперную характеристику из-за различий в процессе производства. Это так же приведет к тому, что через каждый светодиод будет течь разный ток. Чтобы свести к минимуму разницу в токе, светодиоды, подключенные в параллель, обычно имеют балластный резистор для каждого звена.
Сопротивления
в электрических цепях могут быть
соединены последовательно, параллельно,
по смешанной схеме и по схемам «звезда»,
«треугольник». Расчет сложной схемы
упрощается, если сопротивления в этой
схеме заменяются одним эквивалентным
сопротивлением Rэкв,
и вся схема представляется в виде схемы
на рис. 1.3, где R=Rэкв,
а расчет токов и напряжений производится
с помощью законов Ома и Кирхгофа.
Электрическая
цепь с последовательным соединением
элементов
|
|
|
Последовательным
называют такое соединение элементов
цепи, при котором во всех включенных в
цепь элементах возникает один и тот же
ток I (рис. 1.4).
На
основании второго закона Кирхгофа (1.5)
общее напряжение U всей цепи равно сумме
напряжений на отдельных участках:
U
= U1
+ U2
+ U3 или
IRэкв
= IR1
+ IR2
+ IR3,
откуда
следует
(1.5)
Rэкв
= R1
+ R2
+ R3.
Таким
образом, при последовательном соединении
элементов цепи общее эквивалентное
сопротивление цепи равно арифметической
сумме сопротивлений отдельных участков.
Следовательно, цепь с любым числом
последовательно включенных сопротивлений
можно заменить простой цепью с одним
эквивалентным сопротивлением Rэкв
(рис. 1.5). После этого расчет цепи
сводится к определению тока I всей цепи
по закону Ома
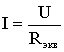 ,
,
и
по вышеприведенным формулам рассчитывают
падение напряжений U1,
U2,
U3
на соответствующих участках электрической
цепи (рис. 1.4).
Недостаток
последовательного включения элементов
заключается в том, что при выходе из
строя хотя бы одного элемента, прекращается
работа всех остальных элементов цепи.
Электрическая
цепь с параллельным соединением элементов
Параллельным
называют такое соединение, при котором
все включенные в цепь потребители
электрической энергии, находятся под
одним и тем же напряжением (рис. 1.6).
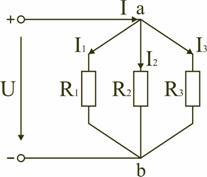
Рис.
1.6
В
этом случае они присоединены к двум
узлам цепи а и b, и на основании первого
закона Кирхгофа (1.3) можно записать, что
общий ток I всей цепи равен алгебраической
сумме токов отдельных ветвей:
I
= I1
+ I2
+ I3,
т.е.
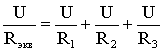 ,
,
откуда
следует, что
(1.6)
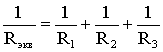 .
.
В
том случае, когда параллельно включены
два сопротивления R1
и R2,
они заменяются одним эквивалентным
сопротивлением
(1.7)
![]() .
.
Из
соотношения (1.6), следует, что эквивалентная
проводимость цепи равна арифметической
сумме проводимостей отдельных ветвей:
gэкв
= g1
+ g2
+ g3.
По
мере роста числа параллельно включенных
потребителей проводимость цепи gэкв
возрастает, и наоборот, общее сопротивление
Rэкв
уменьшается.
Напряжения
в электрической цепи с параллельно
соединенными сопротивлениями (рис. 1.6)
U
= IRэкв
= I1R1
= I2R2 =
I3R3.
Отсюда
следует, что
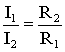 ,
,
т.е.
ток в цепи распределяется между
параллельными ветвями обратно
пропорционально их сопротивлениям.
По
параллельно включенной схеме работают
в номинальном режиме потребители любой
мощности, рассчитанные на одно и то же
напряжение. Причем включение или
отключение одного или нескольких
потребителей не отражается на работе
остальных. Поэтому эта схема является
основной схемой подключения потребителей
к источнику электрической энергии.
Электрическая
цепь со смешанным соединением элементов
Смешанным
называется такое соединение, при котором
в цепи имеются группы параллельно и
последовательно включенных сопротивлений.
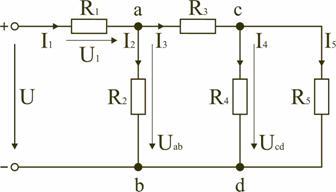
Рис.
1.7
Для
цепи, представленной на рис. 1.7, расчет
эквивалентного сопротивления начинается
с конца схемы. Для упрощения расчетов
примем, что все сопротивления в этой
схеме являются одинаковыми: R1=R2=R3=R4=R5=R.
Сопротивления R4
и R5
включены параллельно, тогда сопротивление
участка цепи cd равно:
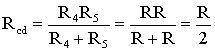 .
.
В
этом случае исходную схему (рис. 1.7)
можно представить в следующем виде
(рис. 1.8):
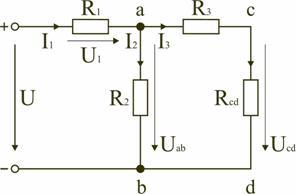
Рис.
1.8
На
схеме (рис. 1.8) сопротивление R3
и Rcd
соединены последовательно, и тогда
сопротивление участка цепи ad равно:
![]() .
.
Тогда
схему (рис. 1.8) можно представить в
сокращенном варианте (рис. 1.9):
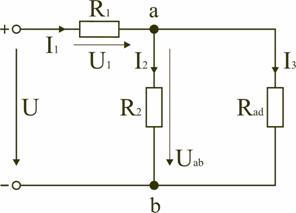
Рис.
1.9
На
схеме (рис. 1.9) сопротивление R2
и Rad
соединены параллельно, тогда сопротивление
участка цепи аb равно
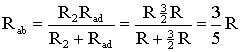 .
.
Схему
(рис. 1.9) можно представить в упрощенном
варианте (рис. 1.10), где сопротивления
R1
и Rab
включены последовательно.
Тогда
эквивалентное сопротивление исходной
схемы (рис. 1.7) будет равно:
![]() .
.
|
|
|
В
результате преобразований исходная
схема (рис. 1.7) представлена в виде
схемы (рис. 1.11) с одним сопротивлением
Rэкв.
Расчет токов и напряжений для всех
элементов схемы можно произвести по
законам Ома и Кирхгофа.
Соединение
элементов электрической цепи по схемам
«звезда» и «треугольник»
В
электротехнических и электронных
устройствах элементы цепи соединяются
по мостовой схеме (рис. 1.12). Сопротивления
R12,
R13,
R24,
R34
включены в плечи моста, в диагональ 1–4
включен источник питания с ЭДС Е, другая
диагональ 3–4 называется измерительной
диагональю моста.
|
|
|
В
мостовой схеме сопротивления R13,
R12,
R23
и R24,
R34,
R23
соединены по схеме «треугольник».
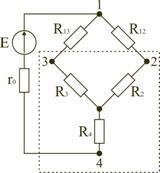
Эквивалентное сопротивление этой схемы
можно определить только после замены
одного из треугольников, например
треугольника R24
R34
R23
звездой R2
R3
R4
(рис. 1.13). Такая замена будет
эквивалентной, если она не вызовет
изменения токов всех остальных элементов
цепи. Для этого величины сопротивлений
звезды должны рассчитываться по следующим
соотношениям:
(1.8)
 ;
;
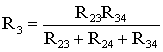 ;
;
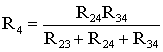 .
.
Для
замены схемы «звезда» эквивалентным
треугольником необходимо рассчитать
сопротивления треугольника:
(1.9)
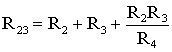 ;
;
![]() ;
;
![]() .
.
После
проведенных преобразований (рис. 1.13)
можно определить величину эквивалентного
сопротивления мостовой схемы (рис. 1.12)
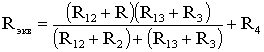 .
.