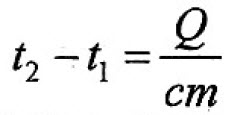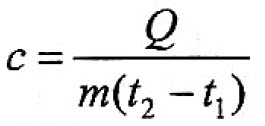как узнать количество теплоты если известен объём нагреваемой воды и разница температур в промежутке времени?
xxx xxx
Ученик
(65),
закрыт
5 лет назад
нагревается с помощью кипятильника.
Лучший ответ
Игорь Листерман
Ученик
(54)
13 лет назад
не играет роли чем вода нагревается!
Формула кол-ва теплоты
Q=cm(t2-t1)= с*рV*(t2-t1)
с – удельная теплоемкость… для воды 4200
масса вещества m = рV (плотность на объем) плотность для воды 1000
t2-t1 – измененние температуры
Источник: собственная голова
Остальные ответы
Похожие вопросы
Приветствую вас, уважаемые читатели, на своем канале!
В данной статье разберем вопрос 27 – расчеты теплового эффекта (по термохимическим уравнениям).
Теорию по данному заданию можно посмотреть здесь.
Данное задание не претерпело изменений. Рассмотрим пять примеров.
Пример 1 (из демонстрационного варианта ЕГЭ 2022)
Синтез аммиака протекает в соответствии с термохимических уравнением реакции:
N2(г) + 3H2(г) = 2NH3(г) + 92 кДж.
Определите количество теплоты, которое выделится в результате образования 560 мл (н.у.) газообразного аммиака. (Запишите число с точностью до сотых.)
Решение
1) Перепишем уравнение реакции, укажем мольное соотношение и тепловой эффект по реакции:
2) Переведем объем в литры – 0,56 л, количество теплоты обозначим за Q. Все эти данные подпишем над уравнением реакции:
3) Так как известен объем аммиака (NH3), то по реакции объем равен: 2*22,4:
4) Составим пропорцию и решим ее:
0,56/44,8 = Q/92
Q = 1,15 кДж.
Ответ: 1,15
Пример 2 (авторы: Е.А. Дацук и A.А. Степенин 2022)
В реакцию, термохимическое уравнение которой
C2H5OH(ж) + 3O2(г) = 2CO2(г) + 3H2O(ж) + 1374 кДж,
вступило 16,1 г этанола. Вычислите количество выделившейся при этом теплоты (в кДж). Ответ запишите с точностью до десятых.
Решение
1) Перепишем уравнение реакции, укажем мольное соотношение и тепловой эффект по реакции:
2) Масса этанола (С2H5OH) равна 16,1 г; количество теплоты обозначим за Q. Все эти данные подпишем над уравнением реакции:
3) Так как известна масса этанола (С2H5OH), то по реакции масса равна: 1*46:
4) Составим пропорцию и решим ее:
16,1/46 = Q/1374
Q = 480,9 кДж.
Ответ: 480,9
Пример 3 (авторы: Е.А. Дацук и A.А. Степенин 2022)
Теплота образования оксида алюминия из простых веществ составляет 1676 кДж/моль. Вычислите объем кислорода (при н.у.), вступивший в реакцию с алюминием, если в результате получено 502,8 кДж тепла. Ответ запишите с точностью до сотых.
Решение
1) Запишем уравнение реакции и укажем тепловой эффект реакции:
Откуда взялось число 3352? В условии сказано, что для 1-го моль оксида алюминия теплота составляет 1676 кДж, соответственно, для 2-х моль – 3352 кДж.
2) Объем кислорода (O2) обозначим за V, теплота равна 502,8 кДж. Все эти данные подпишем над уравнением реакции:
3) Необходимо найти объем кислорода (O2), поэтому по реакции объем равен: 3*22,4:
4) Составим пропорцию и решим ее:
V/67,2 = 502,8/3352
V = 10,08 л.
Ответ: 10,08
Пример 4 (автор: Ю. Н. Медведев 2022)
Определите тепловой эффект реакции
2С2H2 + 5O2 = 4CO2 + 2H2O + Q,
если известно, что при сгорании 3,36 л (при н.у.) ацетилена выделяется 195,75 кДж теплоты. (Запишите число с точностью до целых.)
Решение
1) Перепишем уравнение реакции, укажем мольное соотношение и тепловой эффект по реакции:
Тепловой эффект – неизвестный параметр, который необходимо найти.
2) Известен объем ацетилена (С2H2) 3,36 л и теплота 195,75 кДж. Все эти данные подпишем над уравнением реакции:
3) Так как известен объем ацетилена (С2H2), то объем по реакции равен: 2*22,4:
4) Составим пропорцию и решим ее:
3,36/44,8 = 195,75/Q
Q = 2610 кДж.
Ответ: 2610
Пример 5 (авторы: С.И. Широкопояс и И.С. Борисов 2022)
При сгорании навески неизвестного органического вещества выделяется 560 кДж теплоты и образуется 60 л углекислого газа. Вычислите количество теплоты, выделяющееся при образовании 108 л углекислого газа в тех же условиях. (Запишите ответ с точностью до целых)
Решение
Данную задачу можно решить через пропорцию без уравнения реакции, так как даны одинаковые условия.
Составим пропорцию:
60 л – 560 кДж
108 л – Q кДж, где Q – теплота, выделяющаяся при образовании 108 л углекислого газа (CO2).
Q = 1008 кДж.
Ответ: 1008
Если есть вопросы, то пишите в комментариях.
Разборы примеров предыдущих вопросов можно посмотреть здесь:
– вопрос 1;
– вопрос 2;
– вопрос 4.
Не забываем поставить лайк этой статье и подписаться на канал!
Всем успехов в изучении химии!
Вы познакомились с понятиями количества теплоты и удельной теплоемкости. В уроке «Расчет количества теплоты, необходимого для нагревании тела или выделяемого им при охлаждении» вы познакомились с основной формулой, которую мы будем использовать и в этом уроке:
$Q = cm(t_2 — t_1)$
В данном уроке мы рассмотрим задачи на нахождение различных величин, связанных с нагреванием и охлаждением тел. При их решении вам может понадобиться таблица значений удельной теплоемкости различных веществ из прошлого урока.
Задача №1 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое для нагрева $15 space кг$ меди на $80 degree C$.
Дано:
$m = 15 space кг$
$c = 400 frac{Дж}{кг cdot degree C}$
$Delta t = 80 degree C$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Для решения этой задачи мы будем использовать формулу для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
В данном случае нам не известны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = cm Delta t$.
Подставим значения всех величин и рассчитаем количество теплоты:
$Q = 400 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 80 degree C = 480 space 000 space Дж = 480 space кДж$.
Ответ: $Q = 480 space кДж$.
Задача №2 на расчет количества теплоты
Рассчитайте количество теплоты, необходимое, чтобы нагреть бассейн объемом $300 space м^3$ на $10 degree C$.
В задаче идет речь о бассейне, а значит, о пресной воде. Она имеет плотность, равную $1000 frac{кг}{м^3}$. Запишем условия задачи и решим ее.
Дано:
$V = 300 space м^3$
$Delta t = 10 degree C$
$c = 4200 frac{Дж}{кг cdot degree C}$
$rho = 1000 frac{кг}{м^3}$
$c = 4200 frac{Дж}{кг cdot degree C}$
$Q — ?$
Показать решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам неизвестна масса воды в бассейне, но известен ее объем и плотность. Плотность по определению:
$rho = frac{m}{V}$.
Тогда масса будет равна:
$m = rho V$.
Также нам неизвестны начальная и конечная температуры тела ($t_2$ и $t_1$). Нам известно изменение этой температуры: $Delta t = t_2 — t_1$. Тогда формула для расчета количества теплоты примет вид:
$Q = c rho V Delta t$.
Рассчитаем количество теплоты:
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1000 frac{кг}{м^3} cdot 300 space м^3 cdot 10 degree C = 12.6 cdot 10^9 space Дж = 12.6 space ГДж$.
Ответ: $Q = 12.6 space ГДж$.
Задача №3 на расчет массы
Найдите массу глицерина, если при нагревании от $10 degree C$ до $15 degree C$ он поглотил $12 space кДж$ теплоты. Удельная теплоемкость глицерина равна $2430 frac{Дж}{кг cdot degree C}$.
Дано:
$Q = 12 space кДж$
$t_1 = 10 degree C$
$t_2 = 15 degree C$
$c = 2430 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 12 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу глицерина:
$m = frac{Q}{c(t_2 — t_1)}$.
Рассчитаем:
$m = frac{12 cdot 10^3 space Дж}{2430 frac{Дж}{кг cdot degree C} cdot (15 degree C — 10 degree C)} approx 1 space кг$.
Ответ: $m approx 1 space кг$.
Задача №4 на расчет плотности
Определите плотность машинного масла объемом $1 space л$, если известно, что для увеличения температуры на $30 degree C$ ему требуется передать $45 space кДж$ теплоты. Удельная теплоемкость масла равна $1.67 frac{кДж}{кг cdot degree C}$.
Дано:
$V = 1 space л$
$Q = 45 space кДж$
$c = 1.67 frac{кДж}{кг cdot degree C}$
$Delta t = 30 degree C$
СИ:
$V = 10^{-3} space м^3$
$Q = 45 cdot 10^3 space Дж$
$c = 1.67 cdot 10^3 frac{Дж}{кг cdot degree C}$
$rho — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Нам известны изменение температуры ($Delta t = t_2 — t_1$), количество теплоты и удельная теплоемкость машинного масла. Выразим массу и рассчитаем ее:
$m = frac{Q}{c Delta t} = frac{45 cdot 10^3 space Дж}{1.67 cdot 10^3 frac{Дж}{кг cdot degree C} cdot 30 degree C} approx 0.9 space кг$.
По определению плотности:
$rho = frac{m}{V}$.
Рассчитаем плотность машинного масла:
$rho = frac{0.9 space кг}{10^{-3} space м^3} = 0.9 cdot 10^3 frac{кг}{м^3} = 900 frac{кг}{м^3}$.
Ответ: $rho = 900 frac{кг}{м^3}$.
Задача №5 на расчет удельной теплоемкости
В калориметр было налито $450 space г$ воды, температура которой $20 degree C$. Когда в эту воду погрузили $200 space г$ железных опилок, нагретых до $100 degree C$, температура воды стала равна $24 degree C$. Определите удельную теплоемкость опилок.
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “ж” для обозначения величин, связанных с железными опилками.
Дано:
$m_в = 450 space г$
$m_ж = 200 space г$
$t_{в1} = 20 degree C$
$t_{в2} = 24 degree C$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{ж1} = 100 degree C$
СИ:
$m_в = 0.45 space кг$
$m_ж = 0.2 space кг$
$с_ж — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела и выделяемого при его охлаждении:
$Q = cm(t_2 — t_1)$.
Запишем эту формулу для воды:
$Q_в = c_в m_в (t_{в2} — t_{в1})$.
Запишем формулу количества теплоты для железных опилок:
$Q_ж = c_ж m_ж (t_{ж2} — t_{ж1})$.
Нагретые железные опилки помещают в воду для их охлаждения. Значит, вода будет нагреваться и поглотит некоторое количество теплоты, а опилки будут охлаждаться и выделят некоторое количество теплоты. Т.е., между этими телами будет происходить теплообмен, для которого действует уже известное вам правило:
Если между телами происходит теплообмен, то внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Это значит, что количество теплоты $Q_в$, полученное водой, будет равно количеству теплоту $Q_ж$, которое выделится при охлаждении железных опилок, но с обратным знаком: $Q_в = — Q_ж$.
Подставим выражения, которые дает формула для расчета количества теплоты:
$c_в m_в (t_{в2} — t_{в1}) = — c_ж m_ж (t_{ж2} — t_{ж1})$.
После завершения теплообмена температура воды и температура железных опилок будут равны друг другу: $t_в2 = t_ж2 = t_2$.
Подставим в наше равенство и выразим $c_ж$:
$c_ж = — frac{c_в m_в (t_2 — t_{в1})}{m_ж (t_2 — t_{ж1})}$.
Рассчитаем удельную теплоемкость железных опилок:
$c_ж = — frac{4200 frac{Дж}{кг cdot degree C} cdot 0.45 space кг cdot (24 degree C — 20 degree C)}{0.2 space кг cdot (24 degree C — 100 degree C)} = — frac{7560 space Дж}{- 15.2 space кг cdot degree C} approx 497 frac{Дж}{кг cdot degree C} approx 0.5 frac{кДж}{кг cdot degree C}$.
Ответ: $c_ж approx 0.5 frac{кДж}{кг cdot degree C}$.
Задача №6 на использование графика
Используя график зависимости температуры керосина от сообщенного ему количества теплоты (рисунок 1), определите массу керосина.
Для начала нам нужно записать условия задачи. Из графика мы видим, что начальная температура керосина $t_1$ была равна $0 degree C$. Теперь выберем удобную нам точку на графике. Например, когда керосину сообщили количество теплоты $Q$, равное $2 space кДж$, его температура $t_2$ стала равной $10 degree C$. Теперь мы можем записать условия задачи и решить ее. Удельная теплоемкость керосина известна нам из таблицы.
Дано:
$Q = 2 space кДж$
$t_1 = 0 degree C$
$t_2 = 10 degree C$
$c = 2100 frac{Дж}{кг cdot degree C}$
СИ:
$Q = 2 cdot 10^3 space Дж$
$m — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Формула для расчета количества теплоты, необходимого для нагревания тела:
$Q = cm(t_2 — t_1)$.
Выразим отсюда массу:
$m = frac{Q}{c (t_2 — t_1)}$.
Рассчитаем ее:
$m = frac{2 cdot 10^3 space Дж}{2100 frac{Дж}{кг cdot degree C} cdot (10 degree C — 0 degree C)} approx 0.095 space кг approx 100 space г$.
Ответ: $m approx 100 space г$.
Задача №7 на расчет температуры нагрева
Стальной резец массой $2 space кг$ был нагрет до температуры $800 degree C$ и затем опущен в сосуд, содержащий $15 space л$ воды при температуре $10 degree C$. До какой температуры нагреется вода в сосуде?
Записывая условия задачи, используем индекс “в” для обозначения величин, связанных с водой, и индекс “р” для обозначения величин, связанных со стальным резцом.
Дано:
$V_в = 15 space л$
$m_р = 2 space кг$
$t_{р1} = 800 degree C$
$c_р = 500 frac{Дж}{кг cdot degree C}$
$rho_в = 1000 frac{кг}{м^3}$
$c_в = 4200 frac{Дж}{кг cdot degree C}$
$t_{в1} = 10 degree C$
СИ:
$V_в = 15 cdot 10^3 м^3$
$t_{в2} — ?$
Посмотреть решение и ответ
Скрыть
Решение:
Когда нагретый резец опускают в холодную воду, между этими двумя телами происходит теплообмен. Резец остывает и выделяет энергию, а вода получает эту энергию и нагревается. Соответственно, количество теплоты, которое выделится при остывании стального резца, численно будет равно количеству теплоту, которое получит вода.
Когда теплообмен завершится,температуры стального резца и воды будут одинаковы: $t_{в2} = t_{р2} = t_2$.
Запишем формулу для расчета количества теплоты, которое выделится при остывании резца:
$Q_р = с_р m_р (t_2 — t_{р1})$.
Запишем формулу для расчета количества теплоты, которое получила вода:
$Q_в = с_в m_в (t_2 — t_{в1})$.
Приравняем правые части этих уравнений, не забыв про знак “минус”, которые указывает на выделение энергии при охлаждении тела:
$с_р m_р (t_2 — t_{р1}) = — с_в m_в (t_2 — t_{в1})$.
Раскроем скобки:
$с_р m_р t_2 — с_р m_р t_{р1} = — с_в m_в t_2 + с_в m_в t_{в1}$.
Перенесем множители с $t_2$ на одну сторону уравнения и выразим эту температуру, до которой нагреется вода:
$с_р m_р t_2 + с_в m_в t_2 = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 (с_р m_р + с_в m_в) = с_в m_в t_{в1} + с_р m_р t_{р1}$,
$t_2 = frac{с_в m_в t_{в1} + с_р m_р t_{р1}}{с_р m_р + с_в m_в}$.
Нам неизвестна масса воды, но известны ее плотность и объем. Выразим и рассчитаем массу через эти величины:
$m_в = rho_в V_в = 1000 frac{кг}{м^3} cdot 15 cdot 10^3 м^3 = 15 space кг$.
Теперь мы можем рассчитать температуру $t_2$:
$t_2 = frac{4200 frac{Дж}{кг cdot degree C} cdot 15 space кг cdot 10 degree C + 500 frac{Дж}{кг cdot degree C} cdot 2 space кг cdot 800 degree C}{500 frac{Дж}{кг cdot degree C} cdot 2 space кг + 4200 frac{Дж}{кг cdot degree C} cdot 15 space кг} = frac{630 cdot 10^3 space Дж + 800 cdot 10^3 space Дж}{1 cdot 10^3 frac{Дж}{degree C} + 63 cdot 10^3 frac{Дж}{degree C}} = frac{1430 cdot 10^3 space Дж}{64 cdot 10^3 frac{Дж}{degree C}} approx 22.3 degree C$.
Ответ: $t_2 approx 22.3 degree C$.
Какой температуры получится вода, если смешать $0.02 space кг$ воды при $15 degree C$, $0.03 space кг$ воды при $25 degree C$ и $0.01 space кг$ воды при $60 degree C$?
Дано:
$m_1 = 0.02 space кг$
$t_1 = 15 degree C$
$m_2 = 0.03 space кг$
$t_2 = 25 degree C$
$m_3 = 0.01 space кг$
$t_3 = 60 degree C$
$t — ?$
Посмотреть решение и ответ
Скрыть
Решение:
При смешивании жидкостей разных температур, мы знаем, что внутренняя энергия всех нагревающихся тел увеличивается на столько, на сколько уменьшается внутренняя энергия остывающих тел.
Для смешивания двух жидкостей мы можем записать, что $Q_1 = — Q_2$ или $Q_1 + Q_2 = 0$.
Сначала рассмотрим смешивание первых двух порций воды. Первая порция с температурой $15 degree C$ будет нагреваться (получать энергию), а вторая порция с температурой $25 degree C$ будет охлаждаться (выделять энергию). Эти энергии будут численно равны друг другу, но противоположны по знаку:
$cm_1(t_{1+2} — t_1) = — cm_2(t_{1+2} — t_2)$.
Найдем конечную температуру этой смеси:
$m_1(t_{1+2} — t_1) = — m_2 (t_{1+2} — t_2)$,
$m_1 t_{1+2} — m_1 t_1 = -m_2 t_{1+2} + m_2 t_2$,
$t_{1+2} (m_1 + m_2) = m_1 t_1 + m_2 t_2$,
$t_{1+2} = frac{m_1 t_1 + m_2 t_2}{m_1 + m_2} = frac{0.02 space кг cdot 15 degree C + 0.03 space кг cdot 25 degree }{0.02 space кг + 0.03 space кг} = frac{0.3 space кг cdot degree + 0.75 space кг cdot degree C}{0.05 space кг} = 21 degree C$.
Так мы получили смесь первой и второй порций воды массой $m_{1+2} = 0.05 space кг$ и температурой $t_{1+2} = 21 degree C$.
Теперь добавим третью порцию воды в полученную смесь. Смесь будет нагреваться (получать энергию), а третья порция воды будет охлаждаться (выделять энергию):
$Q_{1+2} = — Q_3$.
$cm_{1+2} (t — t_{1+2}) = — cm_3 (t — t_3)$,
$m_{1+2} (t — t_{1+2}) = — m_3 (t — t_3)$.
Выразим отсюда конечную температуру смеси из трех порций воды $t$:
$m_{1+2} t — m_{1+2} t_{1+2} = -m_3 t + m_3 t_3$,
$t (m_{1+2} + m_3) = m_{1+2} t_{1+2} + m_3 t_3$,
$t = frac{m_{1+2} t_{1+2} + m_3 t_3}{m_{1+2} + m_3}$.
Рассчитаем ее:
$t = frac{0.05 space кг cdot 21 degree C + 0.01 space кг cdot 60 degree}{0.05 space кг + 0.01 space кг} = frac{1.05 space кг cdot degree C + 0.6 space кг cdot degree C}{0.06 space кг} = 27.5 degree C$.
Ответ: $t = 27.5 degree C$.
Задача №9 на расчет количества теплоты, рассеиваемого в окружающую среду
Электрочайник с водой нагревается от температуры $70 degree C$ до температуры $80 degree C$ за $3 space мин$, а остывает от температуры $80 degree C$ до температуры $70 degree C$ за $9 space мин$. Какая часть количества теплоты, выделяемой спиралью чайника при нагревании воды, рассеивается в окружающую среду? Тепловые потери считать постоянными.
Внесем необходимые пояснения. Спираль чайника передает воде определенное количество теплоты $Q_2$. Часть ее ($Q_1$) рассеивается в окружающую среду. Т.е., количество теплоты $Q_2$, выделяемое спиралью, больше количества теплоты $Q$, необходимого для нагрева воды.
Дано:
$t_1 = 70 degree C$
$t_2 = 80 degree C$
$T_1 = 3 space мин$
$T_2 = 9 space мин$
$frac{Q_1}{Q_2} — ?$
Показать решение и ответ
Скрыть
Решение:
Сначала рассчитаем количество теплоты, которое необходимо сообщить воде в чайнике, чтобы ее температура увеличилась с $70 degree C$ до $80 degree C$:
$Q = cm(t_2 — t_1)$.
Масса воды в чайнике нам неизвестна, поэтому примем ее, равной $1 space кг$. Тогда,
$Q = 4200 frac{Дж}{кг cdot degree C} cdot 1 space кг cdot (80 degree C — 70 degree C) = 42 space 000 space Дж = 42 space кДж$.
Когда вода в чайнике остывает с температуры $80 degree C$ до температуры $70 degree C$, она выделяет в окружающую среду точно такое же количество энергии $Q$. Остывание происходит за $9 space мин$. Значит, количество теплоты, которое выделяется в окружающую среду за $1 space мин$ будет равно:
$Q_0 = frac{42 space кДж}{9 space мин} approx 4.7 frac{кДж}{мин}$.
В условиях задачи сказано, что тепловые потери постоянны. Это означает, что вода массой $1 space кг$ отдает $4.7 space кДж$ каждую минуту, в том числе, и при ее нагревании.
Нагревается вода за 3 минуты. За это время она отдает в окружающую среду следующее количество теплоты:
$Q_1 = 4.7 space кДж cdot 3 = 14.1 space кДж$.
Тем не менее, чайник нагрел воду до нужной температуры. Значит, он сообщил воде количество энергии, равное $Q_2 = Q + Q_1$.
$Q_2 = 42 space кДж + 14.1 space кДж = 56.1 space кДж$.
Теперь мы можем рассчитать отношение $frac{Q_1}{Q_2}$, и узнать какая часть теплоты, выделяемая спиралью чайника, рассеивается в окружающую среду:
$frac{Q_1}{Q_2} = frac{14.1 space кДж}{56.1 space кДж} approx 0.25$.
Т.е., в окружающую среду рассеивается $frac{1}{4}$ часть энергии, сообщаемая воде в чайнике.
Можно доказать, что это соотношение останется постоянным для воды любой массы в этой задаче. Чем больше будет масса воды, тем больше энергии ей будет нужно, чтобы нагреться до определенной температуры. Больше будут и тепловые потери. Искомое соотношение же останется неизменным.
Ответ: $frac{Q_1}{Q_2} approx 0.25$.
Физика под удельной теплоемкостью понимает количество теплоты, которое термодинамическое вещество или система способно поглотить до повышения температуры.
Определение из учебника говорит, что это количество тепла, необходимое для создания температуры при нагревании.
Количество теплоты
Единица измерения – джоуль. Другой распространенной формой измерения является использование калорий.

Обозначается латинской буквой Q.
Удельная теплоемкость вещества
Это физическая величина, выражающая количество тепла, необходимое веществу на единицу массы для повышения температуры на одну единицу.
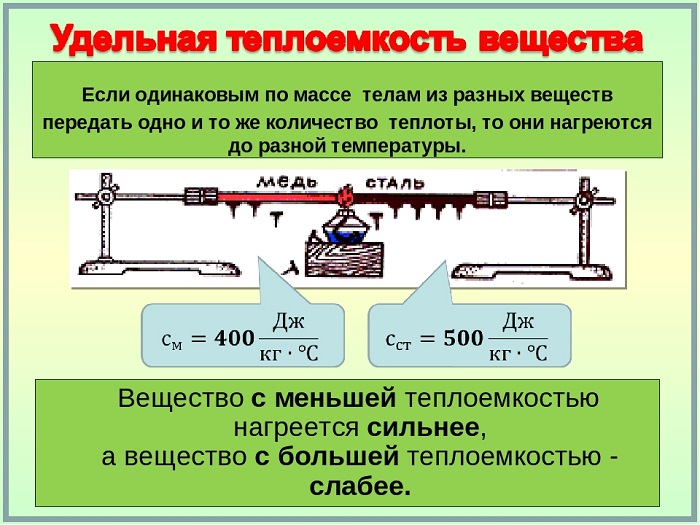
Таким образом, удельная теплоёмкость является свойством вещества, поскольку его значение является репрезентативным для каждого вещества, каждое из которых, в свою очередь, имеет различные значения в зависимости от того, в каком состоянии оно находится (жидкое, твердое или газообразное).
Удельная теплоёмкость обозначается маленькой буквой c и измеряется в Дж/кг∗°С, представляет собой коэффициент повышения температуры в одной единице всей системы или всей массы вещества.
Кроме того, удельная теплоёмкость меняется в зависимости от физического состояния вещества, особенно в случае твердых частиц и газов, поскольку его молекулярная структура влияет на теплопередачу в системе частиц. То же самое относится и к условиям атмосферного давления: чем выше давление, тем ниже удельное тепло.
Основной состав удельной теплоты вещества должен быть с = С/m, т. е. удельная теплота равна соотношению калорийности и массы. Однако когда это применяется к данному изменению температуры, говорят о средней удельной теплоемкости, которая рассчитывается на основе следующей формулы:
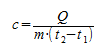
где:
Q – передача тепловой энергии между системой и средой (Дж);
m – масса системы (кг);
Δt или (t2 – t1) – повышение температуры, которой она подвергается (°C).
Формула для нахождения количества теплоты Q:
Q = c∗m(t2 – t1)
Чем выше удельная теплоёмкость вещества, тем больше тепловой энергии потребуется, чтобы его температура повысилась. Например, для нагрева воды (своды = 4200 Дж/кг∗°С) потребуется больше тепловой энергии, чем для нагрева свинца (ссвинца = 140 Дж/кг∗°С).
Уравнение теплового баланса:
Q отданное + Q полученное = 0.
Ниже представлена таблица значений удельной теплоёмкости некоторых веществ:

Примеры решения задач
Следующие задачи покажут примеры расчета необходимого количества теплоты.
Задача №1
Сколько теплоты нужно, чтобы изо льда массой 2 кг, взятого при температуре -10°С, получить пар при 100°С?
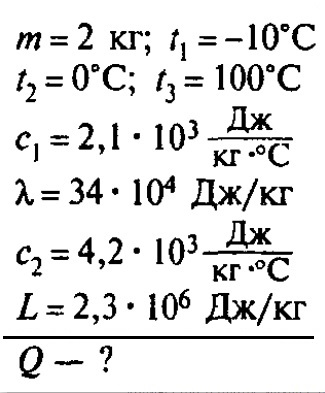
Решение:
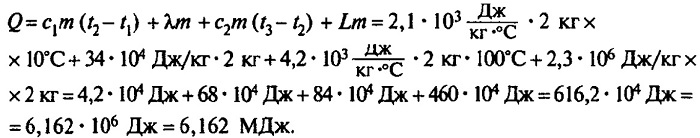
Ответ: чтобы изо льда массой 2 кг, взятого при температуре -10°С, получить пар при 100°С, нужно взять 6,162 мегаджоулей теплоты.
Задача №2
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100°С?
Начнем решение и отметим, что нагреваться будет и котёл, и вода. Разница температур составит 1000С — 100С = 900С. Т. е. и температура котла изменится на 90 градусов, и температура воды также изменится на 90 градусов.
Количества теплоты, которые получили оба объекта (Q1
– для котла и Q2 — для воды), не будут одинаковыми. Мы найдем общее количество теплоты по формуле теплового баланса Q = Q1 + Q2.
Задачи на количество теплоты с решениями
Формулы, используемые на уроках «Задачи на количество теплоты,
удельную теплоемкость».
Название величины |
Обозначение |
Единица измерения |
Формула |
Масса |
m |
кг |
|
Температура |
t |
°С |
|
Удельная теплоемкость |
c |
Дж/кг•°С |
|
Количество теплоты |
Q |
Дж |
|
1 г = 0,001 кг; 1 т = 1000 кг; 1 кДж = 1000 Дж; 1 МДж = 1000000 Дж

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В железный котёл массой 5 кг налита вода массой 10 кг. Какое количество теплоты нужно передать котлу с водой для изменения их температуры от 10 до 100 °С?
При решении задачи нужно учесть, что оба тела — и котёл, и вода — будут нагреваться вместе. Между ними происходит теплообмен. Их температуры можно считать одинаковыми, т. е. температура котла и воды изменяется на 100 °С — 10 °С = 90 °С. Но количества теплоты, полученные котлом и водой, не будут одинаковыми. Ведь их массы и удельные теплоёмкости различны.

Задача № 2.
Смешали воду массой 0,8 кг, имеющую температуру 25 °С, и воду при температуре 100 °С массой 0,2 кг. Температуру полученной смеси измерили, и она оказалась равной 40 °С. Вычислите, какое количество теплоты отдала горячая вода при остывании и получила холодная вода при нагревании. Сравните эти количества теплоты.

Задача № 3.
Стальная деталь массой 3 кг нагрелась от 25 до 45 °С. Какое количество теплоты было израсходовано?

Задача № 4.
В сосуде содержится 3 л воды при температуре 20 °С. Сколько воды при температуре 45 °С надо добавить в сосуд, чтобы в нём установилась температура 30 °С? Необходимый свободный объём в сосуде имеется. Теплообменом с окружающей средой пренебречь

Задача № 5.
На сколько градусов изменилась температура чугунной детали массой 12 кг, если при остывании она отдала 648000 Дж теплоты?

Задача № 6.
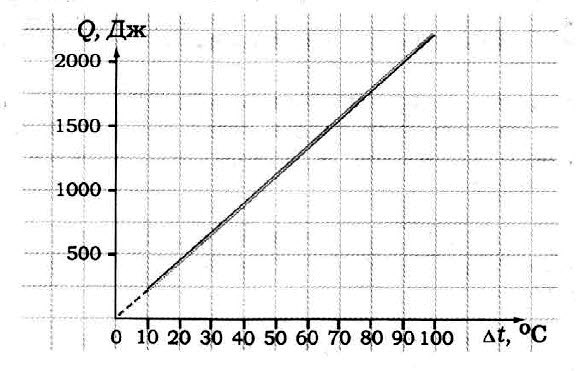
По графику определите удельную теплоёмкость образца, если его масса 50 г.

Задача № 7.
Для нагревания медного бруска массой 3 кг от 20 до 30 °С потребовалось 12000 Дж теплоты. Какова удельная теплоемкость меди?

Задача № 8.
Нагретый камень массой 5 кг, охлаждаясь в воде на 1 °С, передает ей 2,1 кДж энергии. Чему равна удельная теплоемкость камня?
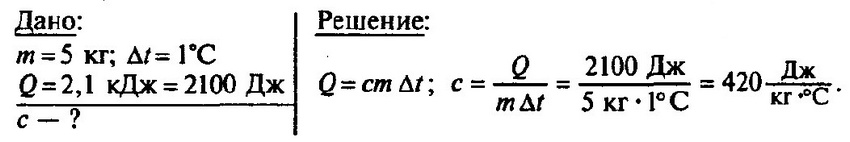
Задача № 9.
Какое количество теплоты потребуется для нагревания на 1 °С воды объемом 0,5 л; олова массой 500 г; серебра объемом 2 см3; стали объемом 0,5 м3; латуни массой 0,2 т?

Задача № 10.
Какое количество теплоты получили алюминиевая кастрюля массой 200 г и находящаяся в ней вода объемом 1,5 л при нагревании от 20 °С до кипения при температуре 100 °С?

Задача № 11.
а) Воздух, заполняющий объем 0,5 л в цилиндре с легким поршнем, нагрели от 0 до 30 °С при постоянном атмосферном давлении. Какое количество теплоты получил воздух?
б) В порожнем закрытом металлическом баке вместимостью 60 м3 под действием солнечного излучения воздух нагрелся от 0 до 20 °С. Как и на сколько изменилась внутренняя энергия воздуха в баке? (Удельная теплоемкость воздуха при постоянном объеме равна 720 Дж/кг-°С.)

Задача № 12.
ОГЭ
Металлический цилиндр массой m = 60 г нагрели в кипятке до температуры t = 100 °С и опустили в воду, масса которой mв = 300 г, а температура tв = 24 °С. Температура воды и цилиндра стала равной Θ = 27 °С. Найти удельную теплоёмкость металла, из которого изготовлен цилиндр. Удельная теплоёмкость воды св = 4200 Дж/(кг К).

Задача № 13.
В теплоизолированном сосуде сначала смешивают три порции воды 100 г, 200 г и 300 г с начальными температурами 20 °C, 70 °C и 50 °C соответственно. После установления теплового равновесия в сосуд добавляют новую порцию воды массой 400 г при температуре 20 °C. Определите конечную температуру в сосуде. Ответ дайте в °C, округлив до целого числа. Теплоёмкостью калориметра пренебрегите.
Решение.

Ответ: 39 °С.
Задача № 14. (повышенной сложности)
Стальной шарик радиусом 5 см, нагретый до температуры 500 ˚С, положили на лед, температура которого 0 ˚С. На какую глубину погрузится шарик в лед? (Считать, что шарик погрузился в лед полностью. Теплопроводностью шарика и нагреванием воды пренебречь.)
Дано: R = 0,05 м; t1 = 500 ˚С; t2 = 0 ˚С;
ρ1 (плотность стали) = 7800 кг/м3.;
ρ2 (плотность льда) = 900 кг/м3.
c (удельная теплоемкость стали) = 460 Дж/кг •˚С,
λ (удельная теплота плавления льда) = 3,3 • 105 Дж/кг,
Найти: h – ?

Краткая теория для решения Задачи на количество теплоты.

Конспект урока «Задачи на количество теплоты».
Посмотреть конспект урока по теме «Количество теплоты. Удельная теплоемкость»
Следующая тема: «ЗАДАЧИ на сгорание топлива с решениями».