Создатель теории приближенных вычислений А. Н. Крылов говорил: «При производстве всяких численных вычислений надо руководствоваться правилом: точность вычислений должна соответствовать точности данных и той практической потребности, для которой вычисления производятся». Ему же принадлежат слова: «Помните, что каждая неверная цифра — это ошибка, всякая лишняя цифра — это пол-ошибки».
Приближенные числа записываются, как правило, при помощи десятичных дробей. Между записью приближенных и точных чисел есть различия. Если перед нами точное число, то вес его цифры являются верными, точными. Что же касается приближенного числа, то некоторые его цифры верны, а другие являются сомнительными.
Цифра десятичного разряда приближенного числа 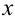 приближения
приближения 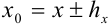 называется верной, если в том же десятичном разряде чисел
называется верной, если в том же десятичном разряде чисел 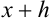 и
и 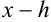 стоит эта же цифра. В противном случае она называется сомнительной.
стоит эта же цифра. В противном случае она называется сомнительной.
Проверку на верные и сомнительные цифры нужно начинать слева направо с наивысшего разряда. Все цифры, стоящие правее первой найденной сомнительной цифры, автоматически считаются сомнительными.

Пример №45.4.
Найдите верные и сомнительные цифры в записи числа 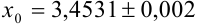 .
.
Решение:
Поскольку 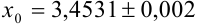 , запишем диапазон возможных значений
, запишем диапазон возможных значений  в виде двойного неравенства:
в виде двойного неравенства:
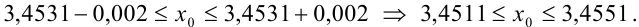
Начинаем проверку на верные и сомнительные цифры с наивысшего разряда — единиц. Видим, что цифры 3,45 одинаковы в левой и правой части двойного неравенства (т.е. в записи  и
и 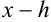 ), следовательно, по определению в записи приближенного числа 3,4531 эти цифры являются верными.
), следовательно, по определению в записи приближенного числа 3,4531 эти цифры являются верными.
Цифры в разряде тысячных в правой и левой части двойного неравенства отличаются (1 и 5), следовательно, в записи приближенного числа 3,4531 цифра 3, стоящая в разряде тысячных, и цифра 1, стоящая за ней, являются сомнительными.
Итак, точное число  обязательно начинается с цифр 3,45. Какие цифры стоят в остальных разрядах числа, точно сказать невозможно.
обязательно начинается с цифр 3,45. Какие цифры стоят в остальных разрядах числа, точно сказать невозможно.
Ответ:
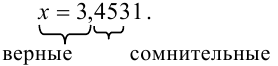
Для записи приближенных чисел существуют следующие правила:
- Оставлять в записи числа только верные цифры.
- Если в десятичной дроби последние верные цифры нули, то их надо выписывать.
- Если число содержит на конце целой части сомнительные цифры, то они должны быть заменены на
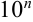 , где
, где  — число цифр, которые нужно заменить.
— число цифр, которые нужно заменить. - Граница абсолютной погрешности числа, содержащего только верные цифры, равна единице последнего разряда.
Проиллюстрируем применение данных правил на конкретных примерах.
1. Поскольку в записи числа следует оставлять только верные цифры, то в примере 45.4 точное значение  будет записано следующим образом:
будет записано следующим образом: 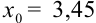 . В этом случае граница абсолютной погрешности
. В этом случае граница абсолютной погрешности 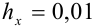 .
.
2. Если задано число 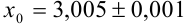 , то нетрудно показать, что в записи приближенного числа 3,005 цифры 3,00 являются верными, а 5 — сомнительной. Для записи точного числа
, то нетрудно показать, что в записи приближенного числа 3,005 цифры 3,00 являются верными, а 5 — сомнительной. Для записи точного числа  выпишем все его верные цифры, включая нули на конце:
выпишем все его верные цифры, включая нули на конце: 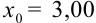 . Эта запись показывает, что граница абсолютной погрешности равна единице последнего разряда, т.е. 0,01. Если бы мы записали это число как
. Эта запись показывает, что граница абсолютной погрешности равна единице последнего разряда, т.е. 0,01. Если бы мы записали это число как 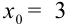 , то граница абсолютной погрешности была бы равна 1, а это значительно более низкая точность, чем заданная в примере 0,01.
, то граница абсолютной погрешности была бы равна 1, а это значительно более низкая точность, чем заданная в примере 0,01.
3. Пусть задано число 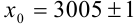 . В записи приближенного числа 3005 цифры 300 являются верными, а 5 — сомнительной. Для записи точного числа
. В записи приближенного числа 3005 цифры 300 являются верными, а 5 — сомнительной. Для записи точного числа  выпишем вес его верные цифры 300, а вместо одной сомнительной цифры 5 запишем умножение на
выпишем вес его верные цифры 300, а вместо одной сомнительной цифры 5 запишем умножение на 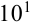 , поскольку заменяем только одну цифру. Тогда
, поскольку заменяем только одну цифру. Тогда 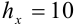 .
.
В науке принято записывать числа в стандартном виде, т.е. в виде 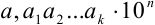 , где
, где 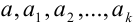 — цифры, причем
— цифры, причем 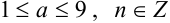 (в целой части числа стоит только одна цифра, отличная от нуля). Число
(в целой части числа стоит только одна цифра, отличная от нуля). Число 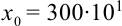 в стандартном виде будет представлено как
в стандартном виде будет представлено как 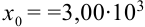 .
.
Значащими цифрами числа называют все его верные цифры, за исключением нулей, стоящих левее первой отличной от нуля цифры.
Например, число 0,712 содержит три значащие цифры: 7, 1, 2. Число 0,00012 — две значащие цифры: 1 и 2. Число 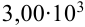 — три значащие цифры: 3, 0, 0.
— три значащие цифры: 3, 0, 0.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Предмет высшая математика
Другие лекции по высшей математике, возможно вам пригодятся:

Верные значащие цифры приближенного числа
Определение
5:
Значащими
цифрами
числа а
называют все цифры в его записи, начиная
с первой ненулевой слева.
Пример 5:
Числа 0,001405и 5,0300 имеют соответственно
4 и 5 значащих цифр. Ноль, записанный в
конце десятичной дроби, всегда значащая
цифра. В числе 5,0300 последний ноль
показывает, что число задано с точностью
до десятитысячных.
Определение
6:
Значащую цифру числа
а
называют верной,
если абсолютная погрешность числа не
превосходит половины единицы разряда,
соответствующего этой цифре.
Пример 6:
Сколько верных значащих цифр содержит
приближенное число
![]()
?
Решение:
Поскольку
![]()
,
то верными будут цифры 5, 8, 2.
Погрешности математических операций Абсолютная погрешность суммы и разности
Теорема 1:
Абсолютная
погрешность
алгебраической
суммы
нескольких приближенных чисел не
превышает суммы алгебраических
погрешностей этих чисел.
Доказательство:
Пусть
![]()
– алгебраическая сумма точных чисел.
![]()
– сумма приближенных значений этих
чисел.
Абсолютные
погрешности их соответственно равны:
![]()
.
Вычитая из точного значения суммы её
приближенное значение, имеем:
![]()
или, переходя к
модулям:
![]()
,
следовательно
![]()
,
что требовалось
доказать.
Из последней
формулы следует, что абсолютная
погрешность алгебраической суммы не
может быть меньше абсолютной погрешности
наименее точного из слагаемых.
Пример 7:
![]()
,
где числа 204,4 и
144,2 верны с точностью до 0,1.
Значит, остальные
нужно округлить с точностью до 0,01,
сложить и округлить результат до 0,1.
Итак
![]()
Относительная погрешность произведения нескольких приближенных чисел
Теорема 2:
Относительная
погрешность произведения
нескольких
приближенных чисел, отличных от нуля,
не превышает суммы относительных
погрешностей этих чисел.
Доказательство:
Пусть
![]()
(1), где
![]()
– положительные
приближенные числа и их абсолютные
погрешности:
![]()
.
Логарифмируя (1),
получим:
![]()
.
По теореме об
абсолютной погрешности суммы:
![]()
.
Используя то, что
![]()
,
получим
![]()
,
что требовалось
доказать.
Относительная погрешность частного
Теорема 3:
Относительная
погрешность частного не превышает суммы
относительных погрешностей делимого
и делителя.
Доказательство:
Пусть
![]()
– приближенные числа, а
![]()
– абсолютные погрешности этих чисел.
По теореме об абсолютной погрешности
алгебраической суммы:
![]()
,
что требовалось
доказать.
Относительная погрешность натуральной степени и корня
Теорема 4:
Относительная погрешность m-й
степени
приближенного числа (m-натуральное)
в m
раз больше относительной
погрешности
самого числа.
Доказательство:
Пусть
![]()
,
тогда
![]()
,
что требовалось
доказать.
Вывод:
В результате вычисления степени
приближенного числа следует оставить
столько верных значащих цифр, сколько
верных значащих цифр в основании.
Теорема 5:
Относительная
погрешность
корня m-й
степени в m
раз меньше предельной относительной
погрешности
подкоренного числа.
Доказательство:
Пусть
![]()
,
тогда
![]()
,
т.е.
![]()
.
Правила подсчета цифр
При массовых
вычислениях с приближенными или точными
числами, а также с числами, у которых
погрешность отсутствует, используют
правила
подсчета цифр:
-
промежуточные
вычисления следует получать хотя бы
с одной запасной цифрой, по отношению
к значащим цифрам
чисел,
участвующим в промежуточном вычислении, -
окончательный
результат вычисления содержит то
количество значащих цифр, которое
имеет исходное число с наименьшим
числом значащих цифр.
Пример 8:
Вычислить выражение: Y
= 0,125а2
(8b-c),
где a
= 18; b
= 2,75; c
= 3,232.
Решение:.
Так как погрешность чисел а,b,с
отсутствует
то вычисления производим в соответствии
с правилами подсчета цифр.
Преобразуем
исходное выражение к следующему, более
рациональному виду :
Y =.0,125а2
(8b-c)
= a2
(b-c/8)
Исходное выражение
содержало 5 действий, а окончательное
выражение содержит 4 действия.
Далее последовательно
производим необходимые вычисления (в
соответствии с числом а
= 18, у которого
две значащие цифры) и записываем результат
в форме с плавающей запятой:
Y
= 324 • (2,75 –
0,404) = 324 • 2,346 = 760 = 7,6 • 102.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Абсолютная погрешность приближенного значения числа, граница абсолютной погрешности, верные и значащие цифры числа
Верные и значащие цифры числа. Округление чисел.
Наша система счета или счисления называется десятичной системой счисления, а 10 – основанием этой системы:
разряд единиц, разряд десятков, разряд сотен и т.д. Аналогично, разряды десятичных дробей: десятые, сотые, тысячные и т.д.
|
Дробь |
Целая часть |
Дробная часть |
||||||
|
разряды |
тысячи |
сотни |
десятки |
единицы |
, |
десятые |
сотые |
тысячные |
|
258,034 |
– |
2 |
5 |
8 |
, |
0 |
3 |
4 |
В приближенном числе различают верные и сомнительные цифры. Цифра какого-либо разряда приближенного числа а считается верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записана эта цифра.
Если же граница абсолютной погрешности больше единицы какого-либо разряда, то цифра этого разряда и все цифры, расположенные справа от нее считаются сомнительными. Граница абсолютной погрешности ∆а находится непосредственно по записи приближенного значения а числа х.
Например:
24,5 ± 0,3 (| х – а | ≤ ∆а )
Приближенное значение 24,5
Граница абсолютной погрешности 0,3
0,3 < 1, значит верные цифры (в широком смысле) – это 2 и 4, а цифра 5 – сомнительная.
375 ± 20
Приближенное значение 375
Граница абсолютной погрешности 20
20 < 100, значит верная цифра 3, а цифры 7 и 5 сомнительные.
Когда рассматриваем верные цифры в широком смысле, то достаточно посмотреть на границу абсолютной погрешности и взять цифры приближенного числа, которые на разряд больше, чем граница абсолютной погрешности.
Цифра какого-либо разряда приближенного числа а считается верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана эта цифра. Если же граница абсолютной погрешности больше половины единицы какого-либо разряда, то цифра этого разряда и все цифры, расположенные справа от нее считаются сомнительными.
В числах, полученных в результате измерений или вычислений и используемых при расчётах в качестве исходных данных, а также в десятичной записи приближенного значения числа, все цифры должны быть верными.
Значащими цифрами приближенного числа, выраженного десятичной дробью считаются все верные цифры этой дроби, кроме нулей, стоящих перед первой цифрой (слева направо), отличной от нуля.
Например:
Приближенное число 10,408 имеет 5 значащих цифр, так как крайняя слева цифра числа отлична от нуля (она равна 1)
Приближенное число 0,01104 имеет 4 значащие цифры:1, 1, 0, 4. Два нуля, стоящие слева от 1 не считаются значащими цифрами
Приближенное число 0,030 имеет 2 значащие цифры: 3 и 0 справа, по правилу два нуля, стоящие слева от цифры 3, не относятся к значащим.
Значащими цифрами приближенного целого числа считаются все его цифры, кроме нулей, поставленных взамен отброшенных или
неизвестных цифр.
Например: Частное
Число 6000 имеет 3 значащие цифры, так как один последний нуль поставлен вместо отброшенной цифры (единицы).
Округление чисел. При округлении числа а его заменяют числом а1 с меньшим количеством значащих цифр. Абсолютная величина разности
| а – а1 | называется погрешностью округления.
При округлении числа до m значащих цифр отбрасываются все цифры, стоящие правее m-й значащей цифры, или при сохранении разрядов заменят их нулями. При этом, если первая слева от отброшенных цифр больше или равна 5, то последнюю оставшуюся цифру увеличивают на 1.
При применении этого правила погрешность округления не превосходит половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой.
Округление приближенных значений чисел с сохранением в записи только верных цифр производится до разряда, в котором записана первая справа верная цифра.
Например:
Округлите до первого справа верного разряда приближенные значения данных чисел:
0,3281 ± 0,05
Граница абсолютной погрешности 0,05 (разряд – сотые) цифры справа налево:1 – сомнительная, 8 – сомнительная, 2 – сомнительная, 3 – верная цифра 3
Погрешность округления:
|0,3281 – 0,3| = 0,0281
0,05 + 0,0281 = 0,0781
Ответ 0,3 ± 0,08
Значащие цифры десятичного числа – это все его цифры, начиная с первой ненулевой слева.
Пример 1
x = 0.002036, цифры 2036 являются значащими;
x = 2.27×106, значащими цифрами являются цифры 2, 2, 7;
x = 2270000, все цифры этого числа являются значащими.
Значащая цифра в записи числа верна, если абсолютная погрешность числа меньше или равна пяти единицам разряда, следующего за этой цифрой.
Пример 2
Определить, сколько верных значащих цифр содержит число:
x = 0.002306 ± 0.00001.
Для определения числа верных значащих цифр запишем x и Dx таким образом, чтобы легко было сравнить разряды этих чисел:
x = 0.002306, абсолютная погрешность Dx = 0.00001.
x = 0.002306,
Dx = 0.00001.
Третья значащая цифра (0) не может быть верной, так как она одного порядка с погрешностью. Верными могут быть цифры, которые стоят перед ней (2, 3). Цифра 3 будет верной, если Dx £ 0.00005. В нашем случае это условие выполнено, следовательно, 2, 3 – верные значащие цифры.
Цифры в записи числа, следующие за верными, называются сомнительными.
Пример 3
x = 1.121 ± 0.003;
x = 1.121;
Dx = 0.003.
В числе x = 1.121 три верные значащие цифры (1, 1, 2) и одна сомнительная (1).
Пример 4
x = 0.002306 ± 0.00007;
x = 0.002306;
Dx = 0.00007.
В числе x = 0.002306 одна верная значащая цифра (2), три сомнительные (3, 0, 6).
Пример 5
x = 12.3 ± 0.5;
x = 12.3;
Dx = 0.5.
В числе x = 12.3 три значащие цифры, две верные значащие цифры (1, 2), одна сомнительная (3).
Пример 6
x = 12.3 ± 0.8;
x = 12.3;
Dx = 0.8.
В числе x = 12.3 одна верная значащая цифра (1), две сомнительные (2, 3).
При записи абсолютной и относительной погрешностей используют, как правило, одну-две значащие цифры. Приближенные числа принято записывать следующим образом: сначала записывают все верные значащие цифры, затем одну-две сомнительные. То есть в записи приближенного числа, как правило, число значащих цифр на одну-две больше, чем число верных значащих цифр.
Практическое правило. Одна верная значащая цифра в записи числа соответствует приблизительно относительной погрешности 10 %. И наоборот, относительная погрешность 10 % соответствует приблизительно одной верной значащей цифре. Две верные значащие цифры соответствуют относительной погрешности 1 %, три верные значащие цифры – относительной погрешности 0.1 %.
