29
Июн 2013
Категория: Справочные материалы
Значения тангенса и котангенса на тригонометрическом круге
2013-06-29
2016-08-04
В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.
Как же быть с тангенсом и котангенсом? Об этом и поговорим сегодня.
Где же на тригонометрическом круге оси тангенсов и котангенсов?
Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).
Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).
На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?
Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и
Изучаем картинку:

Собственно, картинка за себя сама говорит.
Если не очень все же понятно, разберем примеры:
Пример 1.
Вычислить
Решение:
Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что
Ответ:
Пример 2.
Вычислить
Решение:
Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.
не существует.
Ответ: не существует
Пример 3.
Вычислить
Решение:
Находим на круге точку (это та же точка, что и
) и от нее по часовой стрелке (знак минус!) откладываем
(
). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как
. Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение
.
Так значит,
Ответ:
Пример 4.
Вычислить
Решение:
Поэтому от точки (именно там будет
) откладываем против часовой стрелки
.
Выходим на ось котангенсов, получаем, что
Ответ:
Пример 5.
Вычислить
Решение:
Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что
Ответ:
 Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройти тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».
Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройти тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».
Автор: egeMax |
комментариев 6
Печать страницы

Объяснение и обоснование
Напомним, что . Таким образом, областью определения функции y=будут все значения аргумента, при которых , то есть все значения x, kZ. Получаем
Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.
Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все
Значенияx входят в область определения функции y=tgx.
Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т
очек на линии тангенсов принимают
все значения до +, поскольку для любого действительного числа
мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов. Учитывая, что точка О лежит
внутри окружности, а точка вне ее (или на самой окружности), получаем, что прямая имеет с окружностью хотя бы одну общую точку
(на самом деле их две). Следовательно, для любого действительного числа
найдется аргумент х, такой, что tan x равен данному действительному числу.
Поэтому область значений функции y= tg x – все действительные числа,
то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.
Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.
Тангенс — периодическая функция с наименьшим положительным периодом
Поэтому при построении графика
этой функции достаточно построить график на любом промежутке длиной π,
а потом полученную линию перенести параллельно вправо и влево вдоль оси
Ox на расстоянияkT = πk, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,
при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при
а также, учитывая период, при всех
![]()

Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,
Промежутки возрастания и убывания.
Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,
например на промежутке . Если x (рис. 92), то при увеличении аргумента x (x2>x1) ордината соответствующей точки линии
тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом
промежутке функция tgx возрастает. Учитывая периодичность функции
tgx, делаем вывод, что она возрастает также на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график
функции y = tg x. Учитывая периодичность этой функции (с периодом π),
сначала построим график на любом промежутке длиной π, например на промежутке . Для более точного построения точек графика воспользуемся также тем, что значение тангенса — это ордината соответствующей точки
линии тангенсов. На рисунке 93 показано построение графика функции
y = tg x на промежутке.
Далее, учитывая периодичность тангенса (с периодом π), повторяем вид
графика на каждом промежутке длиной π (то есть параллельно переносим
график вдоль оси Ох на πk, где k — целое число).
Получаем график, приведенный на рисунке 94, который называется тангенсоидой.

14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК

Объяснение и обоснование
Так как =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,
D (ctg x): x ≠ πk, k ∈ Z.
Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии
котангенсов (рис. 95).
.png)
Поскольку точки А и В единичной окружности лежат на прямых ОА
и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.
Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом, область значений функции y = ctg x — все действительные числа, то есть R.
Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.
Как было показано в § 13, котангенс — нечетная функция: ctg (-x) = -ctgx, поэтому ее график симметричен относительно начала координат.
Там же было обосновано, что котангенс — периодическая функция с наименьшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.
На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D(рис. 95), то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения функции котангенс положительны (то есть абсцисса соответствующей точки линии котангенсов положительна) в I и III четвертях (рис. 96). Тогда ctgx> 0 при всех . Учитывая период, получаем, что ctgx> 0 при всех
Значения функции котангенс отрицательны (то есть абсцисса соответствующей точки линии котангенсов отрицательна) во II и IV четвертях, таким образом, ctgx< 0 при .


Промежутки возрастания и убывания
Учитывая периодичность функции ctg x (наименьший положительный период T = ), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке (0; ). Если (0; ) (рис. 97), то при увеличении аргумента x (x2>x1) абсцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx2<ctgx1), следовательно, на этом промежутке функция ctg x убывает. Учитывая периодичность функции y= ctgx, делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет построить график функции y= ctg x аналогично тому, как был построен график функции y= tg x. Но график функции у = ctg x можно получить также с помощью геометрических преобразований графика функции у = tg х. По формуле, приведенной на с. 172, , то есть Поэтому график функции у = ctg x можно получить из графика функции у = tg х параллельным переносом вдоль оси Ох на (− ) и симметричным отображением полученного графика относительно оси Ох. Получаем график, который называется котангенсоидой (рис. 98).

Значения тангенса и котангенса на тригонометрическом круге
В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.
Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.
Где же на тригонометрическом круге оси тангенсов и котангенсов?
Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).
Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).
На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?
Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и
Собственно, картинка за себя сама говорит.
Если не очень все же понятно, разберем примеры:
Пример 1.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что
Ответ:
Пример 2.
Вычислить
Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.
не существует.
Ответ: не существует
Пример 3.
Вычислить
Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .
Так значит,
Ответ:
Пример 4.
Вычислить
Поэтому от точки (именно там будет ) откладываем против часовой стрелки .
Выходим на ось котангенсов, получаем, что
Ответ:
Пример 5.
Вычислить
Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что
Ответ:
Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Тангенс
Тангенс – одна из тригонометрических функций. Как и для всех других функций, значение тангенса определяется для конкретного угла или числа (в этом случае используют числовую окружность.
Аргумент и значение тангенса
Аргументом тангенса может быть:
– как число или выражение с Пи: (1,3), (frac<π><4>), (π), (-frac<π><3>) и т.п.
– так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.
Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).
Тангенс острого угла
Тангенс можно определить с помощью прямоугольного треугольника – он равен отношению противолежащего катета к прилежащему.
1) Пусть дан угол и нужно определить тагенс этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить тангенс.
Вычисление тангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших (360°) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
Пример. Вычислите (tg:0).
Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус (0). И то, и другое найдем с помощью тригонометрического круга :
Точка (0) на числовой окружности совпадает с (1) на оси косинусов, значит (cos:0=1). Если из точки (0) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку (0), значит (sin:0=0). Получается: (tg:0=) (frac) (=) (frac<0><1>) (=0).
Пример. Вычислите (tg:(-765^circ)).
Решение: (tg: (-765^circ)=) (frac)
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).
Однако можно определять тангенс и напрямую через тригонометрический круг – для этого надо на нем построить дополнительную ось:
Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.
Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.
Чтобы определить тангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу тангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов.
3) Найти координату пересечения этой прямой и оси тангенсов.
2) Проводим через данную точку и начало координат прямую.
3) В данном случае координату долго искать не придется – она равняется (1).
Пример. Вычислите (tg: 45°) и (tg: (-240°)).
Решение:
Для угла (45°) ((∠KOA)) тангенс будет равен (1), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось тангесов. А для угла (-240°) ((∠KOB)) тангенс равен (-sqrt<3>) (приблизительно (-1,73)).
Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
В отличие от синуса и косинуса значение тангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.
При этом тангенс не определен для:
1) всех точек (A) (значение в Пи: …(-) (frac<7π><2>) ,(-) (frac<3π><2>) , (frac<π><2>) , (frac<5π><2>) , (frac<9π><2>) …; и значение в градусах: …(-630°),(-270°),(90°),(450°),(810°)…)
2) всех точек (B) (значение в Пи: …(-) (frac<9π><2>) ,(-) (frac<5π><2>) ,(-) (frac<π><2>) , (frac<3π><2>) , (frac<7π><2>) …; и значение в градусах: …(-810°),(-450°),(-90°),(270°)…) .
Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).
Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ .
Знаки по четвертям
С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.
Связь с другими тригонометрическими функциями:
– котангенсом того же угла: формулой (ctg:x=) (frac<1>)
Другие наиболее часто применяемые формулы смотри здесь .
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
[spoiler title=”источники:”]
http://cos-cos.ru/math/186/
http://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskij-krug/
[/spoiler]
Примеры:
(tg:30^° =frac{1}{sqrt{3}})
(tg:(frac{π}{3})=sqrt{3})
(tg:2=-2,185…)
Содержание:
- Аргумент и значение
Тангенс острого угла
Тангенс числа или любого угла
Знаки по четвертям
Связь с другими функциями
Аргумент и значение тангенса

Аргументом тангенса может быть:
– как число или выражение с Пи: (1,3), (frac{π}{4}), (π), (-frac{π}{3}) и т.п.
– так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.
Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).
Значение тангенса – всегда действительное число (возможно, иррациональное): (1), (sqrt{3}), (-frac{1}{sqrt{3}}), (-0,1543…)
Тангенс острого угла
Тангенс можно определить с помощью прямоугольного треугольника – он равен отношению противолежащего катета к прилежащему.
Пример:
1) Пусть дан угол и нужно определить тагенс этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить тангенс.

Вычисление тангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших (360°) тангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
(tg: t=)(frac{sin:t}{cos:t})
Пример. Вычислите (tg:0).
Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус (0). И то, и другое найдем с помощью тригонометрического круга:

Точка (0) на числовой окружности совпадает с (1) на оси косинусов, значит (cos:0=1). Если из точки (0) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку (0), значит (sin:0=0). Получается: (tg:0=)(frac{sin:0}{cos:0}) (=)(frac{0}{1})(=0).
Ответ: (0).
Пример. Вычислите (tg:(-765^circ)).
Решение: (tg: (-765^circ)=)(frac{sin:(-765^circ)}{cos:(-765^circ)})
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).

(sin(-765^°)=-frac{sqrt{2}}{2});
(cos(-765^°)=frac{sqrt{2}}{2}) ;
получается (tg(-765^°)= -frac{sqrt{2}}{2} ∶ frac{sqrt{2}}{2}=-1).
Ответ: (-1).
Пример. Вычислите (tg:frac{π}{3}).
Решение: (tg: frac{π}{3}=)(frac{sin:frac{π}{3}}{cos:frac{π}{3}}). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
(sin(frac{π}{3})=frac{sqrt{3}}{2});
(cos(frac{π}{3})=frac{1}{2}) ;
получается (tg(frac{π}{3})= frac{sqrt{3}}{2} ∶ frac{1}{2}= frac{sqrt{3}}{2} cdot frac{2}{1}=sqrt{3}).
Ответ: (sqrt{3}).
Однако можно определять тангенс и напрямую через тригонометрический круг – для этого надо на нем построить дополнительную ось:
Прямая проходящая через начало отсчета на числовой окружности и параллельная оси ординат (синусов) называется осью тангенсов. Направление оси тангенсов и оси синусов совпадает.

Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.
Чтобы определить тангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу тангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов.
3) Найти координату пересечения этой прямой и оси тангенсов.
Пример. Вычислите (tg:frac{π}{4}).
Решение:
1)Отмечаем (frac{π}{4}) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется (1).
Ответ: (1).
Пример. Вычислите (tg: 45°) и (tg: (-240°)).
Решение:
Для угла (45°) ((∠KOA)) тангенс будет равен (1), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось тангесов. А для угла (-240°) ((∠KOB)) тангенс равен (-sqrt{3}) (приблизительно (-1,73)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
В отличие от синуса и косинуса значение тангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.

При этом тангенс не определен для:
1) всех точек (A) (значение в Пи: …(-)(frac{7π}{2}),(-)(frac{3π}{2}),(frac{π}{2}), (frac{5π}{2}), (frac{9π}{2}) …; и значение в градусах: …(-630°),(-270°),(90°),(450°),(810°)…)
2) всех точек (B) (значение в Пи: …(-)(frac{9π}{2}),(-)(frac{5π}{2}),(-)(frac{π}{2}), (frac{3π}{2}), (frac{7π}{2}) …; и значение в градусах: …(-810°),(-450°),(-90°),(270°)…) .
Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).
Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ.
Знаки по четвертям
С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

Связь с другими тригонометрическими функциями:
– косинусом того же угла: формулой (1+tg^2x=)(frac{1}{cos^2x})
– синусом и косинусом того же угла: (tg:x=)(frac{sin:x}{cos:x})
– котангенсом того же угла: формулой (ctg:x=)(frac{1}{tg:x})
Другие наиболее часто применяемые формулы смотри здесь.
Смотрите также:
Формулы приведения
Содержание:
Построим точку 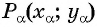
По определению тангенса острого угла получим: 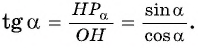
Определение тангенса угла
Определение:
Тангенсом угла 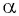 называется отношение синуса угла
называется отношение синуса угла 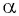 к косинусу угла
к косинусу угла 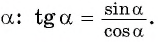
Например, 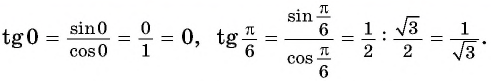
Используя определение тангенса угла и значения синуса и косинуса этого угла, найдем также значения тангенсов углов 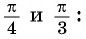
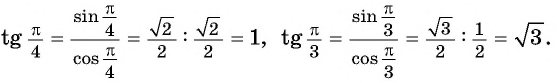
Поскольку 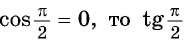 не существует.
не существует.
Через точку 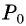 проведем прямую, перпендикулярную оси абсцисс, и продолжим луч
проведем прямую, перпендикулярную оси абсцисс, и продолжим луч 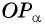 до пересечения с этой прямой в точке
до пересечения с этой прямой в точке 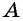 (рис. 52). Получим треугольник
(рис. 52). Получим треугольник 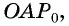 подобный треугольнику
подобный треугольнику 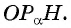
Из подобия треугольников 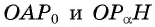 запишем равенство отношений их сторон:
запишем равенство отношений их сторон: 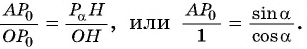
Поскольку 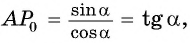 то ордината точки
то ордината точки 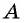 равна тангенсу угла
равна тангенсу угла 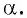
Прямая, перпендикулярная оси абсцисс, проходящая через точку 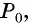 называется осью тангенсов.
называется осью тангенсов.
Нахождение тангенса произвольного угла
Для того чтобы найти тангенс произвольного угла а с помощью оси тангенсов, нужно:
- Построить точку
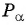 на единичной окружности.
на единичной окружности. - Продолжить прямую
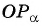 до пересечения с осью тангенсов.
до пересечения с осью тангенсов. - Найти ординату точки пересечения прямой
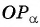 с осью тангенсов.
с осью тангенсов.
Найдите тангенс угла 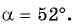
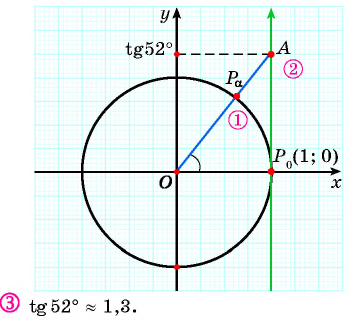
Значения тангенса произвольного угла с помощью оси тангенсов можно указать только приближенно. Для нахождения значения тангенса произвольного угла используют четырехзначные таблицы значений тангенса (синуса, косинуса)* или калькулятор. Методы высшей математики позволяют вычислять значения тангенса (синуса, косинуса) с любой заданной степенью точности.
Пример №1
Определите с помощью оси тангенсов:

Решение:
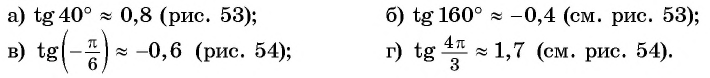
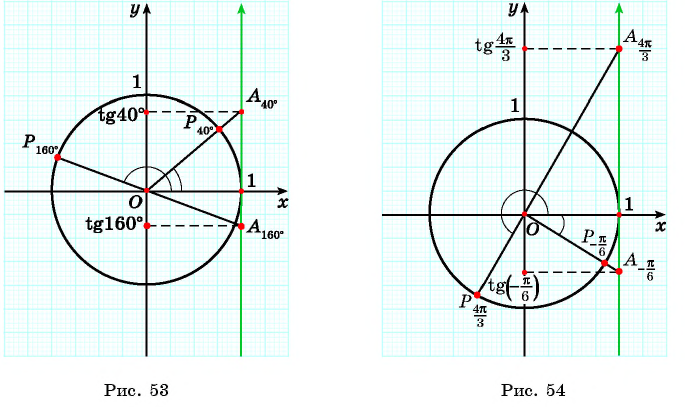
Пример №2
С помощью оси тангенсов сравните значения выражений 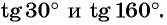
Решение:
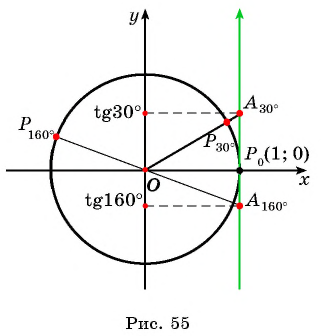
Отметим на оси тангенсов точки, соответствующие углам 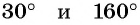 (рис. 55), и сравним ординаты этих точек. Ордината точки
(рис. 55), и сравним ординаты этих точек. Ордината точки 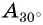 больше ординаты точки
больше ординаты точки 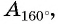 значит,
значит, 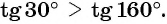
Для углов 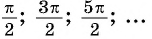 тангенс не существует, так как косинусы этих углов равны нулю. Например,
тангенс не существует, так как косинусы этих углов равны нулю. Например, 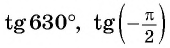 не существуют.
не существуют.
Построим точку 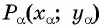 единичной окружности поворотом точки
единичной окружности поворотом точки 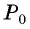 вокруг начала координат на угол
вокруг начала координат на угол 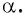 Рассмотрим прямоугольный треугольник
Рассмотрим прямоугольный треугольник 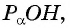 , в котором гипотенуза
, в котором гипотенуза 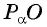 равна 1 (радиусу единичной окружности), а его катеты равны:
равна 1 (радиусу единичной окружности), а его катеты равны: 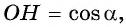
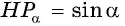 (рис. 56).
(рис. 56).
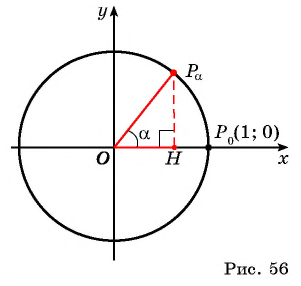
По определению котангенса острого угла получим: 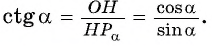
Определение котангенса угла
Определение:
Котангенсом угла 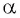 называется отношение косинуса угла
называется отношение косинуса угла 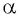 к синусу угла
к синусу угла 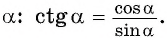
Например, 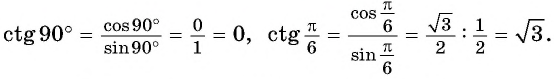
Поскольку 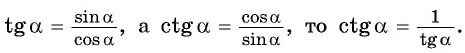
Воспользуемся полученным равенством и найдем значения котангенсов углов 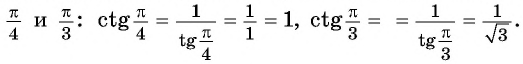
Поскольку 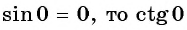 не существует.
не существует.
Найденные значения синуса, косинуса, тангенса и котангенса углов 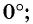
 занесем в таблицу.
занесем в таблицу.
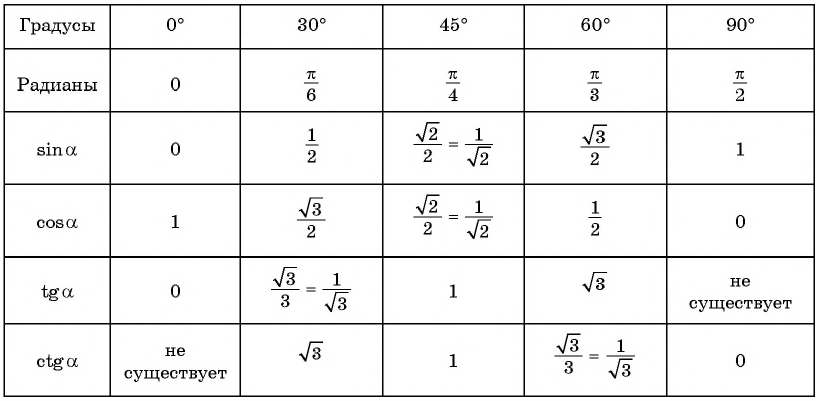
Нахождение котангенса произвольного угла
Для того чтобы найти котангенс произвольного угла 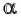 с помощью оси котангенсов, нужно:
с помощью оси котангенсов, нужно:
- Построить точку
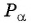 на единичной окружности.
на единичной окружности. - Продолжить прямую
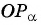 до пересечения с осью котангенсов.
до пересечения с осью котангенсов. - Найти абсциссу точки пересечения прямой
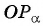 с осью котангенсов.
с осью котангенсов.
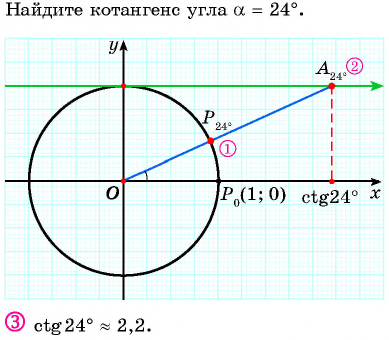
Значения котангенса произвольного угла с помощью оси котангенсов можно указать только приближенно.
- Заказать решение задач по высшей математике
Пример №3
Найдите значение выражения
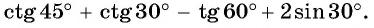
Решение:
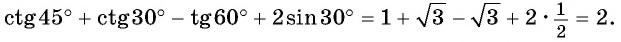
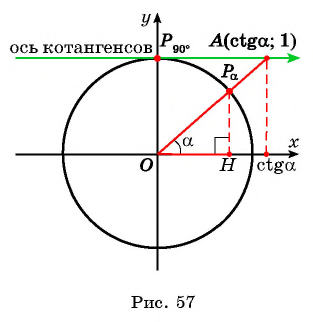
Через точку 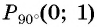 проведем прямую, перпендикулярную оси ординат, и продолжим луч
проведем прямую, перпендикулярную оси ординат, и продолжим луч 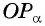 до пересечения с этой прямой в точке
до пересечения с этой прямой в точке 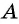 (рис. 57).
(рис. 57).
Получим треугольник 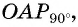 подобный треугольнику
подобный треугольнику 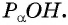
Из подобия треугольников 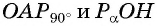 запишем равенство отношений их сторон:
запишем равенство отношений их сторон: 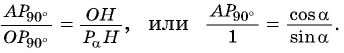 Поскольку
Поскольку 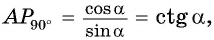 то абсцисса точки
то абсцисса точки 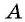 равна котангенсу угла
равна котангенсу угла 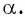
Прямая, перпендикулярная оси ординат, проходящая через точку 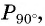 называется осью котангенсов.
называется осью котангенсов.
Пример №4
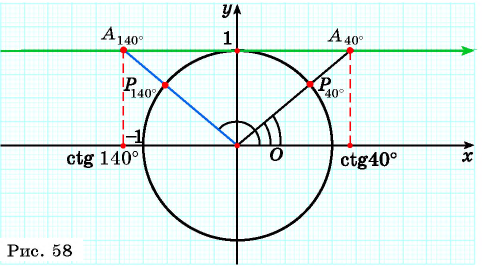
Определите с помощью оси котангенсов:

Решение:
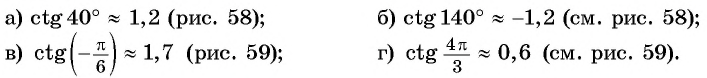
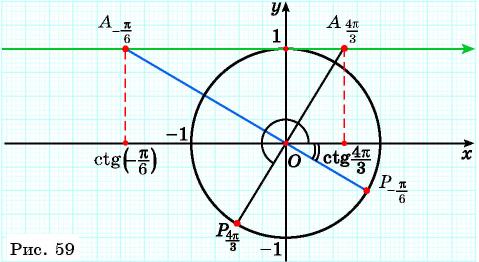
Пример №5
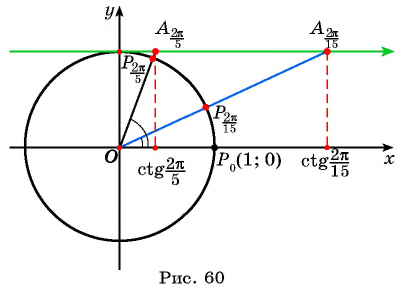
С помощью оси котангенсов сравните значения выражений 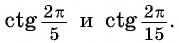
Решение:
Отметим на оси котангенсов точки, соответствующие углам 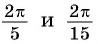 (рис. 60), и сравним абсциссы этих точек. Абсцисса точки
(рис. 60), и сравним абсциссы этих точек. Абсцисса точки 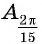 больше абсциссы точки
больше абсциссы точки 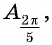 значит,
значит, 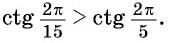
Для углов 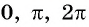 и т. д. котангенс не существует, так как синусы этих углов равны нулю. Например,
и т. д. котангенс не существует, так как синусы этих углов равны нулю. Например, 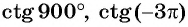 не существуют.
не существуют.
Пример №6
С помощью оси:
а) тангенсов найдите один из углов, тангенс которого равен 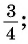
б) котангенсов найдите один из углов, котангенс которого равен 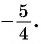
Решение:
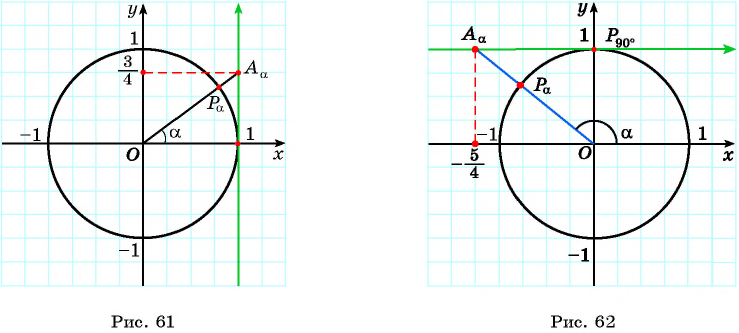
а) 1 Отметим на оси тангенсов точку 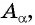 ордината которой равна
ордината которой равна 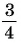 (рис. 61).
(рис. 61).
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 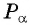 на единичной окружности.
на единичной окружности.
4 Отметим один из углов, соответствующий этой точке (см. рис. 61).
б) 1 Отметим на оси котангенсов точку 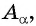 абсцисса которой равна
абсцисса которой равна 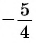 (рис. 62).
(рис. 62).
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 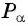 на единичной окружности.
на единичной окружности.
4 Отметим один из углов, соответствующий этой точке (см. рис. 62).
Пример №7
Точка 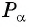 единичной окружности имеет координаты
единичной окружности имеет координаты 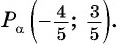 Используя определение тангенса и котангенса произвольного угла, найдите
Используя определение тангенса и котангенса произвольного угла, найдите 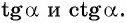
Решение:
Так как точка 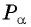 единичной окружности имеет координаты
единичной окружности имеет координаты 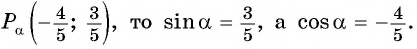
По определению тангенса: 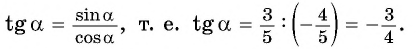
По определению котангенса: 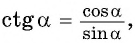 значит,
значит, 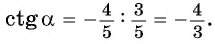
Пример №8
Найдите значение выражения 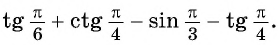
Решение:
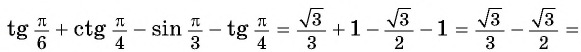
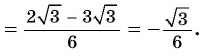
Пример №9
Найдите, если это возможно, значение выражения: 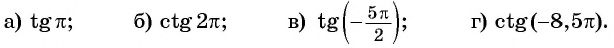
Решение:
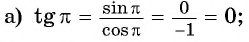
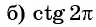 не существует, так как
не существует, так как 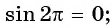
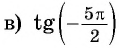 не существует, так как
не существует, так как 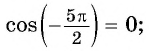
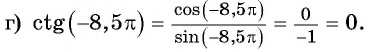
Пример №10
Если 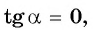 то
то 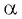 может принимать значения:
может принимать значения: 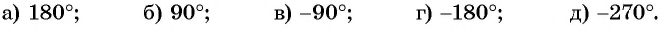
Выберите правильные ответы.
Решение:
Так как тангенсом угла 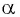 называется отношение синуса угла
называется отношение синуса угла 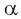 к косинусу угла
к косинусу угла 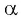 , то нужно найти те углы
, то нужно найти те углы 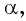 синус которых равен нулю. Среди предложенных углов это углы
синус которых равен нулю. Среди предложенных углов это углы 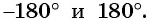
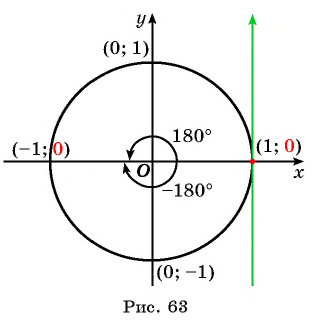
Можно также использовать ось тангенсов: найти точку на оси тангенсов, у которой ордината равна нулю (рис. 63), и определить соответствующие углы. Правильные ответы а) и г).
Пример №11
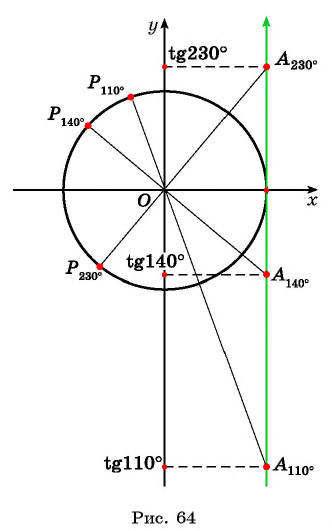
Расположите в порядке возрастания: 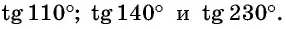
Решение:
Отметим на оси тангенсов точки, соответствующие углам 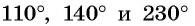 (рис. 64), и сравним ординаты этих точек. Поскольку ордината точки
(рис. 64), и сравним ординаты этих точек. Поскольку ордината точки 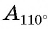 меньше ординаты точки
меньше ординаты точки 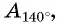 а ордината точки
а ордината точки 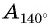 меньше ординаты точки
меньше ординаты точки 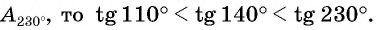
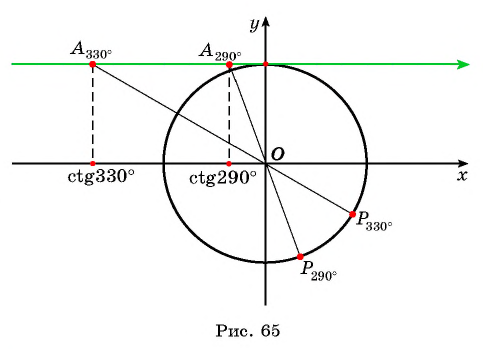
Пример №12
Верно ли, что 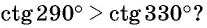
Решение:
Отметим на оси котангенсов точки, соответствующие углам 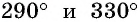 (рис. 65), и сравним абсциссы этих точек. Поскольку абсцисса точки
(рис. 65), и сравним абсциссы этих точек. Поскольку абсцисса точки 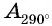 больше абсциссы точки
больше абсциссы точки 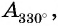 то неравенство
то неравенство 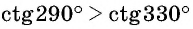 верное.
верное.
Пример №13
Определите знак выражения: 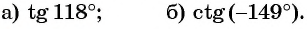
Решение:
а) Первый способ. По определению тангенса: 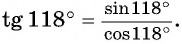 Так как угол
Так как угол 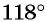 находится во второй четверти, то
находится во второй четверти, то 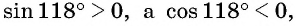 значит,
значит, 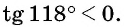 Второй способ. Отметим на оси тангенсов точку, соответствующую углу
Второй способ. Отметим на оси тангенсов точку, соответствующую углу 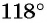 (рис. 66). Ордината точки
(рис. 66). Ордината точки 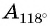 равна
равна 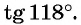 Поскольку точка
Поскольку точка 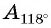 имеет отрицательную ординату, то
имеет отрицательную ординату, то 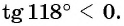
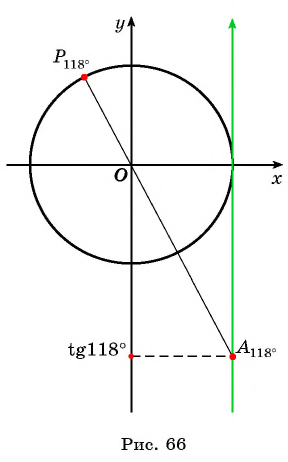
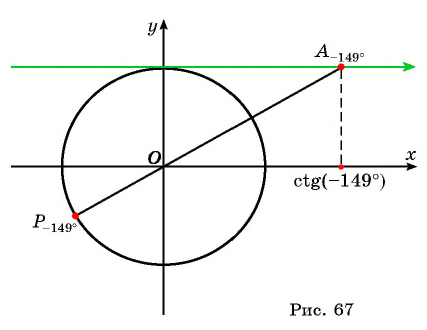
б) Первый способ. По определению котангенса 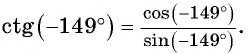 Так как угол
Так как угол 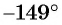 находится в третьей четверти, то
находится в третьей четверти, то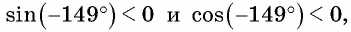 значит,
значит, 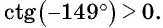
Второй способ. Отметим на оси котангенсов точку, соответствующую углу 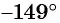 (рис. 67). Абсцисса точки
(рис. 67). Абсцисса точки 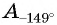 равна
равна 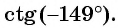 Поскольку точка
Поскольку точка 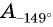 имеет положительную абсциссу, то
имеет положительную абсциссу, то 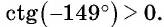
Пример №14
Определите знак произведения 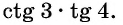
Решение:
Так как угол 3 радиана находится во второй четверти, а угол 4 радиана — в третьей, то 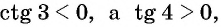 значит,
значит, 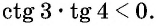
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x – их свойства, графики
- Дробно-рациональные неравенства
- Прогрессии в математике – арифметическая, геометрическая
- Единичная окружность – в тригонометрии
- Определение синуса и косинуса произвольного угла
