
§ 3.3. Программирование линейных алгоритмов ГДЗ по Информатике 8 Класс
Известны длины сторон треугольника а, b, с. Напишите программу, вычисляющую площадь этого треугольника.
| Пример входных данных | Пример выходных данных |
| а=3 | S=6 .0 |
| b=4 | |
| с=5 |
Ответ
program test;
var a, b, c:integer; s, p: real;
begin
write(‘Enter a: ‘);
readln(a);
write(‘Enter b: ‘);
readln(b);
write(‘Enter c: ‘);
readln(c);
p:=(a+b+c)/2;
s:=sqrt(p(p-a)(p-b)*(p-c));
writeln(‘S = ‘, s);
readln;
end.
Честно, отвечаю не сам, задал этот вопрос ИИ. Посмотри, может это что-то дельное:
«Ошибка в коде заключается в отсутствии логических операторов между условиями в операторе if. Вы должны использовать либо and операторы, либо or для объединения нескольких условий. Вот исправленный код:
print("Задайте длины сторон треугольника.")
a = int(input("Длина первой стороны:"))
b = int(input("Длина второй стороны:"))
c = int(input("Длина третьей стороны:"))
print("Существует ли такой треугольник?")
if (a < b + c) and (b < a + c) and (c < a + b):
print("Существует!")
else:
print("Не существует!")
В этом случае я использовал and оператор, чтобы убедиться, что все три условия верны для допустимого треугольника».
Роман Самойлов Мастер (1207)
2 месяца назад
Зачем тогда отвечаете? ИИ каждый дурак может вопрос задать, mail.ru для того и создан, чтобы спрашивать мнение не ботов, а настоящих людей
Дан треугольник с углами 30, 60 и 90 градусов. Напишите функцию, которая будет принимать длину самой короткой стороны треугольника (т.е. одного из катетов) и возвращать длину гипотенузы и второго катета.
Примечания
- В прямоугольном треугольнике, один из углов которого равен 30 градусам, самая короткая сторона ровно в два раза короче самой длинной.
- По теореме Пифагора в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
- Числа округляем до двух знаков после запятой.
Примеры
returnsides(1) ➞ (2, 1.73)
returnsides(2) ➞ (4, 3.46)
returnsides(3) ➞ (6, 5.2)
Варианты решений
def returnsides(length):
a = ()
b = length * 2
c = round(length * (3 ** (1/2)),2)
a = (b,c)
return a
returnsides=lambda l:(2*l,round(1.7320*l,2))
Определить существование треугольника по трем сторонам
С клавиатуры вводятся длины трех отрезков. Определить, можно ли из них составить треугольник.
Решение задачи на языке программирования Python
У треугольника сумма любых двух сторон должна быть больше третьей. Иначе две стороны просто “лягут” на третью и треугольника не получится.
Пользователь вводит длины трех сторон. Программа должна определять, может ли существовать треугольник при таких длинах. Это значит, необходимо сравнить суммы всех пар сторон с оставшейся третьей стороной. Чтобы треугольник существовал, сумма всегда должна быть больше отдельной стороны или, по крайней мере, не меньше, если учитывать так называемый вырожденный треугольник.
Поскольку всего три стороны, то можно составить три варианта сложения двух сторон: a + b, b + c, a + c. Первую сумму сравниваем с оставшейся стороной c, вторую – с a и третью – с b. Если хотя бы в одном случае сумма окажется не больше третьей стороны, то делается вывод, что треугольник не существует.
print("Стороны:") a = float(input("a = ")) b = float(input("b = ")) c = float(input("c = ")) if a + b > c and a + c > b and b + c > a: print("Треугольник существует") else: print("Треугольник не существует")
Можно решить задачу сложнее. Если требуется также определить, какая из сторон больше суммы двух других, то решение может быть таким:
print("Длины сторон треугольника:") a = float(input("a = ")) b = float(input("b = ")) c = float(input("c = ")) flag = '' if a + b > c: if a + c > b: if b + c > a: print("Треугольник есть") else: flag = 'a' else: flag = 'b' else: flag = 'c' if flag != '': print("Треугольника нет") print("'%s' > суммы других" % flag)
Особого смысла использовать переменную flag здесь нет. Она просто позволяет лишний раз не писать в программе строки, информирующие о том, что треугольник не существует.
Пример выполнения программы:
Длины сторон треугольника: a = 4 b = 5 c = 10 Треугольника нет 'c' > суммы других
Более изящным решением является использование оператора множественного ветвления языка программирования Python: if-elif-else.
print("Длины сторон треугольника:") a = float(input("a = ")) b = float(input("b = ")) c = float(input("c = ")) flag = '' if a + b <= c: flag = 'c' elif a + c <= b: flag = 'b' elif b + c <= a: flag = 'a' else: print("Треугольник есть") if flag != '': print("Треугольника нет") print("'%s' > суммы других" % flag)
Здесь сравнение происходит от обратного: утверждается, что сумма двух сторон меньше или равна третьей. Если это так (утверждение верно), то треугольника не существует. “Слишком длинная сторона” определяется в зависимости от того, в заголовке какой ветки логическое выражение возвращает истину.
Больше задач в PDF
09 Apr 2017
Оглавление
Первое приложение
Программа считывает три целочисленных значения из консоли. Эти значения интерпретируются как длины сторон треугольника. Программа выводит сообщение о том, каким является данный треугольник – разносторонним, равнобедренным или равносторонним.
Напишем, функцию, которая принимает на вход три стороны треугольника, которые заданы целыми числами и возвращает тип треугольника. Сохраним написанный код в файле triangle.php.
/**
* Не треугольник
*/
define('TRIANGLE_BAD', 0);
/**
* Равносторонний треугольник
*/
define('TRIANGLE_EQUILATERAL', 1);
/**
* Прямоугольный треугольник
*/
define('TRIANGLE_RIGHT', 2);
/**
* Равнобедренный треугольник
*/
define('TRIANGLE_ISOSCELES', 3);
/**
* Разносторонний треугольник
*/
define('TRIANGLE_SIDED', 4);
/**
* По длинам сторон $a, $b и $c возвращает тип треугольника.
* Если стороны не являются целочисленными, то выбрасывает исключение.
*
* @param $a
* @param $b
* @param $c
* @return int
* @throws Exception
*/
function triangle_type($a, $b, $c)
{
// Вполне ожидаемо,
// что нецелочисленные значения должны приводить к исключительной ситуации.
if (!is_int($a) or !is_int($b) or !is_int($c))
{
throw new Exception('Invalid triangle definition');
}
$max = null;
$min1 = null;
$min2 = null;
if (($a+$b)>$c and ($a+$c)>$b and ($b+$c)>$a)
{
if (($a>$b) and ($a>$c))
{
$max = $a;
$min1 = $b;
$min2 = $c;
}
else if (($b>$c) and ($b>$a))
{
$max = $b;
$min1 = $a;
$min2 = $c;
}
else
{
$max = $c;
$min1 = $a;
$min2 = $b;
}
if (pow($max, 2) == pow($min1, 2) + pow($min2, 2))
{
return TRIANGLE_RIGHT;
}
else if (($max==$min1) and ($max==$min2))
{
return TRIANGLE_EQUILATERAL;
}
else if (($max==$min1) or ($max==$min2) or ($min1==$min2))
{
return TRIANGLE_ISOSCELES;
}
else
{
return TRIANGLE_SIDED;
}
}
else
{
return TRIANGLE_BAD;
}
}
Функция достаточно тривиальна, поэтому мы не будем останавливаться на ее реализации. Нас будет интересовать, как найти в ней ошибки.
Для начала потребуется реализовать механизм, который позволит вводить данные с консоли и получать результат. Сохраним следующий код в файле main.php. Чуть позже вы поймете, почему мы используем разные файлы для самой функции и для кода, который обрабатывает пользовательский ввод.
// здесь мы подключим ранее написанную функцию для определения типа треугольника
require __DIR__ . DIRECTORY_SEPARATOR . 'triangle.php';
function main()
{
// проинициализируем переменные
$a = $b = $c = 0;
// получим длины сторон со стандартного ввода
$num = fscanf(STDIN, "%d %d %dn", $a, $b, $c);
// если мы смогли считать длины трех сторон,
// то вызовем нашу функцию и покажем результат
if ($num == 3)
{
switch (triangle_type($a, $b, $c))
{
case TRIANGLE_BAD:
echo "Это не треугольникn";
break;
case TRIANGLE_EQUILATERAL:
echo "Это равносторонний треугольникn";
break;
case TRIANGLE_ISOSCELES:
echo "Это равнобедренный треугольникn";
break;
case TRIANGLE_RIGHT:
echo "Это прямоугольный треугольникn";
break;
case TRIANGLE_SIDED:
echo "Это разносторонний треугольникn";
break;
}
}
}
main();
Код также достаточно тривиален. Теперь мы можем запустить полученное приложение (да, это именно приложение – последовательность инструкций, определяющих процедуру решения конкретной задачи компьютером).
Откроем терминал, перейдем в каталог, с проектом и выполним следующую команду (для того, чтобы все сработало у вас должен быть установлен интерпретатор php в системе).
Программа будет ожидать ввод трех чисел, разделенных пробелами.
И вот что мы можем увидеть на экране.

Поэкспериментируйте немного с программой вводя разные наборы чисел.
А теперь рассмотрим эту программу с точки зрения разработчика, которому досталось ее тестировать. Какие наборы тестов он должен разработать, чтобы отыскать все возможные баги? Прежде чем читать дальше подумайте и попробуйте посчитать то количество, которое придумали вы.
Итак. Ниже приведен набор тестовых сценариев, которые должны быть написаны для нашей функции.
- тест для проверки действительно неравностороннего треугольника (наборы [1, 2, 3], [2, 5, 10] треугольниками не являются).
- проверка на действительно равносторонний треугольник
- проверка на равнобедренный треугольник (наборы вида [2, 2, 4] треугольником не являются)
- как минимум три теста для проверки равнобедренного треугольника, которые представляют собой перестановки одного и того же набора чисел ([3, 3, 4], [3, 4, 3], [4, 3, 3])
- тест на нулевую длину одной из сторон
- тест на сторону, имеющую длину меньше нуля
- проверка набора чисел, в котором сумма длин двух сторон равна третьей
- тест перестановок для троек чисел из теста 7
- проверка набора чисел, в котором сумма длин двух сторон меньше третьей ([12, 15, 30])
- тест перестановок для троек чисел из теста 9
- проверка на нулевую длину всех трех сторон
- проверка на передачу нецелочисленных значений
- проверка на передачу неполного набора значений
- проверка не только входных данных, но и ожидаемого выходного значения в каждом из тестов 1-13
Если вы не смогли назвать все кейсы, то не пугайтесь. Среднее число тестов, которые называли в разное время опытные разработчики составило 7,8.
Конечно нет никаких гарантий того, что набор тестов, удовлетворяющих перечисленным условиям, обнаружит все возможные ошибки. Но поскольку случаи 1-13 представляют ошибки, реально встречающиеся в различных версиях данной программы, адекватное тестирование должно обнаружить хотя бы их.
Это упражнение должно было продемонстрировать вам, что тестирование простых программ наподобие вышеприведенной является отнюдь не тривиальной задачей. А теперь попытайтесь представить себе, насколько трудоемким окажется тестирование, скажем, бухгалтерской программы крупного предприятия, компилятора или же системы управления воздушным движением, объем кода которых может достигать сотен тысяч строк. Еще большие трудности возникают с приложениями, которые написаны с использованием объектно-ориентированных языков (куда входит и php) и подходов. В частности, тесты для подобных приложений должны выявлять ошибки с созданием экземпляров объектов и взаимодействия между ними.
Однако, какой бы устрашающей ни казалась задача, адекватное (достаточно полное) тестирование программ является ключевой и, как вы убедитесь далее, вполне реализуемой частью процесса разработки программного обеспечения.
Тестируем
Конечно же самым простым решением будет просто закодировать все тестовые случаи для нашего проекта и написать нечто вроде следующего кода (файл triangle_test_simple.php).
require __DIR__ . DIRECTORY_SEPARATOR . 'triangle.php';
function testForIsoscelesTriangle()
{
echo "Test for [3, 4, 4]: ";
if (triangle_type(3, 4, 4) == TRIANGLE_ISOSCELES) {
echo "okn";
} else {
echo "failn";
}
}
function main()
{
testForIsoscelesTriangle();
}
main();
И такое часто практикуется. Особенно в среде разработчиков на CC++. На каждый логически связанный набор тестовых случаев создается свой файл. Который содержит множество функций обрабатывающих по одному сценарию каждая.
В этом нет ничего плохого. Единственный минус такого подхода – отсутствие готового инструментария, который реализует все необходимые операции по обслуживанию и запуску тестов. Весь инструментарий приходится для каждого проекта реализовывать заново. Либо изготавливать свою собственную обвязку, которая будет кочевать из проекта в проект.
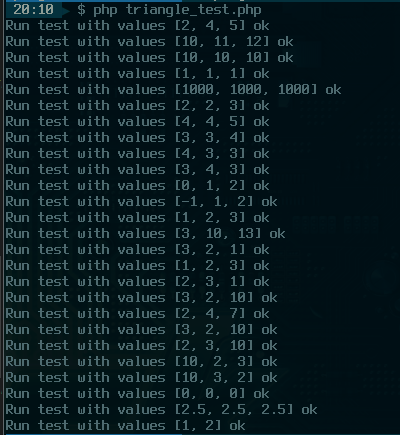
Один из вариантов создания инструмента для работы с подобными тестами вы можете увидеть в файле triangle_test.php. Запустите его и увидите на экране подробный лог тестирования проекта.
Литература
- “Искусство тестирования программ” Гленфорд Майерс, Том Баджетт, Кори Сандлер, ISBN: 978-5-8459-1974-8
- “PHP 7” Дмитрий Котеров, Игорь Симдянов, ISBN 978-5-9775-3725-4
Исходные тексты программ
- github
Оглавление
Теги:
тестирование по
php
Категории:
Разработка
