Емкостное сопротивление конденсатора – величина, измеряемая в омах, создается непосредственно самим конденсатором, который включен в любую цепь. Оно должно иметь большую величину, то есть быть большим. Если на них происходит подача переменного тока, в устройстве происходят процессы заряда и последующего разряда. Последнее происходит по требованию цепи. При включении электрического тока, напряжение будет равно 0. Само устройство при этом начнет заряжаться, следовательно его величина напряжения постепенно растет. В случае необходимости, при достижении максимального заряда, произойдет разряд конденсатора.
В статье, посвященной теме расчета сопротивления конденсатора, приведена вся информация о процессе, как происходит заряд-разряд. В качестве бонуса есть интересный материал по теме, который можно скачать, и видеоролик в конце статьи.
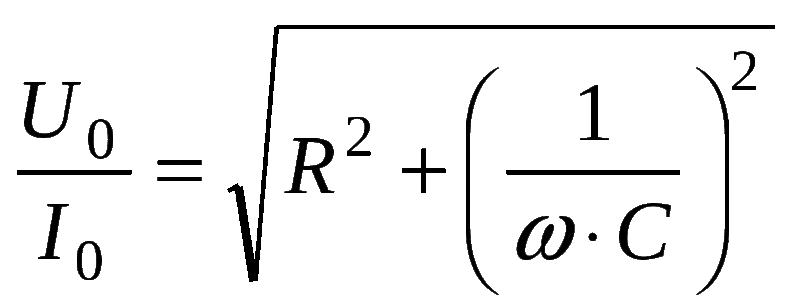
Формула сопротивления
Формула ёмкостного сопротивления выводится следующим образом:
- Вначале следует вычислить угловую частоту. Для этого частоту протекающего по цепи тока (в герцах) необходимо умножить на удвоенное число «пи».
- Затем полученное число следует перемножить на ёмкость конденсатора в фарадах.
Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление. Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.
Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
- Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
- Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
- Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.
В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними. Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.
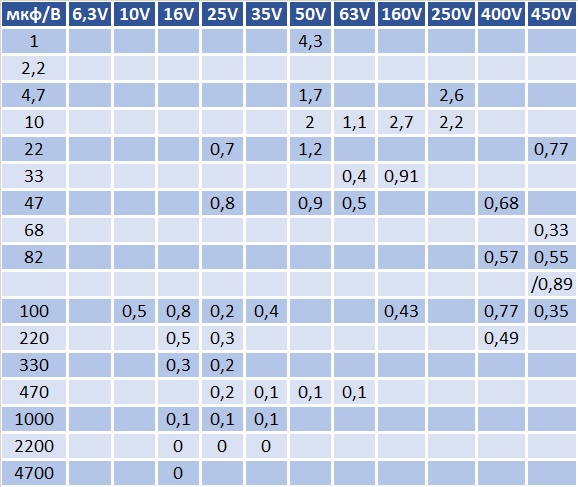
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
[stextbox id=’info’]Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.[/stextbox]
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Материал в тему: все о переменном конденсаторе.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
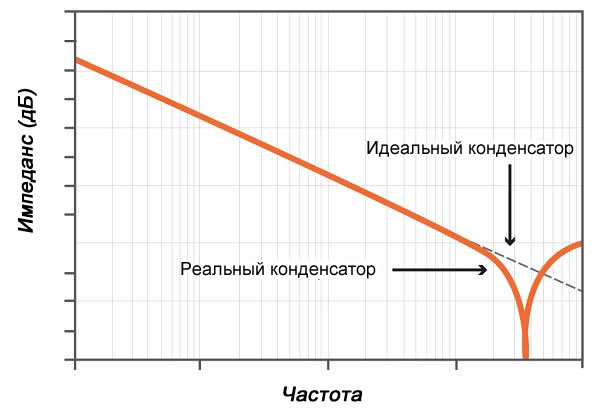
Пример расчёта
Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R 2 +Xc 2 ) ½.
Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.
Стоит почитать: все об электролитических конденсаторах.
В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет
Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.
По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.
Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (50002+32002)½ = 5 936 Ом =5,9 кОм.
[stextbox id=’info’]Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.[/stextbox]
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
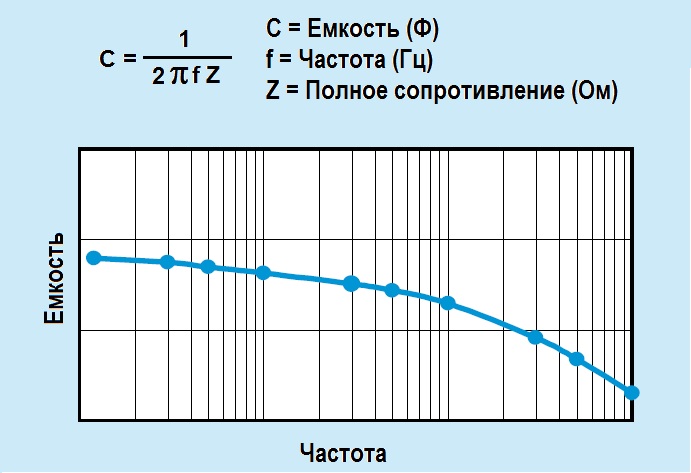
Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
[stextbox id=’info’]Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.[/stextbox]
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:
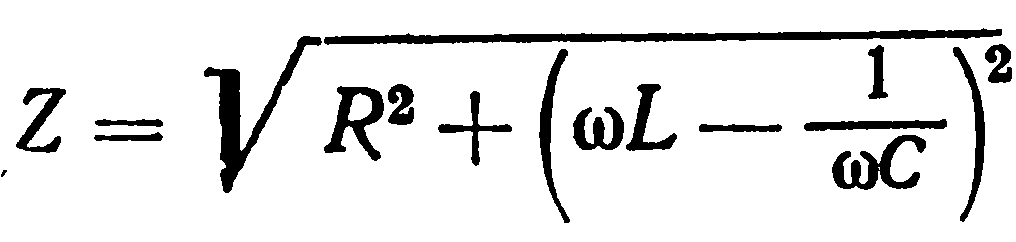
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Z = R + i X , где Z – импеданс, R – величина активного сопротивления , X – величина реактивного сопротивления, i – мнимая единица . В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:
- X > 0 – элемент проявляет свойства индуктивности .
- X = 0 – элемент имеет чисто активное сопротивление .
- X < 0 – элемент проявляет ёмкостные свойства.
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений.
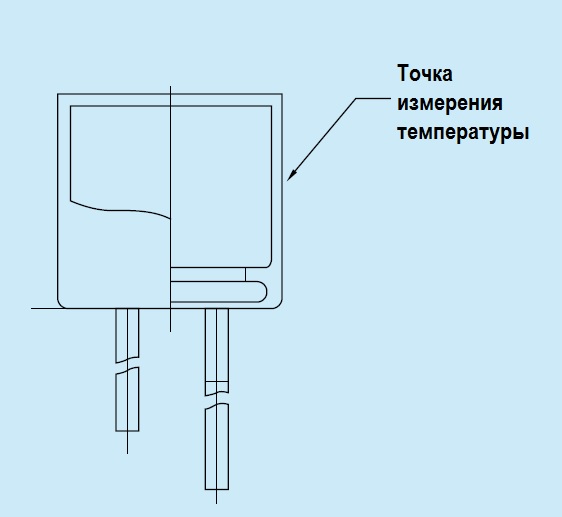
Индуктивное сопротивление (X L ) обусловлено возникновением ЭДС самоиндукции . Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока. Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
Заключение
В данной статье были рассмотрены основные вопросы расчета сопротивления конденсаторов. Больше информации можно найти в скачиваемой версии учебника по электромеханике “Что такое конденсаторы”
В нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессиональных электронщиков. Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vk.com/electroinfonet. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:
www.amperof.ru
www.eduspb.com
www.beasthackerz.ru
www.electroandi.ru
www.websor.ru
Предыдущая
КонденсаторыСколько стоят керамические конденсаторы?
Следующая
КонденсаторыЧто такое ионистор?
Калькулятор электрического сопротивления ёмкости
При подключении конденсатора в цепь переменного тока возникает совокупность процессов заряда и разряда ёмкости,
т.е. накопление и отдача энергии электрическим полем между обкладками. По мере заряда ёмкости, ток через нее уменьшается.
Конденсатор будет заряжаться до максимального значения, пока ток не сменит направление на противоположное.
В моменты максимального значения напряжения на конденсаторе, ток в нём будет равен нулю.
Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
Ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току Xc.
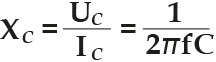
X C — сопротивление, Ом;
f — частота, Гц;
C — ёмкость, Ф.
Сопротивление конденсатора переменному току это отношение действующих значений напряжения к току.
Оно обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Фазы кривых тока и напряжения на конденсаторе смещены на 90 градусов, при этом ток опережает напряжение.
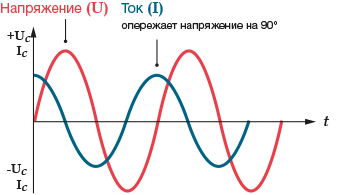
Расчет электрического сопротивления ёмкости
Для расчета введите значение ёмкости конденсатора и частоту переменного тока
Калькулятор вычисления действующих значений тока или напряжения на конденсаторе.
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Что такое емкостное сопротивление
Содержание
- 1 Определение
- 2 Принцип работы
- 3 Расчет
- 4 Характеристики элемента
- 5 Импеданс
- 6 Расчет
- 7 Применение
- 8 Измерение и проверка
- 8.1 Проверка
- 8.2 Замер
- 8.3 Измерение емкости
- 9 Заключение
- 10 Видео по теме
При проектировании электрический цепей, оборудования и электроприборов учитываются многие свойства проводников. Одним из важных свойств считается емкостное сопротивление.
В данной статье будет подробно описано — что такое емкостное сопротивление конденсатора. Так же будет приведена формула расчета такого параметра, описана работа конденсатора в цепи переменного тока и сферы применения ёмкостного сопротивления.
Определение
Сопротивлением называют физический эффект противодействия протеканию тока по любой электрической цепи. Этим свойством обладают все проводники электрического тока. Данная величина измеряется в Ом.
Емкостное электрическое сопротивление является величиной, благодаря которой можно понять, что в цепи присутствует конденсатор. Емкостные сопротивления конденсатора рассчитываются только для цепей переменного тока, без учета наличия в них резисторов.
Конденсатор обозначается на схеме буквой «С», а его ёмкостное сопротивление «Xc».
Принцип работы
Конденсатор с определенной ёмкостью работает по принципу периода, который состоит из заряда и разряда элемента. Период делится на 4 части:
- Первая часть предполагает рост напряжения. В этот момент сопротивление конденсатора минимально, а зарядный ток очень высокий.
- Во второй четверти происходит наполнение его ёмкости за счет зарядного тока.
- В третьей четверти конденсатор полностью заряжается, при этом происходит снижение тока вплоть до 0. ЭДС возрастает с эффектом смены своей направленности.
- В последней четверти происходит разряд элемента. На этом этапе ЭДС будет в пределах 0, а ток постепенно нарастать.
Все описанные процессы за один период определяют дальнейший фазный сдвиг на 90 градусов.
Природа возникновения емкостного сопротивления полностью зависит от нескольких факторов:
- Обязательно наличие конденсатора в цепи.
- По цепи должен течь только переменный ток.
- Сопротивление проводника должно быть меньше емкости конденсатора.
Все эти факторы помогают рассчитать наиболее правильное значение ёмкостных характеристик для наиболее эффективной работы электроцепи.
Расчет
Расчет электрического емкостного сопротивления цепи делается по формуле. Она состоит из следующих значений:
- «Xc» — является емкостным сопротивлением в Омах.
- «1» — период полного заряда и разряда элемента.
- «w» — круговая частота переменного тока с емкостью, рад/сек.
- «C» — емкость конденсатора, единицы измерения Фарад.
Сама формула при этом выглядит следующим образом:
При помощи этой формулы легко рассчитывается Xc. Для этого требуется просто умножить циклическую частоту переменного тока на известную величину емкости конденсатора. Далее необходимо будет один период разделить на полученное значение. Таким образом можно всегда найти сопротивление конденсатора в Ом.
Рассчитываться емкостное сопротивление может так же с помощью и другой формулы, которая приведена на рисунке ниже.
При расчетах по данной формуле прослеживаются следующие зависимости:
- Емкость конденсатора и частота тока всегда выше сопротивления.
- От величин емкости и частоты зависит скорость одного периода заряда/разряда конденсатора.
Также стоит учесть, что после подключения конденсатора в цепь постоянного тока, его сопротивление сильно увеличивается. Объясняется причина такого явления довольно просто — отсутствует частота протекания электричества.
Характеристики элемента
Для того чтобы понять, что такое емкостное сопротивление, необходимо разобраться с его основной характеристикой, которая называется емкостью. Емкостью называется накопительная способность элемента. Она заключается в накоплении определенной доли электрического тока за определённый промежуток времени. Единицей измерения этой величины является Фарад (Ф или F).
Элемент заряжается электричеством до определенного момента, после которого он начинает разряжаться и отдавать ток дальше по электроцепи. Время полного разряда напрямую зависит от величины сопротивления цепи. Чем выше это значение, тем меньше времени тратится на разрядку элемента. Для расчета ёмкостной характеристики используется следующее выражение:
Так же конденсаторы обладают рядом дополнительных характеристик. К ним относят:
- Общую удельную емкость. Является отношением массы диэлектрических пластин и емкостных параметров.
- Напряжение. Параметр определяется как рабочее напряжение, которое способен выдержать элемент.
- Температурная стойкость или стабильность. Это температурный параметр, который не влияет на изменение емкости.
- Изоляционное сопротивление. Является величиной точки утечки и саморазряда.
- Эквивалентная нагрузка. Значение, определяющее потери на выводе или контактах устройства.
- Абсорбция. Разность потенциалов в момент разряда до 0.
- Полярность. Параметр свойственен элементам, которые работают строго при подаче на обкладку потенциала определенного значения (плюс или минус).
- Индуктивность. Свойство конденсатора образовывать на контактах индуктивное сопротивление. Такое свойство может наделить элемента параметрами колебательного контура.
Все эти значения строго учитываются при проектировании цепей или схем электрического оборудования.
Импеданс
Кроме емкостного, конденсатор еще имеет общее сопротивление или импеданс. Данное значение определяется с учетом значений трех параметров: индуктивного, резистивного и емкостного сопротивления.
Для вычисления импеданса применяется следующая формула:
В данном выражении используются следующие сопротивления:
- xL — индуктивное;
- xC — емкостное;
- R — активное.
Активное сопротивление цепи появляется вследствие возникновения в ней ЭДС. Так как переменный ток по своей природе импульсный, то электромагнитный поток может довольно незначительно изменяться, а это приводит к сдвигу постоянного значения ЭДС.
Емкостные и индуктивные величины взаимосвязаны. По разнице между ними легко находят реактивную составляющую цепи.
Отсюда легко проследить, от чего зависит само реактивное сопротивление:
- Если реактивная величина больше 0, то устройство больше нагружено индуктивным значением.
- Если реактивное значение равно 0, то емкость не нагружается активным сопротивлением.
- Если реактивность меньше 0, то элемент имеет высокое емкостное сопротивление.
Активное сопротивление считается невосполнимой величиной. Она тратится на преобразование тока в иной вид энергии. Реактивная величина неизменна для актуальной цепи переменного тока.
Расчет
Узнав, по какой формуле делаются необходимые вычисления и поняв смысл емкостного сопротивления, можно заняться расчетом данной величины.
Например, сделаем расчет на основе следующих данных:
- Емкость конденсатора C=1мкФ;
- В цепи также имеется активное сопротивление R, которое равно 5 кОм;
- Индуктивное сопротивление цепи xL составляет 4.5 кОм;
- Частота переменного тока равна 50 Гц;
- Напряжение 50 вольт.
На основе этих данных необходимо будет найти сопротивление конденсатора.
Емкостное сопротивление определим следующим образом:
xC=1/(2πfC)=1/(2×3.14×50×1×10-6)=3184 Ом или округленно 3.2 кОм.
Для определения величины тока в этой цепи воспользуемся законом Ома:
I=U/xC=50/3184=0.0157 ампер или 15.7мА.
После этого определяются параметры общего сопротивления:
Z=(R²+(xL-xC)²)½=(5000²+(4500–3184)²)½=5170 Ом или 5.1 кОм.
По данным расчётам можно определить влияние емкостного элемента на электроцепь. Главное понимать, какие физические величины используются в данных формулах для выполнения правильных вычислений.
Применение
В электронных цепях очень часто конденсатор используется в качестве фильтрующего элемента. При этом инженеры учитывают способ подключения данного элемента:
- При параллельном соединении конденсатора с цепью, устройство способно задерживать ток высокой частоты. Такой фильтр работает по принципу зависимости сопротивления от частоты тока. Чем выше частота, тем ниже будет сопротивление.
- При последовательном включении фильтр уже отсеивает низкочастотные импульсы. Вторым свойством такого фильтра является возможность не пропускать постоянный ток.
Также большая доля использования таких устройств приходится на звуковые усилители. Конденсатор способен отделить переменный и постоянный ток, а значит работать в качестве усилителя низкой частоты. При этом подбираются элементы с наименьшей емкостью.
Так же устройства используются для блоков питания постоянного тока или стабилизаторов. Тут применяется свойство разделения постоянной и переменной составляющей. Например, разделение ее между потребителями с помощью отдельных выходов для постоянного и переменного тока. В таких устройствах конденсатор разряжается, если нагрузка на цепь увеличивается за счет подключения нового устройства. Тем самым общая пульсация в цепи сглаживается. При необходимости можно передать ток обоих значений по одному проводнику. Делается это следующим образом — контакты с постоянным напряжением подключают к выводу емкости для прямого контакта с переменным напряжением. Таким образом происходит фильтрация частоты, сглаживание импульсов и передача постоянного тока потребителю. Такая схема используется в антенных усилителях, которые подключаются к телевизорам.
Измерение и проверка
Измерить целостность конденсатора и его сопротивление можно при помощи мультиметра. Перед этим элемент обязательно необходимо отсоединить от цепи.
Проверка
Диагностика целостности конденсатора начинается с визуально осмотра его состояния. Любые трещины, вздутия или деформации корпуса можно считать неисправностью элемента. Если визуальный осмотр не дал никаких результатов, то элемент проверяется на пробой при помощи тестера.
Делается такая проверка следующим образом:
- Элемент необходимо выпаять из схемы, а его контактные выводы замкнуть металлическим предметом для разрядки.
- Мультиметр перемести в режим замера сопротивления.
- Измерительные щупы соединить с контактами устройства.
- Сопротивление исправного элемента будет измеряться бесконечным значением, которое будет превышать значение сопротивления утечки. Величина этой утечки при этом составляет 2 кОм.
Если показания меньше этого значения, значит элемент неисправен и пробит.
Замер
Замерить сопротивление можно так же с помощью мультиметра. Его надо будет перевести в режим измерения сопротивлений более 100 кОм. Далее необходимо соединить щупы прибора с контактами устройства. Некоторое время потребуется на полную зарядку элемента. После этого он покажет конечный результат, который не должен быть выше 100 кОм. Если этот порог преодолен, то можно сделать однозначный вывод о неисправности элемента.
Измерение емкости
Для замера емкости потребуется тестер с режимом СX. Если такого режима нет, проверить элемент будет невозможно. Далее требуется:
- Полностью разрядить конденсатор.
- На мультиметре выбирается режим СX.
- Измерительные щупы соединить с контактными выводами устройства, строго соблюдая полярность.
- Прибор должен показать величину больше 1, но при этом ее значение должно быть в пределах тех значений, которые указаны на корпусе детали. Если значение равняется 0 или находится за пределами указанных значений, то конденсатор можно признать неисправным.
Полученные мультиметром данные также можно считать ёмкостным значением, так как в момент проверки элемент проходит зарядку током.
Заключение
Емкостным сопротивлением обладают все цепи, в которых задействованы конденсаторы. Зная, какой по параметрам элемент включен в данную цепь, можно легко рассчитать его емкостное влияние на цепь, используя представленные в статье формулы для расчётов.
Видео по теме
Конденсатор используется в схемах для разделения переменной и постоянной составляющей напряжения, при этом он хорошо проводит высокочастотный сигнал, и плохо – низкочастотный. Находясь в цепи постоянного тока, его импеданс принимается бесконечно большим. Для переменного тока ёмкостное сопротивление конденсатора не имеет постоянной величиной. Поэтому расчёт этого значения крайне важен при проектировании различных радиоэлектронных приборов.
- Общее описание
- Характеристики прибора
- Импеданс элемента
- Ёмкостное сопротивление
- Индуктивная составляющая
- Пример расчёта
Общее описание
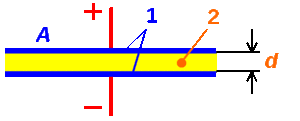
Физически электронное устройство – конденсатор – представляет собой две обкладки, выполненные из проводящего материала, между которыми находится диэлектрический слой. С поверхности пластин выводятся два электрода, предназначенные для подключения в электрическую цепь. Конструктивно прибор может быть различного размера и формы, но его структура остаётся неизменной, то есть всегда происходит чередование проводящего и диэлектрического слоев.
Слово “конденсатор” произошло от латинского “condensatio” – “накопление”. Научное определение гласит, что накопительный электрический прибор — это двухполюсник, характеризующийся постоянным и переменным значениями ёмкости и большим сопротивлением. Предназначен он для накопления энергии и заряда. За единицу измерения ёмкости принят фарад (F).
На схемах конденсатор изображается в виде двух прямых, соответствующих проводящим пластинам прибора, и перпендикулярно к их серединам нарисованными отрезками — выводами устройства.
Принцип действия конденсатора заключается в следующем: при включении прибора в электрическую цепь напряжение в ней будет иметь нулевую величину. В этот момент устройство начинает получать и накапливать заряд. Электрический ток, подающийся в схему, будет максимально возможным. Через некоторое время на одном из электродов прибора начнут накапливаться заряды положительного знака, а на другом – отрицательного.
Длительность этого процесса зависит от ёмкости прибора и активного сопротивления. Расположенный между выводами диэлектрик мешает перемещению частиц между обкладками. Но это будет происходить лишь до того момента, пока разность потенциалов источника питания и напряжение на выводах конденсатора не сравняются. В этот момент ёмкость станет максимально возможной, а электроток – минимальным.
Если на элемент перестают подавать напряжение, то при подключении нагрузки конденсатор начинает отдавать свой накопленный заряд ей. Его ёмкость уменьшается, а в цепи снижаются уровни напряжения и тока. Иными словами, накопительный прибор сам превращается в источник питания. Поэтому если конденсатор подключить к переменному току, то он начнёт периодически перезаряжаться, то есть создавать определённое сопротивление в цепи.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.
Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние.
Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
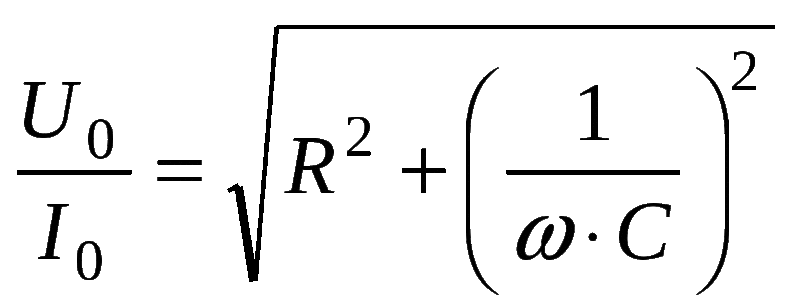
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
Ёмкостное сопротивление
Для понимания процесса следует представить конденсатор в электрической цепи, по которой течёт переменный ток. Причём в этой цепи нет других элементов. Значение тока, проходящего через конденсатор, и напряжения, приложенного к его обкладкам, изменяется по времени. Зная любое из этих значений, можно найти другое.
Пускай ток изменяется по синусоидальной зависимости I (t) = Im * sin (w*t+ f 0). Тогда напряжение можно описать как U (t) = (Im/C*w) *sin (w*t+ f 0 -p/2). При учёте в формуле сдвига фаз на 90 градусов, возникающего между сигналами, вводится комплексная величина j, называемая мнимой единицей. Поэтому формула для нахождения тока будет выглядеть как I = U /(1/j*w*C). Но учитывая, что комплексное число только обозначает смещение напряжения относительно тока, а на их амплитудные значения не влияет, его можно убрать из формулы, тем самым значительно её упростив.
Так как по закону Ома сопротивление прямо пропорционально напряжению на участке цепи и обратно пропорционально току, то преобразуя формулы, можно будет получить следующее выражение:
- Xc = 1/w*C = ½*p*f*C. Единица измерения – ом.
Становится понятно, что ёмкостное сопротивление зависит не только от ёмкости, но и от частоты. При этом чем больше эта частота, тем меньшее сопротивление конденсатор будет оказывать проходимому через него току. По отношению к ёмкости это утверждение будет обратным. Вот поэтому для постоянного тока, частота которого равна нулю, сопротивление накопителя будет бесконечно большим.
На практике всё немного по-другому. Чем ближе частота сигнала приближается к нулевому значению, тем больше становится сопротивление конденсатора, но при этом разрыв цепи наступить всё равно не может. Связанно это с током утечки. В случае когда частота стремится к бесконечности, сопротивление конденсатора должно становиться нулевым, но этого тоже не происходит – из-за присутствия паразитной индуктивности и всё того же тока утечки.
Индуктивная составляющая
При прохождении переменного сигнала через накопитель, его можно представить в виде последовательно включённой с источником питания катушки индуктивности. Эта катушка характеризуется большим сопротивлением в цепи переменного сигнала, чем постоянного. Значение силы тока в определённой точке времени находится как I = I 0 * sinw .
Приняв во внимание, что мгновенная величина напряжения U 0 обратна по знаку мгновенному значению ЭДС самоиндукции E 0, а также используя правило Ленца, можно получить выражение E = L * I, где L — индуктивность.
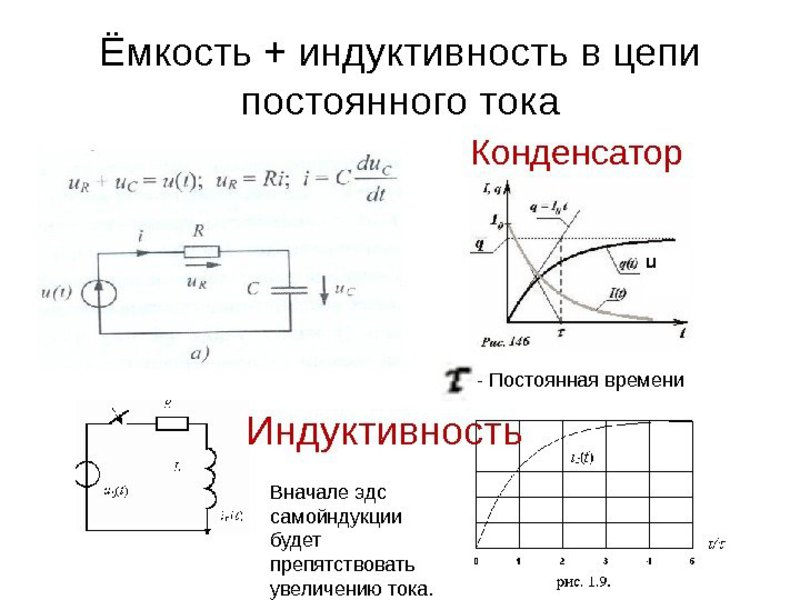
Следовательно: U = L*w * I 0 *cosw*t = U 0 *sin (wt + p /2) , причём ток отстаёт от напряжения на p /2. Используя закон Ома и приняв, что сопротивление катушки равно w * L, получится формула для участка электрической цепи, имеющая только индуктивную составляющую: U 0 = I 0 / w * L.
Таким образом, индуктивное сопротивление будет равно Xl = w * L, измеряется оно также в омах. Из полученного выражения видно, что чем больше частота сигнала, тем сильнее будет сопротивление прохождению тока.
Пример расчёта
Ёмкостное и индуктивное сопротивления относятся к реактивным, то есть таким, которые не потребляют мощности. Поэтому закон Ома для участка схемы с ёмкостью имеет вид I = U/Xc, где ток и напряжение обозначают действующие значения. Именно из-за этого конденсаторы используются в цепях для разделения не только постоянных и переменных токов, но и низкой и высокой частот. При этом чем ёмкость будет ниже, тем более высокой частоты сможет пройти ток. Если же последовательно с конденсатором включено активное сопротивление, то общий импеданс цепи находится как Z = (R 2 +Xc 2 ) ½.
Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.
В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет
Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.
По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.
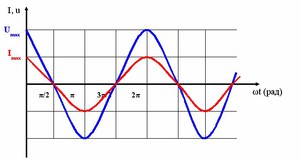
Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (50002+32002)½ = 5 936 Ом =5,9 кОм.
Таким образом, подсчитать полное сопротивление на любом участке цепи несложно. При этом можно воспользоваться и так называемыми онлайн-калькуляторами, куда вводят начальные данные, такие как частота и ёмкость, а все расчёты выполняются автоматически. Это удобно, так как нет необходимости запоминать формулы и вероятность ошибки при этом стремится к нулю.
Господа, как-то раз чудесным летним деньком я взял ноутбук и вышел из дома на дачный участок. Там, усевшись в кресле-качалке в тени яблонь, я и решил написать данную статью. Ветерок шумел в ветвях деревьев, раскачивая их из стороны в сторону, и в воздухе была та самая атмосфера, благоприятствующая течению мыслей, которая так порой необходима…
Впрочем, хватит лирики, пора переходить непосредственно к существу обозначенного в заголовке статьи вопроса.
Итак, параллельное соединение конденсаторов… Что вообще такое параллельное соединение? Те, кто читал мои прошлые статьи, безусловно, помнят значение этого определения. Оно нам встречалось, когда мы говорили про параллельное соединение резисторов. В случае конденсаторов определение будет иметь абсолютно такой же вид. Итак, параллельное соединение конденсаторов – это такое соединение, когда одни концы всех конденсаторов соединены в один узел, а другие – в другой.
Конечно, лучше один раз увидеть, чем сто раз услышать, поэтому на рисунке 1 я привел изображение трех конденсаторов, которые соединены параллельно. Пусть емкость первого равна С1, второго – С2, а третьего – С3.
Рисунок 1 – Параллельное соединение конденсаторов
В данной статье мы разберем, по каким законам изменяются токи, напряжения и сопротивления переменному току при параллельном соединении конденсаторов, а также какова будет суммарная емкость такой конструкции. Ну и, само собой, поговорим, зачем вообще такое соединение может быть нужно.
Предлагаю начать с напряжения, ибо с ним здесь все предельно ясно. Господа, должно быть совершенно очевидно, что при параллельном соединении конденсаторов напряжения на них равны между собой. То есть напряжение на первом конденсаторе точно такое же, как на втором и на третьем
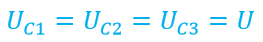
Почему, собственно, это так? Да очень просто! Напряжение на конденсаторе считается как разность потенциалов между двумя ножками конденсатора. А при параллельном соединении «левые» ножки всех конденсаторов сходятся в один узел, а «правые» – в другой. Таким образом, «левые» ножки всех конденсаторов имеют один потенциал, а «правые» другой. То есть разность потенциалов между «левой» и «правой» ногами будет одинаковая для любого конденсатора, а это как раз и значит, что на всех конденсаторах одно и то же напряжение. Чуть более строгий вывод этого утверждения вы можете глянуть вот в этой статье. В ней мы приводили его для параллельного соединения резисторов, но и здесь он будет звучать абсолютно так же.
Итак, мы выяснили, что напряжение на всех параллельно соединенных конденсаторах одно и то же. Это, кстати, верно для любого вида напряжения – как для постоянного, так и для переменного. Вы можете присоединить к трем параллельно включенным конденсаторам батарейку на 1,5 В. И на всех них будет постоянные 1,5 В. А можете присоединить к ним генератор синусоидального напряжения с частотой 50 Гц и амплитудой 310 В. И на каждом конденсатор будет синусоидальное напряжение с частотой 50 Гц и амплитудой 310 В. Важно помнить, что у параллельно соединенных конденсаторов одной и той же будет не только амплитуда, но и частота, и фаза напряжения.
И если с напряжением все вот так вот просто, то с током ситуация посложнее. Когда мы говорим про ток через конденсатор, то обычно имеем ввиду переменный ток. Вы ведь помните, что постоянные токи через конденсаторы не текут? Конденсатор для постоянного тока – это все равно, что разрыв цепи (на деле есть некоторое сопротивление утечки конденсатора, но им обычно пренебрегают, потому что оно очень велико). Переменные же токи вполне себе текут через конденсаторы, причем могут иметь при этом весьма и весьма большие амплитуды. Очевидно, что эти переменные токи вызываются некоторым переменными напряжениями, приложенными к конденсаторам. Итак, пусть у нас по-прежнему имеется три параллельно соединенных конденсатора с емкостями С1, С2 и С3. К ним приложено некоторое переменное напряжение с комплексной амплитудой 
. Из-за этого приложенного напряжения через конденсаторы будут течь некоторые переменные токи с комплексными амплитудами 
. Для наглядности давайте нарисуем картинку, на которой будут все фигурировать все эти величины. Она представлена на рисунке 2.
Рисунок 2 – Ищем токи через конденсаторы
Прежде всего надо понять, как связаны токи с суммарным током 
источника. А связаны они, господа, все по тому же самому первому закону Кирхгофа, с которым мы уже знакомились в отдельной статье. Да, тогда мы его рассматривали в контексте постоянного тока. Но, оказывается, первый закон Кирхгофа остается верным и в случае переменного тока! Просто в этом случае надо использовать комплексные амплитуды токов. Итак, суммарный ток трех параллельно соединенных конденсаторов связан с общим током вот так
То есть общий ток фактически просто разделяется между тремя конденсаторами, тогда как суммарная его величина остается той же самой. Важно помнить еще одну важную вещь – частота тока и его фаза будет одна и та же для всех трех конденсаторов. Точно такая же частота и фаза будет и у суммарного тока I. Таким образом, различаться они будут только лишь амплитудой, которая будет у каждого конденсатора своя. Как же найти эти самые амплитуды токов? Очень просто! В статье про сопротивление конденсатора мы связали между собой ток через конденсатор и напряжение на конденсаторе через сопротивление конденсатора. Сопротивление конденсатора мы легко можем посчитать, зная его емкость и частоту протекающего через него тока (помним, что для разной частоты конденсатор имеет разное сопротивление) по общей формуле:
Воспользовавшись этой замечательной формулой, мы можем найти сопротивление каждого конденсаторы:
Комплексная амплитуда тока связана с комплексной амплитудой напряжения по закону Ома для сетей переменного тока (более подробно про это мы говорили в предыдущей статье):
Воспользовавшись этой формулой, мы легко находим ток через каждый из трех параллельно соединенных конденсаторов:
Общий ток в цепи, который втекает в узел А и вытекает потом из узла В, очевидно, равен
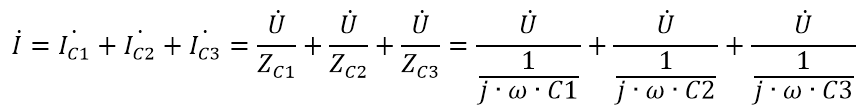
На всякий случай напомню еще раз, что это получилось на основании первого закона Кирхгофа. Заметьте, господа, один важный факт – чем больше емкость конденсатора, тем меньше его сопротивление и тем большая часть тока будет течь через него.
Давайте представим общий ток через три параллельно соединенных конденсатора как отношение приложенного к ним напряжения и некоторого эквивалентного общего сопротивления Zc∑ (которое нам пока неизвестно, но которое мы потом найдем) трех параллельно включенных конденсаторов:
Сокращая левую и правую части на U, получаем
Таким образом, получаем важный вывод: при параллельном соединении конденсаторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных конденсаторов. Если вы помните, то точно такой же вывод мы получили и при параллельном соединении резисторов.
А что происходит с емкостью? Какая будет общая емкость у системы из трех параллельно соединенных конденсаторов? Можно ли это как-то найти? Безусловно, можно! И, более того, мы почти это сделали. Давайте в нашу последнюю формулу подставим расшифровку сопротивлений конденсаторов. Тогда у нас получится примерна такая запись
После элементарных математических преобразований, доступных даже пятикласснику, получаем, что
Это наш очередной чрезвычайной важный вывод: суммарная емкость системы из нескольких параллельно соединенных конденсаторов равна сумме емкостей отдельных конденсаторов.
Итак, мы рассмотрели основные моменты, касающиеся параллельного соединения конденсаторов. Давайте в сжатой форме резюмируем их все:
- Напряжение на всех трех параллельно соединенных конденсаторах одно и то же (по амплитуде, фазе и частоте);
- Амплитуда тока в цепи, содержащей параллельно соединенные конденсаторы, равна сумме амплитуд токов через отдельные конденсаторы. Чем больше емкость конденсатора, тем больше амплитуда тока через него. Фазы и частоты токов на всех конденсаторов одни и те же;
- При параллельном соединении конденсаторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных конденсаторов;
- Суммарная емкость параллельно соединенных конденсаторов равна сумме емкостей всех конденсаторов.
Господа, если вы запомните и поймете эти четыре пункта, то, можно сказать, статью я писал не зря
.
А теперь давайте для закрепления материала попробуем решить какую-нибудь задачу на параллельное соединение конденсаторов. Потому что, весьма вероятно, если вы ничего не слышали раньше про параллельное соединение конденсаторов, то все написанное выше может восприниматься просто как набор абстрактных буковок, которые не очень понятно как применять на практике. Поэтому, на мой взгляд, наличие приближенных к практике задач является неотъемлемой частью образовательного процесса. Итак, задача.
Допустим, у нас есть три параллельно соединенных конденсаторов с емкостями С1=1 мкФ, С2=4,7 мкФ и С3=22 мкФ. К ним приложено переменное синусоидальное напряжение с амплитудой Umax=50 В и частотой f=1 кГц. Требуется определить
а) напряжение на каждом из конденсаторов;
б) ток через каждый конденсатор и суммарный ток в цепи;
в) сопротивление каждого конденсатора переменному току и общее сопротивление;
г) общую емкость такой системы.
Начнем с напряжения. Мы помним, что на всех конденсаторах напряжение у нас одно и то же – то есть синусоидальное с частотой f=1 кГц и амплитудой Umax=50 В. Предположим, что оно изменяется по синусоидальному закону. Тогда можно записать следующее
Вот мы и ответили на первый вопрос задачи. Осциллограмма напряжения на наших конденсаторах приведена на рисунке 3.
Рисунок 3 – Осциллограмма напряжения на конденсаторах
Дальше, пользуясь общими формулами для сопротивления конденсатора, посчитаем сопротивление каждого конденсатора току с частотой f=1 кГц:
Да, мы видим, что сопротивления у нас получились не только комплексные, но еще и со знаком минус. Однако вас это не должно смущать, господа. Это значит только то, что ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга, причем ток опережает напряжение. Да, мнимая единичка показывает тут только фазовый сдвиг и ничего больше. Для расчета амплитуды тока нам потребуется только модуль этого комплексного числа. Про все это говорилось уже в прошлых двух статьях (раз и два). Возможно, это не совсем очевидно и требуется какая-либо наглядная иллюстрация этого дела. Это можно сделать на тригонометрическом круге и, надеюсь, немного позже, я подготовлю отдельную статью, посвященную этому, либо вы можете сами придумать, как это показать наглядно, пользуясь данными из моей статьи про комплексные числа в электротехнике.
Теперь ничего не мешает найти обратное общее сопротивление:
Находим общее сопротивление трех наших параллельно соединенных конденсаторов
Следует помнить, что это сопротивление верно исключительно для частоты 1 кГц. Для других частот значение сопротивления, очевидно, будет другое.
Следующим шагом рассчитаем амплитуды токов через каждый конденсатор. В расчете будем использовать модули сопротивлений (отбросим мнимую единицу), помня при этом, что сдвиг фаз между током и напряжением будет 90 градусов (то есть, если напряжение у нас меняется по закону синуса, то ток будет меняться по закону косинуса). Можно вести расчет и с комплексными числами, используя комплексные амплитуды тока и напряжения, но, на мой взгляд, в данной задаче проще просто учесть потом фазовые соотношения. Итак, амплитуды токов равны
Суммарная амплитуда тока в цепи, очевидно, равна
Мы можем себе позволить вот так вот складывать амлитуды сигналов, потому что у всех токов через параллельно соединенные конденсаторы у нас одна и та же частота и фаза. В случае невыполнения этого требования вот так вот просто взять и сложить нельзя.
Теперь, помня про фазовые соотношения, нам никто не мешает записать законы изменения тока через каждый конденсатор
И суммарный ток в цепи
Осциллограммы токов через конденсаторы приведены на рисунке 4.
Рисунок 4 – Осциллограммы токов через конденсаторы
Ну и в завершении задачи самое простое – найдем общую емкость системы как сумму емкостей:
Кстати, эту емкость вполне можно использовать для расчета суммарного сопротивления трех параллельно соединенных конденсаторов. В качестве упражнения читателю предлагается самому в этом убедиться .
В заключение хотелось бы выяснить один, возможно, самый важный вопрос: а зачем вообще нужно на практике соединять конденсаторы параллельно? Что это дает? Какие возможности нам открывает? Ниже по пунктам я обозначил основные моменты:
- Параллельное соединение конденсаторов дает увеличение емкости системы. Пожалуй, это самый основной и главный пункт. Например, в нашей системе нужна емкость не менее 1000 мкФ, а в нашем распоряжении только конденсаторы на 220 мкФ. Что делать? Правильно, взять этих конденсаторов штук пять и получить требуемую емкость.
- Конденсаторы часто используют для сглаживания пульсаций напряжения. Бывает, что в этом случае через конденсатор текут весьма значительные импульсные токи (например, в импульсных источниках питания). Каждый конденсатор может выдержать отнюдь не бесконечно большую величину импульсного тока. Таким образом, если величина импульсного тока в системе превышает максимально допустимый ток для данного типа конденсаторов, то их соединяют несколько штук параллельно. При этом ток распределяется между этими конденсаторами.
- Существует такое понятие, как “резонанс конденсатора”. Подробно о нем мы погорим позднее. Если быть кратким, то суть явления заключается в том, что на высоких частотах, начиная с некоторой резонансной частоты, из-за паразитных индуктивностей конденсатор перестает быть конденсатором и начинает вести себя как дроссель. У разных конденсаторов эта резонансная частота различна: у кого-то она больше, у кого-то меньше. Так вот, когда нужна фильтрация сигнала в широком диапазоне частот, применяют параллельное соединение конденсаторов с разными резонансными частотами. Например, соединяют параллельно конденсаторы с емкостью 0,1 мкФ, 10 нФ, 100 пФ, 22 пФ. Такое соединение даст эффективное подавление помех в широком диапазоне. Более подробно обсудим это интересное явление в другой раз.
Ну а мы на этом заканчиваем, господа. Спасибо за внимание и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
