Задачи на смеси и сплавы — подробнее
Концентрация какого-то вещества в растворе – это отношение массы или объема этого вещества к массе или объему всего раствора.
То же самое относится и к сплавам: содержание одного из металлов в сплаве – это отношение массы этого металла к массе всего сплава.
Обычно концентрация измеряется в процентах.
Что такое процент?
Напомню, что это сотая доля числа. То есть, если массу или объем разделить на ( displaystyle 100), получим ( displaystyle 1%) этой массы или объема.
Чтобы вычислить концентрацию в процентах, достаточно полученное число умножить на ( displaystyle 100%).
Почему?
Сейчас покажу: пусть масса всего раствора равна ( displaystyle M), а масса растворенного вещества (например, соли или кислоты) – ( displaystyle m). Тогда один процент от массы раствора равен ( displaystyle frac{M}{100}).
Как узнать, сколько таких процентов содержится в числе ( displaystyle m)?
Просто: поделить число ( displaystyle m) на этот один процент: ( displaystyle frac{m}{frac{M}{100}}=frac{m}{M}cdot 100), но ведь ( displaystyle frac{m}{M}) – это концентрация.
Вот и получается, что ее надо умножить на ( displaystyle 100), чтобы узнать, сколько процентов вещества содержится в растворе.
Более подробно о процентах – в темах «Дроби, и действия с дробями»и «Проценты».
Поехали дальше.
Масса раствора, смеси или сплава равна сумма масс всех составляющих.
Логично, правда?
Например, если в растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг соли, то сколько в нем воды? Правильно, ( displaystyle 7)кг.
И еще одна очевидность:
При смешивании нескольких растворов (или смесей, или сплавов), масса нового раствора становится равной сумме масс всех смешанных растворов.
А масса растворенного вещества в итоге равна сумме масс этого же вещества в каждом растворе отдельно.
Например: в первом растворе массой ( displaystyle 10) кг содержится ( displaystyle 3) кг кислоты, а во втором растворе массой ( displaystyle 14) кг – ( displaystyle 5) кг кислоты.
Когда мы их смешаем, чему будет равна масса нового раствора?
( displaystyle 10+14=24) кг.
А сколько в новом растворе будет кислоты? ( displaystyle 3+5=8) кг.
Перейдем к задачам.
Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике
ЕГЭ №11. Задачи на растворы, смеси и сплавы (и на проценты)
В этом видео мы научимся решать текстовые задачи на проценты, а так же на растворы, смеси и сплавы — на все, что содержит разные вещества в каком-то соотношении.
Задачи на смеси и сплавы очень часто попадаются на ОГЭ (№23) и профильном ЕГЭ (под номером 12).
Мы научимся очень простому способу сводить эти задачи к обычному линейному уравнению или к системе из двух таких уравнений.
Также мы научимся решать сложные задачи на проценты — в основном они на банковские вклады и кредиты и прочие финансовые штуки.
Это, в том числе, даст нам очень большой задел для “ экономической» задачи №17 (которая стоит аж 3 первичных балла).
ЕГЭ №17 Экономическая задача. Вклады
Экономические задачи в основном довольно простые, но дают аж 3 первичных балла!
Но это не совсем 3 балла нахаляву. Эти задачи требуют очень подробного и чёткого описания решения.
По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.
Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!
На этом уроке мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.




















Тема: «Способы решения задач на растворы, смеси и сплавы»
Оглавление:
1.Введение……………………………………………………………………………………………..
2. Задачи на растворы, смеси и сплавы…………………………………………..
2.1. Теоретические основы решения задач на растворы, смеси и сплавы ………………………………………………………………………………………
2.2. Способы решения задач на растворы, сплавы и смеси…………….
2.3. Решение задач на растворы, смеси и сплавы…………………………….
3. Заключение………………………………………………………………………………….
4. Список источников информации………………………………………………..
5. Приложение…………………………………………………………………………………
Введение
При подготовке к сдаче ЕГЭ по математике на профильном уровне встретила задачи на растворы, смеси и сплавы, которые в школьном курсе математики почти не рассматриваются.
Они также встречаются на уроках химии и физики.
Имеют практическое значение в повседневной жизни. Например, как правильно приготовить маринад для консервирования, как смешать клей для обоев, приготовить раствор для заливки фундамента дома, разбавить уксусную кислоту для употребления в пищу, приготовить различной концентрации растворы.
Задачи на растворы, смеси и сплавы являются хорошим средством развития логического мышления, средством к углублению свои знаний .
Одним из возможных путей подготовки к ЕГЭ является изучение методов (способов, алгоритмов) решения задач на растворы, смеси и сплавы. В данной ситуации будет полезным не только самому научиться решать такого типа задачи, но и научить одноклассников.
Объект исследования: Задачи на смеси и сплавы
Предмет исследования: Способы решения задачи на растворы, смеси и сплавы
Цель: Изучить способы решения задач на смеси и сплавы.
Задачи: 1. Изучить способы решения задачи на растворы, смеси и сплавы.
2.Выявить алгоритм решения задач данного вида.
3. Научиться решать задачи на растворы, смеси и сплавы. Гипотеза: все задачи на растворы, сплавы и смеси делятся на несколько типов, а каждый из типов имеет конкретный способ решения.
Человеку часто приходится смешивать различные жидкости, порошки, газообразные или твердые вещества, или разбавлять что-либо водой.
В задачах такого типа эти операции приходится проводить мысленно и выполнять расчеты.
Текстовые задачи на смеси, сплавы и растворы входят в различные сборники заданий по подготовке к итоговой аттестации по математике за курс основной школы, включаются в варианты ЕГЭ.
Теоретические основы решения задач на растворы, смеси, сплавы.
Чтобы лучше понимать условия задач, необходимо знать следующие понятия:
-
Все получающиеся сплавы или смеси однородны.
-
При решении этих задач считается, что масса смеси нескольких веществ равна сумме масс компонентов.
-
Процент – одна сотая любого вещества.
-
Производительность объекта – скорость работы
-
Процентным содержанием ( концентрацией) вещества в смеси называется отношение его массы к общей массе всей смеси. Она показывает долю вещества в растворе.
-
Это отношение может быть выражено либо в дробях, либо в процентах.
-
Сумма концентраций всех компонент, составляющих смесь, равна единице.
Глава 2. Типы задач «на смеси сплавы, растворы». Способы их решения.
Все задачи на растворы, смеси, сплавы, можно разделить на три типа:
-
на вычисление концентрации;
-
на вычисление количества чистого вещества в смеси (или сплаве);
-
на вычисление массы смеси (сплава).
Существуют следующие способы решения задач:
-
с помощью таблиц;
-
с помощью схемы;
-
старинным арифметическим способом;
-
алгебраическим способом;
-
с помощью графика;
-
с помощью расчетной формулы.
-
правило квадрата
-
приравнивание площадей равновеликих прямоугольников
-
Способ Л.Ф.Магницкого для трех веществ
-
Правило креста
Алгоритм решения задачи на сплавы, растворы и смеси:
-
Изучить условия задачи;
-
Выбрать неизвестную величину (обозначить ее буквой);
-
определить все взаимосвязи между данными величинами;
-
Составить математическую модель задачи (выбрать способ решения задачи, составить пропорцию или уравнение относительно неизвестной величины) и решить ее;
-
провести анализ результата.
Глава 3. Рассмотрим несколько задач и решим их различными способами.
Задача 1. Сколько нужно добавить воды в сосуд, содержащий 200 г
70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?
Решение: 1 способ – с помощью таблицы:
Наименование веществ, смесей
Наименование веществ, смесей
Масса
раствора (г)
Масса вещества (г)
Исходный раствор
70 % = 0,7
200
0,7·200
Воды долили
–
x
–
Новый раствор
8 % = 0,08
200 + x
0,08(200 + x)
Так как подливали только воду, масса уксусной кислоты в растворе не изменилась. Составляем уравнение : 0,08(200 + х) = 0,7·200
16 + 0,08х = 140
0,08х = 124
х = 1550г
Ответ :1,55 кг воды.
2способ: с помощью схемы: Пусть в сосуд долили х литров воды. Получаем схему:
Уксусная кислота
Уксусная кислота
70%
8%
+ х литров воды
200 (200 + х) г.
0,08(200 + х) = 0,7·200; 16 + 0,08х = 140; 0,08х = 124; х = 1550г Ответ :1,55 кг воды.
Задача 2: В сосуд, содержащий 5 литров 12–процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
 Решение – с помощью формулы:
Решение – с помощью формулы:
Концентрация раствора равна
Объем вещества в исходном растворе равен 0,12*5=0,6 литра. При добавлении 7 литров воды общий объем раствора увеличится, а объем растворенного вещества останется прежним. Таким образом, концентрация полученного раствора равна:

Ответ: 5.
Задача 3: Сначала приготовили 25%-ый водный раствор поваренной соли. Затем одну треть воды выпарили. Найдите концентрацию получившегося раствора.
Решение – с помощью схемы:
До выпаривания: 
 После выпаривания:
После выпаривания: 
Сейчас соль стала составлять третью часть всего раствора, т.е. 100% : 3 = %
 Ответ: %.
Ответ: %.
Задача 4: Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение: 1 способ – с помощью формулы.
 Пусть количество каждого из растворов было V. Тогда количество сухого вещества в первом растворе 0,15V , а во втором – 0,19V. После того как растворы смешали их общий объем стал 2V, а количество сухого вещества в смеси стало 0,15V+0,19V. Концентрация раствора равна:
Пусть количество каждого из растворов было V. Тогда количество сухого вещества в первом растворе 0,15V , а во втором – 0,19V. После того как растворы смешали их общий объем стал 2V, а количество сухого вещества в смеси стало 0,15V+0,19V. Концентрация раствора равна:
Таким образом, концентрация полученного
 раствора равна:
раствора равна:
Ответ: 17.
2 способ – правило креста или прямоугольника
15
19-х
х
19
Х-15
Запишем исходные концентрации в левый столбец таблицы, искомую полученную концентрацию х запишем в центральный столбец. Правый столбец таблицы заполним разностями исходных и полученной концентрации, вычитая из
большей концентрации меньшую.
Отношение полученных разностей
равно отношению долей, в которых требуется смешать растворы для получения из растворов исходной концентрации раствора с требуемой концентрацией. Так как объемы смешиваемых растворов равны, имеем:

Ответ: 17.
Задача 5. Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Решение – с помощью схемы:

Задача 6 Свежие абрикосы содержат 80 % воды по массе, а курага (сухие абрикосы) – 12 % воды. Сколько понадобится килограммов свежих абрикосов, чтобы получить 10 кг кураги?
Решение: (с помощью схемы)
При высыхании абрикосов испаряется вода, количество сухого вещества не изменяется. Выразим количество сухого вещества в свежих абрикосах и в кураге. Пусть взяли х кг свежих абрикосов. Тогда схема для решения такой задачи имеет вид: вода
вода
с.в.
с.в.
20%
88%
х кг *0,2
10 кг *0,88
80%
12%
=
Составим уравнение, подсчитав количество сухого вещества в левой и правой части схемы:
0,2х=8,8
х=44.
Ответ:44кг.
Задача 7. При смешивании 5% -ного раствора кислоты с 40% -ным раствором кислоты получили 140 г 30% -ного раствора. Сколько грамм каждого раствора надо было взять?
5
10
30
40
25
Решение – старинным арифметическим способом.
Рассмотрим пары 30 и 5; 30 и 40. В каждой паре их большего числа вычтем меньшее и результат запишем в конце соответствующей чёрточки. Получилась схема:
Из неё делается заключение, что 5% раствора следует
взять 10 частей, а 40 % – 25 частей. Узнав, сколько
приходится на одну часть 140: (10+25) = 4 г., получаем,
что 5% – ного раствора необходимо взять 40г,
а 40% -ного -100 г
Ответ: 40 г – 5% -ного раствора и 100г – 40% – ного раствора.
Задача 8 : В 100г 20%-ного раствора соли добавили 300г её 10%-ного раствора. Определите процентную концентрацию раствора
с помощью расчетной формулы
m1=100г .
m2=300г . а= а=
а= =0,125
=0,125
а1=0,2 .
а2=0,1 .
………….
а -? Ответ:12,5%
с помощью правила креста
0,2 Х- 0,1
Х
0,1 0,2- Х
1:3=(х-0,1):(0,2-х);
Х=0,125; х=12,5%.
Ответ: х=12,5%.
Задача 9: Смешали 30%-й раствор соляной кислоты с 10%-ым раствором и получили 600 г 15%-го раствора. На сколько граммов масса первого раствора меньше массы второго?
Решение: 1 способ – алгебраический.
Обозначим x массу первого раствора, тогда масса второго (600 – x).
Составим уравнение:
0,3x + 0,1* (600 – x) = 600 * 0,15; 0,3х + 60 – 0,1х = 90 0,2х = 3
x = 150 ( г.) масса 1 раствора
600 – 150 = 450 (г.) масса 2 раствора
450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора
2 способ – графический:
Рассмотрим прямоугольники с площадями S1 и S2. Прямоугольники равновелики, так как количество соляной кислоты в обоих растворах после смешивания одинаково (Масса смеси умноженная на концентрацию равна количеству чистого вещества.) Приравняв площади, равновеликих прямоугольников получаем
15x = 5 (600- x); 15х = 3000 – 5х; 15х + 5х = 3000
20х = 3000 Х = 150; 600 – 150 = 450г; . 450-150 = 300 (г.)
Ответ: на 300 г. масса 1 раствора меньше массы 2 раствора
Задача 10: Первый сплав содержит 10% меди, второй – 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Решение – старинный арифметический способ:
10
10
30
40
20
Пусть масса первого сплава равна m кг,
тогда масса второго сплава m+3 кг.
Заполним таблицу:
Отношение полученных масс равно отношению
 долей, в которых требуется сплавлять исходные сплавы. Поэтому
долей, в которых требуется сплавлять исходные сплавы. Поэтому
Тогда масса второго сплава равна 6 кг, а масса третьего сплава равна 9 кг.
Ответ: 9.
Задача 11.Имеются сплавы золота и серебра. В одном эти металлы находятся в отношении 2: 3, а в другом в отношении 3: 7. Сколько нужно взять от каждого сплава, чтобы получить 1 кг нового, в котором золото и серебро находились бы в отношении 5: 11?
золото:серебро
2:3
золото:серебро
3:7
золото:серебро
5:11
Х У
По этой схеме уравнение х + у =1 показывает массу нового сплава.
Определяем массу золота в каждом сплаве и получаем уравнение
 *х +
*х +  * у =
* у =  * 1
* 1
Аналогично массу серебра и получаем уравнение
 * х +
* х +  * у =
* у =  * 1
* 1
Записываем одну из систем:
х + у = 1 {  х +
х +  у =
у =  {
{
х + у = 1
 х +
х +  у =
у = 
Решая ее, получаем х = 0,125 и у = 0,875
Ответ: 125 г и 875 г.
Задача12:Имеется два кислотных раствора: один 20%, другой 30%. Взяли 0,5 л первого и 1,5 л второго раствора и образовали новый раствор. Какова концентрация кислоты в новом растворе?
Решение:Так как первый раствор 20 % – й, то в нем 0,2 объема занимает «чистая» кислота. Так как объем первого раствора равен 0,5л, то в этом количестве содержится 0,2*0,5=0,1 л «чистой» кислоты.
Аналогично во втором растворе будет содержаться 0,3*1,5=0,45л «чистой» кислоты.
При смешивании растворов получим 0,5+1,5=2л кислотного раствора, в котором 0,1+0,45=0,55л «чистой» кислоты.
Отсюда следует, что концентрация кислоты в новом растворе есть отношение 0,55:2=0,275, т.е.27,5%.
Ответ: концентрация кислоты в новом растворе 27,5%
Задача 13.От двух кусков сплава с массами 3 кг и 2 кг и с концентрацией меди 0,6 и 0,8 отрезали по куску равной массы. Каждый из отрезанных кусков сплавлен с остатком другого куска, после чего концентрация меди в обоих сплавах стала одинаковой. Какова масса каждого из отрезанных кусков?
Так как в обоих сплавах концентрация меди после двух операция
стала одинаковой, то массы сплавов и массы меди в этих сплавах
пропорциональны.
Первоначально массы меди в сплавах равны 0,6*3(кг) и 0,8*2(кг).
После того, как отрезали куски массой х(кг), содержание меди стало 0,6(3-х) и 0,8(2-х),
а после сплавления

0,6(3-х) + 0,8х и 0,8(2-х) +0,6х  mm (кг)
mm (кг)
 =
=  , х = 1,2
, х = 1,2
2 3 mc(кг)
Ответ: 1,2 кг
Задача 14. Латунь – сплав меди и цинка. Кусок латуни содержит меди на 11 кг больше, чем цинка. Этот кусок латуни сплавили с 12 кг меди и получили латунь, в котором 75% меди. Сколько килограммов меди было в куске латуни первоначально?
Обозначим искомую величину за х.
Тогда масса первоначального куска латуни 2х – 11, а его содержание меди составляет р =  процентов.
процентов.
Поскольку «медность» куска меди 100%, то по правилу квадрата получаем: р 25
75  =
= х= 22,5
х= 22,5
100 75-р
Ответ: 22,5 кг меди было в куске латуни
Задача 15. В бидон налили 4л молока трехпроцентной жирности и 6л молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?
Обозначим искомую величину за Х.
По правилу квадрата получим: 3 6-х
Х
6 х-3
Составим пропорцию: =
= х= 4,8
х= 4,8
Ответ: 4,8 % – жирность молока
Способ Л.Ф.Магницкого для трех веществ
Задача 16. Некто имеет чай трех сортов –цейлонский по 5 гривен за фунт,
индийский по 8 гривен за фунт и китайский по 12 гривен за фунт.
В каких долях нужно смешать эти сорта, чтобы получить чай
стоимостью 6 гривен за фунт?
5 6 6
6
12 1 2/8
…………………………………………………………………………..
5 2 1
6
8 1 1/10
Взять 6+2=8 частей чая ценой по 5 гривен и по одной части ценой 8 гривен и 12 гривен за один фунт.
Возьмем 8/10 фунта чая ценой по 5 гривен за фунт и по1/10 фунта чая ценой 8 и 12 гривен за фунт, то получим 1 фунт чая ценой
8/10*5 + 1/10*8 + 1/10*12 = 6 гривен
Задача17.Имеется два сплава меди и свинца. Один сплав содержит 15% меди, а другой 65% меди. Сколько нужно взять каждого сплава, чтобы получилось 200г сплава, содержащего 30% меди?
Изобразим каждый из сплавов в виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). Кроме того на модели отобразим характер операции – сплавление, поставим знак «+» между первым и вторым прямоугольниками. Поставив знак «=» между вторым и третьим прямоугольниками, мы тем самым показываем, что третий сплав получен в результате сплавления первых двух. Полученная схема имеет следующий вид:
Теперь заполняем получившиеся прямоугольники в соответствии с условием задачи:
-
Над каждым прямоугольником («маленьким») указываем соответствующие компоненты сплава. При этом обычно бывает достаточно использовать первые буквы их названия (если они различны). Удобно сохранять порядок соответствующих букв.
-
Внутри прямоугольников вписываем процентное содержание (или часть) соответствующего компонента. Понятно, что если сплав состоит из двух компонентов, то достаточно указать процентное содержание одного из них. В этом случае процентное содержание второго компонента равно разности 100% и процентного содержания первого.
-
Под прямоугольником записываем массу (или объем) соответствующего сплава (или компонента).
Рассматриваемый в задаче процесс можно представить в виде следующей модели- схемы:
медь
свинец
медь
свинец
свинец
медь
65%
=
+
30%
15%
200г
Решение.
1-й способ. Пусть хг – масса первого сплава. Тогда, (200-х)г – масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему:
свинец
свинец
свинец
медь
медь
медь
15%
65%
30%
х г
(200-х) г
200 г
+
=
Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):

Решив это уравнение, получаем х=140. При этом значении х выражение 200-х=60. Это означает, что первого сплава надо взять140г, а второго-60г.
Ответ:140г. 60г.
2-й способ. Пусть х г и у г – масса соответственно первого и второго сплавов, то есть пусть исходная схема имеет вид:
свинец
свинец
медь
медь
15%
65%
х г
y г
свинец
медь
30%
200 г
+
=
Легко устанавливается каждое из уравнений системы двух линейных уравнений с двумя переменными:

Решение системы приводит к результату: Значит, первого сплава надо взять 140 г, а второго-60 г.
Значит, первого сплава надо взять 140 г, а второго-60 г.
Ответ: 140г,60г.
Задача18. В 4кг сплава меди и олова содержится 40% олова. Сколько килограммов олова надо добавить к этому сплаву, чтобы его процентное содержание в новом сплаве стало равным 70%?
Решение: Пусть х кг – искомое количество олова. Тогда масса полученного сплава равна (4+х) кг. Составим схему и внесем эти выражения на схему:
олово
олово
олово
медь
медь
100%
4кг
х г
хкг
(4+х)кг
40%
70%![]()
+
=
Составим уравнение, подсчитав массу олова слева и справа от знака равенства на схеме. Получаем уравнение: (1), корнем которого служит
(1), корнем которого служит 
Отметим, что уравнение можно составить и на основе подсчета массы меди слева и справа от знака равенства. Для этого понадобится знать процентное содержание меди в данном и полученном сплавах. Внесем эти данные в схему:
олово
олово
олово
медь
медь
60%
30%
4 кг
х г
х кг
(4+х) кг
+
=
В этом случае получаем следующее уравнение:
 (2).
(2).
Уравнение (1) равносильно уравнению (2). В этом легко убедиться, решив последнее уравнение. Его корень равен 4. Обычно решают то уравнение, которое проще. В нашем случае разница не так заметна. Вместе с тем, второе уравнение содержит переменную только в одной (правой) части и его обе части сразу можно разделить на 0,3. Поэтому предпочтение можно отдать второму уравнению.
Ответ:4кг.
Задача 19. К некоторому количеству сплава меди с цинком, в котором эти металлы находятся в отношении 2:3, добавили 4 кг чистой меди. В результате получили новый сплав, в котором медь и цинк относятся как 2:1. Сколько килограмм нового сплава получилось?
Решение.
Прежде чем составлять схему, уточним, что в первом сплаве медь составляет  , а в полученном сплаве –
, а в полученном сплаве –  . Обозначим массу полученного сплава х кг, и внеся указанные части в соответствующие фрагменты схемы, получаем:
. Обозначим массу полученного сплава х кг, и внеся указанные части в соответствующие фрагменты схемы, получаем:
цинк
медь
медь
медь
цинк
2/5
1
(x-4) кг
х г
4 кг
х кг


 2/5
2/5
2/3
+
=
Нетрудно составить уравнение, подсчитав количество меди слева от знака неравенства, и приравняв его к количеству меди, справа от него. Получаем уравнение: Решив его, получаем искомое значение: х=9.
Решив его, получаем искомое значение: х=9.
Замечание. Можно было составить уравнение на основе подсчета массы цинка в обеих частях неравенства. Для этого внесем в схему необходимые данные:
1)если в первом сплаве медь составляет часть  , то цинк –
, то цинк –  ;
;
медь
медь
медь
цинк
цинк
3/5
1/3
(x-4)кг
х г
4кг
хкг


 2/5
2/5
+
=
2) если в полученном сплаве медь составляет часть  , то цинк –
, то цинк –  .
.
Уравнение в этом случае имеет вид:

Это уравнение равносильно предыдущему.
Ответ х= 9кг.
Задачи на смеси, сплавы, сливы решают на уроках химии, физики, математики. Рассмотрим некоторые
способы решения задач на смеси, сплавы и растворы.
Все
задачи на «смеси, сплавы, растворы» можно разделить на три типа:
·
на
вычисление концентрации;
·
на
вычисление количества чистого вещества в смеси (или сплаве);
·
на
вычисление массы смеси (сплава).
Что
нужно знать для решения зада на смеси, сплавы, сливы:
1.
%
– ное содержание соли, кислоты, других веществ воде составляет 0%;
2.
%
– ное содержание чистой кислоты, чистого вещества составляет 100 %;
3. Массовая
доля растворенного вещества в растворе – это отношение массы этого вещества к
массе раствора. ω = ![]() ,
,
где ω
– массовая доля растворенного вещества в растворе;
![]() – масса растворенного
– масса растворенного
вещества в растворе;
![]() – масса раствора.
– масса раствора.
Введем обозначения:
ω 1–
массовая доля растворенного вещества в первом растворе;
ω 2 –
массовая доля растворенного вещества во втором растворе;
ω –
массовая доля растворенного вещества в новом растворе, полученном при
смешивании первого и второго растворов;
m1(в-ва), m2(в-ва),
m(в-ва) – массы растворенных веществ в соответствующих растворах;
m1(р-ра), m2(р-ра),
m(р-ра) – массы соответствующих растворов.
Предполагают,
что:
а)
все получившиеся смеси и сплавы являются однородными;
б)
объем смеси равен сумме объемов смешиваемых растворов;
в)
объемы растворов и массы сплавов не могут быть отрицательными.
Практика:
Задача № 1:
Сироп содержит 18% сахара. Сколько кг воды
нужно добавить к 40 кг сиропа, чтобы содержание сахара составило 15%?
Решение задачи
№1:
1.
Алгебраический способ. Табличный метод:
Пусть
x (кг) – масса воды, тогда получим таблицу:
|
Концентрация |
m |
m |
|
|
Было |
18% |
40 |
0,18 |
|
Стало |
15% |
(40 |
0,15 · |
Имеем уравнение: 0,15 · (40 + x)
= 0,18
·
40
6 + 0,15 x
= 7,2
0,15 x
= 1,2
x = 8
Ответ: 8 кг воды.
2.
Алгебраический способ. “Правило
смешения” (с помощью химической расчетной формулы):
ω1· m1
+ ω2· m2
=
ω· (m1
+ m2).
Подставим в формулу данные задачи, учитывая, что концентрация сахара в воде 0%,
масса воды x кг.
Имеем уравнение: 18 · 40 + 0 · x
= 15 ·
(40 + x)
720 – 600 = 15 x
x = 120 : 15
x = 8
Ответ:
8 кг воды
Задачи легко решаются, если
применить химическую расчётную формулу.
Задача
№2:
К
100 г 20% раствора соли добавили 300 г её 10% раствора. Определите процентную
концентрацию раствора.
Решение
задачи № 2:
Алгебраический
способ. “Правило смешения”
(с
помощью расчетной формулы):
ω1· m1
+ ω2· m2
=
ω· (m1
+ m2).
Подставим
в формулу данные задачи: 20 · 100 + 10 · 300
= ω
· (100
+ 300);
ω =![]() = 12,5
= 12,5
Ответ:
12,5 % – концентрация полученного раствора.
Задача № 3.
Смешали 10%-ный и 25%-ный растворы соли и
получили 3 кг 20%-ного раствора. Какое количество каждого раствора в килограммах
было использовано?
Алгебраический способ с
помощью расчётной формулы:
ω1· m1
+ ω2· m2
=
ω· (m1
+ m2).
Пусть
х (кг) – масса 1-го раствора, тогда (3 – х) (кг) – масса 2-го раствора.
10•х
(кг) содержится соли в 10 % -ом растворе,
25•(3-х)
(кг) содержится соли в 25 % -ом растворе,
20•3
(кг) содержится соли в смеси.
Подставим в формулу, составим и решим
уравнение:
10•х
+ 25•(3-х) = 20•3;
–
15х = – 15;
х = 1,
1(кг) – масса 10 % -го раствора,
3 – 1 =2 (кг) – масса 25 % -го раствора.
Ответ: 1 кг, 2 кг.
Задача № 4: Имеются
два сосуда. Первый содержит 30 кг, а второй — 20 кг раствора кислоты различной
концентрации. Если эти растворы смешать, то получится раствор, содержащий 68 %
кислоты. Если же смешать равные массы этих растворов, то получится раствор,
содержащий 70 % кислоты. Сколько процентов кислоты содержится в первом сосуде?
Решу задачу алгебраическим способом, с
помощью расчётной формулы:
ω1· m1
+ ω2· m2
=
ω· (m1
+ m2).
![]()
![]()
![]() Составлю
Составлю
систему уравнений. Пусть х (%) – в первом растворе кислоты, у
(%) – во втором растворе кислоты, 30x + 20![]() =
=
68 ·
50; 30x + 20![]() = 3400; x = 60
= 3400; x = 60
20x
+ 20y
= 70 · 40
/ ·
(-1)
– 20x
– 20y
= – 2800 y = 80;
Ответ: 60 % кислоты в первом растворе.
Задачи для
самостоятельного решения
1. Водно-солевой
раствор содержал 4 кг соли. Через некоторое время 4 кг воды испарилось,
вследствие чего концентрация соли в растворе увеличилась на 5%. Какой была
первоначальная масса раствора? Ответ: 20
кг.
2. Сколько
килограммов 30-процентного и сколько килограммов 40-процентногосплавов меди
надо взять, чтобы получить 50 кг 36-процентного
сплава?
Ответ: 20 кг и 30 кг.
3. После
смешивания двух растворов, один из которых содержал 48 г, а другой — 20 г
безводного йодистого калия, получилось 200 г нового раствора. Найдите
концентрацию каждого из первоначальных растворов, если концентрация первого на
15% больше концентрации второго. Ответ:40%
и 25%.
4. Слиток
сплава меди и цинка массой 36 кг содержит 45% меди. Какую массу меди надо
добавить к этому куску, чтобы полученный сплав содержал 60% меди?
Ответ:13,5кг.
5. Смешали
30%-ный раствор соляной кислоты с ее 10%-ным раствором и получили 600 г
15%-ного раствора. Сколько граммов 30 % -ного раствора было взято?
Ответ:150г.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF
Введение
Практическая цель в обучении математике – научить школьников решать задачи из повседневной жизни, что связано с умением составить математическое описание модели. Главная цель в обучении математике – развитие логического мышления, которая предполагает умение учащихся оперировать с логическими цепочками умозаключений. Это достигается путем введения текстовых задач различных типов. Предлагаемые темы рассчитаны на школьников 10-11 классов.
Задачи на смеси и сплавы при первом знакомстве вызывают у обучающихся в школах затруднения. Многие ученики не могут сами справиться с такими задачами. Задачи этого типа ранее встречались только на вступительных экзаменах в вузах, теперь добавлены в контрольные измерительные материалы (КИМы) для подготовки и проведения экзамена по математике за курс основной школы. Такие задачи представляю собой средство хорошего развития мышления у обучающихся, и имеют практическое значение. Именно поэтому данная тема является актуальной на сегодняшний день.
Предполагается, что анализ тематики достаточно актуален и представляет научный и практический интерес, поскольку данные термины прочно вошли в нашу повседневную жизнь и требуют детального анализа с целью выявления в них общего и различий.
Для решения задач на концентрации нужно уметь рассуждать и решать задачи на дроби и проценты, на составление уравнений и их систем. Эти задачи решаются арифметически, с применением дробей, линейного уравнения и их систем.
Объект исследования – текстовые задачи на смеси и сплавы.
Предмет исследования – особенности решения задач на смеси и сплавы.
Цель исследования – систематизация теоретического материала по теме «Задачи на смеси и сплавы» и его применение к решению данного типа задач.
Теоретическая часть
Большой объем расчетных математических задач приходится на решение систем линейных алгебраических уравнений. Многие задачи управленческого, экономического, технологического характера строятся как линейные алгебраические, либо сводятся к ним. Ровно также как и задачи на смеси и сплавы.
Задачи, которые мы сейчас называем задачами на составление уравнений, возникали в самых различных цивилизациях древности, вероятно, в связи с практическими потребностями: эти задачи описывали жизненные ситуации, возникающие при обмене каким-либо имуществом и при его распределении (при торговых отношениях, наследовании, сборе налогов и т. д.). Но не исключено, что некоторые задачи служили просто для упражнения ума или вызывали теоретический интерес.
Так, например, в Древнем Египте был класс задач, в котором фигурировало слово аха – буквально «куча»; этим словом обозначалось неизвестное количество. Вот пример условия такой задачи: «Количество [аха] и его четвертая часть дают вместе 15».
Современный школьник записал бы это условие так: . Далее он, видимо, сложил бы коэффициенты при x, получил бы уравнение или , затем для определения x поделил бы 15 на (или вначале умножил бы обе части уравнения на 4, получив 5x = 60, а уже потом поделил бы на 5; а может быть, наоборот, поделил бы обе части на 5, а потом умножил на 4).
Однако Египтяне так не делали. Этому препятствовало отсутствие необходимой символики для соединения подобных членов. Решение, излагаемое египетским автором, начинается так. «Считай с 4; от них ты должен взять четверть, вместе 5». После этого 15 делится на 5, получается 3, а затем 3 умножается на 4 и получается 12. Как и в других сохранившихся египетских математических текстах, никаких объяснений не приводится. По-видимому, метод заключался в следующем: предположим, что искомое количество равно 4; тогда его четвертая часть была бы равна 1; количество и его четвертая часть вместе были бы равны 5; однако на самом деле они равны 15; поэтому настоящее искомое количество больше предполагаемых 4 во столько же раз, во сколько 15 больше 5, то есть в 3 раза, и равно 12.
Именно потому, что многие были заинтересованы задачами данного типа, к настоящему времени люди научились правильно решать такие задачи, и составили определенные правила:
Неизвестные величины нужно обозначить буквами;
Используя соотношения между известными и неизвестными величинами, которые есть в условии, составить уравнения;
Решить систему уравнений;
Ответить на вопросы, поставленные задаче.
Например:
Задача. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской, чтобы получить концентрацию соли 1,5%?
Решение:
В 30 кг морской воды содержится
Если добавить x кг пресной воды, то полная масса будет (30+x) кг, а концентрация соли (в %) составит
Таким образом, нужно добавить 70 кг пресной воды.
А также, при решении задач на смеси и сплавы такое понятие, как «процент».
Процент (лат. per cent — на сотню) – одна сотая часть. Обозначается знаком «%». Используется для обозначения доли чего-либо по отношению к целому. Например, 17 % от 500 кг означает, что 17 частей по 5 кг каждая, то есть 85 кг. Справедливо также утверждение, что 200 % от 500 кг составляет 1000 кг, поскольку 1 % от 500 кг равен 5 кг, и 5 ∙ 200 = 1000.
В Древнем Риме, задолго до существования десятичной системы счисления, вычисления часто производились с помощью дробей, которые были кратны . Например, Октавиан Август взимал налог в размере на товары, реализовавшиеся на аукционе, это было известно как Centesima Rerum Venalium (сотая доля продаваемых вещей). Подобные расчёты были похожи на вычисление процентов.
При деноминации валюты в средние века вычисления со знаменателем 100 стали более привычными, а с конца XV века до начала XVI века данный метод расчёта стал повсеместно использоваться, судя по содержанию изученных материалов, содержащих арифметические вычисления. Во многих из этих материалов данный метод применялся для расчёта прибыли и убытка, процентных ставок, а также в правиле трёх. В XVII веке данная форма вычислений стала стандартом для представления процентных ставок в сотых долях.
В России понятие процента впервые ввёл Пётр I. Но считается, что подобные вычисления начали применяться в Смутное время, как результат первой в мировой истории привязки чеканных монет 1 к 100, когда рубль сначала состоял из 10 гривенников, а позже из 100 копеек
В тексте знак процента используется только при числах в цифровой форме, от которых при наборе отделяется неразрывным пробелом (доход 67 %), кроме случаев, когда знак процента используется для сокращённой записи сложных слов, образованных при помощи числительного и прилагательного процентный.
Иногда бывает удобным сравнивать две величины не по разности их значений, а в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного товара больше или меньше цены другого в процентах. Если сравнение по разности вполне однозначно, то есть всегда можно найти, насколько одна величина больше или меньше другой, то для сравнения в процентах нужно указывать, относительно какой величины вычисляется процент. Такое указание, впрочем, необязательно в том случае, когда говорят, что одна величина больше другой на число процентов, превышающее 100. В этом случае остается только одна возможность вычисления процента, а именно деление разности на меньшее из двух чисел с последующим умножением результата на 100.
Рассмотрим связь между процентами и десятичными дробями:
0 % = 0;
5 % = 0,05;
20 % = 0,2;
50% = 0,5;
0,07 % = 0,0007;
45,1 % = 0,451;
100 % = 1;
146 % = 1,46.
После того, как мы рассмотрели, что такое процент числа, следует подробнее остановиться на понятии «концентрация вещества».
Концентрацией (процентным содержанием) веществав смеси(сплаве, растворе) называют число процентов, выраженное формулой
Для массовой концентрации вещества:
, где
– число процентов.
–масса вещества А в смеси.
– масса всей смеси.
Для объемной концентрации вещества:
, где
– число процентов;
– объем вещества в растворе;
– объем всего раствора.
Продемонстрируем использование данных понятий при решении задач, с использованием понятия процента.
Задача 1. К 190 г воды добавим 10 г уксусной кислоты, получим раствор, масса которого равна 190 + 10 = 200 грамм.
Концентрация кислоты – это отношение количества уксуса к количеству раствора, записанное в процентах:
.
Процентное содержание воды:
.
Задача 2(смесь).
Взяли одно ведро песка и три ведра извести. Смешав содержимое всех четырех ведер, получили смесь извести с песком, её масса равна 1 + 3 = 4 (единиц массы). Концентрация – это отношение количества песка к количеству смеси, записанное в процентах:
.
Процентное содержание извести:
.
Задача 3(сплав).
Возьмем сплав меди и свинца, в котором 100 грамм меди и 150 грамм свинца. Получим концентрацию:
.
Как можно заметить, во всех задачах на сплавы, растворы, смеси используется всего одна формула:
.
где K — процентное содержание чистого вещества в сплаве или растворе,
m – масса чистого вещества
M – масса сплава или раствора.
Задачи на смеси и сплавы бывают двух основных видов: КАКИХ?
Две смеси определенной массы с некоторой концентрацией вещества смешивают в одной емкости. Нужно определить массу и концентрацию этого вещества в новой смеси.
В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
Строго говоря, подход к решению от этого не меняется.
Во втором случае мы тоже смешиваем две смеси, просто в одной концентрация вещества больше 0, а в другой равна 0.
А также существует стандартная таблица (табл.1) для решения задач данного типа:
Таблица 1
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1-ое вещество |
|||
|
2-ое вещество |
|||
|
Раствор |
Задачи на составление линейных уравнений:
Большой объем расчетных математических задач приходится на решение систем линейных алгебраических уравнений. Многие задачи управленческого, экономического, технологического характера строятся как линейные алгебраические, либо сводятся к ним. Ровно также как и задачи на смеси и сплавы.
Задачи, которые мы сейчас называем задачами на составление уравнений, возникали в самых различных цивилизациях древности, вероятно, в связи с практическими потребностями: эти задачи описывали жизненные ситуации, возникающие при обмене каким-либо имуществом и при его распределении (при торговых отношениях, наследовании, сборе налогов и т. д.). Но не исключено, что некоторые задачи служили просто для упражнения ума или вызывали теоретический интерес.
Основные понятия задач на смеси и сплавы.
Для более ясного понимания задач данного типа, необходимо знать следующие понятия:
В решении задач на смеси и сплавы считается, что сумма масс компонентов равна массе смеси нескольких веществ.
При смешивании смесей и сплавов их результат всегда однороден.
Процент – это одна сотая любого вещества.
Производительность объекта – скорость работы.
Долю вещества в растворе показывает отношение массы процентного содержания вещества в смеси к общей массе всей смеси.
Сумма концентраций – компонент, составляющих смесь, равняется единице.
В математике используются задачи на смеси и сплавы следующих типов:
Типы задач:
На вычисление концентрации;
Задача 1. В графине с чаем содержится 5% сахара. Сколько килограммов воды надо выпарить из 10 кг чая, чтобы концентрация сахара в нем увеличилась до 10%?
Решение: Для более удобного решения построим таблицу (табл.2) .
Таблица 2
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1раствор |
0,5 кг |
10 кг |
5% |
|
2 раствор |
0,5 кг |
5 кг |
10% |
(кг) – масса твердого вещества:
(кг):
(кг).
Ответ: 5 кг.
На вычисление количества чистого вещества в сплаве (или смеси);
Задача 2. Имеются два сплава с содержанием бронзы. В первом содержится 40% бронзы, а во втором – 50%. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 15% бронзы ?
Решение: Для более удобного решения построим таблицу (табл.3) .
Таблица 3
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1 сплав |
0,4х |
х |
40% |
|
2 сплав |
0,5у |
у |
50% |
|
Новый сплав |
15% |
,
,
,
,
.
Ответ: 1,4,1.
На вычисление массы сплава (смеси).
Задача 3. В сплаве меди и цинка содержится 25% меди, масса сплава 1500г. Найти сколько содержится меди в сплаве?
Решение: Для решения данной задачи воспользуемся формулой благодаря которой получаем вычисление (г).
Ответ: 300 г.
Рассмотрим способы решения задач на смеси и сплавы:
Арифметический способ;
Алгебраический способ;
С помощью таблиц;
С помощью графиков;
С помощью схем.
Существует определенный алгоритм для решения задач на смеси и сплавы:
Рассмотреть условия задачи;
Выбрать неизвестную величину (обозначить ее как неизвестное);
Определить все взаимосвязи между данными величинами;
Выбрать способ решения задачи, составить пропорцию или уравнение относительно неизвестной величины;
Решить задачу;
Сделать анализ результата.
Применение представленного алгоритма будет представлено в следующей главе.
Практическая часть
Рассмотрим алгебраический способ решения задач на нескольких примерах.
Задача 1. Имеются два раствора соли массой 50 г и 140г. В первом растворе содержится 8г соли, а во втором – 20 г соли. Какова концентрация этих растворов? Какой будет концентрация, если смешать два этих раствора?
Решение: Для более удобного решения построим таблицу (табл.4).
Таблица 4
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1 раствор |
8 г |
50 г |
|
|
2 раствор |
20 г |
140 г |
|
|
Смесь |
28 г |
190 г |
– концентрация 1-го раствора:
– концентрация 2- го раствора:
– концентрация 2-х растворов.
Ответ: 16%, 14%, 14,7%.
Задача 2. Смешали 300 г 10% -го клубничного сиропа и 400 г 20% -го ванильного сиропа. Какова концентрация полученной смеси?
Решение: Для более удобного решения построим таблицу (табл.5) .
Таблица 5
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1раствор |
30 г |
300 г |
10% |
|
2 раствор |
80 г |
400 г |
20% |
|
Смесь |
110 г |
700 г |
(г) – в 1-ом растворе:
(г) – в 2-ом растворе:
(г) – в смеси растворов:
.
Ответ: 16%.
Задача 3. Какое количество соли содержится в 100 г 5% -го морского раствора? В каком количестве 10% -го раствора содержится такое же количество этого вещества?
Решение: Для более удобного решения построим таблицу (табл.6) .
Таблица 6
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1раствор |
100 г |
5% |
|
|
2 раствор |
100 г |
10% |
(г) –вещества в 1-ом растворе:
(г) –вещества во 2-ом растворе.
Ответ: 5 г, 10 г.
Задача 4. Морская вода содержит 7% соли. Сколько килограммов воды надо выпарить из 140 кг морской воды, чтобы концентрация соли в ней увеличилась до 25%?
Решение: Для более удобного решения построим таблицу (табл.7) .
Таблица 7
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1раствор |
9,8 кг |
140 кг |
7% |
|
2 раствор |
9,8 кг |
39,2 кг |
25% |
(кг) – масса твердого вещества:
(кг):
(кг).
Ответ: 100,8 кг.
Задача 5. Сколько килограммов воды нужно добавить к 40 кг яблочного сока, чтобы концентрация сахара уменьшилась с 8% до 5%?
Решение: Для более удобного решения построим таблицу (табл.8) .
Таблица 8
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1раствор |
3,2 кг |
40 кг |
8% |
|
2 раствор |
3,2 кг |
64 кг |
5% |
(кг):
(кг):
(кг).
Ответ: 24 кг.
Задача 6. Имеются два сплава с содержанием меди. В первом содержится 40% меди, а во втором – 70%. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 25% меди?
Решение: Для более удобного решения построим таблицу (табл.9) .
Таблица 9
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1 сплав |
0,4х |
х |
40% |
|
2 сплав |
0,7у |
у |
70% |
|
Новый сплав |
45% |
,
,
,
,
.
Ответ: 5,1.
Алгебраический способ решения данных задач является универсальным. С помощью данного способа можно решить любую задачу на смеси и сплавы.
Далее для примера рассмотрим арифметический способ решения задач на смеси и сплавы.
Задача 7.В 200 г 30% -го раствора соли добавили 400 г ее 15% -го раствора. Найдите процентную концентрацию раствора.
Решение: Выполним вычисления по действиям:
(г) – в 200 г 30% – го раствора:
(г) – в 400 г 15% -го раствора:
(г) – соли в растворе:
(г) – масса всего раствора:
– концентрация раствора.
Ответ: 20%.
Арифметический способ решения задач на смеси и сплавы не сложен, но требует хорошего понимания сути задачи, и занимает достаточно много времени.
Задача 8. В сосуд, содержащий 5 литров 12% -го водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Решение:Концентрация раствора
:
(л):
(л):
.
Ответ: 5%.
Задача 9.Смешали некоторое количество 15% -го раствора некоторого вещества с таким же количеством 19% -го раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение: Масса получившегося раствора 2m. Тогда, концентрация получившегося раствора равна:
Ответ: 17%.
Задача 10. Имеется два сплава. Первый содержит 10% никеля, второй – 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше второго?
Решение:
(кг)
Ответ: 100 кг.
Далее мы рассмотрим графический способ решения задач на смеси и сплавы.
Задача 11. В 150г 30%-ного раствора соли добавили 500г её 15%-ного раствора. Определите процентную концентрацию раствора.
Решение:
Ответ: 18,5.
Данный способ является наглядным и дает приближенное решение. При использовании миллиметровой бумаги можно получить достаточно точный ответ.
Задача 12. Собрали 50 кг свежих ягод, содержащих по массе 95% воды. Когда их подсушили, они стали весить 5 кг. Каков процент содержания воды по массе в сухих ягод?
Решение: Модели в данных задачах оформляем в виде кружочков, поделённых пополам. В нижней его части записываем содержание воды в %, в верхней – массу вещества.
20кг 100% у 100%
х 80%
20%
масса
Х 28%
72%
Х 28%
72%
Х 28%
72%
вода
Свежие фрукты сухие фрукты
Если свежие фрукты содержали 72% воды, то «не воды» в них было 28%. Всего 100%. Массу сухого вещества назвали х, а по условию задачи свежих фруктов было 20 кг. Все эти сведения отмечены в первом кружочке. Аналогично заполняем второй кружочек.
Из рисунка видим две пропорции. Решим их.
.
кг.
Ответ: 7 кг.
Заключение.
Таким образом, согласно информации в теоретической части, мы рассмотрели такие понятия, как процент числа, концентрация вещества. Выделили типы задач на смеси и сплавы:
На вычисление концентрации;
На вычисление количества чистого вещества в сплаве (или смеси);
На вычисление массы сплава (смеси).
Рассмотрели, какие бывают типы задач, выделили способы решения данных задач:
Арифметический способ;
Алгебраический способ;
С помощью таблиц;
С помощью графиков;
С помощью схем.
А также ознакомились со стандартной таблицей:
|
Масса твердого вещества (m тв) |
Масса вещества (m р-ра) |
Концентрация, % (К) |
|
|
1-ое вещество |
|||
|
2-ое вещество |
|||
|
Раствор |
В практической части мы решали задачи алгебраическим, арифметическим способами, с помощью таблиц, схем и графиков.
А также решали с помощью стандартной таблицы (табл.1), с которой ознакомились в теоретической части.
Вследствие чего можно сделать вывод, что табличный способ решения задач данного типа более удобный для решения задач на смеси и сплавы.
Следовательно, цель данной работы достигнута, а задачи – решены.
Список использованных источников
Бродский, И.Л. Сборник текстовых задач по математике для профильных классов [Текст] / И.Л. Бродский, А.М. Видус, А.Б. Коротаев. – М.: АРКТИ, 2004. – 424 с.
Видео уроки в интернет –http://videouroki.net
Галицкий и др. Сборник задач по алгебре для 8-9 классов: Учебное пособие для учащихся шк. и классов с углубл. изуч. математики / М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич.-2-е изд. – М.: Просвещение, 1994. – 271с.
Геллер Ю.А., Рахштадт А.Г. Материаловедение. – Москва: Металлургия, 1975. – 445 с.
Демидова, Т.Е. Теория и практика решения текстовых задач [Текст] / Т.Е. Демидова, А.П. Тонких. – М.: Издательский центр «Академия» 2002. – 286 с.
Ерина, Т.М. Математика. Профильный уровень. Высший балл [Текст] / Т.М. Ерина. – М.: Издательство «Экзамен», 2017. – 350 с.
Задачи на смеси и сплавы. Журнал «Математика в школе». №17. №11 2004г.
Захарова А.Е. Учимся решать задачи на смеси и сплавы // Математика для школьников. 2006.- №3. – С.18-21.
Интернет ресурс -[ эл.ресурс]- режим доступа, http://ru.wikipedia.org
Колачев Б.А., Ливанов В.А., Елагин В.И.. Металловедение и термическая обработка цветных металлов и сплавов. – Москва: Металлургия, 1972. – 480 с.
Лахтин Ю.М. Металловедение и термическая обработка металлов. Учебник для вузов. – 3-е. – Москва: Металлургия, 1983. – 360 с.
Лурье, М. В. Задачи на составление уравнений: Учеб. руководство / М.В. Лурье, Б.И. Александров. – 3-е изд., перераб. – М. Наука. Гл. ред. Физ.-мат. Лит., 1990-96с.
Ляпин С.Е. Методика преподавания математики. М.; Л., 1952. – 315 с.
Маланичева, Т.А. О решении задач на работу. Математика в школе [Текст] / Т.А. Маланичева, 2015, №5, 64 с.
Образовательный портал для подготовки к экзаменам.- http://reshuege.ru
Овчинникова, М.В. Методика работы над текстовыми задачами в начальных классах (общие вопросы) [Текст]: учебно-методическое пособие для студентов специальностей «Начальное обучение. Дошкольное воспитание». / М.В. Овчинникова. – К.: Пед.пресса, 2001.
Пойа, Д. Как решить задачу [Текст] / Д. Пойа. – М.: Просвещение, 1959. – 206 с.
Прокопенко Н.И. Задачи на смеси и сплавы / Н.И. Прокопенко. – М. : Чистые пруды, 2010. – 32 с.
Сафронова Т.М., Симоновская Г.А., Черноусова Н.В. Компетентностный подход в современном российском образовании и его реализация при подготовке учащихся к единому государственному экзамену по математике // Вестник Елецкого государственного университета им. И.А. Бунина. – Вып.28.: Серия «Педагогика» (История и теория математического образования). – Елец: ЕГУ им. И.А.Бунина, 2011. – 216 с.
Стефанова, Н.Л. Методика и технология обучения математике [Текст] / Н.Л. Стефанова. – М.: 2007. – 406 с.
Стойлова, Л.П. Математика [Текст]: учебник для студ. учреждений высш. проф. образования. / Л.П. Стойлова. – 3-е изд., стер. – М.: Академия, 2013. – 464 с.
Фридман Л.М., Турецкий Е.Н. Как научиться решать задачи: Кн. для учащихся ст. классов сред.школы. – 3-е изд., доработанное. М.: Просвещение, 1989. 329с.
Цыганов Ш.И. Все задачи ЕГЭ по математике прошлых лет: Учебное пособие / Ш. И. Цыганов – 4-е изд., дополненное – Уфа: Центр педагогических измерений, 2008-324с.
Шевкин, А.В. Материалы курса «Текстовые задачи в школьном курсе математики» [Текст]: лекции 1-4. / А.В. Шевкин. – М.: Педагогический университет «Первое сентября», 2006. 88 с.
Шульга, Р.П. Решение текстовых задач разными способами – средство повышения интереса к математике [Текст] / Р.П. Шульга. – М.: «Просвещение», 1990. – с. 181.
Задачи на смеси и сплавы. В задачах на смеси и сплавы важно уметь определять концентрацию и массу вещества.
Задачи на смеси и сплавы
Задачи на смеси и сплавы бывают двух видов:
ü Две смеси определенной массы с некоторой концентрацией вещества сливают вместе. Нужно определить массу и концентрацию этого вещества в новой смеси.
ü В некоторый раствор, с некоторой концентрацией вещества, добавляют, например, чистую воду (с нулевой концентрацией этого вещества). Нужно определить, какой стала концентрация вещества.
В задачах на смеси и сплавы важно уметь определять концентрацию и массу вещества.
 Концентрация вещества – это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах.
Концентрация вещества – это отношение массы или объема вещества к массе или объему всего раствора. Как правило, концентрация выражается в процентах.
где MA – масса вещества A в смеси (сплаве, растворе), а M – масса всей смеси (сплава, раствора).
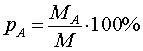
Масса раствора равна сумме масс всех составляющих.
При смешивании нескольких растворов (смесей, сплавов) масса нового раствора становится равной сумме всех смешанных растворов.
Масса растворенного вещества при смешивании двух растворов суммируется.
Алгоритм решения задач на смеси и сплавы:
1. Определить, какое вещество влияет на концентрацию раствора (главное вещество).
2. Следить за весом главного вещества при добавлении других веществ в раствор.
3.  Исходя из данных об изменениях состояния главного вещества – сделать выводы.
Исходя из данных об изменениях состояния главного вещества – сделать выводы.
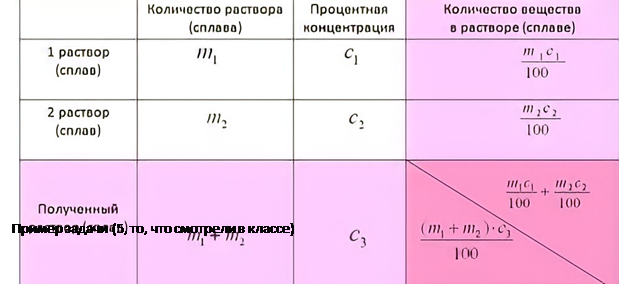 |
| Раствор | % | Количество вещества | |
| | | х | 0,1x | |
| || |  y y
|
0,35y | |
| |+|| | x + y | 0,3 * 150 |
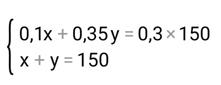
Задача 7
| Раствор | % | Количество вещества | |
| | | х | 100 х | |
| || | y | 60y | |
|
41% х y
50% |
|||
|
