Ромб — это параллелограмм, в котором все стороны являются взаимно одинаковыми. Соответственно, ромб
включает в себя абсолютно все свойствами параллелограмма и является его частным случаем. Также ещё
существуют такие важные факты о ромбе, как например, то что в каждый отдельно взятый ромб можно
включить окружность. Необходимо запомнить, что центр окружности, которая уже включена и находится в
ромбе является точкой, в которой пересекаются абсолютно все существующие диагонали рассматриваемой
фигуры. В то же время, место в котором пересекаются все существующие диагонали является центром
симметрии данного ромба.
- Сторона ромба через площадь ромба и высоту
- Сторона ромба через площадь и синус угла
- Сторона ромба через площадь и радиус вписанной
окружности - Сторона ромба через диагонали
- Сторона ромба через длинную диагональ и острый угол
- Сторона ромба через короткую диагональ и тупой угол
- Сторона ромба через периметр
Через площадь и высоту
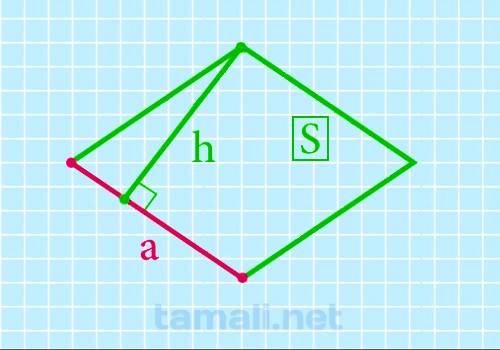
Для того чтобы найти сторону ромба через площадь и высоту, необходимо воспользоваться следующей
формулой:
A = S /h
где S — площадь ромба, h — высота исследуемого ромба.
Цифр после
запятой:
Результат в:
Пример. Найти сторону ромба, если площадь равна 30 см, а высота, опущенная на эту сторону — 3 см.
Решение. a=S/ha=30/3=10 см.
Сторона ромба через периметр
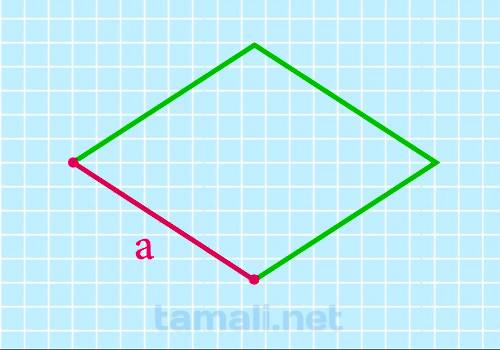
Для того чтобы найти одну из сторон ромба через периметр, нужно воспользоваться следующей
формулой:
a = P / 4
где P — периметр ромба.
Цифр после
запятой:
Результат в:
Пример. Периметр ромба равен 28 см. Найти сторону ромба.
Решение. а = 28 / 4 = 7 см.
Через площадь и синус угла
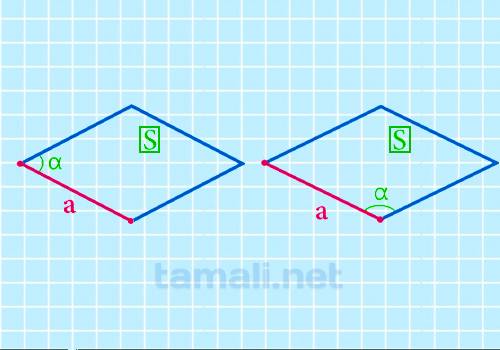
Для нахождения стороны ромба через площадь и синус угла необходимо использовать формулу,
представленную ниже:
a = √S / √sinɑ
где S — площадь ромба, a — сторона ромба, ɑ — острый угол ромба.
Цифр после
запятой:
Результат в:
Пример. Найти сторону ромба, если площадь равна 18 см, а острый угол — 30º.
Решение. a = √S/√sinɑ = a² =18/0.5=36 см a= 6 см.
Через площадь и радиус вписанной окружности
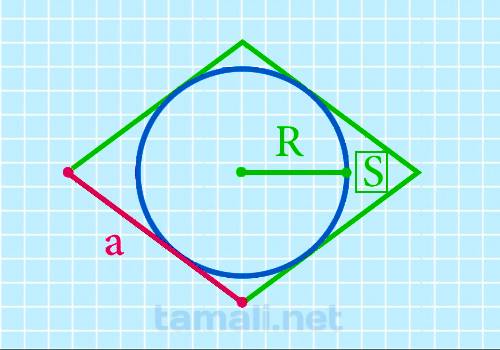
Для того чтобы рассчитать стороны ромба через площадь и радиус вписанной окружности, нужно
воспользоваться следующей формулой:
a = S/2r
где a — сторона ромба, S — площадь, r – радиус.
Цифр после
запятой:
Результат в:
Пример. Найти сторону ромба, если радиус вписанной окружности равен 2 см, а площадь — 12 см. a = 12/2*2=3 см.
Через длинную диагональ и острый угол
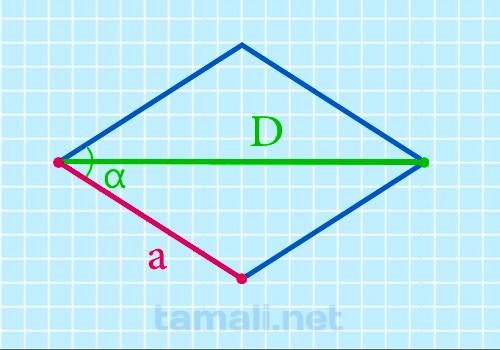
Чтобы найти сторону ромба через длинную диагональ и острый угол следует воспользоваться данной
формулой:
a = D / 2 + 2*cosɑ
где D — длинная диагональ, ɑ — острый угол ромба.
Цифр после
запятой:
Результат в:
Пример. Длинная диагональ ромба равна 12 см, а острый угол — 60º. Найти сторону ромба.
Решение. A= 12/2 + 2*1/2=6+1= 7 см.
Через короткую диагональ и тупой угол
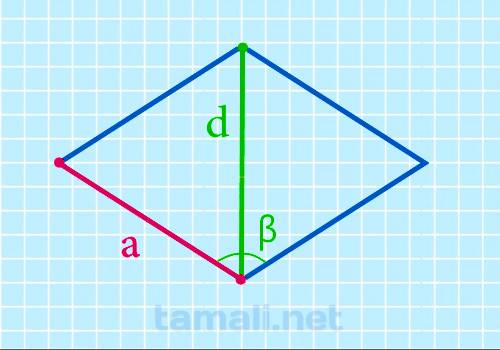
Для того чтобы найти сторону ромба необходимо воспользоваться следующей формулой:
a = d/2 – 2cosβ
где d — короткая диагональ, β — тупой угол ромба.
Цифр после
запятой:
Результат в:
Пример. Тупой угол ромба равен 120º, а короткая диагональ — 6 см. Найти сторону ромба.
Решение: a = 6 / 2 – 2 * (-0.5) = 3 + 1 = 4 см.
Сторона ромба через диагонали
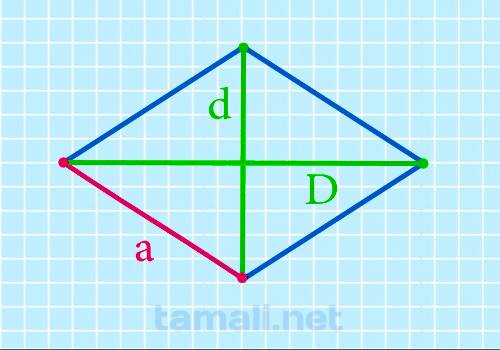
Для нахождения стороны ромба через диагонали необходимо произвести следующие расчёты:
a = D² + d²/2
где a — сторона ромба, которую необходимо найти, D — наибольшая из диагоналей, d – наименьшая
диагональ ромба.
Цифр после
запятой:
Результат в:
Пример. Найти сторону ромба, если диагонали равны 24 см и 10 см.
Решение. АС² + ВD² = 2(АВ² + ВС²), 100 + 576 = 4 · АВ²; АВ²= 169; АВ = 13 см. АВ = ВС = СD = АD = 13 см.
Примеры
Пример 1. Длины двух диагоналей d1 и d2 ромба равны 5 и 10 единицам соответственно.
Найдите площадь ромба.
Решение: d1 = 5 единиц и d2 = 10 единиц. Площадь = (d1 × d2) / 2 = (5 ×
10) / 2 квадратных единиц = 25 квадратных единиц.
Пример 2: Длины двух диагоналей d1 и d2 ромба равны 14 и 17 единицам соответственно.
Найдите площадь ромба.
Решение: d1 = 14 единиц и d2 = 17 единиц. Площадь = (d1 × d2) / 2 = (14
× 17) / 2 квадратных единиц = 70 квадратных единиц.
Пример 3: Длины двух диагоналей d1 и d2 ромба равны 3 единицам и 6 единицам
соответственно. Найдите площадь ромба.
Решение: d1 = 3 единицы и d2 = 6 единиц. Площадь = (d1 ×
d2) / 2 = (3 × 6) / 2 квадратных единиц = 9 квадратных единиц.
Стоит подчеркнуть свойство о том, что диагонали в рассматриваемой фигуре будут характеризоваться как
биссектрисы углов ромба, а также, то, что все существующие диагонали представляются
перпендикулярными. Соответственно, все перечисленные определения ромба доказывают, что он имеет
абсолютно все свойства параллелограмма.
Для того чтобы понять природу ромба необходимо также рассмотреть параллелограмм, его определение и
свойства. Параллелограмм представляет из себя четырёхугольник, в котором все стороны, лежащие
напротив друг друга, являются параллельными Ромб — частный случай параллелограмма.
Как и у любой фигуры, у ромба есть различные свойства, которые определяют, что он собой представляет.
К таким свойствам относятся:
- Четыре прямые стороны равной длины (AB = CD = DA = BC)
- Диагонали пересекают друг друга под углом 90°, или можно также сказать, что каждая из двух
диагоналей ромба является перпендикулярной биссектрисой другой (диагонали DB и CA пересекают
друг друга под углом 90°) - Противоположные углы равны, а противоположные стороны параллельны CD || AB и BC || AD; ∠A = ∠C и
∠D = ∠B - Смежные углы в сумме составляют 180° (∠A + ∠B = 180°; ∠B + ∠C = 180°; ∠C + ∠D = 180°; ∠A + ∠D =
180°) - Четыре вершины.
- Две линии симметрии.
- Четыре внутренних угла — два острых и два тупых.
- Две пары параллельных прямых.
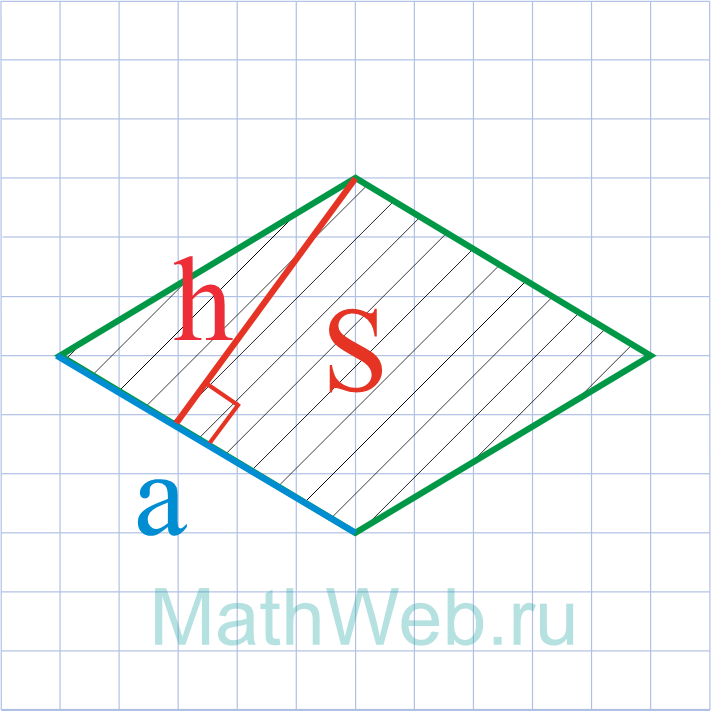
Где S – площадь ромба,h – его высота.
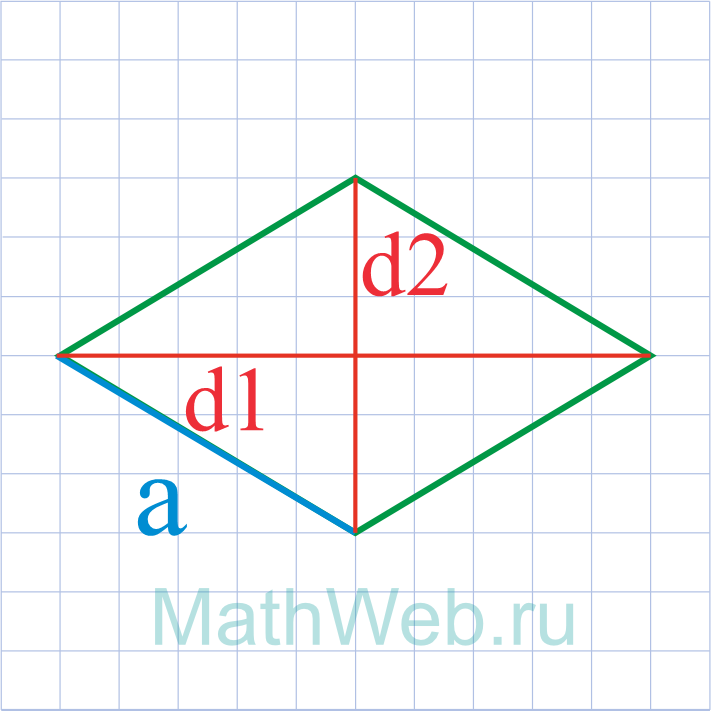
Где d1 – большая диагональ,d2 – меньшая диагональ.
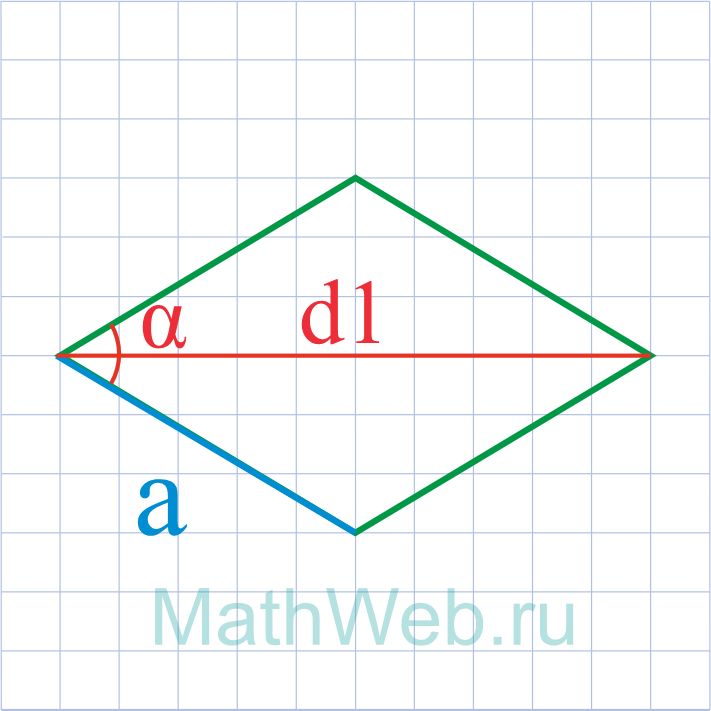
Где d1 – большая диагональ,α – острый угол.
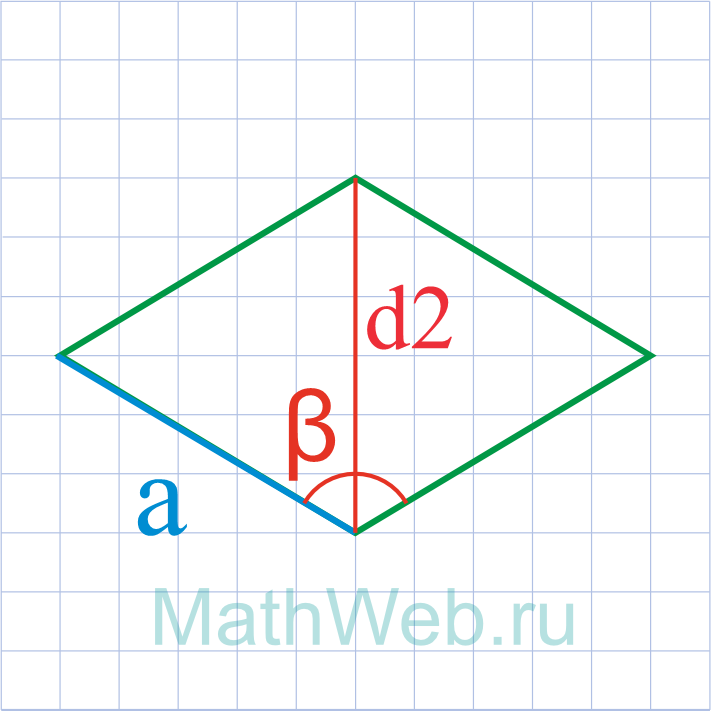
Где d2 – меньшая диагональ,β – тупой угол.
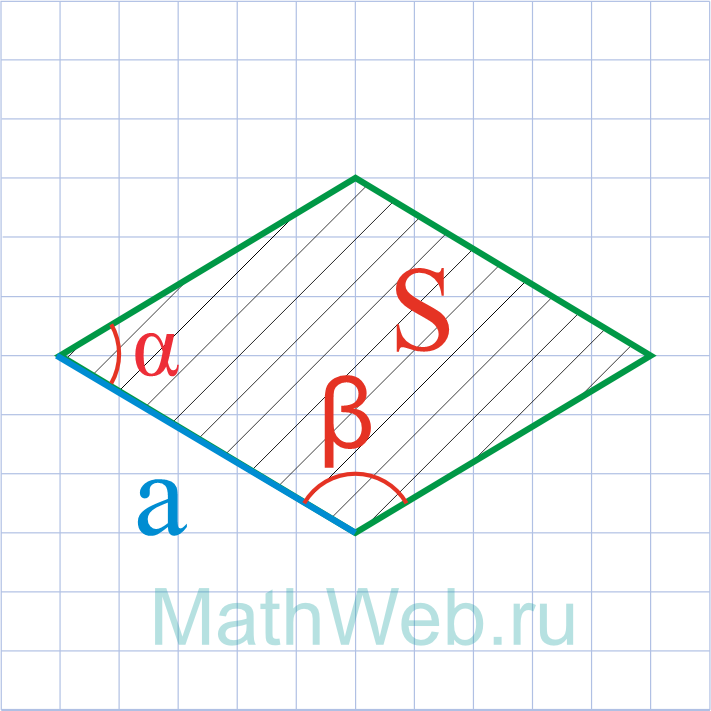
Где S – площадь ромба, α°,β° – его углы.
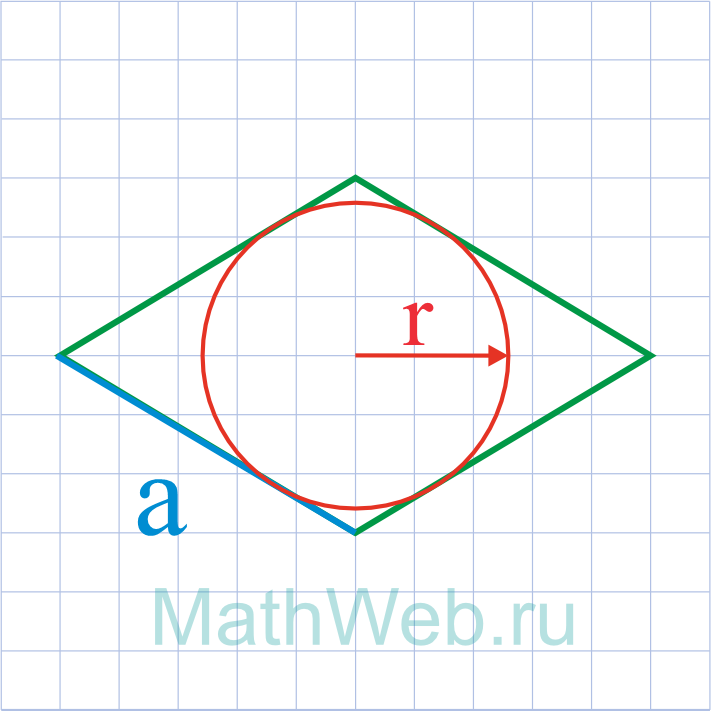
Где S – площадь ромба,r – радиус вписанной окружности.
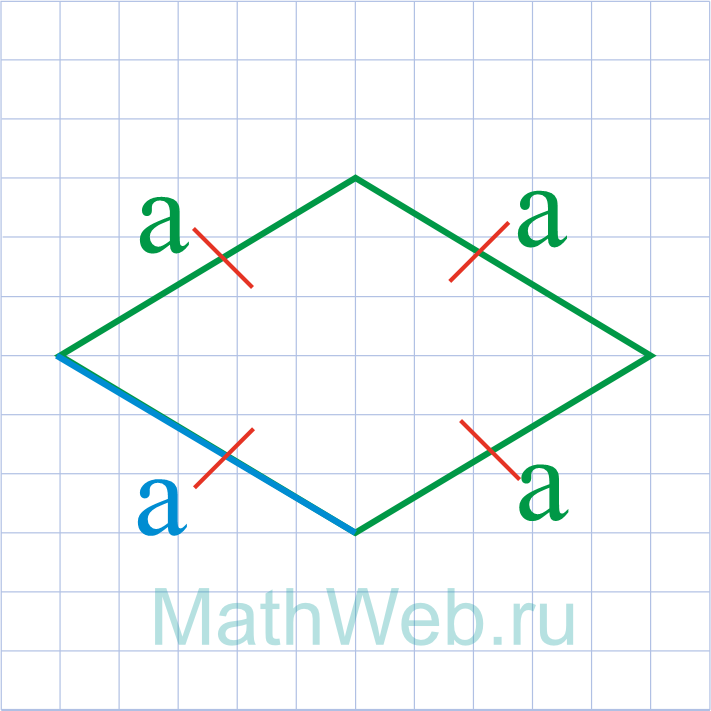
Где P – периметр ромба.
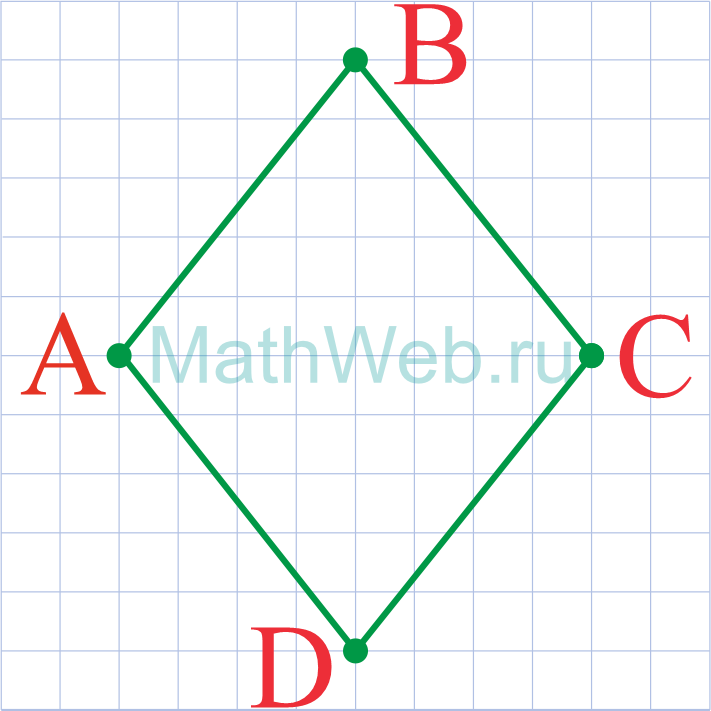
- Ромб – это параллелограмм у которого все стороны равны.
- Противоположные стороны ромба параллельны.
- Все ромбы различаются между собой только размером стороны и углов.
Как найти длину стороны ромба?
Сторона ромба может быть легко найдена с помощью нашего онлайн калькулятора. Так же Вы можете воспользоваться формулами ниже для самостоятельного расчета.
 |
a = S h |
 |
a = √d12 ― d22 2 |
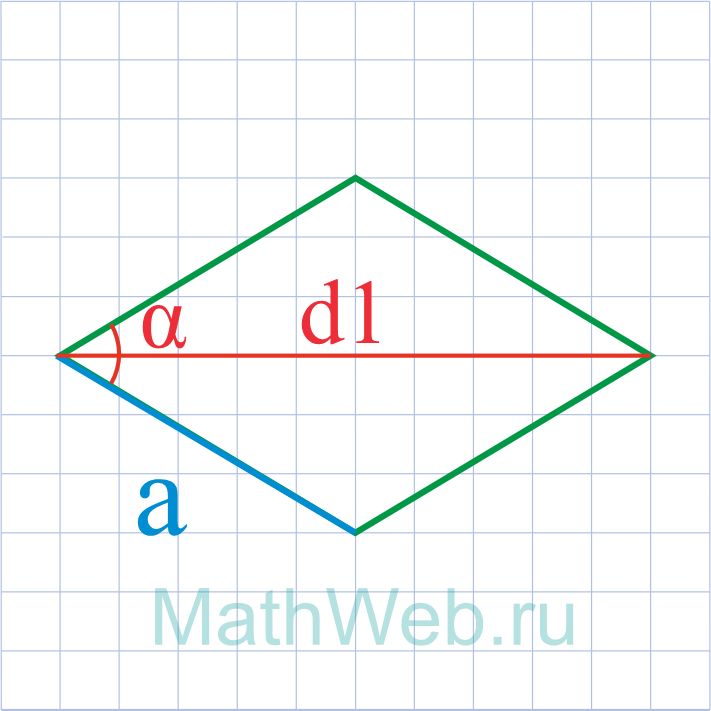 |
a = d1 √2 + 2·cos(α°) |
 |
a = d2 √2 – 2·cos(β°) |
 |
a = √S √sin(α°) = √S √sin(β°) |
 |
a = S 2r |
 |
a = P 4 |
Так как в ромбе все четыре стороны равны, совсем несложно найти одну из них, если известен его периметр – просто делим на четыре.

И опять несложно определить одну из сторон, если известны площадь ромба и его высота:
нужно площадь разделить на высоту

Немножко сложнее, если известны диагонали – здесь без теоремы Пифагора и извлечением из под корня не обойтись:
сторона ромба равна половине корня квадратного от суммы квадратов диагоналей

Примечание:
на рисунке d1=D и d2=d
Также есть много других формул (более сложных), где сторону ромба можно найти через площадь и угол, через диагональ и угол и другие
Допустим, нам известны длины диагоналей ромба. Как найти длину стороны ромба?
Так как диагонали ромба (AC, BD) пересекаются под прямым углом и делятся точкой пересечения (O) пополам, то сторона ромба (AB) будет диагональю прямоугольного треугольника (ABO) с катетами, образованными половинками диагоналей ромба (AO, BO). Тогда по теореме Пифагора получается: квадрат длины стороны ромба равняется сумме квадратов половин длин его диагоналей.
|AB|^2=|AO|^2+|BO|^2=(|AC|/2)^2+(|BD|/2)^2.
Соответственно, длина стороны ромба будет равняться корню квадратному из суммы квадратов половинок его диагоналей.
|AB|=√((|AC|/2)^2+(|BD|/2)^2).
Пусть нам известны площадь ромба (ABCD) и его высота (BH), т. е. длина перпендикуляра, опущенного из вершины (B) на сторону (AD) (или ее продолжение). Как определить сторону ромба (AB) в этом случае?
Как видно из рисунка, ромб состоит из двух треугольников (ABD и DBC) площадь каждого из которых равняется половине произведения высоты на основание. Следовательно площадь ромба будет равна произведению высоты на длину стороны. Отсюда получается простая формула для вычисления длины стороны ромбы: нужно его площадь разделить на длину высоты.
|AB|=S/|BH|
Если известна величина угла ромба и длина одной из диагоналей, то нахождение стороны ромба производится аналогично первому случаю, только вместо теоремы Пифагора необходимо использовать тригонометрические соотношения. При этом следует учесть, что диагонали ромба являются одновременно биссектрисами углов, то есть делят их пополам.
Пусть, например, нам известна величина угла BAD и длина выходящей из него диагонали АС. Исходя из тригонометрических зависимостей в прямоугольном треугольнике ABO, получаем, что длина стороны ромба будет равна частному от половины исходящей диагонали на синус половины угла.
В виде формулы эта зависимость будет выглядеть следующим образом:
|AB|= (|AC|/2)/sin(α/2), где α – величина угла BAD.
Аналогично вычисляется длина стороны ромба в случае, когда заданы другие параметры – длина противоположной углу диагонали, соотношение диагоналей и т. д. Для определения стороны ромба достаточно лишь выбрать подходящую тригонометрическую функцию – косинус, тангенс и т. п.
Подробнее: http://www.kakprosto.ru/kak-3743-kak-nayti-storony-romba#ixzz46UEQzvte
Свойства ромба:
1. Ромб – частный случай параллелограмма
2. Противоположные стороны – параллельны
3. Все четыре стороны – равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами

a – сторона ромба
D – большая диагональ
d – меньшая диагональ
α – острый угол
β – тупой угол
Формула стороны через диагонали, ( a ):
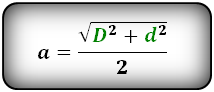
Формулы стороны через диагональ и угол, ( a ):
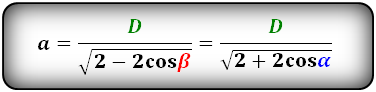
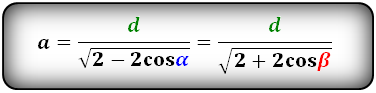
Формулы стороны через диагональ и половинный угол, ( a ):


Формулы стороны через диагонали и угол, ( a ):
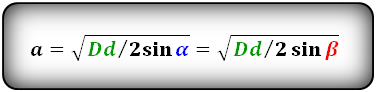
Формулы стороны через площадь ромба ( S ) и угол, ( a ):
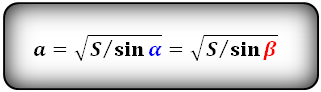
Формулы стороны через периметр ромба ( P ) и угол, ( a ):

Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 27 ноября 2011
-
Обновлено: 13 августа 2021
