3.3. Математические ожидания и ковариации векторов и матриц
При работе с линейными моделями удобно представлять данные в виде векторов или матриц. Элементы некоторых векторов или матриц статистических линейных моделей являются случайными переменными. Определение случайной переменной было дано. Значение этой переменной зависит от случайного результата опыта.
В этой книге рассматривается такой тип векторов случайных переменных отклика, элементы которого могут быть коррелированы, а влияющие на них переменные являются контролируемыми и неслучайными. В конкретной линейной модели, влияющие на отклик переменные, имеют выбранные или полученные в результате расчёта детерминированные значения. Таким образом, в рассматриваемых линейных моделях имеются два вектора случайных переменных:
у= и e=
и e= .
.
Значения i-й переменной уi (i=1, 2, …, n) отклика наблюдаются в результате проведения i-го опыта эксперимента, а значения переменной ei случайной ошибки не наблюдаются, но могут оцениваться по наблюдаемым значениям переменной отклика и значениям влияющих на неё переменных.
При рассмотрении линейных моделей широко используются векторы и матрицы случайных переменных, поэтому в первую очередь для них необходимо обобщить идеи математического ожидания, ковариации и дисперсии.
Математические ожидания
Математическое ожидание вектора у размеров пх1 случайных переменных y1, y2, …, уп определяется как вектор их ожидаемых значений:
Е(у)=Е =
= =
= =y, (3.3.1)
=y, (3.3.1)
Рекомендуемые материалы
где E(уi)=yi получается в виде E(уi)= , используя функцию fi(уi) плотности вероятности безусловного распределения переменной уi.
, используя функцию fi(уi) плотности вероятности безусловного распределения переменной уi.
Если х и у – векторы случайных переменных размеров пх1, то, в силу (3.3.1) и (3.2.7), математическое ожидание их суммы равно сумме их математических ожиданий:
Е(х+у)=Е(х)+Е(у). (3.3.2)
Пусть уij (i=1, 2, …, m; j=1, 2, …, п) набор случайных переменных с ожидаемыми значениями E(уij). Выражая случайные переменные и их математические ожидания в матричной форме, можно определить общий оператор математического ожидания матрицы Y=(yij) размеров mхп следующим образом:
Определение 3.3.1. Математическое ожидание матрицы Y случайных переменных равно матрице математических ожиданий её элементов
E(Y)=[E(yij)].
По аналогии с выражением (3.3.1), ожидаемые значения матрицы Y случайных переменных представляются в виде матрицы ожидаемых значений:
E(Y)= =
= . (3.3.3)
. (3.3.3)
Вектор можно рассматривать как матрицу, следовательно, определение 3.3.1 и следующая теорема справедливы и для векторов.
Теорема 3.3.1. Если матрицы А=(аij) размеров lхm, B=(bij) размеров nхp, С=(cij) размеров lхp – все имеют элементами постоянные числовые значения, а Y – матрица размеров mхn случайных переменных, то
E(AYB+C)=AE(Y)B+C. (3.3.4)
Доказательство дано в книгах [Себер (1980) стр.19; Seber, Lee (2003) стр.5]
□
Там же доказывается, что, если матрицы A и В размеров mхn, элементами которых являются постоянные числовые значения, а х и у – векторы случайных переменных размеров пх1, то
E(Aх+Bу)=AE(х)+BE(у).
Если f(Y) – линейная функция матрицы Y, то её ожидаемое значение находится по формуле Е[f(Y)]=f[Е(Y)] [Boik (2011) cтр.134]. Например, если матрицы А размеров рхm, B размеров пхр и С размеров рхр – все имеют элементами постоянные числовые значения, а матрица Y размеров тхп случайных переменных, то
E[след(AYB+C)]=след[E(AYB+C)], так как след матрицы – линейный оператор
=след[AE(Y)B+C], так как AYB+C – линейная функция матрицы Y
=след[AE(Y)B]+след(C). (3.3.5)
Ковариации и дисперсии
Аналогичным образом можно обобщить понятия ковариации и дисперсии для векторов. Если векторы случайных переменных х размеров mх1 и у размеров nх1, то ковариация этих векторов определяется следующим образом.
Определение 3.3.2. Ковариацией векторов х и у случайных переменных является прямоугольная матрица ковариаций их элементов
C(х, у)=[C(хi, уj)].
Теорема 3.3.2. Если случайные векторы х и у имеют векторы математических ожиданий E(x)=x и Е(у)=y, то их ковариация
C(х, у)=E[(x–x)(y–y)T].
Доказательство:
C(х, у)=[C(хi, уj)]
={E[(хi–xi)(yj–yj)]} [в силу (3.2.9)]
=E[(x–x)(y–y)T]. [по определению 3.3.1]
□
Применим эту теорему для нахождения матрицы ковариаций векторов х размеров 3х1 и у размеров 2х1
C(х, у)=E[(x–x)(y–y)T]
=E
=Е
= .
.
Определение 3.3.3. Если х=у, то матрица ковариаций C(у, у) записывается в виде D(у)=E[(y–y)(y–y)T] и называется матрицей дисперсий и ковариаций вектора у. Таким образом,
D(у)=E[(y–y)(y–y)T]=[C(уi, уj)]
= . (3.3.4)
. (3.3.4)
А так как C(уi, уj)=C(уj, уi), то матрица (3.3.4) симметричная и квадратная.
Матрица дисперсий и ковариаций вектора у представляется в виде ожидаемого значения произведения (y–y)(y–y)T. В силу (П.2.13), произведение (yi–yi)(yj–yj) является (ij)-м элементом матрицы (y–y)(y–y)T. Таким образом, в силу (3.2.9) и (3.3.4), математическое ожидание E[(yi–yi)(yj–yj)]=sij является (ij)-м элементом Е[(y–y)(y–y)T]. Отсюда
E[(y–y)(y–y)T]= . (3.3.5)
. (3.3.5)
Дисперсии s11, s22, …, sпп переменных y1, y2, …, уп и их ковариации sij, для всех i≠j, могут быть удобно представлены матрицей дисперсий и ковариаций, которая иногда называется ковариационной матрицей и обозначается прописной буквой S строчной s:
S=D(у)= (3.3.6)
(3.3.6)
В матрице S i-я строка содержит дисперсию переменной уi и её ковариации с каждой из остальных переменных вектора у. Чтобы быть последовательными с обозначением sij, используем для дисперсий sii=si2, где i =1, 2, …, n. При этом дисперсии расположены по диагонали матрицы S и ковариации занимают позиции за пределами диагонали. Отметим различие в значении между обозначениями D(у)=S для вектора и С(уi, уj)=sij для двух переменных.
Матрица S дисперсий и ковариаций симметричная, так как sij=sji [см. (3.2.9)]. Во многих приложениях полагается, что матрица S положительно определённая. Это обычно верно, если рассматриваются непрерывные случайные переменные, и между ними нет линейных зависимостей. Если между переменными есть линейные зависимости, то матрица S будет неотрицательно определённой.
Для примера найдём матрицу дисперсий и ковариаций вектора у размеров 3х1
D(у)=E[(y–y)(y–y)T]
=E
=E
= .
.
= .
.
Как следует из определения 3.3.3,
D(у)=E[(у–y)(y–y)T], (3.3.7)
что после подобного сделанному в (3.2.4) преобразованию приводится к выражению
D(y)=E(yyT)–yyT. (3.3.8)
Последние два выражения являются естественным обобщением одномерных результатов данных выражениями (3.2.2) и (3.2.4).
Пример 3.3.1. Если а – какой-либо вектор числовых значений тех же размеров пх1, что и вектор у, то
D(y–а)=D(y).
Это следует из того, что yi–ai–E(yi–ai)=yi–ai–E(yi)+ai=yi–E(yi), так что
C(yi–ai, yj–aj)=C(yi, yj).
□
Напомним, что симметричная матрица А является положительно определенной, если для всех векторов у≠0 квадратичная форма уТАу>0. В дальнейшем будет использоваться часто следующая теорема.
Теорема 3.3.3. Если у – вектор случайных переменных, в котором ни одна из переменных не является линейной комбинации остальных, то есть, нет вектора а≠0 и числа b таких, что аТу=b для любого у, то D(у)=S – положительно определенная матрица.
Доказательство этой теоремы дано в [Себер (1980) стр.22].
□
Обобщенная дисперсия и нормированный вектор
Матрица S содержит дисперсии и ковариации всех п случайных переменных вектора у и всесторонне представляет полную их вариацию. Обобщённой мерой, характеризующей вариацию случайных переменных вектора у, может служить определитель матрицы S:
Обобщенная дисперсия =det(S). (3.3.9)
В качестве статистики обобщённой дисперсии используется обобщённая выборочная дисперсия, определяемая детерминантом матрицы S=YT(I–Е/n)Y/(n–1) вариаций и ковариаций выборочных значений переменных вектора у, представленных матрицей Y=[y1, y2, …, yk], где её столбцы составлены из векторов значений переменных вектора у [Rencher, Christensen (2012) стр.81]:
Обобщенная выборочная дисперсия =det(S). (3.3.10)
Если det(S) малый, то значения переменных вектора у располагаются ближе к их усреднённым значениям вектора  , чем, если бы det(S) был большим. Малое значение det(S) может указывать также на то, что переменные y1, y2,…, уп вектора у сильно взаимно коррелированы и стремятся занимать подпространство меньшее, чем п измерений, что соответствует одному или большему числу малых собственных значений [Rencher (1998) раздел 2.1.3; Rencher, Christensen (2012) стр.81].
, чем, если бы det(S) был большим. Малое значение det(S) может указывать также на то, что переменные y1, y2,…, уп вектора у сильно взаимно коррелированы и стремятся занимать подпространство меньшее, чем п измерений, что соответствует одному или большему числу малых собственных значений [Rencher (1998) раздел 2.1.3; Rencher, Christensen (2012) стр.81].
Для получения полезной меры разности между векторами у и y необходимо учитывать дисперсии и ковариации переменных вектора у. Как для одной нормированной случайной переменной, получаемой по формуле z=(у–y)/s и имеющей среднее равное 0 и дисперсию равную 1, нормированная разность между векторами у и y определяется в виде
Нормированная разность =(у–y)ТS–1(у–y). (3.3.11)
Использование матрицы S–1 в этом выражении нормирует (трансформирует) переменные вектора у так, что нормированные переменные имеют средние равные 0 и дисперсии равные 1, а также становятся и некоррелированными. Это получается потому, что матрица S положительно определённая. По теореме П.6.5 её обратная матрица тоже положительно определённая. В силу (П.12.18), матрица S–1=S–1/2S–1/2. Отсюда
(у–y)ТS–1(у–y)=(у–y)ТS–1/2S–1/2(у–y)
=[S–1/2(у–y)]Т[S–1/2(у–y)]
=zТz,
Вам также может быть полезна лекция “Построение формы в ранне многоголосии”.
где z=S–1/2(у–y) – вектор нормированных случайных переменных. Математическое ожидание вектора z получается
Е(z)=Е[S–1/2(у–y)]=S–1/2[Е(у)–y]=0
и его дисперсия
D(z)=D[S–1/2(у–y)]=S–1/2D(у–y)S–1/2=S–1/2SS–1/2=S–1/2S1/2S1/2S–1/2=I.
Следовательно, по пункту 2 теоремы 4.5.2 следующей главы вектор S–1/2(у–y) имеет нормальное распределение N(0, I).
Для нормированной разности, как параметра, есть соответствующая статистика, а именно, выборочная нормированная дистанция, определяемая формулой (у– )ТS–1(у–
)ТS–1(у– ) и называемая часто дистанцией Махаланобиса [Mahalanobis (1936); Seber (2008) cтр.463]. Некоторый п-мерный гиперэллипсоид (у–
) и называемая часто дистанцией Махаланобиса [Mahalanobis (1936); Seber (2008) cтр.463]. Некоторый п-мерный гиперэллипсоид (у– )ТS–1(у–
)ТS–1(у– )=а2, центрированный вектором
)=а2, центрированный вектором  и базирующийся на S–1 для нормирования расстояния до центра, содержит выборочные значения переменных вектора у. Гиперэллипсоид (у–
и базирующийся на S–1 для нормирования расстояния до центра, содержит выборочные значения переменных вектора у. Гиперэллипсоид (у– )ТS–1(у–
)ТS–1(у– ) имеет оси пропорциональные квадратным корням собственных значений матрицы S. Можно показать, что объём гиперэллипсоида пропорционален [det(S)]1/2. Если минимальное собственное значение матрицы S равно нулю, то в этом направлении нет оси и гиперэллипсоид расположен в (п–1)-мерном подпространстве п-мерного пространства. Следовательно, его объём в п-мерном пространстве равен 0. Нулевое собственное значение указывает на избыточность переменных вектора у. Для устранения этого необходимо убрать одну или более переменных, являющихся линейными комбинациями остальных.
) имеет оси пропорциональные квадратным корням собственных значений матрицы S. Можно показать, что объём гиперэллипсоида пропорционален [det(S)]1/2. Если минимальное собственное значение матрицы S равно нулю, то в этом направлении нет оси и гиперэллипсоид расположен в (п–1)-мерном подпространстве п-мерного пространства. Следовательно, его объём в п-мерном пространстве равен 0. Нулевое собственное значение указывает на избыточность переменных вектора у. Для устранения этого необходимо убрать одну или более переменных, являющихся линейными комбинациями остальных.
Как найти математическое ожидание?
Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание – это первый начальный момент заданной СВ.
Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины – срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).
Формула среднего случайной величины
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$: $$ M(X)=sum_^. $$ Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx. $$
Пример нахождения математического ожидания
Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.
Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом: $$ x_i quad -1 quad 2 quad 5 quad 10 quad 20 \ p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1 $$
Используем формулу для м.о. дискретной случайной величины: $$ M(X)=sum_^. $$ Получаем: $$ M(X)=sum_^ =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8. $$ Вот в этом примере 2 описано также нахождение дисперсии Х.
Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.
Используем для нахождения мат. ожидания формулу: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx. $$ Подставляем из условия плотность вероятности и вычисляем значение интеграла: $$ M(X)=int_<-infty>^ <+infty>f(x) cdot x dx = int_<0>^ <1>12(x^2-x^3) cdot x dx = int_<0>^ <1>12(x^3-x^4) dx = \ =left.(3x^4-frac<12><5>x^5) right|_0^1=3-frac<12> <5>= frac<3><5>=0.6. $$
Вычисление математического ожидания онлайн
Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$.
Видео. Полезные ссылки
Видеоролики: что такое среднее (математическое ожидание)
Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Полезные ссылки
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по терверу. Для закрепления материала – еще примеры решений по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
3.3 Математические ожидания и ковариации векторов и матриц
3.3. Математические ожидания и ковариации векторов и матриц
При работе с линейными моделями удобно представлять данные в виде векторов или матриц. Элементы некоторых векторов или матриц статистических линейных моделей являются случайными переменными. Определение случайной переменной было дано. Значение этой переменной зависит от случайного результата опыта.
В этой книге рассматривается такой тип векторов случайных переменных отклика, элементы которого могут быть коррелированы, а влияющие на них переменные являются контролируемыми и неслучайными. В конкретной линейной модели, влияющие на отклик переменные, имеют выбранные или полученные в результате расчёта детерминированные значения. Таким образом, в рассматриваемых линейных моделях имеются два вектора случайных переменных:
у=  и e=
и e= .
.
Значения i-й переменной уi (i=1, 2, …, n) отклика наблюдаются в результате проведения i-го опыта эксперимента, а значения переменной ei случайной ошибки не наблюдаются, но могут оцениваться по наблюдаемым значениям переменной отклика и значениям влияющих на неё переменных.
При рассмотрении линейных моделей широко используются векторы и матрицы случайных переменных, поэтому в первую очередь для них необходимо обобщить идеи математического ожидания, ковариации и дисперсии.
Математическое ожидание вектора у размеров пх1 случайных переменных y1, y2, . уп определяется как вектор их ожидаемых значений:
Е(у)=Е =
= =
= =y, (3.3.1)
=y, (3.3.1)
Рекомендуемые файлы
где E(уi)=yi получается в виде E(уi)= , используя функцию fi(уi) плотности вероятности безусловного распределения переменной уi.
, используя функцию fi(уi) плотности вероятности безусловного распределения переменной уi.
Если х и у – векторы случайных переменных размеров пх1, то, в силу (3.3.1) и (3.2.7), математическое ожидание их суммы равно сумме их математических ожиданий:
Пусть уij (i=1, 2, . m; j=1, 2, . п) набор случайных переменных с ожидаемыми значениями E(уij). Выражая случайные переменные и их математические ожидания в матричной форме, можно определить общий оператор математического ожидания матрицы Y=(yij) размеров mхп следующим образом:
Определение 3.3.1. Математическое ожидание матрицы Y случайных переменных равно матрице математических ожиданий её элементов
По аналогии с выражением (3.3.1), ожидаемые значения матрицы Y случайных переменных представляются в виде матрицы ожидаемых значений:
E(Y)= =
= . (3.3.3)
. (3.3.3)
Вектор можно рассматривать как матрицу, следовательно, определение 3.3.1 и следующая теорема справедливы и для векторов.
Теорема 3.3.1. Если матрицы А=(аij) размеров lхm, B=(bij) размеров nхp, С=(cij) размеров lхp – все имеют элементами постоянные числовые значения, а Y – матрица размеров mхn случайных переменных, то
Доказательство дано в книгах [Себер (1980) стр.19; Seber, Lee (2003) стр.5]
Там же доказывается, что, если матрицы A и В размеров mхn, элементами которых являются постоянные числовые значения, а х и у – векторы случайных переменных размеров пх1, то
Если f(Y) – линейная функция матрицы Y, то её ожидаемое значение находится по формуле Е[f(Y)]=f[Е(Y)] [Boik (2011) cтр.134]. Например, если матрицы А размеров рхm, B размеров пхр и С размеров рхр – все имеют элементами постоянные числовые значения, а матрица Y размеров тхп случайных переменных, то
Ковариации и дисперсии
Аналогичным образом можно обобщить понятия ковариации и дисперсии для векторов. Если векторы случайных переменных х размеров mх1 и у размеров nх1, то ковариация этих векторов определяется следующим образом.
Определение 3.3.2. Ковариацией векторов х и у случайных переменных является прямоугольная матрица ковариаций их элементов
Теорема 3.3.2. Если случайные векторы х и у имеют векторы математических ожиданий E(x)=x и Е(у)=y, то их ковариация
Применим эту теорему для нахождения матрицы ковариаций векторов х размеров 3х1 и у размеров 2х1
=E
=Е
= .
.
= . (3.3.4)
. (3.3.4)
E[(y–y)(y–y) T ]= . (3.3.5)
. (3.3.5)
Дисперсии s11, s22, . sпп переменных y1, y2, . уп и их ковариации sij, для всех i≠j, могут быть удобно представлены матрицей дисперсий и ковариаций, которая иногда называется ковариационной матрицей и обозначается прописной буквой S строчной s:
S=D(у)=  (3.3.6)
(3.3.6)
В матрице S i-я строка содержит дисперсию переменной уi и её ковариации с каждой из остальных переменных вектора у. Чтобы быть последовательными с обозначением sij, используем для дисперсий sii=si 2 , где i =1, 2, . n. При этом дисперсии расположены по диагонали матрицы S и ковариации занимают позиции за пределами диагонали. Отметим различие в значении между обозначениями D(у)=S для вектора и С(уi, уj)=sij для двух переменных.
Матрица S дисперсий и ковариаций симметричная, так как sij=sji [см. (3.2.9)]. Во многих приложениях полагается, что матрица S положительно определённая. Это обычно верно, если рассматриваются непрерывные случайные переменные, и между ними нет линейных зависимостей. Если между переменными есть линейные зависимости, то матрица S будет неотрицательно определённой.
Для примера найдём матрицу дисперсий и ковариаций вектора у размеров 3х1
=E
=E
= .
.
= .
.
Как следует из определения 3.3.3,
что после подобного сделанному в (3.2.4) преобразованию приводится к выражению
Последние два выражения являются естественным обобщением одномерных результатов данных выражениями (3.2.2) и (3.2.4).
Пример 3.3.1. Если а – какой-либо вектор числовых значений тех же размеров пх1, что и вектор у, то
Напомним, что симметричная матрица А является положительно определенной, если для всех векторов у≠0 квадратичная форма у Т Ау>0. В дальнейшем будет использоваться часто следующая теорема.
Теорема 3.3.3. Если у – вектор случайных переменных, в котором ни одна из переменных не является линейной комбинации остальных, то есть, нет вектора а≠0 и числа b таких, что а Т у=b для любого у, то D(у)=S – положительно определенная матрица.
Доказательство этой теоремы дано в [Себер (1980) стр.22].
Обобщенная дисперсия и нормированный вектор
Матрица S содержит дисперсии и ковариации всех п случайных переменных вектора у и всесторонне представляет полную их вариацию. Обобщённой мерой, характеризующей вариацию случайных переменных вектора у, может служить определитель матрицы S:
Обобщенная дисперсия =det(S). (3.3.9)
В качестве статистики обобщённой дисперсии используется обобщённая выборочная дисперсия, определяемая детерминантом матрицы S=Y T (I–Е/n)Y/(n–1) вариаций и ковариаций выборочных значений переменных вектора у, представленных матрицей Y=[y1, y2, …, yk], где её столбцы составлены из векторов значений переменных вектора у [Rencher, Christensen (2012) стр.81]:
Обобщенная выборочная дисперсия =det(S). (3.3.10)
Если det(S) малый, то значения переменных вектора у располагаются ближе к их усреднённым значениям вектора  , чем, если бы det(S) был большим. Малое значение det(S) может указывать также на то, что переменные y1, y2. уп вектора у сильно взаимно коррелированы и стремятся занимать подпространство меньшее, чем п измерений, что соответствует одному или большему числу малых собственных значений [Rencher (1998) раздел 2.1.3; Rencher, Christensen (2012) стр.81].
, чем, если бы det(S) был большим. Малое значение det(S) может указывать также на то, что переменные y1, y2. уп вектора у сильно взаимно коррелированы и стремятся занимать подпространство меньшее, чем п измерений, что соответствует одному или большему числу малых собственных значений [Rencher (1998) раздел 2.1.3; Rencher, Christensen (2012) стр.81].
Для получения полезной меры разности между векторами у и y необходимо учитывать дисперсии и ковариации переменных вектора у. Как для одной нормированной случайной переменной, получаемой по формуле z=(у–y)/s и имеющей среднее равное 0 и дисперсию равную 1, нормированная разность между векторами у и y определяется в виде
Использование матрицы S –1 в этом выражении нормирует (трансформирует) переменные вектора у так, что нормированные переменные имеют средние равные 0 и дисперсии равные 1, а также становятся и некоррелированными. Это получается потому, что матрица S положительно определённая. По теореме П.6.5 её обратная матрица тоже положительно определённая. В силу (П.12.18), матрица S –1 =S –1/2 S –1/2 . Отсюда
где z=S –1/2 (у–y) – вектор нормированных случайных переменных. Математическое ожидание вектора z получается
и его дисперсия
Следовательно, по пункту 2 теоремы 4.5.2 следующей главы вектор S –1/2 (у–y) имеет нормальное распределение N(0, I).
Для нормированной разности, как параметра, есть соответствующая статистика, а именно, выборочная нормированная дистанция, определяемая формулой (у– ) Т S –1 (у–
) Т S –1 (у– ) и называемая часто дистанцией Махаланобиса [Mahalanobis (1936); Seber (2008) cтр.463]. Некоторый п-мерный гиперэллипсоид (у–
) и называемая часто дистанцией Махаланобиса [Mahalanobis (1936); Seber (2008) cтр.463]. Некоторый п-мерный гиперэллипсоид (у– ) Т S –1 (у–
) Т S –1 (у– )=а 2 , центрированный вектором
)=а 2 , центрированный вектором  и базирующийся на S –1 для нормирования расстояния до центра, содержит выборочные значения переменных вектора у. Гиперэллипсоид (у–
и базирующийся на S –1 для нормирования расстояния до центра, содержит выборочные значения переменных вектора у. Гиперэллипсоид (у– ) Т S –1 (у–
) Т S –1 (у– ) имеет оси пропорциональные квадратным корням собственных значений матрицы S. Можно показать, что объём гиперэллипсоида пропорционален [det(S)] 1/2 . Если минимальное собственное значение матрицы S равно нулю, то в этом направлении нет оси и гиперэллипсоид расположен в (п–1)-мерном подпространстве п-мерного пространства. Следовательно, его объём в п-мерном пространстве равен 0. Нулевое собственное значение указывает на избыточность переменных вектора у. Для устранения этого необходимо убрать одну или более переменных, являющихся линейными комбинациями остальных.
) имеет оси пропорциональные квадратным корням собственных значений матрицы S. Можно показать, что объём гиперэллипсоида пропорционален [det(S)] 1/2 . Если минимальное собственное значение матрицы S равно нулю, то в этом направлении нет оси и гиперэллипсоид расположен в (п–1)-мерном подпространстве п-мерного пространства. Следовательно, его объём в п-мерном пространстве равен 0. Нулевое собственное значение указывает на избыточность переменных вектора у. Для устранения этого необходимо убрать одну или более переменных, являющихся линейными комбинациями остальных.
Математическое ожидание
Математическое ожидание — это ожидаемый результат от какого-то действия.
Например, можно рассчитать ожидаемую стоимость инвестиции в определённый момент в будущем. Рассчитывая математическое ожидание перед тем, как инвестировать, можно выбрать наилучший сценарий который, по мнению инвестора, даст наилучший результат.
Случайная величина может быть двух типов:
- Дискретной: число возможных значений X — это числимое конечное или бесконечное множество точек; пример: количество дефектных устройств в производстве фабрики.
- Непрерывной: X может принимать любое значение в заданном диапазоне; пример: концентрация углекислого газа в воде.
Математическое ожидание дискретной случайной величины рассчитывается этой формулой:
Математическое ожидание дискретной случайной величины рассчитывается:
1. Сначала нужно умножить каждое из возможных результатов на свою вероятность (например: вероятность, что выпадет “1” — 1/6, “2” — 1/3, значит умножаем 1 на 1/6, 2 на 1/3, и т.д.),
2. Затем суммируем все эти значения (1 × 1/6 + 2 × 1/3 и т.д.).
Для непрерывной случайной величины используется эта формула:
В этом случае рассчитывается интеграл в заданном интервале.
Примеры вычисления математического ожидания
- если в задаче даётся таблица с данными, то перемножаем каждое событие на его вероятность и потом всё складываем;
- если в задаче дают функцию с заданным интервалом, то вычисляем интеграл с этим интервалом.
Пример 1
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | −1 | 1 | 2 | 3 | 4 |
| pi | 0,1 | 0,2 | 0,3 | 0,1 | 0,3 |
Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = −1×0,1+ 1×0,2 + 2×0,3 + 3×0,1 + 4×0,3 = −0,1 + 0,2 + 0,6 + 0,3 + 1,2 = 2,2
Пример 2
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = 2x, при x∈(0,1) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:


Пример 3
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | 1 | 2 | 3 | 4 | 5 |
| pi | 0,3 | 0,3 | 0,1 | 0,1 | 0,2 |
Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = 1×0,3 + 2×0,3 + 3×0,1 + 4×0,1 + 5×0,2 = 0,3 + 0,6 + 0,3 + 0,4 + 1 = 2,6
Пример 4
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = (1/10).(3x²+1), при x∈(0,2) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:
[spoiler title=”источники:”]
http://studizba.com/lectures/47-matematika/680-statisticheskie-metody-eksperimentalnyh-issledovaniy/13066-33-matematicheskie-ozhidaniya-i-kovariacii-vektorov-i-matric.html
http://www.uznaychtotakoe.ru/matematicheskoe-ozhidanie/
[/spoiler]
46
Случайный вектор
– это упорядоченный набор (система)
случайных величин. Ранее уже встречались
наборы независимых случайных величин.
В этой главе рассматриваются системы
случайных величин, зависящих друг от
друга. Примеры случайных векторов:
вектор скорости зенитной ракеты,
наводимой на цель, совершающей
противоракетный маневр; вектор состояния
реальной атмосферы (температура,
давление, плотность, влажность, направление
и скорость ветра); вектор свойств
конструкционного материала (плотность,
временное сопротивление , модуль
упругости и пр.).
4.1. Ковариация
Ковариацией двух
скалярных случайных величин X
и Y
называется математическое ожидание
произведения центрированных X
и Y.
Слово ковариация
происходит от латинского co
– вместе и
variatio
– изменение.
![]()
Здесь и далее нулем
отмечены центрированные случайные
величины.
Если X
и Y
– непрерывные случайные величины, то
![]()
![]() (4.1)
(4.1)
где
![]() – плотность совместного распределения
– плотность совместного распределения
случайных величин.
За характеристику
линейной зависимости между X
и Y
применяется отношение ковариации к
произведению средних квадратических
отклонений называемое коэффициентом
корреляции
![]()
Ковариация и
коэффициент корреляции независимых
случайных величин равны нулю. Если X
= Y,
то
![]() ЕслиX
ЕслиX
= –Y,
то
![]()
Величина ковариации
обычно устанавливается опытным путем.
Статистическая оценка ковариации
находится по соотношениям
![]()
Обработка опытных
данных должна включать также оценку
точности определения ковариации.
4.2. Математическое ожидание и ковариационная матрица случайного вектора
Как правило, под
вектором будем понимать матрицу-столбец
![]()
Учтем, что
математическое ожидание матрицы равно
матрице, составленной из математических
ожиданий ее элементов.
![]()
Ковариационной
матрицей случайного вектора называется
матрица, составленная из дисперсий и
ковариаций проекций вектора.
 (4.2)
(4.2)
Ковариационная
матрица симметрична относительно
главной диагонали так как
![]() .
.
Это означает, что![]() .
.
4.3. Линейное преобразование случайного вектора
Из определения
математического ожидания следует, что

Здесь A,B,C – неслучайные
матрицы, структура которых допускает
приведенные операции сложения и
умножения.
Для линейного
преобразования случайного вектора
![]()
справедливо
следующее
![]()
Действительно

Последний результат
очень важен и будет часто использоваться.
4.4. Собственные векторы ковариационной матрицы
Как следует из
4.2, случайный вектор X
с m
компонентами имеет квадратную и
симметричную относительно главной
диагонали ковариационную матрицу
K порядка m.
Вектор Z
и переменная
![]() называются собственным вектором и
называются собственным вектором и
собственным значением матрицы, если
они удовлетворяют равенству
![]() ,
,
(4.3)
из которого следует,
что умножение собственного вектора
слева на матрицу K
изменяет его модуль, но не изменяет
направления.
Перепишем приведенное
равенство в виде однородной системы
линейных уравнений
![]() (4.4)
(4.4)
Здесь E
– единичная матрица порядка m.
Отличное от нуля решение этой системы
существует только тогда, когда определитель
системы равен нулю.

Это уравнение
степени m
относительно неизвестной
![]() .
.
Оно называется характеристическим
уравнением матрицы. Доказано, что если
матрица вещественна и симметрична, то
все ееm
корней
![]() – вещественны и различны. Подстановка
– вещественны и различны. Подстановка
собственных значений матрицы в исходную
систему уравнений (4.4) дает возможность
определить собственные векторы![]()
Собственные векторы
ортогональны, то есть
![]()
Для доказательства
этого важного свойства составим
произведение
![]() и раскроем его двумя различными способами,
и раскроем его двумя различными способами,
используя равенство (4.3). Во-первых,
![]()
Во-вторых,
![]()
Поскольку
![]() ,
,
полученные выражения равны только при
условии ортогональности векторов![]() .
.
Система (4.4)
определяет лишь направление, но не длину
(модуль) собственных векторов. Действительно
вектор W=CZ,
отличающийся от собственного вектора
только длиной, также удовлетворяет
равенству (4.4).
![]() .
.
Поэтому будем
считать, что модуль каждого собственного
вектора равен единице
![]()
Образуем из векторов
Z
квадратную матрицу F
порядка m:
F![]()
 (4.5)
(4.5)
Как установлено,
столбцы этой матрицы, во-первых,
ортогональны, а во-вторых, нормированы.

Установим еще одно
свойство матрицы F. Умножим матрицу F
слева на матрицу F транспонированную и
раскроем произведение.

![]() Таким
Таким
образом, транспонирование матрицы F
одновременно является операцией
обращения:
![]()
В заключение, не
смотря на очевидность, подчеркнем, что
также как сама ковариационная матрица
случайного вектора, ее собственные
векторы и собственные значения неслучайны.
Соседние файлы в папке MD_DOC
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
Найти мат. ожидание
|
|
22/05/16 |
|
|
|
|
|
Otta |
Re: Найти мат. ожидание
|
||
09/05/13 |
dima_1985 Вы бы обозначение для транспонированной матрицы путем написали, а?
|
||
|
|
|||
|
zykov |
Re: Найти мат. ожидание
|
|
18/09/21 |
|
|
|
|
|
Otta |
Re: Найти мат. ожидание
|
||
09/05/13 |
zykov Обычно оно зависит от Впрочем, это дело ТС.
|
||
|
|
|||
|
zykov |
Re: Найти мат. ожидание
|
|
18/09/21 |
Otta Да, эксперимент был для
|
|
|
|
|
dima_1985 |
Re: Найти мат. ожидание
|
|
22/05/16 |
|
|
|
|
|
Otta |
Re: Найти мат. ожидание
|
||
09/05/13 |
Почитайте про пфаффиан, хоть и в википедии. Раскрывать скобки, считая квадрат суммы – не лучший ход. Особенно в общем случае. Проще посчитать распределение
|
||
|
|
|||
|
Евгений Машеров |
Re: Найти мат. ожидание
|
||
11/03/08 |
Элементы матрицы A были независимыми, элементы матрицы C – нет.
|
||
|
|
|||
|
Otta |
Re: Найти мат. ожидание
|
||
09/05/13 |
Элементы матрицы A были независимыми, элементы матрицы C – нет. А независимость всех и не нужна.
|
||
|
|
|||
|
Евгений Машеров |
Re: Найти мат. ожидание
|
||
11/03/08 |
Я о первоначальном рассуждении ТС.
|
||
|
|
|||
|
ihq.pl |
Re: Найти мат. ожидание
|
|
18/05/15 |
dima_1985 , а если воспользоваться определением определителя через перестановки?
|
|
|
|
|
dima_1985 |
Re: Найти мат. ожидание
|
|
22/05/16 |
|
|
|
|
|
Otta |
Re: Найти мат. ожидание
|
||
09/05/13 |
|||
|
|
|||
|
dima_1985 |
Re: Найти мат. ожидание
|
|
22/05/16 |
В общем виде получим
|
|
|
|
|
svv |
Re: Найти мат. ожидание
|
||
23/07/08 |
|||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Макеты страниц
Математическое ожидание  случайной величины X с ф. p. F определяется равенством
случайной величины X с ф. p. F определяется равенством

Говорят, что математическое ожидание  существует в том и только в том случае, когда существует интеграл в (1). Математическое ожидание
существует в том и только в том случае, когда существует интеграл в (1). Математическое ожидание  случайной величины X называют также средним значением (или просто средним) случайной величины
случайной величины X называют также средним значением (или просто средним) случайной величины 
Более общим образом, предположим, что  случайный вектор с ф. p. F, и пусть
случайный вектор с ф. p. F, и пусть  интегрируемая функция от
интегрируемая функция от  Математическое ожидание
Математическое ожидание  определяется соотношением
определяется соотношением

Это определение математического ожидания корректно в силу следующего обстоятельства: если  — случайная величина, задаваемая равенством
— случайная величина, задаваемая равенством  и
и  ее ф. р., то интеграл в (2) равен интегралу
ее ф. р., то интеграл в (2) равен интегралу

Для всякой случайной величины X и всякого натурального числа  среднее
среднее  называется
называется  моментом
моментом  Моменты
Моменты  относительно среднего значения называются центральными моментами
относительно среднего значения называются центральными моментами  Конечно, для некоторых случайных величин существуют не все эти математические ожидания.
Конечно, для некоторых случайных величин существуют не все эти математические ожидания.
В частности, дисперсия  случайной величины X — это второй центральный момент, определяемый соотношением
случайной величины X — это второй центральный момент, определяемый соотношением

Стандартным отклонением называют квадратный корень из  Если
Если  то коэффициентом вариации X называют отношение
то коэффициентом вариации X называют отношение

Для любых двух случайных величин  их ковариация
их ковариация  определяется следующим образом:
определяется следующим образом:

В частности,  Коэффициентом корреляции между
Коэффициентом корреляции между  называется отношение
называется отношение

Если величина (7) равна, нулю, то говорят, что  некоррелированы.
некоррелированы.
Рассмотрим матрицу

в которой каждый элемент  неслучайная величина. Среднее
неслучайная величина. Среднее  матрицы
матрицы  определяется как матрица, элементы которой равны математическим ожиданиям соответствующих элементов матрицы
определяется как матрица, элементы которой равны математическим ожиданиям соответствующих элементов матрицы  Итак,
Итак,

В частности, для всякого случайного вектора  вектор средних
вектор средних  есть
есть

Матрицей ковариаций (или ковариационной матрицей)  вектора X называется симметрическая
вектора X называется симметрическая  -матрица,
-матрица,  компонента которой равна
компонента которой равна  т. е.
т. е.

Пусть  случайный вектор с вектором средних
случайный вектор с вектором средних  и ковариационной матрицей 2. Пусть, далее, случайный вектор
и ковариационной матрицей 2. Пусть, далее, случайный вектор  определен как
определен как  где А — постоянная
где А — постоянная  -матрица, т. е. матрица с постоянными (неслучайными) элементами,
-матрица, т. е. матрица с постоянными (неслучайными) элементами,  постоянный
постоянный  -мерный вектор. Тогда
-мерный вектор. Тогда  .
.
В частности, дисперсия всякой линейной комбинации  есть
есть  Таким образом, всякая ковариационная матрица 2 неотрицательно определена. Более того, 2 положительно определена, если только дисперсия хотя бы одной линейной комбинации
Таким образом, всякая ковариационная матрица 2 неотрицательно определена. Более того, 2 положительно определена, если только дисперсия хотя бы одной линейной комбинации  а
а  отлична от нуля.
отлична от нуля.
Два следующих важных свойства математических ожиданий таковы. Для любого множества случайных величин  с конечными средними
с конечными средними

Если случайные величины  независимы, то
независимы, то

Характеристические функции и производящие функции моментов. Характеристической функцией (сокращенно х. ф.) случайной величины X называется комплексная функция заданная для каждого  равенством
равенством

X. ф. существует для любой случайной величины, и никакие два различных распределения не имеют одной и той же х. ф. Таким образом, между  существует взаимно однозначное соответствие.
существует взаимно однозначное соответствие.
Вот некоторые из важнейших свойств х. ф. Если  к независимых случайных величин с х. ф. соответственно и случайная величина
к независимых случайных величин с х. ф. соответственно и случайная величина  определена как
определена как

то х. ф.  величины
величины  задается формулой
задается формулой

Если для случайной величины X с х. ф.  существует момент
существует момент  для некоторого натурального
для некоторого натурального  то этот момент может быть найден из равенства
то этот момент может быть найден из равенства

где  обозначает производную функции
обозначает производную функции  порядка
порядка  вычисленную в точке t = 0.
вычисленную в точке t = 0.
X. ф. случайного  -мерного вектора
-мерного вектора  это комплексная функция принимающая в точке
это комплексная функция принимающая в точке  значение
значение

Свойства х. ф.  -мерного случайного вектора аналогичны указанным свойствам х. ф. случайной величины. В частности, если у случайного вектора
-мерного случайного вектора аналогичны указанным свойствам х. ф. случайной величины. В частности, если у случайного вектора  существует математическое ожидание
существует математическое ожидание  для некоторого набора натуральных чисел
для некоторого набора натуральных чисел  то оно может быть вычислено по формуле
то оно может быть вычислено по формуле

Другое полезное свойство х. ф. может быть сформулировано следующим образом. Пусть  случайный вектор с х. ф. А — постоянная
случайный вектор с х. ф. А — постоянная  -матрица,
-матрица,  постоянный
постоянный  -мерный вектор и
-мерный вектор и  случайный вектор, определенный равенством
случайный вектор, определенный равенством  Тогда
Тогда  вектора
вектора  удовлетворяет соотношению
удовлетворяет соотношению

Производящей функцией моментов случайной величины X называется вещественная функция  задаваемая формулой
задаваемая формулой

Отсюда видно, что производящая функция моментов определена для любого вещественного  для которого конечно математическое ожидание!) в (20). Иногда предпочтительнее рассматривать производящие функции моментов, нежели характеристические функции, поскольку первые вещественны, а вторые комплексны. Недостатком же производящих функций является то, что для некоторых случайных величин производящие функции моментов конечны не для всех значений
для которого конечно математическое ожидание!) в (20). Иногда предпочтительнее рассматривать производящие функции моментов, нежели характеристические функции, поскольку первые вещественны, а вторые комплексны. Недостатком же производящих функций является то, что для некоторых случайных величин производящие функции моментов конечны не для всех значений  Однако если производящая функция моментов случайной величины X конечна для всех значений
Однако если производящая функция моментов случайной величины X конечна для всех значений  из некоторого интервала, содержащего внутри себя точку
из некоторого интервала, содержащего внутри себя точку  то существуют все моменты
то существуют все моменты  и их значения могут быть определены посредством дифференцирования производящей функции моментов в точке
и их значения могут быть определены посредством дифференцирования производящей функции моментов в точке 
Аналогично вводятся и многомерные производящие функции моментов, причем справедливы равенства типа (15) и (18).
 🙂
🙂 .
. .
. .
.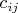 .
.![$E[det(A-A^T)]=(2n-1)!!(2p)^n(1-p)^n$ $E[det(A-A^T)]=(2n-1)!!(2p)^n(1-p)^n$](https://dxdy-04.korotkov.co.uk/f/7/6/d/76d9ae8c9c1b725338e9734ec79a762482.png)
