2013_2014
учебный год II
семестр Лекция № 2.6
стр.
12
Деформация балок при изгибе.
Дифференциальное уравнение изогнутой
оси балки. Метод начальных параметров.
Универсальное уравнение упругой линии.
6.1. Основные понятия и определения
Р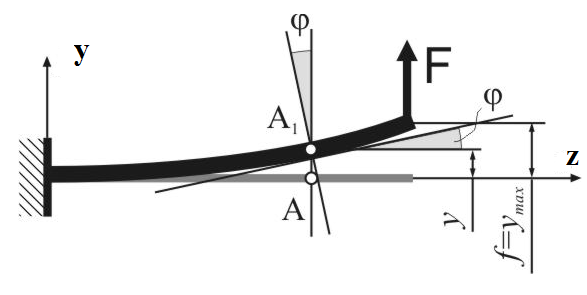 ассмотрим
ассмотрим
деформацию балки при плоском изгибе.
Ось балки под действием нагрузки
искривляется в плоскости действия сил
(плоскость x0y),
при этом поперечные сечения поворачиваются
и смещаются на некоторую величину.
Искривленная ось балки при изгибе
называется изогнутой
осью или
упругой
линией.
Деформацию балок
при изгибе будем описывать двумя
параметрами:
-
прогиб (y)
– смещение центра тяжести сечения
балки по направлению, перпендикулярному
рис. 6.1
к ее оси.
Не путать прогиб
y с
координатой y
точек сечения
балки!
Наибольший прогиб
балки называется стрелой прогиба (f
= ymax);
2) угол
поворота сечения ()
– угол, на который сечение поворачивается
относительно своего первоначального
положения (или угол между касательной
к упругой линии и первоначальной осью
балки).
В общем случае
величина прогиба балки в данной точке
является функцией координаты z
и может быть
записана в виде следующего уравнения:
y = y(z)
Тогда угол между
касательной к изогнутой оси балки и
осью x будет
определяться из следующего выражения:
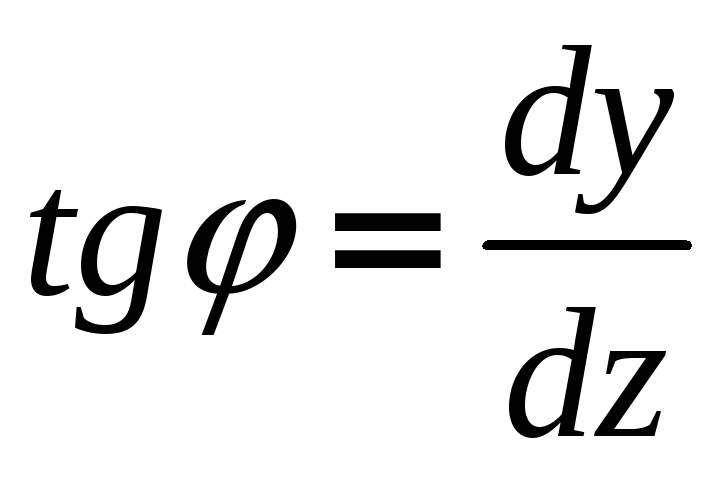 .
.
Ввиду малости
углов и перемещений, можем считать, что
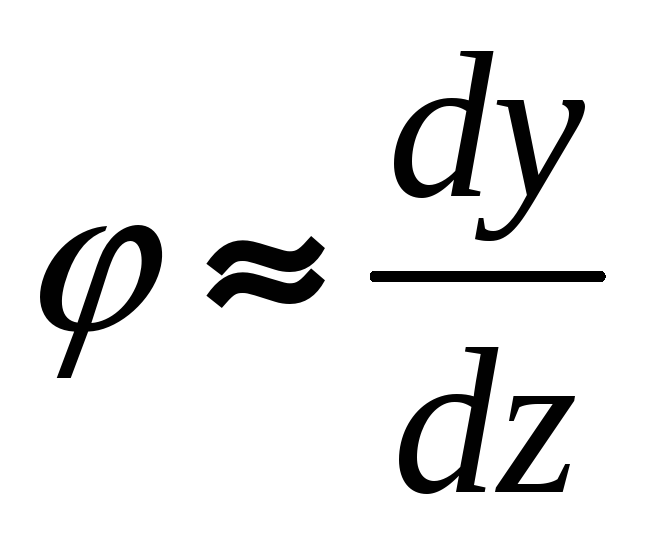
угол поворота
сечения есть первая производная от
прогиба балки по абсциссе сечения.
6.2. Дифференциальное уравнение изогнутой оси балки
Исходя из физической
природы явления изгиба, можем утверждать,
что изогнутая ось непрерывной балки
должна быть непрерывной и гладкой
(неимеющей изломов) кривой. При этом
деформация того или иного участка балки
определяется искривлением его упругой
линии, то есть кривизной оси балки.
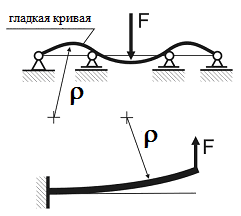
рис. 6.2
Ранее нами была
получена формула для определения
кривизны бруса (1/ρ)
при изгибе
 .
.
С другой стороны,
из курса высшей математики известно,
что уравнение кривизны плоской кривой
выглядит следующим образом:
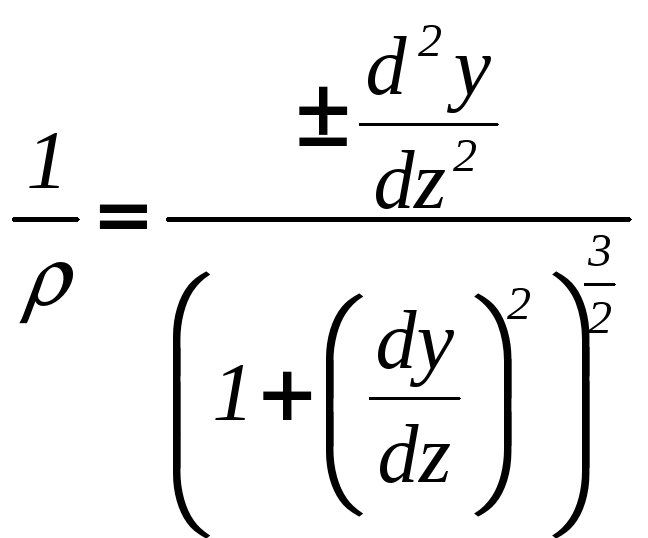 .
.
Приравняв правые
части данных выражений, получим
дифференциальное уравнение изогнутой
оси балки, которое называется точным
уравнением изогнутой оси бруса
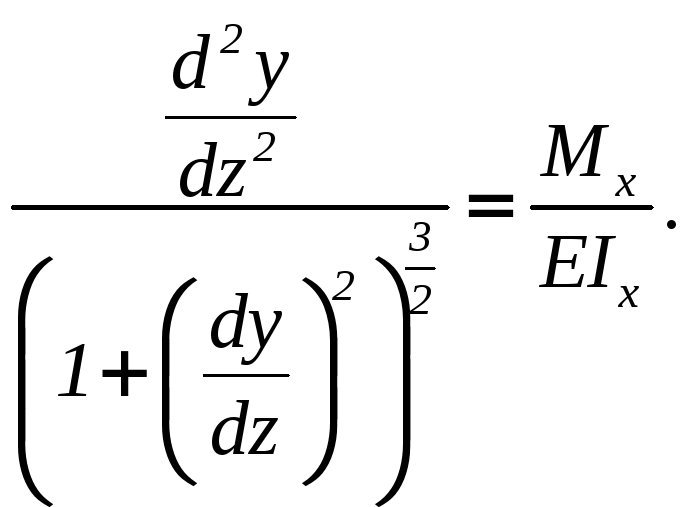
В координатной
системе прогибов z0y,
когда ось y
направлена
вверх, знак момента определяет знак
второй производной от y
по z.
Интегрирование
данного уравнения, очевидно, представляет
некоторые трудности. Поэтому его, как
правило, записывают в упрощенной форме,
пренебрегая величиной в скобках по
сравнению с единицей.
Тогда дифференциальное
уравнение упругой линии балки будем
рассматривать в виде:
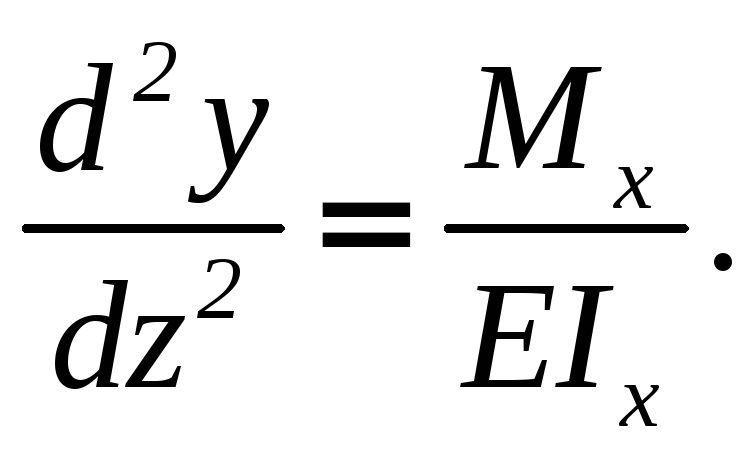 (6.1)
(6.1)
Решение
дифференциального уравнения (6.1) найдем,
интегрируя обе его части по переменной
z:
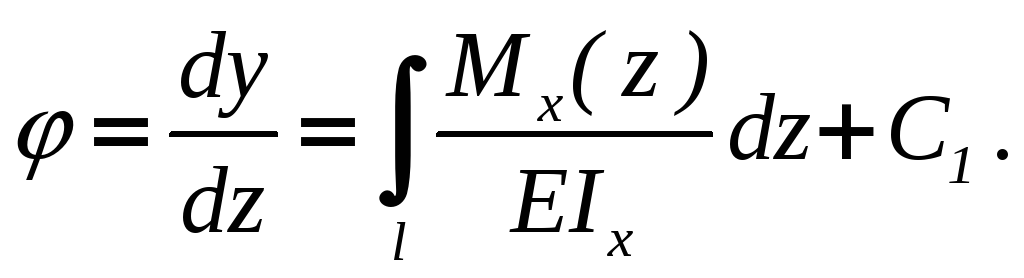 (6.2)
(6.2)
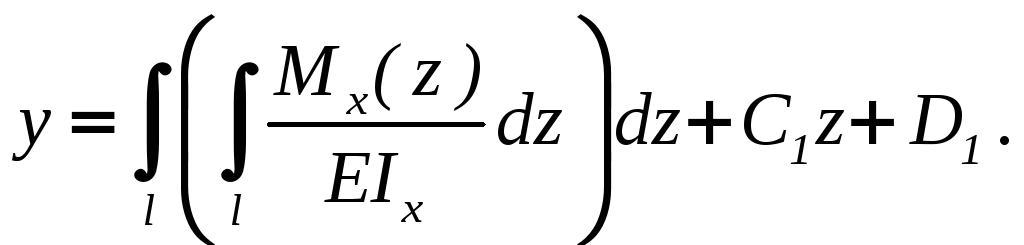 (6.3)
(6.3)
Постоянные
интегрирования C1,
D1
находят из граничных условий – условий
закрепления балки, при этом для каждого
участка балки будут определяться свои
постоянные.
Рассмотрим процедуру
решения данных уравнений на конкретном
примере.
Д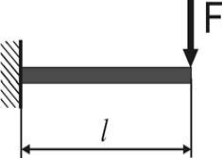 ано:
ано:
Консольная балка
длиной l,
загруженная поперечной силой F.
Материал балки (E),
форму и размеры ее сечения (Ix)
также считаем известными.
О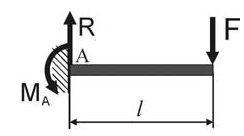 пределить
пределить
закон
изменения угла поворота (z)
и прогиба y(z)
балки по ее длине и их значения в
характерных сечениях.
Решение
а) определим реакции
в заделке
![]()
![]()
 б)
б)
методом сечений определим внутренний
изгибающий момент:
![]()
в) определим угол
поворота сечений балки
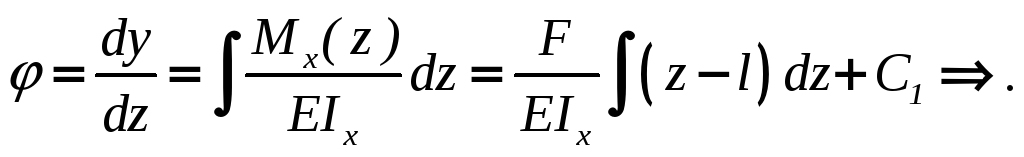
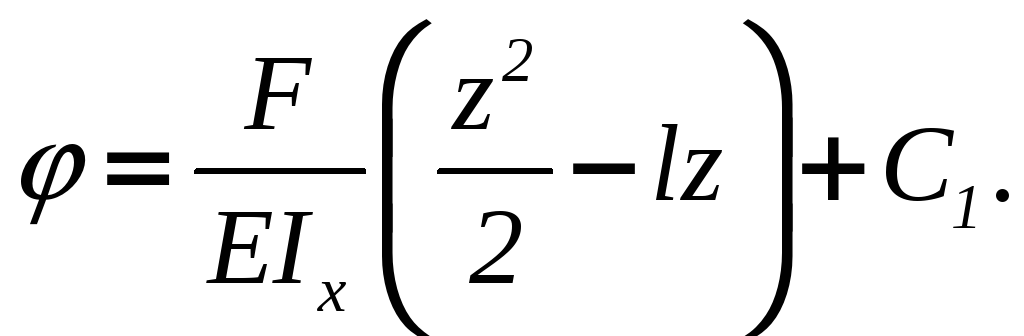
Постоянную C1
найдем из условий закрепления, а именно
– в жесткой заделке угол поворота равен
нулю, тогда
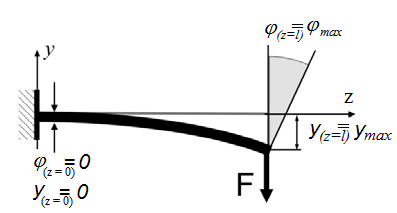 (0)
(0)
= 0
C1=0.
Найдем угол поворота
свободного конца балки (z
= l)
:
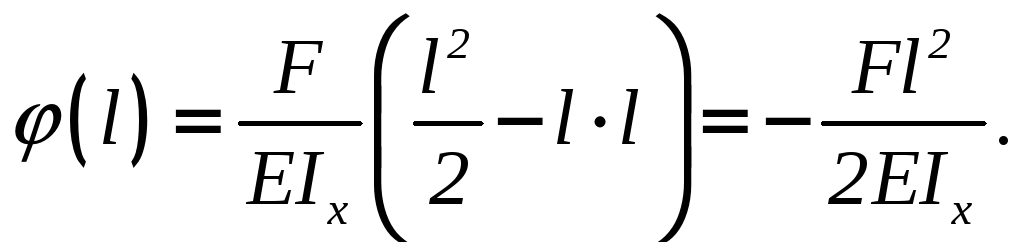
Знак «минус»
показывает, что сечение повернулось по
часовой стрелке.
г) определим прогибы
балки:
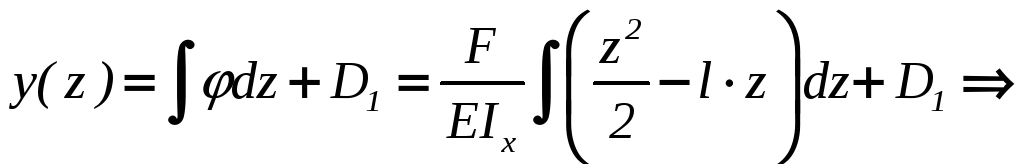
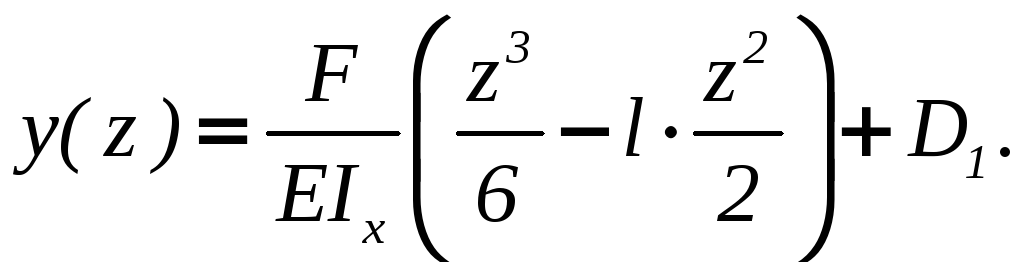
Постоянную D1
найдем из
условий закрепления, а именно – в жесткой
заделке прогиб равен нулю, тогда
y(0) = 0
+ D1
D1
=
0
Найдем прогиб
свободного конца балки (x
= l)
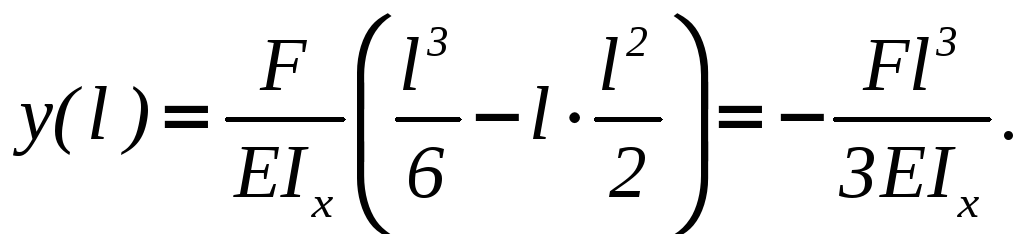 .
.
Знак «минус»
показывает, что сечение опустилось
вниз.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Деформация балки при изгибе проявляется в искривлении ее продольной оси.
Рассмотрим это на примере простой консольной балки, нагруженной изгибающим моментом m.
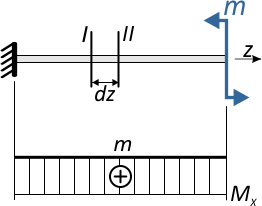
Мысленно вырежем из балки фрагмент длиной dz.
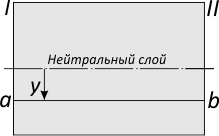
на котором отметим нейтральный слой и отрезок ab соединяющий сечения I-II и равноудаленный от нейтрального слоя на расстояние y.
От действия изгибающего момента данный фрагмент изогнется вместе с балкой
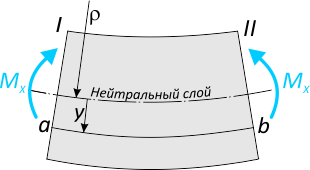
Кривизна рассматриваемого фрагмента балки определяется как
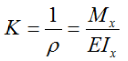
где
ρ – радиус кривизны изогнутой оси балки в данном сечении;
Mx — изгибающий момент в сечении;
E – модуль Юнга материала балки;
Ix — осевой момент инерции поперечного сечения.
Вследствие деформации, поперечные сечения балки, на всех участках, где есть изгибающий момент, повернутся относительно нейтральной оси (линии) на некоторый угол.
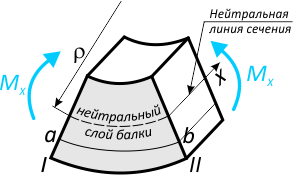
Из-за этого, все слои балки кроме нейтрального будут растягиваться или сжиматься.
В данном примере верхние слои балки сжаты, нижние – растянуты.
Относительное удлинение отрезка (слоя) ab
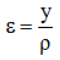
В общем случае нагружения искривление продольной оси упругой линии балки описывается дифференциальным уравнением следующего вида
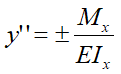
непосредственное интегрирование которого позволяет рассчитывать угловые и линейные перемещения сечений балки при изгибе.
Примеры решения задач >
Лекции по сопромату >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
В этом уроке будем учиться строить эпюры для балок, работающих на поперечный изгиб — эпюры поперечных сил и изгибающих моментов. Важно уметь правильно построить и проанализировать эти эпюры, потому что большинство современных инженерных сооружений состоят из элементов, которые работают на изгиб.
В статье рассмотрим 2 примера: один попроще — консольная балка, загруженная сосредоточенными силами и моментом, другой посложнее — двухопорная балка, загруженная распределённой нагрузкой.
Чтобы освоить материал этого урока, уже нужно знать, как определяются опорные реакции. Умеешь — отлично, но если же нет, то можешь изучить этот урок.
Подробно рассматривать в этом уроке нахождения реакций не будем, я буду приводить только их расчёт.
Поперечные силы и изгибающие моменты
При поперечном изгибе, в поперечных сечениях балки, возникает два внутренних силовых фактора (ВСФ) – поперечная сила (Q) и изгибающий момент (Mизг).


Наша задача, научиться определять их и строить эпюры. Чтобы потом, используя полученные эпюры, можно было проводить различные расчёты. Например, подбирать размеры поперечных сечений балки или проверять прочность балки, если эти размеры уже заданы и т. д.
Поперечные силы и изгибающие моменты определяются с помощью метода сечений. Когда балка мысленно рассекается на две части. Затем действие частей балки друг на друга заменяется внутренними силовыми факторами (ВСФ) – поперечными силами и изгибающими моментами. Потом путём рассмотрения равновесия одной из частей находятся ВСФ.
Если пока не очень понятно — это нормально, когда начнём это всё делать на практике, ты обязательно всё поймёшь!
Обозначения поперечных сил и изгибающих моментов
Теперь поговорим по поводу обозначений для поперечных сил и изгибающих моментов. Как правило, задачи в сопромате, и механике в целом, решаются относительно каких-то координатных осей. А поперечные силы и изгибающие моменты, имеют индексы в зависимости от выбранной системы координат.
Например, если выбрать следующие обозначения для координатных осей:

То, поперечная сила, будет обозначаться, как Qy (параллельна оси y), а изгибающий момент, как Mx (поворачивает относительно оси x). Это наиболее частый вариант. Однако, можно встретить обозначения – Qy, Mz или Qz, Mx. Самые ленивые, предпочитают подписывать данные величины, как просто Q и M. Как видишь, здесь всё зависит от предпочтений твоего преподавателя. Чтобы изучая этот урок, ты не привыкал (- а) к каким-то индексам, т. к. твой преподаватель тебя всё равно будет учить по-своему, я решил использовать в статье для поперечной силы, просто букву – Q, а для изгибающего момента – Mизг. Такое обозначение изгибающего момента, тоже используется часто, а сам индекс «изг» нужен, чтобы не путать внутренний – изгибающий момент, с внешними моментами, которые почти всегда подписываются просто буквой – M.
Расчётная схема балки
Также нужно понимать, что когда мы рассчитываем поперечные силы и изгибающие моменты, мы считаем их непросто для какой-то линии:

А подразумеваем, что мы рассчитываем некоторый элемент конструкции — балку, которая обязательно имеет некоторую форму, либо для которой впоследствии будет рассчитана эта форма, в зависимости от целей расчёта.
К примеру, балка может иметь прямоугольное поперечное сечение:

Если в расчётах эпюр при растяжении (сжатии) или кручении, форма стержня указывалась явно, и в этом был определённый смысл, так как те стержня имели ступенчатую форму – разную жёсткость на участках. То здесь, как правило, балки имеют одинаковое сечение, по всей длине, поэтому для экономии времени, балку показывают в виде такой линии. Затем, после построения эпюр, традиционно, для балки либо подбирается поперечное сечение из условия прочности, либо проверяется прочность уже заданного сечения.
Правила знаков для поперечных сил и изгибающих моментов
В этом разделе поговорим о правилах знаков для поперечных сил и изгибающих моментов. Для примера возьмём самую простую расчётную схему — консольную балку, загруженную сосредоточенной силой (F).
Расчётная схема

Предположим, что нужно определить поперечную силу и изгибающий момент в каком-то поперечном сечении. Пока не будем строить никаких эпюр, а просто поставим перед собой простейшую задачу — рассчитать внутренние силовые факторы (Q и Мизг) для одного, конкретного сечения. Например, рассмотрим сечение в заделке (А).
Чтобы вычислить внутренние силовые факторы для этого сечения, нужно учесть всю внешнюю нагрузку, либо справа от сечения, либо слева. Если учитывать нагрузку справа — нужно учесть силу F, а если учитывать нагрузку слева — нужно учесть тогда реакции в заделке. Чтобы не вычислять реакции, пойдём по короткому пути и учтём всю нагрузку — справа.
Правило знаков для поперечных сил
Поперечная сила в сечении будет равна алгебраической сумме всех внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
А знаки внешних сил определяются следующим образом — если внешняя сила, относительно рассматриваемого сечения, стремится повернуть:
• ПО часовой стрелке, то её нужно учесть с «плюсом»;

• ПРОТИВ часовой стрелки — учитываем её с «минусом».

Таким образом, для нашего случая, поперечная сила в сечении A будет равна:
Правило знаков для изгибающих моментов
Изгибающий момент в сечении будет равен алгебраической сумме всех моментов внешних сил (с учётом знака) по одну сторону от рассматриваемого сечения.
Перед тем как поговорить о правилах знаков для изгибающих моментов. Необходимо понять ещё одну особенность — когда на балку действует какая-то внешняя нагрузка, балка деформируется. При деформации балки принято различать «верхние волокна» и «нижние волокна», относительно линии (нейтральной оси), проходящей через центр тяжести поперечного сечения балки.

Одни волокна при поперечном изгибе, будут растягиваться, а другие сжиматься.

В нашем случае, «верхние волокна», как видишь, будут растянуты, а нижние – сжаты.
На основании этой особенности, часто используется следующее правило для изгибающих моментов — если момент силы стремится растянуть:
• верхние волокна, то учитываем его с «минусом»;

• нижние волокна, то нужно учесть его с «плюсом».

Не забываем, что мы ведём расчёт моментов, поэтому все силы нужно умножать на соответствующие плечи.
Таким образом, в нашем случае, изгибающий момент в сечении A будет равен:
Если на балку действуют сосредоточенные моменты, то правило знаков аналогичное:


Сосредоточенные моменты, конечно, уже не нужно ни на что умножать. Например, для верхней схемы, изгибающий момент в сечении A будет равен:
Как построить эпюры поперечных сил и изгибающих моментов ?
В пределах участков, и эпюра Q и эпюра M меняются по определённому закону. Границами участков являются точки приложения сил, моментов, а также начало и конец распределённой нагрузки (будем рассматривать во второй задаче). Поэтому, чтобы построить эпюры в пределах участка, сначала необходимо написать уравнения, которые будут описывать изменение поперечных сил и изгибающих моментов в пределах участка. А затем, подставляя в уравнения координаты начала и конца участка, получить значения на эпюрах в характерных точках, и построить эпюры на участке. Рассчитав таким образом все участки, можно построить эпюры для балки.
Чувствую, опять перегрузил тебя информацией…давай лучше, наконец, посмотрим, как это всё делается на практике 😉
Построение эпюр для консольной балки
В качестве первого примера, возьмём консольную балку, жёстко закреплённую с левого торца и загруженной следующим образом:

Будем рассчитывать балку справа налево.
Рассмотрим первый участок
Обозначим некоторое сечение 1-1 на расстоянии x1, от свободного торца балки, при этом x1 будет находиться в диапазоне: 0 ≤ x1 ≤ 4м.

Так как расчёт выполняется справа налево, то в уравнениях необходимо учесть всю нагрузку, которая находится правее рассматриваемого сечения. Как видишь, на этом участке действует всего лишь одна сила F. Её и будем учитывать.
Поперечные силы на первом участке
Сила F, относительно сечения 1-1, поворачивает ПО часовой стрелке, поэтому с учётом правила знаков, записываем её с «плюсом»:
Как видишь, поперечная сила будет постоянна на первом участке:
Уже можем отразить это на эпюре поперечных сил:

Изгибающие моменты на первом участке
Теперь запишем уравнение для изгибающих моментов. Сила F растягивает верхние волокна, поэтому с учётом правила знаков, нужно учесть момент силы F со знаком «минус»:
Здесь уже изгибающие моменты будут меняться по линейному закону. Как я уже писал, чтобы построить эпюру изгибающих моментов на участке, нужно вычислить значения на границах участка:

Откладываем полученные значения:

Расчёт второго участка
Переходим ко второму участку. Также будем рассматривать некоторое сечение 2-2, на расстоянии x2 от начала участка (0 ≤ x2 ≤ 6м). Здесь также нужно учесть ВСЮ нагрузку, которая находится справа от сечения 2-2.

Поперечные силы на втором участке
Теперь на участке будут действовать 2 силы (сосредоточенный момент — M, никак не влияет на эпюру поперечных сил), учитываем их с учётом правила знаков:
Теперь можем показать окончательную эпюру поперечных сил:

Изгибающие моменты на втором участке
Для изгибающих моментов, с учётом правила знаков, второе уравнение будет выглядеть следующим образом:
Вычисляем значения на границах второго участка:

Показываем окончательную эпюру изгибащих моментов:

Проверка построенных эпюр
Балку можно рассчитать и слева направо. При этом очевидно, должны получаться те же эпюры. Давай проверим себя и рассчитаем эту балку с другой стороны.
Определение реакций в жёсткой заделке
Первым делом, нам потребуется определить реакции в заделке:


Расчёт эпюр поперечных сил и изгибающих моментов
Рассчитываем все участки теперь слева направо:


Ожидаемо, получили те же эпюры поперечных сил и изгибающих моментов:

Причём не обязательно считать все участки балки только слева направо или справа налево. Можно считать балку с разных сторон:

Такой подход позволяет минимизировать расчёт: когда балка имеет много расчётных участков. Как раз так и будем считать вторую двухопорную балку.
Эпюра моментов со стороны растянутых или сжатых волокон
По построенной эпюре можно явно сказать, какие волокна балки будут растянуты, а какие сжаты. Это очень полезная информация, при проведении прочностных расчётов.
Причем сама эпюра была построенна со стороны растянутых волокон:

Однако, студентов некоторых специальностей учат строить эпюры, с другой стороны – со стороны сжатых волокон:

Как видишь, в первом случае, отрицательные значения на эпюре моментов откладываются выше нулевой линии, а во втором – ниже. При этом правила знаков для расчета эпюр и сами расчёты не меняются. Обычно эпюры «на растянутых волокнах» строят студенты — строители, а эпюры «на сжатых волокнах» строятся студентами машиностроительных специальностей. В конечном счёте с какой стороны ты будешь строить эпюры, будет зависеть от твоего преподавателя, как он учит. В своих уроках я буду строить эпюры моментов со стороны растянутых волокон.
Учёт распределённой нагрузки
Перед тем как пойдём дальше и рассмотрим вторую задачу – двухопорную балку, нужно научиться работать с распределённой нагрузкой.
Давай рассмотрим ещё одну простенькую схему — консольную балку, загруженную распределённой нагрузкой:

Определение поперечной силы и изгибающего момента в сечении A
Чтобы определить поперечную силу в сечении A, первым делом нужно «свернуть» распределённую нагрузку (q) до сосредоточенной силы. Для этого нужно интенсивность нагрузки (q) умножить на длину участка действия нагрузки.
После чего получим силу — ql, приложенную ровно посередине участка, на котором действует распределённая нагрузка:

Тогда поперечная сила QA будет равна:
Изгибающий момент Mизг, A будет равен:

Расчёт эпюр поперечных сил и изгибающих моментов
Для написания уравнений для расчёта эпюр рассмотрим сечение 1-1:

Уравнение для поперечных сил будет следующее:
Рассчитаем значения на эпюре поперечных сил:


Уравнение для изгибающих моментов будет следующее:

Тогда значения на эпюре будут такими:


На участке с распределённой нагрузкой, на эпюре изгибающих моментов всегда будет либо выпуклость, либо вогнутость. Так как эпюра на этом участке будет меняться по квадратичному закону.
Если эпюра моментов откладывается со стороны растянутых волокон, распределённая нагрузка будет направлена «внутрь вогнутости» (выпуклости) эпюры изгибающих моментов:

Если же эпюра моментов откладывается со стороны сжатых волокон, то наоборот:

Построение эпюр для двухопорной балки
А теперь давай рассмотрим более сложную схему – двухопорную балку, загруженную всеми типами нагрузок:

Определим реакции опор:


Рассчитываем первый участок:

Строим эпюры на первом участке:

Определение экстремума на эпюре моментов
Так как эпюра поперечных сил пересекает нулевую линию на первом участке, это значит, что в месте пересечения — на эпюре изгибающих моментов будет экстремум — точка, в которой эпюра моментов часто имеет наибольшее значение. Это значение, обязательно следует рассчитывать, потому — что экстремумы часто являются не только максимальными значениями в пределах участка, но и для всей балки в целом. Поэтому так важно, вычислять это значение, для дальнейшего проведения прочностных расчётов.
Чтобы найти экстремум, сначала нужно найти координату, где эпюра поперечных сил пересекает нулевую линию. Для этого уравнение для поперечных сил нужно приравнять к нулю:
Отсюда найти значение координаты:

Затем подставить это значение в уравнение для изгибающих моментов:

Теперь можем указать экстремум на эпюре:

Расчет эпюр на остальных участках
Расчёты остальных участков не вижу смысла комментировать, потому что здесь будет применяться всё то, о чём я уже рассказывал по ходу урока. Поэтому просто приведу решение:

Определение экстремума:


Оценка правильности построенных эпюр поперечных сил и изгибающих моментов
И напоследок хочу рассказать как можно проверить себя – оценить правильность построенных эпюр визуально. Собственно так, как проверяют эпюры — преподаватели, ведь они не проверяют у всех студентов каждое уравнение, каждый знак или цифру, т.к. это бы занимало слишком много времени.
Вот несколько признаков, правильно построенных эпюр:
- На эпюре поперечных сил, в местах приложения сосредоточенных сил, должны быть скачки на величину этих сил.
- На эпюре изгибающих моментов, в местах приложения сосредоточенных моментов, должны быть скачки на величину этих моментов.
- Эпюра поперечных сил, на участках без распределённой нагрузки, должна быть постоянна. А на участках, где действует распределённая нагрузка – меняться по линейному закону.
- Эпюра изгибающих моментов, на участках без распределённой нагрузки, должна меняться по линейному закону или быть постоянна (если действуют только сосредоточенные моменты). А на участках, где действует распределённая нагрузка – иметь вогнутость или выпуклость.
Универсальное уравнение оси изогнутой балки, вычисление прогибов и углов поворота поперечных сечений

Определение прогибов и углов поворота поперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)
Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):
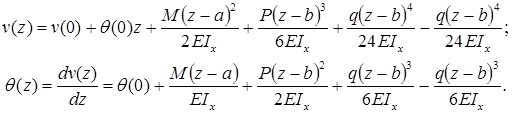
a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.
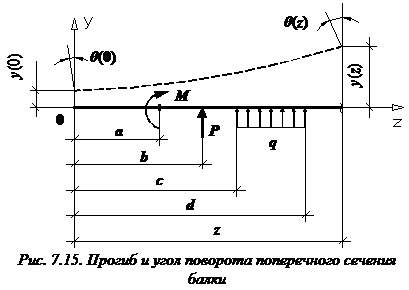
В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.
Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.
Прогиб 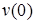 и угол поворота
и угол поворота 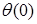 балки в начале координат (начальные параметры) определяются из условий закрепления балки.
балки в начале координат (начальные параметры) определяются из условий закрепления балки.
Уравнение упругой линии балки на примере

Определим прогиб балки на консоли при 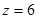 м, то есть
м, то есть 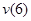 . Запишем универсальное уравнение упругой линии балки :
. Запишем универсальное уравнение упругой линии балки :
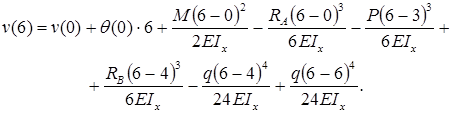
Прогиб балки в начале координат (на левой шарнирной опоре), равен нулю: 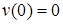 .
.
Для определения угла поворота в начале координат необходимо составить дополнительное условие: прогиб на правой опоре равен нулю.
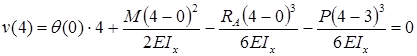 ,
,
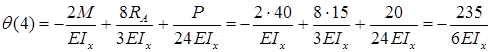 .
.
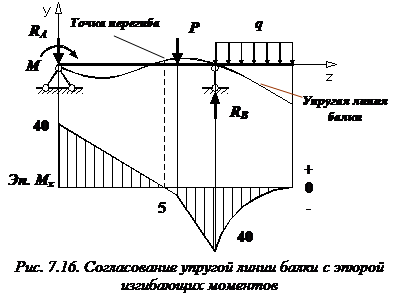
Прогиб консоли при z=6м:
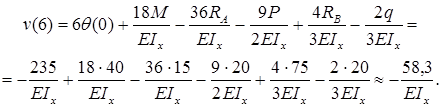
Знак «минус» говорит: прогиб балки на консоли происходит вниз. Число, стоящее в числителе, измеряется в килоньютонах на метр в кубе (кН·м3).
Примерный вид упругой линии балки показан на рис. 7.16.
Упругая линия балки должна быть согласована с эпюрой изгибающих моментов по дифференциальным зависимостям. Точка перегиба находится под сечением балки, в котором изгибающий момент равен нулю, что следует из закона Гука при изгибе.
Экспериментальное определение деформаций при прямом изгибе

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАМЫШИНСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)
ВОЛГОГРАДСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО УНИВЕРСИТЕТА
КАФЕДРА «ОБЩЕТЕХНИЧЕСКИЕ ДИСЦИПЛИНЫ»
ДЕФОРМАЦИЙ ПРИ ПРЯМОМ ИЗГИБЕ
по дисциплине «Сопротивление материалов»
Экспериментальное определение деформаций при прямом изгибе: Методические указания к лабораторной работе № 7 по дисциплине «Сопротивление материалов» / Сост. , ; ; Волгоград. гос. техн. ун-т. – Волгоград, 2007. – 15 с.
Содержат краткую теорию, сведения об используемых в работе оборудовании, приборах и образце, порядок проведения работы и форму отчета, а также перечень контрольных вопросов.
Предназначены в помощь студентам, обучающимся по направлениям 140200.
Ил. 7. Табл. 2. Библиогр.: 4 назв.
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
© Волгоградский государственный
 технический
технический
ЛАБОРАТОРНАЯ РАБОТА № 7
Тема: Определение деформаций при прямом изгибе.
Цель работы: Определить теоретическим и экспериментальным путем линейные и угловые перемещения в заданных сечениях балки и сравнить полученные результаты.
Время проведения: 2 часа.
1. краткие Теоретические сведения
При прямом изгибе в отличие от других видов простого сопротивления (растяжение, сжатие, кручение) продольная ось балки искривляется, превращаясь в плоскую кривую, расположенную в силовой плоскости.
Центры тяжести поперечных сечений балки перемещаются вдоль силовой линии, т. е. линии, перпендикулярной нейтральной оси.

Поперечные сечения балки в результате деформации поворачиваются вокруг нейтральной оси, оставаясь плоскими и перпендикулярными деформированной оси балки (рис. 1).
Плоская кривая, форму которой приобретает продольная ось балки в результате деформации, называется изогнутой осью или упругой линией балки.
При изгибе различают два вида перемещений (рис. 1).
1. Линейное перемещение (прогиб) у(z) – это перемещение центра тяжести сечения балки в направлении перпендикулярном ее недеформированной оси; считается положительным, если происходит вверх, и отрицательным – если вниз, измеряется в мм.
Наибольшее линейное перемещение балки называется стрелой прогиба и обозначается буквой f.
2. Угловое перемещение (угол поворота) φ(z) – это угол, на который поперечное сечение балки поворачивается по отношению к своему первоначальному положению.

Угол поворота считается положительным, если поворот сечения происходит против часовой стрелки и отрицательным, если – по часовой, измеряется в радианах или градусах.
Для проведения перпендикуляра к изогнутой оси в данной точке необходимо провести к ней касательную в этой точке и восстановить из нее перпендикуляр.
Очевидно, что угол φ между поперечными сечениями до и после деформации и угол между недеформированной осью и касательной к изогнутой оси равны, как углы с взаимно перпендикулярными сторонами (рис. 2).
Изогнутая ось балки является графиком, отражающим зависимость прогиба у от текущей координаты z балки:
Первая производная от функции по данному значению аргумента есть тангенс угла наклона касательной к графику функции, в точке, абсцисса которой равна данному значению аргумента.
 . (2)
. (2)
Так как упругие деформации балки весьма малы, а тангенсы малых углов приблизительно равны самим углам, то можно записать:
 . (3)
. (3)
Таким образом, мы получили дифференциальную зависимость между углом поворота φ и прогибом у для одного и того же сечения балки: угол поворота поперечного сечения балки есть первая производная от линейного перемещения центра тяжести его сечения по абсциссе этого сечения.
 Существует несколько методов определения величины перемещений при изгибе. В данной работе предлагается использовать универсальное уравнение упругой линии балки. Так как для нагружения балки будем использовать сосредоточенную силу, то приведем упрощенную форму дифференциальных уравнений для балки, изображенной на рис. 3:
Существует несколько методов определения величины перемещений при изгибе. В данной работе предлагается использовать универсальное уравнение упругой линии балки. Так как для нагружения балки будем использовать сосредоточенную силу, то приведем упрощенную форму дифференциальных уравнений для балки, изображенной на рис. 3:
для определения угла поворота φ:
 , (4)
, (4)
 , (5)
, (5)
φ0 – ‘это угол поворота поперечного сечения в начале координат, будет определяться следующим соотношением:
 ; (6)
; (6)
Ix – осевой момент инерции поперечного сечения балки относительно нейтральной оси;
z – расстояние от левого конца балки (начала координат) до сечения, в котором определяется перемещение;
F – величины сосредоточенных сил, расположенных слева от рассматриваемого сечения;
b – расстояние от начала координат до точки приложения силы;
(z – а) – расстояние от рассматриваемой нагрузки до сечения, в котором определяется перемещение;
Знак перед слагаемым, содержащим нагрузку, выбирается в соответствии со знаком изгибающего момента, который вызывает эта нагрузка в сечении, где определяем перемещения.
Так как все силы расположены слева от рассматриваемого сечения, то силы, направленные вверх, будем брать со знаком «плюс»; а вниз – со знаком «минус». Угол поворота φ0 крайнего левого сечения балки определяется из условия равенства нулю прогиба на правой опоре балки.
Следует помнить, что универсальное уравнение справедливо только в упругой стадии работы балки.
Поэтому до проведения испытания необходимо вычислить наибольшую допустимую нагрузку в области упругой деформации и не превышать ее значение при проведении испытания.
2. Краткие сведения об оборудовании,
измерительных приборах и образце
Опытное определение перемещений производится на настольной лабораторной установке СМ-7, схема которой показана на рис. 4.
Основным элементом установки является стальная балка прямоугольного поперечного сечения и длиной 100 см, опирающаяся на две шарнирные опоры. Одну из опор можно передвигать вдоль балки, получая при этом различные варианты расчетной схемы. Нагрузка в виде сосредоточенной силы передается в любом месте балки через подвижные подвесы.

Рис. 4. Общий вид установки:
1 – образец балки; 2 – шарнирно-подвижная опора; 3 – шарнирно-неподвижная опора;
4 – передвижной подвес для груза; 5 – стойка с индикатором часового типа для замеров прогибов; 6 – стержень для измерения угла поворота сечения; 7 – индикатор часового типа; 8 – станина; 9 – регулировочные винты.
Линейные перемещения (прогибы) замеряются с помощью индикатора часового типа (рис. 5), установленного на передвижной стойке.
Шток индикатора упирается в балку и при ее деформации перемещается вместе с ней. При этом величина перемещения фиксируется в зависимости от направления вращения стрелки. Поворот стрелки на одно деление (цена деления) соответствует перемещению штока на 0,01 мм, а полный оборот стрелки – на 1 мм.
Количество полных оборотов большой стрелки регистрируется на малой шкале.
Для определения углов поворота опорных сечений балка оборудована специальным стержнем, жестко прикрепленным к ней и поворачивающимся вместе с балкой при ее деформации на тот же угол (рис. 6):
 (рад).
(рад).


1 – подвижный шток;
2 – большая шкала (100 делений);
3 – малая шкала (10 делений)
r – длина стержня, (мм)
с – отсчет по индикатору, (мм)
3.1. Подготовка к эксперименту
1. Записать тему и цель работы, данные об образце и оборудовании.
2. Вычислить геометрические характеристики поперечного сечения балки.
3. Из табл. 1 перечертить в отчет вариант расчетной схемы по заданию преподавателя.
4. Вычислить допускаемую нагрузку F.
5. По указанию преподавателя принять ступень нагружения ΔF. При этом должно быть не менее трех ступеней нагружения, в
сумме не превышающих допускаемую нагрузку.
6. Вычислить теоретические значения перемещений (линейного и углового) в заданных сечениях балки на ступень нагружения ΔF, используя универсальное уравнение упругой линии балки.




3.2. Экспериментальная часть
1. Установить опоры, подвесы для нагрузки и индикаторы для замера перемещений в соответствии с заданной расчетной схемой.
2. Стрелки индикаторов установить на «0» путем поворота шкалы относительно корпуса.
3. Положить груз, равный принятой ступени нагружения на подвес, снять показания индикаторов и записать их в таблицу.
4. Добавить еще один груз и снова снять отсчеты по индикаторам, нарастающим итогом. То же для последующих нагружений. Данные занести в таблицу 2 отчета.
3.3. Обработка опытных данных
1. Вычислить приращения отсчетов – Δn индикаторов 1 и 2 на
каждую ступень нагружения по формуле:
где ni+1 – последующее показание индикатора (например, второе);
ni – предыдущее показание индикатора (например, первое).
2. Вычислить среднее значение приращений индикаторов по формуле:
 ,
,
где i – число приращений.
3. Вычислить величину прогиба yк на ступень нагружения по формуле:
4. Вычислить угол поворота по формуле:
 ,
,
r – длина стержня (см. рис. 6).
5. Сравнить теоретические и экспериментальные результаты найти процент расхождения.
6. Записать выводы по работе, в которых отразить следующее:
· соблюдается ли прямая пропорциональная зависимость между перемещениями и нагрузкой при ее возрастании;
· от каких параметров балки зависит величина перемещений, и каким образом;
· соответствует ли величины перемещений, полученных экспериментальным путем, теоретическим значениям.

4. ПРИМЕР ТЕОРЕТИЧЕСКОГО ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
1. Геометрические характеристики сечения.
· осевой момент инерции:
 ,
,
· осевой момент сопротивления:
 .
.
2. Определение величины допускаемой нагрузки.
1.1. Опорные реакции:
2.2. Изгибающие моменты в характерных сечениях балки:
2.3. Величина наибольшего момента в области упругих деформаций:
2.4. Величина наибольшей нагрузки в области упругих деформаций:
 .
.
3. Определим величину (E × Ix ×φ0), для чего запишем выражение для прогиба в сечении на правой опоре (уравнение (5)) и приравняем его к нулю.

Здесь: уВ = 0, z=l=1,0 м, a=0,2м. Силовую нагрузку примем F = 10 (Н), тогда VA = 0,8F = 0,8 × 10 = 8 (Н). Подставим данные, приравняем скобку к нулю и выразим искомое произведение

4. Угол поворота сечения В:

5. Прогиб в сечении К балки (для точки К координата z=0,5м):

Лабораторная работа №7
Прибор для измерения деформаций:
Цена деления прибора:
Модуль упругости I рода Е = 2 × 105 МПА
Нагрузка F = н
Расстояние между опорами l = м
Размеры поперечного сечения:
Геометрические характеристики сечения балки:
Осевой момент инерции:
Осевой момент сопротивления:
Расчетная схема балки
Определение величины допускаемой нагрузки:
Определение расчетных величин прогиба и угла поворота:
отсчет по индикатору
Определение среднего значения приращения прогиба и угла поворота:
Определение расхождений между опытными данными и теоретическими значениями:
Выводы по работе:
Работу выполнил студент:
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что происходит при прямом изгибе с осью балки, с поперечными сечениями балки и их центром тяжести?
2. Что такое изогнутая ось балки (упругая линия)?
3. Какие перемещения имеют место при изгибе?
4. Что такое прогиб? Правило знаков, единицы измерения.
5. Что называется углом поворота? Правило знаков, единицы измерения.
6. Что такое стрела прогиба?
7. Какие линии по отношению к балке образуют угол равный углу поворота?
8. Какая зависимость существует между прогибом и углом поворота?
9. Какие геометрические характеристики поперечного сечения балки используются в данной работе? Как определяется их величина?
10. Что означает выражение (z – а) в универсальном уравнении упругой линии балки?
11. В каком случае перед слагаемым, содержащим нагрузку, следует брать «плюс» и «минус»?
12. Что такое жесткость балки?
Список используемой литературы
1. Феодосьев материалов. М.:Изд-во МГТУ, 2000 – 592c.
2. и др. Сопротивление материалов. Киев: Высшая школа, 1986. – 775с.
3. Степин материалов. М.: Высшая школа, 1988. – 367с.
4. Сопротивление материалов. Лабораторный практикум./, и др. М.: Дрофа, 2004. – 352с.
Составители: Александр Владимирович Белов
Наталья Георгиевна Неумоина
Анатолий Александрович Поливанов
ДЕФОРМАЦИЙ ПРИ ПРЯМОМ ИЗГИБЕ
Методические указания к лабораторной работе № 7
по дисциплине «Сопротивление материалов»
Под редакцией авторов
Темплан 2007 г., поз. №. 16
Подписано в печать г. Формат 60×84 1/16.
Бумага листовая. Печать офсетная.
Усл. печ. л. 0,94. Усл. авт. л. 0,75.
Тираж 100 экз. Заказ №
Волгоградский государственный технический университет
400131 Волгоград, просп. им. , 28.
Волгоградского государственного технического университета
Изгиб деформация универсальное уравнение упругой линии
§1 Понятие изгиба. Нейтральная линия.
Определение: Изгибом называется вид деформации, при котором происходит искривление оси бруса. В дальнейшем будем рассматривать деформацию плоского прямого изгиба, при котором силовая плоскость проходит через одну из главных центральных осей сечения.
Кроме прямого, может возникать косой изгиб, при котором силовая плоскость совпадает только с одной центральной осью, т.е. происходит под некоторым углом к главным центральным осям.
В зависимости от возникающих в балке внутренних силовых факторов (ВСФ) различают чистый и поперечный изгиб (рис. 6.3).
Чистым изгибом называется изгиб, при котором в сечении балки возникает только изгибающий момент, а поперечным называется изгиб, при котором действуют как изгибающий момент, так и поперечная сила.
К
ак показывают расчеты нейтральная линия проходит через главную центральную ось сечения, расположенную перпендикулярно к силовой линии.
Нейтральную линию иногда называют нулевой линией, т.к. в ее точках нормальные напряжения и продольные деформации отсутствуют (σ = 0; ε = 0).
§2 Напряжения при чистом и поперечном изгибе.
Основное условие прочности.
В теории изгиба принимаются такие допущения:
1) Справедлива гипотеза плоских сечений.
2) По высоте сечения бруса волокна не имеют веса, т.е. не давят друг на друга. Принимается упрощенная схема напряженного состояния.
3
) по ширине сечения бруса напряжения являются постоянными.
С учетом принятых допущений и рассматривая четыре стороны задачи для чистого изгиба, при котором возникают только нормальные напряжения можно использовать следующую расчетную зависимость.
где σ(y) – нормальные напряжения в точке
сечения бруса, находящейся на
расстоянии y под нейтральной
Mизг – изгибающий момент в данном
Ix – осевой момент инерции сечения
y – ордината последней точки.
Анализируя зависимость (15.1) можно заключить, что нормальное напряжение изменяется по линейному закону, увеличиваясь от центра сечения к его краям. Причем максимальные напряжения, возникающие в крайних волокнах можно определить по известной формуле:
где – осевой момент сопротивления [м 3 ].
Зависимость (15.1) и (15.2) графически можно представить в виде следующей эпюры напряжений (рис. 6.8).
При проектировании балочных конструкций целесообразно применять профили, имеющие рациональную форму с точки зрения полученной эпюры напряжений. Считается, что профиль (или сечение), у которого большая часть материала располагается в крайних волокнах является рациональным. Например, двутавр, швеллер, пустотелый прямоугольник, сдвоенный уголок.
Расчет на прочность при чистом изгибе производится по следующему условию прочности
Условие (15.3) является основным условием прочности при изгибе. При помощи этого условия можно выполнить известные виды расчетов: проверочный, проектировочный и максимальной нагрузки.
– проверочный по (15.3)
При расчете на прочность балок из разных материалов необходимо учитывать их способность сопротивляться растягивающим и сжимающим напряжениям. При этом следует придерживаться следующих рекомендаций:
1. Если балка изготовлена из пластичного материала, одинаково работающего на растяжение-сжатие, т.е. ([σр] = [σc]), то целесообразно использовать сечения, симметричные относительно нейтральной линии. В этом случае на прочность проверяются крайние точки сечения балки σmax = |σmin| (рис.6.9).
2. Если материал балки хрупкий, лучше работающий на сжатие, чем на растяжение ([σр] >l, в противном случае этими напряжениями можно пренебрегать.
§3 Главные напряжения при изгибе.
Полная проверка прочности балок при изгибе
В общем случае при изгибе в сечениях балки действуют как нормальные, так и касательные напряжения. Любая точка балки находится в упрощенном плоском напряженном состоянии.
Решая обратную задачу можно найти положение главной площадки и величины главных напряжений (σ1, σ3).
Анализируя напряженное состояние при изгибе для опасных точек балки и используя (16.3)-(16.6) можно выполнить полную проверку прочности балки при изгибе, для этого необходимо рассмотреть три типа опасных точек в разных сечениях исследуемой балки. Проведем т0акую проверку, выбрав следующую расчетную схему (рис. 6.15)
Полная проверка прочности балки при изгибе выполняется по трем типам опасных точек. Опасная точка I типа: по длине балки находится сечения, где действует максимальный по модулю изгибающий момент (сечение I-I), а по высоте балки – в крайних волокнах от нейтральной линии, где имеют место максимальные нормальные напряжения (точки 1 и 5). В этих точках имеет место линейное напряженное состояние. Условие прочности для точек I типа имеет такой вид (основное условие прочности)
О
пасные точки II типа располагаются по длине балки в сечениях с максимальной поперечной силой (сечение II-II левое и правое), а по высоте балки – на уровне нейтральной линии (точка 3 левая и правая), где действует максимальное касательное напряжение. В этих точках возникает частный случай плоского напряженного состояния – чистый сдвиг. Условие прочности имеет такой вид
Опасные точки III типа располагаются в сечениях балки, где возникает неблагоприятное сочетание больших изгибающего момента и поперечной силы (сечение III-III левое и правое), а по высоте балки – между крайними волокнами и нейтральной линией, где одновременно большие нормальные и касательные напряжения (точки 2 и 4 левая, правая). в этих точках возникает упрощенное плоско-напряженное состояние. Условие прочности для точек III типа записывается согласно теории прочности (например, для пластичного материала: по III или IV теории).
Если по мере выполнения расчетов прочность по одному из условий не выполняется, то необходимо увеличить размеры сечения балки или увеличить номер профиля согласно таблиц сортамента.
Приведенный выше анализ напряженного состояния балок при изгибе позволяет грамотно конструировать элементы сооружений и рационально выбирать их поперечные сечения, например, для железобетонных конструкций целесообразно использовать стальную арматуру и располагать её по линиям, совпадающим с траекторией главных растягивающих напряжений.
§4 Деформации при изгибе. Общие понятия.
В теории изгиба расчет на прочность в большинстве случаев выполняется расчетом на жесткость. В этом случае оценивается упругая податливость балки и определяются такие её размеры, чтобы возникающие деформации не превышали допустимых пределов, т.е. условие жесткости можно представить в таком виде
где fmax – максимальная расчетная деформация;
[f] – допускаемая деформация.
Рассмотрим основные элементы деформированного состояния балки (рис.6.16).
упругая линия (у.л.) – искривленная ось балки под действием нагрузки;
y – прогиб – вертикальное перемещение, отсчитываемое перпендикулярно к исходной оси балки;
u – горизонтальное перемещение или смещение балки (обычно бесконечно малая величина, ≈ 0);
θ – угол поворота сечения к заданной точке.
При изгибе балки линейная и угловая деформации (y и θ) имеют свои правила знаков согласно следующей схеме (рис.6.17).
Правило знаков для y:
Правило знаков для θ:
против часовой стрелки «+»,
по часовой стрелке «–».
Для левой системы координат наоборот.
Между прогибом и углом поворота существует дифференциальная зависимость, которую можно получить рассматривая координаты некоторой плоской кривой (рис.6.18).
При нахождении линейных или угловых деформаций для реальных балок необходимо знать её уравнение упругой линии УУЛБ (уравнение упругой линии балки), имеющее такой общий вид:
Рассмотрим некоторые методы нахождения деформаций при изгибе, основанные на составлении и решении уравнения упругой линии балки.
§5 Дифференциальное уравнение упругой линии балки и его интегрирование.
Из теории изгиба известна зависимость кривизны балки следующего вида
С другой стороны из курса высшей математики кривизна плоской кривой может быть представлена через её координаты следующим образом:
Приравнивая (18.3) и (18.4) получим точное ДУУЛБ
Полученное дифференциальное уравнение имеет большие трудности при решении, поэтому его упрощают, учитывая известную гипотезу малости деформаций
Учитывая небольшие углы поворота сечений для реальных балок получаем следующее приближенное ДУУЛБ, которое будет называться в дальнейшем основным дифференциальным уравнением упругой линии балки.
Данное уравнение справедливо для правой системы координат.
Полученное уравнение решается путем двойного интегрирования
В этом решении произвольные постоянные интегрирования представляют собой по геометрическому смыслу соответственно угол поворота и прогиб в начале координат
Произвольные постоянные интегрирования определяются из граничных или начальных условий построения расчетной схемы балки. Рассмотрим основные разновидности граничных условий.
Виды граничных условий
Рассмотренный выше метод расчета перемещений при изгибе называется методом непосредственного интегрирования дифференциального уравнения упругой линии балки МНИ ДУУЛБ.
Для его применения необходимо:
- Выбрать систему координат (в крайнем сечении балки)
- Для каждого силового участка балки составляется общее уравнение моментов, которое подставляется в основное ДУУЛБ.
- Решается ДУУЛБ путем двойного интегрирования и определяется произвольная постоянная интегрирования из граничных условий.
- В полученное уравнение упругой линии балки подставляются поочередно абсциссы искомых точек и определяются прогибы. Аналогично находятся углы поворотов с использованием дифференциальной зависимости (18.1).
МНИ обладает существенным недостатком, который заключается в том, что для решения балок с большим количеством силовых участков необходимо определить большое количество произвольных постоянных интегрирования (например, для n участков будет 2n таковых), поэтому данный метод целесообразно использовать только для балок, имеющих один или два участка. Для устранения названного недостатка предлагается более совершенный метод, основанный на ДУУЛБ и более рациональном его решении.
§6 Метод начальных параметров.
Универсальное уравнение упругой линии балки (УУУЛБ).
В отличие от предыдущего метода в предлагаемом методе ДУУЛБ составляется таким образом, что независимо от количества силовых участков балки приходится находить только две произвольных постоянных интегрирования – прогиб и угол поворота в начале координат (y0, θ0). Это достигается путем применения специальных правил при составлении уравнения моментов или уравнений прогибов. В этом случае все решение сводится к составлению УУУЛБ применительно к заданной расчетной схеме балки.
Общий вид УУУЛБ будет следующим:
После дифференцирования (18.13) получим универсальное уравнение углов поворота балки УУУЛБ.
где y0, θ0 – геометрические начальные параметры, т.е. прогиб и угол поворота в начале координат, определяются по граничным условиям;
М0, Q0 – статические начальные параметры, т.е. изгибающий момент и поперечная сила в начале координат; они определяются по условиям нагружения или по уравнениям равновесия.
Mi, Fi, qi – момент, сосредоточенная сила и распределенная нагрузка в i том сечении балки соответственно. Они включаются в уравнение со своими знаками в соответствии с «правилом зонтика» для изгибающего момента.
ki – величина, характеризующая неравномерно распределенную нагрузку, например, треугольную или трапециевидную.
Д
ля решения задач по нахождению перемещений в балках методом начальных параметров необходимо (пример: рис.6.23):
2) Для последнего силового участка балки составляется универсальное уравнение упругой линии балки УУУЛБ.
Для составления выражения для распределенной нагрузки её предварительно продолжают до конца (последнего) сечения и вводят дополнительную компенсирующую нагрузку обратного направления.
3) Определяются начальные параметры УУУЛБ.
Геометрические начальные параметры.
Статические начальные параметры.
4) Подставляются все найденные начальные параметры в исходное УУУЛБ и путем дифференцирования получается универсальное уравнение углов поворота балки УУУЛБ.
В этом же пункте определяются искомые перемещения, для чего в соответствующее уравнение подставляется абсцисса искомой точки и отбрасываются слагаемые, характеризующие внешние нагрузки, которые находятся за пределами рассматриваемого участка.
Рассмотренный метод начальных параметров является достаточно простым и универсальным, но имеет следующие недостатки.
1) Он не применим для балок с ломаной осью, рамным систем и кривых брусьев.
2) Не позволяет определить перемещение в произвольных направлениях, кроме вертикального.
Для устранения этих недостатков в курсе сопротивления материалов широко применяются так называемые энергетические способы, основанные на известном законе сохранения энергии.
§7 Потенциальная энергия упругой деформации (ПЭУД)
в общем случае нагружения бруса. Теорема Кастильяно.
На основании закона сохранения энергии работа внешних сил на перемещениях точек системы равна потенциальной энергии упругой деформации
Основываясь на положениях этого закона можно зная величину энергии, накопленной брусом, найти перемещение ее точек при известных внешних нагрузках. Получим общую зависимость для ПЭУД произвольного бруса, находящегося под воздействием разнообразных внешних нагрузок, для этого составим сумму работ, совершаемых шестью внутренними силовыми факторами.
Учитывая известное выражение работ для простых деформаций получим следующее выражение
kx, ky – безразмерные коэффициенты, характеризующие форму сечения бруса при сдвиге.
Для нахождения перемещений с помощью ПЭУД применяется так называемая теорема Кастильяно:
Обобщенные перемещения в точке приложения некоторой обобщенной нагрузки представляют собой частную производную потенциальной энергии по заданной обобщенной нагрузке.
где δk – обобщенное перемещение в точке К, где приложена внешняя обобщенная нагрузка, по ее направлению.
FK – обобщенная нагрузка, действующая в точке К.
Под обобщенным перемещением понимается перемещение, вызываемое соответствующей обобщенной нагрузкой. В частности,
Д
анная теорема обладает тем недостатком, что позволяет находить только перемещения, соответствующие данной обобщенной нагрузке, только в точке её приложения и только по ее направлению.
§8 Метод для нахождения перемещений в упругих системах.
Недостатки теоремы Кастильяно можно устранить, если использовать прием, предложенный Мором-Максвеллом. Этот метод основан на применении так называемой фиктивной обобщенной нагрузки Φ.
1) В заданной точке системы прикладывается соответствующая обобщенная параметром фиктивная нагрузка, которая условно принимается равной единице.
Направление приложения фиктивной нагрузки соответствует искомому направлению. Для прогиба удобно единичную силу направлять снизу вверх согласно положительному направлению прогиба (см. правило знаков для прогиба). Единичный момент направляется против часовой стрелки в соответствии с положительным направлением угла поворота.
2) Определяется потенциальная энергия упругой деформации всей системы, которая подставляется в зависимость , выражающую теорему Кастильяно и производится расчет частной производной по данной фиктивной нагрузке.
В полученном выражении исключается фиктивная нагрузка, т.к. ее на самом деле нет.
Для удобства практического расчета все преобразования рассмотренные выше исключаются и расчет перемещений выполняется по формуле, называемой интегралом Мора (запишем применительно к деформации изгиба).
где – изгибающий момент от действия единичной фиктивной нагрузки в i том сечении системы.
– изгибающий момент от действия внешней нагрузки для i того сечения.
Рассмотрим следующий пример (рис.6.25).
Выбирается вспомогательная схема, которая загружается соответствующей единичной нагрузкой. Чтобы взять вспомогательную схему, надо на исходной схеме отбросить все внешние нагрузки.
Для исходной и вспомогательной схем составляются общие выражения изгибающих моментов по всем участкам, которые подставляются в интеграл Мора.
Метод Мора является самым сильным по возможности расчета перемещений (его можно применить для любой схемы), однако его недостатком является высокая трудоемкость при расчете систем с большим количеством силовых участков.
Для сокращения сложности таких расчетов интеграл Мора обычно заменяют операцией умножения согласно способа Верещагина (1924 г.).
§9 Способ Верещагина и его применение
Предлагаемый способ является графо-аналитическим способом решения интеграла Мора, который заключается в «перемножении» эпюр изгибающих моментов по силовым участкам заданной системы. Такое решение возможно благодаря тому, что для систем, имеющих прямолинейные участки эпюра изгибающих моментов от единичной нагрузки имеет линейные очертания (прямоугольник, треугольник, трапеция).
Согласно способа Верещагина искомое перемещение представляет собой произведение площади грузовой эпюры на ординату единичной эпюры, которая располагается под центром тяжести грузовой эпюры на данном участке.
где ωi – площадь грузовой эпюры на i том участке.
– ордината единичной эпюры под центром тяжести грузовой на i том участке.
Рассмотрим пример (рис.6.28)
При использовании способа Верещагина для упрощения расчетов можно учитывать следующие рекомендации.
1) При перемножении эпюр, имеющих линейные очертания можно использовать площадь одной из них, а ординату другой в прямом и обратном порядке.
2) Если перемножаемые эпюры имеют сложную форму, то можно их разбивать на простые части и перемножать по отдельности.
3) В некоторых случаях сложные эпюры удобно перемножать, используя прием расслоения эпюр. В этом случае в пределах данного участка строятся эпюры от каждой нагрузки в отдельности, которые перемножаются поочередно с единичной эпюрой.
4) При перемножении эпюры, имеющей форму скрученной трапеции, ее целесообразно дополнить до двух треугольников, которые затем перемножаются по отдельности с другой эпюрой.
5) Когда обе перемножаемые эпюры имеют сложную форму можно использовать так называемую формулу Симпсона.
Способ Верещагина является достаточно удобным и простым для расчета перемещений в упругих системах при любых видах деформаций. Однако его нельзя применить для систем, имеющих криволинейные участки.
§10 Статически неопределимые системы при изгибе.
Каноническое уравнение метода сил (КУМС).
Статически неопределимая система (СНС) при изгибе обладает теми же свойствами, что СНС при растяжении-сжатии и кручении, однако имеют следующую особенность.
Степень неопределимости в таких системах может быть образована как внешними, так и внутренними признаками построения СНС.
Система неопределима внешним образом, если её элементы имеют ограничения по перемещению в пространстве. Такие ограничения накладываются опорными связями и в этом случае степень СНС по внешним признакам находится по известной формуле
где R – число неизвестных реакций опор СНС,
У – число уравнений статики.
Степень СНС образована внутренними признаками, если они накладывают ограничения на относительные перемещения точек системы по отношению друг к другу. К ним относятся дополнительные элементы, шарниры, узлы и прочие геометрические факторы.
В этом случае степень СНС по внутренним признакам находится по следующей формуле
где K – число замкнутых контуров СНС (например, рамок),
У – число шарниров, врезанных в элемент СНС в пересчете на простые шарниры.
П
ростым называется шарнир, в котором сходятся только два стержня.
Сложный шарнир, в котором сходятся более 3 х стержней можно заменить n–1 простыми шарнирами (n – число стержней, сходящихся в сложном шарнире).
Таким образом, степень СНС можно определить сложив зависимости (21.1) и (21.2).
Для решения СНС при изгибе в курсе сопротивления материалов применяются метод сил, метод перемещений и комбинированный метод. Наиболее часто применяется метод сил, в частности прием сравнения перемещений, канонические уравнения метода сил (КУМС) и уравнения трех моментов.
Удобно и математически относительно несложно провести решение СНС с применением КУМС.
Д
ля составления канонических уравнений устанавливается число лишних связей системы. Эти лишние связи (например, реакции опор) обозначаются буквами Xi независимо от того сила это или момент (рис.6.34)
Для каждой лишней опоры составляется уравнение деформаций в виде суммы перемещений, вызванных действиями всех лишних связей и внешних нагрузок, причем эти деформации на опорах должны равняться нулю. Для удобства записи и решения эти уравнения составляются по определенному правилу (или канону).
В общем случае КУМС записывается так:
где δij – перемещение в i той точке под действием единичной силы, приложенной к j той точке.
δ11, δ22, δ33, . δnn – главные коэффициенты КУМС, представляющие собой единичные перемещения в i той точке под действием единичной силы, приложенной в той же точке. Они определяются по способу Верещагина путем перемножения эпюр от единичных сил «самих на себя».
δ12, δ13, . δij – побочные коэффициенты, представляющие собой единичные перемещения, определяемые по способу Верещагина путем перемножения единичных эпюр между собой.
Δ1F, Δ2F, . ΔnF – грузовое перемещение, определяемое как перемещение в i той точке под действием системы внешних нагрузок.
По способу Верещагина оно находится путем перемножения грузовой эпюры момента на единичную эпюру под действием i той единичной силы.
Определив все единичные и грузовые перемещения КУМС, решается данная система и определяются неизвестные усилия X1; X2; X3 . Xi . Xn.
По завершении раскрытия неопределимости СНС строятся необходимые эпюры (для рамы – N, Q и M). и выполняются две проверки – статическая и деформационная.
Статическая проверка заключается в проверке равновесия элементов или узлов системы (см. задачу № 12 РПР-2).
Деформационная проверка сводится к расчету перемещений тех точек системы, где действуют лишние связи (Xi). Обычно проверяется равенство нулю перемещений в опорах системы. Для этого необходимо по способу Верещагина перемножить конечную эпюру изгибающих моментов с единичной эпюрой, построенной для i той лишней связи.
В некоторых случаях при решении СНС можно уменьшить количество перемножений эпюр, если использовать эффект симметрии геометрического построения или силового нагружения системы (рис.6.35).
В следующем случае система рассекается по оси симметрии и в качестве лишних связей выбираются внутренние силовые факторы в проведенном сечении.
Тогда единичные эпюры от соответствующих внутренних силовых факторов будут иметь либо симметричную, либо кососимметричную формы
Следовательно, при перемножении симметричной эпюры на кососимметричную получаем перемещение равное нулю.
Когда животное бьют, глаза его приобретают человеческое выражение. Сколько же должен был выстрадать человек, прежде чем стал человеком. Карел Чапек
ещё >>
[spoiler title=”источники:”]
http://pandia.ru/text/78/495/17974.php
http://davaiknam.ru/text/izgib-1-ponyatie-izgiba-nejtralenaya-liniya
[/spoiler]
В прошлой части мы обсудили, как может изменяться момент стержня и как выяснить, не разрушится ли он под действием нормальных и касательных сил. Однако под воздействием момента стержни могут изгибаться и изменять форму, что может приводить к неправильной работе конструкций или даже их разрушению в процессе эксплуатации. Сегодняшняя статья посвящена вопросу нахождения прогибов и углов наклона при изгибе.
Уравнение кривой
В прошлой части мы выяснили, что для нахождения момента нам необходимо знать какой у дуги изгиба радиус кривизны, какой у сечения статический момент и какой модуль Юнга у материала балки:
Затем мы устранили из уравнения такое значение как радиус кривизны, из наших уравнений, так как нас не столько волновало, как под воздействием изменится балка, сколько не сломается ли она.
Однако сейчас нас интересует именно то, как будет деталь изгибаться под воздействием моментов, как будет меняться геометрия .
В прошлый раз мы не заостряли внимание на вопросе «что такое радиус кривизны», да и просто «что такое кривизна». В этой части мы данную проблему решим, а также объясним как это значение поможет нам в сопромате вычислить деформации изгиба.
Фактически, до этого момента мы оперировали не столько радиусом, сколько кривизной, которая обратно пропорциональна радиусу:
А сейчас мы поговорим о том, какое значение она имеет с точки зрения геометрии.
Если нет желания смотреть, как с точки зрения математики выводятся геометрические характеристики, можно промотать до следующего жирного шрифта и принять за данность выводы.
Кривизна – это то, насколько сильно изменяется угол наклона касательной к нашей кривой за единицу длины дуги.

Так как любую кривую можно представить как сумму бесконечно малых дуг, принадлежащих разным окружностям, стоит посмотреть, на сколько будет изменяться угол в двух точках ее дуги.

Углы будем измерять в радианах (180°=π, 360°=2π). Длина окружности равна удвоенному произведению радиуса на π: l=2πR. Круг — фигура симметричная, и поэтому в любой точке кривизна будет одинакова и равна:
χ=frac{2π}{2π*R}=frac{1}{R}
Вот так и находилась формула кривизны балки. И теперь мы хотим поставить её на службу поиска формы балки.
Нам нужно найти изменение угла за бесконечно малый пройденный путь, и мы имеем некоторую функцию. При этом её первая производная будет равна тангенсу угла с осью x, которую мы обозначим греческой тета θ:

Нам же для вычисления кривизны необходимо найти изменение угла θ:
Гуглим таблицу дифференциалов, находим, что дифференциал от тангенса равен следующему выражению:
d(arctg (x))=frac{dx}{1+x^2}
Так как функция сложная (y’ — тоже какая-то функция, пусть нам и не известная), получившееся значение надо будет домножить на производную от аргумента:
dθ=frac{dx}{(1+(y’)²)}*y’’
Кривизна же — это изменение угла за пренебрежительно малый отрезок длины:
Уравнение угла наклона нам известно. Теперь нам нужно вычислить длину малой дуги. Достаточно малой, чтобы можно было пренебречь кривизной и считать её прямой. Тогда мы сможем воспользоваться теоремой Пифагора:
Где dx – пройденный путь по оси x, а dy – по оси y.
Нам для красоты уравнения хотелось бы избавиться побыстрее от дифференциалов, чтобы в формуле остались только производные. Для этого мы делим все, что было под корнем на (dx)^2:
frac{(dx)^2}{(dx)^2}+frac{(dy)^2}{(dx)^2}=1+(y')^2
Так как (dx)^2/(dx)^2=1, а (dy)/(dx) – это производная y по x.
Чтобы уравновесить данное вмешательство, мы должны домножить все выражение на dx (т.к. √(dx)^2=dx):
Теперь у нас есть все для нахождения кривизны:
χ=frac{dθ}{dl}=frac{dx}{(1+(y’)^2)}*y’’*frac{1}{dxsqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^2}
*frac{1}{sqrt{1+(y’)^2}}=\=frac{y’’}{(sqrt{1+(y’)^2})^{{3}}}
Отсюда стоит читать всем, даже тем, кому математика вывода кривизны не очень интересна.
Итак, мы смогли вычислить чему равна функция кривизны:
χ=frac{1}{R}=frac{y’’}{(sqrt{1+(y’)^2})^{3}}
Где y – прогиб (т.е. расстояние на которое выше или ниже окажется определенная точка балки, по сравнению с недоформированным состоянием), y’ – первая производная от неё, а y» – вторая (или кривизна).
Перед нами же стоит задача вычислить форму. Так как в сопротивлении материалов прогибы достаточно небольшие, изменением длины можно пренебречь. Следовательно, нам остается лишь вычислить изменение координаты y в зависимости от x. И в полученной формуле нам мешает это сделать очень объемный знаменатель (√(1+(y’)²)³.
Если подумать логически, то так как прогибы в сопромате достаточно небольшие, можно было бы не учитывать производную y’, так как она является отношением катетов треугольника, который бы получился опусти мы к оси x перпендикуляр.
Дело в том, что даже если прогиб (координата y) будет составлять 1/10 от x, производная в самом крайнем углу будет чуть больше 0,2x. А ее квадрат 0,04x. А (√(1+(y’)²)³ около 1,06.
Это не назвать пренебрежительно малым значением, однако его проще компенсировать коэффициентами запаса прочности. Да и прогиб этот слишком большой для основ сопротивления материалов (большими деформациями занимается отдельная дисциплина). Вот демонстрация прогиба в натуральном соотношении:
В результате, если мы проигнорируем знаменатель, получим формулу, которую уже можно будет использовать в дальнейших расчетах:
χ=θ’=y’’
Угол поворота и прогиб
Мы уже выяснили, что кривизна балки в каждой части зависит от момента, возникающего в этом сечении, статического момента и модуля Юнга материала, из которого это балка сделана:
Сегодня же мы будем решать обратную задачу и находить изгиб балки. В первой части статьи мы выяснили, что для малых изгибов радиус кривизны (он равен единице деленной на радиус кривизны) практически равен второй производной от прогиба (насколько по оси z поднимется или опустится балка в конкретной точке). В итоге мы, зная как распределяется момент, сможем посчитать вторую производную прогиба для каждой точки балки:
y’’=χ=frac{1}{R}=frac{M_z}{I_z×E}
Нам же интересна форма балки: углы её наклона и на сколько сантиметров выше или ниже она окажется.
Начнём с наклона. Как мы уже выяснили, первая производная будет равна тангенсу наклона. Тангенс равен отношению противолежащего катета к прилежащему:

Углы наклона у нас будут маленькими, поэтому прилежащий катет будет практически равен радиусу. Отношение противолежащей стороны к радиусу является синусом:

А синус малого угла, как мы уже выяснили вначале статьи, численно равен углу в радианах.
Примечание: мы выяснили, что для малых углов тангенс, синус и угол численно равны. Эта закономерность важна не только в сопромате, но и в большинстве других инженерных наук. Например, в геодезии, при определении величины малых скатов.

Как следствие, для того, чтобы найти угол наклона, нам необходимо проинтегрировать кривизну:
θ=∫y''dx=∫frac{M_z*dx}{J_z*E}=frac{1}{J_z*E}∫M_z*dx=y'+C
Углы и прогибы балки под воздействием момента
В простейшем случае к балке приложен только момент:

В таком случае значение момента является константой. Обозначим ее как M. Тогда найти прогиб можно по формуле:
θ=∫y''dx=frac{1}{I_z*E}∫M_z*dx=frac{M_z*x}{I_z*E}+C
Остается найти константу интегрирования. Так как в начале координат балка жестко закреплена, угол в месте закрепления будет равен нулю, как следствие, константа тоже будет равна нулю. Эпюра угла наклона будет выглядеть вот так:

Для того, чтобы найти прогибы надо, соответственно, проинтегрировать получившееся выражение еще раз:
y=∫θdx=∫frac{M_z*x*dx}{I_z*E}+∫Cdx=frac{M_z*x^2*dx}{2*I_z*E}+Cx+D
Константу C мы уже знаем, а константу D можно найти по той же логике: балка жестко закреплена в начальной точке, а значит прогиб y в ней будет равен 0. А полученная нами формула приводит к нулю в начале координат только при нулевой константе:
(M*0)2/2+C*0+D=0, только если D=0
Ну а эпюра прогибов будет выглядеть следующим образом:

Углы и прогибы балки под воздействием силы
В случае же, если момент появляется под воздействием силы, эпюры как бы сдвигаются на одну вперед:

Линейной станет функция момента, а угол будет постепенно увеличиваться (вначале быстро, потом медленнее, так как момент будет меньше).
Mz=P(l-x), где Mz— момент возникающий в балке в точке, которая расположена на расстоянии x от места закрепления балки, а l – длина балки.
Получили мы это уравнение следующим образом: мы знаем что в месте закрепления возникает момент который компенсирует момент от воздействия силы на конце балки:
Также в месте закрепления будет возникать сила, которая будет компенсировать силу внешнюю:
Когда мы будет отдаляться от точки закрепления на величину x, сила реакции опоры будет создавать для нашего сечения момент MRa=Ra*x. Он будет складываться с моментом передавшимся с начала балки:
M_z=M_{z_{0}}-M_{R_{a}}=\=p*l+R_a*x=P*l-P*x=\=P(l-x)
Зная функцию распределения момента мы можем найти функции наклона и прогиба.
Наклон будет увеличиваться по параболе:
θ=∫frac{(P*(l-x))*dx}{I_z*E}=frac{P*(l-x)^2}{2*I_z*E}+C

Ну а прогиб будет изменяться уже по кубическому закону:
y=∫frac{P*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{P*(l-x)^3*dx}{6*I_z*E}+C*x+D
Примечание: если проще, то l-x потому, что в нулевой координате момент равен расстоянию до силы, а затем уменьшается на то расстояние, которое мы до нее прошли

Углы и прогибы балки под воздействием равномерно-распределенной нагрузки
В случае с равномерно-распределенной нагрузкой ситуация абсолютно аналогична: эпюры «сдвигаются» на одну относительно воздействия силы. Поперечная сила изменяется по линейному закону Qy=Ra-qx=ql-qx=q(l-x), момент по параболе Mz=q(l-x)2/2:

Угол наклона, соответственно, будет определяться кубической функцией:
θ=∫frac{q*(l-x)^2*dx}{2*I_z*E}+∫C*dx=\=frac{q*(l-x)^3*dx}{6*I_z*E}+C

А прогиб уже функцией четвёртой степени:
y=∫frac{q*(l-x)^3*dx}{6*I_z*E}=\=frac{q*(l-x)^4*dx}{24*I_z*E}+Cx+D

Расчет балки на прогибы и углы наклона. Метод начальных параметров. Пример
На практике достаточно редко случается ситуация, при которой на конструкцию действует только одна сила, а сама конструкция состоит из одной балки, закрепленной только в одном месте. Разберем как пример расчёт балки, в которой есть все виды воздействий:

Примечание: среди внешних воздействий отсутствует сила. Мы сделали это для того, чтобы не загружать статью лишними расчётами: сила реакции опоры в расчетах ничем не отличается от силы внешней.
Первым делом, нужно заменить места закрепления на силы, которые они создают для поддержания равновесия балки. В данном случае это две вертикальные силы (моментов шарнирные опоры не создают):
Теперь наша задача найти эти силы. Сделать это довольно просто: составляем уравнение сил по оси y и момента для точки закрепления балки.
Уравнение равновесия сил по оси Y:
R_a-ql+R_b=R_a-30+R_b=0, R_a+R_b=30
Уравнение равновесия момента в левой точке закрепления:
M_a=ql*a+frac{15l^2}{2}+M-d*R_b=30+30-10-5R_b=0
Где a — расстояние до начала действия равномерно-распределенной нагрузки, d — расстояние до опоры b.
Из уравнения момента мы можем найти, чему равна сила реакции правой опоры:
Подставляем это значение в уравнение равновесия сил и получаем силу реакции первой опоры:
R_a+R_b=R_a+14=30, R_a=16

Для того, чтобы найти прогибы, нам надо составить уравнения момента для каждого участка. В нашем случае удобнее всего Теперь найдём функцию распределения момента для первого участия. Так как в точке a балка закреплена не жестко, момент в ней по условию равен нулю. В ней возникает только сила реакции опоры Ra=16.
Момент на первом участке будет зависеть от удаления от этой силы:

Для нахождения угла наклона это выражение надо проинтегрировать:
θ_{(I)}=frac{1}{I_zE}∫R_axdx=frac{R_ax^2}{2I_zE}+C
И ещё раз для получения прогиба:
y_{(I)}=frac{1}{I_zE}∫frac{R_ax^2dx}{2}+∫Cdx=frac{R_ax^3}{6I_zE}+Cx+D
Затем нам нужно найти геометрию балки на участке с равномерно-распределенной нагрузкой.

При этом, момент на этом участке будет зависеть от двух составляющих: от силы реакции Ra с первого участка и от нагрузки q.
M_{z_{(II)}}=f(R_a,x)+f(q,x)
Функция момента (Mz(I)=Ra*x=12x) возникающего от силы на первом участке будет справедлива и для нашего участка: момент по-прежнему будет равен произведению плеча на силу.
По мере того, как мы будем отступать от начала действия равномерно-распределенной нагрузки, момент будет увеличиваться по квадратичному закону (почему, можно прочитать в статье посвященной теореме Журавского) M(q)=qx’^2/2, где x’ — расстояние от начала приложения нагрузки.
Нам удобнее все расчёты проводить из одной точки, поэтому для второго участка x’=x-a, где a координата начала приложения нагрузки. Таким образом, уравнение момента на втором участке будет выглядеть так:
Mz_{(II)}=Ra*x-frac{q(x-a)^2}2=16x-frac{15(x-1)^2}2
Интегрируем чтобы найти наклон:
θ_{(II)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6)+C
И ещё раз, чтобы найти прогиб:
y_{(II)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32})
На следующем участке действие равномерно-распределенной нагрузки заканчивается. При этом, мы хотим чтобы q(x-a)2/2 в формуле осталась: всё-таки она вносит вклад в момент и геометрию стержня.
Чтобы эту небольшую проблему исправить, мысленно продолжим распределенную силу до конца конструкции, но приложим в противовес ей точно такую же, направленную в другую сторону:

Таким образом на следующий участок стержня (который начинается в точке b) дополнительно будет приложена распределенная нагрузка q, которая будет создавать момент M=q(b-x)2/2.
Суммарный момент для третьего участка будет равен:
Mz_{(III)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2
Ну и, соответственно, найти наклон и прогибы не составляет трудности:
θ_{(III)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6)+C
y_{(III)}=frac{1}{Iz*E}∫((frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32})+Cx+D
Четвёртый участок начинается в месте приложения момента и заканчивается на второй опоре.
Составляем уравнение момента:
Mz_{(IV)}=Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0=\=16x-frac{15(x-1)^2}2+frac{15(x-3)^2}2+10
Где c — расстояние от начала координат до места приложения момента, а x-c, расстояние между точкой, которую мы рассматриваем и местом приложения момента. В нулевой степени это выражение всегда равно единице, поэтому для уравнения момента это константа. Но после интегрирования это выражение становится важной частью уравнения наклона:
θ_{(IV)}=frac{1}{Iz*E}∫(Ra*x-frac{q(x-a)^2}2+frac{q(x-b)^2}2+M(x-c)^0)dx=\=frac{1}{Iz*E}*(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))+C
А затем и уравнения прогиба:
y_{(IV)}=\frac{1}{Iz*E}∫(frac{Ra*x^2}2-frac{q(x-a)^3}6+frac{q(x-b)^3}6+M(x-c))dx+∫Cdx=\=frac{1}{Iz*E}*(frac{Ra*x^3}6-frac{q(x-a)^4}{32}+frac{q(x-b)^4}{32}+frac{M(x-c)^2}{2})+Cx+D

Остается вычислить константы интегрирования. На первой и последней опоре прогибы (т.е. вертикальные перемещения) будут равны нулю. Подставляем x=0 в уравнение первого отрезка:
y_{(I)}=frac{R_a0^3}{6I_zE}+C*0+D
И выясняем, что константа интегрирования D равна нулю.
Подставляя константу интегрирования D в уравнение последнего участка для закрепленного конца балки (т.е. x=l=5) мы получим следующее уравнение:
0=frac{1}{Iz*E}*(frac{16*5^3}6-frac{15(5-1)^4}{32}+frac{15(5-3)^4}{32}+frac{10(5-4)^2}{2})+С*5+0
Выражение равно нулю по причине того, что прогибы в месте закрепления образовываться никак не могут.
Решив уравнение мы получим значение второй константы интегрирования:
С=frac{225,83}{5*Iz*E}=frac{45,17}{Iz*E}
Дальше остается лишь подставить эти константы в уравнения и мы получим уравнения наклонов и прогибов.

Итак, мы выяснили по каким законам будет прогибаться каждый участок балки.
Если резюмировать, то для получения уклона и прогиба на некотором участке, нам нужно просуммировать все воздействия и их проинтегрировать.
Метод начальных параметров
В общем виде углы наклона будут считаться так:
А прогибы так:
Примечание: не забывайте компенсировать равномерно-распределенную нагрузку в точке, где она заканчиваться!
На практике гораздо целесообразнее считать момент, наклон и прогиб сразу для всей балки, с помощью трех систем уравнений: системы моментов, наклонов и прогибов.
Уравнения моментов для каждого участка
Так их удобнее составлять, так как достаточно просто для каждого нового участка добавлять воздействия:
Уравнения наклонов
Как можно заметить, для того, чтобы из системы уравнений моментов получить систему уравнений наклонов достаточно проинтегрировать каждый член и добавить константу интегрирования C:
Уравнения прогибов
Как ни странно, для того, чтобы их получить, достаточно проинтегрировать каждый из членов уравнения наклона, добавить ещё одну константу интегрирования D, а первую константу C умножить на x.
Итак, подошёл к концу разговор о том, как материалы противодействуют изгибам. В прошлых частях мы уже выяснили, какие нормальные напряжения возникают в материале при попытке его согнуть. Обсудили и как с распределением момента связаны поперечные силы и касательные напряжения. А сейчас выяснили и как будет материал менять свою форму под воздействием изгиба.
Это имеет далекоидущие последствия для всех инженерных дисциплин и опирающихся на них специальностей. Например, ротор турбин, являющийся по своей сути длинным стержнем на опорах, под силой тяжести достаточно сильно изгибается. По этой причине для всех турбин большой мощности противопоказан быстрый старт. Перед тем, как соединять статор и ротор, стержень турбины необходимо повращать, чтобы он избавился от изгибающих деформаций. Иначе лопатки будут цепляться и в лучшем случае деформироваться, а в худшем ломаться. Но это уже совсем другая история.
В следующей части мы поговорим о другом виде воздействия момента на стержень: о кручении.
Автор: К.А.Овчинников
Редактор: Сабуров Даниил
Эксперт: Ершов Марк
За консультативную поддержку по математической части огромная благодарность Гришиной Ольге Андреевне, старшему преподавателю кафедры высшей математики БГТУ ВОЕНМЕХ.
Информация о произведении:
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Источники:
- Горбатовский Александр Александрович Дифференциальное уравнение изогнутой оси балки // Курс лекций по сопротивлению материалов МГТУ ИМ. Н.Э.БАУМАНА
- Лекции по сопротивлению материалов в СПбПУ им. Петра Великого
- Лекции по сопротивлению материалов в БГТУ «ВОЕНМЕХ» им. Устинова
- http://mathhelpplanet.com/static.php?p=krivizna-ploskoi-krivoi
- https://spravochnick.ru/matematika/krivizna_krivoy/krivizna_i_ee_vychislenie/
- iSopromat Метод начальных параметров. Расчет перемещений сечений балки // https://youtu.be/xRp-ViFUl7Y
4 124
