Как составить кинематическую схему редуктора

Составление кинематической схемы редуктора

Необходимо
разобрать редуктор и ознакомиться с
его устройством, обратив внимание на
входной (ведущий) вал, выходной вал и
всю цепь звеньев, передающих вращение
от первого вала к последнему. При этом
надо научиться различать зубчатые
колеса трех видов:

1. вращающиеся
   вокруг неподвижной оси (в неподвижных
   подшипниках) с внешним (рис.2.1 (а)) зубчатым
   ободом или внутренним зубчатым ободом
   (рис.2.1 (б));

2. неподвижные
   колеса, жестко соединенные с корпусом
   редуктора (рис.2.1 (в));

3. зубчатые
   колеса – сателлиты, укрепленные в
   подшипниках на подвижном звене (рычаге),
   которое называется водилом и обозначается
   буквой Н (рис.2.1 (г, д)).

Кинематическая
схема составляется в сечении, в котором
лежат оси всех колес, – от входного вала
редуктора, изображаемого слева, к
выходному.

В
планетарных передачах с целью уменьшения
нагрузки на каждую пару зубьев на одном
водиле устанавливают два, три и большее
число сателлитов (например, колеса 2₁,
2₂,
2₃,
2₄
на рис.2.2 (а)), причем, второй и последующие
сателлиты (2₂,
2₃,
2₄)
дублируют работу первого (2₁)
и накладывают пассивные связи. Поскольку
пассивные связи надо исключать при
подсчете числа степеней свободы, то на
схеме (рис.2.2 (б)) на одном водиле
рекомендуется изображать только один
сателлит или один блок сателлитов, как
на рис.2.1 (д).

Схему редуктора
составляют на черновике, а после проверки
преподавателем чертят в бланке. На схеме
все подвижные звенья от ведущего вала
к ведомому необходимо пронумеровать
арабскими цифрами (рис.2.3), руководствуясь
следующим:

а) два жестко соединенных между собой
колеса образуют одно подвижное звено,
и их полагается нумеровать одинаковым
номером, а одно из колес отмечать штрихом
или звездочкой: например, 2 и 2’ или 3 и
3’ на рис.2.3;

б)
водило имеет номер своего звена (5 и 7 на
рис.2.3) и дополнительно обозначается
буквой Н: например, Н₅
и Н₇;

в) неподвижные колеса и неподвижное
звено имеют особое обозначение – “0”.

Номер
последнего подвижного звена совпадает
с числом подвижных звеньев n.
Для определения числа вращательных пар
Р₅
и высших пар Р₄
следует подсчитать или пронумеровать
римскими цифрами все подшипники, в том
числе и подвижные подшипники между
сателлитом и водилом, а римскими цифрами
в кружке – все зацепления колес. Например,
на рис.2.3 n
= 7, P₅
=7, P₄
= 6.

Число
степеней свободы (пункт 2 бланка)
определяется по формуле Чебышева,
например, для схемы на рис.2.3

Р
едуктор
на кинематической схеме требуется
разделить на отдельные ступени.

Ступенью
называется часть редуктора между двумя
ближайшими валами в неподвижных
подшипниках.

Простая ступень
состоит из пары сцепляющихся колес с
неподвижными геометрическими осями,
например, 1-2 или 2’-3 на рис.2.3.

Планетарная
ступень состоит из водила (Н₅),
сателлитов (4), укрепленных на водиле, и
всех колес (3’ и 0), входящих в зацепление
с этими сателлитами (второй пример:
водило Н₇,
сателлит 6 и колеса 5 и 0), т.е. число
планетарных ступеней совпадает с числом
водил.

Если
ведущий и ведомый валы двух (и большего
числа) простых ступеней находятся на
одной прямой (например, 1 и 3 на рис.2.3),
то такая простая передача называется
соосной,
в противном случае – несоосной.

К
аждая
планетарная ступень всегда бывает
только соосной, так как оси солнечного
и неподвижного колес должны находиться
на одной прямой. В наиболее распространенном
планетарном механизме Джемса (рис.2.2)
соосность выполняется при следующем
соотношении радиусов начальных
окружностей колес:

• п
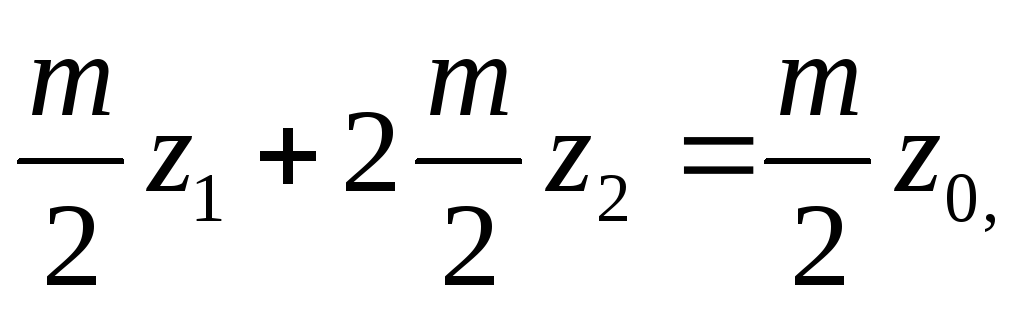
  ри
  нулевом зацеплении начальные окружности
  совпадают с делительными и

где
m
– модуль, одинаковый для всех сцепляющихся
колес (1,2,0).

• п
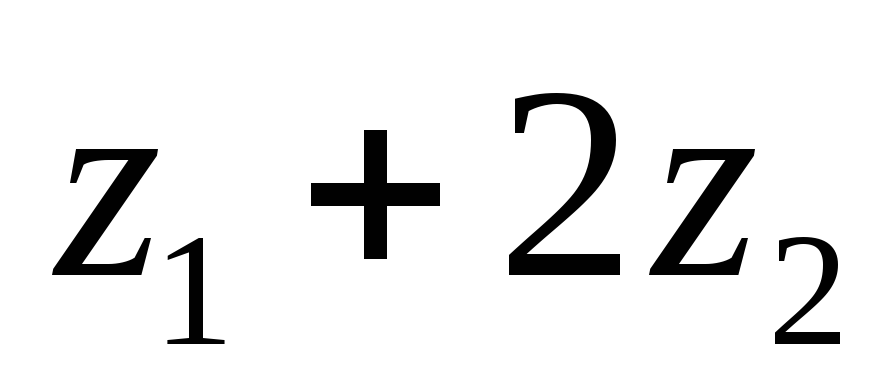
  ри
  корригированном зацеплении сумма
  зубьев колес может быть меньше z
  на один зуб (в исключительном случае
  на два).

П
оэтому
условие соосности для механизма Джемса
имеет вид:

где

= 0 – для нулевого зацепления,

 =
1 – для ненулевого зацепления.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Шпаргалка: Разработка кинематической схемы редуктора

Тульский Государственный Университет.

Кафедра приборов управления.

Приборный редуктор

Пояснительная записка по курсовому проекту

“Прикладная механика”

направление 200203 “Оптотехника”

Выполнил:

студент группы 121641

Проверил

Рогов С. В.

Тула 2007

Содержание:

1. Начальные данные

2. Введение

3. Патентно-библиографический поиск

4. Выбор типа передачи и вида зацепления

5. Разработка кинематической схемы

а) Определение обще-передаточного отношения

б) Определение числа ступеней

в) Этап выбора зубьев колёс

г) Кинематическая схема редукторов

6. Расчёты кинематики и геометрии

а) Определение кинематики редуктора

б) Расчёт геометрии зубчатых колёс

7. Разработка конструкции редуктора

а) Выбор конструкции зубчатых колёс

б) Расчёт валов

в) Выбор опор

г) Прочностной расчёт редукторов

д) Расчёт КПД редуктора

е) Описание конструкции редуктора

ж) Определение коэффициента заполнения

8. Заключение

9. Список литературы

10. Приложение

11. Спецификация

1. Начальные данные:

nвх = 1045

nвых = 19

Мвых = 65*10-3

Условие: минимальные габариты.

2. Введение

Подразделение зубчатых механизмов (редукторы и мультипликаторы):

Редуктором называют механизм, состоящий из зубчатых или червячных передач, выполненный в виде отдельного агрегата и служащий для передачи вращения от вала двигателя к валу рабочей машины. Кинематическая схема привода может включать, помимо редуктора, открытые зубчатые передачи, цепные или ременные передачи.

Назначение редуктора — понижение угловой скорости и соответственно повышение вращающего момента ведомого вала по сравнению с ведущим. Механизмы для повышения угловой скорости, выполненные в виде отдельных агрегатов, называют ускорителямиили мультипликаторами .

Редуктор состоит из корпуса (литого чугунного или сварного стального), в котором помещают элементы передачи — зубчатые колеса, валы, подшипники и т. д. В отдельных случаях в корпусе редуктора размещают также устройства для смазывания зацеплений и подшипников (например, внутри корпуса редуктора может быть помещен шестеренный масляный насос) или устройства для охлаждения (например, змеевик с охлаждающей водой в корпусе червячного редуктора).

Редуктор проектируют либо для привода определенной машины, либо по заданной нагрузке (моменту на выходном валу) и передаточному числу без указания конкретного назначения. Второй случай характерен для специализированных заводов, на которых организовано серийное производство редукторов.

В автоматических, вычислительных, измерительных и других приборах и устройствах широкое применение имеют малогабаритные редукторы и отсчётные механизмы, к которым предъявляются повышенные требования в отношении точности и плавности работ. Несмотря на различную применяемость (в качестве редукторов следящих систем или автоматических устройств, редукторов самопишущих приборов, отсчетных механизмов вычислительных устройств, механизмов настройки радиоэлектронной аппаратуры и т. д.), эти механизмы имеют много общего в методах проектирования, так как они составлены из однородных элементов (мелкомодульных зубчатых передач, валиков, опор, муфт, отсчетных устройств, стопоров и других механических узлов и деталей). Такие составные механизмы, обеспечивающие механические связи между заданными элементами приборов и конструктивно оформленные как единое целое в одном корпусе или на одном общем основании, называют редукторами точных приборов или приборными редукторами. Так как приборные редукторы имеют механические связи с электродвигателями, потенциометрами, вращающимися трансформаторами, сельсинами и другими электроэлементами, то последние обычно устанавливаются на общем корпусе (основании) редуктора.

Редукторы классифицируют по следующим основным признакам:

— типу передачи (зубчатые, червячные или зубчато-червячные);

— числу ступеней (одноступенчатые, двухступенчатые и т. д.);

— типу зубчатых колёс (цилиндрические, конические, коническо-цилиндричские и т. д.);

— относительному расположению валов редуктора в пространстве (горизонтальные, вертикальные);

— особенностям кинематической схемы (развёрнутая, соосная, с раздвоенной ступенью и др.);

А в приборостроении находят применение следующие основные разновидности редукторов точных приборов:

— приводные приборные редукторы следящих и автоматических систем, самопишущих приборов, приборных электродвигателей и т. д.;

— отсчетные механизмы, служащие для передачи точных значений углов поворота в вычислительных или измерительных устройствах, для снятия результатов вычисления или измерения и для контроля за правильностью работы отдельных элементов устройства;

— механизмы ручной настройки радиоаппаратуры или ручного ввода математических величин в вычислительные устройства;

— волновые зубчатые редукторы — новые типы малогабаритных редукторов высокой точности, предназначенные для уменьшения скорости вращения ведомого вала.

Требования, предъявляемые редукторам: прочность, хорошая износостойкость, надёжность, работоспособность, экономичность, технологичность.

3. Библиографический поиск

Библиографический поиск проведен по теме: ”Зубчатые передачи, использованные в оптических приборах ” за период с 1956 по 1995 год по учебным пособиям и справочной литературе.

В результате проведенного поиска найдено девять источников, информация о которых представлена ниже.

Характерной особенностью оптических приборов является органичность сочетания и взаимодействия в них оптических и механических систем. Последние подразделяются на два основных вида: несущие и подвижные системы.

Несущие системы представляют собой комплексы неподвижных элементов (оснований, кронштейнов, плат, стоек и пр.) и предназначаются для базирования и внутреннего взаимного ориентирования оптических и других схемных элементов прибора. Они представляют собой общую компоновку конструкции, ее жесткость, технологичность сборки, надежность. Характерной особенностью является широкое применение в них регулировочно-юстировочных устройств, обусловленное высокими требованиями к точности оптических приборов, а также сравнительно низкий уровень унификации конструктивных решений.

Подвижные системы осуществляют механическое перемещение оптических систем и их элементов, обусловленное их функциональным назначением; образуют измерительные цепи приборов; являются основой устройств управления различными видами позиционирования, широко применяемого в оптических приборах; выполняют разнообразные простейшие транспортирующие функции. Подвижные системы представляют конструктивную реализацию кинематических цепей, поэтому проектирование их базируется на выборе типов исходных механизмов и на определении их параметров. Ведущую роль в данных механизмах играют малогабаритные редукторы.

Функциональное назначение механизмов в оптических приборах. В оптических приборах в основном встречаются три вида задач, решаемых с помощью механизмов: 1) позиционирования исполнительного элемента механизма в заданное положение; 2) передача измерительного сигнала от чувствительного элемента измерительной цепи на регистрирующее устройство; 3) осуществление процесса движения с целью перемещения некоторого рабочего элемента (кино- или магнитной ленты и т.п.).

Совокупность оптических деталей, установленных в положение, заданном расчетом и конструкцией, составляет оптическую систему прибора.

Оптические детали разделяются на следующие виды: линзы, зеркала, призмы и клинья, дифракционные решетки, сетки, экраны, светофильтры, защитные стекла, поляризационные призмы, поляфильтры, компенсаторы, световоды.

В качестве узлов рассматриваются части, состоящие из деталей, соединяемых склеиванием или устанавливаемых на оптическом контакте, а также объективы, окуляры, сложные призмы и типовые призменные системы. Эти детали и узлы являются основными элементами оптических приборов.

Однако, помимо перечисленных узлов, важную роль в оптических приборах играют зубчатые, червячные и ременные передачи.

Примеры зубчатых и других передач представлены в следующих устройствах, приведенных ниже, а также их назначение, основные требования и краткое описание работы.

Механизмы служат для осуществления заданного вида и закона механического движения. По условиям применения в подвижных системах оптических приборах (ПСОП) механизмы подразделяются на силовые, выполняющие простые транспортирующие функции; ходовые (применяются в основном при автоматизированном управлении движением) и точные механизмы. К первым предъявляются требования легкости и плавности хода, ко вторым- требование малости потерь на трение, к третьим- обеспечение заданной точности функционирования. Основные характеристики механизмов- структура и свойства. Структура сложного механизма, применяемого в оптических приборах, определяется числом и типами элементарных механизмов, составляющих его кинематическую цепь. /6, 7/

Классификиция узлов ОП, использующих зубчатые передачи представлено в следующей схеме:

Механическиеузлы ОП

системы визирования узлы перемещения юстировочные уст-ва

червячная червячная зубчато-реечная

цилиндрическая винтовая червячная

винтовая

Примеры узлов, содержащих зубчатые передачи в ОП, представлено на следующих рисунках:

1-оптическая труба; 2-червячное колесо;

Рисунок 1-Угломерное червячное устройство.

Применяется для измерения углового перемещения оптической зрительной трубы 1, соединенной с червячным колесом 2, имеет вход на колесе и выход на отсчетном устройстве, соединенным с червяком. /6/

z1, z2 ,…z10 -цилиндрические зубчатые колеса;

Рисунок 2-Визирная головка с дистанционным приводом.

Указанное устройство используется для дистанционного наведения визира. Устройство состоит из головной призмы и системы следящего электропривода. Исполнительным элементом является управляемый электродвигатель; обратная связь осуществляется с помощью двух вращающихся трансформаторов (ВТ)- грубого и точного отсчета. Наличие двух элементов обратной связи объясняется их невысокой точностью по сравнению с необходимой точностью визирования. Редуктор механизма состоит из цилиндрических прямозубых зубчатых колес (zn ). Для выборки мертвого хода в цепи призма-ВТ точного отсчета применены разрезные зубчатые колеса z2 и z4.

В качестве датчиков обратной связи можно применять потенциометры, сельсины и другие элементы, обеспечивающие необходимую точность. /7/

Фокусировочные механизмы.

Фокусировочные механизмы предназначены для получения резкого изображения объекта в микроскопах и контрольно-юстировочных устройствах. В настоящее время в микроскопостроении известно большое число различных схем и конструкций фокусировочных механизмов. Обычно, они состоят из раздельно функционирующих механизмов для грубого и тонкого перемещения. В качестве механизма грубого и тонкого перемещения чаще всего используют зубчато-реечную передачу, состоящую из косозубой шестерни и рейки. Применение такой передачи обусловлено необходимостью получить плавное перемещение ведомого элемента механизма. Плавность движения ведомых элементов фокусировочных механизмов- основное требование, которое предъявляется к этим механизмам. Пример фокусировочного механизма представлен на рисунке 3.

1-винт; 2-клин; 3-ролик; 4-каретка; 5-пружина;

Рисунок 3-Фокусировочный механизм.

В данном механизме, вращение винта 1 вызывает поступательное перемещение клина 2 вдоль оси винта. Перемещение клина вызывает перемещение каретки 4. Контакт каретки 4 с клином 2 осуществляется силовым замыканием с помощью пружины 5. Для уменьшения трения и увеличения плавности движения каретки 4 контакт ее с клином осуществляется через ролик 3. /6/

1-оправа; 2-качающаяся оправа; 3-основание; 4-червяк; 5-шпонка; 6-втулка;

Рисунок 4- Механизм вертикального наведения.

Механизм вертикального наведения визира состоит из оправы 1, установленной на юстировочных винтах в качающейся оправе 2. Оправа 2 вращается в шарикоподшипниках, закрепленных в кронштейнах на основании 3. Для исключения отклонения плоскости движения визирного луча от вертикальной плоскости призмы должна быть параллельна опорной плоскости основания. Качение призмы производится системой шток-рейка-зубчатый венец, причем в качестве рейки используется червяк. Червяк 4имеет лыску и фиксируется от поворота шпонкой 5, закрепленной во втулке 6, которая может поворачиваться, благодаря чему достигается установка визирного луча без осевого смещения червяка. /7/

Вследствие проведенного библиографического поиска можно сделать вывод, что в оптических приборах наиболее широкое применение нашли червячные и винтовые зубчатые передачи.

4. Выбор типа передачи и вида зацепления

Конические зубчатые передачи: конические зубчатые колёса применяют, когда необходимо получить передачу вращения между валами, оси которых пересекаются под углом. Наиболее часто применяют передачи с межосевым углом равным 90о. Конические колёса выполняют с прямым, косым и криволинейным (дуговым) направлением зубьев. В приборостроении преимущественно применяют конические колёса с прямыми зубьями.

Червячная передача . Показанная на (рис. 1, а)передача состоит из червяка 1, представляющего собой винт с трапецеидальным или близким к нему профилем витка, и червячного колеса 2. Передача вращения осуществляется между вилами, оси которых перекрещиваются. Во многих механизмах приборов такое расположение валов (рис. 1, б) оказывается наиболее оптимальным. Посредством червячной передачи можно осуществить большие передаточные отношения — до 300 и более; однако наиболее часто I =; 7… 100. Передачи характеризуются плавностью и бесшумностью работы. Обычно червячные передачи используют в качестве редукторов, т. е. когда движение передается от червяка к колесу. Наряду с этим в приборостроении применяют червячные передачи в качестве мультипликаторов, когда движение передается от червячного колеса к червяку (регуляторы скорости и др.). Существенным преимуществом червячных передач является возможность исключения обратной передачи вращения, т. е. от колеса к червяку. К недостаткам червячных передач относятся низкий к. п. д. из-за больших потерь на трение в зацеплении витков червяка с зубьями червячного колеса и необходимость по этой же причине выполнять червячные колеса или их зубчатые венцы из дорогих антифрикционных материалов.

Рис.1

Также есть винтовые передачи, они служат для преобразования вращательного движения в поступательное. Основными деталями винтовой передачи являются винт в виде цилиндра с наружной резьбой и гайка в виде кольца с внутренней резьбой. Винтовые передачи разделяют на силовые и кинематические (отсчетные). Силовые передачи работают при значительных нагрузках и должны иметь высокий к. п. д. и достаточную прочность. Кинематические винтовые передачи должны обеспечивать точность перемещения деталей и узлов приборов.

Также существуют и другие виды передач.

Наиболее распространённым среди видов передач является эвольвентное зацепление, предложенное ещё Эйлером. Благодаря своей технологичности и эксплуатационным качествам.

Эвольвентное зацепление . Наиболее распространенным профилем зубьев колес, отвечающим требованиям основной теоремы зацепления, является эвольвента окружности. Эвольвентой называется кривая, представляющая собой траекторию движения любой точки прямой, перекатывающейся без скольжения по окружности 2(рис. 2, а). Прямая 1 называется производящей прямой, а окружность 2— эволютой или (применительно к зубчатому колесу) основной окружностью.

Рис.2

При равномерном вращении колёс точки контакта, перемещаясь с одной и той же скоростью по линии зацепления, будут перемещаться не равномерно по профилю, т. е. два сопряжённых профиля перекатываются друг по другу со скольжением.

Зацепление Новикова применяется для передачи больших крутящих моментов.

Циклоидальные (часовые) зубчатые передачи. Профиль зуба колеса в циклоидальном зацеплении сложный. Он состоит из двух кривых, представляющих собой траектории движения точек двух производящих окружностей 2 и 3 (рис. 3 а) одна (2) их которых катится снаружи, а другая (3) – внутри основной окружности 1.

Рис. 3

При качении производящей окружности 2 образуется эпициклоидальный профиль 3 — гипоциклоидальный профиль М0Мг ножки зуба колеса. При r = r1 |2 профиль ножки — гипоциклоиды – становится радиально направленной прямой (рис. 3 б). В циклоидальной зубчатой передачи основные (они же начальные) окружности (рис. 3 в) соприкасаются в полюсе Р. Одна и та же производящая окружность 3 служит для образования ножки зуба колеса при качении её внутри основной окружности 1 и эпициклоидальной головки зуба шестерни (триба) при её качении снаружи основной окружности 2. Аналогично, производящая окружность 4 при качении внутри основной окружности 2 образует ножку зуба шестерни, а при качении снаружи основной окружности 1 – эпициклоидальный профиль головки зуба. По дугам N1 P и PN2 производящих окружностей перемещается точка контакта профиля зубьев колёс при работе передачи. Из рассмотренного вытекает, что каждому колесу должен соответствовать вполне определённый триб, поскольку головка зуба колеса образовывается производящей окружностью, служащей одновременно для получения ножки зуба триба. И, наоборот, каждому трибу соответствует вполне определённое колесо.

Основным достоинством циклоидальных передач является возможность изготовления трибов с малым числом зубьев (5…6), что позволяет значительно сокращать их габариты. Это послужило поводом к замене эпициклоидального зацепления профиля головок зубьев другой окружности. В отличие от циклоидального, зацепление таких профилей зубьев называется часовым. Соответствующим выбором радиуса ρ1 заменяющей окружности (рис 4) и её положения относительно центра колеса, определяемого радиусом r1, можно улучшить работу зубчатой передачи в реальных условиях, в частности приблизить начало зацепления к линии центров. Это обеспечивает значительное сокращение сил сопротивления вращению колёс в передаче. При замене дуг эпициклоид головок зубьев дугами окружностей значительно упрощается изготовление дисковых фрез для нарезания колёс и трибов, а также и червячных фрез.

Рис. 4

Разновидностью циклоидального является цевочное зацепление. Оно, по существу, мало отличается от часового. Основное отличие состоит лишь в том, что у зубьев шестерни (триба) отброшен прямолинейный участок ножки зуба и оставлен лишь дуговой профиль головки зуба, доведённый до цилиндра, оформленного конструктивно в виде так называемой цевки. Поэтому цевочное зацепление целесообразно назвать цевочным часовым зацеплением.

5. Разработка кинематической схемы

а) Определение обще-передаточного отношения.

Zi+1 – число зубьев ведомого колеса.

б) Определение числа ступеней.

Точность работы будет тем больше, чем меньше число ступеней.

Оптимальное число ступеней: ;

Передаточное отношение каждой ступени: ;

В соответствие с рекомендациями передаточное отношение ступеней в прямозубчатых передачах выбирается: i = 0,2…5. Число 3,8 принадлежит данному интервалу.

==>

∆%

в) Этап выбора зубьев колёс.

; ; ;

№ колёс	Расчётные значения	Значения по ГОСТ
Z1	25	25
Z2	90	92
Z3	25	25
Z4	95	96
Z5	25	25
Z6	100	102

u – количество z1

г) Кинематическая схема редукторов.

Приборные редукторы относятся к отдельно собираемым и самостоятельно регулируемым механизмам, и поэтому для них разрабатывается кинематическая схема. При хорошем выполнении кинематическая схема даёт ясное представление о пространственном расположении взаимодействующих элементов механизма. Для построения схемы обычно применяется изометрическая проекция, хотя разрешается применять и другие виды аксонометрических проекций. Все элементы на схеме изображаются в виде условных графических обозначений, установленных нормалями приборостроения. На контурах подвижных элементов (или около них) стрелками указываются направления вращения или перемещения подвижных элементов, а на линиях валиков стрелками обозначаются направления передачи величин при работе механизма. На схеме возле элементов или на выносках от них указываются основные данные, характеризующие их работу (числа зубьев, модули и степени точности зубчатых колёс, цены оборотов вращающихся элементов и т.п.).

На кинематических схемах буквой Б обозначен входной (быстроходный) вал редуктора, буквой Т – выходной (тихоходный).

Б

Т

6. Расчёты кинематики и геометрии

Исходным для расчёта является передаточное отношение ступеней: i1 =3,6; i2 =3,8; i3 =4.

а) Определение кинематики редуктора

Число оборотов вала:

Определение угловых скоростей валов проводятся по формуле:

Определение вращающих моментов:

№ вала	nоб /мин	ω c-1	M. 10-3 Н. м
1	1045	109,38	1,2
2	290	30,38	4,3
3	76	7,99	16
4	19	1,99	65

б) Расчёт геометрии зубчатых колёс.

Исходным для расчёта геометрии является значение модуля, которое выбирается из стандартного ряда в соответствие с ГОСТ 9563-60.

m = 0,4

Диаметр делительной окружности:

Диаметр окружных выступов:

Диаметр впадин:

Высота зуба:

Ширина венца:

Межосевое расстояние между валами:

№ колеса	zi	m мм	di мм	dв	dвп	hi мм	bi мм	ai
z1	25	0,4	10	10,8	9,6	1	4	23
z2	90	0,4	36	36,8	35,6	1	3
z3	25	0,4	10	10,8	9,6	1	4	24
z4	95	0,4	38	38,8	37,6	1	3
z5	25	0,4	10	10,8	9,6	1	4	25
z6	100	0,4	40	40,8	39,6	1	3

7. Разработка конструкции редуктора.

а) Выбор конструкции зубчатых колёс.

Конструкция определяется ГОСТом 13733-77.

рис. 5 рис. 6 рис. 7

Рисунок 5 – дисковые зубчатые колёса; рисунок 6 – колёса с односторонней ступицей; рисунок 7 – с двусторонней ступицей.

Определяющим, при выборе той или иной конструкции является требование по исключению проскальзывания зубчатых колёс на валу редуктора, поэтому при числе оборотов вала об /мин рекомендуется использовать колёса со ступицей, а для валов с об /мин выбирают дисковые колёса. Поэтому для первого вала выбираем конструкцию, указанную на рис.6, а для второго, третьего и четвёртого валов конструкцию, указанную на рис.5.

б) Расчёт валов.

Он начинается с определения диаметров цапф из расчёта на чистое кручение.

В качестве материала для валов берётся сталь Ст 45 [τ] = 17 Н /мм2

Конструктивно диаметры валов различают на: гладкие и ступенчатые.

Для монтажа колёс на валу предпочтительнее ступенчатые, поэтому для посадки колёс назначают следующие диаметры: dв > dц на 1-2 мм для ступенчатых, и

dв =dц – для гладких.

в) Выбор опор.

Для шарикоподшипников в основном используют опоры с трением качения и трением скольжения. Выбор шарикоподшипников производится по диаметру цапфы в соответствии с ГОСТ 8338-75 с учётом прессовой посадки.

Обозначения подшипников	d	Грузоподъёмность Н
Ср	Сст
1000091	1	125	34
1000092	2	280	86
1000093	3	560	186

Проводим проверку на динамическую грузоподъёмность:

n берётся максимальное (об /мин )

L – долговечность (в часах)

L=10000

Р – эквивалентная динамическая нагрузка.

X – коэффициент нагрузки

V – коэффициент вращения

Кб – коэффициент безопасности

КТ – температурный коэффициент

Для цилиндрической передачи X=V=Кб =КТ =1

Fr – радиальная нагрузка на вал

Для второго вала:

Для предпоследнего вала:

α – угол профиля; α = 20о

Для последнего вала:

г) Прочностной расчёт редуктора.

Он проводится на базе конструктивной схемы.

Расчёт балки на изгиб проводится для наиболее нагруженных валов, то есть для последнего и предпоследнего валов. Для предпоследнего вала величина радиальных сил равна:

Расчётно-проектировочный диаметр вала:

[σ] – предел прочности материала вала

0,4[σ]=[τ]кр

Определяем запас прочности:

Расчёт зубьев на прочность. Рассчитывается зуб шестерня:

Fτ – для предпоследнего вала

КF – коэффициент нагрузки

Для цилиндрической прямозубой передачи КFβ =1,07 КFV =1,15

YF – коэффициент формы зуба выбирается по числу зубьев шестерня.

YF = 3,9

Допустимое напряжение на прочность.

В большинстве случаев напряжение изгиба меняется по прерывистому циклу, то есть зависит от базового числа циклов:

SF – коэффициент безопасности

ЅF =Ѕr ЅF*

Sr =1,75 S*F =1

д) Расчёт КПД редуктора.

КПД редуктора называется отношение величины полезной работы ведомого звена за цикл работы механизма к величине работы ведущего звена.

Расчёт КПД цилиндрической прямозубой передачи ведётся по формуле:

μ – коэффициент трения в передаче

μ=0,1

с – коэффициент, учитывающий увеличение трения при нагрузках.

, где

е) Описание конструкции редуктора.

Редуктор включает в себя 4 вала с закреплёнными на них шестернями, находящихся в позиции 3, 5. Посадка зубчатых колёс позиция 4, 6 на валы и закрепление с помощью штифтов позиция 13.

ж) Определение коэффициента заполнения.

8. Заключение

В соответствии с техническим заданием на базе патентно-библиографического поиска была разработана кинематическая схема редуктора. Прочностные расчёты показали, что редуктор работоспособен. Достоинства: высокий КПД, постоянство передаточного отношения, надёжность, долговечность, простота в эксплуатации.

Недостатки: шум, возникающий во время работы редуктора при неточном изготовлении колёс.

Список литературы

1. Дмитриев Ф. С. «Проектирование редукторов точных приборов» Ленинград «Машиностроение» 1971

2. Курсовое проектирование деталей машин Москва «Машиностроение» 1988

3. Мосягин Р. В., Павлов Б. И. «Детали и узлы малогабаритных редукторов» Справочное пособие, «Машиностроение» Ленинград 1967

4. Элементы приборных устройств в 2 частях под ред. Тищенко О. Ф. Москва «Высшая школа» 1982