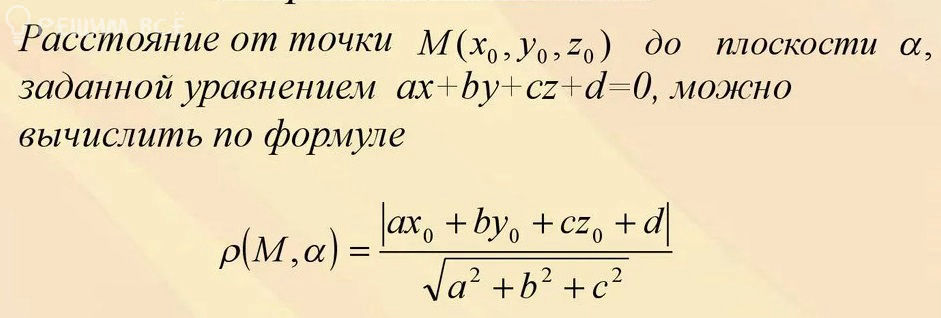Как найти площадь грани а1а2а3а4

Точки A1,A2,A3,A4 являются вершинами пирамиды. Вычислить ее объем, площадь грани А1 А2 А3 и высоту пирамиды, опущенную на данную грань.  

А1(-2,-1,-1), А2(0,3,2), А3(3,1,-4), А4(-4,7,3).

1) Сначала находим площадь грани А1А2А3 как половину модуля векторного произведения векторов А1А2 и А1А3.

Находим векторы:

А1А2 = (0-(-2); 3-(-1); 2-(-1)) = (2; 4; 3).

А1А3 = (3-(-2); 1-(-1); -4-(-1)) = (5; 2; -3).

A1A2*A1A3=  I          j          k|         I           j

         A1A2= 2         4          3|        2          4

         A1A3=  5        2         -3|        5          2 = -12i + 15j + 4k – (-6)j – 6i – 20k =

-18i + 21j – 16k.

Нормальный вектор плоскости А1А2А3 равен (-18; 21; -16).

S(A1A2A3)= 0,5(√(324+441+256) = √1021/2 ≈ 15,9765.

2) Находим вектор А1А4.

А1А4 = (-4-(-2); 7-(-1); 3-(-1)) = (-2; 8; 4).

Объём пирамиды равен 1/6 смешанного произведения векторов (А1А2хА1А3)*А1А4.

(А1А2хА1А3) = -18; 21; -16

            А1А4 =   -2;   8;    4    

                          36 + 168 – 64 =   140.

V = (1/6)*140 = 70/3 ≈ 23,3333.

3) Высоту пирамиды  находим по формуле:

H = 3V/So = (3*(70/3))/( √1021/2 ) =  140/√1021 = 140*√1021/1021 ≈ 4,38142.

Талаев Михаил

Профи

(794),
закрыт

9 лет назад

Даны координаты вершин тетраэдра А1А2А3А4. Вычислить площадь грани А1А2А3 и обьем пирамиды.
A1(-1;0;-2) A2(-6;2;-5) A3(-4;3;-1) A4(1;-3;-1)

— —

Мастер

(1972)


10 лет назад

Источник: Геометрический смысл векторного и смешанного произведения векторов.

Вопрос задан анонимно

18.01.20

1 ответ

11-20. Даны координаты вершин пирамиды А1, А2,А3А4. Найти:
1) синус угла между ребром А1, A4 и гранью А1, A2,A3.
2) площадь грани А1,A2,A3.
3) объем пирамиды А1,A2,A3,A4.
4) длину высоты, опущенной из точки А4 на грань А1А2А3;
5) координаты точки А5, симметричной точке А4 относительно грани
A1A2A3.

17 номер
17. A1 (2;4; -3), A2 (2; 5; -4), A3(-2; 2; 1), A4 (-3; 0; -1).

математика 10-11 класс
191

vector{A_(1)A_{2}}=(2-2;5-4;-4-(-3))=(0;1;-1)
vector{A_(1)A_{3}}=(-2-2;2-4;1-(-3))=(-4;-2;4)
vector{A_(1)A_{4}}=(-3-2;0-4;-1-(-3))=(-5;-4;4)

Пусть M (x;y;z) – произвольная точка плоскости A_(1)A_(2)A_(3)
Тогда векторы
vector{A_(1)M}=(x-2;y-4;z-(-3))=(x-2;y-4;z+3)
vector{A_(1)A_{2}}=(0;1;-1)
vector{A_(1)A_{3}}=(-4;-2;4)

лежат в одной плоскости, значит компланарны.

Условие компланарности – равенство нулю смешанного произведения векторов.

[m](vec{A_{1}M},vec{A_{1}A_{2}},vec{A_{1}A_{3}})=begin {vmatrix} x-2&y-4&z+3\0&1&-1\-4&-2&4end {vmatrix}[/m]

Раскрываем определитель, получаем

[m]=х+2у+2z-4[/m]

Приравниваем к 0 и получаем уравнение плоскости [m]A_{1}A_{2}A_{3}[/m]

[m]=х+2у+2z-4=0[/m]

Нормальный вектор плоскости [m]A_{1}A_{2}A_{3}[/m]

[m]vec{n}=(1;2;2)[/m]

Направляющий вектор прямой [m]A_{1}A_{4}[/m]

[m]vec{A_{1}A_{4}}=(-5;-4;4)[/m]

Находим косинус угла между векторами
[m]vec{n}=(1;2;1)[/m] и [m]vec{A_{1}A_{4}}=(1;1;3)[/m]

[m]vec{n}cdot vec{A_{1}A_{4}}=-5cdot 1+(-4)cdot 1+4cdot 3=3[/m]

[m]|vec{n}|=sqrt{1^2+2^2+2^2}=sqrt{9}=3[/m]

[m]|vec{A_{1}A_{4}}|=sqrt{(-5)^2+(-4)^2+4^2}=sqrt{57}[/m]

[m]cos ∠( vec{n}, vec{A_{1}A_{4}})=frac{6}{sqrt{6}cdot sqrt{11}}=frac{3}{3cdot sqrt{57}}=frac{1}{sqrt{57}}[/m]

Угол φ между прямой и плоскостью дополняет угол между векторами, поэтому синус дополнительного угла и есть найденный косинус

[m]sin φ =sin(90 °- ∠ vec{n}, vec{A_{1}A_{4}}))=cos∠( vec{n}, vec{A_{1}A_{4}})=frac{1}{sqrt{57}}[/m]
2)
[m]S_{A_{1}A_{2}A_{3}}=frac{1}{2}|vec{A_{1}A_{2}} × vec{A_{1}A_{3}}|[/m]

Находим векторное произведение векторов : [m]vec{A_{1}A_{2}}[/m] и [m]vec{A_{1}A_{3}}[/m]

[m]vec{A_{1}A_{2}} × vec{A_{1}A_{3}}]begin {vmatrix} vec{i}&vec{j}&vec{k}\0&1&-1-4&-2&4end {vmatrix}=2vec{i}+4vec{j}+4vec{k}[/m]

[m]S_{A_{1}A_{2}A_{3}}=frac{1}{2}sqrt{2^2+4^2+4^2}=sqrt{36}=6[/m]

3)
[m]V=frac{1}{6}|(vec{A_{1}A_{2}},vec{A_{1}A_{3}},vec{A_{1}A_{4}})|[/m]

[m](vec{A_{1}A_{2}},vec{A_{1}A_{3}},vec{A_{1}A_{4}})=begin {vmatrix}0&1&-1\-4&-2&4\-5&-4&4end {vmatrix}=…=(-10)[/m]

[m]V=frac{1}{6}|-10|=frac{5}{3}[/m]

5)

4)
Найдем расстояние от точки [m]A_{4}[/m] до плоскости [m]A_{1}A_{2}A_{3}[/m] :

[m] ρ =frac{|-3+2cdot 0+ 2cdot 1-4|}{sqrt{1^2+2^2+2^2}}=frac{|-5|}{3}=frac{5}{3}[/m]

По формуле: