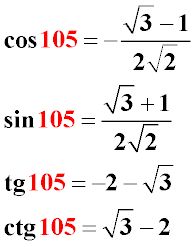
Как найти значения тригонометрических функций для угла 105 градусов
Найдем значения синуса, косинуса и тангенса для угла 105 градусов аналитическим способом.
На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 105 градусов – задача сложная. Однако, это не совсем так.
Прежде всего, мы должны обратить внимание, что для углов, значения которых превышают 90 градусов, у нас есть формулы приведения к углу, меньшему 90 градусов.
Поэтому, для начала, представим себе угол в 105 градусов как (90 + 15)
Тогда
sin ( 90 + α ) = cos α
sin 105 = sin( 90 + 15 ) = cos 15
cos ( 90 + α ) = – sin α
cos 105 = cos( 90 + 15 ) = -sin 15
tg ( 90 + α ) = -ctg α
tg 105 = tg( 90 + 15 ) = -ctg 15
Примечание. Уже на данном этапе можно посмотреть значения в таблицах синуса, косинуса и тангенса 105 градусов, который преобразован в значения тригонометрических функций синуса, косинуса и тангенса угла 15 градусов. Но, представим себе, что мы тоже их не знаем.
Поэтому, на данном этапе нам на помощь придут формулы преобразования двойного угла тригонометрических функций.
Дело в том, что мы можем представить угол в 30 градусов, как двойной угол 15 градусов ( 2 * 15 ).
Тогда, отталкиваясь от тождества:
cos 2α = 1 – 2sin2α
Принимаем двойной угол как 2 * 15 градусов, тогда
cos 30 = 1 – 2sin215
sin215 = ( 1 – cos 30 ) / 2
Значение косинуса для угла 30 градусов легко вычислить. Оно равно √3/2
sin215 = ( 1 – √3/2 ) / 2
sin 15 = √ (( 1 – √3/2 ) / 2 )
cos 105 = – sin 15
cos 105 = – √ (( 1 – √3/2 ) / 2 )
путем несложных агебраических преобразований получаем:
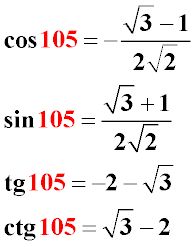
Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 105 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств преобразований двойных углов и половин заданных углов.
См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).
Ниже приведены также значения тригонометрических функций для угла 105 градусов в виде десятичной дроби с четырьмя знаками после запятой.
|
5π/12 |
синус 105 sin 105 |
косинус 105 cos 105 |
тангенс 105 tg 105 |
котангенс 105 ctg 105 |
|
Значение |
0,9659 |
–0,2588 |
–3,7321 |
–0,2679 |
0
Синус, косинус, тангенс угла 30 и 60 градусов (sin cos tg 30 и 60) |
Описание курса
| Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120)
Прискилла
30 декабря, 03:12
-

Виктбрия
30 декабря, 04:19
0
Sin (105) = sin (45+60) = sin60cos45+sin45cos60 = (((корень из6) + (кореньиз2))) / 4
- Комментировать
- Жалоба
- Ссылка
-

Данила
30 декабря, 04:46
+1
Sin (105) = sin (45+60) = sin45*cos60+cos45*sin60=√2/2 * (1/2+√3/2) = √2 (1+√3) / 4
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Вычислите: sin 105 градусов …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
В статье мы расскажем, как находить значения:
(cos300^°), (sin(-540^°)), (cos 510^°), (sin(-135^°))
и других тригонометрических выражений без тригонометрической таблицы.
Как вычисляются синусы и косинусы углов?
Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен – абсциссе, а синус угла – ординате.
Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.
Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Получается, (cos 30^° = frac{sqrt{3}}{2}), а (sin30^° =frac{1}{2}).
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac{1}{2}=±0,5); (±frac{sqrt{2}}{2} ≈±0,707); (±frac{sqrt{3}}{2} ≈±0,866).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Для этого нужно знать несколько фактов:
- Начало отсчета находится в крайней правой точке окружности;
-
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
-
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
-
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:


- Одна точка может соответствовать разным углам;
- Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.
Пример. Отметьте угол в (90^° ) и (-90^°).
Решение:

Пример. Отметьте угол в (225^° ) и (-135^°).
Решение: (225^°=180^°+45^°)
(-135^°=-90^°-45^°)

Пример. Отметьте угол в (420^° ) и (-390^°).
Решение: (420^°=360^°+60^°)
(-390^°=-360^°-30^°)


Задание 1. Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).
Как находить синус и косинус любого угла?
Простой алгоритм:
- Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
- Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
- Найдите координаты точки, используя картинку ниже.

Пример. Вычислите (sin300^°) и (cos300^°) .
Решение: (300^°=360^°-60^°)

(cos 300^°=frac{1}{2}), (sin{300^°}=-frac{sqrt{3}}{2}).
Пример . Вычислите (sin(-540^°)) и (cos(-540^°)) .
Решение. (-540^°=-360^°-180^°).

(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos(-540^°)=-1), а (sin(-540^° )=0).
Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье.
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).

Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения (-18sqrt{2}sin(-135^°)).
Решение. (-135^°=-90^°-45^°)

Получается (-18sqrt{2} sin(-135^° )=-18sqrt{2}cdot-frac{sqrt{2}}{2}=frac{18cdotsqrt{2}cdotsqrt{2}}{2}=9cdot 2=18.)
Ответ: (18).
Пример . Найдите значение выражения (54sqrt{3}cos(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)

(54sqrt{3}cos(510^°)=54sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{54cdot sqrt{3}cdot sqrt{3}}{2}=-27cdot 3=-81.)
Ответ: (-81).
Смотрите также:
Как найти тангенс и котангенс без тригонометрической таблицы? Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
Синус 105 градусов 12 минут равен 0.9650164945
sin(105°12′) = sin(105.2°)
sin(105.2°) = 0.9650164945
| sin(105°12′0″) = 0.9650164945 | sin(105°12′20″) = 0.9649910674 | sin(105°12′40″) = 0.9649656312 |
| sin(105°12′1″) = 0.9650152233 | sin(105°12′21″) = 0.9649897958 | sin(105°12′41″) = 0.9649643591 |
| sin(105°12′2″) = 0.9650139522 | sin(105°12′22″) = 0.9649885241 | sin(105°12′42″) = 0.964963087 |
| sin(105°12′3″) = 0.965012681 | sin(105°12′23″) = 0.9649872525 | sin(105°12′43″) = 0.964961815 |
| sin(105°12′4″) = 0.9650114098 | sin(105°12′24″) = 0.9649859808 | sin(105°12′44″) = 0.9649605428 |
| sin(105°12′5″) = 0.9650101385 | sin(105°12′25″) = 0.9649847092 | sin(105°12′45″) = 0.9649592707 |
| sin(105°12′6″) = 0.9650088673 | sin(105°12′26″) = 0.9649834375 | sin(105°12′46″) = 0.9649579985 |
| sin(105°12′7″) = 0.965007596 | sin(105°12′27″) = 0.9649821657 | sin(105°12′47″) = 0.9649567264 |
| sin(105°12′8″) = 0.9650063247 | sin(105°12′28″) = 0.964980894 | sin(105°12′48″) = 0.9649554542 |
| sin(105°12′9″) = 0.9650050534 | sin(105°12′29″) = 0.9649796222 | sin(105°12′49″) = 0.9649541819 |
| sin(105°12′10″) = 0.965003782 | sin(105°12′30″) = 0.9649783504 | sin(105°12′50″) = 0.9649529097 |
| sin(105°12′11″) = 0.9650025107 | sin(105°12′31″) = 0.9649770786 | sin(105°12′51″) = 0.9649516374 |
| sin(105°12′12″) = 0.9650012393 | sin(105°12′32″) = 0.9649758067 | sin(105°12′52″) = 0.9649503651 |
| sin(105°12′13″) = 0.9649999679 | sin(105°12′33″) = 0.9649745349 | sin(105°12′53″) = 0.9649490928 |
| sin(105°12′14″) = 0.9649986964 | sin(105°12′34″) = 0.964973263 | sin(105°12′54″) = 0.9649478204 |
| sin(105°12′15″) = 0.964997425 | sin(105°12′35″) = 0.9649719911 | sin(105°12′55″) = 0.9649465481 |
| sin(105°12′16″) = 0.9649961535 | sin(105°12′36″) = 0.9649707191 | sin(105°12′56″) = 0.9649452757 |
| sin(105°12′17″) = 0.964994882 | sin(105°12′37″) = 0.9649694472 | sin(105°12′57″) = 0.9649440033 |
| sin(105°12′18″) = 0.9649936105 | sin(105°12′38″) = 0.9649681752 | sin(105°12′58″) = 0.9649427308 |
| sin(105°12′19″) = 0.9649923389 | sin(105°12′39″) = 0.9649669032 | sin(105°12′59″) = 0.9649414584 |
