Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа).
Уравнение Клапейрона-Менделеева (1834 г) устанавливает связь между объемом V, давлением P и абсолютной температурой Т для газа:
n – число молей газа  ;
;
P – давление газа, Па;
V – объем газа, м 3 ;
T – абсолютная температура газа, К;
R – универсальная газовая постоянная 8,314 Дж/моль×K.
Если объём газа выражен в литрах, то уравнение Клапейрона-Менделеева записывается в виде:

Из уравнения Клапейрона-Менделеева следует три закона:
Уравнение состояния идеального газа – основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения 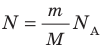
Произведение числа Авогадро 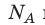 на постоянную Больцмана k называют универсальной газовой постоянной (R): R=
на постоянную Больцмана k называют универсальной газовой постоянной (R): R=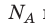 k 8,31 Дж/ (моль⋅К). Заменив в уравнении (*)
k 8,31 Дж/ (моль⋅К). Заменив в уравнении (*) 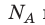 k на R, получим уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
k на R, получим уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
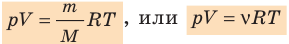
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (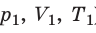 ) в состояние (
) в состояние (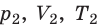 ) (рис. 30.1).
) (рис. 30.1).
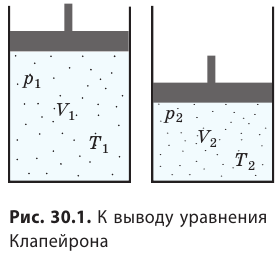
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 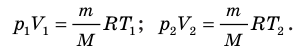 Разделив обе части первого уравнения на
Разделив обе части первого уравнения на 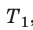 , а второго — на
, а второго — на 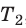 , получим:
, получим: 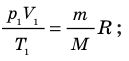
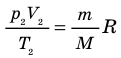 . Правые части этих уравнений равны; приравняв левые части, получим уравнение Клапейрона:
. Правые части этих уравнений равны; приравняв левые части, получим уравнение Клапейрона:
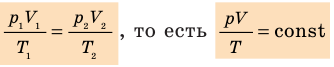
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (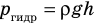 ) давление на глубине больше атмосферного. Температура же внутри пузырька практически не изменяется. В данном случае имеем дело с процессом изотермического расширения.
) давление на глубине больше атмосферного. Температура же внутри пузырька практически не изменяется. В данном случае имеем дело с процессом изотермического расширения.
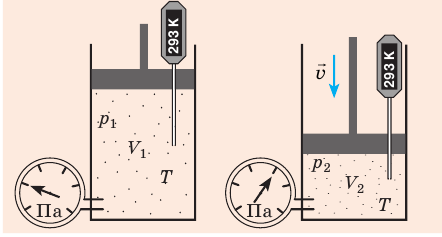
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (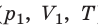 ) в состояние (
) в состояние (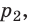
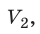 T), то есть температура газа остается неизменной (рис. 30.2). Тогда согласно уравнению Клапейрона имеет место равенство p
T), то есть температура газа остается неизменной (рис. 30.2). Тогда согласно уравнению Клапейрона имеет место равенство p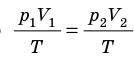 . После сокращения на T получим:
. После сокращения на T получим: 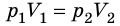 .
.
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
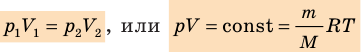
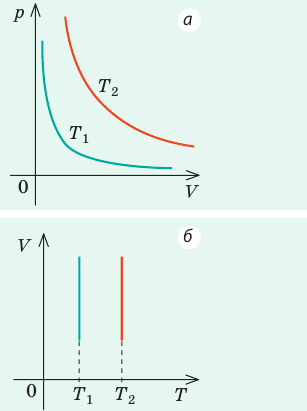
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 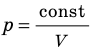 . Эту зависимость в координатах p, V можно представить в виде гиперболы (рис. 30.3, а). Поскольку при изотермическом процессе температура газа не изменяется, в координатах p, T и V, T изотермы перпендикулярны оси температур (рис. 30.3, б, в).
. Эту зависимость в координатах p, V можно представить в виде гиперболы (рис. 30.3, а). Поскольку при изотермическом процессе температура газа не изменяется, в координатах p, T и V, T изотермы перпендикулярны оси температур (рис. 30.3, б, в).

Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (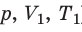 ) в состояние (
) в состояние (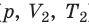 ), то есть давление газа остается неизменным (рис. 30.4). Тогда имеет место равенство
), то есть давление газа остается неизменным (рис. 30.4). Тогда имеет место равенство 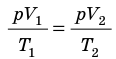 . После сокращения на p получим:
. После сокращения на p получим: 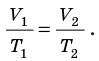
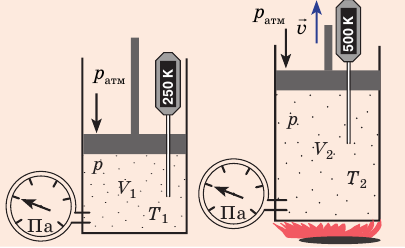
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p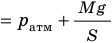
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
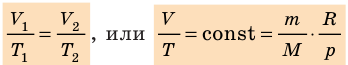
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
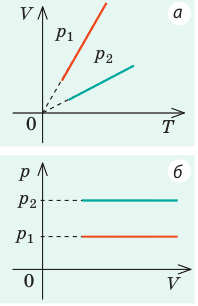

Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (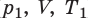 ) в состояние (
) в состояние (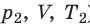 ), то есть объем газа не изменяется (рис. 30.6). В этом случае имеет место равенство
), то есть объем газа не изменяется (рис. 30.6). В этом случае имеет место равенство 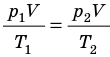 . После сокращения на V получим:
. После сокращения на V получим: 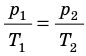
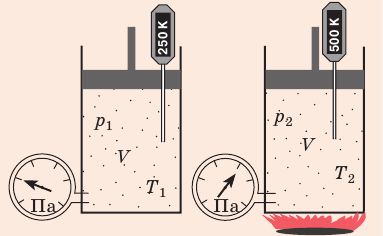
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно: 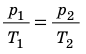
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
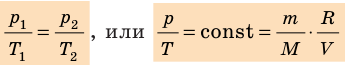
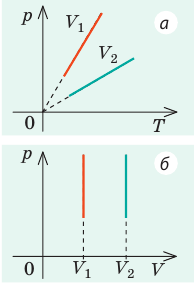
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).

Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
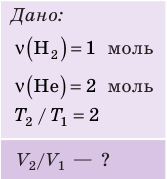
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется: , но использовать закон Бойля — Мариотта нельзя, так как вследствие диссоциации (распада) молярная масса и число молей водорода увеличились в 2 раза:
, но использовать закон Бойля — Мариотта нельзя, так как вследствие диссоциации (распада) молярная масса и число молей водорода увеличились в 2 раза: 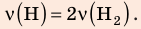
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 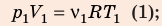
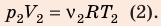 Разделив уравнение (2) на уравнение (1) и учитывая, что
Разделив уравнение (2) на уравнение (1) и учитывая, что  получим:
получим: 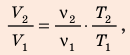 где
где 
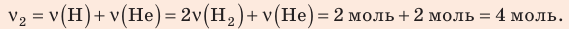 Найдем значение искомой величины:
Найдем значение искомой величины: 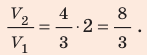
Ответ: примерно в 2,7 раза.
Пример №2
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
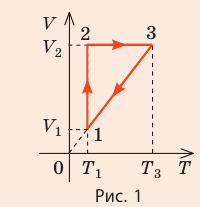
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
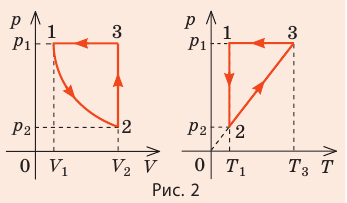
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
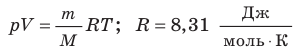 — универсальная газовая постоянная.
— универсальная газовая постоянная. - Уравнение Клапейрона:
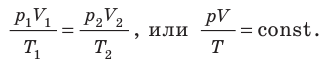
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:

| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Уравнение идеального газа pv vrt
Уравнение Менделеева-Клапейрона – уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем Vm и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:
pV = RT , где R — универсальная газовая постоянная,
R = 8,31 Дж/(моль . К)
Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT. или pV = NАkT,
где NА — число Авогадро, k — постоянная Больцмана.

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров – давление, объем или температура – остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.
Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.

Изотермический процесс – процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля – Мариотта.
Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой – термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P1V1=P2V2=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.

Изобарный процесс – процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.

Изохорный процесс – процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.

Итак, из закона pV = (М/m) . RT выводятся следующие законы:
p = const => V/T = const — закон Гей – Люссака .
V= const => p/T = const — закон Шарля
Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление – это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.

Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро NA = 6,02·10 23 ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.
В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна NA?
Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:
N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.
Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/NA. Отсюда:
NA = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23
PV 7,95 . 10 -4 . 3 . 10 -2
В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.
[spoiler title=”источники:”]
http://www.evkova.org/uravnenie-sostoyaniya-idealnogo-gaza
http://www.sites.google.com/site/opatpofizike/uravnenie-mendeleeva-klapejrona
[/spoiler]
Объем обозначают V и измеряют объем в кубическом метре, в кубическом сантиметре, в кубическом дециметре или литре. Науку геометрию стоит учить с самого начала изучения предмета в школе и формулы стоит хотя бы заучивать, если не можем по памяти доказать теоремы. Объем также измеряют в галлонах и баррелях.
Объем куба высчитывают исходя из длины его грани или ребра, то есть объем куба, который обозначаем V равен длина грани или ребра в кубе. Смотрите формулу

Чтобы узнать объем параллелепипида прямоугольного,смотрите формулу

Объем пирамиды высчитывают по этой формуле

Школьные знания очень пригождаются во взрослой жизни, можно высчитать объем жилого фонда самостоятельно
1
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 700 К, P = 20 941,2 Па, V = 9,5 м3.
2
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите объём V (в м3), если T = 250 К, P = 23 891,25 Па, ν = 48,3 моль.
3
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите давление P (в Паскалях), если T = 250 К, ν = 16,4 моль, V = 8,2 м3.
4
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если P = 77698,5 Па, ν = 28,9 моль, V = 1,7 м3.
5
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите объём V (в м3), если T = 700 К, P = 49444,5 Па, υ = 73,1 моль.
6
Закон Менделеева–Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К ⋅ моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 500 К, P = 65 787,5 Па, V = 5,4 м3.
7
Закон Менделеева–Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К · моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 400 К, P = 13 030,08 Па, V = 5 м3.
8
Закон Менделеева–Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К ⋅ моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 250 К, P = 63 156 Па, V = 1 м3.
9
Закон Менделеева–Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К ⋅ моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 400 К, P = 13 296 Па, V = 4,9 м3.
10
Закон Менделеева–Клапейрона можно записать в виде PV=νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К ⋅ моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 300 К, P = 4986 Па, V = 0,7 м3.
11
Закон МенделееваКлапейрона можно записать в виде
где
давление (в паскалях),
объём (в м
),
количество вещества (в молях),
температура (в градусах Кельвина), а
универсальная газовая постоянная, равная 8,31 Дж/(К
моль). Пользуясь этой формулой, найдите температуру
(в градусах Кельвина), если
моль,
Па,
м
12
Закон МенделееваКлапейрона можно записать в виде
где
давление (в паскалях),
объём (в м
),
количество вещества (в молях),
температура (в градусах Кельвина), а
универсальная газовая постоянная, равная 8,31 Дж/(К
моль). Пользуясь этой формулой, найдите давление
(в паскалях), если
К,
моль,
м
13
Закон МенделееваКлапейрона можно записать в виде
где
давление (в паскалях),
объём (в м
),
количество вещества (в молях),
температура (в градусах Кельвина), а
универсальная газовая постоянная, равная 8,31 Дж/(К
моль). Пользуясь этой формулой, найдите температуру
(в градусах Кельвина), если
моль,
Па,
м
14
Закон МенделееваКлапейрона можно записать в виде
где
давление (в паскалях),
объём (в м
),
количество вещества (в молях),
температура (в градусах Кельвина), а
универсальная газовая постоянная, равная 8,31 Дж/(К
моль). Пользуясь этой формулой, найдите температуру
(в градусах Кельвина), если
моль,
Па,
м
15
Закон МенделееваКлапейрона можно записать в виде
где
давление (в паскалях),
объём (в м
),
количество вещества (в молях),
температура (в градусах Кельвина), а
универсальная газовая постоянная, равная 8,31 Дж/(К
моль). Пользуясь этой формулой, найдите объём
(в м
), если
К,
Па,
моль.
16
Закон МенделееваКлапейрона можно записать в виде
где
давление (в паскалях),
объём (в м
),
количество вещества (в молях),
температура (в градусах Кельвина), а
универсальная газовая постоянная, равная 8,31 Дж/(К
моль). Пользуясь этой формулой, найдите температуру
(в градусах Кельвина), если
моль,
Па,
м
17
Закон МенделееваКлапейрона можно записать в виде
где
давление (в паскалях),
объём (в м
),
количество вещества (в молях),
температура (в градусах Кельвина), а
универсальная газовая постоянная, равная 8,31 Дж/(К
моль). Пользуясь этой формулой, найдите температуру
(в градусах Кельвина), если
моль,
Па,
м
18
Закон МенделееваКлапейрона можно записать в виде
где
давление (в паскалях),
объём (в м
),
количество вещества
(в молях),
температура (в градусах Кельвина), а
универсальная газовая постоянная, равная 8,31 Дж/(К
моль). Пользуясь этой формулой, найдите объём
(в м
), если
К,
Па,
моль.
19
Закон МенделееваКлапейрона можно записать в виде
где
давление (в паскалях),
объём (в м
),
количество вещества (в молях),
температура (в градусах Кельвина), а
универсальная газовая постоянная, равная 8,31 Дж/(К
моль). Пользуясь этой формулой, найдите температуру
(в градусах Кельвина), если
моль,
Па,
м
ОГЭ 2018 Математика Задание 13
Закон Менделеева–Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите количество вещества ν (в молях), если T = 700 К, P = 20941,2 Па, V = 9,5 м3.
Булат Юсупов
Ученик
(121),
на голосовании
7 лет назад
Голосование за лучший ответ
Георгий Тильковский
Мыслитель
(7295)
7 лет назад
T=PV/(vR)
Закон Менделеева-Клапейрона можно записать в виде PV = νRT, где P — давление (в паскалях), V — объём (в м3), ν — количество вещества (в молях), T — температура (в градусах Кельвина), а R — универсальная газовая постоянная, равная 8,31 Дж/(К⋅моль). Пользуясь этой формулой, найдите температуру T (в градусах Кельвина), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м3.
Спрятать решение
Решение.
Выразим температуру из закона Клапейрона-Менделеева: Подставляя, получаем:
Ответ: 400.
Сложность:
Среднее время решения: 3 мин. 21 сек.
ОГЭ по математике 2022 задание 12: номер 16 | Закон Менделеева—Клапейрона …
45
Закон Менделеева—Клапейрона можно записать в виде $PV=ν RT$, где $P$ — давление (в паскалях), $V$ — объём (в м${^3}$), $ν$ — количество вещества (в молях), $T$ — температура (в градусах Кельвина), а $R$ — универсальная газовая постоянная, равная $8{,}31$ Дж/(К$⋅$моль). Пользуясь этой формулой, найдите температуру $T$ (в градусах Кельвина), если $ν=66{,}8$ моль, $P=13877{,}7$ Па, $V=10$ м$^3$.
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
Период колебания математического маятника (в секундах) приближённо можно вычислить по формуле $T=2√ {l}$, где $l$ — длина нити в метрах. Пользуясь этой формулой, найдите длину нити мая…
Зная длину своего шага, человек может приближённо подсчитать пройденное им расстояние $s$ по формуле $s=nl$, где $n$ — число шагов, $l$ — длина шага. Какое расстояние прошёл человек, если …
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой $F=1{,}8C+32$, где $C$ — градусы Цельсия, $F$ — градусы Фаренгейта. Какая температура по шка…
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой $F=1{,}8C+32$, где $C$ — градусы Цельсия, $F$ — градусы Фаренгейта. Какая температура по шка…
Справочные материалы ОГЭ 2022 по математикеadmin2021-11-19T17:47:22+03:00
Скачать справочные материалы в формате pdf.
Комментарии для сайта Cackle
nikoniko2027
Профи
(933),
на голосовании
9 лет назад
Голосование за лучший ответ
Машенька
Профи
(999)
9 лет назад
v = pV/ RT
Похожие вопросы


