Насколько врёт спидометр автомобиля
Если в поездках на автомобиле вы пользуетесь навигатором, то наверняка замечали, что данные о скорости, отражаемые на спидометре и в навигаторе, несколько отличаются друг от друга. Почему так происходит, а также от чего зависит разница – узнаете из этой статьи.

Насколько точно показывает спидометр скорость автомобиля
Точность показаний спидометра зависит от его разновидности. Измерители бывают:
- механическими;
- электронными.
В заднеприводных автомобилях показания механического измерителя напрямую связаны с передаточным числом редуктора. Изменение передаточного числа сказывается на данных о быстроте движения авто. Влияет на погрешность также изношенность редуктора и состояние шин. В сумме неточность показаний может составлять более 10 %.
В переднеприводных авто механический прибор получает данные о скорости от привода левого колеса, расположенного выше главной пары. При правом повороте показания измерителя увеличиваются, при левом – уменьшаются в сравнении с движением по прямому отрезку.
Электронные спидометры получают данные за счёт контроля над вращением ведущего колеса. Несмотря на то что им не страшны люфт, износ троса или катушки и прочие неприятности, свойственные механическим приборам, всё же назвать их абсолютно точными нельзя. Погрешность электронных измерителей составляет примерно 5-7 %.
В среднем погрешность прибора может достигать 10 % при скорости 200 км/ч.
От чего зависит погрешность
Спидометр является измерительным прибором, а ни один из них не может функционировать без погрешностей, которые делятся на:
- инструментальные, зависящие от точности самого измерительного прибора;
- методические, на которые влияет способ измерения той или иной величины (в данном случае — скорости);
- дополнительные, к ним можно отнести, например, использование не предусмотренных производителем автомобиля шин или отличающихся по размеру дисков.
Неточность измерителя различается в зависимости от привода автомобиля:
- у заднеприводных она составляет около 10 %;
- у переднеприводных немного меньше – 5-7 %.
Любой производитель закладывает в спидометр определённую погрешность измерения быстроты движения, выраженную в процентном отношении. И этот процент будет всегда неизменным, независимо от того, насколько быстро движется автомобиль. В то же время реальные цифры, которые можно наблюдать на приборной доске, будут различаться в зависимости от того, едет ли авто со скоростью 50 или 150 км/ч.
В среднем, при движении со скоростью 200 км/ч погрешность измерителя составит 10 %. При замедлении до 110 км/ч, разница может уменьшиться до 5-10 км/ч, а двигаясь не быстрее 60 км/ч, можно наблюдать минимальную неточность либо не наблюдать её вовсе.
Чем выше скорость автомобиля, тем больше погрешность между показаниями измерителя и реальной скоростью, определяемой в абсолютных величинах. При этом выраженная в процентах поправка, заложенная производителем, останется неизменной.
Зачем спидометр врёт
Любой спидометр должен соответствовать техническим требованиям, установленным ЕЭК ООН №39 (ГОСТ 12936-2017). Правила требуют, чтобы погрешность измерителя не отличалась от реальной скорости движения автомобиля больше, чем на 10%+6 км/ч.
То есть, в соответствии с международными правилами и российским государственным стандартом исправный измерительный прибор должен показывать большую скорость, чем в действительности.
Производители не выпускают приборы с нулевой погрешностью по ряду причин:
- ни один измерительный прибор не может быть абсолютно точным;
- в процессе эксплуатации автомобиля датчики теряют чувствительность, а контакты окисляются, что в любом случае сказывается на точности показаний измерительного прибора;
- показания спидометра зависят от таких параметров, как износ шин, диаметр колёс, температура воздуха и т. п.
Если скорость, которую показывает спидометр, будет больше реальной, то ничего страшного не произойдёт (правила разрешают такой вариант). Но если показания измерительного прибора будут меньше, чем в действительности, то водителей можно будет привлекать к ответственности за нарушения скоростного режима, которые они в действительности не совершали.
Как можно повлиять на показания спидометра
Для измерения скорости датчики спидометра пользуются данными о количестве оборотов колёс. В каждом автомобиле датчики настроены на колёса штатного размера. Производители обычно допускают возможность установки на автомобиль нескольких типоразмеров дисков и шин, именно под них измерительный прибор и был откалиброван изначально.
Но если поменять колёса на нестандартные, то есть, на те, которые отличаются по размеру от допускаемых производителем, то показания измерительных приборов изменятся:
- при установке колёс большего диаметра, чем предусмотрено производителем, спидометр будет показывать меньшую скорость;
- установка колёс меньшего диаметра, напротив, приведёт к увеличению показаний измерительного прибора.
Величина неточности будет увеличиваться или уменьшаться пропорционально тому, насколько новые шины будут отличны от стандартных.
Устанавливая на автомобиль нестандартные шины или диски, выполните калибровку спидометра.
Теперь вы знаете, почему реальная скорость автомобиля и та скорость, которую вы можете наблюдать на приборной доске, отличаются друг от друга. Кроме погрешности, предусмотренной производителем, на данные спидометра влияет, к примеру, размер колёс. Зная об этом, будьте внимательны и соблюдайте скоростной режим.
- Распечатать
Оцените статью:
- 5
- 4
- 3
- 2
- 1
(11 голосов, среднее: 2.8 из 5)
Поделитесь с друзьями!
Погрешности измерений, представление результатов эксперимента
- Шкала измерительного прибора
- Цена деления
- Виды измерений
- Погрешность измерений, абсолютная и относительная погрешность
- Абсолютная погрешность серии измерений
- Представление результатов эксперимента
- Задачи
п.1. Шкала измерительного прибора
Шкала – это показывающая часть измерительного прибора, состоящая из упорядоченного ряда отметок со связанной с ними нумерацией. Шкала может располагаться по окружности, дуге или прямой линии.
Примеры шкал различных приборов:
п.2. Цена деления
Цена деления измерительного прибора равна числу единиц измеряемой величины между двумя ближайшими делениями шкалы. Как правило, цена деления указана на маркировке прибора.
Алгоритм определения цены деления
Шаг 1. Найти два ближайшие пронумерованные крупные деления шкалы. Пусть первое значение равно a, второе равно b, b > a.
Шаг 2. Посчитать количество мелких делений шкалы между ними. Пусть это количество равно n.
Шаг 3. Разделить разницу значений крупных делений шкалы на количество отрезков, которые образуются мелкими делениями: $$ triangle=frac{b-a}{n+1} $$ Найденное значение (triangle) и есть цена деления данного прибора.
Пример определения цены деления:
 |
Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале:a = 5 c b = 10 cМежду ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. Цена деления: begin{gather*} triangle=frac{b-a}{n+1}\ triangle=frac{10-5}{24+1}=frac15=0,2 c end{gather*} |
п.3. Виды измерений
Вид измерений
Определение
Пример
Прямое измерение
Физическую величину измеряют с помощью прибора
Измерение длины бруска линейкой
Косвенное измерение
Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений
Определение площади столешницы при измеренной длине и ширине
п.4. Погрешность измерений, абсолютная и относительная погрешность
Погрешность измерений – это отклонение измеренного значения величины от её истинного значения.
Составляющие погрешности измерений
Причины
Инструментальная погрешность
Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.)
Погрешность метода
Определяется несовершенством методов и допущениями в методике.
Погрешность теории (модели)
Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности.
Погрешность оператора
Определяется субъективным фактором, ошибками экспериментатора.
Инструментальная погрешность измерений принимается равной половине цены деления прибора: $$ d=frac{triangle}{2} $$
Если величина (a_0) – это истинное значение, а (triangle a) – погрешность измерения, результат измерений физической величины записывают в виде (a=a_0pmtriangle a).
Абсолютная погрешность измерения – это модуль разности между измеренным и истинным значением измеряемой величины: $$ triangle a=|a-a_0| $$
Отношение абсолютной погрешности измерения к истинному значению, выраженное в процентах, называют относительной погрешностью измерения: $$ delta=frac{triangle a}{a_0}cdot 100text{%} $$
Относительная погрешность является мерой точности измерения: чем меньше относительная погрешность, тем измерение точнее. По абсолютной погрешности о точности измерения судить нельзя.
На практике абсолютную и относительную погрешности округляют до двух значащих цифр с избытком, т.е. всегда в сторону увеличения.
Значащие цифры – это все верные цифры числа, кроме нулей слева. Результаты измерений записывают только значащими цифрами.
Примеры значащих цифр:
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В простейших измерениях инструментальная погрешность прибора является основной.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:
- определение длины с помощью линейки или мерной ленты;
- определение объема с помощью мензурки.
Пример получения результатов прямых измерений с помощью линейки:
 |
Измерим длину бруска линейкой, у которой пронумерованы сантиметры и есть только одно деление между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{1+1}=0,5 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,5}{2}=0,25 text{см} end{gather*} Истинное значение: (L_0=4 text{см}) Результат измерений: $$ L=L_0pm d=(4,00pm 0,25) text{см} $$ Относительная погрешность: $$ delta=frac{0,25}{4,00}cdot 100text{%}=6,25text{%}approx 6,3text{%} $$ |
 |
Теперь возьмем линейку с n=9 мелкими делениями между пронумерованными делениями. Цена деления такой линейки: begin{gather*} triangle=frac{b-a}{n+1}= frac{1 text{см}}{9+1}=0,1 text{см} end{gather*} Инструментальная погрешность: begin{gather*} d=frac{triangle}{2}=frac{0,1}{2}=0,05 text{см} end{gather*} Истинное значение: (L_0=4,15 text{см}) Результат измерений: $$ L=L_0pm d=(4,15pm 0,05) text{см} $$ Относительная погрешность: $$ delta=frac{0,05}{4,15}cdot 100text{%}approx 1,2text{%} $$ |
Второе измерение точнее, т.к. его относительная погрешность меньше.
п.5. Абсолютная погрешность серии измерений
Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки).
Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений.
Алгоритм определения истинного значения и абсолютной погрешности в серии измерений
Шаг 1. Проводим серию из (N) измерений, в каждом из которых получаем значение величины (x_1,x_2,…,x_N)
Шаг 2. Истинное значение величины принимаем равным среднему арифметическому всех измерений: $$ x_0=x_{cp}=frac{x_1+x_2+…+x_N}{N} $$ Шаг 3. Находим абсолютные отклонения от истинного значения для каждого измерения: $$ triangle_1=|x_0-x_1|, triangle_2=|x_0-x_2|, …, triangle_N=|x_0-x_N| $$ Шаг 4. Находим среднее арифметическое всех абсолютных отклонений: $$ triangle_{cp}=frac{triangle_1+triangle_2+…+triangle_N}{N} $$ Шаг 5. Сравниваем полученную величину (triangle_{cp}) c инструментальной погрешностью прибора d (половина цены деления). Большую из этих двух величин принимаем за абсолютную погрешность: $$ triangle x=maxleft{triangle_{cp}; dright} $$ Шаг 6. Записываем результат серии измерений: (x=x_0pmtriangle x).
Пример расчета истинного значения и погрешности для серии прямых измерений:
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.
Составим расчетную таблицу:
| № опыта | 1 | 2 | 3 | Сумма |
| Масса, г | 99,8 | 101,2 | 100,3 | 301,3 |
| Абсолютное отклонение, г | 0,6 | 0,8 | 0,1 | 1,5 |
Сначала находим среднее значение всех измерений: begin{gather*} m_0=frac{99,8+101,2+100,3}{3}=frac{301,3}{3}approx 100,4 text{г} end{gather*} Это среднее значение принимаем за истинное значение массы.
Затем считаем абсолютное отклонение каждого опыта как модуль разности (m_0) и измерения. begin{gather*} triangle_1=|100,4-99,8|=0,6\ triangle_2=|100,4-101,2|=0,8\ triangle_3=|100,4-100,3|=0,1 end{gather*} Находим среднее абсолютное отклонение: begin{gather*} triangle_{cp}=frac{0,6+0,8+0,1}{3}=frac{1,5}{3}=0,5 text{(г)} end{gather*} Мы видим, что полученное значение (triangle_{cp}) больше инструментальной погрешности d.
Поэтому абсолютная погрешность измерения массы: begin{gather*} triangle m=maxleft{triangle_{cp}; dright}=maxleft{0,5; 0,05right} text{(г)} end{gather*} Записываем результат: begin{gather*} m=m_0pmtriangle m\ m=(100,4pm 0,5) text{(г)} end{gather*} Относительная погрешность (с двумя значащими цифрами): begin{gather*} delta_m=frac{0,5}{100,4}cdot 100text{%}approx 0,050text{%} end{gather*}
п.6. Представление результатов эксперимента
Результат измерения представляется в виде $$ a=a_0pmtriangle a $$ где (a_0) – истинное значение, (triangle a) – абсолютная погрешность измерения.
Как найти результат прямого измерения, мы рассмотрели выше.
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.
Погрешность суммы и разности
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, то
- абсолютная погрешность их суммы равна сумме абсолютных погрешностей
$$ triangle (a+b)=triangle a+triangle b $$
- абсолютная погрешность их разности также равна сумме абсолютных погрешностей
$$ triangle (a-b)=triangle a+triangle b $$
Погрешность произведения и частного
Если (a=a_0+triangle a) и (b=b_0+triangle b) – результаты двух прямых измерений, с относительными погрешностями (delta_a=frac{triangle a}{a_0}cdot 100text{%}) и (delta_b=frac{triangle b}{b_0}cdot 100text{%}) соответственно, то:
- относительная погрешность их произведения равна сумме относительных погрешностей
$$ delta_{acdot b}=delta_a+delta_b $$
- относительная погрешность их частного также равна сумме относительных погрешностей
$$ delta_{a/b}=delta_a+delta_b $$
Погрешность степени
Если (a=a_0+triangle a) результат прямого измерения, с относительной погрешностью (delta_a=frac{triangle a}{a_0}cdot 100text{%}), то:
- относительная погрешность квадрата (a^2) равна удвоенной относительной погрешности
$$ delta_{a^2}=2delta_a $$
- относительная погрешность куба (a^3) равна утроенной относительной погрешности
$$ delta_{a^3}=3delta_a $$
- относительная погрешность произвольной натуральной степени (a^n) равна
$$ delta_{a^n}=ndelta_a $$
Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса.
п.7. Задачи
Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно? 
Составим таблицу для расчета цены деления:
| № мензурки | a, мл | b, мл | n | (triangle=frac{b-a}{n+1}), мл |
| 1 | 20 | 40 | 4 | (frac{40-20}{4+1}=4) |
| 2 | 100 | 200 | 4 | (frac{200-100}{4+1}=20) |
| 3 | 15 | 30 | 4 | (frac{30-15}{4+1}=3) |
| 4 | 200 | 400 | 4 | (frac{400-200}{4+1}=40) |
Инструментальная точность мензурки равна половине цены деления.
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):
| № мензурки | Объем (V_0), мл | Абсолютная погрешность (triangle V=frac{triangle}{2}), мл |
Относительная погрешность (delta_V=frac{triangle V}{V_0}cdot 100text{%}) |
| 1 | 68 | 2 | 3,0% |
| 2 | 280 | 10 | 3,6% |
| 3 | 27 | 1,5 | 5,6% |
| 4 | 480 | 20 | 4,2% |
Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке.
Ответ:
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Задача 2. В двух научных работах указаны два значения измерений одной и той же величины: $$ x_1=(4,0pm 0,1) text{м}, x_2=(4,0pm 0,03) text{м} $$ Какое из этих измерений точней и почему?
Мерой точности является относительная погрешность измерений. Получаем: begin{gather*} delta_1=frac{0,1}{4,0}cdot 100text{%}=2,5text{%}\ delta_2=frac{0,03}{4,0}cdot 100text{%}=0,75text{%} end{gather*} Относительная погрешность второго измерения меньше. Значит, второе измерение точней.
Ответ: (delta_2lt delta_1), второе измерение точней.
Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.
Абсолютная погрешность скорости каждой машины равна инструментальной, т.е. половине деления спидометра: $$ triangle v_1=frac{10}{2}=5 (text{км/ч}), triangle v_2=frac{1}{2}=0,5 (text{км/ч}) $$ Показания каждого из спидометров: $$ v_1=(54pm 5) text{км/ч}, v_2=(72pm 0,5) text{км/ч} $$ Скорость сближения равна сумме скоростей: $$ v_0=v_{10}+v_{20}, v_0=54+72=125 text{км/ч} $$ Для суммы абсолютная погрешность равна сумме абсолютных погрешностей слагаемых. $$ triangle v=triangle v_1+triangle v_2, triangle v=5+0,5=5,5 text{км/ч} $$ Скорость сближения с учетом погрешности равна: $$ v=(126,0pm 5,5) text{км/ч} $$ Относительная погрешность: $$ delta_v=frac{5,5}{126,0}cdot 100text{%}approx 4,4text{%} $$ Ответ: (v=(126,0pm 5,5) text{км/ч}, delta_vapprox 4,4text{%})
Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины.
Инструментальная погрешность линейки (d=frac{0,1}{2}=0,05 text{см})
Результаты прямых измерений длины и ширины: $$ a=(90,20pm 0,05) text{см}, b=(60,10pm 0,05) text{см} $$ Относительные погрешности (не забываем про правила округления): begin{gather*} delta_1=frac{0,05}{90,20}cdot 100text{%}approx 0,0554text{%}approx uparrow 0,056text{%}\ delta_2=frac{0,05}{60,10}cdot 100text{%}approx 0,0832text{%}approx uparrow 0,084text{%} end{gather*} Площадь столешницы: $$ S=ab, S=90,2cdot 60,1 = 5421,01 text{см}^2 $$ Для произведения относительная погрешность равна сумме относительных погрешностей слагаемых: $$ delta_S=delta_a+delta_b=0,056text{%}+0,084text{%}=0,140text{%}=0,14text{%} $$ Абсолютная погрешность: begin{gather*} triangle S=Scdot delta_S=5421,01cdot 0,0014=7,59approx 7,6 text{см}^2\ S=(5421,0pm 7,6) text{см}^2 end{gather*} Ответ: (S=(5421,0pm 7,6) text{см}^2, delta_Sapprox 0,14text{%})

Научно-практическая конференция
«Погрешность показаний спидометра автомобиля.»
Автор: Никифоров Алексей Учащийся 7а класса МОУ «СОШ № 4» Научный руководитель: Страмилова Г.В. Учитель физики МОУ «СОШ № 4»
Петровск-Забайкальский 2021

- Актуальность темы определяется, прежде всего, тем, что в современных условиях, точность таких данных в первую очередь будет влиять на исполнение всех требований ПДД, соответственно водитель сможет правильно выбирать скоростной режим в зависимости от ограничений на дороге, что избавит его от получения штрафов.

- Объектом исследования становятся, таким образом, различные интернет-ресурсы, а также зарубежная и российская литература, посвященная спидометрам автомобиля.
- Предмет исследования – виды спидометров и причины, влияющие на показания спидометра автомобиля.

- Цель исследования состоит в том, чтобы сравнить показания спидометра нашего автомобиля с показаниями различных альтернативных мобильных программ для измерения скорости.

Задачи:
- 1. Рассмотреть виды и принцип работы спидометра;
- 2. Используя интернет-ресурсы, рассмотреть причины, влияющие на показания спидометра;
- 3. Провести собственное исследование для сравнения показания спидометра нашего автомобиля с показаниями различных альтернативных мобильных программ измерения скорости.

Методы , использованные при выполнении работы:
- 1.Описательно-повествовательный (использовался при описании причин влияющих на показания спидометра и принцип работы спидометра);
- 2.Сравнительный (использовался при рассмотрении видов автомобильных спидометров и альтернативных программ для измерения скорости);
- 3. Анализ и синтез (использовался при анализе и обобщении различных фактов данного исследования).

Все спидометры можно разделить на три большие группы:
- Механические спидометры;
- Электромеханические спидометры;
- Электронные спидометры.
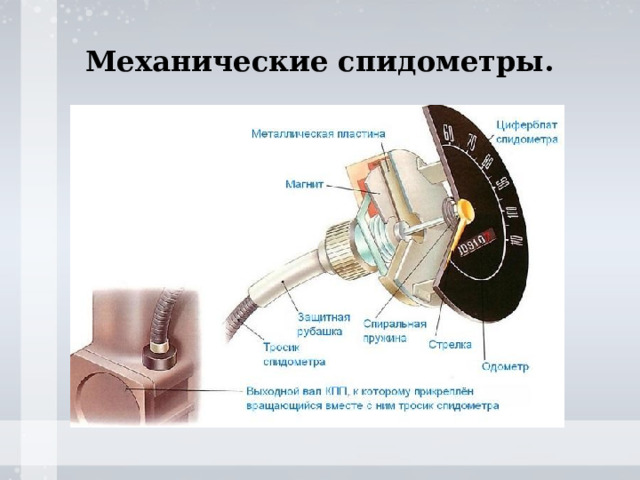
Механические спидометры.

Электромеханические спидометры.

Электронные спидометры.

Причины погрешности спидометра.
- Автопроизводители допускают расхождение в 5-7 процентов.
- Износ шестерни датчика и в некоторой степени с износом шестерни привода датчика на вторичном валу КПП дает погрешность до 10%.
- Погрешность в 2,5% и более возникает при установке на автомобиль колес уменьшенного или увеличенного диаметра, а также при езде на спущенных покрышках.
- Дополнительную погрешность измерения скорости дают спидометры на переднеприводных автомобилях.
Яндекс навигатор – бесплатный универсальный помощник для водителей автотранспорта и вставших в пробку пассажиров общественного транспорта .
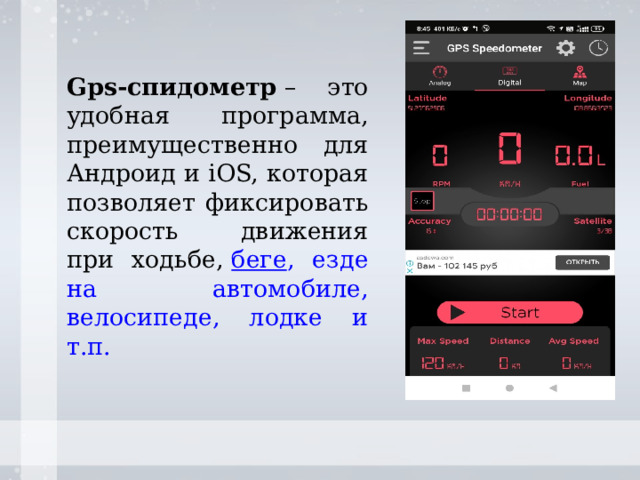
Gps-спидометр – это удобная программа, преимущественно для Андроид и iOS, которая позволяет фиксировать скорость движения при ходьбе, беге , езде на автомобиле, велосипеде, лодке и т.п.

Формула для расчета погрешности.
Погрешность в % = (1 — VGPS / Vсп )* 100;
где:
VGPS — скорость по GPS;
Vсп — скорость по спидометру.
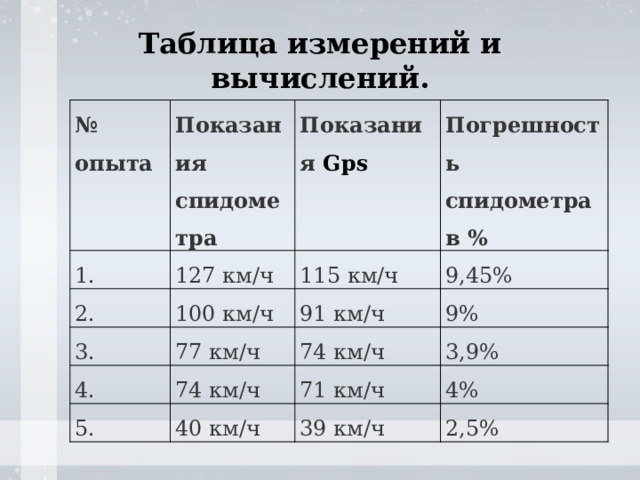
Таблица измерений и вычислений.
№ опыта
Показания спидометра
1.
Показания Gps
127 км/ч
2.
Погрешность спидометра в %
115 км/ч
100 км/ч
3.
77 км/ч
9,45%
91 км/ч
4.
5.
74 км/ч
9%
74 км/ч
3,9%
71 км/ч
40 км/ч
4%
39 км/ч
2,5%

Сравнение показаний Яндекс – навигатора и Gps-спидометра

Сравнение показаний Яндекс- навигатора, Gps-спидометра и спидометра автомобиля .

Сравнение показаний Gps-спидометр и спидометра автомобиля на различных скоростях.
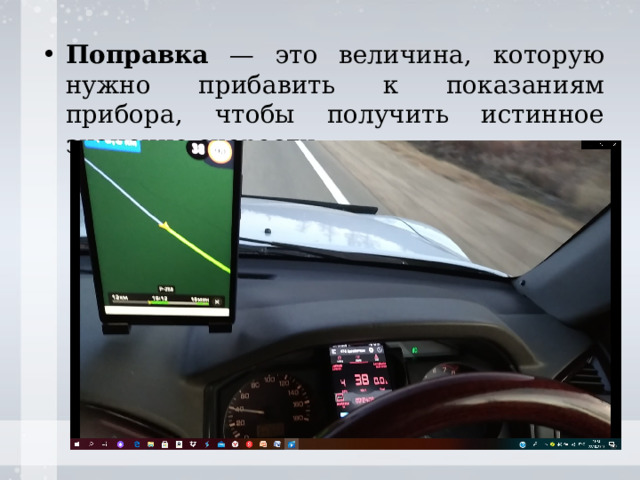
- Поправка — это величина, которую нужно прибавить к показаниям прибора, чтобы получить истинное значение скорости.

Скорость
Погрешность
100 км/ч
Поправка
9%,
-9%.
- На скорости 80 км/ч по спидометру, реальная скорость будет равна 80 — 9% от 80-ти = 80 × 0,91 = 72,8 км/ч≈ 73 км/ч .
- А на скорости 110 км/ч, реальная скорость будет 110 — 9% = 100,1 км/ч, и так далее.

Подведем итоги.
1. Спидометр «врет» (завышает скорость) всегда, и чем выше скорость — тем больше он ее завышает.
2. GPS определят скорость точнее спидометра, но тоже привирает, просто поменьше, чем спидометр (в пределах 1% от измеренной скорости).
3. Поправки к спидометру (с достаточной степенью точности) можно вычислить сравнив его показания с показаниями GPS и учитывать их при поездках.

Спасибо за внимание!
Вот мания у меня такая — проверять приборы на правильность показаний =) Первым был указатель температуры ОЖ.
Теперь настала очередь не менее важного спидометра. А проверял я его так: взял навигатор, как известно GPS-навигация один из самых точных способов проверить много чего (место положения, скорость, расстояние и т.д.) и поставил рядом со спидометром для наглядности показаний.
Предварительно правильность работы спидометра в навигаторе проверил на таких авто как Форд Гэлэкси, БМВ е34, Мазда 626, УАЗе и даже на тепловозах серий М62, ЧМЭ3, 2ТЭ10У/УМ/М(и всех его модификациях) везде показания спидометров и навигации грешили от -5-и до +3 км/ч. Самые точные показания были у Гэлэкси — там всё по нулям сошлось. Так вот, я всё это дело и профотать еще постарался, так что смотрим и читаем описание фото.

Собственно сам телефон с навигационной программой Navitel 9.0.0.2.

Общая картина происходящего.

Показания обоих приборов на стоянке.Навигтор — 0 км/ч и спидак 0 км/ч
А вот дальше интересное начинается…

И так, скорость спидометра — примерно 60,5/61 км/ч. При этом показания Навитела — 51…

спидометр: 99 — 100 км/ч навител: 88,5 км/ч

спидометр: 109 км/ч навител: 99 км/ч

спидометр: 121 км/ч навител: 111 км/ч
Итог таков: погрешность моего спидометра +10 км/ч. Факт налицо, к тому же при проезде возле ГАИ с “пистолетом” на скорости (по моему спидометру) примерно в 70 км/ч в черте города, меня не тормозили, значит, я не превысил скорость 60 =) Кстати, на старой приборке у меня было тоже самое.
Но фиг его на самом деле знает. Еще есть теория о скорости по оборотам двигателя. Стоят 13-е диски с шинами 175/70/R13, КПП 4-х ступка. Вот такие у меня обороты показывает тахо:

Скорость где-то 133 км/ч И обороты в 4 500 об/м.
Так вот у меня просьба к тем Гольфоводам, у которых примерно такое же оснащение/комплектация, проверить у кого какие обороты на той или иной скорости по спидометру.
Ну и на последок: вот такие у меня циферки уже на новом спидометре)))

И раз)

и 282222 И еще 400
Цена вопроса: 10 $
Пробег: 282 222 км
Почему «врет» автомобильный спидометр?


Спидометр автомобиля определяет скорость машины, ведь глаз водителя «замыливается» – и немалые 100 км/ч кажутся черепашьим шагом.
Что такое автомобильный спидометр?
Автомобильный спидометр — это измерительный прибор для определения мгновенной скорости движения автомобиля. Показания выводятся в километрах в час (км/ч), или, как в Америке, — мили в час. В основном, бывают двух видов: аналоговые (или механические) и цифровые спидометры.
Что показывает спидометр автомобиля? На заднеприводных автомобилях спидометр обычно контролирует вращение вторичного вала коробки передач и по нему рассчитывается скорость. Значит, показания зависят от размера шин, передаточного числа редуктора заднего моста и собственной погрешности прибора.
Спидометры переднеприводных автомобилей измеряют скорость с помощью привода левого колеса. Значит, к погрешности спидометра и влиянию размера шины прибавляется эффект от закругления дороги: на поворотах влево «приборная скорость» чуть меньше, чем посередине машины, а вправо – чуть больше.
Что касается автомобильного спидометра — нетрудно догадаться, почему он именно «преувеличивает» и показывает большую скорость. Во-первых, у водителя будет меньше шансов нарушить скоростной режим и получить штраф. Во-вторых, если бы спидометр занижал реальную скорость, водители затаскали бы автопроизводителей по судам, доказывая, что все аварии и штрафы случились из-за неверных показаний приборов.
Среднее значение погрешности у современных спидометров — 10% на скорости в 200 км/ч. Причем зависимость, как правило, нелинейная. Это значит, что на 110 км/ч разница с реальной скоростью может составлять 5-10 км/ч, а на скоростях до 60 км/ч погрешности почти нет или она минимальная.
Но почему спидометр обязательно должен «врать»? Дело в том, что ему труднее быть точным, чем многим другим приборам. Ведь скорость движения обычно определяется по скорости вращения колеса. Эта скорость зависит от диаметра колеса, а это — параметр нестабильный.
Как сказываются шины нештатного размера на показания спидометра? Замена шины 185/60R14 на шину 195/55R15 или наоборот меняет показания спидометра на 2,5%. Немного? Но вопрос еще в том, как эта ошибка сложится с погрешностью самого спидометра, как скажется износ шин, давление в них. Низкое давление также искажает показания спидометра.
Если спидометр автомобиля показывает скорость в милях в час, то как перевести в километры в час? Особенно, это касается машин из Америки, где изначально спидометры калибруются в милях в час. Считайте, что 1 миля равна 1,6 км. Значит, если спидометр показывает скорость 90 миль в час, то это 144 км/ч (90 х 1,6 = 144 км/ч). Обратный подсчет из км/ч в миль/ч производиться путем деления на 1,6.
Источник
На сколько врет спидометр и зачем?
Спидометр высчитывает скорость автомобиля косвенно, через обороты выходного вала коробки передач, поэтому не всегда отражает реальную картину передвижения в пространстве. Он имеет свою погрешность, которая колеблется в рамках 0,5 %. Кроме того, есть масса иных факторов, заставляющих измерительную технику ошибаться.
Хозяин машины может поставить нештатные колеса, или при тюнинге заменят главную пару. Случаются и непредвиденные ситуации: если вдруг спустит шина или придется ехать на докатке. Тогда истинная скорость машины тоже изменится, а показания спидометра останутся прежними.
Поэтому, чтобы водитель вдруг не решил, что едет слишком медленно, на законодательном уровне предписано вносить в техническую часть спидометра положительные коррекции.
Приборы измерения скорости сознательно настроены на завышение. Того требует ГОСТ Р 41.39-99. И сделано это по соображениям безопасности.
Согласно пункту 5.3 технического регламента «скорость по прибору не должна быть меньше истинной». Другими словами, завышать прибор может, а вот занижать ему запрещено законом. Поэтому конструкторы закладывают в показания скорости запас, который, как демпфер, оставляет их в рамках разрешенного коридора.

Определить этот запас можно самому. Достаточно посмотреть на экран навигатора во время движения и сравнить с положением стрелки спидометра. Но для любителей точных цифр существует утвержденная методика. В пункте 5.2 ГОСТа Р 41.39-99 (Правила ЕЭК ООН N 39) приводится формула расчета коррекций.
«Между скоростью, указываемой на шкале спидометра (V1) и истинной скоростью (V2) должно соблюдаться следующее отношение: 0
Источник
Какая погрешность спидометра автомобиля
СПИДОМЕТРЫ АВТОМОБИЛЬНЫЕ С ЭЛЕКТРОПРИВОДОМ
Технические требования и методы испытаний
Automobile speedometer with electric drive. Technical requirements and test methods
Дата введения 2019-04-01
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-2015 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-2015 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены»
Сведения о стандарте
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Центральный ордена Трудового Красного Знамени научно-исследовательский автомобильный и автомоторный институт «НАМИ» (ФГУП «НАМИ»), Обществом с ограниченной ответственностью «Научно-технический центр «Автоэлектроника» (ООО «НТЦ «Автоэлектроника»)
2 ВНЕСЕН Межгосударственным техническим комитетом по стандартизации МТК 56 «Дорожный транспорт»
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 30 ноября 2017 г. N 52)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97
Сокращенное наименование национального органа по стандартизации
Минэкономики Республики Армения
Госстандарт Республики Казахстан
4 Приказом Федерального агентства по техническому регулированию и метрологии от 10 июля 2018 г. N 409-ст межгосударственный стандарт ГОСТ 12936-2017 введен в действие в качестве национального стандарта Российской Федерации с 1 апреля 2019 г.
ВНЕСЕНЫ: поправка, опубликованная в ИУС N 2, 2020 год; поправка, опубликованная в ИУС N 4, 2020 год
Поправки внесены изготовителем базы данных
1 Область применения
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие межгосударственные стандарты:
ГОСТ 515-77 Бумага упаковочная битумированная и дегтевая. Технические условия
ГОСТ 9142-2014 Ящики из гофрированного картона. Общие технические условия
ГОСТ 10958-78 Стекла защитные для приборов общепромышленного применения. Технические условия
ГОСТ 14254-2015 Степени защиты, обеспечиваемые оболочками (код IP)
ГОСТ 15150-69 Машины, приборы и другие технические изделия. Исполнения для различных климатических районов. Категории, условия эксплуатации, хранения и транспортирования в части воздействия климатических факторов внешней среды
ГОСТ 16536-90 Ящики деревянные для продукции автомобильной промышленности. Технические условия
ГОСТ 25651-2015 Приборы автомобилей контрольно-измерительные. Технические требования и методы испытаний
3 Технические требования
Внешний вид спидометра должен соответствовать образцу, утвержденному в установленном порядке.
3.2 Спидометры изготавливают на номинальные напряжения постоянного тока 12 или 24 В.
3.3 Верхний предел диапазона показаний спидометра следует выбирать из ряда: 60, 80, 100, 120, 140, 160, 180, 200, 220 и т.д. через 20 км/ч.
3.4 Спидометры изготавливают с итоговым счетчиком, указывающим пройденный путь.
Емкость итогового счетчика пройденного пути должна быть 999999,9 или 999999 км. Допускается изготавливать итоговый счетчик емкостью 99999 км.
Показания итогового счетчика спидометров, выпущенных предприятием-изготовителем, должны быть не более 10 км.
По согласованию с потребителем спидометры могут изготавливать с дополнительным счетчиком, позволяющим вручную устанавливать его показания на ноль. Емкость этого счетчика должна быть 999,9 км.
3.5 Передаточное отношение механизма спидометра от приводного вала к счетному узлу должно соответствовать 624:1 и 1000:1, если другое не оговорено в КД на спидометры конкретного типа.
3.7 При постоянной частоте вращения привода спидометра стрелка указателя скорости на отметках шкалы более 20 км/ч не должна иметь колебаний, превышающих ±2% верхнего предела диапазона показаний.
3.8 Основная погрешность спидометра должна быть положительной.
Основная погрешность указателя скорости показывающего прибора спидометра при температуре окружающего воздуха (20±5)°С указана в таблице 1.
Источник
Почему пробег по одометру не сходится со спутниковой навигацией GPS/ГЛОНАСС

Многие наши клиенты при списании топлива и закрытии путевых учетных листов техники задаются вопросом почему показания пробега по одометру транспортного средства расходиться с показаниями системы мониторинга и в некоторых случаях очень значительно. В интернете существует множество статей, на эту тему которые пытаются раскрыть этот вопрос. Но исчерпывающей информации представлено мало. Мы же решили разобраться полностью. Итак, начнем.
Измерение пробега с помощью одометров
Для полного понимания вопроса нужно иметь представление что такое одометр и как говорится «с чем его едят». Так вот одометр — это прибор для измерения пройденного пути транспортным средством. В подавляющем большинстве случаев исполняются в корпусе спидометра и являются полностью взаимозависимыми как конструктивно, так и по предоставляемым показаниям. Бортовые спидометры (одометры) всех видов не относятся к классу точных приборов. Для каждого вида данных устройств установлены допустимые погрешности. Данные погрешности установлены только для самих приборов. Все конструктивные изменения, а также физический износ некоторых узлов и агрегатов автомобиля в эту погрешность не включены. Так же по техническим требованиям ЕЭК ООН №39 спидометры не могут занижать показания. Средняя погрешность спидометра по этим правилам (ГОСТ Р 41.39-99) может быть только положительной и не превышать истинную скорость движения более чем на 10% + 6 км/ч. Поэтому и одометр, конструктивно связанный со спидометром, так же даёт завышенные показания.
По нашему опыту работы, показания скорости и пробега приборов «с завода» по факту завышены на 5-10%. Об этом ведётся множество разговоров и бурные обсуждения на форумах автолюбителей. Возможно, что автопроизводители заботятся не только о безопасности водителей, но и вполне законно (опираясь на правила ЕЭК ООН №39) сокращают реальный гарантийный пробег на неизвестную величину, так как требования к точности измерения пробега отсутствуют.
Несомненно, производители постоянно пытаются усовершенствовать приборы для повышения их точности. На протяжении времени спидометры автомобилей изменялись. Можно составить некую классификацию по их конструктивным особенностям: механические, электромеханические или электронные.
Механический одометр представляет собой счетчик, приводимый в движение гибким валом, а проще говоря тросиком от редуктора техники. При монтаже такого прибора измерения для каждой определенной модели выставляется передаточное число, по которому будет высчитываться скорость и пробег. По мимо собственной погрешности в 5% при общем износе редуктора техники погрешности могут превышать 10%. А средний срок службы некоторых спидометров по данным из руководств по эксплуатации, составляет 115 000 км. Так же свои «5 пять копеек» в погрешность вносят неоригинальные запчасти, а изменение передаточного числа с 4,44 на 3,9 меняет показания дополнительно на рекордные 14%!
Электромеханические одометры берут свои показания от электронного измерителя числа импульсов от датчика скорости, который в свою очередь электромеханическим путем считывает данные с коробки передач.

Рис.1 Одометр ВАЗ 2107
Действительно с приходом нового типа спидометров общая погрешность измерения скорости и пробега несколько снизилась, ведь они избавились лишь от нескольких слабых мест механической части, но все же погрешность большинства из них находится в пределах 5-7%. К тому же, например, в ТУ для электромеханических спидометров 56.3802 прямо прописаны дополнительные погрешности от изменения напряжения на спидометре +-2%, а от температуры +-3%. Таким образом стендовая допустимая погрешность 10% + 6 км/ч прирастает 2-3% в зависимости от условий эксплуатации.
Электронные одометры — следующая ступень развития приборостроения. Механический счетчик километража был заменен на жидкокристаллический дисплей. Вид спидометра стал намного более современным, но существенных изменений в части съёма показаний скорости и пройденного пути осталась практически на том же уровне.

Рис.2 Одометр Skoda Rapid
Принцип учета пройденного километража все так же зависим от механических частей транспортного средства. По нашему опыту при проведении калибровки тахографов на тестовом участке пути (на заводе-изготовителе эта процедура в принципе не происходит), погрешность данных устройств редко снижается ниже 5%. Но приятная глазу электронная часть принесла свои узкие места в надежность показаний одометра. При замене механической части на электронную появилась возможность программировать спидометры на накрутку километража причем на электронно строгое, точное значение, например, +10%. Такие услуги часто рекламируются на форумах водителей грузовиков.
Мы прекрасно видим, что изначально погрешности спидометров составляют довольно весомые величины, но на работу одометров так же влияют и другие факторы:
ü Радиус колеса. Визуально может показаться что колеса с разной размерностью шин, а тем более износом не отличаются друг от друга, но это не так. На грузовой технике согласно средним значениям высоты рисунка новой резины 18-23 мм и минимально разрешенной остаточной глубиной протектора в 1 мм вполне за период эксплуатации может образоваться разница более 1 см в радиусе одной и той же резины. Предлагаем посчитать с помощью нехитрой математики какую разницу по километражу будут показывать автомобили с использованием идеальных одометров без погрешностей о которых говорилось выше. Для примера мы взяли стандартное колесо Камаза с шиной КАМА 280 Р 508. Данные по расчетам приведены в таблице:
Источник
Насколько врёт спидометр автомобиля
Если в поездках на автомобиле вы пользуетесь навигатором, то наверняка замечали, что данные о скорости, отражаемые на спидометре и в навигаторе, несколько отличаются друг от друга. Почему так происходит, а также от чего зависит разница – узнаете из этой статьи.

Насколько точно показывает спидометр скорость автомобиля
Точность показаний спидометра зависит от его разновидности. Измерители бывают:
В заднеприводных автомобилях показания механического измерителя напрямую связаны с передаточным числом редуктора. Изменение передаточного числа сказывается на данных о быстроте движения авто. Влияет на погрешность также изношенность редуктора и состояние шин. В сумме неточность показаний может составлять более 10 %.
В переднеприводных авто механический прибор получает данные о скорости от привода левого колеса, расположенного выше главной пары. При правом повороте показания измерителя увеличиваются, при левом – уменьшаются в сравнении с движением по прямому отрезку.
Электронные спидометры получают данные за счёт контроля над вращением ведущего колеса. Несмотря на то что им не страшны люфт, износ троса или катушки и прочие неприятности, свойственные механическим приборам, всё же назвать их абсолютно точными нельзя. Погрешность электронных измерителей составляет примерно 5-7 %.
В среднем погрешность прибора может достигать 10 % при скорости 200 км/ч.
От чего зависит погрешность
Спидометр является измерительным прибором, а ни один из них не может функционировать без погрешностей, которые делятся на:
Неточность измерителя различается в зависимости от привода автомобиля:
Любой производитель закладывает в спидометр определённую погрешность измерения быстроты движения, выраженную в процентном отношении. И этот процент будет всегда неизменным, независимо от того, насколько быстро движется автомобиль. В то же время реальные цифры, которые можно наблюдать на приборной доске, будут различаться в зависимости от того, едет ли авто со скоростью 50 или 150 км/ч.
В среднем, при движении со скоростью 200 км/ч погрешность измерителя составит 10 %. При замедлении до 110 км/ч, разница может уменьшиться до 5-10 км/ч, а двигаясь не быстрее 60 км/ч, можно наблюдать минимальную неточность либо не наблюдать её вовсе.
Чем выше скорость автомобиля, тем больше погрешность между показаниями измерителя и реальной скоростью, определяемой в абсолютных величинах. При этом выраженная в процентах поправка, заложенная производителем, останется неизменной.
Зачем спидометр врёт
Любой спидометр должен соответствовать техническим требованиям, установленным ЕЭК ООН №39 (ГОСТ 12936-2017). Правила требуют, чтобы погрешность измерителя не отличалась от реальной скорости движения автомобиля больше, чем на 10%+6 км/ч.
То есть, в соответствии с международными правилами и российским государственным стандартом исправный измерительный прибор должен показывать большую скорость, чем в действительности.
Производители не выпускают приборы с нулевой погрешностью по ряду причин:
Если скорость, которую показывает спидометр, будет больше реальной, то ничего страшного не произойдёт (правила разрешают такой вариант). Но если показания измерительного прибора будут меньше, чем в действительности, то водителей можно будет привлекать к ответственности за нарушения скоростного режима, которые они в действительности не совершали.
Как можно повлиять на показания спидометра
Для измерения скорости датчики спидометра пользуются данными о количестве оборотов колёс. В каждом автомобиле датчики настроены на колёса штатного размера. Производители обычно допускают возможность установки на автомобиль нескольких типоразмеров дисков и шин, именно под них измерительный прибор и был откалиброван изначально.
Но если поменять колёса на нестандартные, то есть, на те, которые отличаются по размеру от допускаемых производителем, то показания измерительных приборов изменятся:
Величина неточности будет увеличиваться или уменьшаться пропорционально тому, насколько новые шины будут отличны от стандартных.
Устанавливая на автомобиль нестандартные шины или диски, выполните калибровку спидометра.
Теперь вы знаете, почему реальная скорость автомобиля и та скорость, которую вы можете наблюдать на приборной доске, отличаются друг от друга. Кроме погрешности, предусмотренной производителем, на данные спидометра влияет, к примеру, размер колёс. Зная об этом, будьте внимательны и соблюдайте скоростной режим.
Источник
