Число групп в зависимости от числа наблюдений
|
n |
31-100 |
300-1000 |
|
r |
5-6 6-8 |
10-15 |
1.3. Этапы построения сгруппированного вариационного ряда.
Построение сгруппированного ряда
складывается из нескольких этапов (рис.
1):

Рис. 1. Этапы построения сгруппированного
вариационного ряда.
I этап: определение
количества групп в вариационном ряду.
При большом количестве групп ряд
получается громоздким, что ведет к
трудностям вычисления показателей. При
малом числе групп в ряду интервал велик.
Это приводит к крайне нежелательному
снижению точности характеристик ряда,
рассчитываемых на следующем этапе
работы.
При большом колебаний признака его
максимальные величины могут не
соответствовать размерам последней
группы и будут вне ее. В этом случае
необходимо увеличить число групп с тем,
чтобы можно было включить эти крайние
варианты.
II этап: определение
величины интервала (i)
между группами.Определяя величину
интервала между группами, амплитуду
вариационного ряда (разность между
максимальным и минимальным значениями
вариант) делят на число групп (см. табл.1)n= 50 и тогдаr= 10.
Величина интервала i= =
= =
= = 4,6 сек.
= 4,6 сек.
Полученный интервал округляется до
целого числа – 5.
III этап: определение
начала, середины и конца группы. Прежде
всего, необходимо определить середину
для первой группы. В нашем примере
максимальная варианта равна 64. Поскольку
середина группы должна делиться на
величину интервала, то за середину
первой группы следует взять варианту,
равную 65, которая будет ближайшей к
максимальному значению и без остатка
разделится на величину интервала,
равного 5. Середины для других групп
находят следующим образом: от середины
каждой предыдущей группы отнимают
величину интервала. Так, если середина
первой группы – 65, то середина второй
группы равна 60 (65-5), середина третьей
группы – 55 (60-5) и т. д. (табл. 3).После
составления ряда из величин, принятых
за середину группы – 65, 60, 55, 50 и т.д.,
нужно определить границы (начало и
конец) этих групп. При этом следует иметь
в виду, что границы не должны повторяться,
иначе трудно будет распределить варианты
по группам и построить вариационный
ряд.
Определяя начало группы, к ее середине
прибавляют величину
 ,
,
вычитая же ее из середины, получают
конец группы. В нашем примере Прибавив 2 к середине первой группы,
Прибавив 2 к середине первой группы,
получим 67 (начало группы), ее концом
будет: 65-2 = 63 (см. табл. 3).
Границы должны составленный так, чтобы
значения вариант не оказывались между
группами, нежелательны также открытые
группы. Например, «свыше 60» или «менее
20» и т. д.
Таблица 3
Распределение женщин 30-44 лет по времени задержки дыхания после вдоха (в секундах)
|
Начало |
Середина |
Конец |
Варианты |
Частоты |
|
67 62 57 52 47 42 37 32 27 22 |
65 60 55 50 45 40 35 30 25 20 |
63 58 53 48 43 38 33 28 23 18 |
67-63 62-58 57-53 52-48 47-43 42-38 37-33 32-28 27-23 22-18 |
1 1 3 2 5 13 8 8 5 4 ∑p = 50 ∑p |
IV этап: распределение
случаев наблюдения по группам.Для
разноски рекомендуется использовать
карточки, на каждой из которых записана
величина варианты. Карточки раскладывают
по пачкам соответственно размерам
показателей в группе. Подсчитывают
количество карточек в каждой пачке и
результаты записывают по группам,
получая, таким образом, частоты (p)
вариационного ряда.
V этап: графическое
изображение вариационного ряда.Для
углубленного анализа полученных данных
большее значение имеет правильное
построение графического изображения
вариационных рядов (рис. 2).
Основные правила построения графических
изображений вариационных рядов
заключается в следующем:
– необходимо построить оси координат:
ось абсцисс (x) и ось ординат
(y). Ось абсцисс служит для
изображения градации (середины групп)
изучаемого признака (рост, масса тела,
уровень белка в крови и т. д.), ось ординат
– для изображения числа случаев с данной
величиной признака;
– при построений осей координат надо
соблюдать определенные соотношения
между длиной осей абсцисс и ординат
(x:y= 4:3).
Вариационный ряд является одним из
типов распределения признака в
статистической совокупности и служит
для вычисления средних величин.
Например:
вариационный ряд: 18, 18, 19, 20, 21, 26, …, 64 n= 50
-
r(число групп) = 10
-
i=

Интервал всегда целое число, округляем
до 5.
3) Находим границы группы [18,19,20,21,22], 5
возможных числовых значений, т.к. i= 5
Находим середину группы(20 – середина
группы).
4) Распределяем совокупность по группам
В 1 группу войдут Vот 18
до 22
1группа [5 вариант]
2 группа……………
3группа……………. и т.д.
5) Строим графическое изображение
(делается для наглядности)
а) строим оси: абсцисс ( х ), ординат ( у
)
у
х
б) ось абсцисс (х) служит для изображения
середины групп, ось ординат
(у) – числа вариант в группе

Рис. 2. Графическое изображение
вариационного ряда.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти середину интервала
При статистической обработке результатов исследований самого разного рода полученные значения часто группируются в последовательность интервалов. Для расчета обобщающих характеристик таких последовательностей иногда приходится вычислять середину интервала – «центральную варианту». Методы ее расчета достаточно просты, но имеют некоторые особенности, вытекающие как из используемой для измерения шкалы, так и из характера группировки (открытые или закрытые интервалы).

Инструкция
Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте обычные математические методы вычисления среднеарифметического значения. Минимальное значение интервала (его начало) сложите с максимальным (окончанием) и разделите результат пополам – это один из способов вычисления среднеарифметического значения. Например, это правило применимо, когда речь идет о возрастных интервалах. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.
Иногда бывает удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала. В этом варианте сначала определите ширину диапазона – отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя граница соответствует значению 47,15, а верхняя – 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.
Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.
Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий – если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал имеет такую же размерность. В противном случае вам надо определить динамику изменения ширины интервалов, предшествующих открытому, и вывести его условную ширину, исходя из полученной тенденции изменения.
Источники:
- что такое открытый интервал
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Решение статистических задач в EXCEL: Практикум , страница 3
Количественные данные следует определить как «Числовые».
2. Для выполнения расчета необходимо закрыть имеющиеся открытые интервалы – первый – «до 500», последний — «от 700».
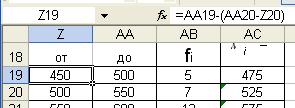
Формула вычисления левой границы первого интервала вводится в ячейку Z19 : «=АА19-(АА20-Z20)» (– из ячейки АА19 вычесть разницу между содержимым ячейки АА20 и Z20).
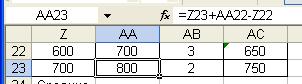
Правая граница последнего интервала в ячейку АА23 устанавливается формулой «=Z23+АА22-Z22» (от значения в ячейке Z23 откладывается размер предшествующего интервала «АА22-Z22»).
3. 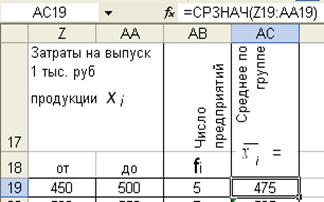 Рассчитывается среднее по каждой группе , как середина интервала. Для этого в ячейку первой группы (АС19) устанавливается функция СРЗНАЧ(Z19;AA19). После появления среднего значения первого интервала формула копируется в соседние ячейки. При этом автоматически смещаются координаты исходных данных в соответствии со смещением координат ячейки результата.
Рассчитывается среднее по каждой группе , как середина интервала. Для этого в ячейку первой группы (АС19) устанавливается функция СРЗНАЧ(Z19;AA19). После появления среднего значения первого интервала формула копируется в соседние ячейки. При этом автоматически смещаются координаты исходных данных в соответствии со смещением координат ячейки результата.
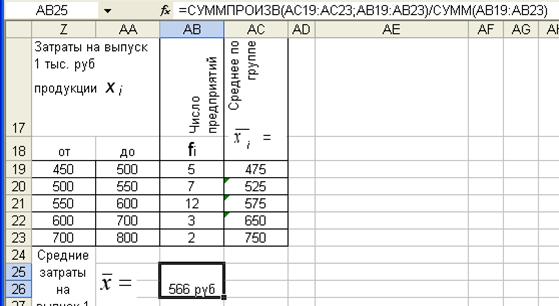
4. Рассчитывается величина средней взвешенной (в примере в ячейку АВ25)
СУММПРОИЗВ (АС19:АС23;АВ19:АВ23) реализует числитель
СУММ (АВ19:АВ23) – знаменатель;
«/» — знак деления.
Дисперсия. Среднее квадратическое
отклонение.
Дисперсия и среднее квадратическое отклонение (СКО) могут вычисляться по простой и взвешенной формулам.
Дисперсия, среднее квадратическое отклонение
по простой форме.
Для расчетов дисперсии по простой форме в Excel используется функция:
ДИСПР (диапазон данных).
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».
Рассмотрим методику расчета на примере расчета дисперсии и СКО зарплаты подразделения:

1. Исходные значения признака хi надо записать в массив ячеек расположенных в столбце или строке (в примере в строке (AF42:AQ42)).
Количественные данные следует определить как «Числовые».
2. В ячейку результата дисперсии (например «AF44») установить функцию ДИСПР(AF42:AQ42)
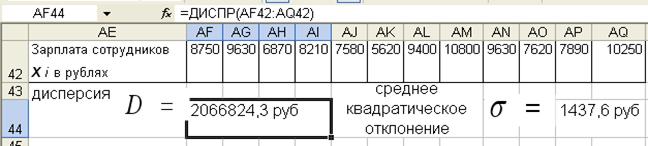
1. В ячейку результата СКО (например «AР44») установить функцию (ДИСПР(AF42:AQ42))^0,5.
Знак «^0,5» — означает возведение в степень 0,5 величины стоящей перед ним.
Дисперсия, среднее квадратическое
отклонение по взвешенной форме.
Для расчетов дисперсии по взвешенной форме в Excel используется функция:
СУММ (диапазон данных) и
СУММПРОИЗВ (диапазоны перемножаемых данных),
СКО определяется как квадратный корень дисперсии, реализуемый оператором возведения в степень «^».
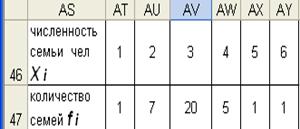 Рассмотрим методику расчета на примере расчета дисперсии и СКО размера семьи группы
Рассмотрим методику расчета на примере расчета дисперсии и СКО размера семьи группы
1. Исходные значения признака хi и частоту fi надо записать в массивы ячеек расположенных в столбце или строке (в примере в строках (АТ46:AY46) и (АТ47:AY47).
Количественные данные следует определить как «Числовые».
1. Рассчитать среднее арифметическое взвешенное — в примере в ячейке AW49 установлена формула =СУММПРОИЗВ (AT46:AY46;AT47:AY47)/СУММ(AT47:AY47)
Задача №6. Расчёт показателей вариации
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, руб. | До 400 | 400 — 600 | 600 — 800 | 800 — 1000 | Свыше 1000 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
Определите:
1) размах вариации;
2) средний размер вклада;
3) среднее линейное отклонение;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
| Размер вклада, руб. | 200 — 400 | 400 — 600 | 600 — 800 | 800 — 1000 | 1000 — 1200 |
|---|---|---|---|---|---|
| Число вкладчиков | 32 | 56 | 120 | 104 | 88 |
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
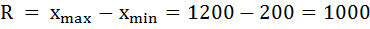
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
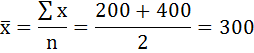
второго — 500 и т. д.
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
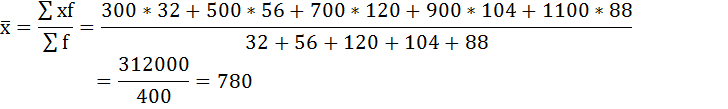
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
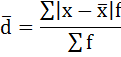
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
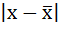
3. Полученные отклонения умножаются на частоты:
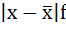
4. Находится сумма взвешенных отклонений без учёта знака:
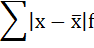
5. Сумма взвешенных отклонений делится на сумму частот:
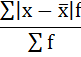
Удобно пользоваться таблицей расчётных данных:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  |
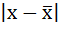 |
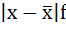 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Итого | 400 | — | — | — | 81280 |
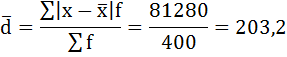
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
4) Дисперсия — это средняя арифметическая квадратов отклонений каждого значения признака от средней арифметической.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
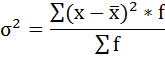
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:

3. Возводят в квадрат отклонения каждой варианты от средней:
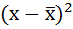
4. Умножают квадраты отклонений на веса (частоты):
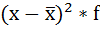
5. Суммируют полученные произведения:
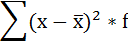
6. Полученная сумма делится на сумму весов (частот):
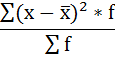
Расчёты оформим в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  |
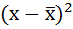 |
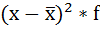 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Итого | 400 | — | — | — | 23040000 |
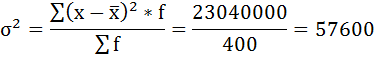
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
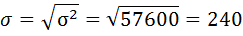
6) Коэффициент вариации — это отношение среднего квадратического отклонения к средней арифметической:
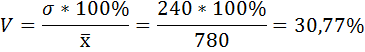
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Как найти середину?
Чтобы найти середину, нарисуйте числовую линию, содержащую точки и. Затем рассчитайте расстояние между двумя точками. В этом случае расстояние между и составляет. Разделив расстояние между двумя точками на 2, вы установите расстояние от одной точки до средней точки.
Тем не менее, как найти середину?
Чтобы найти середину любого диапазона, сложите два числа и разделите на 2. В этом случае 0 + 5 = 5, 5/2 = 2.5.
следующий: как найти середину интервала?
Разделите сумму верхнего и нижнего пределов на 2.. Результат — середина интервала. В этом примере 12, разделенное на 2, дает 6 как среднюю точку между 4 и 8.
тогда какова середина между двумя числами?
Середина между двумя числами — число точно посередине двух чисел. Вычисление средней точки — это то же самое, что вычисление среднего двух чисел. Следовательно, вы можете вычислить среднюю точку между любыми двумя числами, сложив их вместе и разделив на два.
Какова формулировка теоремы о средней точке?
Теорема о средней точке утверждает, что «Отрезок в треугольнике, соединяющий середину двух сторон треугольника, считается параллельным его третьей стороне и также составляет половину длины третьей стороны.«.
Как найти середину частотного распределения?
«Средняя точка» (или «отметка класса») каждого класса может быть рассчитана как: Средняя точка = нижний предел класса + верхний предел класса 2 . «Относительная частота» каждого класса — это доля данных, попадающих в этот класс.
Какова середина академического интервала?
«Средняя точка» (или «отметка класса») каждого класса может быть рассчитана как: Средняя точка = нижний предел класса + верхний предел класса 2 . «Относительная частота» каждого класса — это доля данных, попадающих в этот класс.
Что вы называете серединой урока?
Знак класса определяется как среднее значение нижнего и верхнего пределов. Следовательно, средняя точка интервала между занятиями называется отметкой класса.
Какая средняя точка гистограммы?
На полпути между соседними интервалами реальные пределы интервала, которые определяют, где конкретная точка данных будет «подсчитана» на гистограмме. Например, обратите внимание на третью полосу на этой гистограмме. Средняя точка равна 5. Нижний реальный предел находится на полпути между 2.5 и 5, или 3.75.
Какая средняя точка 25 и 50?
Таким образом, число, находящееся посередине между 25 и 50, равно 37.5. Как видите, среднее число на 12.5 больше, чем 25, и на 12.5 меньше, чем 50. Таким образом, наш средний ответ 37.5 выше правильный.
Какая средняя точка 15 и 20?
Когда вы спрашиваете: «Какое число находится посередине между 15 и 20?» мы предполагаем, что вы имеете в виду число точно посередине двух чисел на числовой строке, как показано ниже, где X = 15 и Y = 20. Таким образом, число, находящееся на полпути между 15 и 20, равно 17.5. Как видите, среднее число на 2.5 больше 15 и 2.5 меньше 20.
Как найти середину частотного распределения?
Вы можете добавить дополнительную информацию в свою таблицу распределения частот. «Средняя точка» (или «отметка класса») каждого класса может быть рассчитана как: Средняя точка = нижний предел класса + верхний предел класса 2 . «Относительная частота» каждого класса — это доля данных, попадающих в этот класс.
Как работает формула средней точки?
Средняя точка M тогда определяется как М = ((х + Х) / 2, (у + Y) / 2). … Чтобы показать, что M действительно является средней точкой отрезка PQ, нам нужно показать, что расстояние между M и Q такое же, как расстояние между M и P, и что это расстояние составляет половину расстояния от P до Q.
Какая середина треугольника?
Середина треугольника — это отрезок, соединяющий середины двух сторон треугольника. На рисунке D — это середина ¯AB, а E — середина ¯AC. Итак, ¯DE — это мидсегмент.
Как проверить теорему о средней точке?
Математические лаборатории с активным отдыхом — проверьте теорему о средней точке
- ЗАДАЧА.
- Теория. Теорема о средней точке: отрезок, соединяющий середины любых двух сторон треугольника, параллелен третьей стороне.
- Процедура. Шаг 1. Наклейте на картон один лист белой бумаги. …
- Наблюдения.
- Результат. Теорема о середине проверена.
В чем разница между теоремой о средней точке и ее определением?
В чем разница между теоремой о средней точке и ее определением? Определение: для данного сегмента линии существует середина. Теорема: средняя точка делит отрезки на два равных отрезка. Определение: высоты треугольника пересекаются в общей точке, называемой ортоцентром.
Что такое середина статистики?
Гистограмма, показывающая средние точки. Средняя точка класса (или отметка класса) — это определенная точка в центре интервалов (категорий) в таблице частотного распределения; Это также центр полосы на гистограмме. … Средняя точка определяется как среднее значение верхнего и нижнего пределов класса.
Как найти середину гистограммы?
Полигон частот можно создать из гистограммы или путем вычисления средних точек интервалов из таблицы распределения частот. Средняя точка бункера рассчитывается по формуле сложение верхнего и нижнего граничных значений ячейки и деление суммы на 2.
Как найти середину учебного интервала?
Для нахождения середины интервала классов мы используем формулу: Средняя точка = нижний предел класса + верхний предел класса 2 а для нахождения диапазона данных мы должны найти разницу между наивысшим и наименьшим баллами.
Какова середина интервала 10 класса?
Size = 20-10 = 10. Следовательно, размер интервала каждого класса равен 10. Следовательно, средняя точка класса 30-40 равна
35
. Диапазон = 64-12 = 52.
| Интервал класса | Счетные отметки | частота |
|---|---|---|
| 10-20 | |||| | 9 |
| 20-30 | 12 | |
| 30-40 | ||| | 8 |
| 40-50 | || | 7 |
Какая средняя точка у класса 15-20?
Отметка класса также известна как средняя точка класса — это особая точка в середине интервала классов. он определяется выражением, где a = нижний предел и b = верхний предел. Таким образом, размер класса и оценка класса 15-20 составляет 5 и 17.5.
Какова средняя точка доверительного интервала?
Важной темой в статистике является доверительный интервал, который сообщает нам наиболее вероятный интервал, в котором будет находиться среднее значение или пропорция. Часто дается нижняя и верхняя границы доверительного интервала, но средняя точка этих двух чисел является наилучшим предположением. для того, что мы ищем.
Какая средняя точка в таблице частот?
Средние значения точки: средние числа в каждой из групп. Самый простой способ найти их — сложить верхнюю и нижнюю границы и разделить ответ на два. Последний столбец находится путем умножения средней точки на частоту. Например, 1250 х 9 = 11250.
Что такое мидпойнт в статистике?
Средняя точка класса (или отметка класса) — это определенная точка в центре интервалов (категорий) в таблице частотного распределения; Это также центр полосы на гистограмме. Посмотрите видео, чтобы узнать, как рассчитать отметки / середины классов:… Средняя точка определяется как среднее значение верхнего и нижнего пределов класса.
Как найти середину сгруппированных данных?
Чтобы найти средние точки, сложите начальную и конечную точки, а затем разделите на 2. Середина 0 и 4 равна 2, потому что. Мы не знаем точное значение каждого из 11 элементов данных в группе 0 <m ≤ 4, поэтому лучшая оценка, которую мы можем сделать, состоит в том, что каждый элемент данных был равен средней точке, 2.
Какая середина класса высшего класса?
Нижний предел для каждого класса — это наименьшее значение в этом классе. С другой стороны, верхний предел для каждого класса является наибольшим значением в этом классе. Средняя точка класса нижний предел класса плюс верхний предел класса, деленный на 2.
Как найти середину открытого интервала по статистике?!
Знаток
(371),
закрыт
14 лет назад
заУчка
Мудрец
(19674)
14 лет назад
в статистике в случае открытых интервалов принято считать ширину последнего интервала равной ширине предпоследнего, а ширину первого – равной ширине второго. поэтому у вас при закрытии интервала получается 201-300, а середина соответственно 250.
Анна
Гуру
(3285)
14 лет назад
Вообще, чтобы найти середину интервала, надо найти длину и поделить пополам. Сложите начальное значение с конечным и разделите на 2….
Примеры решений задач по статистике
Решение задач по статистике и выводы к ним
Задача по статистике №1. Найти параметры интервального ряда распределения по данным таблицы, а именно: моду, медиану, среднюю арифметическую величину, среднюю взвешенную величину, коэффициент вариации, среднее квадратическое отклонение.
|
№ группы |
Группы компаний по основным производственным фондам, млн. руб. (х) |
Число компаний (fi) |
Середина интервала (Xi) = (начало интервала+конец интервала)/2 |
|
1 |
10 – 25 |
2 |
17,5 |
|
2 |
25 – 33 |
8 |
29 |
|
3 |
33 – 42 |
14 |
37,5 |
|
4 |
42 – 49 |
9 |
45,5 |
|
5 |
49 – 62 |
3 |
55,5 |
|
Всего: |
36 |
— |
Мы сразу добавили столбец «середина интервала». Для первой группы компаний рассчитали следующим образом: (10+25)/2=17,5 млн. руб. Для 2-5 групп расчеты произведены аналогично.
Теперь рассчитаем среднюю арифметическую величину.
 средняя арифметическая =
средняя арифметическая =  = (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.
= (17,5+29+37,5+45,5+55,5)/5=37 млн. руб.
Далее рассчитаем среднюю взвешенную величину.
 средняя взвешенная =
средняя взвешенная =  = (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.
= (17,5*2+29*8+37,5*14+45,5*9+55,5*3)/36=38 млн. руб.
Значение средневзвешенной величины можно считать более корректным, чем значение средней арифметической величины, поэтому далее в расчетах будем использовать среднюю взвешенную.
Теперь добавим в таблицу столбцы, данные которых нам понадобятся для расчета дисперсии.
|
Число компаний (f) |
Середина интервала (Xi) = (начало интервала+конец интервала)/2 |
Xi*fi |
|
|
|
|
2 |
17,5 |
35 |
-20,5 |
420,25 |
840,5 |
|
8 |
29 |
232 |
-9 |
81 |
648 |
|
14 |
37,5 |
525 |
-0,5 |
0,25 |
3,5 |
|
9 |
45,5 |
409,5 |
7,5 |
56,25 |
506,25 |
|
3 |
55,5 |
166,5 |
17,5 |
306,25 |
918,75 |
|
Итого: 36 |
— |
1368 |
— |
— |
2917 |
Рассчитаем дисперсию.
 =2917/36=81,03. (дисперсия не имеет размерности)
=2917/36=81,03. (дисперсия не имеет размерности)
Среднеквадратическое отклонение рассчитывается как корень квадратный из дисперсии.
 =9 (млн. руб.).
=9 (млн. руб.).
Рассчитаем коэффициент вариации по формуле:
 =(9/38)*100%=23,68%.
=(9/38)*100%=23,68%.
Рассчитаем моду и медиану.
Найдем моду по формуле. 
Модальный интервал находим по наибольшей частоте. Наибольшая частота, т.е. частота модального интервала fМо=14. Модальный интервал от 33 до 42 млн. руб. Значит величина модального интервала i = 42-33=9.
Нижняя граница модального интервала  равна 33.
равна 33.
Частота предмодального интервала  равна 8.
равна 8.
Частота постмодального интервала  равна 9.
равна 9.
Мода будет равна = 33 + 9*((14-8)/(14-8+14-9))=37,9 млн. руб.
Найдем медиану по формуле. 
Медианный интервал находим по накопленной частоте. Суммируются f частоты, пока не достигается значение, превышающее середину совокупности (36/2=18 млн. руб.).
|
Группы компаний по основным производственным фондам, млн. руб. (х) |
Число компаний (f) |
Накопленная частота S |
|
10 – 25 |
2 |
2 |
|
25 – 33 |
8 |
10 |
|
33 – 42 |
14 |
24 |
|
42 – 49 |
9 |
33 |
|
49 – 62 |
3 |
36 |
Таким образом, медианный интервал от 33 до 42 млн. руб. Значит величина медианного интервала i = 42-33=9.
Частота медианного интервала fМе=14.
Нижняя граница медианного интервала  равна 33.
равна 33.
Накопленная частота предмедианного интервала  равна 10.
равна 10.
Медиана будет равна = 33 + 9*((36/2-10)/(14))=38,14 млн. руб.
Расчеты по теме “индексы”
Пример по выборке.
Задача по группировке.
Решение задачи по расчету средней.
Задача по кореляционному анализу
Контрольные и курсовые работы по общей теории статистики и экономической статистике по этим и другим темам представлены в соответствующем разделе сайта.



