Связь между
молярной (Cm)
и удельной (с) теплоемкостями газа
Cm=cM,
где М
— молярная
масса газа.
Молярные
теплоемкости*
при
постоянном объеме и постоянном давлении
соответственно равны
Cv=iR/2;
Cp=(i+2)R/2
где i
— число
степеней свободы; R
— молярная
газовая постоянная.
Удельные
теплоемкости при постоянной объеме и
постоянном давлении соответственно
равны
![]() ,
,
![]() .
.
Уравнение Майера
Cр—Сv=R.
Показатель
адиабаты
![]() ,
,
или
![]() ,
,
или![]() .
.
Внутренняя
энергия идеального газа
U=N<>
или U=vCvT,
где <>—средняя
кинетическая энергия молекулы;
N—число
молекул газа;
v
— количество
вещества.
Работа, связанная
с изменением объема газа, в общем случае
вычисляется по формуле
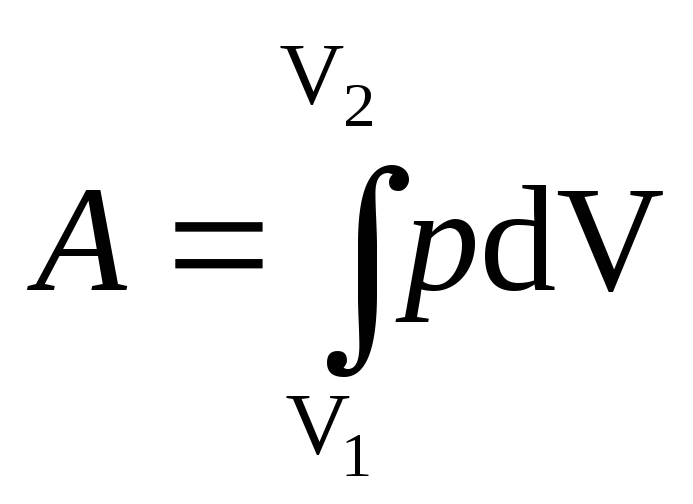 ,
,
где V1
— начальный
объем газа; V2
— его
конечный объем.
Работа газа:
а) при изобарном
процессе (p=const)
A=p(V2
–
V1);
б) при изотермическом
процессе (T=const)
![]() ;
;
*
Здесь и далее
в целях упрощения записи в индексах
обозначений молярной теплоемкости при
постоянном давлении и постоянном объеме
букву «m»
будем опускать.
в) при адиабатном
процессе
![]() ,
,
или
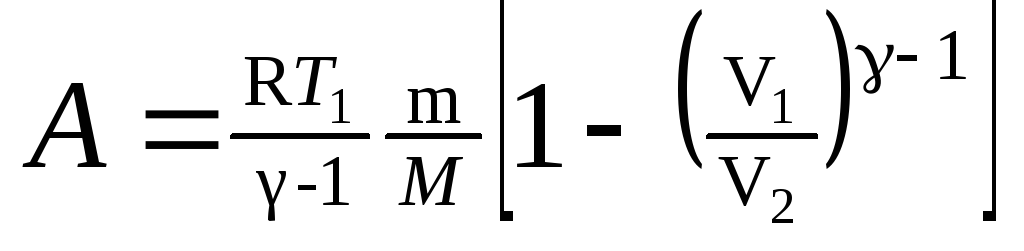 ,
,
где T1
— начальная
температура газа; T2
— его
конечная температура.
Уравнение Пуассона
(уравнение газового состояния при
адиабатном процессе)
![]() .
.
Связь между
начальным и конечным значениями
параметров состояний газа при адиабатном
процессе:
![]() .
.
Первое начало
термодинамики в общем случае записывается
в виде
Q=U+A,
где Q
– количество теплоты, сообщённое газу;
U—изменение
его внутренней энергии; А
—
работа, совершаемая газом против внешних
сил.
Первое начало
термодинамики:
а) при изобарном
процессе
![]()
б) при изохорном
процессе (A=0)
![]() ;
;
в) при изотермическом
процессе (U=0)
![]() ,
,
г) при адиабатном
процессе (Q=0)
![]() .
.
Термический
коэффициент полезного действия (КПД)
цикла
в
общем случае
![]() ,
,
где Q1—количество
теплоты, полученное рабочим телом
(газом) от нагревателя; Q2—количество
теплоты, переданное рабочим телом
охладителю.
КПД цикла Карно
![]() ,
,
или
![]() ,
,
где T1
— температура
нагревателя; T2
— температура
охладителя.
Изменение энтропии
![]()
где A
и B
— пределы
интегрирования, соответствующие
начальному и конечному состояниям
системы. Так как процесс равновесный,
то
интегрирование проводится по любому
пути.
Формула Больцмана
S=klnW,
где
S — энтропия
системы;
W
—
термодинамическая вероятность ее
состояния; k
—
постоянная Больцмана.
Примеры решения задач
Пример
1. Вычислить
удельные теплоемкости неона и водорода
при постоянных объеме (сv)
и давлении (cp),
принимая эти газы за идеальные.
Решение.
Удельные теплоемкости идеальных газов
выражаются формулами
![]() ; (1)
; (1)
![]() . (2)
. (2)
Для неона (одноатомный
газ) i1=3,
M1=2010-з
кг/моль.
Подставив в формулы
(1) и
(2) значения
i1,
M1
и R
и произведя вычисления, найдем:
сv1=
624
Дж/(кгК);
сp1=1,04
кДж/(кгК).
Для водорода
(двухатомный газ) i2=5,
M2=210-3
кг/моль.
Вычисление по
формулам
(1) и
(2) дает
следующие значения удельных теплоемкостей
водорода:
сv2=10,4
кДж/(кгK);
сp2=14,6
кДж/(кгK).
Пример
2. Вычислить
удельные теплоемкости сv
и сp
смеси неона и водорода. Массовые доли
газов соответственно равны 1=0,8
и 2=0,2.
Значения удельных теплоемкостей газов
взять из примера
1.
Решение.
Удельную теплоемкость смеси при
постоянном объеме сv
найдем из следующих рассуждений. Теплоту,
необходимую для нагревания смеси на
T,
выразим двумя соотношениями:
Q=сv(m1+m2)T
(1)
где сv
— удельная
теплоемкость смеси; m1
— масса
неона; m2
— масса
водорода, и
Q=(сv1m1+
сv2m2)T (2)
где сv1
и сv2
— удельные
теплоемкости неона и водорода
соответственно.
Приравняв правые
части выражений
(1) и
(2) и разделив
обе части полученного равенства на
T,
найдем
сv(m1+m2)=
сv1m1+
сv2m2,
откуда
![]()
Отношения
1=m1/(m1+m2)
и 1=m2/(m1+m2)
выражают массовые доли соответственно
неона и водорода. С учетом этих обозначений
последняя формула, примет вид
сv=сv11+
сv22.
Подставив в эту
формулу числовые значения величин,
найдем
сv=2,58
кДж/(кгК).
Рассуждая
таким
же
образок, получим формулу для вычисления
удельной теплоёмкости смеси при
постоянном давлении:
cp=сp11+
сp22
Произведя вычисления
по этой формуле, найдем
cp=3,73
кДж/(кгК).
Пример
3. Определить
количество теплоты, поглощаемой
водородом массой m=0,2
кг при нагревании его от температуры
t1=0°С
до температуры t2=100
°С при постоянном давлении. Найти также
изменение внутренней энергии газа и
совершаемую им работу.
Решение.
Количество теплоты Q,
поглощаемое газом при изобарном
нагревании, определяется по формуле
Q=mcpT,
(1)
где m
— масса
нагреваемого газа; cp
— его
удельная теплоемкость при постоянном
давлении; T
— изменение температуры газа.
Как известно,
![]() .
.
Подставив это выражение cp
в формулу
(1), получим
![]()
Произведя вычисления
по этой формуле, найдем
Q=291
кДж.
Внутренняя энергия
выражается формулой
![]() ,
,
следовательно, изменение внутренней
энергии
![]() .
.
После подстановки
в эту формулу числовых значений величин
и вычислений получим U=208
кДж.
Работу расширения газа
определим по формуле, выражающей первое
начало термодинамики: Q=U+A,
откуда
A=Q – U.
Подставив значения
Q и U,
найдем
А
=83 кДж.
Пример
4. Кислород
занимает объем V1=1
м3
и находится под давлением р1=200
кПа. Газ нагрели сначала при постоянном
давлении до объема V2=3
м2,
a
затем при постоянном объеме до давления
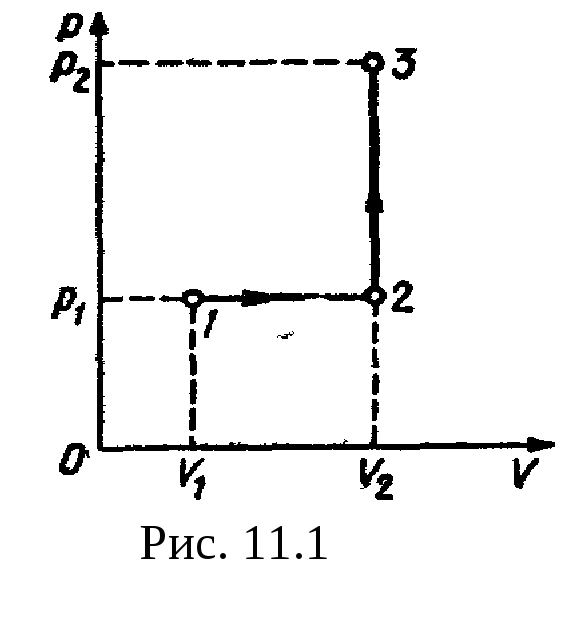
Рис
11.1 р2=500
кПа. Построить график процесса и найти:
1) изменение
U
внутренней энергии газа; 2)
совершенную им работу A;
3) количество
теплоты
Q,
переданное
газу.
Решение.
Построим график процесса (рис.
11.1). На
графике точками
1, 2, 3
обозначены состояния газа, характеризуемые
параметрами (р1,
V1,
T1),
(р1,
V2,
T2),
(р2,
V2,
T3).
1.
Изменение внутренней энергии газа при
переходе его из состояния
1 в состояние
3 выражается
формулой
U=cvmT,
где cv
— удельная
теплоемкость газа при постоянном объеме;
m
— масса
газа; T
— разность
температур, соответствующих конечному
3 и
начальному 1 состояниям, т. е. T=T3—
T1.
Так как
![]() ;
;
где М
— молярная
масса газа, то
![]() .
.
(1)
Температуры T1
и T3
выразим из уравнения Менделеева
— Клапейрона
(![]() ):
):
![]()
С учетом этого
равенство
(1) перепишем
в виде
U=(i/2)(p2V2–p1V1).
Подставим сюда
значения величин (учтем, что для кислорода,
как двухатомного газа, i=5)
и произведем вычисления:
U=3,25
МДж.
2.
Полная работа, совершаемая газом, равна
A=A1+A2,
где A1
— работа
на участке
1—2; A2
— работа
на участке
2—3,
На участке
1—2 давление
постоянно (p=const).
Работа в этом случае выражается формулой
A1=p1V=p1(V2—V1).
На участке 2—3
объем газа не изменяется и, следовательно,
работа газа на этом участке равна нулю
(A2=0).
Таким образом,
A=A1=p1(V2—V1).
Подставив в эту
формулу значения физических величин,
произведем вычисления:
A=0,4
МДж
3.
Согласно первому началу термодинамики,
количество теплоты Q,
переданное газу, равно сумме работы
A,
совершенной газом, и изменению U
внутренней энергии:
Q=A+U,
или
Q=3,65 МДж.
Пример
5. Идеальный
двухатомный газ, содержащий количество
вещества v=l
моль, находится под давлением p1=250кПа
и занимает объем V1==10
л. Сначала газ изохорно нагревают до
температуры T2=400
К. Далее, изотермически расширяя, доводят
его до первоначального давления.
После этого путем изобарного сжатия
возвращают газ в начальное состояние.
Определить термический КПД
цикла.
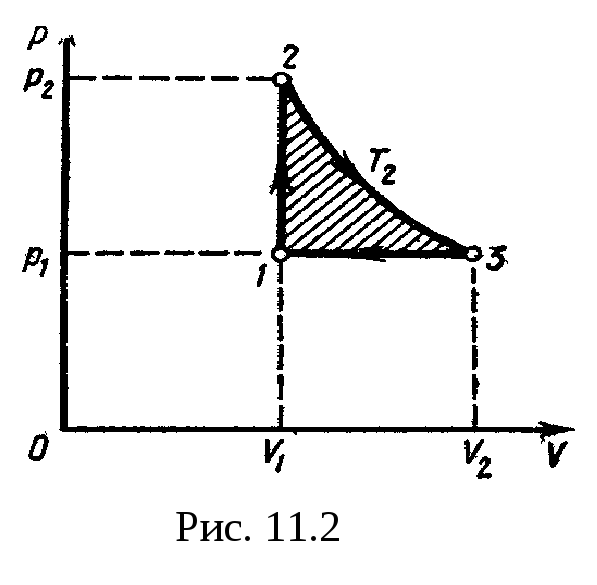
Решение.
Для наглядности построим сначала график
цикла, который состоит из изохоры,
изотермы и изобары. В координатах р,
Vэтот
цикл имеет вид. представленный на рис.
11.2. Характерные
точки цикла обозначим
1, 2, 3.
Термический КПД
любого цикла определяется выражением
=(Q1
– Q2)/Q1,
или =l
– Q2/Q1,
(1) где
Q1
—
количество теплоты, полученное газом
за цикл от нагревателя; Q2
— количество теплоты, отданное газом
за цикл охладителю.
Заметим, что разность
количеств теплоты Q1
– Q2
равна работе A,
совершаемой газом за цикл.
Эта
работа на графике в координатах р,
V (рис.
11.2)
изображается площадью цикла (площадь
цикла заштрихована).
Рабочее вещество
(газ) получает количество теплоты
Q1
на двух участках: Q1-2
на участке
1—2 (изохорный
процесс) и Q2-3
на участке
2—3
(изотермический процесс). Таким образом,
Q1=Q1-2+Q2-3.
Количество теплоты,
полученное газом при изохорном процессе,
равно
Q1-2=Cvv(T2
–
T1),
где Cv
— молярная
теплоемкость газа при постоянном объеме;
v
— количестве вещества. Температуру T1
начального состояния газа найдем,
воспользовавшись уравнением Клапейрона
— Менделеева:
T1=p1V1/(vR).
Подставив числовые
значения и произведя вычисления, получим
![]()
Количество теплоты,
полученное газом при изотермическом
процессе, равно
Q2-3=vRT2ln(V2/V1),
где V2
—
объем, занимаемый газом при температуре
T2
и давлении p1
(точка
3 на графике).
На участке
3—1 газ
отдает количество теплоты Q2,
равное
Q2=Q3-1=Cpv(T2
–T1),
где Cp
— молярная
теплоемкость газа при изобарном процессе.
Подставим найденные
значения
Q1
и Q2
в формулу
(1):
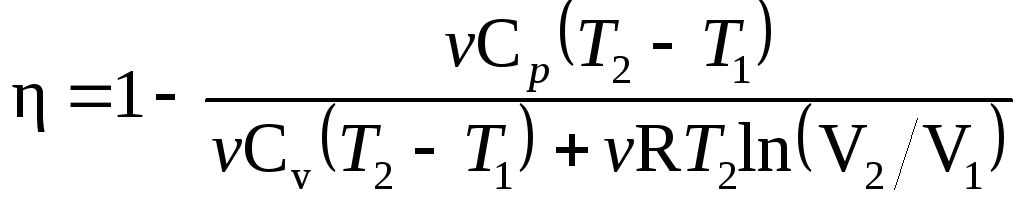
В полученном
выражении заменим отношение объемов
V2/V1,
согласно закону Гей-Люссака, отношением
температур (V2/V1=T2/T1)
и выразим Cv
и Cp
через число степеней свободы молекулы
[Cv=iR/2,
Cp=(i+2)R/2].
Тогда после сокращения на
v
и R/2
получим
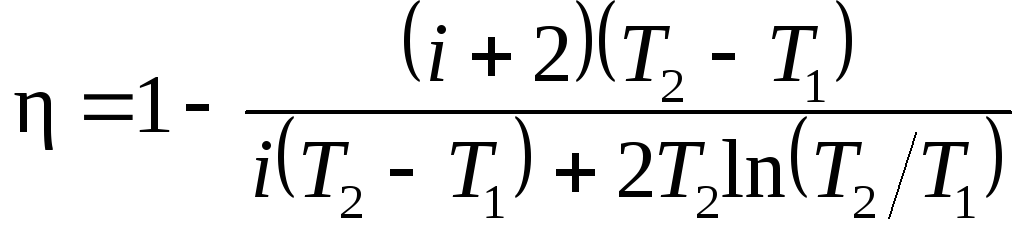 .
.
Подставив значения
i,
T1,
T2
и R
и произведя вычисления, найдем
![]()
Пример 6.
В цилиндре под поршнем находится водород
массой m=0,02
кг при температуре T1=300K.
Водород начал расширяться адиабатно,
увеличив свой объем в пять раз, а затем
был сжат изотермически, причем объем
газа уменьшился в пять раз. Найти
температуру Т2,
в конце адиабатного расширения и работу
А,
совершенную газом. Изобразить процесс
графически.
Решение.
Температуры и объемы газа, совершающего
адиабатный процесс, связаны между
собой соотношением
![]() ,
,
где —
показатель адиабаты (для водорода как
двухатомного газа =1,4).
Отсюда получаем
выражение для конечной температуры T2:
![]() .
.
Подставляя числовые
значения заданных величин, находим
![]() .
.
Прологарифмируем
обе части полученного выражения:
lgT2=lg300+0,4(lgl
– lg5)=2,477+0,4( -0,699)=2,477—0,280=2,197.
Зная lgT2,
по таблицам антилогарифмов находим
искомое значение T2:
T2=157
К.
Работа A1
газа при адиабатном расширении
определяется по формуле
![]() .
.
Подставив сюда
числовые значения величин, после
вычисления получим
![]()
Работа A2
газа при изотермическом сжатии выражается
формулой
A2=RT2(m/M)ln(V2/V1).
Произведя вычисления
по этой формуле, найдем
A2=
-21 кДж.
Знак минус показывает,
что при сжатии газа работа совершена
внешними силами.
Общая работа,
совершенная газом при рассмотренных
процессах, А=A1+A2=29,8кДж
+ (-21 кДж)=8,8 кДж.
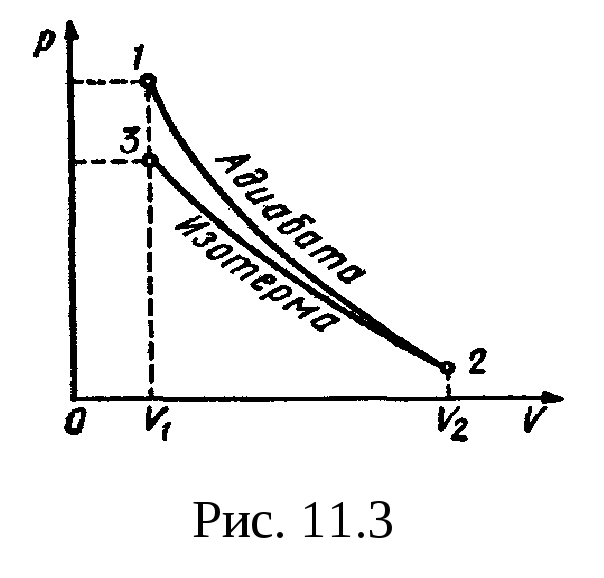
График процесса
приведен на рис.
11.3.
Пример
7. Нагреватель
тепловой машины, работающей по обратимому
циклу Карно, имеет температуру
t1==200°С.
Определить температуру Т2,
охладителя, если при получении от
нагревателя количества теплоты Q1=
1 Дж машина
совершает работу A=0,4
Дж? Потери на трение и теплоотдачу не
учитывать.
Решение.Температуру охладителя найдем, использовав
выражение для термического КПД машины,
работающей по циклу Карно,=(T1—
T2)/T1.
Отсюда
T2=
T1(1-).
(1)
Термический КПД
тепловой машины выражает отношение
количества теплоты, которое превращено
в механическою работу A,
к количеству теплоты Q1,
которое получено рабочим телом тепловой
машины из внешней среды (от нагревателя),
т. е. =A/Q1.
Подставив это выражение в формулу
(1), найдем
T2=
T1(1-A/Q).
(2)
Учтя, что T1=473
К, после вычисления по формуле
(2) получим
T2=284
К.
Пример
8. Найти
изменение S
энтропии при нагревании воды массой
m=100
г от температуры t1=0°C
до температуры
t2=100
°С и последующем превращении воды в пар
той же температуры.
Решение.
Найдем отдельно изменение энтропии S’
при нагревании воды и изменение энтропии
S”
при превращении ее в пар. Полное изменение
энтропии выразится суммой S’
и S”.
Как известно,
изменение энтропии выражается общей
формулой
![]() (1)
(1)
При бесконечно
малом изменении dT
температуры нагреваемого тела
затрачивается количество теплоты
dQ=mcdT,
где m
— масса
тела; с
— его
удельная теплоемкость. Подставив
выражение dQ
в равенство
(1), найдем
формулу для вычисления изменения
энтропии при нагревании воды:
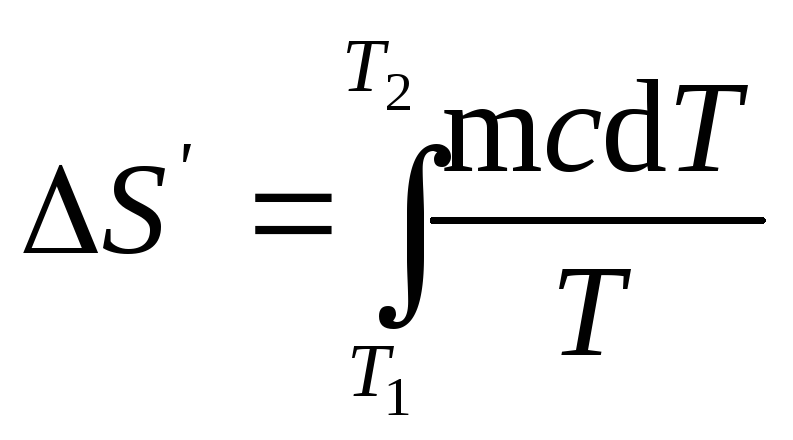 .
.
Вынесем за знак
интеграла постоянные величины и
произведем интегрирование, тогда получим
S’=mcln(T2/T1).
После вычислений
найдем S’=132
Дж/К.
При вычислении по
формуле
(1) изменения
энтропии во время превращения воды в
пар той же температуры постоянная
температуpa
T
‘выносится
за знак интеграла. Вычислив интеграл,
найдем
![]() (2)
(2)
где Q
—
количество теплоты, переданное при
превращении нагретой воды в пар той
же температуры.
Подставив в равенство
(2) выражение
количества теплоты Q=m,
где
— удельная
теплота парообразования, получим
![]()
(3)
Произведя вычисления
по формуле
(3), найдем
S”=605
Дж/К.
Полное изменение
энтропии при нагревании воды и последующем
превращении ее в пар S=S’+S”=737
Дж/К.
Пример
9. Определить
изменение S
энтропии при изотермическом расширении
кислорода массой m=10
г от объема V1=25
л до объема V2=100
л.
Решение.
Так как процесс изотермический, то в
общем выражении энтропии
![]()
температуру выносят за знак интеграла.
Выполнив это, получим
![]() (1)
(1)
Количество теплоты
Q, полученное
газом, найдем по первому началу
термодинамики: Q=U+A.
Для изотермического процесса U=0,
следовательно,
Q=A,
(2) а
работа А для этого процесса определяется
по формуле
A=(m/M)RT
ln(V2/V1).
(3)
С учетом
(2) и
(3) равенство
(1) примет
вид
S=(m/M)R
ln(V2/V1).
(4)
Подставив в
(4) числовые
значения и произведя вычисления, получим
S=(1010-3/(3210-3))
8,31
ln(10010-3/(2510-3))
Дж/К=3,60
Дж/К.
Первое начало термодинамики (первый закон термодинамики) представляет собой закон сохранения энергии в тепловых процессах.
Первое начало термодинамики
Внутренняя энергия идеального газа изменяется двумя способами: за счет теплопередачи или при совершении работы.
±ΔU=±Q±A‘
Пояснение:
- +∆U — внутренняя энергия газа увеличивается.
- –∆U — внутренняя энергия газа уменьшается.
- +Q — газ нагревают (газу передают количество теплоты).
- –Q — газ охлаждается (газ отдает тепло окружающей среде).
- +A’ — газ сжимает внешняя сила.
- –A’ — газ расширяется, совершая работу.
Внимание! Знак перед работой показывает, как процесс совершения работы влияет на изменение внутренней энергии газа.
Пример №1. В некотором процессе внутренняя энергия газа уменьшилась на 300 Дж, а газ совершил работу 500 Дж. Какое количество теплоты было сообщено газу?
Чтобы рассчитать количество теплоты, сообщенное газу, нужно найти разность между изменением внутренней энергии и работой, совершенным газом. Для этого нужно правильно определить их знаки. Так как внутренняя энергия уменьшилась, она отрицательна. Но работа положительна. Поэтому газу было сообщено следующее количество теплоты:
Q = A – U = 500 – 300 = 200 (Дж)
Зависимость физических величин
Выясним, от чего зависят величины, входящие в формулу первого начала термодинамики. Изменение внутренней энергии идеального газа зависит от изменения температуры:
ΔU=32νRΔT
Работа идеального газа зависит от изменения его объема:
A‘=pΔV
Первое начало термодинамики для изопроцессов
| Изотермический процесс (T = const) |
ΔU=0, Q=A‘ |
| Изохорный процесс (V = const) |
A‘=0, ΔU=Q |
| Изобарное расширение газа (p = const) |
ΔU=Q−pΔV ΔU=Q−νRΔT |
| Адиабатный (система не получает тепло извне и не отдает его окружающей среде, или Q = 0) |
Q=0, ΔU=A‘ |
Пример №2. Идеальный одноатомный газ находится в сосуде с жесткими стенками объемом 0,6 куб. м. При нагревании его внутренняя энергия увеличилась на 18 кДж. На сколько возросло давление газа?
18 кДж = 18000 Дж
Внутреннюю энергию газа можно определить по формуле:
ΔU=32νRΔT
Отсюда изменение температуры равно:
ΔT=2ΔU3νR
Уравнение состояния идеального газа для 1 и 2 состояния:
p1V=νRT1
p2V=νRT2
Отсюда давления равны:
p1=νRT1V
p2=νRT2V
Разность давлений:
p2−p1=νRT2V−νRT1V=νRVΔT=νRV·2ΔU3νR=2ΔU3V
p2−p1=2·180003·0,6=20000 (Па)=20 (кПа)
Графические задачи на первое начало термодинамики
Рассмотрим графический способ решения задачи на первое начало термодинамики на конкретном примере.
Задача: Один моль идеального одноатомного газа сначала изотермически расширился (T1 = 300 К). Затем газ охладили, понизив давление в 3 раза (см. рисунок). Какое количество теплоты отдал газ на участке 2–3?
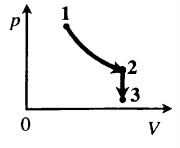
Порядок решения:
1. Определить температуры для всех указанных точек, учитывая графики процессов, масштаб и условие задачи.
T1 = T2 = 300 К; T3 = 100 К
2. Определить, к какому изопроцессу относится тот участок графика, о котором спрашивают в задаче.
Участок 2–3 на графике — это изохорный процесс, так как давление остается постоянным.
3. Записать для него первое начало термодинамики.
В данном процессе:
ΔU=Q
4. Учитывая характер изменения величин, правильно расставить знаки: −ΔU=−Q.
5. Подставляя в первое начало термодинамики формулы для расчета изменения внутренней энергии и работы газа, решить задачу.
Формула изменения внутренней энергии газа:
ΔU=32νRΔT
Формула работы газа:
A‘=pΔV
Так как процесс изохорный, работа газа равна нулю. Поэтому количество теплоты, отданное газом на участке 2–3, равно изменению внутренней энергии газа:
Изменение внутренней энергии равно:
Q23=32νRΔT23=32·1·8,31·200=2493 (Дж)
Задание EF17492
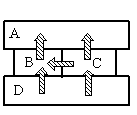 Четыре металлических бруска положили вплотную друг к другу, как показано на рисунке. Стрелки указывают направление теплопередачи от бруска к бруску. Температуры брусков в данный момент 100°С, 80°С, 60°С, 40°С. Температуру 40°С имеет брусок
Четыре металлических бруска положили вплотную друг к другу, как показано на рисунке. Стрелки указывают направление теплопередачи от бруска к бруску. Температуры брусков в данный момент 100°С, 80°С, 60°С, 40°С. Температуру 40°С имеет брусок
- A
- B
- C
- D
Алгоритм решения
- Определить тип теплопередачи.
- Вспомнить, как происходит этот тип теплопередачи.
- Сделав анализ рисунка, установить, какой брусок имеет указанную в задаче температуру.
Решение
Так как это твердые тела, поверхности которых соприкасаются друг с другом, и перенос тепла происходит без переноса вещества, то этот вид теплопередачи является теплопроводностью. Тепло всегда направлено от более нагретого тела к менее нагретому.
На рисунке видно, что самым нагретым телом является нижний брусок, так как он только отдает тепло, но не принимает его. Средний брусок справа менее нагрет, чем нижний, так как принимает от него тепло. Но он более теплый по сравнению со средним бруском слева, так как он делится с ним теплом. И оба этих бруска отдают свою энергию верхнему бруску, который сам только принимает тепло, но не отдает его. Следовательно, именно он имеет температуру +40 оС.
Ответ: A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A

pазбирался: Алиса Никитина | обсудить разбор
Задание EF17562
Газу передали изохорно количество теплоты 300 Дж. Как изменилась его внутренняя энергия в этом процессе?
Ответ:
а) увеличилась на 300 Дж
б) уменьшилась на 300 Дж
в) увеличилась на 600 Дж
г) уменьшилась на 600 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 300 Дж.
Первое начало термодинамики:
ΔU=Q+A
Так как по условию задачи это изохорный процесс, то работа равна 0. Следовательно, изменение внутренней энергии газа равно количеству теплоты:
ΔU=Q=300 (Дж)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17597
Находясь в цилиндре двигателя, газ получил от нагревателя количество теплоты, равное 10 кДж. Затем он расширился, совершив работу 15 кДж. В результате всех этих процессов внутренняя энергия газа уменьшилась на
Ответ:
а) 5 кДж
б) 10 кДж
в) 15 кДж
г) 25 кДж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 10 кДж.
• Работа, совершенная газом: A = 15 кДж.
Первое начало термодинамики:
ΔU=Q+A
В этой формуле за работу принимается та работа, что совершается над газом. Но в данном случае газ сам совершает работу. Поэтому первое начало термодинамики примет вид:
ΔU=Q−A=10−15=−5 (кДж)
Знак «–» указывает на то, что внутренняя энергия газа уменьшилась на 5 кДж.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17579
При постоянном давлении гелий нагрели, в результате чего он совершил работу 5 кДж? Масса гелия 0,04 кг. Насколько увеличилась температура газа?
Ответ:
а) 60 К
б) 25 К
в) 15 К
г) 3 К
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Записать первое начало термодинамики.
3.Записать формулу для расчета работы газа.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и выполнить вычисления искомой величины.
Решение
Запишем исходные данные:
• Газ совершил работу: A = 5 кДж.
• Масса гелия: m = 0,04 кг.
5 кДж = 5000 Дж
Первое начало термодинамики:
ΔU=Q+A
Учтем, что не над газом совершают работу, а сам газ совершает ее:
Отсюда:
ΔU=Q−A
Так как газ нагревали изобарно, часть тепла ушла на изменение внутренней энергии газа, а часть — на совершение этим газом работы.
Работа, совершенная газом, равна:
A=pΔV=mMRΔT
Молярная масса гелия равна 4∙10–3 кг/моль.
Отсюда:
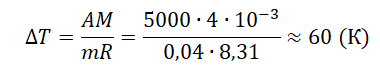
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 3.9k
В случае, если результатом теплообмена становится передача телу некоего количества теплоты Q, то его температура и внутренняя энергия претерпевают изменения.
Необходимое для нагревания 1 кг вещества на 1 К количество теплоты Q носит название удельной теплоемкости вещества c, а ее формула выглядит следующим образом:
c=Qm∆T.
В большом количестве ситуаций удобной для использования является молярная теплоемкость C:
C=M·c, где M представляет собой молярную массу вещества.
Теплоемкость, полученная таким способом, не является однозначной характеристикой вещества. Исходя из первого закона термодинамики, можно сказать, что изменение внутренней энергии тела зависимо не только от количества полученной теплоты, но и от величины совершенной телом работы. В разных условиях осуществления процесса теплопередачи тело может совершать различную работу. Таким образом, переданное телу одинаковое количество теплоты способно провоцировать изменения его внутренней энергии и, соответственно, температуры.
Подобной неоднозначностью при определении теплоемкости характеризуются только газообразные вещества. Объем в процессе нагрева практически не меняет своей величины, что сводит работу расширения к нулю. По этой причине вся полученная телом теплота уходит на изменение его внутренней энергии. Газ в процессе теплопередачи может значительно менять свой объем и совершать работу, чем отличается от твердых тел и жидкостей. Таким образом, теплоемкость газообразного вещества имеет зависимость от характера термодинамического процесса.
Изопроцессы в газах
Чаще всего рассматриваются два значения теплоемкости газов:
- CV являющаяся молярной теплоемкостью в изохорном процессе (V=const);
- Cp представляющая собой молярную теплоемкость в изобарном процессе (p=const).
При условии постоянного объема газ не совершает работы: A=0. Исходя из первого закона термодинамики для 1 моля газа, можно сказать, что справедливым является следующее выражение:
QV=CV∆T=∆U.
Изменение величины ΔU внутренней энергии газа прямо пропорционально изменению значения ΔT его температуры.
В условиях процесса при постоянном давлении первый закон термодинамики дает такую формулу:
Qp=∆U+p(V2-V1)=CV∆T+pV.
В котором ΔV является изменением объема 1 моля идеального газа при изменении его температуры на ΔT. Таким образом, можно заявить, что:
Cp=Qp∆T=CV+p∆V∆T.
Из уравнения состояния идеального газа, записанного для 1 моля, может выражаться отношение ΔVΔT:
pV=R.
В котором R представляет собой универсальную газовую постоянную. При условии постоянства давления p=const, можно записать следующее:p∆V=R∆T или ∆V∆T=Rp.
Из этого следует, что выражающее связь между молярными теплоемкостями Cp и CV соотношение имеет вид (формула Майера):
Cp=CV+R.
В процессе с неизменным давлением молярная теплоемкость Cp газа всегда превышает молярную теплоемкость CV в процессе с не подверженным изменениям объемом, что демонстрируется на рисунке 3.10.1.
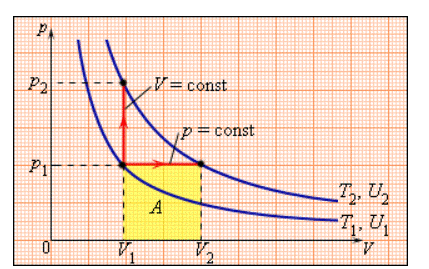
Рисунок 3.10.1. Два возможных процесса нагревания газа на ΔT=T2 –T1. При p=const газ совершает работу A=p1(V2 – V1). Поэтому Cp>CV.
Отношение теплоемкостей в процессах с постоянным давлением и постоянным объемом занимает важное место в термодинамике и обозначается в виде греческой буквы γ.
γ=CpCV.
Данное отношение включено в формулу для адиабатического процесса.
Между двумя изотермами, обладающими температурами T1 и T2 на диаграмме (p, V) реальны различные варианты перехода. Так как для всех подобных переходов изменение величины температуры ΔT=T2 –T1 является одним и тем же, выходит, что изменение значения
ΔU внутренней энергии тоже одинаково. С другой стороны, совершенные при этом работы A и количества теплоты Q, полученные в результате теплообмена, выйдут разными для различных путей перехода. Из этого следует, что газа имеет относительно приближенное к бесконечности число теплоемкостей. Cp и CV представляют собой частные, однако, очень важные для теории газов, значения теплоемкостей.
Рисунок 3.10.2. Модель теплоемкости идеального газа.
Термодинамические процессы, в которых теплоемкость газа не подвергается изменениям, носят название политропических.
Каждый изопроцесс являются политропическим. В изотермическом процессе ΔT=0, из-за чего CT=∞. В адиабатическом процессе ΔQ=0, выходит, что Cад=0.
Стоит обратить внимание на то, что «теплоемкость» и «количество теплоты» являются крайне неудачными терминами, доставшимися современной науке в качестве наследства теории теплорода, которая господствовала в XVIII веке.
Данная теория представляла теплоту в виде содержащегося в телах особого невесомого вещества. Считалось, что оно не подвержено уничтожению и не может быть созданным. Явление нагрева объясняли повышением, а охлаждение – понижением содержания в телах теплорода. Однако теория теплорода оказалась несостоятельной, так как не смогла дать ответа на вопрос, почему одинаковое изменение внутренней энергии тела возможно получить, приводя ему разное количество теплоты в зависимости от совершаемой им работы. По этой причине утверждение, что в данном теле содержится некоторый запас теплорода лишено смысла.
Молекулярно-кинетическая теория
В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией E→ поступательного движения молекул и абсолютной температурой T:
E→=32kT.
Внутренняя энергия 1 моля идеального газа эквивалентна произведению E→ на число АвогадроNА:
U=32kNAT=32RT.
При условии изменения температуры на величину ΔT внутренняя энергия изменяется на величину:
U=32R∆T=CV∆T.
Коэффициент пропорциональности между ΔU и ΔT эквивалентен теплоемкости CV в условиях постоянного давления:
CV=32R=12,47 ДЖ/моль·К.
Данное выражение подтверждается экспериментами с газами, которые состоят из одноатомных молекул вроде гелия, неона или аргона. При этом для двухатомных (водород, азот) и многоатомных (углекислый газ) газов такое соотношение не согласуется с полученными в результате опытов данными. Причина этого расхождения заключается в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать энергию как поступательного, так и вращательного их движения.
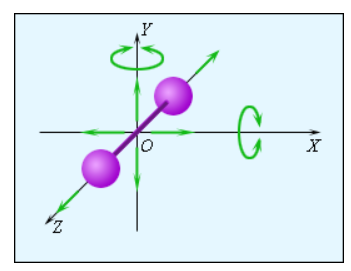
Рисунок 3.10.3. Модель двухатомной молекулы. Точка O совпадает с центром масс молекулы.
Рисунок 3.10.3 иллюстрирует модель двухатомной молекулы. Молекула имеет возможность производить пять независимых типов движений: три поступательных движения вдоль осей X, Y, Z и два вращения относительно осей X и Y.
Опытным путем выяснено, что вращение относительно оси Z, на которой лежат центры обоих атомов, может быть возбуждено только при очень высоких значениях температуры. В условиях обычных температур вращение вокруг оси Z не происходит.
Каждое независимое движение в молекуле носит название степени свободы.
Выходит, что одноатомная молекула обладает 3 поступательными степенями свободы, «жесткая» двухатомная молекула 5 степенями, то есть 3 поступательными и 2 вращательными, а многоатомная молекула 6 степенями свободы, из которых 3 приходятся на поступательные и 3 на вращательные.
В классической статистической физике доказывается теорема о равномерном распределении энергии по степеням свободы:
Если система молекул находится в тепловом равновесии при температуре T, то средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна 12kT.
Из данной теоремы следует, что для молярных теплоемкостей газа Cp и CV и их отношения
γ справедлива запись в следующем виде:
CV=i2R, Cp=Cv+R=i+22R, γ=CpCV=i+2i,
где i представляет собой количество степеней свободы газа.
Для газа, состоящего из одноатомных молекул (i=3)
CV=32R, Cp=Cv+R=52R, γ=CpCV=53=1,66.
Для газа, состоящего из двухатомных молекул (i=5)
CV=52R, Cp=Cv+R=72R, γ=CpCV=75=1,4.
Для газа, состоящего из многоатомных молекул (i=6)
CV=3R, Cp=Cv+R=4R, γ=CpCV=43=1,33.
В обычных условиях экспериментально измеренные теплоемкости многих газов неплохо согласуются с приведенными выражениями, но в целом классическая теория теплоемкости газов вполне удовлетворительной не является. Существует колоссальное число примеров со значительной разницей между результатами эксперимента и теорией. Данный факт объясняется тем, что классическая теория не может полностью учесть, связанную с внутренними движениями в молекуле энергию.
Теорема о равномерном распределении энергии по степеням свободы может быть применена и по отношению к тепловому движению частиц в твердом теле. Входящие в состав кристаллической решетки атомы колеблются около положений равновесия. Энергия данных колебаний представляет собой внутреннюю энергию твердого тела. Каждый конкретный атом может колебаться в кристаллической решетке в трех взаимно перпендикулярных направлениях. Выходит, что каждый атом имеет 3 колебательные степени свободы. При условии гармонических колебаний средняя кинетическая энергия эквивалентна средней потенциальной энергии. По этой причине в соответствии с теоремой о равномерном распределении на каждую колебательную степень свободы приходится средняя энергия kT, а на один атом – 3kT.
Внутренняя энергия 1 моля твердого вещества равна следующему выражению:
U=3RNAkt=3Rt.
Следовательно, молярная теплоемкость вещества в твердом состоянии равняется:
С=3R=25,12 Дж/моль·К.
Данное выражение носит название закона Дюлонга–Пти. Для твердых тел почти нет различия между Cp и CV по причине пренебрежительно малой работы при сжатии или расширении.
Опыт показывает, что молярная теплоемкость у многих твердых тел (химических элементов) при обычных температурах на самом деле близка к 3R. При этом, в условиях низких температур заметны довольно сильные расхождения между теорией и экспериментом. Таким образом, гипотеза о равномерном распределении энергии по степеням свободы может считаться лишь приближением. Заметная в опыте зависимость теплоемкости от температуры объясняется только при условии использования квантовых представлений.
Физическая дисциплина «Термодинамика», имеющая дословный перевод с греческого как θέρμη — «тепло», δύναμις — «сила», занимается изучением общих характеристик макросистем и обращения энергии внутри них. Эту науку относят к феноменологическому типу, хотя опирается она на факты, полученные опытным путем.
Термодинамическая система, рассматриваемая в данном ракурсе, имеет конкретные характеристики, не применимые к единичным атомам и молекулам. К ним относят температуру, энергию, объем, концентрацию растворов, давление.
Определение таких параметров происходит по формулам термодинамики.
Основные формулы термодинамики
Особенностью термодинамики является то, что ее постулаты не касаются взаимодействия отдельных единиц (атомов, молекул), как в молекулярной физике. Предметом изучения предстают общие взаимопревращения энергии, образование теплоты, теплопередача и совершение работы.
Исходя из этого, выделяют основные формулы термодинамики, к которым относятся:
- Уравнение Менделеева-Клайперона: (PV=(m/M)*RT). Его смысл — в изменениях трех входящих величин, которые направлены на характеристику состояния идеального газа.
- Количество вещества, обозначаемое буквой (ν). (nu=N/NA=m/mu)
Величина, выражающая, сколько одинаковых структурных компонентов (единиц) находится в веществе.
- Закон Дальтона: давление смеси газов на стенку сосуда равно сумме давлений каждого входящего в смесь элемента: (p=p1+p2+…pn.)
- Главное уравнение МКТ (молекулярно-кинетической теории): (p=2n/3<varepsilon>n=N/V). Выражает математическое соотношение таких параметров, как давление газа и микропараметров: массы молекул, их скорости движения, концентрации.
- Средняя кинетическая энергия поступательного движения молекулы газа. Для обозначения применяется (E_k), выражается через формулу: (E_k=E_{моля}/NA=3/2ast RT/NA). Ее мерой является абсолютная температура идеального газа, поскольку потенциальная энергия (вследствие взаимодействия молекул друг с другом) равна нулю. Зная, что R/NA=k, получается формула: (E_k=3/2ast kT).
- Давление идеального газа прямо пропорционально концентрации и его температуре: (P=nkT.)
- Скорость молекул определяется по формулам:
(V=surd(2kT/m_o)=surd(2RT/mu)) — наиболее вероятная;
(<V>=surd(8kT/pi m_o)=surd(8RT/pimu)) — среднеарифметическая;
(<Vкв>surd(3kT/m_o)=surd(3RT/mu)) — средняя квадратичная. - Сумма кинетических энергий всех молекул определяет внутреннюю энергию всего идеального газа. Математически выражение выглядит так: (U=i/2ast(m/mu)ast RT.)
- Формула для определения работы, которую совершает идеальный газ при расширении:( A=P(V_2-V_1).)
- Формула первого закона термодинамики: (Q=Delta U+A.)
- Для определения удельной теплоемкости вещества применяется математическое выражение: (С=Delta Q/mdT.)
- Кроме удельной теплоемкости, существует понятие молярной теплоемкости. Для ее определения применяется формула: (C=cmu). Для изохорного процесса правильная формула принимает вид: (C_v=1/2ast R), для изобарного: (C_p=((i+2)/2)ast R).
Первое начало термодинамики
Согласно первому закону термодинамики, (Q) (количество внутренней теплоты), которое получил газ извне, расходуется на совершение работы (А) и изменение внутренней энергии (U). Формула закона: (Q=Delta U+A).
На практике газ может быть нагрет либо охлажден. Однако в данном случае рассматривается изотермический процесс, в котором один из характеризующих параметров остается неизменным.
Если процесс изотермичен, в химии включается закон Бойля-Мариота. В нем говорится, что давление газа соотносится к изначальному объему, при стабильной температуре, обратно пропорционально.
(Q=A)
Когда процесс происходит при неизменном объеме, говорят об изохорности. Здесь вступает в действие закон Шарля. В обозначенных условиях то тепло, которое поступило к газу, расходуется на изменение внутренней энергии. Другими словами, (P) пропорционально (T).
(Q=Delta U)
Протекание процессов в идеальном газе при неизменном давлении носит характер изобарного. Здесь действует закон Гей-Люссака, который выражается уравнением:
(Q=Delta U=pDelta V)
Полная формулировка закона гласит: полученное тепло при изобарном процессе расходуется на совершение работы газом, а также изменяет его внутреннюю энергию.
Часть процессов происходят изолированно от внешней среды. Газ не получает дополнительной энергии. Такая ситуация носит название адиабатной и математически записывается: (Q=0). Работа (А) в таком случае выражается: (A=-Delta U.)
Уравнение идеального газа в термодинамике
Молекулы идеального газа постоянно движутся. От того насколько велика скорость их движения, зависит общее состояние газа, а также величина его воздействия, например, на стенки сосуда. Поэтому одним из основных уравнений термодинамики является Клайперона-Менделеева:
(PV=(m/M)ast RT)
В уравнении (m) — единица массы газа, (M) — его молекулярная масса, (R) — универсальная величина, называемая газовой постоянной. Ее значение = 8,3144598. Измеряется в Дж/(моль*кг).
В основе термодинамики лежат и другие газовые постоянные, например, число Авогадро, постоянная Больцмана. Таким образом, (R=kNA.)
Из уравнения Клайперона-Менделеева можно также вычислить массу. Она будет равна произведению плотности на объем: (m=rho V).
Основное уравнение молекулярно-кинетической теории (МКТ)
Решение части задач зависит от знания особенностей взаимосвязи между давлением газа и характеристикой кинетической энергии его молекул. Математическое выражение такой зависимости носит название основного уравнения МКТ:
(p=2/3ast nE)
В данном выражении кинетическая энергия обозначена буквой (Е), а концентрация молекул — (n). Каждую из этих величин физики можно найти исходя из соответствующих формул, после чего уравнение для молекулярно-кинетической теории (МКТ) приобретает вид:
(p=nkT)
Формула теплоемкости и главная формула КПД в термодинамике
Когда теплообмен проявляется передачей телу определенного количества теплоты, его энергия, как и температура, меняются.
То количество теплоты, обозначаемое (Q), которое понадобится для того, чтобы 1 кг определенного вещества нагреется на 1 К, носит определение теплоемкости вещества и обозначается с.
Математическое выражение относительно переданного количества теплоты выглядит формулой:
(Q=cm(t_2-t_1)=cmDelta t)
Измеряется величина в Дж/(кг∙К).
При t2⟩t1, количество теплоты со знаком плюс, следовательно, вещество нагревается. Если наоборот, то Q — со знаком минус, и вещество остывает.
В физике, характеризуя свойства вещества, говорят о его теплоемкости. Это имеет значение, например, при выборе стройматериалов или сырья для изготовления нагревательных приборов. Теплоемкость равна произведению массы на удельную теплоемкость данного тела:
(C=cm)
Учитывая, что в величине теплоемкости уже отражена масса, то сокращенная формула для определения (Q) выглядит так:
(Q=C(t_2-t_1))
С другой стороны, то количество теплоты, которое отдает источник, можно высчитать по формуле:
(Q=Pt.)
В выражении буквой (P) обозначается мощность нагревателя, а (t) — время их контакта.
Конструкция, состоящая из нагревателя, тела-реципиента теплоты и охладителя, носит название тепловой машины. В качестве примера рассматривается двигатель внутреннего сгорания. Как и любой механизм, она имеет такую характеристику, как КПД — коэффициент полезного действия. Для его расчета применяется формула:
(eta=(Q_н-Q_x)/Q_н)
Внутренняя энергия одноатомного и двухатомного идеального газа
Характерной особенностью идеального газа является отсутствие у его составляющих частей потенциальной энергии. Вся внутренняя энергия — это сумма кинетических энергий всех молекул. Она является величиной, прямо пропорциональной температуре идеального газа:
(mw2/2=alpha T)
В этом уравнении:
(alpha T=3Rmu/2Nmu)
Исходя из приведенных формул, величина кинетической энергии поступательного движения идеального газа должна определяться исходя из выражения:
(mv2/2=(3Rmu/2Nmu)ast T)
Поступательное движение характеризуется тремя степенями свободы. На каждую из них приходится одна треть общей кинетической энергии.
Двух- и более атомные молекулы газа характеризуются степенями свободы, касающимися вращательного движения.
Если обозначить число молекул в одном киломоле за (Nμ), то внутренняя энергия идеального газа будет измеряться по формуле:
(Umu=1/2(Rmu Ti))
В формуле (i) — число степеней свобод.
Если газ одноатомный, (i=3), двуатомный — 5, трех- и более — 6.
Задачи на термодинамику характеризуют распространенные физические процессы, поэтому часть включаются в программы экзаменов. Если для их решения не хватает времени, можно обратиться за помощью в Феникс.Хелп. На профильном сайте вам помогут справиться с любой, даже запутанной задачей, экономя ваши время и силы.
