|
bezdelnik 8 лет назад
R – радиус описанной окружности Rafail d=R*cos(Пи/5). Зачем Вы спрашиваете?
bezdelnik А можно без косинуса и вообще без тригонометрических выражений? Число Пи не имеет точного значения и это не есть хорошо.
Rafail Можно. Отвечая на Ваш вопрос “http://www.bolshoyvopros.ru/questions/1026640-chemu-ravna-ploschad-pravilnogo-5-ti-ugolnika-v-r-cm.html” я приводил величину cos(36°)=(1+√(5))/4. Вот ее и подставьте. Получится d=R*(1+√(5))/4.
bezdelnik Без косинуса Вы всё же не обошлись.
Rafail Читайте внимательно последнюю строку.
все комментарии (еще 2) bezdelnik 7 лет назад Апофема правильного многоугольника есть радиус вписанной в него окружности обычно обозначаемый r. Из графического построения r^2=R^2-(Х^2)/4, где Х длина стороны пятиугольника. Х^2=(5-√5)/2. После преобразований получим r=(√(3+√5)/2))/2=0,809… комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Правильный пятиугольник
Правильный пятиугольник — это такой пятиугольник у которого все пять сторон равны и его пять углов равны.
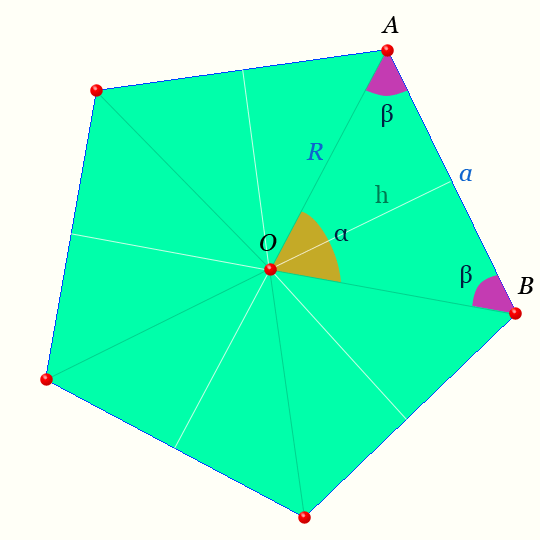
Правильный пятиугольник
Центр правильного пятиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного пятиугольника.
Обозначения на рисунке для правильного пятиугольника
| n=5 | число сторон и вершин правильного пятиугольника, | шт |
|---|---|---|
| α | центральный угол правильного пятиугольника, | радианы, ° |
| β | половина внутреннего угла правильного пятиугольника, | радианы, ° |
| γ | внутренний угол правильного пятиугольника, | радианы, ° |
| a | сторона правильного пятиугольника, | м |
| R | радиусы правильного пятиугольника, | м |
| p | полупериметр правильного пятиугольника, | м |
| L | периметр правильного пятиугольника, | м |
| h | апофемы правильного пятиугольника, | м |
Основные формулы для правильного пятиугольника
Периметр правильного пятиугольника
[ L = 5a ]
Полупериметр правильного пятиугольника
[ p = frac{5}{2}a ]
Центральный угол правильного пятиугольника в радианах
[ α = frac{2}{5}π ]
Центральный угол правильного пятиугольника в градусах
[ α = frac{360°}{5} = 72° ]
Половина внутреннего угла правильного пятиугольника в радианах
[ β = frac{3}{10}π ]
Половина внутреннего угла правильного пятиугольника в градусах
[ β = frac{3}{10}180° = 54° ]
Внутренний угол правильного пятиугольника в радианах
[ γ = 2β = frac{3}{5}π ]
Внутренний угол правильного пятиугольника в градусах
[ γ = frac{3}{5}180° = 108° ]
Площадь правильного пятиугольника
[ S = ph = frac{5}{2}ha ]
Или учитывая формулу Площади правильного пятиугольника получим
[ S = frac{5}{2} a sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]
Отсюда получим апофему правильного пятиугольника
[ h = sqrt{Big(frac{a}{2 sin(π/5)}Big)^2-frac{a^2}{4}} ]
Правильный пятиугольник |
стр. 269 |
|---|
Pentagon is a geometrical shape with 5 sides and is also referred to as five-sided polygon. Apothem is the line from the center point of the pentagon to the middle of one of its sides. Apothem is the line drawn from the midpoint of one of the sides to the center of pentagon. Here is the free online Apothem of pentagon calculator for you to calculate the apothem of a pentagon. This apothem of pentagon calculator requires side length measurement to calculate the area of apothem.
Calculate the Apothem of a Pentagon
Pentagon is a geometrical shape with 5 sides and is also referred to as five-sided polygon. Apothem is the line from the center point of the pentagon to the middle of one of its sides. Apothem is the line drawn from the midpoint of one of the sides to the center of pentagon. Here is the free online Apothem of pentagon calculator for you to calculate the apothem of a pentagon. This apothem of pentagon calculator requires side length measurement to calculate the area of apothem.
Code to add this calci to your website 

Formula:
Apothem of Pentagon = a / [2 tan(π / n)]
Where,
a = Side length
n = 5
Example:
Calculate the apothem of a pentagon with 5 sides and its sides are 20 cm in length.
Solution:
Apothem of pentagon = 20 / [2 tan(180 / 5)]
= 13.7638 cm.
![]()
1
R – радиус описанной окружности
1 ответ:
![]()
0
0
Апофема правильного многоугольника есть радиус вписанной в него окружности обычно обозначаемый r. Из графического построения r^2=R^2-(Х^2)/4, где Х длина стороны пятиугольника. Х^2=(5-√5)/2. После преобразований получим r=(√(3+√5)/2))/2=0,809…
Читайте также
![]()
Зеленую окружность можно чертить произвольным радиусом. В эту окружность будем вписывать правильный пятиугольник. Без циркуля начертить точно окружность нельзя, но это не обязательно. Окружность и все дальнейшие построения можно выполнять от руки. Далее через центр окружности О нужно провести две взаимно перпендикулярные прямые и одну из точек пересечения прямой с окружностью обозначить А. Точка А будет вершиной пятиугольника. Радиус ОВ разделим пополам и поставим точку С. Из точки С проводим вторую окружность радиусом АС. Из точки А проводим третью окружность радиусом АD. Точки пересечения третьей окружности с первой (Е и F)будут также вершинами пятиугольника. Из точек Е и F радиусом АЕ делаем засечки на первой окружности и получаем остальные вершины пятиугольника G и H.
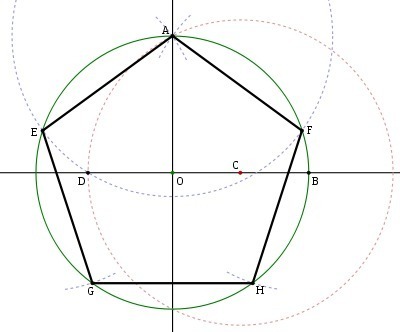
![]()
Это штаб-квартира Министерства обороны США, базирующаяся в 5-этажном здании(плюс 2 подземных) пятиугольной формы, откуда и название. Внешняя длина каждой стороны пятиугольника 281 м, работает в здании более 26 тысяч человек.
Выбор пятиугольника подсказал рельеф местности, где пересекались несколько дорог под углом 108 градусов, проект был создан, но потом решили строить здание в другом месте.
Из интересного можно сказать, что количество туалетов вдвое превышает санитарную норму, но не из-за страха перед противником, а потому что проект включал в себя раздельные туалеты для черных и белых 🙂
![]()
Сколько вершин у пятиугольника?
Вершин у пятиугольника столько же, сколько и углов – пять. Это отображено и в названии данной фигуры. Можем посчитать вместе на примере вот этого пятиугольника, изображенного на картинке ниже:
![]()
Построение возможно, если данный многоугольник, то бишь пятиугольник является правильным, то есть его все стороны и все углы равны.
Строите окружность с центром О.
Затем проводите два взаимно перпендикулярных диаметра АВ и СД.
Радиус АО делите пополам в точке Е.
Из т.Е радиусом ЕС проводите дугу СF, с пересечением диаметра АВ в точке F.
Из т.С радиусом СF проводите дугу FG,с пересечением окружности в т.G.
Получаете СG (=CF) – и это одна из сторон нашего пятиугольника.
Проводите тем же радиусом дугу mn из центра О и получаете ещё одну вершину Н искомого пятиугольника и так далее.
Описание этого построения с чертежом есть в справочнике по элементарной математике.К сожалению, я не умею вставлять картинки или чертить здесь.
![]()
С именем героини этой всем знакомой сказки также не все просто. Так в оригинальной народной сказке “Морозко”, записанной Афанасьевым, героиню, бедную падчерицу увезенную в лес, зовут, как бы вы думали? – Марфушка. Именно так, видимо прошла мода на это старинное русское имя, стали называть уродливую дочь старухи в фильме “Морозко” 1964 года. А бедную, или наоборот счастливую, главную героиню зовут уже Настенька.

Как найти площадь пятиугольника
3 методика:ОсновыВычисление площади пятиугольника: геометрияВычисление площади пятиугольника: формула
Пятиугольник – это многоугольник, у которого пять углов. Пятиугольники бывают правильными, неправильными, выпуклыми, вогнутыми, звездчатыми. Не существует простого и единого способа вычисления площади пятиугольников, но легко найти площадь правильного пятиугольника. Эта статья описывает два основных способа вычисления площади правильного пятиугольника.
Шаги
Часть 1 из 3: Основы
-

1
Правильные и неправильные пятиугольники. Правильный пятиугольник – это пятиугольник, у которого все стороны равны; в противном случае пятиугольник называется неправильным.- Правильный пятиугольник всегда будет выпуклым (см. ниже). Неправильный пятиугольник может быть и выпуклым, и вогнутым.
-

2
Выпуклые и вогнутые пятиугольники. Выпуклый пятиугольник не имеет вершин, направленных внутрь фигуры (другими словами, не имеет внутренних углов более 180 градусов). Вогнутый пятиугольник имеет вершину, направленную внутрь фигуры (другими словами, имеет внутренний угол более 180 градусов). -

3
Периметр пятиугольника. Как и в случае других геометрических фигур, найти периметр пятиугольника легко: просто сложите длины всех пяти сторон. -

4
Апофема правильного пятиугольника. Апофема – отрезок, соединяющий центр пятиугольника и середину любой из его сторон. -

5
Основные тригонометрические функции. Их надо знать, так как площадь пятиугольника можно найти посредством его разбиения на прямоугольные треугольники. Существуют три основных тригонометрических функции: sin угла = противолежащий катет/гипотенуза; cos угла = прилежащий катет/гипотенуза; tg угла = противолежащий катет/прилежащий катет.
Часть 2 из 3: Вычисление площади пятиугольника: геометрия
-

1
Разбейте пятиугольник на пять равнобедренных треугольников. Затем в каждом треугольнике опустите высоту (из центра пятиугольника). Вы получите десять прямоугольных треугольников. Запомните: каждый угол пятиугольника равен 108 градусам.- Например, найдите площадь правильного пятиугольника со стороной 6 см. Для начала разбейте его так, как показано на рисунке.
-

2
Найдите стороны равнобедренного треугольника. Для этого рассмотрите один из прямоугольных треугольников.- В приведенном примере сторона пятиугольника равна 6 см. Следовательно, один катет прямоугольного треугольника равен 3 см (так как высота делит сторону пятиугольника пополам). С помощью тригонометрических функций можно вычислить другие стороны. Вычисления показаны на рисунке.
-

3
Вычислите площадь прямоугольного треугольника. Площадь прямоугольного треугольника вычисляется по простой формуле: А1 = ab/2.- В приведенном выше примере подставьте найденные значения в эту формулу. Вычисления показаны на рисунке.
-

4
Найдите площадь пятиугольника. Напомним, что вы разбили пятиугольник на десять прямоугольных треугольников. Таким образом, общая площадь пятиугольника в десять раз больше площади одного прямоугольного треугольника: А = 10*А1.- В приведенном выше примере площадь пятиугольника вычисляется следующим образом: А = 10*А1 = 10*3,0321 = 30,3210.
Часть 3 из 3: Вычисление площади пятиугольника: формула
-

1
Формула для вычисления площади любого правильного многоугольника: A = Pa/2, где Р – периметр многоугольника, а – апофема многоугольника.- Например, дан правильный пятиугольник со стороной 6 см. Найдите его площадь.
-

2
Найдите периметр пятиугольника. Для этого сложите длины всех его сторон.- В приведенном выше примере: Р = 6+6+6+6+6 = 30.
-

3
Найдите апофему пятиугольника. Если вы знаете сторону многоугольника, то его апофема вычисляется по формуле: а = s/2tan(180/n), где s – сторона многоугольника, n – количество сторон многоугольника.- В приведенном выше примере вычисление апофемы показано на рисунке.
-

4
Вычислите площадь пятиугольника. Для этого используйте основную формулу для вычисления площади пятиугольника.- В приведенном выше примере: А = (30*2,0214)/2 = 30,3210.
Советы
- Если возможно, вычислите площадь пятиугольника, используя оба описанных метода. Затем сравните результаты, чтобы подтвердить правильность ответа.
