Примеры решения задач к теме
8.2. Интерференция света Основные формулы и методические указания
1.
Оптическая длина пути, проходимого
световым лучом в однородной среде с
показателем преломления n
![]() (8.
(8.
2. 4)
где l
–
геометрическая длина пути светового
луча.
2.
Оптическая разность хода двух световых
лучей
![]() (8.
(8.
2. 5)
3.
Условия возникновения максимума и
минимума интенсивности света от 2-х
когерентных источников соответственно
![]() (8.
(8.
2. 6)
и
![]() (8.
(8.
2. 7)
где l
– длина световой волны в вакууме,
![]() –
–
порядок соответствующего максимума
или минимума интенсивности света.
4.
Положение на экране (от его центра)
последовательно расположенных максимумов
и минимумов интенсивности света
соответственно
![]() (8.
(8.
2. 8)
и
![]() (8.
(8.
2. 9)
где ![]() .
.
5.
Расстояние между интерференционными
полосами на экране, полученными от двух
когерентных источников света
![]() (8.
(8.
2. 10)
где ![]() – расстояние от экрана до источников,
– расстояние от экрана до источников,
![]() – расстояние между когерентными
– расстояние между когерентными
источниками, причем![]()
6.
Оптическая разность хода световых
лучей, отраженных от двух поверхностей
тонкой пластины или пленки, по обе
стороны которых одинаковые среды
![]() (8.
(8.
2. 11)
где ![]() – толщина пластины или пленки,
– толщина пластины или пленки,
![]() – показатель их преломления,
– показатель их преломления,
![]() – угол преломления,
– угол преломления,
![]() – длина световой волны в вакууме.
– длина световой волны в вакууме.
7.
Условия образования максимумов и
минимумов интенсивности света в
отраженном свете от тонкой плоскопараллельной
пластины или пленки соответственно:
![]() (8.
(8.
2. 12)
и
![]() (8.
(8.
2. 13)
где ![]() – угол падения светового луча на пластину
– угол падения светового луча на пластину
или пленку.
8.
Радиусы темных и светлых колец Ньютона
в отражении света соответственно, при
условии, что между линзой и пластиной
вакуум (воздух)
![]() (8.
(8.
2. 14)
![]() (8.
(8.
2. 15)
Здесь
![]() – радиус кривизны поверхности линзы,
– радиус кривизны поверхности линзы,
соприкасающейся с параллельной пластиной,![]() – длина световой волны в среде между
– длина световой волны в среде между
линзой и пластиной,![]() – порядковый номер кольца (
– порядковый номер кольца (![]() соответствует центральному темному
соответствует центральному темному
пятну).
Задачи
на интерференцию света делятся в основном
на две группы: на интерференцию волн от
двух когерентных источников и на
интерференцию в тонких пластинах
(пленках). К задачам первой группы
относятся случаи интерференции,
получаемые с помощью щелей Юнга (опыт
Юнга), зеркала Ллойда, зеркал Френеля,
а также бипризмы Френеля. Для расчета
интерференционной картины в этом случае
используются формулы (8.2.7), (8.2.8) и (8.2.9),
предварительно определив (если это
необходимо) положение двух когерентных
источников. Вторую группу составляют
задачи на интерференцию как в
плоскопараллельных, так и в клинообразных
тонких слоях, а так же задачи на кольца
Ньютона. В этом случае соотношение
(8.2.10) позволяет вычислить оптическую
разность 2-х интерферирующих лучей,
отраженных от обеих поверхностей слоя.
По условиям (8.2.11) и (8.2.12) определяют
результат интерференции.
При
интерференции света, известной под
названием колец Ньютона, роль тонкой
пленки играет прослойка (обычно воздушная)
между пластиной и выпуклой поверхностью
прижатой к ней линзы. Формулы (8.2.13) и
(8.2.14) для радиусов колец выведены в
предположении, что эта прослойка окружена
одинаковыми средами, то есть пластинка
и линза должны иметь одинаковые показатели
преломления.
В
качестве примера решения задач по этой
теме, рассмотрим следующие задачи.
З а д а ч а 8. 2. 1
Свет от точечного монохроматического
источника
![]() с длиной волны
с длиной волны![]() м
м
падает на экран “Э” (рис. 8.2), в
котором имеются два маленьких отверстия![]() и
и![]() (опыт Юнга), расположенных на расстоянии
(опыт Юнга), расположенных на расстоянии![]() 3 м
3 м
от экрана. Расстояние между![]() и
и![]()
![]() м
м
(![]() ).
).
Определить расстояние между максимумами
интенсивности света смежных
интерференционных полос (ширину светлой
или темной полосы) на экране.
|
Дано:
|
Решение
|
|
|
Искомое
расстояние между максимумами интенсивности
смежных интерференционных полос на
экране
![]() определяется
определяется
как разность расстояний от центра
картины (т. 0) до двух соседних темных
полос с номерами![]() и
и![]() ,
,
то есть
![]()
Для
нахождения
![]() и
и![]() воспользуемся
воспользуемся
условием образования минимума
интенсивности света от 2-х когерентных
источников для чего из рис. 8.2 найдем
геометрическую разность хода 2-х лучей
![]()
где: ![]()
Вычитая
из первого второе, получим
![]() или
или
![]()
Откуда
![]() так как
так как![]()
Из
условия минимума
![]() находим, что
находим, что
![]() (для
(для
![]()
![]() ).
).
Следовательно,
ширина темных и светлых полос одинакова,
и равна
![]() .
.
Подставляя
числовые значения, рассчитаем
![]()
![]() м.
м.
Ответ:
![]() м.
м.
З а д а ч а 8. 2. 2
Два когерентных источника, расстояние
между которыми
![]() мм
мм
удалены от экрана на![]() м.
м.
На длине экрана![]() см
см
располагается![]() полос. Чему равна длина волны
полос. Чему равна длина волны
монохроматического света, падающего
на экран.
|
Дано:
|
Решение
Так
Откуда |
|
|
|
Ответ:
![]() м.
м.
З а д а ч а 8. 2. 3
В опыте Юнга на пути одного из лучей
монохроматического света с длиной волны
![]() м
м
поместили перпендикулярно лучу тонкую
стеклянную пластину с показателем
преломления![]() .
.
При этом центральная светлая полоса
сместилась в положение, первоначально
занимаемое пятой светлой полосой. Какова
толщина стеклянной пластины![]() ?
?
|
Дано:
|
Решение
Внесенная
Так, |
|
|
![]() .
.
Откуда
![]() м.
м.
Ответ:
![]() м.
м.
З а д а ч а 8. 2. 4
На мыльную пленку с
![]() падает под углом 600
падает под углом 600
параллельный пучок белого света.
Определить наименьшую толщину пленки,
при которой в отраженном свете пленка
имеет желтую окраску (![]() м).
м).
|
Дано:
|
Решение
В интерференции |
|
|
![]()
![]()
Отсюда
толщина пленки равна
![]() .
.
Минимальную
толщину пленки будем иметь при
![]() .
.
![]() м.
м.
Ответ:
![]() м.
м.
З а д а ч а 8. 2. 5
Для уменьшения потерь света при отражении
от линзы фотоаппарата на поверхности
объектива (линзы) с показателем преломления
![]() наносится тонкая прозрачная пленка с
наносится тонкая прозрачная пленка с![]() .
.
При какой наименьшей ее толщине произойдет
максимальное ослабление отраженного
света, длина волны которого приходится
на среднюю часть видимого спектра с![]() м.
м.
Считать, что лучи падают нормально к
поверхности объектива.
|
Дано:
|
Решение Свет, |
|
|
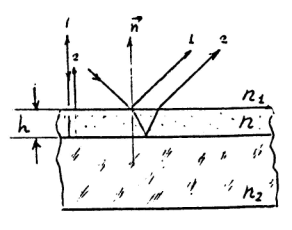
Рис.
8.3
величину
![]() и тогда, с учетом того, что в задаче угол
и тогда, с учетом того, что в задаче угол
падения равен нулю, полная разность
хода световых лучей составит![]() ,а
,а
условие минимума интенсивности света
теперь будет таким
![]() .
.
Откуда
![]()
Следовательно,
искомая минимальная толщина пленки
будет при условии
![]() то есть
то есть
![]() м.
м.
Это
очень тонкая пленка, поэтому на практике
изготовляют пленку толщиной
![]() ,
,
естественно увеличивая![]() в нечетное число раз.
в нечетное число раз.
Ответ:
![]() м.
м.
З а д а ч а 8. 2. 6
На стеклянный клин с
![]() нормально к его грани подает параллельный
нормально к его грани подает параллельный
пучок лучей монохроматического света
с длиной волны![]() м.
м.
Число![]() интерференционных полос приходящихся
интерференционных полос приходящихся
на![]() см
см
равно![]() .
.
Определить угол![]() клина.
клина.
|
Дано:
|
Решение Лучи |
|
|

Рис. 8.
4
Темные
полосы в отраженном свете видны на тех
участках клина, для которых полная
разность хода световых лучей кратна
нечетному числу половин длин волн, то
есть определяются тем же условием
минимума интенсивности света, что и для
плоскопараллельной пластины соответствующей
толщине клина
![]()
![]() (1)
(1)
Здесь
учтено, что угол падения лучей равен
нулю.
Из
(1) следует, что
![]() ;
;![]() . (2)
. (2)
Искомый
угол
![]() при основании клина найдем из прямоугольного
при основании клина найдем из прямоугольного
треугольника, с учетом (2):
![]()
Так
как угол
![]() <<1,
<<1,
то![]() ,
,
и тогда
![]() рад.
рад.
Для
того, чтобы выразить
![]() в градусах, воспользуемся соотношением
в градусах, воспользуемся соотношением
между радианом и градусом, получим
![]() .
.
Используя
соотношение между радианом и секундой:
![]() рад
рад![]() ,
,
получим ![]() .
.
Ответ:
![]() или
или![]() .
.
З а д а ч а 8. 2. 7
Найти радиус кривизны плосковыпуклой
линзы, лежащей на плоскопараллельной
стеклянной пластине, освещаемая нормально
падающим на неё монохроматическим
светом длиной волны
![]() м.
м.
Радиус восьмого темного кольца Ньютона
в отраженном свете равен 2 мм.
|
Дано:
|
Решение
Пучок Падающий |
|
|
о

Рис.
8.5
т стеклянной пластины (луч 2). Лучи
1, 2 когерентны. И в результате их положения
на выпуклой стороне линзы наблюдается
интерференция кольца. Темные кольца
видны в тех местах, где полная разность
хода этих лучей![]() равна нечетному числу половин длин
равна нечетному числу половин длин
волн, то есть
![]()
(1)
где ![]() – толщина
– толщина
воздушной прослойки в том месте, где
видно интерференционное кольцо;
![]() – длина
– длина
волны падающего света;
![]() – номер темного кольца.
– номер темного кольца.
Величина
![]() в (1) – добавочная разность хода,
в (1) – добавочная разность хода,
возникающая при отражении луча 2 от
оптически более плотной среды (пластина).
После
упрощений, равенство (1) дает
![]() . (2)
. (2)
Из
прямоугольного треугольника ОАВ
(рис. 8.5) имеем
![]() .
.
С
учетом того, что
![]() ,
,
получаем
![]() . (3)
. (3)
Из
(2) и (3) следует, что
![]() ,
,
откуда искомый радиус кривизны линзы
равен
![]() м.
м.
Ответ:
![]() м.
м.
Соседние файлы в папке Кононенко_Зеневич Методич. указания
- #
13.02.20164.13 Кб37._MU KZ (chast 3, page 23).doc
- #
13.02.20164.1 Кб31._MU KZ(chast 3, page 03_23).doc
- #
13.02.20164.1 Кб39._МУиКЗ по ФИЗИКЕ, часть1.doc
- #
- #
- #
Содержание:
Интерференция света:
Фаза — аргумент периодической функции, определяющий значение физической величины в любой момент времени t. Она определяет состояние колебательной системы (координаты, скорости, ускорения) в любой момент времени при заданной амплитуде. Монохроматической волной называется электромагнитное излучение постоянной частоты.
Рассмотрим процесс наложения волн длиной 
Монохроматические волны одной и той же частоты, приходящие от этих источников в некоторую точку пространства Р, возбуждают в ней гармонические колебания той же частоты.
В силу этого, разность фаз колебаний, возбуждаемых рассматриваемыми источниками в точке Р, остается постоянной с течением времени, даже если начальные фазы этих колебаний различны.
Волны называются когерентными, если разность фаз колебаний, возбуждаемых ими, не изменяется с течением времени. Соответственно, свойство, характеризующее согласованность протекания в пространстве и времени нескольких колебательных или волновых процессов, называется когерентностью (от латинского слова cohaerens — связанный, сцепленный).
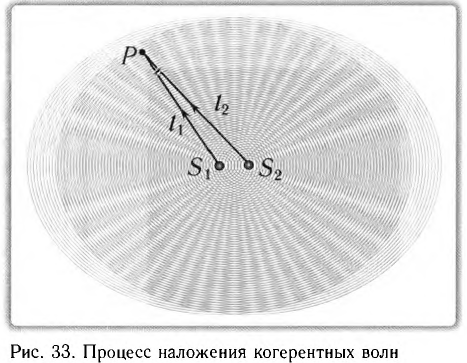
Опыт показывает, что амплитуда результирующего колебания в точке Р, создаваемого двумя одинаковыми источниками, зависит от геометрической разности хода волн до рассматриваемой точки:

Если разность хода волн  равна целому числу длин волн
равна целому числу длин волн 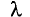 (четному числу полуволн
(четному числу полуволн 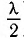 ) то волны приходят в точку Р (см. рис. 33) синфазно и усиливают друг друга. В этом случае говорят о выполнении условия максимума:
) то волны приходят в точку Р (см. рис. 33) синфазно и усиливают друг друга. В этом случае говорят о выполнении условия максимума:
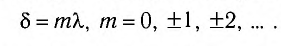
Действительно, разность фаз колебаний в рассматриваемой точке в этом случае
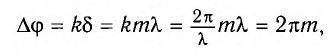
т. е. кратна 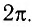 .
.
В случае, когда разность хода волн равна нечетному числу полуволн, волны приходят в точку Р в противофазе и ослабляют друг друга. Это соответствует выполнению условия минимума:
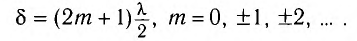
Убедитесь самостоятельно, что разность фаз колебаний в этом случае
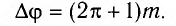
Таким образом, в результате сложения колебаний, возбуждаемых когерентными волнами на поверхности воды, образуется устойчивая картина распределения минимумов и максимумов результирующего колебания (рис. 34). Это означает, что когерентные волны интерферируют друг с другом.

Интерференция (от латинских слов inter — взаимно, между собой и fеrio — ударяю, поражаю) — явление сложения двух или более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующихся максимумов и минимумов амплитуд результирующего колебания.
Пространственная картина устойчивого во времени распределения амплитуд результирующего колебания при интерференции называется интерференционной картиной.
Вследствие того, что энергия волны пропорциональна квадрату амплитуды, энергия результирующего колебания в общем случае не равна сумме энергий складываемых колебаний, так как 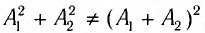 . Так, в точках максимума результирующая амплитуда колебаний возрастает в два раза, а энергия, соответственно, в четыре. Однако не будем забывать, что в точках минимума колебания отсутствуют вовсе. Таким образом, явление интерференции приводит к перераспределению энергии в пространстве, причем суммарная энергия колебаний во всех точках среды при этом остается равной сумме энергий интерферирующих волн.
. Так, в точках максимума результирующая амплитуда колебаний возрастает в два раза, а энергия, соответственно, в четыре. Однако не будем забывать, что в точках минимума колебания отсутствуют вовсе. Таким образом, явление интерференции приводит к перераспределению энергии в пространстве, причем суммарная энергия колебаний во всех точках среды при этом остается равной сумме энергий интерферирующих волн.
Отметим, что если бы в точке Р складывались две некогерентные волны с одинаковыми амплитудами, то энергия результирующего колебания была бы равна сумме энергий отдельных волн, независимо от положения точки Р относительно источника. Это означало бы просто удвоение энергии, принесенной одной из волн в данную точку.
Закономерности интерференции волн носят универсальный характер, т. е. справедливы для волн любой природы.
При рассмотрении интерференции света (электромагнитных волн) следует учесть, что длина волны света в веществе изменяется в зависимости от показателя преломления вещества. Это эквивалентно замене геометрической разности хода на оптическую разность хода
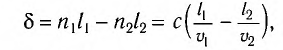
т. е. разность расстояний, пройденных волнами, с учетом различных скоростей 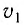 и
и 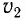 их распространения в средах с показателями преломления
их распространения в средах с показателями преломления 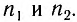
В вакууме (с =  =
= ) оптическая разность хода совпадает с геометрической. При оптической разности хода, кратной четному числу полуволн (целому числу длин волн), наблюдается максимум интерференции света, а при оптической разности хода, кратной нечетному числу полуволн, — минимум.
) оптическая разность хода совпадает с геометрической. При оптической разности хода, кратной четному числу полуволн (целому числу длин волн), наблюдается максимум интерференции света, а при оптической разности хода, кратной нечетному числу полуволн, — минимум.
Распространенные бытовые источники света (лампы накаливания, лампы дневного света, свечи и т. д.) не являются когерентными, т. е. не позволяют наблюдать явление интерференции.
Изобретение и распространение когерентных источников излучения — лазеров — сделало демонстрацию явления интерференции достаточно простой.
Для получения интерференционной картины при отсутствии лазеров пользуются классической интерференционной схемой (схемой Юнга), где пучок света разделяется на два пучка с помощью отверстий В и С в ширме (рис. 35). Поскольку эти пучки созданы одним и тем же источником, они являются когерентными. На экране в области DE наблюдается интерференционная картина.
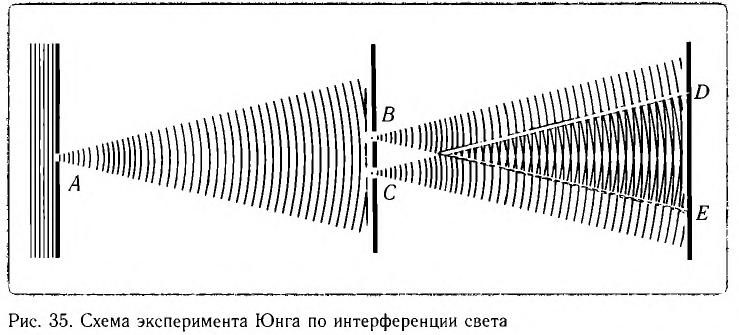
Классический эксперимент по наблюдению интерференции Томас Юнг провел в 1801 г. Это позволило измерить длину световой волны и убедительно подтвердить волновую природу света.
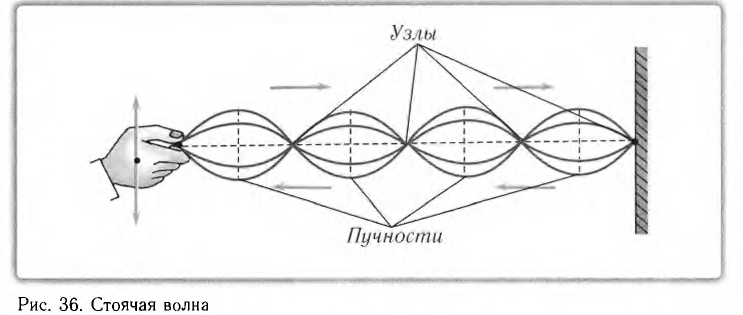
Рассмотрим еще один распространенный случай интерференции — сложение волн с одинаковыми частотами, распространяющихся в противоположных направлениях (например, падающей и отраженной волны), приводящее к образованию в пространстве устойчивой картины чередования максимумов амплитуды колебаний (пучностей) и минимумов (узлов).
Волна, возникающая в результате сложения двух волн одинаковой частоты, распространяющихся в противоположных направлениях, называется стоячей волной (рис. 36).
Пример решения задачи:
Рассчитайте положения максимумов и минимумов интерференционной картины на экране MN, находящемся на расстоянии L = АО = 2,0 м от двух одинаковых когерентных источников света 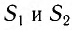 , которые расположены в вакууме на расстоянии
, которые расположены в вакууме на расстоянии 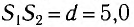 мм друг от друга (рис. 37). Длина волны излучения источников
мм друг от друга (рис. 37). Длина волны излучения источников 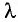 = 600 нм. Найдите расстояние
= 600 нм. Найдите расстояние 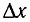 между соседними максимумами.
между соседними максимумами.
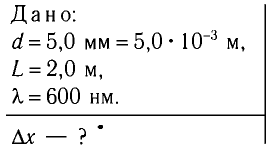
Решение
До некоторой точки Р на экране волны проходят пути 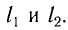
Максимумы интенсивности будут наблюдаться при условии
а минимумы при условии – 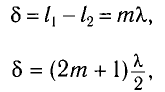
где m = 0, ±1, ±2…..
По теореме Пифагора из треугольников 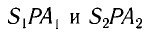 находим
находим
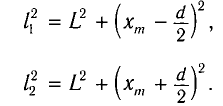
Откуда
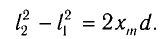
С учетом того, что 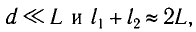 находим
находим
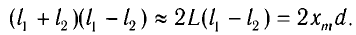
С учетом условия максимумов получаем
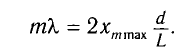
Откуда расстояние от центра экрана до т-й светлой полосы находится из соотношения
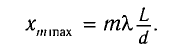
Из условия минимумов находим положение темных полос:
Откуда 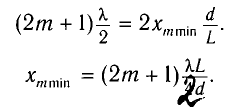
Расстояние между соседними максимумами 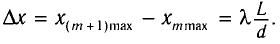
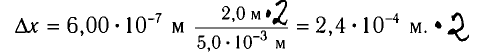
Из полученной формулы видно, что ширина интерференционных полос увеличивается при уменьшении расстояния d между когерентными источниками.
Ответ: 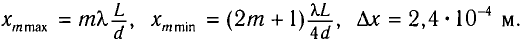
Волновая природа света и дисперсия света
Показатель преломления среды относительно вакуума называется абсолютным показателем преломления этой среды. Абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше скорости света в вакууме:
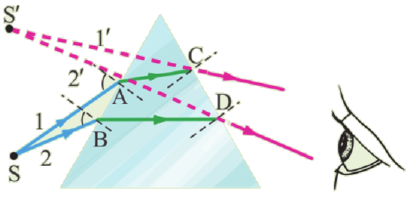
Луч света, падающий на боковую грань треугольной призмы, отклоняется к основанию призмы.
Природа света
Несколько веков имели место два разных представления о природе света: корпускулярная и волновая природа света.
Основоположником представлений о корпускулярной природе света является И. Ньютон. Он считал, что свет является потоком частиц (корпускул). Прямолинейное распространение света и его отражение легко объяснялись согласно этому представлению.
Основоположником представлений о волновой природе света является голландский ученый Христиан Гюйгенс (1629-1695). Основной причиной возникновения этих представлений является прохождение световых лучей сквозь друг друга при распространении подобно волнам. В XIX веке английский ученый Томас Юнг (1773-1829) провел эксперименты, в которых обнаружил многочисленные факты, подтверждающие волновую природу света. Основоположник теории электромагнитного поля Дж. Максвелл теоретически обосновал электромагнитную волновую природу света. Согласно современным представлениям свет и другие электромагнитные волны обладают двойной – корпускулярной и волновой природой.
- Заказать решение задач по физике
Дисперсия света
Одним из явлений, доказывающих волновую природу света, является дисперсия света.
Дисперсия света — это зависимость показателя преломления среды от частоты (длины волны) падающего света.
Впервые это явление исследовал Исаак Ньютон. Он поместил прозрачную стеклянную треугольную призму на пути тонкого пучка солнечного света, попадающего в затемненную комнату через маленькое отверстие в ставнях. Пройдя призму, солнечный луч разделился на спектр из семи составных цветных лучей. Последовательность цветов составных частей в дисперсионном спектре всегда одинакова: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.
Среди монохроматических (содержащих свет одного цвета) лучей наиболее сильно преломляются фиолетовые лучи, а меньше других – красные (см: а). Причина явления объясняется на основе волновых представлений о свете. Так, абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше, чем в вакууме:

Здесь 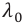 – длина световой волны в вакууме.
– длина световой волны в вакууме. 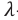 – длина световой волны в среде. Значит, подвергающийся наименьшему преломлению красный свет имеет наименьший показатель преломления. А это означает, что красный свет обладает наибольшей длиной волны (или наименьшей частотой). Фиолетовый свет, наоборот, обладает наибольшим показателем преломления и наименьшей длиной волны (или наибольшей частотой). Из проведенных в дальнейшем экспериментов было определено, что дисперсионный спектр видимого света охватывает в шкале электромагнитных волн часть с длинами волн от
– длина световой волны в среде. Значит, подвергающийся наименьшему преломлению красный свет имеет наименьший показатель преломления. А это означает, что красный свет обладает наибольшей длиной волны (или наименьшей частотой). Фиолетовый свет, наоборот, обладает наибольшим показателем преломления и наименьшей длиной волны (или наибольшей частотой). Из проведенных в дальнейшем экспериментов было определено, что дисперсионный спектр видимого света охватывает в шкале электромагнитных волн часть с длинами волн от 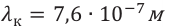 (красный) до
(красный) до 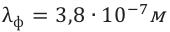 (фиолетовый).
(фиолетовый).
Результат. Таким образом, явление дисперсии показало, что белый свет обладает сложным строением – состоит из монохроматических световых лучей разного цвета. Каждый монохроматический луч света обладает собственной частотой и длиной волны. Поэтому при прохождении монохроматического луча через стеклянную призму он, только преломляясь, изменяет своё направление (не разлагается на составные, не меняет окраски). Если разложенный призмой свет, состоящий из монохроматических составляющих, направить на вторую перевернутую призму, то на выходе из второй призмы опять получится белый свет.
Согласно физике цвета, ни один из трех основных цветов – красный, зеленый и синий, не могут получиться при смешивании двух других. Однако смешиванием основных цветов можно получить все остальные цвета и их оттенки.
Многоцветное восприятие нами окружающего мира объясняется явлениями поглощения, преломления и отражения света. Например, лист бумаги воспринимается нашим зрением белым потому, что он отражает падающий на него белый свет полностью. Если тело полностью поглощает падающий на него свет, то он воспринимается как черный, например, сажа.
Интерференция волн и интерференция света
• Самые часто встречаемые колебания в природе являются колебаниями в связанных системах. В связанных колебательных системах колебания передаются от одного звена системы другой. Например, бросив в воду камень, можно наблюдать распространение концентрических водных кругов из точки падения камня. Нам кажется, что происходит распространение воды в виде выпуклостей и впадин.
Какая связанная система создает волну в воде?
Какие явления происходят в среде при распространении волны?
Обратите внимание на картину, образованную на неподвижной поверхности воды поплавками удочек рыболовов (а). При встрече волн друг с другом происходит их сложение. В результате в определенных точках пространства они усиливают друг друга (а, 1), а в других ослабляют (а, 2).

Интерференция волн
В исследовании вы наблюдали результат сложения когерентных волн, созданных на поверхности воды гармоническими колебаниями шариков генератора с одинаковой частотой.
Когерентные волны — это волны, созданные различными источниками колебания, имеющими одинаковую частоту колебаний и постоянную разность фаз, не зависящую от времени.
Результирующие колебания, образованные сложением когерентных волн, в зависимости от разности между расстояниями от источника колебаний до точки их встречи или усиливаются, или ослабляются – происходит интерференция волн.
Интерференция волн -усиление или ослабление амплитуды колебаний результирующей волны в результате сложения когерентных волн (лат. “интер” взаимно, “ферио” – ударю).
Усиление или ослабление амплитуды результирующей волны определяется условиями максимума и минимума интерференции.
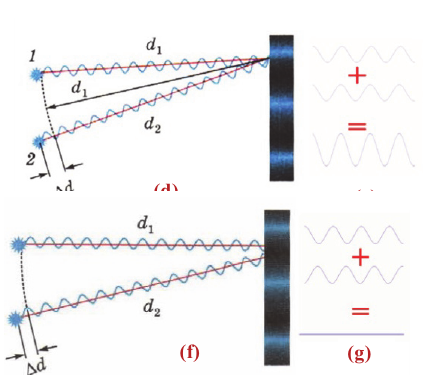
Условие максимума интерференции
Максимум интерференции наблюдается в точках пространства (поверхности), в которых максимумы слагаемых волн накладываются друг на друга. Это зависит от разницы пройденных волнами путей от источника колебаний до этой точки.
Интерференционный максимум результирующей волны образуется в точках, в которых разность хода складываемых волн равна нулю или четному числу полудлин волн (разность фаз равна нулю или четному количеству 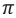 ) (d):
) (d):
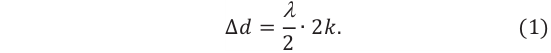
Здесь 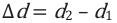 – разность путей, проходимых волнами до точки сложения (разность хода), k– порядок максимума, является целым числом: k= 0,1, 2,…. Между разностью фаз и разностью хода когерентных волн существует такая связь:
– разность путей, проходимых волнами до точки сложения (разность хода), k– порядок максимума, является целым числом: k= 0,1, 2,…. Между разностью фаз и разностью хода когерентных волн существует такая связь:
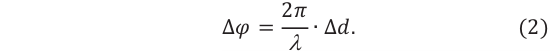
Учитывая выражение (1) в формуле (2), для разницы фаз максимума интерференции получим:
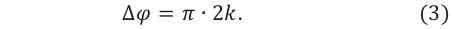
В этом случае при равенстве амплитуд складываемых волн амплитуда результирующего колебания будет равна сумме амплитуд исходных волн (е):
Условие минимума интерференции
Минимумы интерференции наблюдаются в тех точках пространства, в которые волны доходят в противофазе. При этом максимум одной волны совпадает с минимумом другой. В результате волны ослабляют друг друга.
Минимум интерференции наблюдается в точках, в которых разность хода слагаемых волн равна нечетному числу полудлин волн (разность фаз равна нечетному количеству 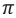 ) (f):
) (f):
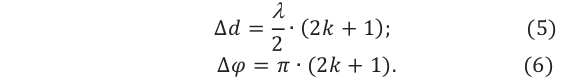
Если при этом амплитуды складываемых волн равны, то в точке минимума интерференции амплитуда результирующей волны уменьшается до нуля (g):
Интерференция света
Интерференция – характерное свойство всех видов волн, в том числе и световых. Так, две световые волны при сложении в пространстве могут усиливать или ослаблять друг друга, даже может случиться и такой вариант: свет + свет = темнота.
Интерференция света – явление увеличения или уменьшения амплитуды результирующих световых колебаний в разных точках пространства вследствие сложения двух когерентных световых волн.
Долгие годы не могли найти способ получения когерентных световых волн, поэтому невозможно было доказать способность световых волн интерферировать.
Только в начале XIX века с помощью несложного устройства Томас Юнг смог наблюдать интерференцию света (h).
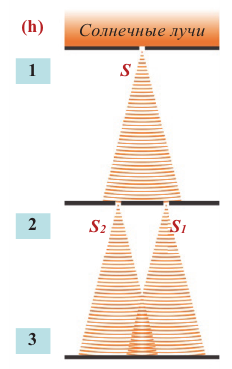

Классический опыт по наблюдению интерференции света состоит в следующем: солнечный свет освещает непрозрачный экран 1 и, пройдя через малое отверстие S в этом экране (проделанное булавкой), попадает на экран 2. Световые лучи, вышедшие из малых отверстий S1 и S2 на втором экране, являются когерентными. В результате интерференции этих волн на экране 3 появляются интерференционные полосы. В центральной части экрана наблюдаются чередующиеся цветные и темные полосы. По мере удаления от центра интерференционная картина ослабевает. Используя условие максимумов в этих опытах, Юнг смог на основе формулы (1) измерить длины световых волн для разных цветов. Как ни странно, первый опыт по интерференции света был проведен отрицающим его волновую природу Исааком Ньютоном. Поместив на стеклянной пластине плоско-выпуклую стеклянную линзу выпуклой стороной вниз, он осветил её сверху (i, 1). Посмотрев на линзу сверху, Ньютон увидел чередующиеся светлые и темные концентрические круги (i, 2), которые впоследствии стали называть кольцами Ньютона. Но ни Ньютон, ни повторявшие этот интересный опыт в течение более чем 100 лет ученые не смогли объяснить причину возникновения этих колец. И только в 1802 году Юнгу удалось объяснить происхождение колец Ньютона. Он объяснил кольца Ньютона таким образом: когда пучок света падает на плоскую поверхность линзы, то он, проходя сквозь нее, частично отражается от нижней сферической поверхности линзы (см. i-З, луч 1), а частично – от поверхности стеклянной пластинки, на которой лежит линза (см. i-З, луч 2). Вследствие такого многократного отражения образуются два когерентных луча. Эти лучи, складываясь, в соответствии с максимумами и минимумами интерференции создают интерференционную картину чередующихся темных и светлых концентрических кольца.
Определение длины световой волны
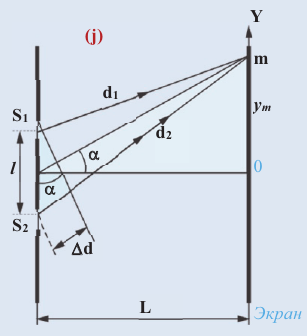
Представим, что расстояние между источниками когерентных волн S1 и S2 намного меньше расстояния от источников до экрана (j): 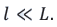 В таком случае световые волны, исходящие из этих источников и дошедшие до точки экрана m с координатой
В таком случае световые волны, исходящие из этих источников и дошедшие до точки экрана m с координатой 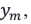 , можно считать параллельными. Разность хода между этими лучами:
, можно считать параллельными. Разность хода между этими лучами:
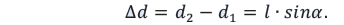
Вследствие малости угла 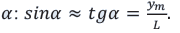
Условие интерференционного максимума в этом случае будет:

Отсюда можно найти длину волны:

- Дифракция света
- Принцип Гюйгенса — Френеля
- Прохождение света через плоскопараллельные пластинки и призмы
- Поляризация света
- Преломление света
- Полное отражение
- Дисперсия света
- Электромагнитная природа света
У этого термина существуют и другие значения, см. Интерференция.

Интерфере́нция све́та (лат. interferens, от inter — между + -ferens — несущий, переносящий) — интерференция электромагнитных волн (в узком смысле – прежде всего, видимого света) — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких световых волн. Это явление обычно характеризуется чередующимися в пространстве максимумами и минимумами интенсивности света. Конкретный вид такого распределения интенсивности света в пространстве или на экране, куда падает свет, называется интерференционной картиной.
Поскольку явление интерференции прямо зависит от длины волны, то при интерференции света, содержащего различные спектральные составляющие (цвета), например, белого света, происходит разделение этих спектральных составляющих, глазом видимые в случае белого света как радужные полосы.
История открытия[править | править код]
Впервые явление интерференции было независимо обнаружено Гримальди (для луча, прошедшего через два близких отверстия), Робертом Бойлем и Робертом Гуком (для интерференции в тонких слоях прозрачных сред, таких как мыльные плёнки, тонкие стенки стеклянных шаров, тонкие листки слюды; они наблюдали при этом возникновение разноцветной окраски; при этом Гук заметил и периодическую зависимость цвета от толщины слоя). Гримальди впервые и связал явление интерференции с идеей волновых свойств света, хотя ещё в довольно туманном и неразвитом виде.
В 1801 году Томас Юнг (1773—1829 гг.), введя «принцип суперпозиции», первым дал достаточно детальное и, по сути, не отличающееся от современного объяснение этого явления и ввёл в научный обиход термин «интерференция» (1803). Он также выполнил демонстрационный эксперимент по наблюдению интерференции света, получив интерференцию от двух щелевых источников света (1802); позднее этот опыт Юнга стал классическим.
Интерференция света в тонких плёнках[править | править код]

Интерференция в тонкой плёнке. 

Получить устойчивую интерференционную картину для света от двух разделённых в пространстве и независящих друг от друга источников света не так легко, как для источников волн на воде. Атомы испускают свет цугами очень малой продолжительности, и когерентность нарушается. Сравнительно просто такую картину можно получить, сделав так, чтобы интерферировали волны одного и того же цуга[1]. Так, интерференция возникает при разделении первоначального луча света на два луча при его прохождении через тонкую плёнку, например плёнку, наносимую на поверхность линз у просветлённых объективов. Луч света длиной волны 

Изменение фазы проходящего через плёнку луча, в общем случае, зависит от показателя преломления плёнки и окружающих её сред. Кроме того, надо учитывать, что свет при отражении от оптически более плотной среды меняет свою фазу на половину периода. Так, например, в случае для воздуха (





То есть 
Для деструктивной интерференции в данном примере необходимо, чтобы разность фаз между лучами была кратна 
То есть 
Полное гашение лучей произойдет для толщин плёнки: 
Если 


Интерференция света на мыльном пузыре
При 

Лучи соседних участков спектра по обе стороны от 
Явление интерференции наблюдается в тонком слое несмешивающихся жидкостей (керосина или масла на поверхности воды), в мыльных пузырях, бензине, на крыльях бабочек, в цветах побежалости, и т. д.
Кольца Ньютона[править | править код]
Другим методом получения устойчивой интерференционной картины для света служит использование воздушных прослоек, основанное на одинаковой разности хода двух частей волны: одной — сразу отраженной от внутренней поверхности линзы и другой — прошедшей воздушную прослойку под ней и лишь затем отразившейся. Её можно получить, если положить плосковыпуклую линзу на стеклянную пластину выпуклостью вниз. При освещении линзы сверху монохроматическим светом образуется тёмное пятно в месте достаточно плотного соприкосновения линзы и пластинки, окружённое чередующимися тёмными и светлыми концентрическими кольцами разной интенсивности. Тёмные кольца соответствуют интерференционным минимумам, а светлые — максимумам, одновременно тёмные и светлые кольца являются изолиниями равной толщины воздушной прослойки. Измерив радиус светлого или тёмного кольца и определив его порядковый номер от центра, можно определить длину волны монохроматического света. Чем круче поверхность линзы, особенно ближе к краям, тем меньше расстояние между соседними светлыми или тёмными кольцами[2].
Математическое описание[править | править код]
Интерференция двух плоских волн[править | править код]
Пусть имеются две плоские волны:


По принципу суперпозиции результирующее поле в области пересечения этих волн будет определяться суммой:

Интенсивность задается соотношением:

Откуда с учётом:


Для простоты рассмотрим одномерный случай 
![I=I_{1}+I_{2}+2E_{{1_{{0}}}}E_{{2_{{0}}}}cdot cos[(k_{{1_{x}}}-k_{{2_{x}}})x+{varphi }_{1}-{varphi }_{2}]](https://wikimedia.org/api/rest_v1/media/math/render/svg/15f6e55923b03b3ae6cef3a8e03efc2ec909fd6b)
Интерференционная картина представляет собой чередование светлых и темных полос, шаг которых равен: 
Примером этого случая является интерференционная картина в отраженном от поверхностей плоскопараллельной пластинки свете.
Случай неравных частот[править | править код]
В некоторых учебниках и пособиях говорится о том, что интерференция света возможна только для волн, образованных от одного источника света путём амплитудного либо полевого деления волновых фронтов. Это утверждение является неверным. С точки зрения принципа суперпозиции интерференция существует всегда, даже когда интерферируют волны от двух разных источников света. Правильно было бы говорить о наблюдении или возможности наблюдения интерференционной картины. Последняя может быть нестационарна во времени, что приводит к замазыванию и исчезновению интерференционных полос.
Рассмотрим две плоские волны с разными частотами:


По принципу суперпозиции результирующее поле в области пересечения этих волн будет определяться суммой:

Пусть некоторый прибор, обладающий некоторым характерным временем регистрации (экспозиции), фотографирует интерференционную картину. В физической оптике интенсивностью называют усредненный по времени поток световой энергии через единичную площадку ортогональную направлению распространения волны. Время усреднения определяется временем интегрирования фотоприемника, а для устройств, работающих в режиме накопления сигнала (фотокамеры, фотоплёнка и т. п.), временем экспозиции. Поэтому приемники излучения оптического диапазона реагируют на среднее значение потока энергии. То есть сигнал с фотоприемника пропорционален:

где под <> подразумевается усреднение. Во многих научно технических приложениях данное понятие обобщается на любые, в том числе и не плоские волны. Так как в большинстве случаев, например в задачах связанных с интерференцией и дифракцией света, исследуется в основном пространственное положение максимумов и минимумов и их относительная интенсивность, постоянные множители, не зависящие от пространственных координат, часто не учитываются. По этой причине часто полагают:

Квадрат модуля амплитуды задается соотношением:

Откуда, подставляя напряженность электрического поля, получим:




С учётом определения интенсивности можно перейти к следующему выражению:
[1] 

Взятие интеграла по времени и применение формулы разности синусов даёт следующие выражения для распределения интенсивности:

![{displaystyle I=I_{1}+I_{2}+2{mathbf {E} }_{1_{0}}{mathbf {E} }_{2_{0}}cdot cos left[Delta omega left(t_{0}+{frac {tau }{2}}right)+Delta mathbf {kr} +Delta varphi right]cdot operatorname {sinc} left({frac {Delta omega tau }{2}}right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c41f92082a9806009c703f9435674ee3ffa7270)
Здесь и далее используется обозначение 
В итоговом соотношении слагаемое, содержащее тригонометрические множители, называется интерференционным членом. Оно отвечает за модуляцию интенсивности интерференционными полосами. Степень различимости полос на фоне средней интенсивности называется видностью или контрастом интерференционных полос:

Условия наблюдения интерференции[править | править код]
Рассмотрим несколько характерных случаев:
1. Ортогональность поляризаций волн.
При этом 

Далее, без потери общности, можно положить, что поляризации волн одинаковы.
2. В случае равенства частот волн 

3. В случае 

Контраст полос, как и в случае ортогональных поляризаций, равен 0
4. В случае 
Общий случай интерференции[править | править код]
При взятии интеграла в соотношении [1] полагалось, что разность фаз 



Оно называется общим законом интерференции стационарных оптических полей.
Интерференция отдельных фотонов[править | править код]
Интерференция света происходит не в результате сложения разных фотонов, а в результате интерференции фотона самого с собой.[3] При этом временная когерентность не требуется для формирования статистической интерференционной картины — фотоны могут проходить один за одним с неограниченным периодом следования.[3][4]
В 1909 году английский учёный Джеффри Тейлор провёл опыт с использованием чрезвычайно слабого источника света и установил, что волновое поведение присуще отдельным фотонам.
См. также[править | править код]
- Дисперсия света
- Дифракция света
- Интерференция волн — общее описание интерференции как волнового процесса.
- Каустика
- Поляризация волн
- Цуг волн
Примечания[править | править код]
- ↑ Мякишев Г. Я., Буховцев Б. Б. §58. Интерференция света // Физика: Учеб. для 10 кл. сред. шк. — 9-е изд. — М.: Просвещение, 1987. — С. 158—161. — 319 с.
- ↑ Ландсберг Г.С. §126. Кольца Ньютона // Элементарный учебник физики. — 13-е изд. — М.: Физматлит, 2003. — Т. 3. Колебания и волны. Оптика. Атомная и ядерная физика. — С. 249-266. — 656 с. — ISBN 5922103512.
- ↑ 1 2 3 Интерференция света / М. Д. Галанин // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ 1 2 Видео из опыта Юнга при очень слабом потоке фотонов Архивная копия от 30 июня 2014 на Wayback Machine – Лейденский университет
Литература[править | править код]
- Яштолд-Говорко В. А. Фотосъёмка и обработка. Съёмка, формулы, термины, рецепты, — Изд. 4-е, сокр. — М.: «Искусство», 1977.
- Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
Ссылки[править | править код]
- Интерференция света // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Интерференция света — статья из Физической энциклопедии
- Flex приложение, демонстрирующее принципы работы интерферометра Фабри-Перо
- Энергия электромагнитных волн. Интенсивность света
- Свойства источника света и материала. Типы источников света. Суммарное освещение
Интерференция света – явление ослабления или усиления интенсивности света в зависимости от соотношения фаз складываемых световых когерентных волн, линейно поляризованных в одной плоскости. Для уровня школьной физики данное определение является излишним. По умолчанию, световые волны являются когерентными и линейно поляризованными.
Таким образом, для нас в задачах на интерференцию важно наличие нескольких (чаще всего двух) волн и разности фаз (разности хода) между ними.
В школьных задачах на интерференцию основным вопросом является результат интерференции в наблюдаемой точке (усиление или ослабление света).
Для математического описания явления интерференции вводят оптическую длину пути () — произведение показателя преломления среды, по которой проходит свет, на геометрическую длину пути, которую прошёл луч. Тогда для двух лучей (рис. 1):
(1)
- где

Рис. 1. Интерференция
Пусть от точечного источника системой зеркал два луча развели по двум областям с различными показателями преломления ( и
). Пути лучей в этих системах
и
соответственно. Затем, вышедшие из областей, лучи обратно свели в точку
. За счёт того, что в средах с различным показателем преломления луч от одного и того же источника движется с разной скоростью, к одной и той же точке они приходят с ненулевой разностью хода (1).
Тогда результат интерференции (усиление или ослабление света) диктуется соотношениями:
- максимум интерференции (максимальное усиление):
(2)
(3)
Тогда для ответа на вопрос об усилении и ослаблении света можно анализировать приведённое уравнение (2):
(4)
Тогда, если полученное целое или ближе к целому, то в точке
наблюдается усиление света, в случае, если
полуцелое или близко к полуцелому, в точке
— темнота.
Вывод: фактически задачи на интерференцию сводятся к анализу уравнения (4) и поиску оптической длины пути для (1).
Пример: Оптическая разность хода волн от двух когерентных источников в некоторой точке пространства мкм. Каков будет результат интерференции в этой точке, если длина волны будет:
нм,
нм.
Исходя из аналитической формулы (4):
(5)
(6)
Таким образом, получившийся параметр получился целым числом, это говорит о том, что при данных параметрах в точке соединения лучей будет наблюдаться усиление света. Параметр
оказался ближе к полуцелому, таким образом, в исследуемой точке будет наблюдаться ослабление света.
Интерференция – это одно из наиболее ярких проявлений волновой природы света. Мы можем наблюдать такое интересное и красивое явление, если наложить друг на друга 2 или более световых пучков. В месте перекрывания пучков интенсивность волны света обладает характером чередующихся светлых и темных полос, при этом в точках максимумов интенсивность больше, а в точках минимумов меньше суммы интенсивностей пучков.
При белом свете интерференционные полосы окрашиваются в разные цвета светового спектра. На практике интерференционные явления окружают нас повсюду. Это и цвета масляных пятен на асфальте, и окрашивание замерзающих оконных стекол, и чудесные цветные рисунки на крыльях отдельных бабочек и жуков.
Первый научный эксперимент проявления интерференции света
Первый научный эксперимент по наблюдению интерференции света провел в лабораторных условиях И. Ньютон. Ученый рассматривал интерференционную картину, которая возникала при отражении света в тонкой воздушной прослойке между плоской стеклянной пластиной и плосковыпуклой линзой большого радиуса кривизны. Наблюдение Ньютона графически изображено на рис. 3.7.1.
Интерференционная картина выглядела в виде концентрических колец, которые впоследствие получили название колец Ньютона (рис. 3.7.2).
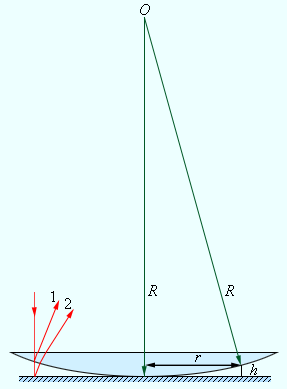
Рисунок 3.7.1. Наблюдение колец Ньютона. Интерференционная картина возникает при сложении волн, отразившихся от 2-х сторон воздушной прослойки. «Лучи» 1 и 2 – направления распространения волн;
h – толщина воздушного зазора.

Рисунок 3.7.2. Кольца Ньютона в зеленом и красном свете.
У И. Ньютона не получилось с позиции корпускулярной теории дать объяснение тому, почему возникают кольца. Но ученый понимал, что это имеет отношение к какой-то периодичности световых процессов.
Интерференционный опыт Юнга
В 1802 году ученый Юнга провел первый интерференционный опыт, которому есть подтверждение в волновой теории света. В данном эксперименте свет от источника – узкой щели S попадал на экран с
2-мя близко расположенными друг к другу щелями S1 и S2, как показано на рис. 3.7.3. Минуя каждую из щелей, световой пучок уширялся из-за дифракции, а потому на белом экране Э световые пучки, которые прошли через щели S1 и S2, перекрывались. В месте перекрытия световых пучков находится интерференционная картина, выступающая в виде чередующихся светлых и темных полос.
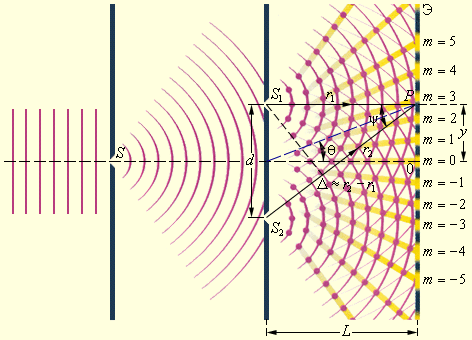
Рисунок 3.7.3. Схема интерференционного опыта Юнга.
Ученый Юнг – первый, кто догадался, что невозможно увидеть интерференцию, если сложить волны от 2-х независимых источников. Потому в его эксперименте щели S1 и S2, которые по принципу Гюйгенса можно рассматривать в качестве источников вторичных волн, освещались светом одного источника S. Если симметрично расположить щели, то вторичные волны от источников S1 и S2 находятся в фазе, однако волны проходят до точки наблюдения P различные расстояния r1 и r2. Можно сделать вывод, что фазы колебаний, которые создаются волнами от источников S1 и S2 в точке P, различные. Следует, что задача об интерференции волн – это задача о сложении колебаний одинаковой частоты, но с различными фазами.
Высказывание о том, что волны от источников S1 и S2 распространяются независимым образом, а в точке наблюдения они складываются друг с другом, – это опытный факт, который называется принципом суперпозиции.
Монохроматическую (или синусоидальную) волну, распространяющуюся в направлении радиус-вектора r→, записывают в виде
E=a cos (ωt – kr),
где a – это амплитуда волны, k=2πλ – это волновое число, λ – это длина волны, ω=2πν – это круговая частота. При решении оптических задач под E предполагают модуль вектора напряженности электрического поля волны. При вкладывании 2-х волн в точке P итоговое колебание также случается на частоте ω и обладает некоторой амплитудой A и фазой φ:
E=a1·cos (ωt–kr1)+a2·cos (ωt – kr2)=A·cos (ωt-φ).
Приборы, которые могли бы следить за быстрыми изменениями поля световой волны в оптическом диапазоне, не существуют. Наблюдаемая величина – это поток энергии, прямо пропорциональный квадрату амплитуды электрического поля волны.
Физическая величина, равная квадрату амплитуды электрического поля волны, называется интенсивностью: I=A2.
Путем простых тригонометрических вычислений можно прийти к следующему выражению для интенсивности результирующего колебания в точке P:
I=A2=a12+a22+2a1a2 cosk∆=I1+I2+2I1I2 cos k∆ (*),
где Δ=r2–r1 – это разность хода.
Из данного выражения можно сделать вывод, что интерференционный максимум (то есть светлая полоса) достигается в таких точках пространства, в которых Δ=mλ (m=0, ±1, ±2, …). Причем Imax=(a1+a2)2=I1+I2. Интерференционный минимум (то есть темная полоса) достигается при Δ=mλ+λ2. Минимальное значение интенсивности Imin=(a1–a2)2<I1+I2. Рис. 3.7.4 наглядно показывает, как распределяется интенсивность света в интерференционной картине, смотря от того, каким будет ход Δ.
Рисунок 3.7.4. Распределение интенсивности в интерференционной картине. Целое число m – это порядок интерференционного максимума.
Предположим, что если I1=I2=I0, то есть длина 1 и 2 световой волны одинакова, то выражение (*) выглядит следующим образом:
I=2I0(1+cos kΔ) (**).
В данном случае Imax=4I0, Imin=0.
Формулы (*) и (**) – универсальные. Они подходят для любой интерференционной схемы, в которой складываются 2 монохроматические волны одинаковой частоты.
Обозначим в схеме Юнга смещение точки наблюдения от плоскости симметрии y, тогда в случае, когда d≪L и y≪L (как правило, в оптических экспериментах данные условия соблюдаются), можно приблизительно получить:
∆≈d·θ≈d·yL.
Разность хода Δ меняется на одну длину волны λ при смещении от одного интерференционного максимума к другому, то есть на расстояние, эквивалентное ширине интерференционной полосы Δl. Получается,
d·∆lL=λ или ∆l=L·λd≈λψ,
где ψ – это угол схождения «лучей» в точке наблюдения P.
Сделаем количественную оценку. Предположим, что расстояние d между 2-мя щелями S1 и S2 равняется 1 мм, а расстояние от щелей до экрана Э равно L=1 м, в таком случае ψ=dL=0,001 рад. Для света зеленого цвета (λ=500 нм) получаем Δl =λ ψ=5·105 нм=0,5 мм. Для света красного цвета (λ=600 нм) Δl=0,6 мм. Именно так Юнг в первый раз измерил длины световых волн, хоть и точность данных измерений была невысока.
Подчеркнем, что в волновой оптике понятие “луч света” теряет физический смысл в отличие от геометрической оптики. Определение «луч» в волновой оптике употребляется для краткости обозначения направления распространения волны.
Далее данный термин будет упоминаться без кавычек.
При рассмотрении эксперимента И. Ньютона (рис.3.7.1) при нормальном падении волны на плоскую поверхность линзы разность хода примерно равняется удвоенной толщине 2h воздушного промежутка между линзой и плоскостью. Если радиус кривизны R линзы огромен в сравнении с h, можно приблизительно получить формулу:
h≈r22R,
где r – это смещение от оси симметрии. Вычисляя разность хода, следует учитывать, что волны 1 и 2 отражаются при различных условиях. 1-я волна отражается от границы стекло–воздух, а 2-я – от границы воздух–стекло. В последнем варианте фаза колебаний отраженной волны изменяется на π, что равно увеличению разности хода на λ2. А потому
∆=2h+λ2≈r2R+λ2.
При условии r=0, то есть в центре (точка соприкосновения) Δ = λ2; потому в центре колец И. Ньютона всегда находится интерференционный минимум (зрительно это выглядит, как темное пятно). Радиусы rm следующих темных колец вычисляются по формуле
rm=mλR.
По данной формуле рассчитывается длина световой волны λ при известном радиусе кривизны R линзы.
Проблема когерентности волн
С помощью теории Юнга объясняются интерференционные явления, которые возникают при сложении 2-х монохроматических волн одинаковой частоты. Но сегодняшний опыт показывает, что интерференцию света на самом деле наблюдать не так-то просто. Если комнату осветить 2 одинаковыми лампочками, то в любой точке сложатся интенсивности света и здесь не будет никакой интерференции. Тогда появляется вопрос, когда нужно сложить напряженности (учитывая фазовые соотношения), а когда – интенсивности волн, то есть квадраты напряженностей полей? К сожалению, теория интерференции монохроматических волн не дает ответ на данный вопрос.
Реальные световые волны – не строго монохроматические. По фундаментальным физическим причинам излучение всегда происходит статистически (или случайно). Атомы источника света излучают независимо друг от друга в какие-то моменты времени, и каждый атом излучает свет очень короткий промежуток времени (τ≤10–8 с). Итоговое излучение источника света в определенный момент времени складывается из вкладов огромного количества атомов. Спустя время порядка τ совокупность излучающих атомов полностью обновляется. Потому суммарное излучение будет с другой амплитудой и, что очень важно, с другой фазой. Фаза волны, которая излучается реальным источником света, примерно постоянна только лишь на интервалах времени порядка τ.
Отдельные «обрывки» излучения длительности τ называют цуги. Они обладают пространственной длиной, равной cτ, где c – это скорость света.
Колебания в различных цугах не согласованы друг с другом. Выходит, что реальная световая волна – это последовательность волновых цугов с беспорядочно меняющейся фазой. В физике принято считать, что колебания в различных цугах некогерентны. Временной интервал τ, в течение которого фаза колебаний примерно постоянна, называется временем когерентности.
Интерференция возникает только лишь при сложении когерентных колебаний, то есть колебаний, которые относятся к одному цугу. Хоть и фазы каждого колебания также подвергаются случайным временным изменениям, но данные изменения одинаковы, потому разность фаз когерентных колебаний постоянна. В данном случае наблюдается устойчивая интерференционная картина и, значит, выполняется принцип суперпозиции полей. При сложении некогерентных колебаний разность фаз – это случайная функция времени. В этом случае интерференционные полосы подвергаются беспорядочным перемещениям из одной стороны в другую, и за время Δt их регистрации, которая в оптических экспериментах существенно превышает время когерентности (Δt≫τ), наблюдается полное усреднение. Глаз, фотопластинка или фотоэлемент фиксирует в точке наблюдения усредненную величину интенсивности, равную сумме интенсивностей I1+I2 этих колебаний. Здесь соблюдается закон сложения интенсивностей.
Итак, интерференция возникает только лишь при сложении когерентных колебаний. Волны, которые создают в точке наблюдения когерентные колебания, тоже называют когерентными. Волны от 2-х независимых источников некогерентны и не дают интерференцию. Ученый Юнг интуитивно догадался для того, чтобы получить интерференцию света нужно волну от источника разделить на 2 когерентные волны и потом смотреть на экране результат их сложения. Так устроены все интерференционные схемы. Но даже в данном случае интерференционная картина пропадает, если разность хода Δ превышает длину когерентности cτ.
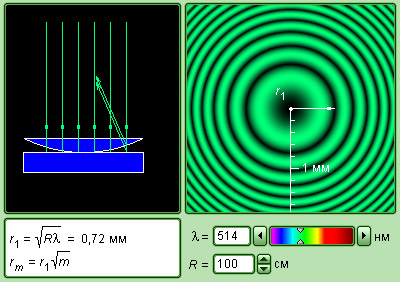
Рисунок 3.7.5. Модель кольца Ньютона.
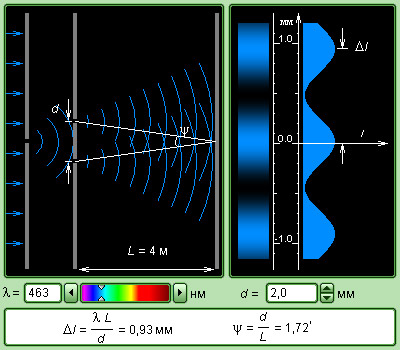
Рисунок 3.7.6. Модель интерференционый опыт Юнга.
 Рис. 8.
Рис. 8.

