velmititine320
Вопрос по геометрии:
Площадь сечения шара плоскостью, проходящей через его центр, равна 9п см^2.найдите объем шара.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 2
hentaisotre709
Сечение шара, проходящее через его центр представляет из себя окружность с радиусом, равным радиусу шара
Площадь сечения
S = πr² = 9π
πr² = 9π
r² = 9
r = 3 см
Площадь шара
S = 4πr² = 4π*3² = 36π см²
rlockexcl
Объём шара находим по формуле: V=4/3πr³;Sсеч. = πr² = 9π (по условию). Следовательно, r² = 9, r = √9 = 3.
V=4/3π3³ = 4/3π27 = 36π см³.
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Приветствую Вас, уважаемые Читатели! Сегодня я хочу поговорить с Вами о формуле объема шара, которую в школьном курсе геометрии давали без вывода, во всяком случае в начале.
Единственное, её могли определять через описанный вокруг шара многогранник. Если это было в школьной программе, напишите, пожалуйста, в комментариях.
Итак, для вычисления объема шара нам потребуется простая схема и “немножко интеграла”. Нарисуем сферу, которую рассечем плоскостью на высоте х от начала координат, совпадающего с центром сферы:
Очевидно, что сечение шара будет являться окружность, площадь которой нам нужно для начала найти. Выразим её радиус через прямоугольный треугольник СОМ:
Основная мысль нахождения объема шара в том, что мы можем “составить” всю сферу из очень тонких слоёв (толщиной dx) такой площади. Величина х у нас изменяется от -R до R: слои как бы пробегают шар сверху до низу. Записываем интеграл и решаем его:
Получилась знакомая формула! Спасибо за внимание!
- Ставьте “Нравится” и подписывайтесь на канал прямой сейчас, даже если считаете мои рассуждения “игрой в бисер”. На канале есть статьи на любой вкус!
- TELEGRAM и Facebook – там я публикую не только интересные статьи, но и математический юмор и многое другое.
Содержание:
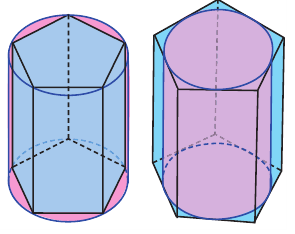
Говоря об объеме, имеют ввиду вместимость пространственной фигуры. Как вы думаете, емкость какого из цилиндров на рисунке больше?

Призмой, вписанной (описанной) в цилиндр, называется призма, основания которой вписаны (описаны) в основания цилиндра.
Объем цилиндра
Пусть в цилиндр с радиусом 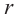
При бесконечном возрастании 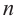 площадь оснований данных призм приближаются к площади основания
площадь оснований данных призм приближаются к площади основания 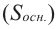 цилиндра, а их объемы к объему цилиндра:
цилиндра, а их объемы к объему цилиндра:
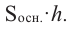
Объем цилиндра равен произведению площади основания на высоту.
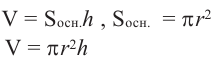
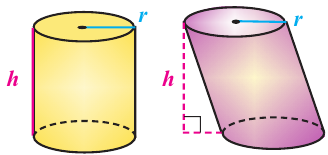
Практическая работа. Какая связь существует между объемами призмы и пирамиды, если они имеют одинаковые высоты и основания? Можно ли эту связь применить для объемов цилиндра и конуса?
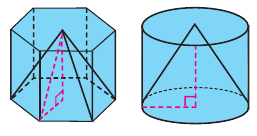
Сделайте из картона модели сосудов в виде конуса и цилиндра, радиусы оснований и высоты которых одинаковы. Заполните цилиндрический сосуд при помощи сосуда в виде конуса (песком, рисом, и т. п.).
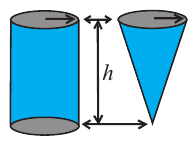
Сколько таких сосудов понадобится, чтобы заполнить цилиндрический сосуд? Верно ли утверждение, что цилиндрический сосуд можно заполнить тремя полными сосудами в виде конуса?
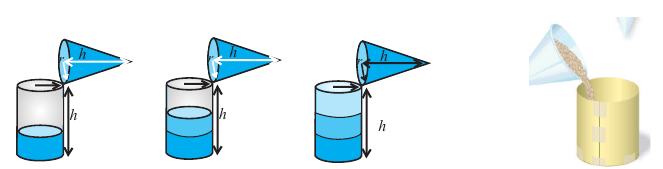
Обобщите соответствующую информацию о вычислении объема призмы, цилиндра, пирамиды и конуса, записав ответ в закрашенные ячейки.
Объем призмы и цилиндра:
Объем = площадь основания 
Объем пирамиды и конуса:
Объем =  объем призмы или цилиндра, имеющих одинаковые
объем призмы или цилиндра, имеющих одинаковые
основание и высоту.
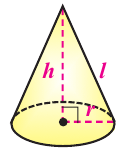
Объем конуса
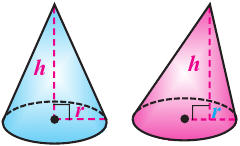
Объем конуса равен произведению одной третьей площади основания на высоту.
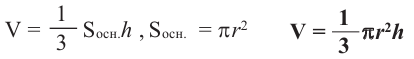
Пример №1
Образующая конуса 9 см, высота 6 см. Найдите объем конуса.
Решение:
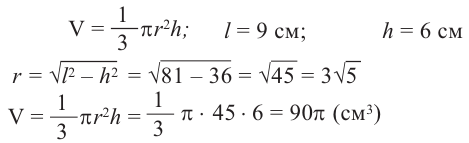
Объем шара и его частей
Практическая работа.
1. Возьмите мяч. Определите его диаметр.
2. Изобразите на бумаге развертку цилиндра, диаметр и высота которого равны диаметру шару.
3. Вырежьте и сверните полученную развертку в цилиндр без верхней крышки. Скрепите развертку при помощи клейкой ленты. Разделите высоту цилиндра на 3 равные части и сделайте соответствующие разметки.

4. Обверните мяч фольгой или плотным материалом и сделайте мешок сферической формы. Наполните его песком.

5. Пересыпьте песок в цилиндр. Какая часть цилиндра заполнится?
Если разделить поверхность шара сеткой из вертикальных и горизонтальных линий и маленький “прямоугольный” кусочек сферы соединить с центром шара, то можно представить, что шар состоит из множества “маленьких пирамид”.

Объем шара можно выразить через сумму объемов “маленьких пирамид” 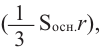 высота которых равна радиусу шара. Бесконечно уменьшая размеры оснований, количество пирамид будет бесконечно расти.
высота которых равна радиусу шара. Бесконечно уменьшая размеры оснований, количество пирамид будет бесконечно расти.
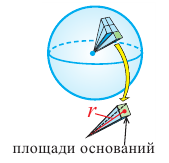
Сумма площадей оснований “маленьких пирамид” будет равна площади поверхности шара. Учитывая, что площадь поверхности шара равна 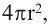 получим формулу для нахождения объема шара:
получим формулу для нахождения объема шара:
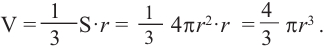
Объем шара:
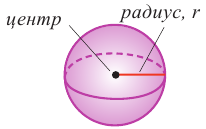
Объем шара равен произведению 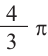 и куба радиуса.
и куба радиуса.
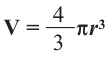
Пример №2
Найдите: а) объем шара радиуса 3 см
b) радиус шара объемом 288 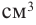
Решение:
а) 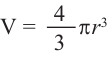
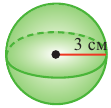
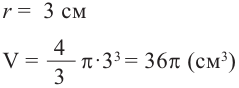
b) 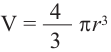

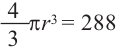
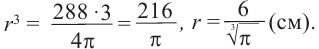
Сектор шара и сегмент шара
Шаровой сектор — это часть шара, ограниченная конической поверхностью с вершиной в центре шара. Шаровой сектор-объеденение конуса и шарового сегмента.
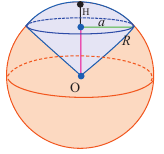
Так как шаровой сектор можно рассмотреть как предел суммы объемов маленьких пирамид, вершины которых находятся в центре шара, а основания касаются его поверхности, то
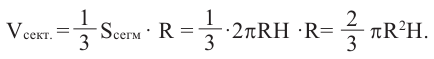
Здесь 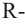 радиус шара,
радиус шара, 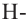 высота соответствующего сегмента
высота соответствующего сегмента
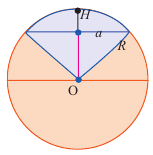
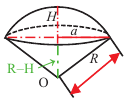
С другой стороны,
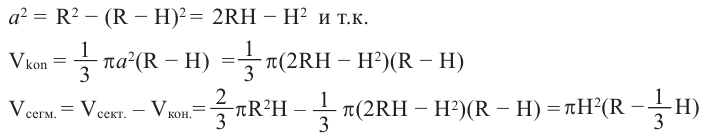
Проектная работа.
Отношение между объемами цилиндра, конуса и шара, которое получил Архимед.
Архимед нашел формулу для нахождения объема шара, исследовав связь между объемом цилиндра, описанного вокруг шара радиуса и объемом конуса, вписанного в данный цилиндр. Попробуйте и вы выполнить это исследование.

Если 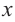 – расстояние от центра шара до плоскости сечения, то для шара радиуса
– расстояние от центра шара до плоскости сечения, то для шара радиуса 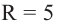 представьте зависимость площади сечения от
представьте зависимость площади сечения от 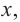 выполнив следующие шаги.
выполнив следующие шаги.
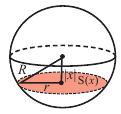
a) Вычислите следующие значения функции 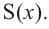
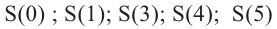
Для примера найдено значение 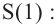
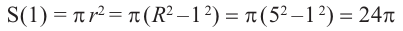
b) Представьте свои суждения о значениях 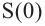 и
и 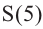 сечений.
сечений.
c) Запишите общую формулу для определения площади сечения, расположенного на расстоянии 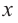 от центра шара радиуса
от центра шара радиуса 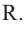
d) Свяжите формулу, полученную в пункте 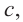 и следующий рисунок.
и следующий рисунок.

e) Чтобы понять умозаключения Архимеда, вернемся к начальному рисунку.
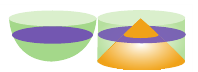
При “извлечении” конуса из цилиндра в поперечном сечении получаем кольца, параллельные основанию.
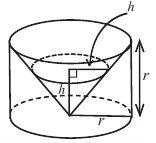
На одном и том же уровне поперечное сечение шара является кругом. Из подобия треугольников можно доказать, что площадь кольца каждого слоя равна 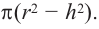 Поскольку площади этих плоских сечений равны, по принципу Кавальери равны и объемы этих тел.
Поскольку площади этих плоских сечений равны, по принципу Кавальери равны и объемы этих тел.
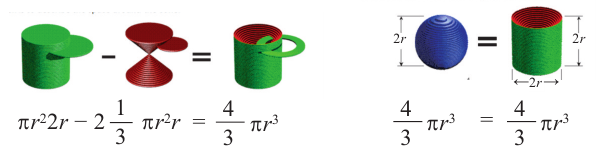
Объемы подобных фигур
Отношения соответствующих линейных размеров подобных пространствнных фигур должны быть равны.
По заданным соответствующим размерам подобных пространственных фигур можно найти неизвестные размеры.
Пример №3
Конусы  и
и  подобны. По данным рисунка найдите образующую конуса
подобны. По данным рисунка найдите образующую конуса 
Решение: Запишем отношение линейных размеров: Радиус А Образующая А
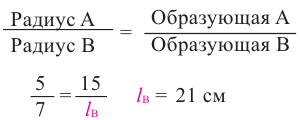
Известно, что отношение площадей поверхностей двух подобных пространственных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия:
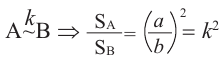
Объемы подобных пространственных фигур
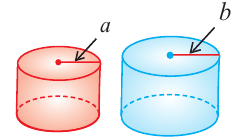
Отношение объемов подобных пространственных фигур 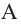 и
и 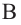 равно кубу отношения соответствующих линейных размеров или кубу коэффициента подобия:
равно кубу отношения соответствующих линейных размеров или кубу коэффициента подобия:
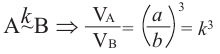
Пример №4
Отношение боковых поверхностей двух подобных цилиндров равно 4:9. Зная, что разность объемов равна 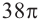 куб.ед., найдите объемы цилиндров.
куб.ед., найдите объемы цилиндров.
Решение: по условию 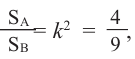 тогда
тогда 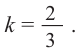 Значит
Значит 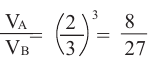 С другой стороны, принимая во внимание, что
С другой стороны, принимая во внимание, что 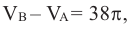 получим:
получим:
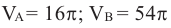
Объемы тел в высшей математике
Под телом Т будем подразумевать ограниченное множество в пространстве.
Будем рассматривать тела, имеющие внутренние точки и границу, которая также принадлежит телу (замкнутые тела), причем такие, что любые две внутренние
точки можно соединить непрерывной линией, проходящей внутри тела.
Определение 1. Рассмотрим тело 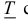 составленное из конечного числа многогранников, содержащихся в Т, и тело
составленное из конечного числа многогранников, содержащихся в Т, и тело 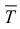 , составленное из многогранников и покрывающее тело Т:
, составленное из многогранников и покрывающее тело Т: 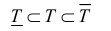
Пусть 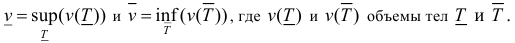 Тело называется кубируемым, если
Тело называется кубируемым, если 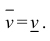 . При этом число
. При этом число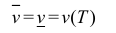 (1) называется объемом тела Т (по Жордану).
(1) называется объемом тела Т (по Жордану).
Замечание. Для кубируемости тела Т необходимо и достаточно, чтобы 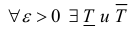 такие, что
такие, что 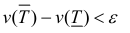 (2)
(2)
Пусть для кубируемого тела Т известны площади s=s(x) его сечения плоскостями перпендикулярными оси Ох, проходящими через точки (х, 0, 0),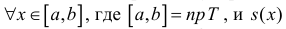 – непрерывна
– непрерывна
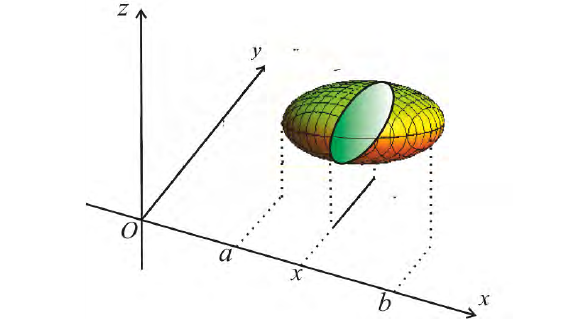
Разобьем отрезок [ a b ] на n частичных отрезков точками 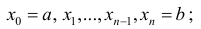
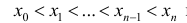 и обозначим это разбиение
и обозначим это разбиение 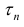 . Пусть
. Пусть 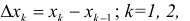
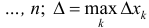 – диаметр разбиения, тогда
– диаметр разбиения, тогда 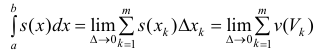 (3)
(3)
Где 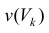 это – объем цилиндрического тела высотой
это – объем цилиндрического тела высотой 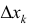 и площадью основания
и площадью основания
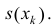 Пусть
Пусть 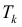 k − -ый слой тела Т между плоскостями, проходящими через точки
k − -ый слой тела Т между плоскостями, проходящими через точки 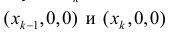 и перпендикулярными оси Ох.
и перпендикулярными оси Ох.
Так как Т – кубируемо, то 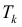 – также кубируемо и
– также кубируемо и 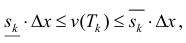 где
где
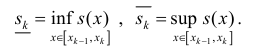
Тогда 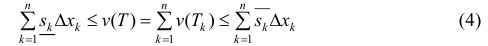
∀n ∈ N, или 
Где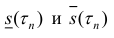 это – нижняя и верхняя суммы Дарбу функции s(x) для разбиения
это – нижняя и верхняя суммы Дарбу функции s(x) для разбиения
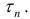 Поэтому
Поэтому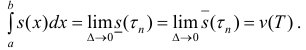 Таким образом
Таким образом 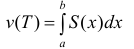 (6)
(6)
Замечание. Нужно заметить, что неравенство (4), которое использовалось для вывода формулы (6), выполняется, когда любые два рассматриваемые сечения
тела Т при проекции на плоскость yOz полностью содержатся одно в другом.
Однако формула (6) верна и в общем случае. Для этого достаточно потребовать,
чтобы тело Т было кубируемым и функция s (x) – непрерывной.
Пример №5
Найти объем тела ограниченного поверхностями 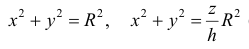 (ниже параболоида).
(ниже параболоида).
Решение.
Из системы уравнений 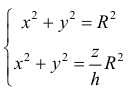 следует, что z=h.
следует, что z=h.
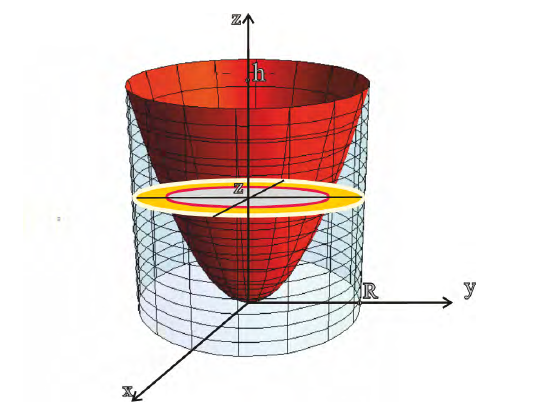
В сечении тела плоскостью проходящей через точку (0, 0, z) перпендикулярно оси Оz получается кольцо
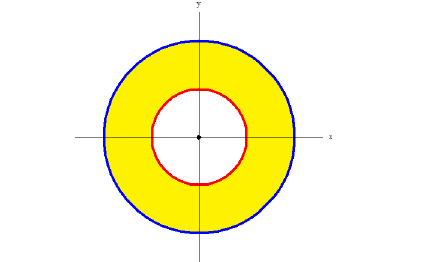
Радиус внешней окружности равен R, радиус внутренней равен 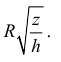
Поэтому по формуле (6):
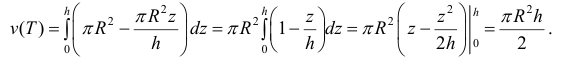
Формулу (6) удобно применять к телам вращения. Пусть y=f(x) – непрерывна на отрезке 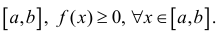 Будем вращать криволинейную трапецию
Будем вращать криволинейную трапецию
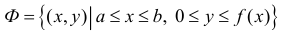
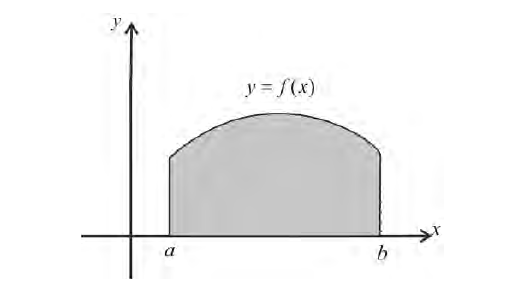
вокруг оси Ох. Получим тело:
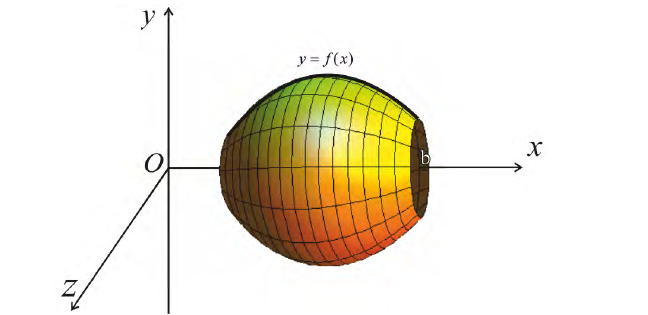
Тогда сечением полученного тела плоскостью проходящей через точку (х,0,0) и перпендикулярной оси Ох будет круг радиуса 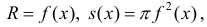 и по формуле (6):
и по формуле (6): 
Где y=f(x).
Аналогично, если 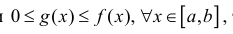 то при вращении вокруг оси Ох фигуры
то при вращении вокруг оси Ох фигуры 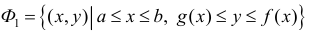
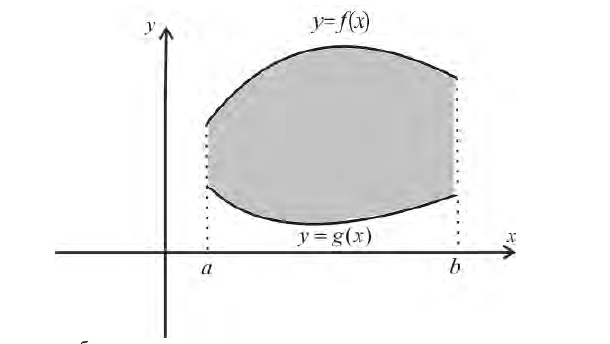
Получим тело, объем которого 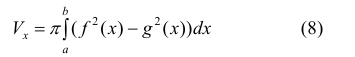
Пример №6
Рассмотрим фигуру Φ ограниченную эллипсом 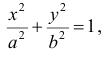
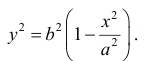
Найдем объем эллипсоида полученного при вращении вокруг оси Ох фигуры Φ .
Решение.
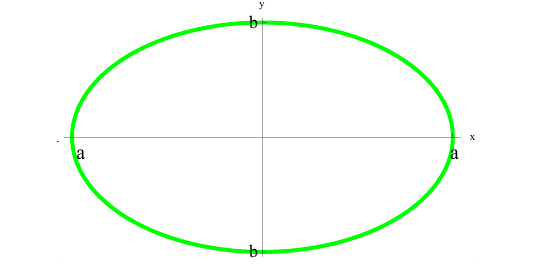
По формуле (7): 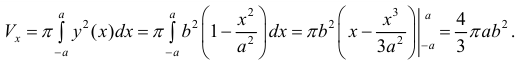
Пусть функция x=x(y) – непрерывна при 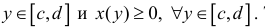 Тогда, аналогично, при вращении вокруг оси Оу фигуры
Тогда, аналогично, при вращении вокруг оси Оу фигуры 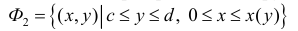
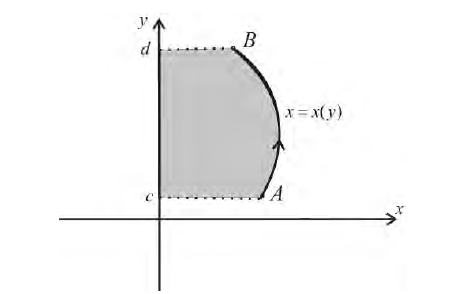
Получим тело, объем которого 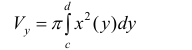 (9)
(9)
Если же вращать вокруг оси Оу трапецию 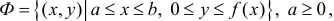
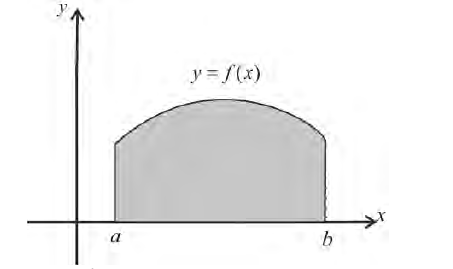
то 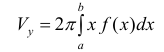 (10)
(10)
Пример №7
Рассмотрим тело Т из примера 1. Оно получается, если вращать вокруг оси Oz фигуру, ограниченную линиями:
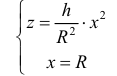
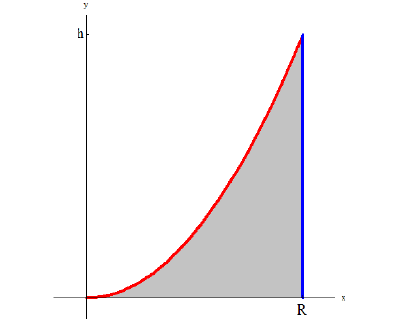
Из первого уравнения найдем 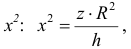 поэтому по формуле (9):
поэтому по формуле (9):
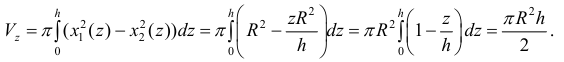
Пример №8
Объем 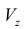 при вращении фигуры
при вращении фигуры 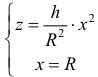 из примера 3 вокруг оси Oz можно также найти и по формуле (10):
из примера 3 вокруг оси Oz можно также найти и по формуле (10): 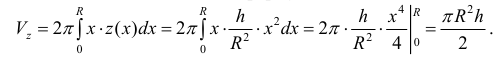
Пример №9
Фигура Ф ограничена линиями 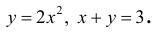 Найти
Найти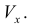
Решение.
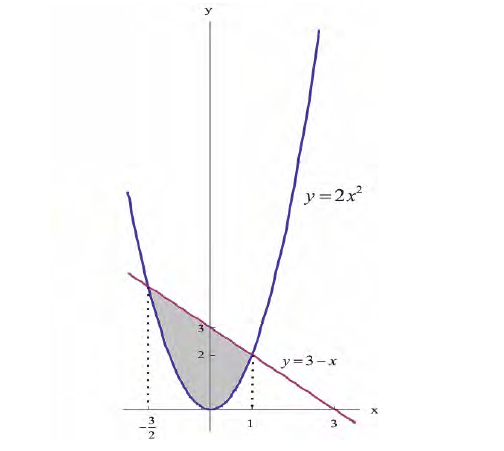
Абсциссы точек пересечения: 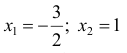 (см. пример 1 § 30). По формуле (8):
(см. пример 1 § 30). По формуле (8):
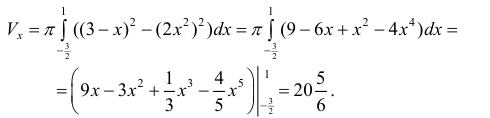
Замечание. Для непрерывной функции 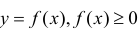 рассмотрим криволинейную трапецию
рассмотрим криволинейную трапецию 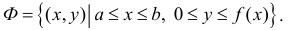
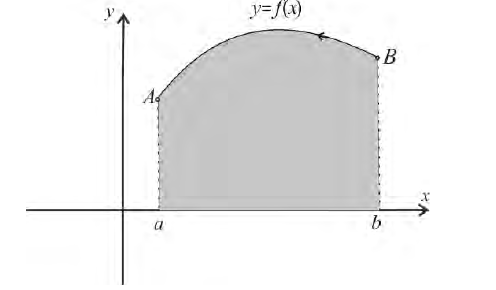
Пусть 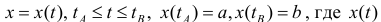 – непрерывно-дифференцируема на промежутке
– непрерывно-дифференцируема на промежутке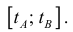 Тогда по формуле (7):
Тогда по формуле (7): 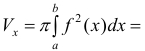 по формуле (1) § 26
по формуле (1) § 26
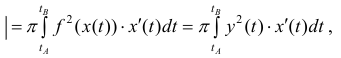
Где 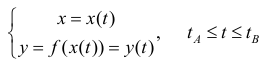 – параметрическое задание линии
– параметрическое задание линии 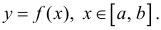 Таким образом
Таким образом 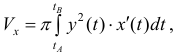 или
или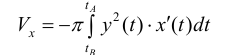 (12)
(12)
(кривая обходится так, чтобы область Ф оставалась слева).
Аналогично, для непрерывной функции 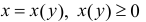 рассмотрим криволинейную трапецию
рассмотрим криволинейную трапецию 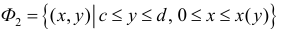
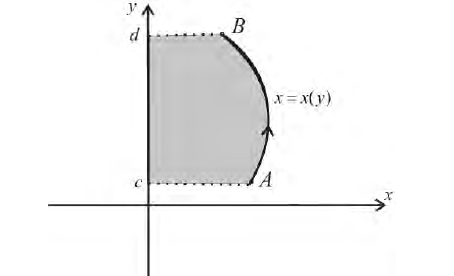
Пусть 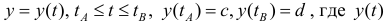 – непрерывно-дифференцируема на промежутке
– непрерывно-дифференцируема на промежутке 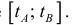 Тогда по формуле (9):
Тогда по формуле (9): 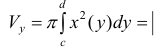 по формуле (1) § 26
по формуле (1) § 26
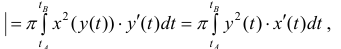
Где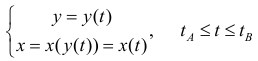 – параметрическое задание линии
– параметрическое задание линии 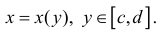
Таким образом 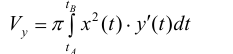 (13) (кривая обходится так, чтобы область Ф оставалась слева).
(13) (кривая обходится так, чтобы область Ф оставалась слева).
Рассмотрим область ,ограниченную простой замкнутой кривой
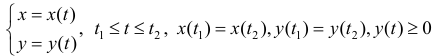 (кривая лежит по одну сторону от оси Ox ). Тогда объем
(кривая лежит по одну сторону от оси Ox ). Тогда объем  можно находить по формуле (12):
можно находить по формуле (12): 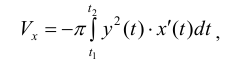
(кривая обходится так, чтобы область оставалась слева).
Аналогично ,для области ограниченной простой замкнутой кривой
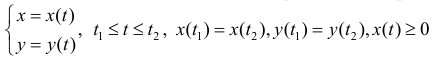 (кривая лежит по одну сторону от оси Oy )объем
(кривая лежит по одну сторону от оси Oy )объем 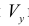 можно находить по формуле (13):
можно находить по формуле (13): 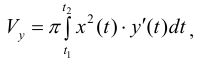 (кривая обходится так, чтобы область оставалась слева).
(кривая обходится так, чтобы область оставалась слева).
Пример №10
Дана астроида 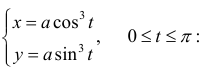
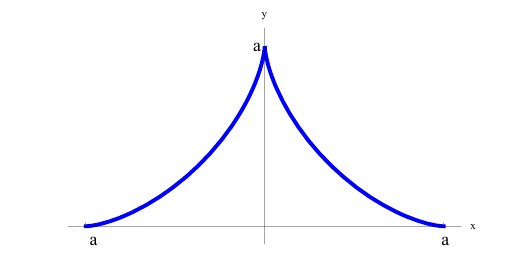
Найдем  .
.
Решение.
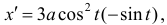 по формуле (12):
по формуле (12):
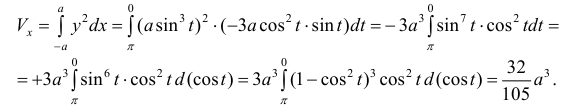
Пример №11
Петля кривой 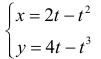 вращается вокруг оси Ox .Найти
вращается вокруг оси Ox .Найти  .
.
Решение.
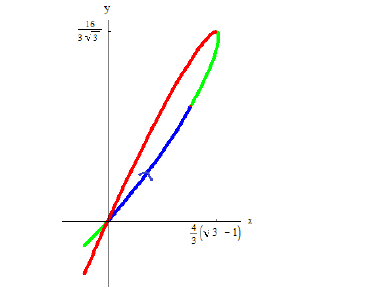
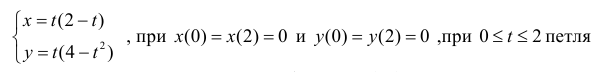 петля обходится против часовой стрелки. По формуле (12):
петля обходится против часовой стрелки. По формуле (12):
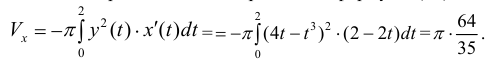
Пусть 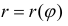 – кривая в полярной системе координат, r (ϕ) – непрерывна при
– кривая в полярной системе координат, r (ϕ) – непрерывна при 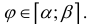 Рассмотрим на плоскости хОу криволинейный сектор
Рассмотрим на плоскости хОу криволинейный сектор
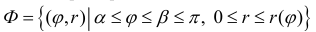
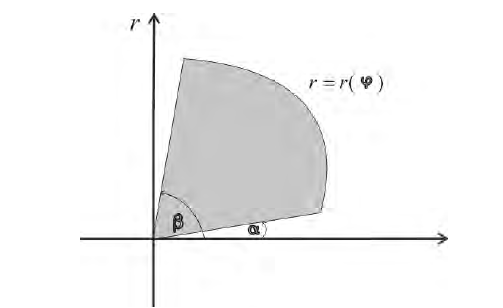
Тогда объем тела при вращении фигуры ϕ вокруг полярной оси равен
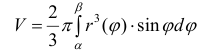 (14)
(14)
Пример №12
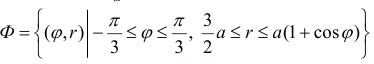 (см. пример 4 § 31).
(см. пример 4 § 31).
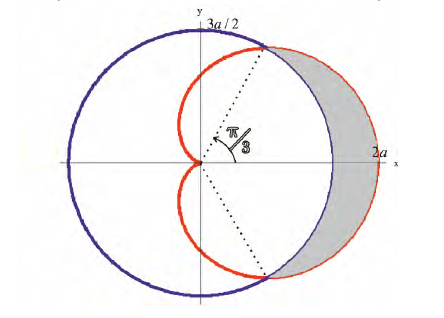
Найдем  .
.
Решение.
По формуле (14):
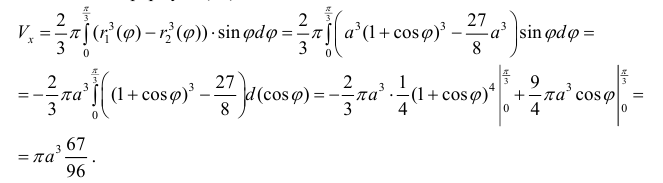
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры – виды, изображения, свойства
- Площадь прямоугольника
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
Введение
Сколько чугуна нужно, чтобы отлить пушечное ядро? Что занимает больше места: арбузная корка или мякоть арбуза? Сколько воздуха поместится внутри воздушного шара? Чтобы ответить на все эти и многие другие вопросы, необходимо уметь находить объем шара. Сделать это не так просто. Разбить его на «кубики», треугольные призмы или другие фигуры, как это делалось раньше, не получится. Можно вычислить объем шара с помощью определенного интеграла. Но как же тогда вычисляли объем, например, древние греки – при отсутствии определенных интегралов? Метод, придуманный Архимедом, был очень красив и по сути своей являлся предшественником метода доказательства через интеграл. Он доказал формулу объема шара понятийно, представив половину шара через конус и цилиндр, объемы которых уже известны.
Метод Архимеда для вычисления объема шара
Идея Архимеда была такова.
Замечание: формулы объемов цилиндра и конуса Архимед уже знал.
Рассмотрим весы и такую конструкцию. На левой чаше – цилиндр радиуса ![]() и его высота
и его высота ![]() . На правой чаше – конус радиуса
. На правой чаше – конус радиуса ![]() и высотой
и высотой ![]() (см. Рис. 1).
(см. Рис. 1).

Рис. 1. Исходная конструкция
Разобьем каждую из этих фигур на ![]() равных слоев (цилиндриков). Будем считать, что конус тоже составлен из цилиндриков. (радиус у них у всех –
равных слоев (цилиндриков). Будем считать, что конус тоже составлен из цилиндриков. (радиус у них у всех – ![]() , а высота слоя –
, а высота слоя – ![]() , все колечки из одного и того же материала). Справа находится конус, составленный также из цилиндриков, высота каждого из которых –
, все колечки из одного и того же материала). Справа находится конус, составленный также из цилиндриков, высота каждого из которых – ![]() , а радиус уменьшается от
, а радиус уменьшается от ![]() до
до ![]() на
на ![]() в арифметической прогрессии, а также из полушар радиуса
в арифметической прогрессии, а также из полушар радиуса ![]() (см. Рис. 2).
(см. Рис. 2).

Рис. 2. Разбиение фигур на «цилиндрики»
Докажем, что чаши уравновешены. Чтобы уравновесить чаши, необходимо добавить к каждому колечку конуса недостающее колечко так, чтобы суммарный их вес дал вес «цилиндрика» слева. Разумеется, можно приравнивать не массы, а объемы – в силу одинаковости материала. Но высоты у колечек одинаковы, значит, должны совпасть площади оснований.
У цилиндра площадь основания каждого колечка ![]() . У очередного слоя конуса –
. У очередного слоя конуса – ![]() . Значит, на фигуру, стоящую правее от конуса, остается
. Значит, на фигуру, стоящую правее от конуса, остается ![]() . Но если предположить, что справа находится «полушар», то радиус его сечения плоскостью, отстоящей от основания на
. Но если предположить, что справа находится «полушар», то радиус его сечения плоскостью, отстоящей от основания на ![]() как раз и будет равен
как раз и будет равен ![]() (см. Рис. 3).
(см. Рис. 3).

Рис. 3. Полушар со своими измерениями
Осталось устремить ![]() к нулю (что и дает, по сути, определенный интеграл).
к нулю (что и дает, по сути, определенный интеграл).
Значит, объем полушара ищется как разность между объемами цилиндра и конуса.
Вычислим: ![]() , откуда
, откуда ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
Выведение формулы объема шара через интеграл
Рассмотрим произвольную ось ![]() , проходящую через центр шара – точку
, проходящую через центр шара – точку ![]() . Тогда объем шара можно найти по формуле:
. Тогда объем шара можно найти по формуле:
![]() , где
, где ![]() – площадь сечения шара плоскостью, перпендикулярной оси
– площадь сечения шара плоскостью, перпендикулярной оси ![]() и проходящей через точку этой оси с абсциссой
и проходящей через точку этой оси с абсциссой ![]() . Почему именно от
. Почему именно от ![]() до
до ![]() ? Потому что если ось проходит через центр, то точки пересечения оси с границей шара находятся на расстоянии
? Потому что если ось проходит через центр, то точки пересечения оси с границей шара находятся на расстоянии ![]() от начала координат: одна – в положительном направлении, а другая – в отрицательном (см. Рис. 4).
от начала координат: одна – в положительном направлении, а другая – в отрицательном (см. Рис. 4).

Рис. 4. Ось ![]() пересекает шар в точках
пересекает шар в точках ![]() и
и ![]()
Найдем ![]() . Пусть
. Пусть ![]() – точка с абсциссой
– точка с абсциссой ![]() на оси. Рассмотрим такую точку
на оси. Рассмотрим такую точку ![]() , что она лежит на границе шара и при этом в плоскости сечения. В этом случае радиус сечения
, что она лежит на границе шара и при этом в плоскости сечения. В этом случае радиус сечения ![]() находится из треугольника
находится из треугольника ![]() по теореме Пифагора
по теореме Пифагора ![]() . А так как сечение – круг данного радиуса, то его площадь равна:
. А так как сечение – круг данного радиуса, то его площадь равна: ![]() (см. Рис. 5).
(см. Рис. 5).

Рис. 5. Радиус сечения ![]() из треугольника
из треугольника ![]()
Тогда:


Пример
Предположим, что вы купили арбуз, имеющий форму шара. Арбуз этот состоит из мякоти (также в форме шара) и корки. При этом толщина корки в ![]() раза меньше радиуса мякоти
раза меньше радиуса мякоти ![]() . Какую часть от объема всего арбуза составляет объем мякоти
. Какую часть от объема всего арбуза составляет объем мякоти ![]() ? (См. Рис. 3.)
? (См. Рис. 3.)

Рис. 6. Купленный арбуз
Решение. Пусть радиус (толщина) корки ![]() , тогда радиус мякоти
, тогда радиус мякоти ![]() , а радиус всего арбуза
, а радиус всего арбуза ![]() . (См. Рис. 4.)
. (См. Рис. 4.)

Рис. 7. Иллюстрация к условию
Имеем: объем мякоти ![]() а объем арбуза
а объем арбуза ![]() , значит, их отношение
, значит, их отношение ![]() .
.
Ответ: ![]() .
.
Шаровой сегмент
Шаровой сегмент в пространстве чем-то похож на круговой сегмент в плоскости. Вспомним, что такое круговой сегмент. Фигура, которая образовалась при отсечении проведенной в круге хордой, называется сегментом. Хорда рассекает круг на два сегмента (см. Рис. 8).

Рис. 8. Два круговых сегмента – маленький и большой
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Не забывайте слово «шаровой»: хоть по контексту это обычно и понятно, но тем не менее сегмент – это плоская фигура. Соответственно, если проводить любую секущую плоскость, шар разбивается на два шаровых сегмента (см. Рис. 9).

Рис. 9. Два шаровых сегмента – маленький и большой
Круг в сечении – основание сегмента (см. Рис. 10).

Рис. 10. Основание сегмента
Отрезок ![]() – высота сегмента (см. Рис. 11).
– высота сегмента (см. Рис. 11).

Рис. 11. Высота сегмента
Сегмент задают либо радиусом шара и высотой сегмента, либо радиусом основания и высотой сегмента.
Объем шарового сегмента выводится точно так же, как и объем шара.
Пусть дан шар радиуса ![]() , от него отсекли сегмент высотой
, от него отсекли сегмент высотой ![]() . Рассмотрим ось
. Рассмотрим ось ![]() , проходящую через центр шара
, проходящую через центр шара ![]() и центр секущей плоскости
и центр секущей плоскости ![]() (см. Рис. 12).
(см. Рис. 12).

Рис. 12. Данный шар
Тогда объем сегмента равен (подставляем уже выведенную формулу для ![]() ):
):

![]()
![]() .
.
Шаровой слой
Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями (см. Рис. 13).

Рис. 13. Шаровой слой
Объем шарового слоя находится по формуле: ![]() .
.
Шаровой сектор
Рассмотрим произвольную секущую плоскость данного шара, не проходящую через его центр. Она отсекает сегмент (рассмотрим тот из них, который не содержит центр шара, то есть меньший). Кроме того, рассмотрим конус, основанием которого будет сечение шара плоскостью, а вершиной – центр шара. Объединение конуса и сегмента называют шаровым сектором (см. Рис. 14).

Рис. 14. Шаровой сектор
Объем шарового сектора находится как сумма объемов конуса и шарового сегмента ![]()
Пусть дан шар, в котором ![]() ,
, ![]() , тогда
, тогда ![]() и
и ![]() (по теореме Пифагора из треугольника
(по теореме Пифагора из треугольника ![]() ) (см. Рис. 15).
) (см. Рис. 15).

Рис. 15. Данный шар
Имеем: ![]()
![]() .
.
То есть ![]() , где
, где ![]() – радиус шара и
– радиус шара и ![]() – высота сегмента.
– высота сегмента.
Заключение
Была выведена формула для нахождения объема шара ![]() , были разобраны части шара – шаровой слой, шаровой сегмент, шаровой сектор – и были выведены формулы нахождения их объема:
, были разобраны части шара – шаровой слой, шаровой сегмент, шаровой сектор – и были выведены формулы нахождения их объема: ![]() ,
, ![]() ,
, ![]() .
.
Список литературы
- Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
- А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
- Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия. 11 класс. Рабочая тетрадь. 8-е изд. – М.: Просвещение, 2013. – 78 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Bymath.net (Источник).
- Yaklass.ru (Источник).
- Sites.google.com (Источник).
Домашнее задание
- Шар пересечен плоскостью. Диаметр окружности сечения равен
 см. Вычислите объем меньшего сегмента, если радиус шара равен
см. Вычислите объем меньшего сегмента, если радиус шара равен  см.
см. - Два шара, радиусы которых
 см и
см и  см, имеют общий центр. Найдите объем тела, содержащегося между поверхностями этих шаров.
см, имеют общий центр. Найдите объем тела, содержащегося между поверхностями этих шаров. - Радиус шара равен
 см. Найдите объем шарового сектора этого шара, если дуга в его осевом сечении содержит
см. Найдите объем шарового сектора этого шара, если дуга в его осевом сечении содержит  .
.
На этом уроке мы дадим определение шара.
Выведем формулу для вычисления объёма шара. А затем с её помощью выведем
формулу для вычисления площади сферы.
Прежде чем приступить к рассмотрению данной
темы, давайте вспомним, что такое шар.
Определение:
Шар – это совокупность всех
точек пространства, находящихся от данной точки на расстоянии, не больше
данного. Причём, данная точка называется центром шара, а данное
расстояние – радиусом шара.
Радиусом шара называют всякий отрезок, соединяющий центр шара с
любой точкой шаровой поверхности.
Отрезок,
соединяющий две точки шаровой поверхности и проходящий через центр шара,
называется диаметром шара. Диаметр шара равен двум радиусам.
Отрезок,
соединяющий две точки шаровой поверхности и не являющийся диаметром шара, т.е.
не проходящий через центр шара, называется хордой шара.
Понятно, что сечение
шара плоскостью есть круг.
Сечение шара
плоскостью, проходящей через его центр, называется большим кругом
шара.
Итак, справедлива
следующая теорема: объём шара радиуса равен
.
Докажем теорему. Пусть нам дан шар радиуса с
центром в точке .
Выберем ось так, чтобы
начало оси совпадало с центром шара.
Тогда отрезок это есть радиус
шара .
Докажем, что
объём шара равен .
На оси отметим
произвольную точку и
рассмотрим сечение шара плоскостью проходящее через эту точку перпендикулярно к
оси .
Заметим, что такое сечение шара плоскостью является кругом с центром в точке .
Отрезок .
Обозначим
радиус этого круга через ,
а его площадь через ,
где –
абсцисса точки .
Выразим площадь
через
и
радиус шара .
Из
прямоугольного треугольника по теореме
Пифагора найдём радиус круга. Тогда имеем .
Площадь круга .
Заменим радиус круга выражением
.
Тогда получаем, что .
Заметим, что
эта формула верна для любого положения точки на
диаметре .
Иначе говоря, верна для всех ,
удовлетворяющих условию .
Так как мы с
вами выразили площадь через ,
то можем вычислить объём шара с помощью основной формулы объёма тела. Вспомним
её: объем тела равен .
Итак, применяя
основную формулу для вычисления объёмов тел получаем, что объём шара равен .
Этим мы с вами доказали, что объём шара с
радиусом равным можно
вычислить по формуле .
Что и требовалось доказать.
Ранее мы с вами без доказательства привели
формулу для вычисления площади сферы. Напомню, что площадь сферы можно
вычислить по формуле: .
Теперь давайте выведем эту формулу, пользуясь
формулой объёма шара.
Итак, рассмотрим сферу радиуса с центром в точке О и описанный
около неё многогранник, имеющий граней.
Напомним, что многогранник называется
описанным около сферы (шара), если сфера касается всех его граней. При этом
сфера называется вписанной в многогранник.
Занумеруем грани в произвольном порядке и
обозначим через – площадь -й грани.
Затем соединим центр О сферы отрезками со
всеми вершинами многогранника. При этом получим эн пирамид с общей вершиной О,
основаниями которых являются грани многогранника, а высотами – радиусы сферы,
проведенные в точки касания граней многогранника со сферой.
Следовательно, объём -й пирамиды равен , а объём всего описанного
многогранника равен: . Где
– площадь поверхности
многогранника.
Отсюда получаем: .
Теперь будем неограниченно увеличивать таким образом, чтобы наибольший
размер каждой грани описанного многогранника стремился к нулю. При этом объём описанного многогранника будет
стремиться к объёму шара. В самом деле, если наибольший размер каждой грани
описанного многогранника не превосходит , то описанный многогранник
содержится в шаре радиуса с центром в точке
.
Но ведь с другой стороны, описанный
многогранник содержит исходный шар радиуса . Значит, объём
.
Так как выражение при
, то и объем
при
(
).
Переходя затем к пределу, получаем, что .
По определению площади сферы , следовательно,
.
Что и требовалось доказать.
Задача: объём шара равен равен см3. Найдите диаметр
шара.
Решение: запишем формулу для
вычисления объёма шара.
По условию задачи объём шара равен см3.
Отсюда видим, что радиус шара равен (см). Напомним, что диаметр
шара вдвое больше его радиуса. Тогда диаметр нашего шара равен (см).
Запишем ответ.
Задача: радиус шара увеличили в раза. Во сколько раз увеличился
объём шара?
Решение: запишем формулу для
вычисления объёма шара.
Так как по условию задачи радиус исходного
шара увеличили в 2 раза, то радиус данного шара будет равен . Подставляя данный радиус в
формулу для вычисления объёма шара видим, что объём исходного шара
увеличился в 8 раз. Следовательно, ответ: объём шара увеличился в 8 раз.
Задача: в цилиндр вписан шар.
Найдите отношение объёма шара к объёму цилиндра.
Решение: шар, вписанный в
цилиндр, касается оснований цилиндра в их центрах и боковой поверхности
цилиндра по окружности большого круга, параллельной основаниям цилиндра. Отсюда
следует, что , а высота цилиндра равна
.
Объём шара вычисляется по формуле , а объём данного цилиндра можно
вычислить по формуле , где
– это площадь основания,
–
высота цилиндра. Так как высота данного цилиндра равна двум радиусам, а площадь
основания равна , то объём цилиндра равен
.
Найдём отношение объёма шара к объёму
цилиндра. Получаем, что объём шара относится к объёму цилиндра, как .
Эту задачу называют «Задачей Архимеда». Во
времена Архимеда формула объёма шара была неизвестна. Поэтому данная задача
считалась очень трудной и, решив ее, Архимед испытал большую радость. На могиле
Архимеда был поставлен памятник с изображением шара и описанного около него
цилиндра.
Итоги:
На этом уроке мы дали определение шара. Вывели
формулу для вычисления объёма шара. А затем с её помощью вывели формулу для
вычисления площади сферы.
