12. Исследование функций с помощью производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
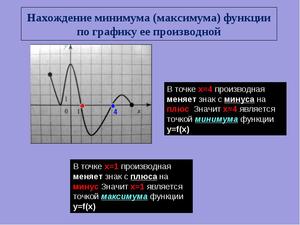
Поиск точек экстремума локального минимума и максимума функций
(blacktriangleright) Если функция задана как частное двух других функций, то [{Large{left(dfrac fgright)’=dfrac{f’cdot
g-fcdot g’}{g^2}}}]
(blacktriangleright) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).
[begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]
Задание
1
#881
Уровень задания: Равен ЕГЭ
Найдите точку локального минимума функции
(y = -dfrac{x^2 + 2016^2}{x}).
ОДЗ: (x neq 0). Решим на ОДЗ:
1) [y’ = -dfrac{2x^2 – (x^2 + 2016^2)}{x^2} = dfrac{2016^2 – x^2}{x^2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует):
[dfrac{2016^2 – x^2}{x^2} = 0qquadLeftrightarrowqquad x^2 = 2016^2] – на ОДЗ, откуда находим корни (x_1 = -2016, x_2 = 2016). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = dfrac{(2016-x)(2016+x)}{x^2}.] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
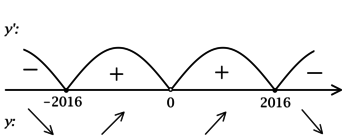
3) Эскиз графика (y):
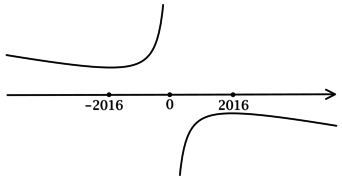
Таким образом, (x = -2016) – точка локального минимума функции (y).
Ответ: -2016
Задание
2
#882
Уровень задания: Равен ЕГЭ
Найдите точку локального максимума функции
(y = dfrac{3,2}{x} + 5x + 1024).
ОДЗ: (x neq 0). Решим на ОДЗ:
1) [y’ = -dfrac{3,2}{x^2} + 5 = dfrac{5x^2-3,2}{x^2} = 5dfrac{x^2 – 0,64}{x^2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [5dfrac{x^2 – 0,64}{x^2} = 0qquadLeftrightarrowqquad x^2 – 0,64] – на ОДЗ, откуда находим корни (x_1 = -0,8, x_2 = 0,8). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = 5dfrac{(x – 0,8)(x + 0,8)}{x^2}.] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
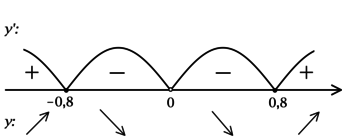
3) Эскиз графика (y):
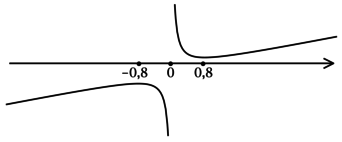
Таким образом, (x = -0,8) – точка локального максимума функции (y).
Ответ: -0,8
Задание
3
#6920
Уровень задания: Равен ЕГЭ
Найдите точку локального максимума функции
(y = dfrac{3x^2 + 1875}{x}).
ОДЗ: (x neq 0). Решим на ОДЗ:
1) [y’ = dfrac{6x^2 – (3x^2 + 1875)}{x^2} = dfrac{3x^2 –
1875}{x^2} = 3cdot dfrac{x^2 – 625}{x^2}.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3cdot dfrac{x^2 – 625}{x^2} = 0qquadLeftrightarrowqquad x^2-625=0, xne 0] – на ОДЗ, откуда находим корни (x_1 = 25, x_2 = -25). Производная функции (y) не существует при (x = 0), но (x = 0) не входит в ОДЗ. Таким образом, [y’ = 3cdot dfrac{(x – 25)(x + 25)}{x^2}.] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
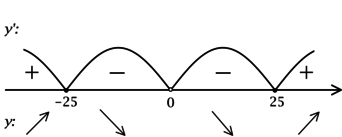
3) Эскиз графика (y):
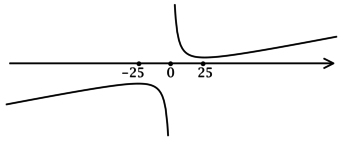
Таким образом, (x = -25) – точка локального максимума функции (y).
Ответ:
-25
Задание
4
#884
Уровень задания: Равен ЕГЭ
Найдите точку локального минимума функции
(y = dfrac{e^x}{x + 1}).
ОДЗ: (x neq -1). Решим на ОДЗ:
1) [y’ = e^xleft(dfrac{1}{x + 1} – dfrac{1}{(x + 1)^2}right) = dfrac{e^x}{(x + 1)^2}x.]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{e^x}{(x + 1)^2}x = 0qquadLeftrightarrowqquad x = 0] – на ОДЗ (так как (e^{x} > 0) при любом (x)). Производная функции (y) не существует при (x = -1), но (x = -1) не входит в ОДЗ. Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства (y’):
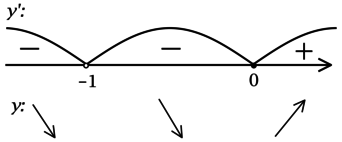
3) Эскиз графика (y):
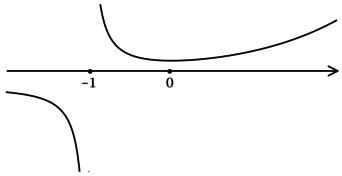
Таким образом, (x = 0) – точка локального минимума функции (y).
Ответ: 0
Задание
5
#2359
Уровень задания: Равен ЕГЭ
Найдите точку максимума функции (y = dfrac{x}{e^x}).
ОДЗ: (x) – произвольный.
1) [y’ = dfrac{1cdot e^x – e^xcdot x}{e^{2x}} = dfrac{1 – x}{e^x}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{1 – x}{e^x} = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:
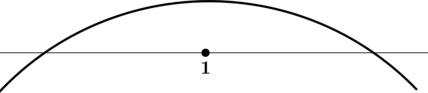
Таким образом, (x = 1) – точка максимума функции (y).
Ответ: 1
Задание
6
#2360
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции (y = dfrac{x^2 – 1}{x^2 + 1}) на отрезке ([-15; 15]).
ОДЗ: (x) – произвольный.
1) [y’ = dfrac{2xcdot (x^2 + 1) – 2xcdot(x^2 – 1)}{(x^2 + 1)^2} = dfrac{4x}{(x^2 + 1)^2}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{4x}{(x^2 + 1)^2} = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-15; 15]):

4) Эскиз графика на отрезке ([-15; 15]):
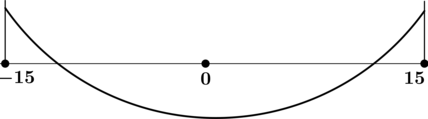
Таким образом, (x = 0) – точка минимума функции (y) на отрезке ([-15; 15]).
Ответ: 0
Задание
7
#2361
Уровень задания: Равен ЕГЭ
Найдите точку минимума функции (y = dfrac{x^2}{x^3 + 1}) на промежутке ((-1; 1]).
ОДЗ: (xneq -1).
1) [y’ = dfrac{2x(x^3 + 1) – 3x^2cdot x^2}{(x^3 + 1)^2} = dfrac{-x^4 + 2x}{(x^3 + 1)^2}]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [dfrac{-x^4 + 2x}{(x^3 + 1)^2} = 0qquadLeftrightarrowqquad
left[
begin{gathered}
x = 0\
x = sqrt[3]{2}
end{gathered}
right.] Производная не существует при (x = – 1).
2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом промежутке ((-1; 1]):

4) Эскиз графика на промежутке ((-1; 1]):
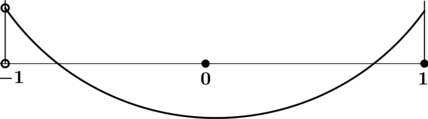
Таким образом, (x = 0) – точка минимума функции (y) на промежутке ((-1; 1]).
Ответ: 0

УСТАЛ? Просто отдохни
§ 16. Возрастание и убывание функции в точке и на интервале
Дадим определение возрастания и убывания
функции в точке. Мы будем говорить, что
функция y=f(x)возрастает (убывает) в точкеc,
если найдётся такая окрестность точкиc, в пределах которой
при![]() а при
а при![]()
(при
![]() а при
а при![]() ).
).
Напомним определения монотонных и
строго монотонных функций на интервале.
Функция называется неубывающей
(невозрастающей) на интервале, если для
любых x1иx2из этого интервала, удовлетворяющих
условиюx1<
x2,
справедливо неравенство
![]() (
(![]() ). Неубывающие и невозрастающие функции
). Неубывающие и невозрастающие функции
называются монотонными.
Функция называется возрастающей
(убывающей) на интервале, если для любых
x1иx2из этого интервала, удовлетворяющих
условиюx1<
x2, справедливо
неравенство
![]() (
(![]() ). Возрастающие и убывающие функции
). Возрастающие и убывающие функции
называются строго монотонными.
Докажем теорему, устанавливающую
достаточные условия возрастания
(убывания) функции.
Теорема 16.1.Если функцияf(x)дифференцируема в точкеcи![]() (
(![]() ), то эта функция возрастает (убывает)
), то эта функция возрастает (убывает)
в точкеc.
Доказательство. Рассмотрим случай
![]() .
.
Из определения производной следует,
что![]() .
.
Поскольку![]() ,
,
то (по теореме о сохранении знака функции,
имеющей предел) найдётся такая окрестность
точкиc, в пределах
которой отношение![]() остаётся положительным. Но это значит,
остаётся положительным. Но это значит,
что в пределах данной окрестности при![]() а при
а при![]() ,
,
т.е. функцияf(x)возрастает в точкеc.
Аналогично доказывается, что при![]() функцияf(x)убывает в точкеc.
функцияf(x)убывает в точкеc.
Теорема доказана.
§ 17. Локальный максимум и локальный минимум функции.
Дадим определение локального максимума
и локального минимума функции.
Говорят, что функция f(x)имеет в точкеcлокальный максимум (минимум), если
найдётся такая окрестность точкиc,
в пределах которой значение![]() является наибольшим (наименьшим) среди
является наибольшим (наименьшим) среди
всех значений функции в этой окрестности,
то есть всюду в этой окрестности
выполняется условие![]() (
(![]() ).
).
Для обозначения локального максимума
и локального минимума функции употребляется
единое название локальный экстремум.
Следующая теорема устанавливает
необходимое условие экстремума
дифференцируемой функции.
Теорема 17.1(называется иногда
теоремой Ферма). Если функцияf(x)дифференцируема в точкеcи имеет в этой точке локальный экстремум,
то![]() .
.
Доказательство. Так как функция f(x)имеет в точкеcлокальный экстремум, то она не может в
этой точке ни возрастать, ни убывать.
Следовательно, в силу теоремы 16.1
производная![]() не может быть ни положительна, ни
не может быть ни положительна, ни
отрицательна, то есть![]() .
.
Теорема доказана.
Геометрический смысл этой теоремы
заключается в том, что если в точке
локального экстремума график функции
имеет касательную, то эта касательная
параллельна оси абсцисс (рис. 5).

Отметим, что равенство нулю производной
является необходимым, но не достаточным
условием локального экстремума.
Рассмотрим в качестве примера функцию
![]() ( рис.6).
( рис.6).

Производная этой функции
![]() .
.
В точке![]()
![]() .
.
Однако функция![]() возрастает на всей числовой оси и не
возрастает на всей числовой оси и не
имеет в точке![]() локального экстремума.
локального экстремума.
§ 18. Теорема Ролля
Теорема 18.1 (теорема Ролля). Пусть
функцияf(x)непрерывна на отрезке [a;b],
дифференцируема во всех внутренних
точках этого отрезка и на концах отрезка
принимает равные значения:![]() .
.
Тогда внутри отрезка [a;b]
найдётся такая точкаc,
в которой производная![]() равна нулю.
равна нулю.
Доказательство. Так как функция f(x)непрерывна на отрезке [a;b],
то, как следует из теоремы Вейерштрасса,
она достигает на этом отрезке своего
наибольшего значенияMи своего наименьшего значенияm.
ЕслиM = m,
то функцияf(x)постоянна на отрезке [a;b],
а, следовательно, в любой точкеxэтого отрезка![]() .
.
Если жеM > m,
то хотя бы одно из двух значенийM
или mдостигается
в некоторой внутренней точкеcотрезка [a;b]
(так как![]() ,
,
то не равные между собой значенияM
и mне могут
оба достигаться на концах отрезка [a;b]
). Но тогда в этой точкеcфункцияf(x)имеет локальный экстремум. Так как
функцияf(x)дифференцируема в точкеc,
то по теореме 17.1![]() .
.
Теорема доказана.

Функция (синяя) и её производная (красная). Глобальный максимум функции обозначен символом 
Экстре́мум (лат. extremum — крайнее) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Задачи нахождения экстремума возникают во всех областях человеческого знания: теория автоматического управления, проблемы экономики, биология, физика и т. д.[1]
Определения[править | править код]
Пусть дана функция 


Если неравенства выше строгие, то 
Значение функции 
Замечание[править | править код]
Функция 


Необходимые условия существования локальных экстремумов[править | править код]
- Из леммы Ферма вытекает следующее[2]:
- Пусть точка
является точкой экстремума функции
, определенной в некоторой окрестности точки
.
- Тогда либо производная
не существует, либо
.
Эти условия не являются достаточными, так, функция может иметь нуль производной в точке, но эта точка может не быть точкой экстремума, а являться, скажем, точкой перегиба, как точка (0,0) у функции 
Достаточные условия существования локальных экстремумов[править | править код]

то 
Заметим, что при этом функция не обязательно дифференцируема в точке 
и

и
то 
Если 


Если 


Если 
См. также[править | править код]
- Критическая точка (математика)
- Методы оптимизации
- Условный экстремум
Примечания[править | править код]
- ↑ Пшеничный, 1969, с. 7.
- ↑ Кудрявцев Л. Д. Математический анализ. — 2-е изд. — М.: Высшая школа, 1973. — Т. 1.
Литература[править | править код]
- Пшеничный Б.Н. Необходимые условия экстремума. — М.: Наука, 1969. — 150 с.
 Поиск точки максимума и минимума функции – довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом “экстремум” подразумевают наибольшее или наименьшее значение функции. Это не совсем верно. Значение может быть наибольшим или минимальным, но не являться экстремумом.
Поиск точки максимума и минимума функции – довольно распространенная задача в математическом анализе. Иногда требуется экстремум. Многие думают, что под словом “экстремум” подразумевают наибольшее или наименьшее значение функции. Это не совсем верно. Значение может быть наибольшим или минимальным, но не являться экстремумом.
Содержание:
- Глобальный и локальный максимум
- Исследование
- Область допустимых аргументов
- Асимптоты
- Производная и экстремумы
- Концы интервала и сравнение результатов
- Видео
Глобальный и локальный максимум
Максимум бывает локальным или глобальным. Точка локального максимума – это аргумент, который при подстановке в f(x) даёт значение не меньше, чем в других точках из области около этого аргумента. Для глобального максимума эта область расширяется до всей области допустимых аргументов. Для минимума всё наоборот. Экстремум – это локальное экстремальное – минимальное или максимальное – значение.
Как правило, если математиков интересует глобально самое большое значение f(x), то в интервале, не на всей оси аргументов. Подобные задачи обычно сформулированы фразой “найдите точку максимума функции на отрезке”. Здесь подразумевается, что надо выявить аргумент, при котором она не меньше, чем на всём остальном указанном отрезке. Поиск локального экстремума является одним из шагов решения такой задачи.
Дано y = f(x). Требуется определить пик функции на указанном отрезке. f(x) может достигать его в точке:
- экстремума, если она попадает в указанный отрезок,
- разрыва,
- ограничивающей заданный отрезок.
Исследование
Пик f(x) на отрезке или в интервале находится путём исследования данной функции. План исследования для нахождения максимума на отрезке (или интервале):
 Найти область допустимых аргументов и пересечения этой области с областью исследования.
Найти область допустимых аргументов и пересечения этой области с областью исследования.- Выявить асимптоты. Они равны пределу при стремлении аргумента к точкам разрыва.
- Определить первую производную и вычислить экстремальные точки и выяснить поведение функции в окрестности этих точек.
- Рассчитать значение f(x) в точках, ограничивающих область исследования.
- Сравнить экстремум со значением функции в точках разрыва и на концах интервала. Определить среди них наибольшее.
Теперь подробно разберем каждый шаг и рассмотрим некоторые примеры.
Область допустимых аргументов
Область допустимых аргументов – это те x, при подстановке которых в f(x) она не престаёт существовать.Область допустимых аргументов ещё называют областью определения. Например, y = x^2 определена на всей оси аргументов. А y = 1/x определена для всех аргументов, кроме x = 0.
Найти пересечение области допустимых аргументов и исследуемого отрезка (интервала) требуется для того, чтобы исключить из рассмотрения ту часть интервала, где функция не определена. Например, требуется найти минимум y = 1/x на отрезке от -2 до 2. На самом деле требуется исследовать два полуинтервала от -2 до 0 и от 0 до 2, так как уравнение у = 1/0 не имеет решения.
Асимптоты
 Асимптота – это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность.
Асимптота – это такая прямая, к которой функция тянется, но не дотягивается. Если f(x) существует на всей числовой прямой и неразрывна на ней, то вертикальной асимптоты у неё нет. Если же она разрывна, то точка разрыва является вертикальной асимптотой. Для y = 1/x асимптота задаётся уравнением x = 0. Эта функция тянется к нулю по оси аргументов, но дотянется до него, только устремившись в бесконечность.
Если на исследуемом отрезке имеется вертикальная асимптота, около которой функция стремится в бесконечность с плюсом, то пик f(x) на здесь не определяется. А если бы определялся, то аргумент, при котором достигается максимум, совпал бы с точкой пересечения асимптоты и оси аргументов.
Производная и экстремумы
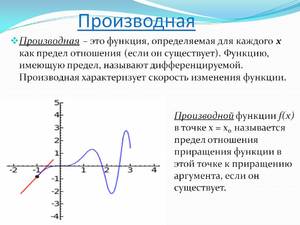 Производная – это предел изменения функции при стремящемся к нулю изменении аргумента. Что это значит? Возьмём небольшой участок из области допустимых аргументов и посмотрим как изменится здесь f(x), а потом уменьшим этот участок до бесконечно малого размера, в этом случае f(x) станет изменяться так же, как и некая более простая функция, которая именуется производной.
Производная – это предел изменения функции при стремящемся к нулю изменении аргумента. Что это значит? Возьмём небольшой участок из области допустимых аргументов и посмотрим как изменится здесь f(x), а потом уменьшим этот участок до бесконечно малого размера, в этом случае f(x) станет изменяться так же, как и некая более простая функция, которая именуется производной.
Значение производной в определенной показывает под каким углом проходит касательная к функции в выбранной точке. Отрицательное значение говорит о том, что функция здесь убывает. Аналогично положительная производная говорит о возрастании f(x). Отсюда появляются два условия.
1) Производная в точке экстремума либо нулевая, либо неопределенная. Это условие необходимое, но недостаточно. Продифференцируем y = x^3, получим уравнение производной: y = 3*x^2. Подставим в последнее уравнение аргумент “0”, и производная обратится в нуль. Однако, это не экстремум для y = x^3. У неё не может быть экстремумов, она убывает на всей оси аргументов.
2) Достаточно, чтобы при пересечении точки экстремума у производной менялся знак. То есть, до максимума f(x) растёт, а после максимума она убывает – производная была положительной, а стала отрицательной.
После того как аргументы для локального максимума были найдены их надо подставить в исходное уравнение и получить максимальное значение f(x).
Концы интервала и сравнение результатов
При поиске максимума на отрезке необходимо проверить значение на концах отрезка. Например, для y = 1/x на отрезке [1; 7] максимум будет в точке x = 1. Даже если внутри отрезка есть локальный максимум, нет никакой гарантии, что значение на одном из концов отрезка не будет больше этого максимума.
Теперь необходимо сравнить значения в точках разрыва (если f(x) здесь не стремится в бесконечность), на концах исследуемого интервала и экстремум функции. Наибольшее из этих значений и будет максимумом функции на заданном участке прямой.
Для задачи с формулировкой “Найдите точку минимума функции” необходимо выбрать наименьшее из локальных минимумов и значений на концах интервала и в точках разрыва.
Видео
Отыскание локальных максимумов и минимумов не обходится без дифференцирования и является необходимым при исследовании функции и построении ее графика.
Точка 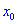 называется точкой локального максимума (или минимума) функции
называется точкой локального максимума (или минимума) функции 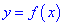 , сли существует такой окрестность
, сли существует такой окрестность 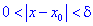 этой точки, принадлежащий области определения функции, и для всех
этой точки, принадлежащий области определения функции, и для всех 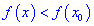 из этого окрестности выполняется неравенство
из этого окрестности выполняется неравенство 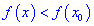 (или
(или 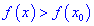 ).
).
Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках – ее экстремальными значениями.
НЕОБХОДИМОЕ УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА:
Если функция имеет в точке 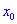 локальный экстремум, то либо производная равна нулю
локальный экстремум, то либо производная равна нулю 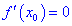 , либо не существует.
, либо не существует.
Точки которые удовлетворяют выписанным выше требованиям называют критическими точками.
Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.
ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ
Теорема І. Пусть функция 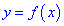 непрерывна в некотором интервале, содержащем критическую точку
непрерывна в некотором интервале, содержащем критическую точку 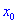 и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки
и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки 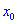 ).
).
Тогда для точки 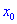 функция имеет максимум, если для аргументов
функция имеет максимум, если для аргументов 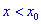 выполняется условие, что производная больше нуля
выполняется условие, что производная больше нуля 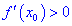 , а для
, а для 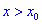 условие – производная меньше нуля
условие – производная меньше нуля 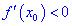 .
.
Если же для 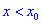 производная меньше нуля
производная меньше нуля 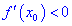 , а для
, а для 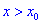 больше нуля
больше нуля 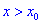 , то для точки
, то для точки 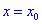 функция имеет минимум.
функция имеет минимум.
Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки 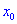 и производная равна нулю
и производная равна нулю 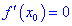 . Тогда в точке
. Тогда в точке 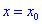 функция имеет локальный максимум, если вторая производная меньше нуля
функция имеет локальный максимум, если вторая производная меньше нуля 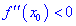 и локальный минимум, если наоборот
и локальный минимум, если наоборот 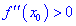 .
.
Если же вторая производная равна нулю 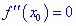 , то точка
, то точка 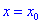 может и не быть точкой экстремума.
может и не быть точкой экстремума.
При исследовании функций на экстремумы используют обе теоремы. Первая на практике проще, поскольку не требует нахождения второй производной.
ПРАВИЛА НАХОЖДЕНИЯ ЕКСТРЕМУМОВ (МАКСИМУМОВ И МИНИМУМОВ) С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ
1) найти область определения 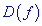 ;
;
2) найти первую производную 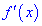 ;
;
3) найти критические точки;
4) исследовать знак производной 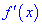 на интервалах, которые получили от разбиения критическими точками области определения
на интервалах, которые получили от разбиения критическими точками области определения 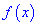 .
.
При этом критическая точка 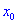 является точкой минимума, если при переходе через нее слева направо производная
является точкой минимума, если при переходе через нее слева направо производная 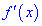 меняет знак с отрицательного
меняет знак с отрицательного 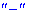 на положительный
на положительный  , в противном случаэ
, в противном случаэ 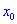 является точкой максимума.
является точкой максимума.
Вместо данного правила можно определять вторую производную 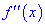 и исследовать согласно второй теоремы.
и исследовать согласно второй теоремы.
5) вычислить значения функции в точках экстремума.
Рассмотрим теперь исследование функции на экстремумы на конкретных примерах.
———————————–
Примеры.
Сборник В.Ю. Клепко, В.Л. Голец “Высшая математика в примерах и задачах”
1. (4.53.7)
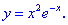
1) Областью определения будет множество действительных чисел
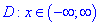 ;
;
2) Находим производную
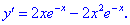
3) Вычисляем критические точки
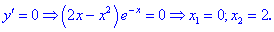
Они разбивают область определения на следующие интервалы
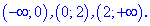
4) Исследуем знак производной на найденных интервалах методом подстановки значений
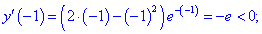
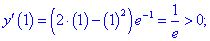
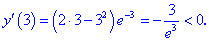
Таким образом первая точка 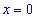 является точкой минимума, а вторая
является точкой минимума, а вторая 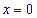 – точкой максимума.
– точкой максимума.
5) Вычисляем значение функции
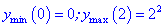
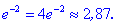
——————————
2. (4.53.9)
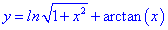
1) Областью определения будет множество действительных чисел  , так корень всегда больше единицы
, так корень всегда больше единицы
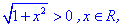
и функция арктангенс определена на всей действительной оси.
2) Находим производную
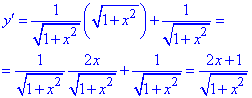
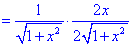
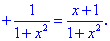
3) С условия равенства производной нулю находим критическую точку

Она разбивает область определения на два интервала
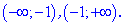
4) Определим знак производной в каждой из областей
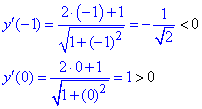
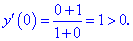
Таким образом находим, что в критической точке 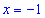 функция принимает минимальное значение.
функция принимает минимальное значение.
5) Вычислим экстремум функции

——————————
3. (4.53.13)
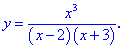
1) Функция определена когда знаменатель не превращается в ноль
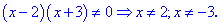
Из этого следует, что область определения состоит из трех интервалов
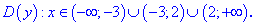
2) Вычисляем производную
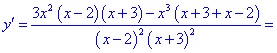
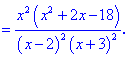
3) Приравниваем производную к нулю и находим критические точки.
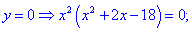
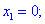
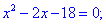
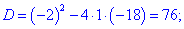
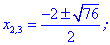
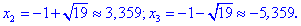
4) Устанавливаем знак производной в каждой из областей, подстановкой соответствующих значений.
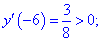
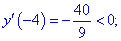
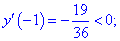
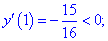
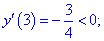
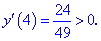
Таким образом точка 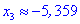 является точкой локального максимума, а
является точкой локального максимума, а 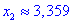 локального минимума. В
локального минимума. В 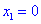 имеем перегиб функции, но о нем будет больше материала в следующих статьях.
имеем перегиб функции, но о нем будет больше материала в следующих статьях.
5) Находим значение в критических точках
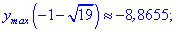
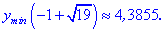
Несмотря на то, что значение функции 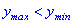 , первая точка является точкой локального максимума, а дуга – минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.
, первая точка является точкой локального максимума, а дуга – минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.
———————————————-
Посмотреть материалы:
- Исследования функции и построения графика
- Интервалы монотонности функции
- Наибольшее и наименьшее значение функции на отрезке
- Выпуклость и вогнутисть графика функции
- Асимптоты функции
- Область определения функции




