Что такое относительное стандартное отклонение?
Относительное стандартное отклонение (RSD) измеряет отклонение набора чисел, рассеянных вокруг среднего значения. Его можно рассчитать как отношение стандартного отклонения к среднему для набора чисел. Чем больше отклонение, тем дальше цифры от среднего. Чем меньше отклонение, тем ближе числа к среднему.
Оглавление
- Что такое относительное стандартное отклонение?
- Формула относительного стандартного отклонения
- Как рассчитать относительное стандартное отклонение? (Шаг за шагом)
- Примеры
- Актуальность и использование
- Рекомендуемые статьи
Формула относительного стандартного отклонения
Относительное стандартное отклонение = (стандартное отклонение / среднее значение) * 100

Стандартное отклонение σ = √ [Σ(x- μ)2 / N]
Например, на финансовых рынках это соотношение помогает количественно оценить волатильность. Формула RSD помогает оценить риск, связанный с безопасностью движения на рынке. Если это отношение к безопасности высокое, то цены будут разбросаны, и ценовой диапазон будет широким. Это означает, что волатильность ценной бумаги высока. Если коэффициент по безопасности низкий, то и цены будут меньше разбросаны. Это означает, что волатильность ценной бумаги низкая.
Как рассчитать относительное стандартное отклонение? (Шаг за шагом)
Выполните следующие шаги:
- Первый, рассчитать среднее значение (µ), т. е. среднее число чисел
- Получив среднее значение, вычтите среднее значение из каждого числа, что даст нам отклонение, и возведите отклонения в квадрат.
- Добавьте квадраты отклонений и разделите это значение на общее количество значений. Это дисперсия.
- Квадратный корень из дисперсии даст нам стандартное отклонение (σ).
- Разделите стандартное отклонение на среднее значение и умножьте на 100.
- Ура! Вы только что взломали, как рассчитать формулу относительного стандартного отклонения.
Подводя итог, можно сказать, что деление стандартного отклонения на среднее значение и умножение на 100 дает относительное стандартное отклонение. Вот как это просто!
Прежде чем мы двинемся дальше, есть некоторая информация, которую вы должны знать. Во-первых, когда данные представляют собой совокупность сами по себе, приведенная выше формула идеальна, но если данные представляют собой выборку из совокупности (скажем, кусочки из большего набора), расчет изменится.
Изменение формулы выглядит следующим образом:
Стандартное отклонение (выборка) σ = √ [Σ(x- μ)2 / N-1]
Когда данные представляют собой совокупность, их следует разделить на N.
Когда данные представляют собой выборку, их следует разделить на N-1.
Примеры
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:»»;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel формулы относительного стандартного отклонения здесь — Формула относительного стандартного отклонения Шаблон Excel
Пример №1
Оценки, полученные тремя учащимися за тест, следующие: 98, 64 и 72. Но сначала рассчитайте относительное стандартное отклонение.
Решение:
Ниже приведены данные для расчета

Иметь в виду
Расчет среднего

μ = Σx/n
где м среднее значение; Σxi представляет собой сумму всех значений, и н это количество предметов
мк = (98+64+72) / 3
м= 78
Среднеквадратичное отклонение
Следовательно, расчет стандартного отклонения выглядит следующим образом:

Складываем значения всех (х — м)2 мы получаем 632
Поэтому, Σ(х-м)2 = 632
Расчет стандартного отклонения:
σ = √ [Σ(x- μ)2 / N]
=√632/3
σ = 14.51
РСД

Формула = (стандартное отклонение / среднее значение) * 100
= (14,51/78)*100
Стандартное отклонение будет –

РСД = 78 +/- 18,60%
Пример #2
В следующей таблице показаны цены на акции XYZ. Найдите RSD за 10-дневный период.
Решение:
Ниже приведены данные для расчета относительного стандартного отклонения.

Иметь в виду
Расчет среднего

μ = (53,73+ 54,08+ 54,14+ 53,88+ 53,87+ 53,85+ 54,16+ 54,5+ 54,4+ 54,3) / 10
м = 54.091
Среднеквадратичное отклонение
Следовательно, расчет стандартного отклонения выглядит следующим образом:

Расчет стандартного отклонения:
σ = 0,244027
РСД

Формула = (стандартное отклонение / среднее значение) * 100
= (0,244027/54,091)*100
Стандартное отклонение будет –

РСД = 0,451141
Пример формулы №3
Организация провела медосмотр своих сотрудников и обнаружила, что у большинства сотрудников избыточный вес, вес (в кг) для 8 сотрудников указан ниже, и вам необходимо рассчитать относительное стандартное отклонение.
Решение:
Ниже приведены данные для расчета относительного стандартного отклонения.

Иметь в виду
Расчет среднего

μ = (130 + 120 + 140 + 90 + 100 + 160 + 150 + 110) / 8
м = 125
Среднеквадратичное отклонение
Следовательно, расчет стандартного отклонения выглядит следующим образом:

Расчет стандартного отклонения:
σ = 24.4949
РСД

Формула = (стандартное отклонение / среднее значение) * 100
= (24,49490/125)*100
Стандартное отклонение будет –

РСД = 19,6
Поскольку данные представляют собой выборку из совокупности, необходимо использовать формулу RSD.
Актуальность и использование
Относительное стандартное отклонение помогает измерить дисперсию. В статистике дисперсия (или разброс) является средством описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных о наборе значений, связанных со средним значением. Это позволяет нам анализировать точность набора значений. Значение RSD выражается в процентах. Это помогает понять, является ли стандартное отклонение маленьким или огромным по сравнению со средним значением для набора значений.
Знаменатель для расчета RSD является абсолютным значением среднего, и он никогда не может быть отрицательным. Следовательно, RSD всегда положителен. Стандартное отклонение анализируется в контексте среднего значения с помощью RSD. RSD используется для анализа волатильности ценных бумаг. Кроме того, RSD позволяет сравнивать отклонения при контроле качества лабораторных тестов.
Рекомендуемые статьи
Эта статья была руководством по относительному стандартному отклонению и его определению. Здесь мы узнаем, как рассчитать относительное стандартное отклонение, используя его формулу, примеры и загружаемый шаблон Excel. Вы можете узнать больше о моделировании в Excel из следующих статей:
- Формула стандартного отклонения ExcelФормула стандартного отклонения ExcelСтандартное отклонение показывает отклонение значений данных от среднего (среднего). В Excel СТАНДОТКЛОН и СТАНДОТКЛОН.С вычисляют стандартное отклонение выборки, а СТАНДОТКЛОН и СТАНДОТКЛОН.П вычисляют стандартное отклонение совокупности. СТАНДОТКЛОН доступен в Excel 2007 и предыдущих версиях. Однако СТАНДОТКЛОН.П и СТАНДОТКЛОН.С доступны только в Excel 2010 и последующих версиях. читать далее
- ФормулаФормулаСтандартное отклонение выборки относится к статистической метрике, которая используется для измерения степени отклонения случайной величины от среднего значения выборки.Подробнее о Стандартное отклонение выборки Стандартное отклонение выборкиСтандартное отклонение выборки относится к статистической метрике, используемой для измерения степень отклонения случайной величины от среднего значения выборки.Подробнее
- Рассчитать стандартное отклонение портфеляРассчитать стандартное отклонение портфеляСтандартное отклонение портфеля относится к волатильности портфеля, рассчитанной на основе трех основных факторов: стандартного отклонения каждого из активов, присутствующих в общем портфеле, соответствующего веса этого отдельного актива и корреляции между каждой парой активы портфеля.Подробнее
- Сравнить — дисперсия и стандартное отклонение. Сравнить — дисперсия и стандартное отклонение. Дисперсия — это числовое значение, которое определяет изменчивость каждого наблюдения от среднего арифметического, а стандартное отклонение — это мера, позволяющая определить, насколько разбросаны наблюдения от среднего арифметического. читать далее
- Простая случайная выборкаПростая случайная выборкаПростая случайная выборка — это процесс, в котором каждый предмет или объект в генеральной совокупности имеет равные шансы быть отобранными, и использование этой модели снижает вероятность смещения в сторону конкретных объектов.Подробнее
Relative standard deviation is defined as a percentage standard deviation that calculates how much the data entries in a set are distributed around the mean value. It tells whether the regular standard deviation is a small or high number when compared to the data set’s mean. In other words, it indicates the percentage distribution of the data. If a data set has a greater relative standard deviation, it clearly indicates that the numbers are significantly far off from the meanwhile, a lower value means that the figures are closer than the average. It is also called the coefficient of variation. Its formula is equal to the ratio of the standard deviation of the data set to the mean multiplied by 100. Its unit of measurement is a percentage (%).
Relative Standard Deviation Formula
R = (σ / x̄) × 100
Where,
- R is the relative standard deviation,
- σ is the standard deviation,
- x̄ is the mean of data set.
Sample problems
Problem 1: Calculate the relative standard deviation of the data set: 2, 5, 7, 3, 1.
Solution:
We have,
x̄ = (2 + 5 + 7 + 3 + 1)/5 = 3.6
σ = √((2 – 3.6)2 + (5 – 3.6)2 + (7 – 3.6)2 + (3 – 3.6)2 + (1 – 3.6)2)/(5 – 1)
= √(23.2/4)
= 2.4
Using the formula we get,
R = (σ / x̄) × 100
= (2.4/3.6) × 100
= 66.9%
Problem 2: Calculate the relative standard deviation of the data set: 4, 7, 1, 3, 6.
Solution:
We have,
x̄ = (4 + 7 + 1 + 3 + 6)/5 = 4.2
σ = √((4 – 4.2)2 + (7 – 4.2)2 + (1 – 4.2)2 + (3 – 4.2)2 + (6 – 4.2)2)/(5 – 1)
= √(22.8/4)
= 2.38
Using the formula we get,
R = (σ / x̄) × 100
= (2.38/4.2) × 100
= 56.84%
Problem 3: Calculate the relative standard deviation of the data set: 5, 9, 3, 6, 4.
Solution:
We have,
x̄ = (5 + 9 + 3 + 6 + 4)/5 = 5.4
σ = √((5 – 5.4)2 + (9 – 5.4)2 + (3 – 5.4)2 + (6 – 5.4)2 + (4 – 5.4)2)/(5 – 1)
= √(21.2/4)
= 2.30
Using the formula we get,
R = (σ / x̄) × 100
= (2.30/5.4) × 100
= 42.63%
Problem 4: Calculate the standard deviation of the data set if the relative deviation is 45% and the mean is 6.
Solution:
We have,
x̄ = 6
R = 45%
Using the formula we get,
R = (σ / x̄) × 100
=> σ = Rx̄/100
=> σ = (45 × 6)/100
=> σ = (270)/100
=> σ = 27
Problem 5: Calculate the standard deviation of the data set if the relative deviation is 67% and the mean is 3.4.
Solution:
We have,
x̄ = 3.4
R = 67%
Using the formula we get,
R = (σ / x̄) × 100
=> σ = Rx̄/100
=> σ = (67 × 3.4)/100
=> σ = (227.8)/100
=> σ = 22.78
Problem 6: Calculate the mean of the data set if the relative deviation is 47% and the standard deviation is 10.
Solution:
We have,
σ = 10
R = 47%
Using the formula we get,
R = (σ / x̄) × 100
=> x̄ = (σ / R) × 100
=> x̄ = (10/47) × 100
=> x̄ = 21.2
Problem 7: Calculate the mean of the data set if the relative deviation is 78% and the standard deviation is 1.5.
Solution:
We have,
σ = 1.5
R = 78%
Using the formula we get,
R = (σ / x̄) × 100
=> x̄ = (σ / R) × 100
=> x̄ = (1.5/78) × 100
=> x̄ = 1.92
Last Updated :
25 Jun, 2022
Like Article
Save Article
17 авг. 2022 г.
читать 2 мин
Относительное стандартное отклонение — это мера стандартного отклонения выборки относительно среднего значения выборки для данного набора данных.
Он рассчитывается как:
Относительное стандартное отклонение = s / x * 100%
куда:
- s: стандартное отклонение выборки
- x : выборочное среднее
Эта метрика дает нам представление о том, насколько близко наблюдения сгруппированы вокруг среднего значения.
Например, предположим, что стандартное отклонение набора данных равно 4. Если среднее значение равно 400, то относительное стандартное отклонение равно 4/400 * 100% = 1%. Это означает, что наблюдения плотно сгруппированы вокруг среднего значения.
Однако набор данных со стандартным отклонением 40 и средним значением 400 будет иметь относительное стандартное отклонение 10%. Это означает, что наблюдения гораздо более разбросаны вокруг среднего значения по сравнению с предыдущим набором данных.
В этом руководстве приведен пример расчета относительного стандартного отклонения в Excel.
Пример: относительное стандартное отклонение в Excel
Предположим, у нас есть следующий набор данных в Excel:

Следующие формулы показывают, как рассчитать выборочное среднее, выборочное стандартное отклонение и относительное выборочное стандартное отклонение набора данных:
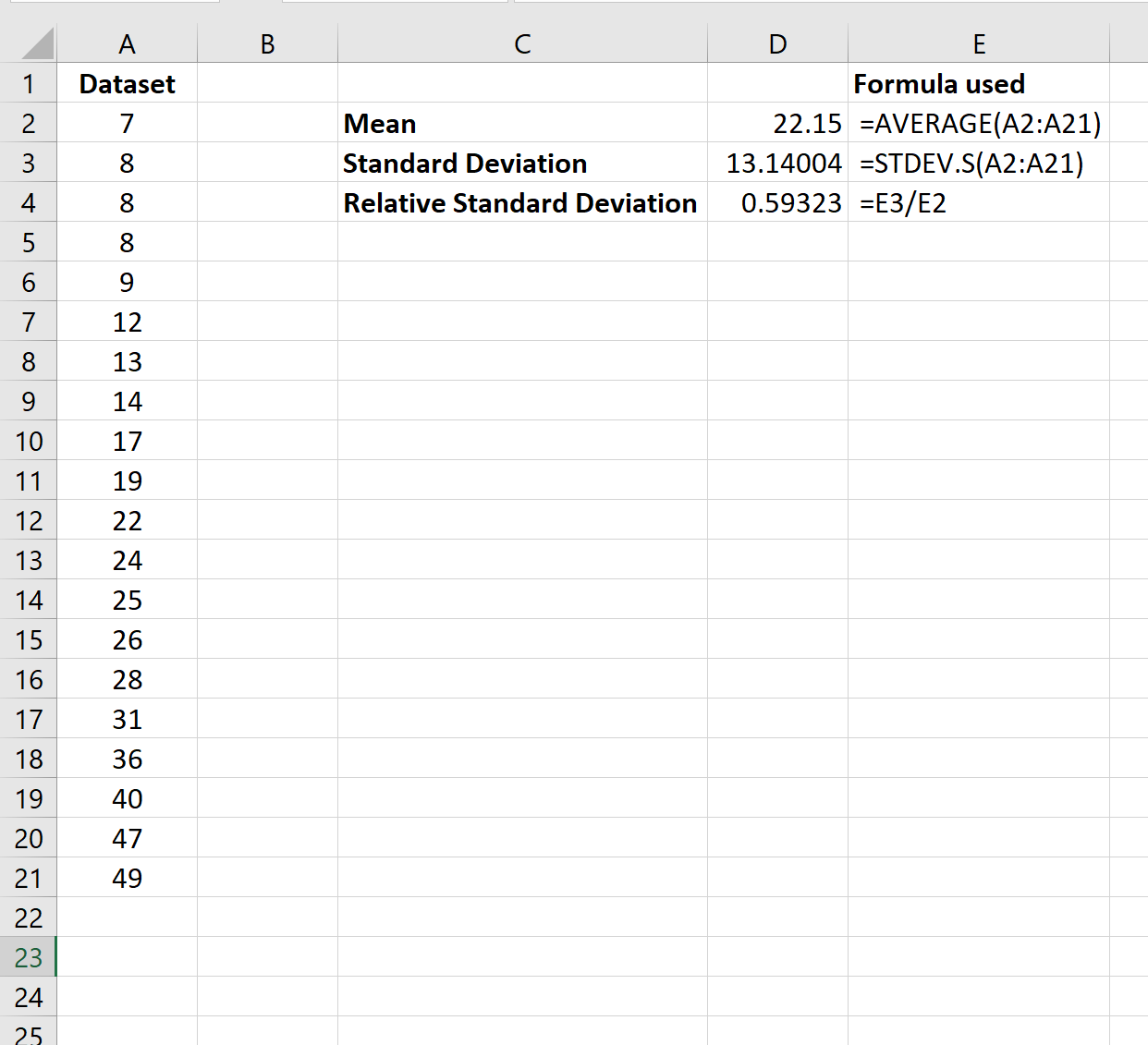
Относительное стандартное отклонение оказывается равным 0,59 .
Это говорит нам о том, что стандартное отклонение набора данных составляет 59% от размера среднего значения набора данных. Это число довольно велико, что указывает на то, что значения довольно сильно разбросаны вокруг среднего значения выборки.
Если у нас есть несколько наборов данных, мы можем использовать одну и ту же формулу для расчета относительного стандартного отклонения (RSD) для каждого набора данных и сравнения RSD по наборам данных:
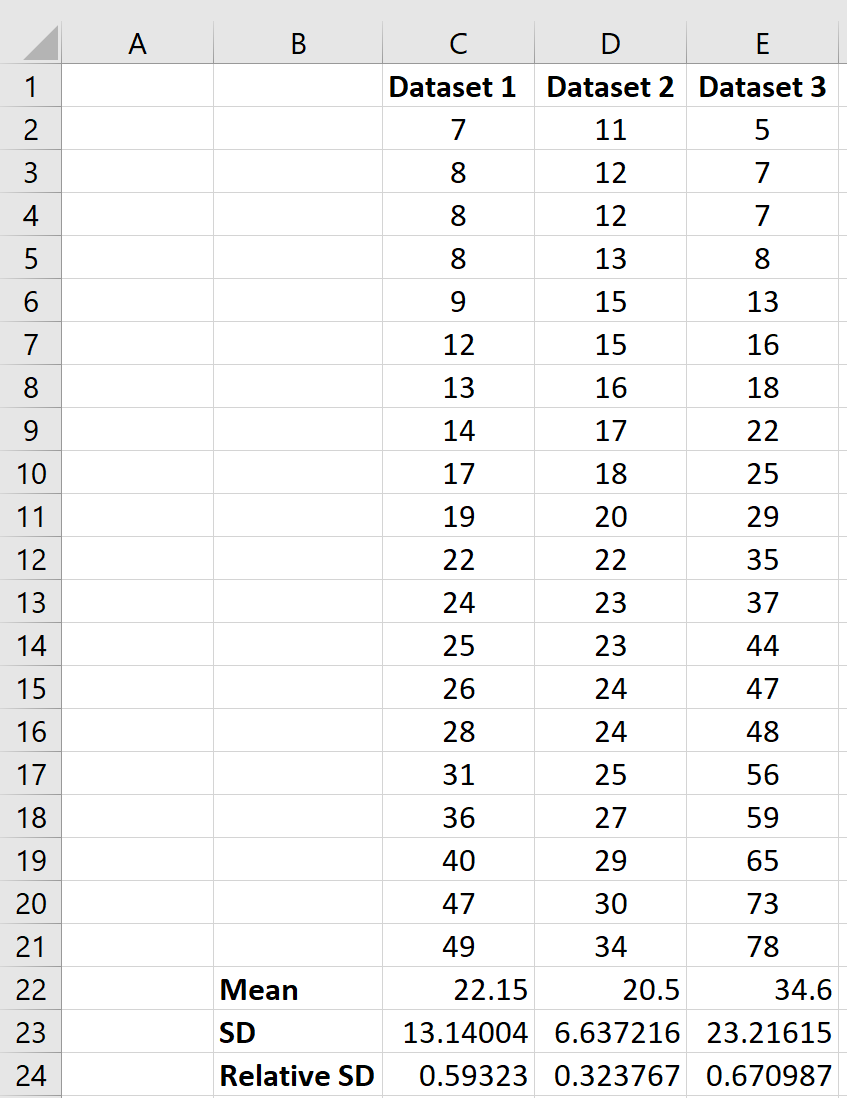
Мы видим, что набор данных 3 имеет наибольшее относительное стандартное отклонение, что указывает на то, что значения в этом наборе данных наиболее разбросаны по отношению к среднему значению набора данных.
И наоборот, мы видим, что набор данных 2 имеет наименьшее относительное стандартное отклонение, что указывает на то, что значения в этом наборе данных наименее разбросаны по отношению к среднему значению этого конкретного набора данных.
Вы можете найти больше руководств по Excel здесь .
- Формула относительного стандартного отклонения

Формула относительного стандартного отклонения (Содержание)
- Формула относительного стандартного отклонения
- Примеры формул относительного стандартного отклонения (с шаблоном Excel)
- Калькулятор формулы относительного стандартного отклонения
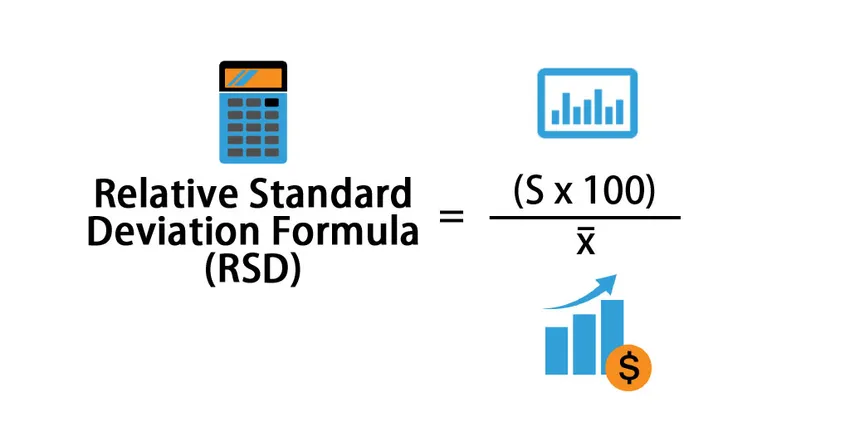
Формула относительного стандартного отклонения
Стандартное отклонение помогает нам понять ценность данных Группы; дисперсия каждого из данных по группе в среднем. Есть данные, близкие к среднему по группе, и есть данные, значение которых выше среднего по группе. Относительное стандартное отклонение – это расчет точности анализа данных. Относительное стандартное отклонение рассчитывается путем деления стандартного отклонения группы значений на среднее значение. RSD выводится из стандартного отклонения и с помощью различных наборов данных, полученных из текущего выборочного теста, проведенного конкретной группой исследований и разработок.
Формула для относительного стандартного отклонения
Relative Standard Deviation (RSD) = (S * 100) / x¯
Где,
- RSD = Относительное стандартное отклонение
- S = стандартное отклонение
- x¯ = среднее значение данных.
Примеры формул относительного стандартного отклонения (с шаблоном Excel)
Давайте рассмотрим пример, чтобы лучше понять расчет относительного стандартного отклонения.
Вы можете скачать этот шаблон относительного стандартного отклонения здесь – шаблон относительного стандартного отклонения
Формула относительного стандартного отклонения – пример № 1
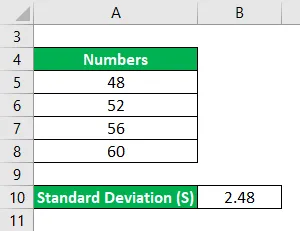
Рассчитайте относительное стандартное отклонение для следующего набора чисел: 48, 52, 56, 60, где стандартное отклонение составляет 2, 48.
Решение:
Среднее значение выборки рассчитывается как:
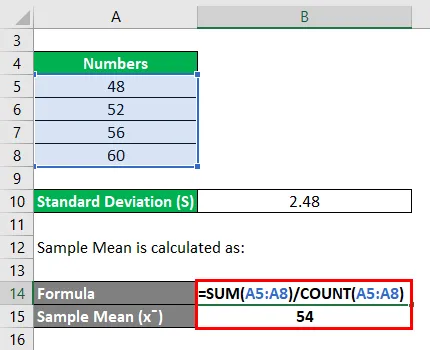
- Среднее значение выборки = (48 + 52 + 56 + 60) / 4
- Образец Среднее = 216/4
- Образец Среднее = 54
Относительное стандартное отклонение рассчитывается по формуле, приведенной ниже
Относительное стандартное отклонение (RSD) = (S * 100) / x
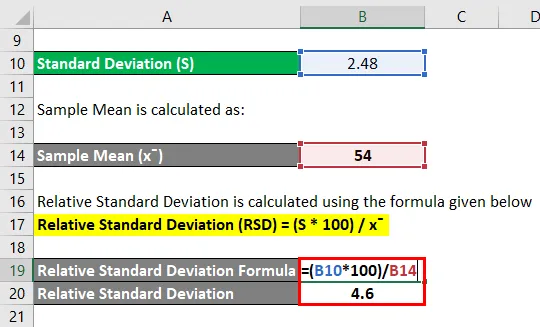
- Относительное стандартное отклонение = (2, 48 * 100) / 54
- Относительное стандартное отклонение = (248) / 54
- Относительное стандартное отклонение = 4, 6
Таким образом, RSD для указанного числа составляет 4, 6.
Формула относительного стандартного отклонения – пример № 2
Рассчитайте относительное стандартное отклонение для следующего набора чисел: 10, 20, 30, 40 и 50, где стандартное отклонение равно 10.
Решение:
Среднее значение выборки рассчитывается как:
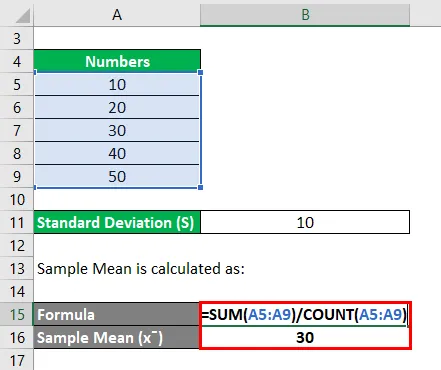
- Образец Среднее = (10 + 20 + 30 + 40 + 50) / 5
- Образец Среднее = 150/5
- Образец Среднее = 30
Относительное стандартное отклонение рассчитывается по формуле, приведенной ниже
Относительное стандартное отклонение (RSD) = (S * 100) / x
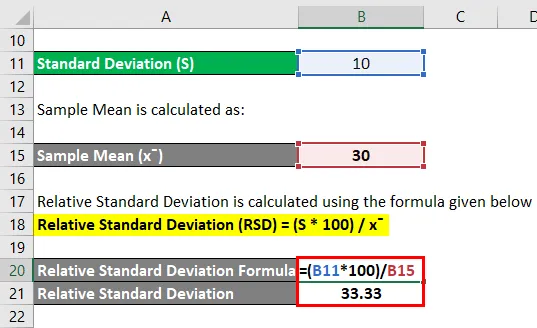
- Относительное стандартное отклонение = (10 * 100) / 30
- Относительное стандартное отклонение = 1000/30
- Относительное стандартное отклонение = 33, 33
Таким образом, RSD для указанного числа составляет 33, 33.
Формула относительного стандартного отклонения – пример № 3
Рассчитайте относительное стандартное отклонение для следующего набора чисел: 8, 20, 40 и 60, где стандартное отклонение равно 5.
Решение:
Среднее значение выборки рассчитывается как:
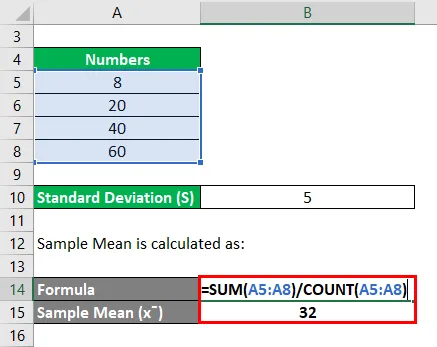
- Образец Среднее = (8 + 20 + 40 + 60) / 4
- Образец Среднее = 128/4
- Образец Среднее = 32
Относительное стандартное отклонение рассчитывается по формуле, приведенной ниже
Относительное стандартное отклонение (RSD) = (S * 100) / x
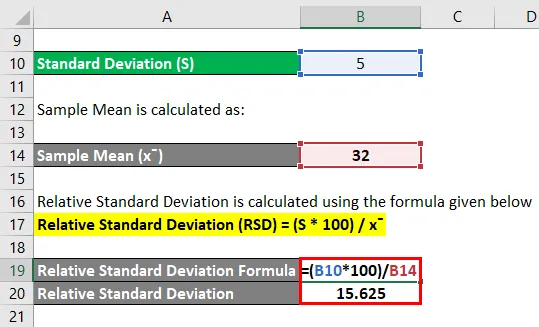
- Относительное стандартное отклонение = (5 * 100) / 32
- Относительное стандартное отклонение = 500/32
- Относительное стандартное отклонение = 15, 625
Таким образом, RSD для указанного числа составляет 15, 625 .
объяснение
Относительное стандартное отклонение получается путем умножения стандартного отклонения на 100 и деления результата на среднее значение по группе. Он выражается в процентах и в основном обозначает, как различные числа располагаются относительно среднего значения. Он обычно используется для соотношения риска и доходности по нескольким инвестиционным предложениям, основанным на его исторической доходности.
Если конкретный продукт имеет более высокое относительное стандартное отклонение, это означает, что числа очень широко распространены от его среднего значения. Иногда, в соответствии с требованиями продукта, команда RSD нуждается в определенных данных, которые на самом деле очень далеки от среднего RSD. В этих случаях учитываются данные, которые хорошо отклоняются от ОСБ.
В случае обратной ситуации, то есть более низкого относительного стандартного отклонения, числа ближе, чем его среднее значение, и также известны как коэффициент вариации. Как правило, это дает представление о реальных прогнозах в рамках данного набора данных.
RSD указывает нам, является ли «обычное» стандартное отклонение минимальным или максимальным с точки зрения количества по сравнению со средним значением из ряда набора данных. Регулярное стандартное отклонение дает четкое представление о распределении баллов по среднему (среднему). Например, при среднем балле 50 и стандартном отклонении 10 большинство людей ожидают, что большинство баллов будет находиться в диапазоне от 40 до 60 и что почти все баллы упадут между 30 и 70.
Актуальность и использование формулы относительного стандартного отклонения
- Относительное стандартное отклонение широко используется при интерпретации отношений между статистическими данными в различных сегментах. Статистика и аналитика стали неотъемлемой частью бизнес-домов, и для прогнозирования ожидаемого спроса на конкретные данные компания должна выбрать различные статистические инструменты. Одним из них является формула относительного стандарта, которая измеряет вероятный спрос на различных этапах на основе исторических статистических данных и кратких сведений об ожидаемом объеме производства.
- В случае каких-либо исследовательских продуктов, не всегда возможно понять точный результат командой RSD. Таким образом, ситуации и результаты обусловлены огромными неопределенностями и вероятностями. Таким образом, консервативный игрок будет достигать среднего уровня. Таким образом, RSD устранит результаты, которые слишком далеко по сравнению с фактическим RSD. Результаты, которые закрыты для ОСБ, будут приняты во внимание.
- Это один из основных инструментов, который показывает, движется ли цена акций по мере роста Бизнеса или нет. Иногда ценовое движение конкретной акции определяется на основе ценового движения индекса. Если цена движется в противоположном направлении, это можно определить с помощью RSD.
- В мире инвестиций преобладают различные аналитические и статистические данные, за которыми следует возврат средств из определенного фонда, управляемого различными фондами. Различная доходность от разных фондовых фондов указывает на диверсификацию и динамику инвестиций. Не всегда можно нормальному человеку выбрать лучшие средства. Таким образом, чтобы оптимизировать конкретный фонд в соответствии со своими требованиями, обычный человек может обратиться к методам ОСБ, применяемым для стандартного отклонения.
- RSD – это усовершенствованная форма Аналитического инструмента, который помогает конечному пользователю понять тенденции, спрос на продукцию и ожидаемые предпочтения клиентов в различных отраслях. Таким образом, чтобы упростить требования, RSD помогает обнаруживать фактические результаты из разных возможностей.
Калькулятор формулы относительного стандартного отклонения
Вы можете использовать следующий калькулятор относительного стандартного отклонения
| S | |
| Икс | |
| Формула относительного стандартного отклонения (RSD) | |
| Формула относительного стандартного отклонения (RSD) | знак равно |
Рекомендуемые статьи
Это было руководство к формуле относительного стандартного отклонения. Здесь мы обсудим, как рассчитать относительное стандартное отклонение вместе с практическими примерами. Мы также предоставляем калькулятор относительного стандартного отклонения с загружаемым шаблоном Excel. Вы также можете посмотреть следующие статьи, чтобы узнать больше –
- Как рассчитать коэффициент Шарпа по формуле
- Формула чистой стоимости реализации
- Руководство по формуле снижения относительного риска
- Примеры формулы отклонения портфеля
1.
Статистическая обработка и представление
результатов
количественного анализа
Выборка
(выборочная совокупность) — совокупность
ограниченного числа статистически
эквивалентных вариант, рассматриваемая
как случайная выборка из генеральной
совокупности. Другими словами, выборочная
совокупность — это совокупность
результатов измерений аналитических
сигналов или определяемых содержаний,
рассматриваемая как случайная выборка
из генеральной совокупности, полученной
в указанных условиях.
Объем
выборки — число
вариант n
составляющих выборку.
При
статистической обработке результатов
количественного анализа используют
выборку, описываемую распределением
Стьюдента.
Распределением
Стьюдента предпочтительно пользоваться
при объеме выборки п<20
Расчет
метрологических параметров.
На
практике в количественном анализе
обычно проводят не бесконечно большое
число определений, а п
=
5—6 независимых определений, т. е. имеют
выборку (выборочную совокупность)
объемом 5—6 вариант. В оптимальном
случае (при
анализе, например, лекарственных
препаратов) рекомендуется
проводить 5 параллельных определений,
т. е. оптимальный рекомендуемый объем
выборки n=5.
При
наличии выборки рассчитывают следующее
метрологические параметры в соответствии
с распределением Стьюдента.
Среднее,
т. е.
среднее значение определяемой величины,
согласно (1.1),
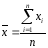
(1.1)
Среднее
из конечной выборки отличается от
действительного значения а
(которое
обычно не известно) и зависит от объема
выборки
lim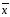
→
а,
при
n→
∞
Отклонение:
di
= xi
–
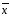
(1.4)
di
— случайное отклонение i-й
варианты xi
от среднего
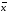 .
.
Дисперсия
V
(иногда
ее обозначают как s2)
показывает
рассеяние вариант относительно
среднего и характеризует воспроизводимость
анализа. Рассчитывается по формуле
(1.5):
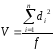
где
f=
п-1
— число степеней
свободы.
Если
известно
действительное значение определяемой,
величины а
(или
истинное значение определяемой величины
µ), например, при работе со стандартным
образцом, то среднее
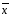
принимают равным а
(или µ); тогда число степеней свободы f
= п.
Дисперсия
среднего V
равна:
V
=
V/n
Стандартное
отклонение (или среднее квадратичное
отклонение) s
— характеристика рассеяния вариант
относительно среднего. Она рассчитывается
как корень квадратный из дисперсии V,
взятый со знаком плюс:
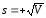
Очевидно,
V
= s2.
Стандартное отклонение s,
как и дисперсия V
характеризует воспроизводимость
результатов количественного анализа.
Стандартное
отклонение среднего s
определяется
как
s
=
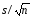
(«старое»
название — средняя квадратичная ошибка
среднего арифметического).
Относительное
стандартное отклонение sr
—
это отношение стандартного отклонения
к среднему значению:
sr
= s/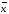
Чем
меньше sr
тем
лучше воспроизводимость анализа.
Доверительный
интервал (доверительный интервал
среднего) —
интервал, в котором с заданной доверительной
вероятностью Р
находится
действительное значение определяемой
величины (генеральное среднее):
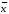
±
∆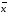 ,
,
(1.7)
где
∆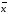
—полуширина
доверительного интервала.
Доверительная
вероятность Р —
вероятность нахождения действительного
значения определяемой величины а
в пределах доверительного интервала.
Изменяется от 0 до 1 или от 0% до 100%. В
количественном анализе при контроле
качества препаратов доверительную
вероятность чаще всего принимают равной
P=
0,95 = 95% и обозначают как Р0,95.
При оценке правильности методик или
методов анализа доверительную вероятность
обычно считают равной Р=
0,99=99%.
Полуширину
доверительного интервала ∆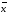
находят по формуле (1.8):
∆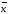
=
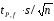
(1.8)
где
tP,f
—
коэффициент нормированных отклонений
(коэффициент Стьюдента, функция Стьюдента,
критерий Стьюдента), который зависит
от доверительной вероятности Р
и
числа степеней свободы f=
п
– 1,
т. е. от числа проведенных определений.
Численные
значения tP,f
рассчитаны для различных возможных
величин Р
и
n
и
табулированы
в справочниках.
В
табл. 1.1 приведены численные значения
коэффициента Стьюдента, рассчитанные
при разных величинах п
и Р.
Чем
больше n,
тем меньше tP,f
. Однако
при n
> 5 уменьшение tP,f
уже сравнительно невелико, поэтому на
практике обычно считают достаточным
проведение пяти параллельных определений
(п
=
5).
Относительная
(процентная) ошибка среднего результата
ε
рассчитывается
по формуле (1.9):
ε
= (∆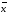 /
/ )∙100%.
)∙100%.
;
(1.9)
Исключение
грубых промахов.
Некоторые
из результатов единичных определений
(вариант), входящих в выборочную
совокупность, могут заметно отличаться
от величин остальных вариант и вызывать
сомнения в их достоверности. Для того
чтобы статистическая обработка
результатов количественного анализа
была достоверной, выборка должна быть
однородной,
т.е.
она не должна быть содержать сомнительные
варианты — так называемые грубые
промахи. Грубые
промахи необходимо исключить из общего
объема выборки, после чего можно проводить
окончательное вычисление статистических
характеристик.
Если
объем выборки невелик 5<
п < 10,
то выявление сомнительных результатов
анализа — исключение
грубых промахов —
чаще всего проводят с
помощью
так называемого Q-критерия
(контрольного
критерия Q),
или Q
–теста.
Для
этого варианты xi
вначале
располагают в порядке возрастания их
численного значения от x1
до
хn
где
n
— объем выборки, т. е. представляют в
виде упорядоченной
выборки. Затем
для крайних вариант — минимальной x1
и
максимальной хn
—
вычисляют величину Q
по
формулам (1.10):
Q1
=(x2-x1)/R;
Qn
= (xn
– xn-1)/R
(1.10)
где
х2
и
xn-1
—
значения вариант, ближайших по величине
к крайним вариантам, а R
=
(xn
– x1)
R
—
размах
варьирования, т.
е. разность между максимальным хn
и
минимальным x1
значениями
вариант, составляющих выборку.
Рассчитанные
значения Q1
и
Qn
сравнивают
с табличными при заданных n
и доверительной вероятности Р.
Если
рассчитанные значения Q1
или
Qn
(или
оба) оказываются больше табличных
Q1
> Qтабл
или Qn
> Qтабл
то
варианты х1
или
хп
(или
обе) считаются грубыми промахами и
исключаются из выборки.
Для
полученной выборки меньшего объема
проводят аналогичные расчеты до тех
пор, пока не будут исключены все грубые
промахи, так что окончательная выборка
окажется однородной и не будет содержать
грубые промахи.
В
табл. 1.2 приведены численные величины
контрольного критерия Q
для
Р
=
0,90—0,99 и п=
3—10.
Таблица
1.1. Численные значения коэффициента
Стьюдента tP,f
для
расчета границ доверительного интервала
при доверительной вероятности P,
объеме выборки n,
числе степеней свободы f=
п
-1
|
п |
f |
Значение |
||||
|
0,80 |
0,90 |
0,95 |
0,99 |
0,999 |
||
|
2 |
1 |
3,08 |
6,31 |
12,07 |
63,7 |
636,62 |
|
3 |
2 |
1,89 |
2,92 |
4,30 |
9,92 |
31,60 |
|
4 |
3 |
1,64 |
2,35 |
3,18 |
5,84 |
12,94 |
|
5 |
4 |
1,53 |
2,13 |
2,78 |
4,60 |
8,61 |
|
6 |
5 |
1,48 |
2,02 |
2,57 |
4,03 |
6,86 |
|
7 |
6 |
1,44 |
1,94 |
2,45 |
3,71 |
5,96 |
|
8 |
7 |
1,42 |
1,90 |
2,36 |
3,50 |
5,41 |
|
9 |
8 |
1,40 |
1,86 |
2,31 |
3,36 |
5,04 |
|
10 |
9 |
1,38 |
1,83 |
2,26 |
3,25 |
4,78 |
|
11 |
10 |
1,37 |
1,81 |
2,23 |
3,17 |
4,59 |
|
12 |
11 |
1,36 |
1,80 |
2,20 |
3,11 |
4,49 |
|
13 |
12 |
1,36 |
1,78 |
2,18 |
3,06 |
4,32 |
|
14 |
13 |
1,35 |
1,77 |
2,16 |
3,01 |
4,22 |
|
15 |
14 |
1,35 |
1,76 |
2,14 |
2,98 |
4,14 |
|
16 |
15 |
1,34 |
1,75 |
2,12 |
2,95 |
4,07 |
|
17 |
16 |
1,34 |
1,75 |
2,11 |
2,92 |
4,02 |
|
18 |
17 |
1,33 |
1,74 |
2,10 |
2,90 |
3,97 |
|
19 |
18 |
1,33 |
1,73 |
2,09 |
2,88 |
3,92 |
|
20 |
19 |
1,33 |
1,73 |
2,09 |
2,86 |
3,88 |
|
21 |
20 |
1,33 |
1,73 |
2,09 |
2,85 |
3,85 |
|
22 |
21 |
1,32 |
1,72 |
2,08 |
2,83 |
3,82 |
|
23 |
22 |
1,32 |
1,72 |
2,07 |
2,82 |
3,79 |
|
24 |
23 |
1,32 |
1,71 |
2,07 |
2,81 |
3,77 |
|
25 |
24 |
1,32 |
1,71 |
2,06 |
2,80 |
3,75 |
|
26 |
25 |
1,32 |
1,71 |
2,06 |
2,79′ |
3,73 |
|
27 |
26 |
1,32 |
1,71 |
2,06 |
2,78 |
3,71 |
|
28 |
27 |
1,31 |
1,70 |
2,05 |
2,77 |
3,70 |
|
29 |
28 |
1,31 |
1,70 |
2,05 |
2,76 |
3,67 |
|
30 |
29 |
1,31 |
1,70 |
2,05 |
2,76 |
3,66 |
|
31 |
30 |
1,31 |
1,70 |
2,04 |
2,75 |
3,65 |
|
41 |
40 |
1,30 |
1,68 |
2,02 |
2,70 |
3,55 |
|
61 |
60 |
1,30 |
1,67 |
2,00 |
2,66 |
3,46 |
|
121 |
120 |
1,29 |
1,66 |
1,98 |
2,62 |
3,37 |
|
∞ |
∞ |
1,28 |
1,64 |
1,96 |
2,58 |
3,29 |
При
проведении Q–mecma
доверительную вероятность чаще всего
принимают равной Р=0,90
= 90%.
Если
из двух крайних вариант х1
и
хп
только
одна вызывает сомнение, то Q-тест
можно проводить лишь в отношении этой
сомнительной варианты.
Таблица
1.2. Численные значения Q-критерия
при доверительной вероятности
Р
и
объеме выборки п
|
п |
||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0,90 |
0,94 |
0,76 |
0,64 |
0,56 |
0,51 |
0,47 |
0,44 |
0,41 |
|
0,95 |
0,98 |
0,85 |
0,73 |
0,64 |
0,59 |
0,54 |
0,51 |
0,48 |
|
0,99 |
0,99 |
0,93 |
0,82 |
0,74 |
0,68 |
0,63 |
0,60 |
0,57 |
|
Примечание. |
Пример.
Пусть
при проведении 5 параллельных анализов
содержание определяемого компонента
в анализируемом образце найдено равным,
%: 3,01; 3,03; 3,04; 3,05 и 3,11. Установите, имеются
ли грубые промахи или же рассматриваемая
выборка однородна.
Решение.
Очевидно,
что сомнительным значением может быть
только одно, равное 3,11. Используем Q
-тест.
Согласно (1.10), можно записать:
Qрассч
= (3,11 – 3,05) / (3,11 – 3,01) = 0,60.
Из
табл. 1.2 при п
=
5 и Р
=
0,90 находим Qтa6л
= 0,64. Поскольку
Qрассч
= 0,60 <
Qтабл
= 0,64,
то
значение варианты 3,11 не является грубым
промахом и не отбрасывается.
Как
отмечалось выше, обычно при проведении
количественного анализа (например,
лекарственных препаратов и т. п. образцов)
рекомендуется объем выборки (число
единичных параллельных определений),
равный п
=
5. В таких случаях грубые промахи устраняют
с использованием Q-теста,
как вписано выше.
Если
объем выборки равен 3 или 4,. т. е.,
n
< 5, то применение Q-теста
не рекомендуется.
Если
объем выборки п
≥
10,
то для устранения грубых промахов (для
проверки однородности выборки) поступают
следующим образом.
Вначале
по результатам единичных независимых
определений предварительно рассчитывают
по формулам (1.1), (1.4), (1.6) среднее значение,
отклонения di
для
всех вариант, стандартное отклонение
s.
Затем
сравнивают абсолютную величину |di|,
и
численное значение 3s.
Если для всех вариант окажется, что
|di|
≤ 3s
(1.11)
то
грубые промахи отсутствуют; выборка
однородна. Если же условие (1.11) выполняется
не для всех вариант, то те варианты, для
которых это условие не выполняется,
признаются грубыми промахами при Р
=
0,95 = 95% и исключаются из общей выборочной
совокупности. Получают выборку меньшего
объема, для которой снова повторяют
весь цикл вычислений и с использованием
соотношения (1.11) снова выясняют наличие
или отсутствие грубых промахов. Так
поступают до тех пор, пока не устранят
все грубые промахи и выборка окажется
однородной.
Объем
выборки больше десяти (п
> 10)
используют чаще всего тогда, когда
оценивают воспроизводимость методик
или методов анализа.
Представление
результатов количественного анализа.
При
представлении результатов количественного
анализа обычно указывают и рассчитывают
следующие статистические характеристики:
xi
,
— результаты
единичных определений (варианты);
п
—
число независимых параллельных
определений (объем выборки);
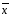
— среднее
значение определяемой величины;
s
—
стандартное отклонение;
∆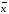
— полуширину
доверительного интервала (с указанием
значения доверительной вероятности
Р);
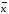
±
∆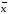 —
—
доверительный интервал (доверительный
интервал среднего);
ε
—относительную (процентную) ошибку
среднего результата.
Эти
характеристики составляют необходимый
и достаточный минимум величин, описывающих
результаты количественного анализа,
при условии, что систематические
ошибки устранены или они меньше случайных.
Иногда
дополнительно указывают также
дисперсию
V
=
s2,
дисперсию
среднего V
стандартное
отклонение среднего s ,
,
относительное
стандартное отклонение sr.
Однако
их перечисление необязательно, так как
все они легко вычисляются из величин,
приведенных выше.
Пример
статистической обработки и представления
результатов количественного анализа.
Пусть
содержание определяемого компонента
в анализируемом образце, найденное в
пяти параллельных единичных определениях
(п
=
5), оказалось равным, %: 3,01; 3,04; 3,08; 3,16 и
3,31. Известно, что систематическая ошибка
отсутствует. Требуется провести
статистическую обработку результатов
количественного анализа (оценить их
воспроизводимость) при доверительной
вероятности, равной Р
=
0,95.

