 |
Два одинаковых груза массой M каждый, соединенные пружиной, лежат на шероховатой горизонтальной плоскости в поле тяжести земли. Какую минимальную горизонтальную силу необходимо приложить к правому грузу, чтобы пришел в движение левый груз? Коэффициент трения грузов о плоскость μ. В начальном состоянии пружина не деформирована. |
Решение
Для того, чтобы сдвинуть тело 2 с места, необходимо приложить к нему горизонтально силу, которая превышает максимальную силу трения покоя, которая в данном случае равна:
В качестве силы, которая сдвигает это тело, выступает сила упругости пружин, модуль которой, согласно закону Гука, равен:
где k — жесткость пружины, Δx — ее удлинение.
Таким образом, необходимо удлинить пружину (т. е. сдвинуть тело 1) на величину:
Если мы приложим к телу 1 постоянную силу F таким образом его движение не будет равноускоренным, так как на него действует, помимо постоянной силы трения Fтр = μmg, сила упругости Fупр = kΔx , которая не является постоянной.
Качественно движение тела 1, при неподвижном теле 2, можно описать следующим образом. Если сила F по модулю превышает силу трения Fmp1, то тело начнет двигаться с положительным ускорением, при этом сила упругости начнет возрастать, в некоторой точке Fупр превысит разность F − Fтp1, и ускорение изменит свой знак. Тело 1 еще некоторое время будет двигаться в положительном направлении и затем остановится.
Максимальная деформация пружины будет в момент остановки тела. Эту максимальную деформацию Δx1 можно найти, воспользовавшись энергетическими соображениями: работа постоянной силы F числено равна изменению энергии пружины плюс работа силы трения. Кинетическая энергия тела в начальный и конечный моменты движения равна нулю.
| F • Δx1 = μmg • Δx1 + | k(Δx1)2 | , (4) |
| 2 |
или
Очевидно, что для ответа на поставленный в задаче вопрос следует положить в (5) Δx1 = Δx, определяемое в (3). Окончательно получим:
| F = μmg + | μmg | = | 3 | μmg. (6) |
| 2 | 2 |
Обратите внимание на два обстоятельства:
- Искомая сила равна сумме силы трения, действующей на тело 1, и половине (!) силы трения, действующей на тело 2.
- Ответ не зависит от величины жесткости пружины. Подумайте, как объяснить эти обстоятельства в том случае, когда жесткость пружины очень велика (скажем, вместо пружины металлический стержень).
Не объясняет ли данная задача старую бурлацкую песню «поддернем, поддернем, да ухнем!»?
Далее: угол максимального отклонения нити [тема: задачи на минимум и максимум]
Брусок
массой 1 кг находится на наклонной плоскости с углом наклона 30°. Какую минимальную горизонтальную
силу необходимо приложить к бруску, чтобы он остался в покое, если коэффициент
трения между ним и поверхностью равен 0,2?
Решение.
Систему
отсчета свяжем с поверхностью Земли и будем считать ее инерциальной.
Начало
координат выберем в точке, совпадающей с центром масс бруска, ось OX направим вверх вдоль наклонной
плоскости, а ось OY
– вверх перпендикулярно
к ней.
В качестве физической
системы рассмотрим брусок. Допустим, что его можно принять за материальную
точку. Земля, наклонная плоскость, воздух и источник силы, которую необходимо
найти, по отношению к выделенной физической системе являются внешними телами.
Взаимодействия
выделенной системы и внешних тел можно описать при помощи соответствующих сил.
Выделенная физическая система является незамкнутой, кроме того, относительно
выбранной инерциальной системы отсчета она находится в состоянии равновесия
(покоя). Поэтому геометрическая сумма сил, действующих на рассматриваемую
физическую систему, равна нулю (первое условие равновесия под действием внешних
сил в инерциальной системе отсчета).
В
соответствии с результатами анализа физической ситуации, если не учитывать
взаимодействие бруса с воздухом, то на него действуют: сила тяжести mg , направленная перпендикулярно вниз;
сила реакции наклонной плоскости N , направленная перпендикулярно к плоскости; сила трения
покоя Fтр ,направленная вдоль наклонной
плоскости, и сила F
, которую необходимо найти.
Поскольку
брусок в состоянии равновесия, то в соответствии с первым условием равновесия имеем.
Если спроецировать
векторные величины на оси OX
и OY, а также учесть, что брусок не движется
по наклонной плоскости, т.е. Fтр ≤ µN , получим систему уравнений.
Решение этой системы
для случая, когда Fтр направлена вдоль наклонной плоскости.
Если Fтр направлена вниз вдоль наклонной плоскости то получаем.
Минимальное значение силы в первом случае
F1min
и во втором случае F2min .
Из полученных выражений для F1min
и F2min
видно, что F1min
< F2min .
Таким образом,
минимальное значение горизонтальной силы которую необходимо приложить для того,
чтобы он оставался в состоянии покоя будет F2min .
Ответ: F
= 3.3 Н.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
How to find the minimum horizontal force?
-
Thread starter
Angela_vaal -
Start date
Nov 2, 2016 -
-
Tags -
Force
Horizontal
Horizontal force
Minimum
-
- Nov 2, 2016
- #1
Homework Statement
What is the minimum horizontal force F needed to make the box start moving in (Figure 1) ? The coefficients of kinetic and static friction between the box and the floor are 0.28 and 0.39, respectively.
Homework Equations
fk=mu N
fs=mu N
The Attempt at a Solution
Im not sure that the N pointing downward is the normal force or not because I though normal force = 25kg* 9.81m/s2=245?
so would the minimum force be Fs= mu N… (.39)(245)=96?
i just don’t know what the 31 N signifies since it is pointing downward? help please
[/B]
Answers and Replies
- Nov 2, 2016
- #2
The equation you wrote for the normal force would be correct for a block of 25 kg sitting on a flat surface with no other forces acting on it.
- Nov 2, 2016
- #3
- Nov 2, 2016
- #4
- Nov 2, 2016
- #5
When the block is just about ready to slide, as you know, friction force Ff = μsN. So you have to find the normal force N.
- Nov 2, 2016
-
- #6
- Nov 2, 2016
- #7
- Nov 2, 2016
- #8
Now we have an extra force of 31N pushing down on the block, yet the block is still not sinking/merging into the ground, therefore the normal reaction force must again be accounting for this extra force: Nf = weight + extra downward force = 245 + 31 = 276N
As discussed above when the vlock is about to slide: Ff = μsNf
Sub you values in, what do you get?
- Nov 2, 2016
- #9
Let’s say I have a crate sitting on a scale and the scale reads 100 pounds. Now let’s say I throw 5 more 10-pound boxes on top of that crate. What is the normal force acting on the crate? I will give you a hint: The scale knows the answer. That is the same situation you have in your problem. You have a block that has weight and you are adding more weight on top of it.
- Nov 2, 2016
- #10
why are we adding the downward force and not subtracting it?
- Nov 2, 2016
- #11
Forget about the friction force for now. Before you can find the friction force, you have to find the normal force. Once you find the normal force, then you can calculate the friction force. To find the normal force, you have to sum all of the vertical components of force.Let’s say I have a crate sitting on a scale and the scale reads 100 pounds. Now let’s say I throw 5 more 10-pound boxes on top of that crate. What is the normal force acting on the crate? I will give you a hint: The scale knows the answer. That is the same situation you have in your problem. You have a block that has weight and you are adding more weight on top of it.
makes sense! thankyou
- Nov 2, 2016
- #12
Suggested for: How to find the minimum horizontal force?
- Apr 23, 2023
- Oct 17, 2022
- Apr 3, 2023
- Jan 24, 2021
- Mar 30, 2023
- Feb 15, 2022
- Mar 8, 2022
- Apr 6, 2021
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
Условие задачи:
С какой минимальной силой, направленной горизонтально, нужно прижать плоский брусок массой 5 кг к вертикальной плоскости, чтобы он не соскользнул вниз? Коэффициент трения между бруском и стеной 0,1.
Задача №2.1.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=5) кг, (mu=0,1), (F-?)
Решение задачи:
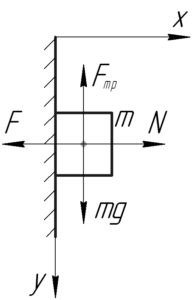Изобразим на схеме плоский брусок и силы, действующие на него: это искомая сила (F), сила нормальной реакции опоры (N), сила тяжести (mg) и сила трения покоя (F_{тр}). Так как брусок не движется, то запишем первый закон Ньютона в проекции на оси декартовой системы координат.
[left{ begin{gathered}
ox:F = N ;;;;(1)hfill \
oy:mg = {F_{тр}} ;;;;(2)hfill \
end{gathered} right.]
Сила трения покоя равна внешней силе, приложенной к бруску (это и видно из выражения (2)), но не превышает силы трения скольжения:
[{F_{тр}} leq mu N]
Условие же минимальности силы (F) соответствует тому крайнему случаю, когда сила трения покоя уже равна силе трения скольжения, но тело ещё не движется.
[{F_{тр}} = mu N]
Подставим эту формулу в выражение (2).
[mg = mu N Rightarrow N = frac{{mg}}{mu }]
Из выражения (1) следует:
[F = frac{{mg}}{mu }]
Подставим численные данные задачи в дробь и посчитаем нужный нам ответ.
[F = frac{{5 cdot 10}}{{0,1}} = 500; Н = 0,5; кН]
Ответ: 0,5 кН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.42 С каким ускорением будет опускаться груз на нити, если сила натяжения нити в 1,25
2.1.44 С какой силой давит человек массой 70 кг на пол лифта, движущегося вниз с ускорением
2.1.45 С какой силой следует придавить тело массой 4,5 кг к вертикальной стене, чтобы
Легче всего решать задачу, если все приложенные к телу силы параллельны – тогда можно получить ответ, используя лишь правило моментов. Если же силы непараллельные, то иногда для получения ответа требуется дополнительно применять второй закон Ньютона.
Параллельные силы
Алгоритм решения задач на правило моментов (параллельные силы)
- Выполнить чертеж. Указать на нем все силы с точкой их приложения и направлением действия. В этом вам поможет таблица.
| Сила | Точка приложения | Направление |
| Сила тяжести, действующая на груз | Центр груза | Вертикально вниз |
| Сила тяжести, действующая на однородный стержень | Центр тяжести | Вертикально вниз |
| Сила тяжести, действующая на неоднородный стержень | Центр масс, положение которого указывают в условии задачи | Вертикально вниз |
| Вес | Точка опоры или подвеса | Вес тела направлен противоположно вектору силы нормальной реакции опоры или вектору силы натяжения подвеса |
| Сила реакции опоры | Точка соприкосновения стержня и опоры | Перпендикулярно вверх |
| Сила натяжения нити | Точка соединения с подвесом | Вдоль оси подвеса |
- Выбрать положение оси вращения. Обычно ось выбирают в месте, где находится неизвестная сила или сила, искать которую не нужно.
- Указать значение плеч. Если в задаче нужно указать некоторое расстояние (к примеру, от центра стержня или от места приложения некоторой силы), то это расстояние следует обозначать за x. Размер плеч сил нужно определять с учетом размеров стержня и расстояния x.
- Записать правило моментов и решить задачу.
Типовы задачи на правило моментов при параллельных силах
| Прямая неоднородная балка длиной l и массой m подвешена за концы на вертикально натянутых тросах. Балка занимает горизонтальное положение. Найдите силу натяжения первого троса T2, если центр тяжести балки находится на расстоянии a от левого конца балки. |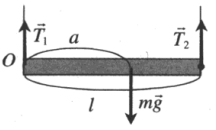 
Для решения задачи в качестве положения оси вращения удобно выбрать точку приложения силы натяжения первого троса (потому что ее искать не нужно). Тогда плечом силы тяжести будет расстояние a, а плечом силы натяжения второго троса — l. Поэтому правило моментов можно записать так: T2l = mga T2 = mga/l |
| Рельс длиной l и массой m поднимают равномерно в горизонтальном положении на двух вертикальных тросах, первый из которых укреплен на конце рельса, а второй — на расстоянии x от другого конца. Определите натяжение второго троса. |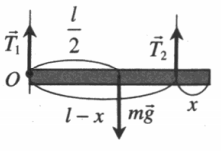 
В этой задаче положение оси вращения также удобно выбрать в точке О, соответствующей точке приложения силы натяжения нити первого троса (так как ее искать не нужно). Тогда плечом силы натяжения второго троса будет служить разность длины рельса и расстояния x, а плечом силы тяжести — половина длины рельса. Поэтому правило моментов примет вид: mgl/2 = T2(l – x) T2 = mgl2(l−x) |
Пример №1. К левому концу невесомого стержня прикреплен груз массой 3 кг (см. рисунок). Стержень расположили на опоре, отстоящей от груза на 0,2 длины. Груз какой массы надо подвесить к правому концу, чтобы стержень находился в равновесии?
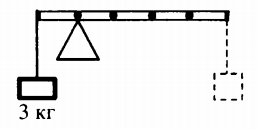
Условие равновесие будет выполняться, если произведение силы тяжести первого груза на ее плечо будет равно произведению силы тяжести второго груза на ее плечо:
Fтяж1d1 = Fтяж2d2
Согласно рисунку, второй груз будет подвешен на расстоянии 0,8 от опоры. Следовательно:
Fтяж2=Fтяж2d1d2=m1gd1d2
m2g=m1gd1d2
m2=m1d1d2=3·0,20,8=0,75 (кг)
Непараллельные силы
Алгоритм решения задач на правило моментов (непараллельные силы)
- Выполнить чертеж и указать все силы. Правильно определить точку приложения и направление сил поможет таблица:
| Сила | Точка приложения | Направление |
| Сила реакции опоры | Точка соприкосновения с опорой | Перпендикулярно плоскости опоры |
| Сила трения покоя | Точка соприкосновения с опорой | В сторону возможного движения |
| Сила тяжести | Центр масс (у однородных тел центр масс совпадает с центром тела) | Вертикально вниз |
| Архимедова сила | Центр масс погруженной части тела | Вертикально вверх |
- Определить плечи сил как кратчайшее расстояние между осью вращения и направлением действия силы.
- Записать правило моментов и решить задачу.
Внимание! Иногда для решения задачи может потребоваться использование второго закона Ньютона в проекциях на оси Ox и Oy.
Типовы задачи на правило моментов при непараллельных силах
| Рабочий удерживает за один конец доску массой m так, что она образует угол α с горизонтом, опираясь о землю другим концом. С какой силой рабочий удерживает доску, если эта сила перпендикулярна доске? |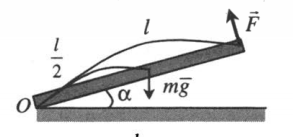 
За точку равновесия примем точку касания доски с землей. Плечо силы тяжести будет равно нижнему катету треугольника, образованного при опускании перпендикуляра к земле из точки приложения этой силы: d1 = l cosα/2 Плечо силы, с которой рабочий поднимает доску, равно длине доски: d2 = l Отсюда: mglcosα2=Fl F=2lmglcosα=2mgcosα |
| В гладкий высокий цилиндрический стакан с внутренним радиусом R помещают карандаш длиной l и массой m. С какой силой действует на стакан верхний конец карандаша? |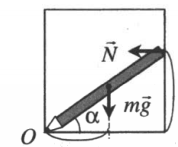 
За точку равновесия примем нижнюю точку карандаша. Сила давления верхнего конца карандаша на стакан по модулю будет равна силе нормальной реакции опоры в этой точке. Поэтому плечо ее силы будет равно произведению длины карандаша на синус угла между ним и дном стакана: d1 = l sinα Минимальным расстоянием между линией действия силы тяжести и точкой равновесия будет половина произведения длины карандаша на косинус угла между ним и дном стакана: d2 = l сosα/2 Отсюда: Nl sinα = mgl сosα/2 N=mglcosα2lsinα Плечо силы тяжести также равно радиусу стакана, а плечо силы реакции опоры можно найти из теоремы Пифагора. Отсюда: N=mgR√l2−4R2 |
| Колесо радиусом R и массой m стоит перед ступенькой высотой h. Какую наименьшую горизонтальную силу надо приложить, чтобы оно могло подняться на ступеньку? Сила трения равна нулю. |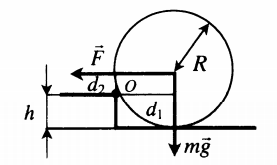 
За точку равновесия примем точку касания колеса со ступенькой. Плечо силы тяжести является катетом треугольника, образованного с радиусом колеса и плечом прикладываемой силы. Плечо этой силы равно разности радиуса и высоты ступеньки. d1=√R2−d22 d2 = R – h Отсюда: mg√R2−d22=F(R−h) F=mg√R2−d22R−h=mg√h(2R−h)R−h |
| Лестница массой m приставлена к гладкой вертикальной стене пол углом α. Найдите силу давления лестницы на стену. Центр тяжести лестницы находится в ее середине. |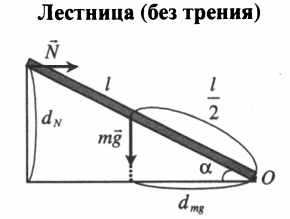 
Плечо силы тяжести равно половине произведения длины лестницы на косинус угла α. Плечо силы реакции опоры равно произведению этой длины на синус α. Поэтому правило моментов записывается так: Nlsinα=mglcosα2 Отсюда: N=mglcosα2lsinα=mg2tanα |
| Лестница длиной l приставлена к идеально гладкой стене под углом α к горизонту. Коэффициент трения между лестницей и полом μ. На какое расстояние x вдоль лестницы может поднять человек, прежде чем лестница начнет скользить? Массой лестницы пренебречь. |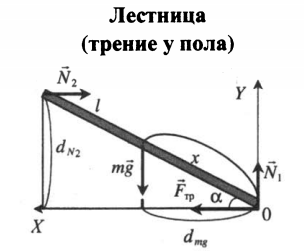 
Правило моментов: mgxcosα=N2lsinα Второй закон Ньютона в проекциях на оси Ox и Oy соответственно: Fтр – N2 = 0 N1 – mg = 0 Сила трения: Fтр = μmg = N2 Следовательно: mgxcosα=μmglsinα x=μmglsinαmgxcosα=μltanα |
| Однородная лестница приставлена к стене. При каком наименьшем угле α между лестницей и горизонтальным полом лестница сохранит равновесие, если коэффициент трения между лестницей и полом μ1, а между лестницей и стеной — μ2? |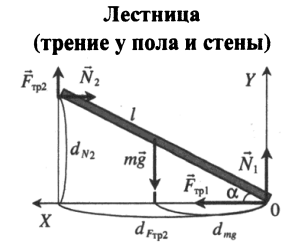 
Правило моментов: mgl2cosα=Fтр2lcosα+N2lsinα Второй закон Ньютона в проекциях на ось Ox: Fтр1 – N2 = 0 μ1N1 – N2 = 0 На ось Oy: Fтр2 + N1 – mg = 0 μ2N2 +N2μ1 = mg N2(μ2+1μ1)=mg N2=mgμ2+1μ1=mgμ1μ1μ2+1 Fтр2=mg−N1=mg−N2μ1=mg−mgμ1μ2+1=mg(1−1μ1μ2+1) mgl2cosα=mg(1−1μ1μ2+1)lcosα+mgμ1μ1μ2+1lcosα Преобразуем выражение и получим: tanα=1−μ1μ21μ1 |
| Какую минимальную горизонтальную силу нужно приложить к верхнему ребру куба массой m, находящегося на горизонтальной плоскости, чтобы перекинуть его через нижнее ребро? |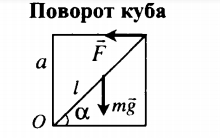 
Правило моментов примет вид: mgl2cosα=Flsinα У куба угол α равен 45 градусам, а синус и косинус этого угла равны. Длины диагонали взаимоуничтожаются. Остается: F=mg2 |
Пример №2. Невесомый стержень длиной 1 м, находящийся в ящике с гладким дном и стенками, составляет угол α = 45о с вертикалью (см. рисунок). К стержню на расстоянии 25 см от его левого конца подвешен на нити шар массой 2 кг. Каков модуль силы N, действующий на стержень со стороны левой стенки ящика?
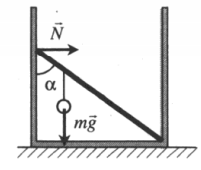
25 см = 0,25 м
Пусть точкой равновесия будет точка касания нижнего конца стержня с дном ящика. Тогда плечом силы тяжести будет:
d1 = (l – 0,25)sinα
Плечом силы реакции опоры будет:
d2 = l cosα
Запишем правило моментов:
mg(l−0,25)sinα=Nlcosα
Отсюда:
N=mg(l−0,25)sinαlcosα
Так как косинус и синус угла 45о равны, получим:
N=mg(l−0,25)l=2·10(1−0,25)1=15 (Н)
Задание EF17982
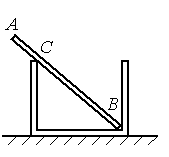Однородный стержень АВ массой 100 г покоится, упираясь в стык дна и стенки банки концом В и опираясь на край банки в точке С (см. рисунок). Модуль силы, с которой стержень давит на стенку сосуда в точке С, равен 0,5 Н. Чему равен модуль горизонтальной составляющей силы, с которой стержень давит на сосуд в точке В, если модуль вертикальной составляющей этой силы равен 0,6 Н? Трением пренебречь.
Ответ:
а) 0,3 Н
б) 0,25 Н
в) 0,6 Н
г) 0,13 Н
Алгоритм решения
- Записать исходные данные и перевести единицы измерения величин в СИ.
- Выполнить чертеж. Выбрать ось вращения. Указать силы и их плечи.
- Использовать второй и третий законы Ньютона, чтобы выполнить общее решение.
- Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
- Масса стержня: m = 100 г.
- Модуль силы, с которой стержень давит на стенку сосуда в точке С: FC = 0,5 Н.
- Модуль вертикальной составляющей силы, с которой стержень давит на сосуду в точке В: FBy = 0,6 Н.
Переведем единицы измерения в СИ:
100 г = 0,1 кг
Выполним чертеж:
Поскольку стержень покоится, согласно второму закону Ньютона, равнодействующая всех сил, действующих на него, должна быть равна нулю. На стержень действует три силы:
- сила тяжести (mg);
- сила реакции опоры в точке С (FC);
- сила реакции опоры в точке В (FВ).
Поэтому:
m→g+→FC+→FB=0
Запишем проекции на оси Ox и Oy соответственно:
FCx=FBx
FCy+FBy=mg
Модуль горизонтальной составляющей силы в точке В можно выразить через теорему Пифагора:
FCx=√F2C−F2Cy
Но вертикальная составляющая силы в точке C равна разности силы тяжести и горизонтальной составляющей силы в точке В:
FCy=mg−FBy
Отсюда:
FBx=FCx=√F2C−F2Cy=√F2C−(mg−FBy)2
Подставим известные данные и вычислим:
FBx=√0,52−(0,1·10−0,6)2=√0,25−0,16=0,3 (Н)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18697
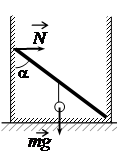Невесомый стержень, находящийся в ящике с гладкими дном и стенками, составляет угол 45° с вертикалью (см. рисунок). К середине стержня подвешен на нити шарик массой 1 кг. Каков модуль силы упругости N, действующей на стержень со стороны левой стенки ящика?
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Угол между стержнем и стенкой ящика: α = 45o.
• Масса шарика: m = 1 кг.
Чтобы записать правило моментов, нужно определить плечи силы тяжести и силы упругости. В качестве точки равновесия выберем точку опоры нижнего конца стержня. Тогда плечо силы тяжести будет равно произведению половины длины стержня на косинус угла между дном ящика и стержнем. Он тоже будет равен 45 градусам, так как он равен разности 180 градусов и угла α = 45o. Отсюда:
dmg=l2cosα
Плечо силы упругости будет равно расстоянию от дна ящика до верхней точки стержня. Оно определяется как произведение длины стержня на синус угла α:
dN=lsinα
Запишем правило моментов:
mgl2cosα=Nlsinα
Отсюда:
N=mgl2lsinαcosα
Длина стержня в числителе и знаменателе сократится, косинус и синус угла тоже, так как при 45 градусах они одинаковые. Следовательно:
N=mg2=1·102=5 (Н)
Ответ: 5
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.9k
