Как найти ребро куба
![]()
Полезные советы
Загрузка…
Отказаться от подписки на канал “Полезные советы”?
Обработка…
15,9 тыс.
Загрузка…
Загрузка…
Обработка…
Хотите сохраните это видео?
Войдите в аккаунт и добавьте его в плейлист.
Войти
-
Пожаловаться на видео?
Выполните вход, чтобы сообщить о неприемлемом контенте.
Войти
Поработать над переводом
16 530 просмотров
Понравилось видео?
Войдите в аккаунт, чтобы поставить отметку.
Войти
Не понравилось?
Войдите в аккаунт, чтобы поставить отметку.
Войти
- Математика – уроки для подготовки к экзаменам ЕГЭ ОГЭ
- Математика online
- КАК НАЙТИ РЕБРО КУБА, ЗНАЯ ПЛОЩАДЬ ПОВЕРХНОСТИ? Примеры | МАТЕМАТИКА 5 класс
КАК НАЙТИ РЕБРО КУБА, ЗНАЯ ПЛОЩАДЬ ПОВЕРХНОСТИ? Примеры | МАТЕМАТИКА 5 класс

Смотреть видео:
#математикаогэ #гвэ #егэответы #репетиторпоматематике #репетитор_по_математике #огэматематика #огэответы #арифметика #ответы_огэ
Свежая информация для ЕГЭ и ОГЭ по Математике (листай):
С этим видео ученики смотрят следующие ролики:
Облегчи жизнь другим ученикам – поделись! (плюс тебе в карму):
- Комментарии
Нет комментариев. Ваш будет первым!
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
-
Свойства куба
- Свойство 1
- Свойство 2
- Свойство 3
-
Формулы для куба
- Диагональ
- Диагональ грани
-
Площадь полной поверхности
- Периметр ребер
- Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.

- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
- a – ребро куба;
- d – диагональ куба или его грани.
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
![]()
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
![]()
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
![]()
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
![]()
Объем
Объем куба равен длине его ребра, возведенной в куб.

Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
![]()
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
![]()
На одном из предыдущих занятий мы с вами познакомились с таким
многогранником, как прямоугольный параллелепипед.
Решая задачу со спичками, получили геометрическую фигуру, которую
называют пирамидой.
Впереди вас ожидает знакомство и с другими многогранниками. А
сейчас давайте вернёмся к прямоугольному параллелепипеду.
Итак, поверхность прямоугольного параллелепипеда состоит из 6
прямоугольников. Эти прямоугольники называются гранями параллелепипеда.
Обратите внимание, что два соседних прямоугольника имеют общую
сторону, которая называется ребром прямоугольного параллелепипеда. Концы
рёбер называются вершинами прямоугольного параллелепипеда.
Таким образом, прямоугольный параллелепипед имеет 6 граней, 12
рёбер и 8 вершин.
Отметим, что при всём различии многогранников поверхность каждого
из них состоит из плоских многоугольников, которые называют гранями
многогранника. Два соседних плоских многоугольника имеют общую сторону – ребро
многогранника. Концы рёбер являются вершинами многогранника.
Этот многогранник называется октаэдром. У него 8 граней,
которые являются треугольниками, 12 рёбер и 6 вершин.
Куб – это такой прямоугольный
параллелепипед, в котором все рёбра равны между собой. Обратите внимание, что
рёбра куба, которые не видны, мы изображаем пунктирными линиями. Это позволяет
получить полное представление о фигуре и её расположении по отношению к нам.
Все грани куба – равные между собой квадраты. Поверхность куба
состоит из 6 равных квадратов. Посмотрите, что грани, расположенные друг против
друга, не имеют общих рёбер. Эти грани называются противоположными.
Грани, которые имеют общее ребро,
называются смежными.
А теперь давайте проведём небольшой эксперимент. Возьмём коробку,
которая имеет форму куба. Откроем её, потом разрежем по четырём вертикальным
рёбрам, а затем развернём.
Фигуру, которая у нас получилась, называют развёрткой куба.
Она состоит из 6 равных квадратов.
Следующие фигуры также являются развёртками куба.
С помощью любой из развёрток вы можете изготовить модель куба. Для
этого можно поступить следующим образом. Начертить на листе бумаги развёртку
куба. Вырезать её. Согнуть по отрезкам, которые соответствуют рёбрам куба, и
склеить.
Теперь давайте проведём с вами отрезок, который соединит наиболее
удалённые друг от друга вершины куба. Эти вершины называют противоположными.
Отрезок, соединяющий две противоположные вершины куба, называется
диагональю куба.
А теперь давайте с вами решим несколько задач.
Задача первая. Определите, какой кубик
получится из данной развёртки.
Решение.
Давайте мысленно представим, какие грани кубика являются смежными,
то есть имеют общее ребро, и сравним с предложенными вариантами, чтобы найти
верный. Для этого нам удобнее всего сравнивать грани, которые отличаются по
нанесённому на них рисунку. Обратите внимание на грань с жёлтым треугольником и
грань с зелёным треугольником. Очевидно, что эти грани будут смежными при
сборке кубика. При этом возможны четыре варианта взаимного расположения этих
граней при различных поворотах кубика.
Теперь сравним с четырьмя предложенными вариантами. Сразу видим,
что вариант первый неверный. Вариант второй неверный. Очевидно, что вариант
третий тоже неверный. А вот вариант четвёртый верный, так как грани, на которых
изображены треугольники, расположены верно. При этом на верхней грани должен
быть изображён синий круг. Действительно так.
Таким образом, мы с вами выяснили, что из данной развёртки
получится куб под номером 4.
Данную задачу вы можете решить ещё одним способом. А именно
нарисовать данную развёртку на бумаге. Причём удобнее это сделать на листочке в
клеточку, тогда вам не надо будет использовать линейку, чтобы соблюдать размеры
кубика. Вы просто будете отсчитывать нужное количество клеточек.
Затем нужно будет раскрасить нарисованную развёртку и вырезать. Потом
свернуть из неё куб и склеить его. После чего вы легко можете сравнить
получившийся куб с каждым из предложенных вариантов и выбрать верный.
Задача вторая. Модель куба с длиной
ребра 4 сантиметра окрасили в серую краску и распилили вдоль рёбер на кубики с
длиной ребра 1 см. Сколько среди полученных кубиков: а) окрашенных с трёх
сторон; б) окрашенных с двух сторон?
Решение.
Задача третья. На рисунке изображён
каркас куба. Проведите видимые рёбра так, чтобы куб был «виден»: а) сверху
слева; б) снизу справа.
Решение.
Задача четвёртая. На рисунке изображена
фигура, сложенная из пяти кубиков. Какой вид будет иметь данная фигура, если
смотреть на неё: а) спереди; б) слева; в) сверху?
Решение.
Содержание:
- § 1 Куб и элементы куба
- § 2 Изображение куба на плоскости
§ 1 Куб и элементы куба
В этом уроке познакомимся с геометрическим телом «куб» и научимся его изображать на плоскости.

Одна из первых детских игр – «кубики».
Возьмем один из кубиков.
В математике его называют «куб».
Рассмотрим это геометрическое тело.
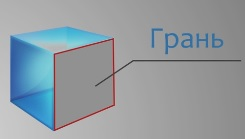
Поверхность куба состоит из квадратов.
У квадрата все стороны равны.
Все квадраты, из которых состоит поверхность куба, одинаковы.
Их называют гранями.
Поэтому куб называют многогранником.
У куба 6 граней.
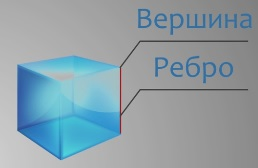
У каждой грани есть стороны.
Стороны называют ребрами.
У куба 12 ребер.
Каждое ребро относится к двум граням куба.
Так как у квадрата все стороны равны, то и все грани куба имеют одинаковую длину.
Концы ребер называются вершинами.
Каждое ребро соединяет две вершины.
Вершин у куба – 8.
Грань, ребро, вершина – это элементы куба.
В одной вершине сходится 3 ребра, каждая грань имеет 4 соседних грани, у каждой грани – 4 ребра.
§ 2 Изображение куба на плоскости
Возьмем куб, выполненный из бумаги. Попробуем его развернуть. Получится развертка куба.

Развертка – это выкройка куба.
Она состоит из 6 квадратов, расположенных в таком порядке, что из них можно сложить или склеить модель куба.
Перейдем к практической части.
Как изобразить куб на плоскости, например, на листе бумаги?
Куб – объемный предмет. Если обвести основание куба – получится квадрат. Это не является изображением куба.
Для наглядного изображения куба достаточно показать три его грани, например, верхняя, правая и передняя. Также можно сделать чертеж куба.
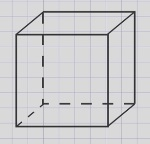
Для выполнения чертежа построим сначала переднюю грань, сзади выше и правее – заднюю грань, проведем нижние и верхние ребра боковых граней.
Ребра, которые не видны, изображают пунктирной линией, остальные сплошной линией.
Отметим, что на рисунке и чертеже мы не можем передать реальные размеры всех ребер куба.
Итак, в этом уроке Вы познакомились с геометрическим телом «куб», а также научились его изображать на плоскости.
Список использованной литературы:
- Чекин А.Л. Математика: 3 кл.: Учебник: В 2 ч./А.Л. Чекин; под ред. Р.Г. Чураковой.- М.: Академкнига / Учебник, 2013.
- Чуракова Р.Г. Математика. Поурочное планирование методов и приемов индивидуального подхода к учащимся в условиях формирования УУД.3 кл.: В 4 ч. Ч. 1/Р.Г. Чуракова, Г.В. Янычева. — М.: Академкнига /Учебник, 2014.
Использованные изображения:
