Как найти предельную норму замещения пример – Сайт, где вы сможете решить свои вопросы

Помощь студентам

Но в какой мере может потребитель отказаться, например, от апельсинов, чтобы приобрести дополнительно еще одно яблоко? Это помогает определить т.н. предельная норма замещения.

Предельная норма замещения Y на Х (МRSху) – количество товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X, при этом оставаясь на данной кривой безразличия. Кривизна изображенных ранее кривых безразличия означает, что количество Y, от которого потребитель хочет отказаться ради еще одной единицы X, уменьшается по мере увеличения количества X, замещающего Y в наборе.

Чтобы увидеть это начнем двигаться вдоль кривой безразличия, изображенной на рис. 6.4. Q_у – недельное потребление товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X. Выигрыш в недельном потреблении единицы товара Х составляет Q_х = 1.

Количество товара Y, которое будет обменено на единицу товара X, между любыми двумя точками на кривой может быть записано как Q_у/Q_х. Это наклон кривой безразличия, вдоль которой движется потребитель, отказываясь от единиц товара Y, для получения единиц товара X. Однако наклон кривых безразличия отрицателен.

Такое рассмотрение MRSху приводит к получению отрицательного числа. Предельная же норма замещения определяется как положительное количество товара Y, от которого потребитель желает отказаться ради дополнительной единицы X. Поэтому он есть произведение наклона кривых безразличия на -1.

наклон кривых безразличия

Кривизна кривой безразличия, изображенная на рис. 6.4. подразумевает уменьшение предельной нормы замещения Y на X. Обратите внимание, как их наклон изменяется по мере того, как потребитель, следуя по данной кривой, замещает Y на X. По мере того, как Х замещает Y вдоль кривой, она становится менее крутой.

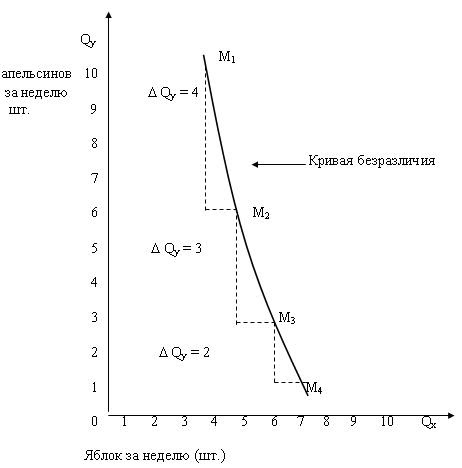
Уменьшение MRSху вдоль кривой безразличи

Рис. 6.4 – Уменьшение MRSху вдоль кривой безразличия

Таблица 6.2 – Предельная норма замещения Y на X

Набор

Qу

Qх

MRSху

М1

М2

М3

М4

4 ед. Y за 1 ед. Х

3 ед. Y за 1 ед. Х

2 ед. Y за 1 ед. Х

Анализ кривых безразличия не требует, чтобы полезность была количественно измерима, достаточно только предположить, что потребители способны ранжировать альтернативы, то есть, что полезность порядково измерима (позиция ординалистов).

Если бы полезность была количественно измерима (позиция кардиналистов), была бы возможность вычислить, сколько полезности при добавлении в набор еще одной единицы товара или услуги. То есть предельную норму замещения вдоль кривой безразличия можно связать с предельными полезностями благ на каждой из осей.

Изъятие Q_у единиц товара Y из набора наносит потребителю ущерб. Потеря полезности составляет Q_у MU_у, где МU_у – предельная полезность Y для потребителя. При замене потерянного количества Y тем количеством X, которое необходимо для возвращения потребителя в состояние прежней удовлетворенности, приобретенная полезность составила бы

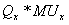
приобретенная полезность

(где МU_х – предельная полезность X). Если потребителю необходимо вернуться на ту же самую кривую безразличия, прирост полезности от добавления Х равен потери полезности от изъятия Y. Таким образом:

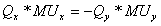
прирост полезности от добавления Х равен потери полезности от изъятия Y

Следовательно,

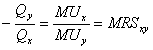
Предельная норма замещения Y на Х поэтому может рассматриваться как отношение предельной полезности Х к предельной полезности Y.

В нашем примере предельная полезность яблок (товар Х) уменьшается, когда его количество растет, и, соответственно она увеличивается у апельсинов (товар Y), когда их количество уменьшается. Поскольку МUх уменьшается, когда товар Х (яблоки) замещает товар Y (апельсины), в то время как МU_у увеличивается, отношение МU_х/МU_у равное МRSху уменьшается.

Отсюда вытекает, что предельная норма замещения Y на Х тоже должна падать при замене Y на X, если предельные полезности Х и Y находятся в обратном отношении к количествам этих товаров, покупаемых за период.

Уменьшение предельной полезности товаров, при предположении количественной измеримости полезности, объяснило бы выпуклую форму кривых безразличия.

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете заказать решение задач, написание учебных работ и онлайн помощь

Подробнее

Источник

Преде́льная но́рма замеще́ния в микроэкономике — величина, определяющая количество товара, от которого потребитель готов отказаться ради увеличения другого товара на единицу. При этом происходит замещение одного товара другим, а интенсивность замещения как раз показывает предельная норма замещения.
Предельную норму замещения обозначают через MRS (от англ. marginal rate of substitution) и вычисляют по формуле:

$MRS_{{xy}}=-(Delta y/Delta x),,$

где $x$ — количество одного блага, $y$ — количество другого блага, соответственно $Delta x$ и ${displaystyle Delta y}$ изменение соответствующих благ.
Также предельная норма замещения может быть определена (при количественном (кардиналистском) подходе к теории полезности) через отношения предельных полезностей товаров $x$ и $y$ :

${displaystyle MRS_{xy}=MU_{x}/MU_{y}}$

Если опираться на понятие кривой безразличия (линия, показывающая все комбинации двух благ в выборе между которыми потребитель безразличен, то есть все эти комбинации приносят ему один и тот же уровень полезности), то предельную норму замещения можно рассматривать как наклон кривой безразличия. То есть считается, что для сохранения достигнутого уровня полезности потребитель может отказаться от какого-то одного блага для получения того же количества общей полезности путём потребления какого-то количества другого блага. Геометрически MRS равна тангенсу угла наклона касательной кривой безразличия в данной точке, взятому с обратным знаком.

Пример[править | править код]

Например, потребителю безразличен выбор между следующими наборами: три яблока и один апельсин — первый набор, и два яблока и два апельсина — второй набор. Хотя через эти две точки нельзя однозначно провести кривую безразличия, предельную норму замещения апельсинов яблоками можно посчитать следующим образом:

$MRS_{{xy}}=-{frac {Delta y}{Delta x}}=-{frac {2-1}{2-3}}=1,,$

где $x$ — количество яблок, $y$ — количество апельсинов, соответственно $Delta x$ — изменение потребления яблок во втором наборе относительно первого, ${displaystyle Delta y}$ — изменение потребления апельсинов во втором наборе относительно первого. То есть в данном примере предельная норма замещения апельсинов яблоками равна единице и потребитель готов сократить потребление яблок на единицу и увеличить потребление апельсинов на единицу, чтобы его удовлетворённость от потребления этих фруктов не изменилась.

А вот при переходе от набора 10:2 к набору 8:3 каких-то двух благ при условии, что эти точки лежат на одной кривой безразличия, предельная норма замещения первого блага вторым будет равна двум, ${displaystyle MRS=2}$ .

Примечания[править | править код]

Ссылки[править | править код]

Экономико-математический словарь (недоступная ссылка с 14-06-2016 [2512 дней])

См. также[править | править код]

Функция полезности
Предельная полезность
Ординалистская теория полезности
Кривая безразличия
Бюджетная прямая
Предельная норма технического замещения

Источник

Что такое предельная норма замещения?

Предельная норма замещения (MRS) — это скорость, с которой некоторые единицы товара могут быть заменены другими, обеспечивая такой же уровень удовлетворения потребителя. Концепция MRS описывает отношения между потреблением двух товаров или ресурсов, когда потребители принимают рациональные решения.

Предельная норма замещения показывает баланс, достигнутый между двумя желательными товарами или ресурсами без ущерба для полезности.
MRS является частью теории кривой безразличия, которая измеряет, как потребители реагируют на разные товары, чтобы получить одинаковый уровень удовлетворения.
Формула расчета MRS = Изменение товара y/Изменение товара x
Кроме того, графическое представление MRS включает в себя построение кривой безразличия для двух продуктов.
Теория имеет ограничения, поскольку приложение ограничено двумя товарами.

Оглавление

Что такое предельная норма замещения?
- Как работает предельная норма замещения?
- Как представлена MRS?
- Уменьшение предельной нормы замещения
- Формула предельной нормы замещения
- Ограничения
- Пример
- Часто задаваемые вопросы
- Рекомендуемые статьи

Как работает предельная норма замещения?

В исследованиях поведения потребителей важно научиться рассчитывать предельную норму замещения. Обычно потребители принимают рациональные решения при нехватке ресурсов или финансовых ограничениях. Поэтому MRS оценивает поведение потребителей в таких ситуациях. Например, вы можете быть голодны, но не иметь финансовых средств для покупки товара в желаемом количестве. Хотя за ту же сумму денег вы можете удовлетворить свой аппетит с таким же уровнем удовлетворения, заменив часть желаемой суммы на аналогичную еду.

Рассмотрим следующий пример:

Клиент А хотел купить финики для приготовления торта с финиками. Однако она не смогла найти необходимое количество фиников в ближайшем магазине, поэтому заменила оставшееся количество изюмом.

На приведенном выше графике кривая безразличияКривая безразличияКривая безразличия (IC) представляет собой графическое представление различных комбинаций или наборов потребления двух товаров или товаров, обеспечивающих равные уровни удовлетворения и полезности для потребителя. финики и изюм, которые можно принести и использовать для приготовления чайного пирога. Каждая комбинация принесет одинаковый уровень удовлетворения и полезности.

Как представлена MRS?

Экономисты используют график для анализа и объяснения MRS. Значение MRS равно наклону кривой безразличия, построенной для двух продуктов. Например, на приведенном выше графике фиников и изюма точки на кривой безразличия показывают различные комбинации двух продуктов, приносящие одинаковое удовлетворение. График наклонен вниз и выпукл к началу координат.

Мы можем изобразить более одной кривой безразличия для двух продуктов, но комбинации, лежащие на разных кривых, имеют различную полезность. Например, по сравнению с комбинациями на более низких кривых безразличия комбинации на более высоких кривых безразличия предлагают большую полезность.

Типы кривых безразличия зависят от характера товаров.

Типы кривой безразличия

Убывающая Нормальные товары (несовершенные заменители) Выпуклые к началу координат Один товар увеличивается, а другой уменьшается MRS уменьшается Постоянная Совершенные заменители Прямые Сохраняет соотношение 1:1 MRS постоянна Возрастающая Совершенные комплименты Г-образная форма указывает на прямой угол Увеличение обоих продуктов MRS равно либо бесконечность, либо нуль

Уменьшение предельной нормы замещения

Согласно правилу убывания увеличение одного ресурса уравновешивается уменьшением другого ресурса. Для представления уменьшающейся MRS используются следующие допущения:

Кривая безразличия никогда не касается обеих осей графика.
Две кривые безразличия никогда не пересекаются
Кривая безразличия имеет нисходящий наклон
Кривая безразличия выпукла к началу координат, что указывает на уменьшение MRS.
Заменители никогда не бывают совершенными заменителями или идеально дополняющими друг друга по своей природе. Скорее, это должны быть обычные товары с взаимозаменяемыми свойствами.
Мы не будем увеличивать количество обоих продуктов одновременно; скорее, изменения в количестве будут в противоположных направлениях.

Формула предельной нормы замещения

Предельная норма замещения

Расчет МРС:

Мы можем использовать следующие шаги для получения MRS.

Миссис хорошего x для хорошего y«=» изменение товара Y/изменение товара X

X: представляет замену
Y: Существующий или текущий ресурс заменяется

Предельная норма замещающей формулы «=» △Г/△Х

где,

△Y Изменение товара Y
△X Изменение товара X

Формула MRS показывает, что при увеличении числа заменителей на последующих фазах и уменьшении количества текущих ресурсов MRS падает.

Представление MRS в терминах предельной полезности Предельная полезность Предельная полезность покупателя — это удовлетворение или выгода, получаемая от одной дополнительной единицы потребленного продукта. Его можно рассчитать, разделив дополнительную полезность на количество дополнительных единиц.Подробнее

Связка А содержит тринадцать пирожных и один кекс.
Набор B содержит девять пирожных и два кекса. Жертвует четырьмя пирожными за дополнительный кекс.
Набор C содержит семь пирожных и три кекса. Жертвует двумя пирожными за дополнительный кекс.
Набор D содержит шесть пирожных и четыре кекса. Жертвует одну упаковку пирожных за дополнительный кекс.

Наборы A, B, C и D дают одинаковый уровень удовольствия. Таким образом, мы также можем заключить, что вначале покупатель был готов пойти на уступки и заменить кексом большее количество пирожных.

Мы можем наблюдать, что количество замененных кондитерских изделий уменьшается в следующих комбинациях. Таким образом, этот пример показывает, что предельная норма замещения уменьшается.

Часто задаваемые вопросы

Что такое формула MRS?
Формула MRS для товаров x и y = изменение товара Y/изменение товара X.

«=» △Г/△Х

Что означает предельная полезность?

Предельная полезность – это дополнительное удовлетворение, получаемое от приобретения дополнительных единиц товара.

Какова предельная норма замещения? Приведите пример?

MRS интерпретирует баланс, достигнутый между двумя товарами или услугами в процессе выбора или во время покупки.
Пример: Клиент намеревался купить три рубашки, но купил две футболки и одну пару брюк. Покупатель отказался от покупки дополнительной футболки, чтобы приобрести одну пару фирменных джинсов, которые его привлекли.

1.6. Критерий оптимального набора товаров и оптимального производственного плана.

Рассмотрим теперь несколько задач, непосредсвенно связанных с понятием предельной нормы замещения. Если известна функция по-

лезности U =U (x1, x2 ) потребителя (мы ограничимся случаем n = 2 ),

то вполне естетсвенно поставить вопрос о выборе оптимального набора товаров, а именно: о нахождении самого дешевого набора товаров с данным уровнем полезности и о нахождении самого полезного набора товаров с данной стоимостью, если известны цены p1, p2 реа-

лизации товара.

Как легко можно заключить из рис. 1.2, для обеих рассматриваемых задач оптимальным является набор товаров, отвечающий точке касания M линии безразличия и прямой x1 p1 + x2 p2 = I , т.е. набор из

двух товаров M = (x1, x2 ) оптимален тогда и только тогда, когда

MRSX1,X2 (M )=	p1	.	(1.11)

	p2

Аналогично, если рассматривается задача об оптимальном производственном плане, т.е. задача о достижении максимально возможного объема производства при данном уровне издержек и о минимизации уровня издержек при данном объеме производства в предположении, что функция издержек линейна

C (q1, q2 )= q1 p1 +q2 p2 ,

где q1,q2 – объемы используемых ресурсов X1, X2 , а p1, p2 – стоимости единиц этих ресурсов, то производственный план M = (q1, q2 ) является оптимальным тогда и только тогда, когда выполнено соотно-

шение (1.11). При этом MRSX1,X2 (M )=		Qq′1	(M )	– предельная норма

						Qq′
					2
замещения первого ресурса вторым, а Q(q1, q2 )	– соответствующая
производственная функция.
	Пример 1.12.	Для функции	полезности Кобба–Дугласа
U (x , x	)= C x 1/ 4 x 3/ 4	проверьте, будут ли наборы товаров: а) (2, 5),
1	2	1	2

б) (5, 7) самыми дешевыми среди всех наборов, имеющих равные с

ними уровни полезности, если стоимости этих товаров составляют p1 = 20, p2 = 24 .

Решение.

Согласно вычислениям примера 1.11,

предельная

норма замещения товара X

товаром X

имеет вид MRS

X1,X2

3 x1

Тогда

MRSX1,X2

(2,5)=

, MRSX1,X2 (5,7)=

≠

20 .

3 5

Таким образом, набор

(2, 5)

является самым дешевым из всех набо-

ров, имеющих с ним равные уровни полезности,

а набор (5, 7) – яв-

ляется.

Задачи для самостоятельного решения

15.

Для

функции

полезности

Кобба–Дугласа

U (x , x

)= C x 1/ 3 x 3/ 4 проверьте,

будут

ли наборы товаров

а) (1, 8),

б) (3, 5)

самыми дешевыми среди всех наборов,

имеющих равные с

ними уровни полезности, если стоимости этих товаров составляют p1 = 25, p2 = 30.

16. Для функции полезности U (x1, x2 )= (x1 −2)3 (x2 −1)2 выяснить, является ли набор товаров (x1, x2 ) = (3, 5) самым полезным из всех наборов, имеющих равную с ним стоимость, если p1 = 36 , p2 = 6.

17. Для производственной функции CES Q(K, L)= (4 K −1 +3L−1 )−1

и цен на	используемые ресурсы pK	= 2 и	pL = 6	выяснить:
а) обеспечит	ли производственный план	(K, L)	= (6, 3)	наибольший

выпуск продукции при данном уровне издержек; б)будет ли при использовании производственного плана (K, L)= (3, 6) минимальным

уровень издержек для данного объема выпускаемой продукции?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Предельная норма замещения – это норма, при которой потребитель готов заменить один товар другим. При малых изменениях предельная скорость замещения равна наклону кривой безразличия.

Кривая безразличия – это график различных комбинаций двух товаров, к которым потребитель безразличен, то есть он не отдает предпочтения одному товару над другим.

Для сохранения состояния безразличия при уменьшении объемов потребления одного товара придется увеличивать объемы потребления другого товара.

Предельная норма замещения – это норма, при которой уменьшение одного блага должно быть компенсировано увеличением другого.

Рассмотрим потребителя, чье безразличие к двум товарам – кинофильмам и обедам – выглядит следующим образом:

Набор	Фильмы	Обеды
A	1	10.00
B	2	5.00
C	3	3.33
D	4	2.50
E	5	2.00
F	6	1.67

Построенная на основании этих данных кривая безразличия будет иметь следующий вид:

Предельная норма замещения

Если потребитель перемещается из точки B в точку D, то есть смотрит 4 фильма вместо 2, он должен сократить свои обеды. Предельная норма замещения – это норма, которая диктует, от какой части обедов он должен отказаться, чтобы насладиться большим количеством фильмов.

Формула

Закон убывающей предельной полезности гласит, что предельная полезность, то есть дополнительная полезность каждой новой единицы товара, ниже предельной полезности предшествующей единицы, то есть первая единица товара имеет наибольшую полезность, вторая единица имеет вторую наибольшую полезность и так далее.

Теперь, если потребитель заменяет один товар, скажем X, другим товаром, скажем Y, он должен компенсировать потребление самыми высокими единицами Y для первой единицы X, вторыми самыми высокими единицами Y для второй единицы X и так далее.

Предельная норма замещения непрерывно изменяется по мере того, как мы движемся по кривой безразличия.

Для очень малых изменений в одном товаре предельная скорость замещения приближается к наклону кривой безразличия, которая равна изменению Y, деленному на изменение X.

Предельная норма замещения X (то есть фильмов) на Y (то есть обедов) определяется следующим образом:

MRS_XY = – (Y₁ – Y₀) ÷ (X₁ – X₀)

MRS_XY и MRS_YX не одно и то же, на самом деле они взаимны друг другу, то есть:

MRS_XY = 1 / MRS_YX

Предельная норма замещения зависит от относительных предпочтений потребителей, то есть от их относительных предельных полезностей и исходных точек.

Можно показать, что предельная норма замещения Y на X равна цене X, деленной на Y, которая, в свою очередь, равна предельной полезности X, деленной на предельную полезность Y:

MRS_XY = P_X / P_Y = MU_X / MU_Y

Кривые безразличия становятся более плоскими по мере того, как мы перемещаемся от оси Y к оси X.

Это происходит потому, что по мере того, как Y становится дефицитным, а X – изобильным, предельная норма замещения X на Y снижается. Это явление называется снижающейся предельной нормой замещения.

Источник

Ux′ = lim	∆U .
k	∆xk →∞	∆xk

нии количества товара Xk	на одну единицу: Ux′	≈	∆U	. При этом, так
	k		∆x
			k

MRSXk ,Xl (M )=	U ′	(M )
xk	.
Ux′	(M )

	l

Пример[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

См. также[править | править код]

Что такое предельная норма замещения?

Как работает предельная норма замещения?

Как представлена ​​MRS?

Уменьшение предельной нормы замещения

Формула предельной нормы замещения

Часто задаваемые вопросы

Рекомендуемые статьи

1.6. Критерий оптимального набора товаров и оптимального производственного плана.

Формула

Вам также может понравиться

Как найти размер атома формула

Как найти сторону правильного треугольника зная периметр

Как найти свой аромат духов онлайн

Добавить комментарий Отменить ответ

Как представлена MRS?