Расчеты контактных
взаимодействий онлайн
Контактные (герцевские) напряжения и деформации возникают при взаимодействии двух соприкасающихся тел. При этом, вследствие передачи давления по весьма малым площадкам, в зоне контакта возникают значительные напряжения, имеющие местный характер.
Контактные напряжения определяют при расчетах ответственных деталей – например подшипников, зубчатых колес, кулачковых и шарнирных механизмов. Расчеты контактных напряжений выполняются в предположении, что нагрузки создают в зоне контакта только упругие деформации.
В данном разделе можно выполнить онлайн расчет контактных взаимодействий сферических и цилиндрических поверхностей, а так же рассчитать контакт элементов произвольно заданной кривизны.
Контакт сферы с плоской поверхностью
Модуль упругости пластины Е1, Па
Коэффициент Пуассона пластины ν1
Диаметр сферы D2, мм
Модуль упругости сферы Е2, Па
Коэффициент Пуассона сферы ν2
Нагрузка F, Н
Напряжения в зоне контакта σ, МПа
Диаметр пятна контакта d, мм
Совместные деформации Y, мм
www.caetec.ru
©Copyright Кайтек 2020
- Ref 8 Table 14.1
Контакт двух сфер
Диаметр сферы D1, мм
Модуль упругости сферы Е1, Па
Коэффициент Пуассона сферы ν1
Диаметр сферы D2, мм
Модуль упругости сферы Е2, Па
Коэффициент Пуассона сферы ν2
Нагрузка F, Н
Напряжения в зоне контакта σ, МПа
Диаметр пятна контакта d, мм
Совместные деформации Y, мм
www.caetec.ru
©Copyright Кайтек 2020
- Ref 8 Table 14.1
Контакт сферы со сферическим разъемом
Диаметр разъема D1, мм
Модуль упругости разъема Е1, Па
Коэффициент Пуассона разъема ν1
Диаметр сферы D2, мм
Модуль упругости сферы Е2, Па
Коэффициент Пуассона сферы ν2
Нагрузка F, Н
Напряжения в зоне контакта σ, МПа
Диаметр пятна контакта d, мм
Совместные деформации Y, мм
www.caetec.ru
©Copyright Кайтек 2020
- Ref 8 Table 14.1
Контакт цилиндра с плоской поверхностью
Модуль упругости пластины Е1, Па
Коэффициент Пуассона пластины ν1
Диаметр цилиндра D2, мм
Модуль упругости цилиндра Е2, Па
Коэффициент Пуассона цилиндра ν2
Длина цилиндра L, мм
Нагрузка F, Н
Напряжения в зоне контакта σ, МПа
Ширина пятна контакта A, мм
www.caetec.ru
©Copyright Кайтек 2020
- Ref 8 Table 14.1
Контакт двух параллельных цилиндров
Диаметр цилиндра D1, мм
Модуль упругости цилиндра Е1, Па
Коэффициент Пуассона цилиндра ν1
Диаметр цилиндра D2, мм
Модуль упругости цилиндра Е2, Па
Коэффициент Пуассона цилиндра ν2
Длина цилиндров L, мм
Нагрузка F, Н
Напряжения в зоне контакта σ, МПа
Ширина пятна контакта A, мм
www.caetec.ru
©Copyright Кайтек 2020
- Ref 8 Table 14.1
Контакт цилиндра с разъемом
Диаметр разъема D1, мм
Модуль упругости разъема Е1, Па
Коэффициент Пуассона разъема ν1
Диаметр цилиндра D2, мм
Модуль упругости цилиндра Е2, Па
Коэффициент Пуассона цилиндра ν2
Длина цилиндров L, мм
Нагрузка F, Н
Напряжения в зоне контакта σ, МПа
Диаметр пятна контакта A, мм
www.caetec.ru
©Copyright Кайтек 2020
- Ref 8 Table 14.1
Контакт двух перпендикулярных цилиндров
Диаметр цилиндра D1, мм
Модуль упругости цилиндра Е1, Па
Коэффициент Пуассона цилиндра ν1
Диаметр цилиндра D2, мм
Модуль упругости цилиндра Е2, Па
Коэффициент Пуассона цилиндра ν2
Нагрузка F, Н
Напряжения в зоне контакта σ, МПа
Совместные деформации Y, мм
Ширина пятна контакта, мм
www.caetec.ru
©Copyright Кайтек 2020
- Ref 8 Table 14.1
Контакт произвольных поверхностей
Максимальный радиус кривизны R1, мм
Минимальный радиус кривизны r1, мм
Модуль упругости Е1, Па
Коэффициент Пуассона ν1
Максимальный радиус кривизны R2, мм
Минимальный радиус кривизны r2, мм
Модуль упругости Е2, Па
Коэффициент Пуассона ν2
Угол α между плоскостями R1 и R2, °
Нагрузка F, Н
Напряжения в зоне контакта σ, МПа
Совместные деформации Y, мм
Ширина пятна контакта, мм
www.caetec.ru
©Copyright Кайтек 2020
- Выше выполнен расчет напряжений в зоне контакта, размеров пятна контакта и совместных деформаций при контактном взаимодействии двух тел с произвольно заданной кривизной. При выполнении вычислений необходимо принимать во внимание следующее:
- 1. В точке контакта двух тел определяются максимальный R и минимальный r радиусы кривизны для обоих тел;
- 2. В данном расчете, если радиус кривизны образует охватываемую поверхность – он задается положительным значением;
- 3. Если радиус кривизны образует охватывающую поверхность – он задается отрицательным значением;
- 4. Плоскости, содержащие линии наибольшей и наименьшей кривизны перпендикулярны между собой;
- 5. В общем случае, плоскости , содержащие линии наибольшей кривизны обоих тел повернуты между собой на некоторый угол α (например при контакте перпендикулярных цилиндров α = 90°).
©ООО”Кайтек”, 2020. Любое использование либо копирование материалов или подборки материалов сайта, может осуществляться лишь с разрешения автора (правообладателя) и только при наличии ссылки на сайт www.caetec.ru
 Контактные напряжения образуются в месте соприкосновения двух тел в тех случаях, когда размеры площадки касания малы по сравнению с размерами тел (сжатие двух шаров, шара и плоскости, двух цилиндров и т. п.). Если значение контактных напряжений больше допускаемого, то на поверхности деталей появляются вмятины, борозды, трещины или мелкие раковины. Подобные повреждения наблюдаются у зубчатых, червячных, фракционных и цепных передач, а также в подшипниках качения.
Контактные напряжения образуются в месте соприкосновения двух тел в тех случаях, когда размеры площадки касания малы по сравнению с размерами тел (сжатие двух шаров, шара и плоскости, двух цилиндров и т. п.). Если значение контактных напряжений больше допускаемого, то на поверхности деталей появляются вмятины, борозды, трещины или мелкие раковины. Подобные повреждения наблюдаются у зубчатых, червячных, фракционных и цепных передач, а также в подшипниках качения.
Теория контактных напряжений является предметом курса «Теория упругости». Расчеты многих деталей машин, изучаемые в данном курсе, выполняют по контактным напряжениям. Поэтому ниже излагаются краткие сведения о контактных напряжениях и о разрушениях деталей, связанных с этими напряжениями .
При расчете контактных напряжений различают два характерных случая: первоначальный контакт в точке (два шара, шар и плоскость и т. п.); первоначальный контакт по линии (два цилиндра с параллельными осями, цилиндр и плоскость и т. п.).
На рис. 8.7 изображен пример сжатия двух цилиндров с параллельными осями. До приложения удельной нагрузки q цилиндры соприкасались по линии. Под нагрузкой линейный контакт переходит в контакт по узкой площадке. При этом точки максимальных нормальных напряжений σΗ располагаются на продольной оси симметрии контактной площадки. Значение этих напряжений вычисляют по формуле
 Для конструкционных металлов коэффициент Пуассона располагается в пределах μ = 0,25…0,35. Без существенной погрешности принимают μ1=μ2 = 0,3 и получают
Для конструкционных металлов коэффициент Пуассона располагается в пределах μ = 0,25…0,35. Без существенной погрешности принимают μ1=μ2 = 0,3 и получают

где Епр и рпр — приведенные модуль упругости и радиус кривизны; Еи Ε 2, гь Г 2 — модули упругости и радиусы цилиндров.
Формула (8.2) справедлива не только для круговых, но и для любых других цилиндров. Для последних гγ и г2 — радиусы кривизны в точках контакта. При контакте цилиндра с плоскостью г2 = оо. Знак минус в формуле (8.3) относится к случаю внутреннего контакта (когда поверхность одного из цилиндров вогнутая).
При вращении цилиндров под нагрузкой отдельные точки их поверхностей периодически нагружаются и разгружаются, а контактные напряжения в этих точках изменяются по прерывистому от нулевому циклу (рис. 8.8, г). Каждая точка нагружается только в период прохождения зоны контакта и свободна от напряжений в остальное время оборота цилиндра.
Допускаемое
контактное напряжение
![]()
В
этой форме отсутствуют коэффициенты
по ГОСТ 21354-75, учитывающие влияние
шероховатости, смазки, скорости и
размеров коле, которые, для распространенных
на практике показателей, близки к
единице.
Предел
контактной выносливости поверхности
зубьев
![]() зависит от твердости поверхности и
зависит от твердости поверхности и
определяется по таб.5.
Таблица
5
Значения![]() и
и![]()
|
Термическая |
Твердость |
|
|
|
Нормализация, |
НВ |
2НВ+70 |
1.8НВ |
|
Объемная |
НRC |
18НRC+150 |
550 |
|
Поверхностная |
НRC |
17НRC+200 |
650 |
|
Цементация |
НRC |
23НRC |
750 |
|
Азотирование |
НRC |
1050 |
12НRC+300 |
Коэффициент
безопасности
![]() принимается
принимается![]() при нормализации, улучшении или объемной
при нормализации, улучшении или объемной
закалке;![]() при поверхностной закалке, цементации
при поверхностной закалке, цементации
или азотировании.
Коэффициент
долговечности
![]() при переменных режимах нагрузки
при переменных режимах нагрузки
рассчитывается по эквивалентному![]() числу циклов:
числу циклов:![]() .
.
В этой формуле базовое число циклов
напряжений![]() ,
,
зависящее от твердости поверхности
зубьев, определяется по графику 2.
NНО
106
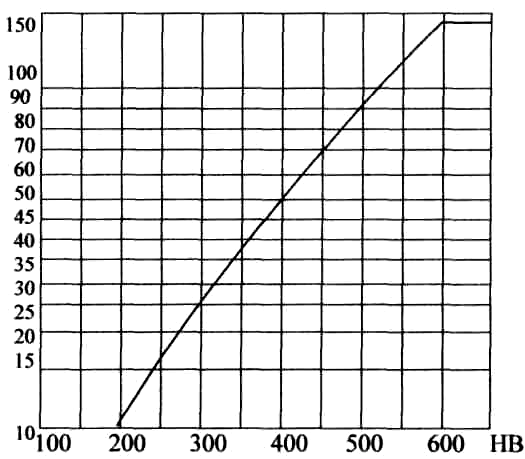
Рис.
2. График для определения базового числа
циклов напряжений
![]() –
–
число циклов перемены напряжений за
весь срок службы (наработка),
![]() .
.
Здесь![]() – угловая скорость соответствующего
– угловая скорость соответствующего
вала,![]() ;
;![]() – срок службы привода,ч.
– срок службы привода,ч.
Для
наших расчетов:
Предел
контактной выносливости
![]() для шестерни
для шестерни
![]() ,
,
для
колеса ![]() ;
;
Базовое
число циклов для шестерни
![]() ,
,
для колеса![]()
Число
циклов перемены напряжений для шестерни
![]() ,
,
для
колеса![]()
Если
![]() ,
,
то принимают![]()
Допускаемое
напряжение для шестерни
 .
.
Для
колеса

В
качестве расчетного напряжения
принимается:
Для
прямозубых передач – меньшее из них,
для
косозубых передач, у которых зубья
шестерни гораздо тверже зубьев колеса:
![]()
Принимаем
для дальнейших расчетов допускаемое
напряжение
![]()
2.3 Определение допускаемых напряжений на изгиб зубьев .
Допускаемое
контактное напряжение на изгиб зубьев
![]()
Предел
выносливости зубьев при изгибе
![]() зависит от твердости поверхности и
зависит от твердости поверхности и
определяется по таб.5.
Коэффициент
безопасности
![]() принимается
принимается![]() при нормализации, улучшении или объемной
при нормализации, улучшении или объемной
закалке;![]() при цементации.
при цементации.
Коэффициент
![]() ,
,
учитывающий влияние двухстороннего
приложения нагрузки, принимается![]() (односторонняя нагрузка) и
(односторонняя нагрузка) и![]() (сателлиты планетарного редуктора).
(сателлиты планетарного редуктора).
Коэффициент
долговечности
![]() определяется:
определяется:
![]()
базовое
число циклов для всех сталей
![]() ,
,![]() ,
,
если![]() ,
,
то принимают![]() .
.
Тогда
допускаемое контактное напряжение на
изгиб зубьев для шестерни
 .
.
Для
колеса

2.4 Проектный расчет цилиндрической зубчатой передачи редуктора
-
Определяем
межосевое расстояние
 ,
,
где
Ка
– вспомогательный коэффициент, для
косозубых передач, Ка=43,
(для прямозубых Ка=49,5);
![]() –коэффициент
–коэффициент
ширины венца колеса, равный 0,2…0,25,
для шестерни, расположенной симметрично
относительно опор для рассматриваемого
варианта; u
– передаточное число редуктора, в нашем
случае u
=5;
Т2–крутящий
момент на тихоходном валу редуктора,
Н![]() м,
м,
для рассматриваемого
варианта Т2=Т3=234,4
Н![]() м;
м;
[H]-
допускаемое контактное напряжение
колеса с менее прочным зубом или среднее
допускаемое контактное напряжение,
Н/мм2;
[H]=637
МПа;
КH
– коэффициент неравномерности нагрузки
по длине зубьев, КH
=1

полученное
значение межосевое расстояние
![]()
округляем до ближайшего стандартного:
стандартные
межосевые расстояния :
1-й
ряд – 40, 50, 63, 80, 100, 125, 160, 200, 250, 315, 400…
2-й
ряд – 140, 180, 225, 280, 355, 450…
получаем
стандартное ближайшее значение межосевого
расстояния 125
мм.
-
Определим
модуль зацепления m,
мм
![]()
где
Кm
– вспомогательный коэффициент,
для косозубых передач, Кm
= 5,8
(для прямозубых Кm
=6,8);
d2
=
2а
u
/ (u+1)
– делительный диаметр колеса, мм;
b2
= а
аw
– ширина венца колеса, мм,
![]()
– допускаемое напряжение изгиба материала
колеса с менее прочным зубом,
![]() .
.
Подставим
известные величины в формулу (25) получим
численное
значение для модуля зацепления :
![]()
полученное
значение модуля округляем до ближайшего
стандартного в большую сторону из ряда
чисел:
m,
мм
1-й
ряд : 1,0 ; 1,5 ; 2 ; 2,5 ; 3 ; 4 ; 5 ; 6 ;
8 ; 10
2-й
ряд : 1,25 ; 1,75 ; 2,25 ; 2,75 ; 3,5 ; 4,5 ; 5,5 ; 7 ; 9
принимаем
m=1,5
мм.
-
Определить
угол наклона зубьев min
для косозубой передачи редуктора:
![]()
В
косозубых передачах угол наклона зубьев
принимают β=8…16.
-
Определим
суммарное число зубьев шестерни и
колеса:
![]()
для
косозубых передач
![]() )
)
Полученное
значение
![]()
округляем
в меньшую сторону до целого числа, имеем:
![]()
-
Уточнить
действительную величину угла наклона
зубьев для косозубых передач

-
Определим
число зубьев шестерни :
![]()
Полученное
значение округлим до ближайшего
целого числа,
![]() .
.
Из условий уменьшения шума и отсутствия
подрезания зубьев рекомендуется![]()
-
Определим
число зубьев колеса
![]()
-
Определим
фактическое передаточное число
 и проверим его отклонение
и проверим его отклонение от заданного
от заданного :
:
![]()
Так
как норма отклонения не выполняется,
пересчитаем
![]() и
и![]() .
.
Примем![]() ,
,![]()
![]()
-
Определим
фактическое межосевое расстояние:
![]()
для
косозубых передач![]()
-
Определим
основные геометрические параметры
передачи:
|
Параметр |
Шестерня |
Колесо |
|||
|
прямозубая |
косозубая |
прямозубая |
косозубая |
||
|
Диаметр |
делительный |
d1=mz1=72 |
d1=mz1/cos |
d2=m |
d2=m |
|
вершин |
dа1=d1+2 |
dа2=d2+2 |
|||
|
впадин |
df1=d1–2,4 |
df2=d2–2,4 |
|||
|
Ширина |
b1=b2+(2..4)мм=40мм |
b2= |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Техническая механика
Сопротивление материалов
Смятие. Контактные напряжения
Расчеты на прочность при смятии
Если детали конструкции, передающие значительную сжимающую нагрузку, имеют небольшую площадь контакта, то может произойти смятие поверхностей деталей.
 Смятие стараются предотвратить различными способами, например, подкладывая различные шайбы и подкладки под контактирующие детали.
Смятие стараются предотвратить различными способами, например, подкладывая различные шайбы и подкладки под контактирующие детали.
Для простоты расчетов напряжений, возникающих при смятии, полагают, что по плоскости контакта возникают только нормальные напряжения, равномерно распределенные по площади контакта. Расчетное уравнение на смятие имеет вид:
где: F – сжимающая сила, Асм – площадь контакта, [σсм] – допускаемое напряжение на смятие.
Если соприкасающиеся детали сделаны из разных материалов, то на смятие проверяют деталь из более мягкого материала.
При контакте двух деталей цилиндрической поверхности (например, заклепочное соединение) закон распределения напряжений смятия по поверхности контакта сложнее, чем по плоскости, поэтому при расчете на смятие цилиндрических отверстий в расчетную формулу подставляют не площадь боковой поверхности полуцилиндра, по которой происходит контакт, а значительно меньшую площадь диаметрального сечения отверстия (условная площадь смятия, (см. рис. 2 ), тогда:

где d — диаметр цилиндра, δ — толщина соединяемой детали (высота цилиндра).
При различной толщине соединяемых деталей, в расчетную формулу подставляют меньшую толщину.
Допустимые напряжения на смятие для разных материалов определяются опытным путем, их значение можно найти в справочниках.
Так, для низкоуглеродистой стали допускаемое напряжение смятия принимается в пределах 100….120 МПа, для клепаных соединений: 240….320 МПа, для древесины: 2,4….11 МПа и т. д.
Контактные напряжения
Контактными называют напряжения и деформации, возникающие при сжатии тел криволинейной формы, причем первоначальный контакт может быть линейным (например, сжатие двух цилиндров с параллельными образующими), или точечным (например, сжатие двух шаров).
В результате деформации контактирующих тел начальный точечный или линейный контакт переходит в контакт по некоторой малой площадке. Решение вопросов о контактных напряжениях и деформациях впервые дано в работах немецкого физика Г. Герца (1857-1894 г. г.).

Для деталей, в поверхностных слоях которых возникают контактные напряжения (например, подшипники качения, фрикционные катки, зубчатые колеса и т. п. ), решающую роль играет прочность рабочих поверхностей – контактная прочность .
Рассмотрим случай контакта двух цилиндров с параллельными образующими (рис 3) .
Определение контактных напряжений в этом случае производится по формуле Герца , выведенной в предположении, что материалы цилиндров подчиняются закону Гука.
Очевидно, что контактные напряжения по ширине площадки контакта неравномерны.
Максимальные напряжения σн определяются по формуле:
σн = √ пр / [2π(1 — ν 2 )ρпр]> , (здесь и далее √ — знак корня)
где:
q – нагрузка на единицу длины линии контакта;
Епр – приведенный модуль упругости, получаемый из соотношения 2/Епр = 1/Е1 + 1/Е2; (здесь 1/Е — некоторая характеристика податливости материала), откуда: Епр = 2 Е1Е2 / Е1 + Е2;
ν — коэффициент Пуассона;
ρпр – приведенный радиус кривизны цилиндров, определяемый из соотношения 1/ρпр = 1/R1 + 1/R2, (здесь 1/ρпр — кривизна поверхности), откуда:
При ν = 0,3 формула Герца приобретает вид:
Формула Герца широко применяется при расчетах на контактную прочность многих деталей машин и механизмов — зубчатых колес, подшипников качения и т. п.
Материалы раздела «Сопротивление материалов»:
Источник
Расчеты контактных взаимодействий
Контактные (герцевские) напряжения и деформации возникают при взаимодействии двух соприкасающихся тел. При этом, вследствие передачи давления по весьма малым площадкам, в зоне контакта возникают значительные напряжения, имеющие местный характер.
Контактные напряжения определяют при расчетах ответственных деталей — например подшипников, зубчатых колес, кулачковых и шарнирных механизмов. Расчеты контактных напряжений выполняются в предположении, что нагрузки создают в зоне контакта только упругие деформации.
В данном разделе можно выполнить онлайн расчет контактных взаимодействий сферических и цилиндрических поверхностей, а так же рассчитать контакт элементов произвольно заданной кривизны.
Расчет контакта сферы с плоской поверхностью
Расчет напряжений в зоне контакта, размеров пятна контакта и совместных деформаций при контактном взаимодействии тел сферической и плоской формы из разнородных материалов.
Исходные данные:
Е1 — модуль упругости материала плоского тела, в паскалях;
D2 — диаметр сферического тела, в миллиметрах;
Е2 — модуль упругости материала сферического тела, в паскалях;
ν2 — коэффициент Пуассона материала сферического тела;
КОНТАКТ СФЕРЫ С ПЛОСКОСТЬЮ
Модуль упругости плиты Е1, Па
Коэффициент Пуассона плиты ν1
Модуль упругости сферы Е2, Па
Коэффициент Пуассона сферы ν2
Напряжения в зоне контакта σ, МПа
Диаметр пятна контакта A, мм
Совместные деформации Y, мм
Расчет контакта двух сфер
Расчет напряжений в зоне контакта, размеров пятна контакта и совместных деформаций при контактном взаимодействии двух тел сферической формы из разнородных материалов.
Исходные данные:
D1 — диаметр первого сферического тела, в миллиметрах;
Е1 — модуль упругости материала первого сферического тела, в паскалях;
ν1 — коэффициент Пуассона материала первого сферического тела;
D2 — диаметр второго сферического тела, в миллиметрах;
Е2 — модуль упругости материала второго сферического тела, в паскалях;
ν2 — коэффициент Пуассона материала второго сферического тела;
Модуль упругости сферы Е1, Па
Коэффициент Пуассона сферы ν1
Модуль упругости сферы Е2, Па
Коэффициент Пуассона сферы ν2
Напряжения в зоне контакта σ, МПа
Диаметр пятна контакта A, мм
Совместные деформации Y, мм
Расчет контакта сферы с разъемом
Расчет напряжений в зоне контакта, размеров пятна контакта и совместных деформаций при контактном взаимодействии двух тел с наружной и внутренней сферической поверхностью из разнородных материалов.
Исходные данные:
D1 — внутренний диаметр сферического тела, в миллиметрах;
Е1 — модуль упругости материала сферического тела с внутренним диаметром, в паскалях;
ν1 — коэффициент Пуассона материала сферического тела с внутренним диаметром;
D2 — наружный диаметр сферического тела, в миллиметрах;
Е2 — модуль упругости материала сферического тела с наружным диаметром, в паскалях;
ν2 — коэффициент Пуассона материала сферического тела с наружным диаметром;
Модуль упругости разъема Е1, Па
Коэффициент Пуассона разъема ν1
Модуль упругости сферы Е2, Па
Коэффициент Пуассона сферы ν2
Напряжения в зоне контакта σ, МПа
Диаметр пятна контакта A, мм
Совместные деформации Y, мм
Расчет контакта цилиндра с плоской поверхностью
Расчет напряжений в зоне контакта и размеров пятна контакта при контактном взаимодействии тел цилиндрической и плоской формы из разнородных материалов.
Исходные данные:
Е1 — модуль упругости материала плоского тела, в паскалях;
D2 — диаметр цилиндрического тела, в миллиметрах;
Е2 — модуль упругости материала цилиндрического тела, в паскалях;
ν2 — коэффициент Пуассона материала цилиндрического тела;
L — длина цилиндрического тела, в миллиметрах;
КОНТАКТ ЦИЛИНДРА С ПЛОСКОСТЬЮ
Модуль упругости плиты Е1, Па
Коэффициент Пуассона плиты ν1
Модуль упругости цилиндра Е2, Па
Коэффициент Пуассона цилиндра ν2
Напряжения в зоне контакта σ, МПа
Ширина пятна контакта A, мм
Расчет контакта двух параллельных цилиндров
Расчет напряжений в зоне контакта и размеров пятна контакта при контактном взаимодействии двух тел цилиндрической формы из разнородных материалов.
Исходные данные:
D1 — диаметр первого цилиндрического тела, в миллиметрах;
Е1 — модуль упругости материала первого цилиндрического тела, в паскалях;
ν1 — коэффициент Пуассона материала первого цилиндрического тела;
D2 — диаметр второго цилиндрического тела, в миллиметрах;
Е2 — модуль упругости материала второго цилиндрического тела, в паскалях;
ν2 — коэффициент Пуассона материала второго цилиндрического тела;
L — длина цилиндрического тела, в миллиметрах;
КОНТАКТ ПАРАЛЛЕЛЬНЫХ ЦИЛИНДРОВ
Модуль упругости цилиндра Е1, Па
Коэффициент Пуассона цилиндра ν1
Модуль упругости цилиндра Е2, Па
Коэффициент Пуассона цилиндра ν2
Напряжения в зоне контакта σ, МПа
Ширина пятна контакта A, мм
Расчет контакта цилиндра с разъемом
Расчет напряжений в зоне контакта и размеров пятна контакта при контактном взаимодействии двух тел с наружной и внутренней цилиндрической поверхностью из разнородных материалов.
Исходные данные:
D1 — внутренний диаметр цилиндрического тела, в миллиметрах;
Е1 — модуль упругости материала цилиндрического тела с внутренним диаметром, в паскалях;
ν1 — коэффициент Пуассона материала цилиндрического тела с внутренним диаметром;
D2 — наружный диаметр цилиндрического тела, в миллиметрах;
Е2 — модуль упругости материала цилиндрического тела с наружным диаметром, в паскалях;
ν2 — коэффициент Пуассона материала цилиндрического тела с наружным диаметром;
L — длина цилиндрического тела, в миллиметрах;
КОНТАКТ ЦИЛИНДРА С РАЗЪЕМОМ
Модуль упругости разъема Е1, Па
Коэффициент Пуассона разъема ν1
Модуль упругости цилиндра Е2, Па
Коэффициент Пуассона цилиндра ν2
Напряжения в зоне контакта σ, МПа
Ширина пятна контакта A, мм
Расчет контакта двух перпендикулярных цилиндров
Расчет напряжений в зоне контакта, размеров пятна контакта и совместных деформаций при контактном взаимодействии двух перпендикулярно расположенных тел цилиндрической формы из разнородных материалов.
Исходные данные:
D1 — диаметр первого цилиндрического тела, в миллиметрах;
Е1 — модуль упругости материала первого цилиндрического тела, в паскалях;
ν1 — коэффициент Пуассона материала первого цилиндрического тела;
D2 — диаметр второго цилиндрического тела, в миллиметрах;
Е2 — модуль упругости материала второго цилиндрического тела, в паскалях;
ν2 — коэффициент Пуассона материала второго цилиндрического тела;
КОНТАКТ ПЕРПЕНДИКУЛЯРНЫХ ЦИЛИНДРОВ
Модуль упругости цилиндра Е1, Па
Коэффициент Пуассона цилиндра ν1
Модуль упругости цилиндра Е2, Па
Коэффициент Пуассона цилиндра ν2
Напряжения в зоне контакта σ, МПа
Совместные деформации Y, мм
Расчет контакта произвольных поверхностей
Ниже выполнен расчет напряжений в зоне контакта, размеров пятна контакта и совместных деформаций при контактном взаимодействии двух тел с произвольно заданной кривизной. При выполнении вычислений необходимо принимать во внимание следующее:
1. В точке контакта двух тел определяются максимальный R и минимальный r радиусы кривизны для обоих тел;
2. В данном расчете, если радиус кривизны образует охватываемую поверхность — он задается положительным значением;
3. Если радиус кривизны образует охватывающую поверхность — он задается отрицательным значением;
4. Плоскости, содержащие линии наибольшей и наименьшей кривизны перпендикулярны между собой;
5. В общем случае, плоскости , содержащие линии наибольшей кривизны обоих тел повернуты между собой на некоторый угол α (например при контакте перпендикулярных цилиндров α = 90°).
Исходные данные:
R1 — максимальный радиус кривизны первого тела, в миллиметрах;
r1 — минимальный радиус кривизны первого тела, в миллиметрах;
Е1 — модуль упругости материала первого тела, в паскалях;
R2 — максимальный радиус кривизны второго тела, в миллиметрах;
r2 — минимальный радиус кривизны второго тела, в миллиметрах;
Е2 — модуль упругости материала второго тела, в паскалях;
ν2 — коэффициент Пуассона материала второго тела;
α — угол между плоскостями, содержащими линии наибольшей кривизны обоих тел, в градусах;
КОНТАКТ ПРОИЗВОЛЬНЫХ ПОВЕРХНОСТЕЙ
Максимальный радиус кривизны R1, мм
Минимальный радиус кривизны r1, мм
Максимальный радиус кривизны R2, мм
Минимальный радиус кривизны r2, мм
Угол α между плоскостями R1 и R2, °
Источник
Контактная прочность

При контактном нагружении сила действует на малом участке поверхности, вследствие чего в поверхностном слое металла возникают высокие местные (локальные) напряжения. Этот вид нагружения встречается при соприкосновении сферических и цилиндрических тел с плоскими, сферическими или цилиндрическими поверхностями.
При теоретическом решении задачи о напряженном состоянии в зоне контакта упругих тел (Герц, Динник, Беляев, Фэппль) предполагают, что нагрузка статическая, материалы тел изотропны, площадка контакта мала по сравнению с поверхностями и действующие силы направлены нормально к этой площадке.
В зоне соприкосновения образуется площадка, размеры которой зависят от упругости материалов и геометрических параметров сжимаемых тел. При сжатии сфер (рис. 215, а) площадка имеет вид окружности диаметром

где Р — нагрузка, Н; Е = 2Е1Е2/(Е1 + Е2) — приведенный модуль упругости материалов сфер, МПа; V = dD/(D ± d) — приведенный диаметр сфер, мм (знак плюс для внешнего контакта — выпуклая поверхность соприкасается с выпуклой поверхностью, минус относится к случаю соприкосновения выпуклой поверхности с вогнутой поверхностью диаметром D).
Давление максимально в центре площадки и в 1,5 раза больше среднего давления:

При сжатии цилиндров (рис. 215, б) площадка имеет вид прямоугольника шириной

где V — приведенный диаметр цилиндров, мм; q — нагрузка на единицу длины цилиндров, Н/мм.

Давление максимально по средней линии площадки и в 1,27 раза превышает среднее давление:

Волокна материала в зоне действия максимальных давлений находятся в состоянии всестороннего сжатия; в них возникают взаимно перпендикулярные напряжения сжатия σx, σy, σz и направленные к ним под углом 45° октаэдрические напряжения сдвига 0,5(σz – σу); 0,5(σz – σx); 0,5(σy – σx). Распределение этих напряжений (в долях максимального давления Рmах на площадке контакта) по глубине поверхностного слоя (в долях ширины b площадки контакта) показано на рис 216.

Нормальные напряжения имеют наибольшую величину (σz = σy = рmax; σx = 0,5pmax) на поверхности; касательные напряжения — на расстоянии (0,25—0,4)b от поверхности (сравни рис. 75).
В условиях всестороннего сжатия предел текучести закаленных сталей высокой прочности достигает 3000—5000 МПа, что примерно в 4—5 раз больше предела текучести при одноосном напряжении сжатия. Допускаемые напряжения 1000—2500 МПа.
В машиностроительных конструкциях нагрузка, как правило, бывает циклической вследствие периодического изменения действующей силы, а также вследствие относительного движения соприкасающихся тел.
Основные схемы работы соединений при контактном нагружении представлены в табл. 27 (в скобках приведены конструктивные аналоги).

В схемах 5—12 нагружение имеет циклический характер, даже если действующая сила статическая, так как нагружению подвергаются последовательно различные точки поверхностей. Относительное перемещение соприкасающихся тел нарушает теоретическое (по Г. Герцу) распределение напряжений в зоне контакта. Поверхностный слой в зоне контакта подвергается сжатию и растяжению в тангенциальном направлении. Расположение зон сжатия и растяжения зависит от характера движения. При чистом качении (схемы 7—9) зоны сжатия на обеих сопрягающихся поверхностях (зачерненные участки) расположены по одну сторону от центра контакта (встречно движению), по другую сторону материал подвергается растяжению.
При скольжении (схема 10) и качении со скольжением (схемы 11, 12) участок сжатия на опережающей поверхности (рис. 217, а) расположен перед центром контакта (встречно движению), а на отстающей поверхности — наоборот; на противоположных участках материал подвергается растяжению (рис. 217, б).

В зоне сжатия опережающей поверхности (рис. 217, в) происходит сближение и сдвиг волокон материала в направлении, указанном стрелками. В зоне растяжения волокна, упруго расправляясь, перемещаются в том же направлении. На отстающей поверхности волокна перемещаются в обратном направлении. В результате на поверхности контакта возникают силы трения, отклоняющие действующие силы от нормали к площадке контакта.
Периодическое сжатие и растяжение волокон вызывает, кроме того, систематическое отставание ведомого тела. Длина поверхности ведущего тела на угле контакта α равна 0,5b – Δb, где Δb — упругое укорочение поверхности. Длина поверхности ведомого тела на том же участке равна 0,5b + Δb’, где Δb’ — упругое удлинение поверхности. Следовательно, скорость вращения ведомого тела меньше скорости ведущего тела в отношении

Из предыдущего ясно, что действительные условия в зоне контакта гораздо сложнее, чем при статическом нагружении, вследствие чего формулы, выведенные для случая статического нагружения, применимы только как первое приближение.
Долговечность циклически нагруженных соединений определяется сопротивлением усталости материала. Кривые сопротивления усталости при контактном нагружении в общем близки к кривым усталости для случаев одноосного напряженного состояния (растяжения, сжатия) с тем различием, что численные значения разрушающих напряжений гораздо выше и кривые не имеют отчетливо выраженного горизонтального участка предела выносливости.

Главное значение для сопротивления усталости в условиях контактного нагружения имеет твердость поверхностного слоя (рис. 218). Процесс усталостного разрушения при контактном нагружении протекает по-особому. Первичные трещины зарождаются в зоне действия максимальных касательных напряжений на глубине, равной 0,3—0,4 размера площадки контакта. Постепенно развиваясь, они выходят на поверхность, образуя характерную точечную сыпь. На дальнейшем этапе точечные дефекты разрастаются и сливаются в цепочки; на участках между цепочками отслаиваются и выкрашиваются крупные частицы металла. Это явление называется питтингом . В результате питтинга соединение, как правило, выходит из строя.
Повышение скорости относительного движения (качение с проскальзыванием) оказывает до известной степени благоприятное влияние. Поврежденный слой в процессе износа постепенно удаляется, вследствие чего выкрашивания не возникает. Долговечность соединения здесь зависит от интенсивности абразивного износа, изменяющего с течением времени первоначальную форму контактных поверхностей.
Типичным примером контактного усталостного разрушения является питтинг рабочих поверхностей зубьев колес. Питтинг сосредоточивается на участках зуба, близких к начальной окружности. Это объясняется тем, что при обычных значениях коэффициента перекрытия (ε = 1,2—1,8) на этих участках нагрузку несет один зуб, а на участках, близких к головке и ножке, — два. Кроме того, на средних участках профиля происходит перекатывание без скольжения, тогда как на участках у головки и ножки имеет место также проскальзывание. Эти участки подвергаются шлифующему действию сопряженных поверхностей, удаляющему поверхностные повреждения, но со временем приводящему к искажению эвольвентного профиля.
Присутствие смазки действует двояко. При умеренных давлениях в зоне контакта масляная пленка способствует более равномерному распределению давлений и увеличению фактической поверхности контакта. Перекатывание поверхностей создает определенный гидродинамический эффект; в пленке, вытесняемой из зазора, возникают повышенные давления, способствующие разделению металлических поверхностей, тем более, что при давлениях, существующих в зоне контакта, увеличивается вязкость масла ( тиксотропический эффект ). В результате нагрузка воспринимается отчасти упругой деформацией выступающих металлических поверхностей, отчасти давлением в масляной пленке ( эластогидродинамическое трение ).
Еще резче выражен гидродинамический эффект при скольжении. Масло, увлекаемое движущейся поверхностью, непрерывно поступает в суживающуюся часть зазора, разделяя металлические поверхности. При благоприятных соотношениях большие скорости скольжения, малые давления, повышенная вязкость масла) в соединении наступает жидкостное трение.
При высоких давлениях в зоне контакта масло оказывает отрицательное влияние. Под действием набегающей поверхности, а также вследствие капиллярности масло внедряется в микротрещины и расширяет их, вызывая ускоренное выкрашивание металла. Особенно резко это явление выражено в случае, если одна из поверхностей в зоне повышенного давления подвергается растяжению (см. рис. 217, в), способствующему раскрытию микротрещин.
Задача повышения прочности контактных соединений заключается прежде всего в снижении давлений на площадке контакта путем придания рациональной формы сопрягающимся поверхностям.
Источник

Контактные напряжения
Местные напряжения, возникающие при взаимном нажатии двух соприкасающихся тел, называют контактными напряжениями. Вследствие деформации материала в месте соприкосновения возникает площадка контакта, по которой и происходит передача давления. Материал вблизи такой площадки, не имея возможности свободно деформироваться, испытывает объемное напряженное состояние.
Контактные напряжения играют основную роль при расчете шариковых и роликовых подшипников, зубчатых колес, элементов кулачковых механизмов и т. д. Эти напряжения определяют методами теории упругости при следующих допущениях: а) в зоне контакта возникают только упругие деформации, следующие закону Гука; б) линейные размеры площадки контакта малы по сравнению с радиусами кривизны соприкасающихся поверхностей; в) силы давления, распределенные по поверхности контакта, нормальны к этим поверхностям; г) на поверхности контакта возникают только нормальные напряжения.
При этих допущениях нормальные напряжения по площадке контакта распределяются по закону поверхности эллипсоида, площадка контакта имеет в общем случае форму эллипса, а максимальное напряжение действует в центре площадки контакта.
Приведем без вывода расчетные формулы для некоторых частных случаев контактной задачи в предположении, что коэффициент Пуассона 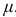 = 0,3. Отметим, что для практических расчетов указанные формулы пригодны и при других значениях
= 0,3. Отметим, что для практических расчетов указанные формулы пригодны и при других значениях 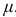 .
.
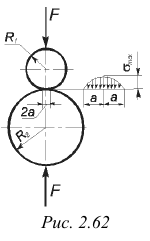
Сжатие шаров. В случае взаимного сжатия силами 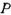 двух упругих шаров радиусов
двух упругих шаров радиусов 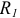 и
и 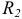 (рис. 2.62) образуется круглая площадка контакта, радиус которой
(рис. 2.62) образуется круглая площадка контакта, радиус которой
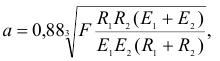
где 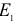 и
и 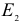 — модули упругости материалов шаров.
— модули упругости материалов шаров.
Максимальное нормальное напряжение в центре площадки контакта
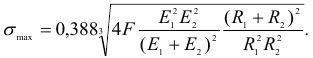
Наиболее напряженная точка находится в центре площадки контакта, где материал испытывает напряженное состояние, близкое к равномерному сжатию (главные напряжения 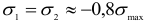 и
и 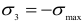 ). Опасная же точка расположена на линии действия сил
). Опасная же точка расположена на линии действия сил 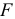 на глубине, примерно равной половине радиуса площадки контакта. Главные напряжения в этой точке
на глубине, примерно равной половине радиуса площадки контакта. Главные напряжения в этой точке
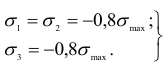
Наибольшее касательное напряжение в опасной точке
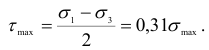
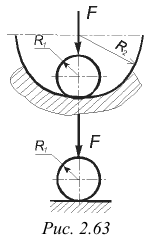
Формула (2.126) справедлива и в случае давления шара на вогнутую сферическую поверхность радиуса 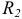 (рис. 2.63, а). Изменив в указанной формуле знак при
(рис. 2.63, а). Изменив в указанной формуле знак при 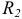 на обратный, имеем
на обратный, имеем
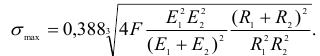
При взаимном давлении шара и плоскости (рис. 2.63, б), полагая 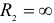 , получим
, получим
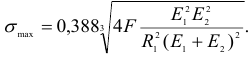
Сжатие цилиндров. Два цилиндра, соприкасающиеся по образующей (рис. 2.64), испытывают взаимное давление по всей длине линии контакта. При равномерно распределенной нагрузке 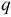 площадка касания имеет вид узкого прямоугольника, ширина которого
площадка касания имеет вид узкого прямоугольника, ширина которого
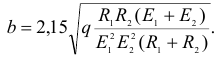
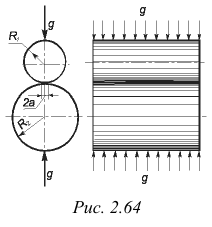
Максимальное напряжение сжатия действует в точках оси площадки контакта:
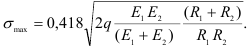
В опасной точке, расположенной на глубине, равной 0,4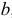 , главные напряжения имеют значения
, главные напряжения имеют значения
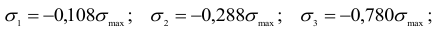
Наибольшее касательное напряжение в опасной точке
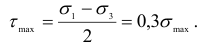
В случае давления цилиндра на деталь с вогнутой цилиндрической поверхностью значение 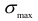 определяют по формуле (2.132), предварительно изменив в ней знак при
определяют по формуле (2.132), предварительно изменив в ней знак при 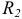 на обратный. Подставив в формулу (2.132) величину
на обратный. Подставив в формулу (2.132) величину 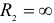 , получим выражение для
, получим выражение для 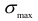 в случае взаимного давления цилиндра и детали с плоской поверхностью.
в случае взаимного давления цилиндра и детали с плоской поверхностью.
На основании формул для определения 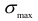 нетрудно установить, что контактные напряжения не являются линейной функцией нагрузки, с ростом сил они возрастают все медленнее. Это объясняется тем, что с увеличением нагрузки увеличивается и площадка контакта. Здесь следует обратить внимание на следующее обстоятельство: если размеры площадки контакта окажутся сопоставимыми с величиной радиусов кривизны соприкасающихся поверхностей, то приведенные выше расчетные зависимости применять нельзя.
нетрудно установить, что контактные напряжения не являются линейной функцией нагрузки, с ростом сил они возрастают все медленнее. Это объясняется тем, что с увеличением нагрузки увеличивается и площадка контакта. Здесь следует обратить внимание на следующее обстоятельство: если размеры площадки контакта окажутся сопоставимыми с величиной радиусов кривизны соприкасающихся поверхностей, то приведенные выше расчетные зависимости применять нельзя.
Аналогичная картина имеет место при определении контактных напряжений между поверхностью тела болта или заклепки и цилиндрической поверхностью отверстия. Местные напряжения в этом случае обычно называют напряжениями смятия и считают, что по площадке контакта (смятия) они распределены равномерно. Такой же закон распределения напряжений по площади контакта принимают и в том случае, если тела до соприкосновения имели плоские поверхности. Учитывая указанное допущение, имеем следующую формулу для определения напряжения смятия:
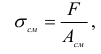
где 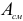 — площадь смятия.
— площадь смятия.
В расчетах на прочность допускаемые напряжения на смятие принимают (на основании опытных данных) в 2-2,5 раза больше допускаемых напряжений на обычное сжатие, т. е.
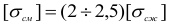
Проверку прочности при контактных напряжениях следует производить по формулам третьей или четвертой теорий прочности.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Предмет прикладная механика
Возможно эти страницы вам будут полезны:

