1. Формула площади равнобедренной трапеции через стороны и угол

b – верхнее основание
a – нижнее основание
c – равные боковые стороны
α – угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):



2. Формула площади равнобокой трапеции через радиус вписанной окружности

R – радиус вписанной окружности
D – диаметр вписанной окружности
O – центр вписанной окружности
H – высота трапеции
α, β – углы трапеции
Формула площади равнобокой трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобокую трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d – диагональ трапеции
α, β – углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

m – средняя линия трапеции
c – боковая сторона
α, β – углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):

5. Формула площади равнобедренной трапеции через основания и высоту

b – верхнее основание
a – нижнее основание
h – высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
![]()
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:

SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
![]()
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:

SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
![]()
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
![]()
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
![]()
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
 ACD
ACD
Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко

Профиль
Благодарили: 0
Сообщений: 1

Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?![]()
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев

Профиль
Благодарили: 0
Сообщений: 8

Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
Формулы площади геометрических фигур
Площадь геометрической фигуры – численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника

-
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты -
Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p – a)(p – b)(p – c)
-
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними. -
Формула площади треугольника по трем сторонам и радиусу описанной окружности
-
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.где S – площадь треугольника,
a, b, c – длины сторон треугольника,
h – высота треугольника,
γ – угол между сторонами a и b,
r – радиус вписанной окружности,
R – радиус описанной окружности,p = a + b + c – полупериметр треугольника. 2
Формулы площади квадрата

-
Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.S = a2
-
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.где S – площадь квадрата,
a – длина стороны квадрата,
d – длина диагонали квадрата.
Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон
S = a · b
где S – Площадь прямоугольника,
a, b – длины сторон прямоугольника.
Формулы площади параллелограмма

-
Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.S = a · b · sin α
-
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.где S – Площадь параллелограмма,
a, b – длины сторон параллелограмма,
h – длина высоты параллелограмма,
d1, d2 – длины диагоналей параллелограмма,
α – угол между сторонами параллелограмма,
γ – угол между диагоналями параллелограмма.
Формулы площади ромба

-
Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.S = a · h
-
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.S = a2 · sin α
-
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.где S – Площадь ромба,
a – длина стороны ромба,
h – длина высоты ромба,
α – угол между сторонами ромба,
d1, d2 – длины диагоналей.
Формулы площади трапеции

-
Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a – b| -
Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высотугде S – площадь трапеции,
a, b – длины основ трапеции,
c, d – длины боковых сторон трапеции,p = a + b + c + d – полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника

-
Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
где S – площадь четырехугольника,
d1, d2 – длины диагоналей четырехугольника,
α – угол между диагоналями четырехугольника. -
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r
-

Формула площади четырехугольника по длине сторон и значению противоположных углов
S = √(p – a)(p – b)(p – c)(p – d) – abcd cos2θ
где S – площадь четырехугольника,
a, b, c, d – длины сторон четырехугольника,
p = a + b + c + d2 – полупериметр четырехугольника,
θ = α + β2 – полусумма двух противоположных углов четырехугольника.
-
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p – a)(p – b)(p – c)(p – d)
Формулы площади круга

-
Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.S = π r2
-
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.где S – Площадь круга,
r – длина радиуса круга,
d – длина диаметра круга.
Формулы площади эллипса
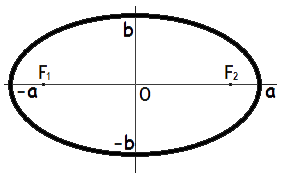
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
S = π · a · b
где S – Площадь эллипса,
a – длина большей полуоси эллипса,
b – длина меньшей полуоси эллипса.
Привет.
Сегодня мы узнаем формулы площадей некоторых фигур.
При решении задач зачастую становится нужным нахождение площадей фигур как по условию задачи, так и в процессе нахождения других каких-то величин. Поэтому давайте сегодня поговорим о них.
Начнем с треугольника и по возрастанию числа вершин.
Для произвольного треугольника существует несколько формул нахождения площади и их применение зависит от ситуации, когда какую будет удобнее применить: которая через высоту, или которая через угол. Когда-то проблематично найти одно, а когда-то выгоднее использовать другое. Формулы следующие:
Однако, есть у нас особый случай – это прямоугольный треугольник. Его площадь можно найти легко, перемножив его катеты. По сути, этот случай использует обе формулы, поскольку за высоту в нем можно принять и катет, да и синус угла 90° это единица. Из чего и получаем данное соотношение:
Также стоит упомянуть ещё одну формулу площади треугольника. Хоть она и выглядит страшно и громоздко, однако иногда, когда не остаётся выхода, ее применить удобнее всего:
Идём далее: четырехугольники. Их большое множество, и для каждого из них есть свои формулы нахождения площади. Однако, есть и формулы, которые применимы для всех четырехугольников. Первая из них требует знание длин диагоналей этого четырехугольника, а также угла между ними, вторая же также, как и для треугольников, требует знание всех сторон для нахождения полупериметра:
Теперь же перейдем к “частным” случаям.
Параллелограмм – по сути, это два равных склеенных треугольника по одной из сторон, поэтому его площадь и равна удвоенной площади треугольника, то есть:
Опять же, если у нас углы в параллелограмме равны по 90°, то мы получаем прямоугольник, и его площадь будет равна длину умножить на ширину (также по сути удвоенная площадь прямоугольного треугольника):
Теперь, что если у нас все стороны в параллелограмме равны. Получаем ромб, площадь которого ищется также, как и у параллелограмма. Однако, у ромба есть одно интересное свойство: его диагонали перпендикулярны. Поэтому, из формулы для произвольного четырехугольника следует ещё и следующая формула, по которой иногда тоже легко считается площадь:
А что если у нас в параллелограмме и все стороны равны, и все углы по 90°? Получаем квадрат. Для него справедливы все формулы, написанные выше, которые даже упрощаются до квадрата стороны.
Далее, у нас идёт трапеция. Для нахождения ее площади формула следующая:
Можно заметить, что полусумма оснований, которая присутствует в этой формуле – это длина средней линии трапеции, вследствие чего получаем:
Перед тем, как идти далее в сторону увеличения вершин фигур, стоит упомянуть кое-что. Зачастую нахождение площадей произвольных фигур – довольно трудная задача. Поэтому часто делаются упрощения: данную фигуру разбивают на более мелкие, и находят их площади, после чего суммируют и получают площадь всей большой фигуры. Однако, это не всегда удобно, поскольку для этого метода нужно знать стороны этих фигур, чтобы ним применить формулы, упомянутые выше. Поэтому далее будем рассматривать формулы площадей для правильных n-угольников – фигур, у которых все стороны и углы равны.
Есть формула, которая использует радиус вписанной окружности:
Кстати, эта формула применима и для некоторых неправильных фигур. Такие фигуры называются выпуклыми. К ним относят фигуры, в которых нет углов превышающих 180°. К ним также относятся треугольники и рассмотренные выше четырехугольники.
Из этой формулы мы можем вывести соотношения для правильных фигур, которые уже разбирали. Так, для правильного треугольника мы получаем следующие соотношения. Для квадрата мы получаем точно такую же формулу, как и ранее – квадрат стороны. Далее идут шестиугольники. Для них формулы следующие. Все формулы приведены на рисунке ниже. Также там указано то, как найти их через радиус описанной окружности.
Далее, что если, у нас 0-угольник. Правильно – это круг, и его площадь ищется по следующей формуле:
Сегодня мы изучили формулы площадей разных плоских фигур. Подписывайтесь на канал, ставьте лайки, пишите свои комментарии. Также предлагайте темы для будущих разборов.
Пока.
#школа #образование #образованиедетей #образованиевроссии #математика #матан
Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.
Некоторые свойства площади фигур
-
Если многоугольники равны, то они имеют равные площади.
-
Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Рис. (1). Нахождение площади многоугольника
Рассмотрим, как найти площадь у разных фигур.
Площадь квадрата
Площадь квадрата равна квадрату его стороны.
, где
a
— длина стороны квадрата.
Площадь прямоугольника
Площадь прямоугольника равна произведению его длины на ширину (смежные стороны).
, где
a
и
b
— длина и ширина.
Площадь параллелограмма равна произведению основания на высоту.

Рис. (2). Параллелограмм
,
a
(
AD
и
CD
) — основание,
h
(
BE
и
BF
) — высота.
Площадь ромба равна половине произведения его диагоналей.

Рис. (3). Ромб

Рис. (4). Треугольник
Площадь треугольника равна половине произведения основания на высоту.
, где
a
(
AD
) — основание,
h
(
BE
) — высота треугольника.
Площадь прямоугольного треугольника равна половине произведения его катетов.

Рис. (5). Трапеция
Площадь трапеции равна половине суммы оснований, умноженной на высоту.
, где
a
(
BC
) и
b
(
AD
) — основания,
h
(
BE
) — высота.
Площадь круга и кругового сектора

Рис. (6). Круг
— площадь кругового сектора.
Более подробно ознакомиться с примерами можно здесь.
