{mu = dfrac{F_{тр}}{mg}}
Ускорение свободного падения g
Приводим 2 варианта нахождения коэффициента трения – зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.
Коэффициент трения представляет собой безразмерную скалярную величину, которая равна отношению силы трения между двумя телами и силы, прижимающей их друг к другу, во время или в начале скольжения.
Коэффициент трения чаще всего обозначают греческой буквой µ («мю»).
Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.
Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).
Содержание:
- калькулятор коэффициента трения
- формула коэффициента трения через силу трения и массу
- формула коэффициента трения через угол наклона
- таблица коэффициентов трения
- примеры задач
Формула коэффициента трения через силу трения и массу

mu = dfrac{F_{тр}}{mg}
Fтр – сила трения
m – масса тела
g – ускорение свободного падения (в большинстве задач можно принять g=9.81 м/с²)
Формула коэффициента трения через угол наклона

mu = tg(alpha)
α – угол наклона
Таблица коэффициентов трения скольжения для разных пар материалов
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Резина по сухому асфальту | 0,95-1,0 | 0,5-0,8 |
| Резина по влажному асфальту | 0,25-0,75 | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,20 | |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лед по льду | 0,05-0,1 | 0,028 |
| Метал по аботекстолиту | 0,35-0,50 | |
| Метал по дереву (в среднем) | 0,60 | 0,40 |
| Метал по камню (в среднем) | 0,42-0,50 | |
| Метал по металу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь(коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примеры задач на нахождение коэффициента трения
Задача 1
Найдите коэффициент трения между полом и ящиком массой 20 кг, который равномерно двигают с силой 50 Н.
Решение
Для решения задачи воспользуемся формулой.
mu = dfrac{F_{тр}}{mg} = dfrac{50}{20 cdot 9.81} = dfrac{50}{196.2} approx 0.25484
Ответ: approx 0.25484
С помощью калькулятора удобно проверить ответ.
Задача 2
Найдите коэффициент трения если угол наклона 30°.
Решение
Для решения этой задачи воспользуемся второй формулой.
mu = tg(alpha) = tg(30°) approx 0.57735
Ответ: approx 0.57735
Проверим полученный ответ с помощью калькулятора .
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 5 августа 2022 года; проверки требует 1 правка.

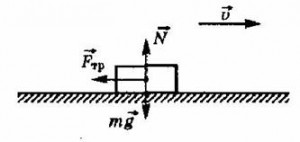
Изображения сил, действующих на скользящее тело.
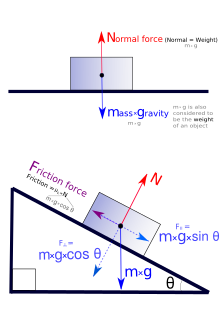
Изображения сил, действующих на тело, находящееся на ровной и наклонной плоскости.
Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении.
Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения, от площади соприкосновения[1].
Величина, характеризующая трущиеся поверхности, называется коэффициентом трения и обозначается обычно латинской буквой 





Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда в большей или меньшей степени происходит преобразование механического движения в другие формы движения материи — чаще всего в тепловую форму движения, и происходит нагревание взаимодействующих тел.
Независимость от площади[править | править код]
Так как никакое тело не является абсолютно ровным, сила трения не зависит от площади соприкосновения, и истинная площадь соприкосновения гораздо меньше наблюдаемой. На самом деле, площадь соприкосновения, казалось бы, ровных поверхностей может находиться в пределах 
Обычно это демонстрируется примером:
Два цилиндра из мягких металлов соединяют плоскими частями, а затем с легкостью отрывают. После этого два цилиндра соединяют и немного двигают относительно друг друга. При этом все неровности поверхности притираются друг к другу, образуя максимальную площадь соприкосновения: появляются силы межмолекулярного притяжения. А после разъединить эти два цилиндра становится очень сложно.
Типы трения скольжения[править | править код]
Если между телами отсутствует жидкая или газообразная прослойка (смазочный материал), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
По физике взаимодействия трение скольжения принято разделять на:
- Сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазочными материалами — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя;
- Сухое с сухой смазкой (графитовым порошком);
- Жидкостное, при взаимодействии тел, разделённых слоем жидкости или газа (смазочного материала) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость;
- Смешанное, когда область контакта содержит участки сухого и жидкостного трения;
- Граничное, когда в области контакта могут содержаться слои и участки различной природы (оксидные плёнки, жидкость и т. д.) — наиболее распространённый случай при трении скольжения;
Также можно классифицировать трение по его области. Силы трения, возникающие при относительном перемещении различных тел, называются силами внешнего трения. Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.
Измерение[править | править код]
В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики. Поэтому нет точной формулы для коэффициента трения. Его оценка производится на основе эмпирических данных: так как по первому закону Ньютона тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения, то для измерения действующей на тело силы трения достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.
Таблица коэффициентов трения скольжения[править | править код]
Значения таблицы взяты из справочника по физике[3]
| Трущиеся материалы (при сухих поверхностях) | Коэффициенты трения | |
|---|---|---|
| покоя | при движении | |
| Алюминий по алюминию | 0,94 | |
| Бронза по бронзе | 0,99 | 0,20 |
| Бронза по чугуну | 0,21 | |
| Дерево по дереву (в среднем) | 0,65 | 0,33 |
| Дерево по камню | 0,46-0,60 | |
| Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
| Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
| Железо по железу | 0,15 | 0,14 |
| Железо по чугуну | 0,19 | 0,18 |
| Железо по бронзе (слабая смазка) | 0,19 | 0,18 |
| Канат пеньковый по деревянному барабану | 0,40 | |
| Канат пеньковый по железному барабану | 0,25 | |
| Каучук по дереву | 0,80 | 0,55 |
| Каучук по металлу | 0,80 | 0,55 |
| Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
| Колесо со стальным бандажем по рельсу | 0,16 | |
| Лёд по льду | 0,028 | |
| Металл по асботекстолиту | 0,35-0,50 | |
| Металл по дереву (в среднем) | 0,60 | 0,40 |
| Металл по камню (в среднем) | 0,42-0,50 | |
| Металл по металлу (в среднем) | 0,18-0,20 | |
| Медь по чугуну | 0,27 | |
| Олово по свинцу | 2,25 | |
| Полозья деревянные по льду | 0,035 | |
| Полозья обитые железом по льду | 0,02 | |
| Резина (шина) по твердому грунту | 0,40-0,60 | |
| Резина (шина) по чугуну | 0,83 | 0,8 |
| Ремень кожаный по деревянному шкиву | 0,50 | 0,30-0,50 |
| Ремень кожаный по чугунному шкиву | 0,30-0,50 | 0,56 |
| Сталь по железу | 0,19 | |
| Сталь (коньки) по льду | 0,02-0,03 | 0,015 |
| Сталь по райбесту | 0,25-0,45 | |
| Сталь по стали | 0,15-0,25 | 0,09 (ν = 3 м/с)
0,03 (ν = 27 м/с) |
| Сталь по феродо | 0,25-0,45 | |
| Точильный камень (мелкозернистый) по железу | 1 | |
| Точильный камень (мелкозернистый) по стали | 0,94 | |
| Точильный камень (мелкозернистый) по чугуну | 0,72 | |
| Чугун по дубу | 0,65 | 0,30-0,50 |
| Чугун по райбесту | 0,25-0,45 | |
| Чугун по стали | 0,33 | 0,13 (ν = 20 м/с) |
| Чугун по феродо | 0,25-0,45 | |
| Чугун по чугуну | 0,15 |
Примечания[править | править код]
- ↑ 1 2 Билимович Б. Ф. Законы механики в технике. – М., Просвещение, 1975. – Тираж 80000 экз. – с. 58
- ↑ Сила трения. ЗФТШ, МФТИ. Дата обращения: 14 февраля 2019. Архивировано 13 февраля 2019 года.
- ↑ Енохович А. С. Справочник по физике. — Просвещение, 1978. — С. 85. — 416 с.
Коэффициент трения скольжения


4
Средняя оценка: 4
Всего получено оценок: 100.
4
Средняя оценка: 4
Всего получено оценок: 100.
Физическая величина, характеризующая трущиеся поверхности, называется коэффициентом трения скольжения. Величина обозначается буквой μ. Коэффициент трения определяют опытным путём.
Сила трения скольжения
На покоящиеся и движущиеся тела всегда действуют силы трения. Они возникают при соприкосновении твердых тел, твердых тел и жидкостей или газов и подчиняются законам Ньютона. Направление сил трения противоположно движению тела и силам, стремящимся изменить его положение.
В случае, когда тело движется относительно другого, говоря о трении скольжения. Она зависит от:
- Силы нормальной реакции опоры $vec N$,
- От скорости движения (но в вычислениях этой зависимостью пренебрегают),
- От безразмерного коэффициента трения скольжения $mu$, который характеризует свойства и состояние поверхностей соприкосновения.

Коэффициент зависит от свойств материала. Чем больше шероховатость поверхности, тем больше значение коэффициента и, соответственно, больше сила трения. Коэффициент трения смазанных поверхностей будет меньше, чем у несмазанных для одной и той же пары материалов. Также коэффициент трения зависит от скорости. Однако эта зависимость минимальна и ей пренебрегают, если не требуется точность измерения. Поэтому коэффициент трения считается постоянным.
Расчет коэффициента трения скольжения
С достаточно большой точностью силу трения скольжения рассчитывают как предельную силу трения покоя по формуле:
$F_{тр} = mu cdot N$.
Тогда формула коэффициента трения скольжения:
$mu ={{F_{тр}} over {N}}$
Значение N рассчитывается как произведение массы тела на ускорение свободного падения и на косинус угла к поверхности приложения:
$N = m cdot g cdot cos alpha$
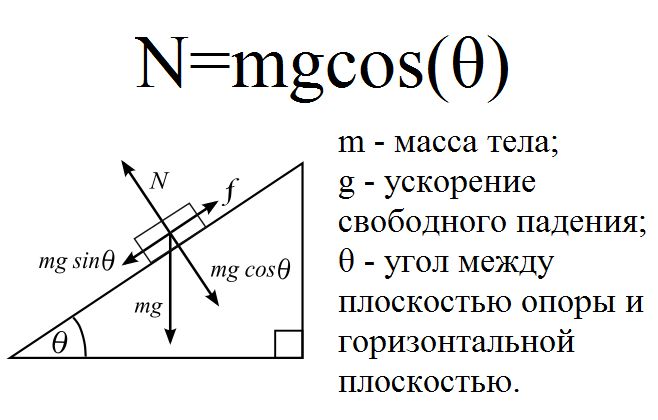
Для большинства пар материалов коэффициент рассчитан опытным путём. Значения находятся в пределах 0,1…0,5. Некоторые значения представлены в таблице.
|
Трущиеся материалы |
Коэффициенты трения |
|
|
Покоя |
При движении |
|
|
Алюминий по алюминию |
0,94 |
|
|
Бронза по бронзе |
0,20 |
|
|
Бронза по чугуну |
0,21 |
|
|
Дерево по дереву |
0,65 |
0,33 |
|
Дерево по камню |
0,46-0,60 |
|
|
Дуб по дубу (вдоль волокон) |
0,62 |
0,48 |
|
Дуб по дубу (перпендикулярно волокнам) |
0,54 |
0,34 |
|
Железо по бронзе |
0,19 |
0,18 |
|
Железо по железу |
0,15 |
0,14 |
|
Железо по чугуну |
0,19 |
0,18 |
|
Каучук по дереву |
0,80 |
0,55 |
|
Каучук по металлу |
0,80 |
0,55 |
|
Кирпич по кирпичу (гладко отшлифованные) |
0,5-0,7 |
|
|
Лёд по льду |
0,028 |
|
|
Медь по чугуну |
0,27 |
|
|
Металл по дереву |
0,60 |
0,40 |
|
Металл по камню |
0,42-0,50 |
|
|
Металл по металлу |
0,18-0,20 |
|
|
Олово по свинцу |
2,25 |
|
|
Полозья деревянные по льду |
0,035 |
|
|
Обитые железом полозья по льду |
0,02 |
|
|
Резина (шина) по твёрдому грунту |
0,40-0,60 |
|
|
Резина (шина) по чугуну |
0,83 |
0,8 |
|
Сталь (коньки) по льду |
0,02-0,03 |
0,015 |
|
Сталь по железу |
0,19 |
|
|
Сталь по стали |
0,15-0,25 |
0,09 при 3 м/с, 0,03 при 27 м/с |
|
Чугун по дубу |
0,65 |
0,30-0,50 |
|
Чугун по стали |
0,33 |
0,13 |
|
Чугун по чугуну |
0,15 |
Коэффициент трения – переменная величина. Поэтому значение коэффициента трения скольжения, приведённые в таблице, являются истинными только при соблюдении определённых условий, в которых были получены.

Что мы узнали?
Коэффициент трения скольжения – физическая величина, характеризующая трущиеся поверхности. Как найти: $mu = {{F_{тр}} over {N}}$. На практике коэффициент рассчитывается исходя из свойств материала эмпирическим путём.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 100.
А какая ваша оценка?
Коэффициент трения скольжения — отношение силы трения к нормальной составляющей внешних сил, действующих на поверхности тела.
![]()
Коэффициент трения скольжения выводится из формулы силы трения скольжения
![]()
Так как сила реакции опоры, это масса умножить на ускорение свободного падения, то формула коэффициента получается:
![]()
Ниже приведена таблица коэффициентов трения скольжения для некоторых материалов:

В Формуле мы использовали :
![]() — Коэффициент трения скольжения
— Коэффициент трения скольжения
![]() — Сила трения скольжения
— Сила трения скольжения
![]() — Сила нормальной реакции опоры
— Сила нормальной реакции опоры
![]() — Масса тела
— Масса тела
![]() — Ускорение свободного падения
— Ускорение свободного падения
Коэффициент трения скольжения — отношение силы трения к силе нормальной реакции опоры.
![]()
Коэффициент трения скольжения выводится из формулы силы трения скольжения: Ft=μ·N
Так как сила реакции опоры N, это масса умножить на ускорение свободного падения, то формула коэффициента получается:
![]()
Ниже приведена таблица коэффициентов трения скольжения для некоторых материалов:

Обозначения:
μ — коэффициент трения скольжения
Ft — сила трения скольжения
N — сила нормальной реакции опоры
m — масса тела
g — ускорение свободного падения