Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июня 2021 года; проверки требуют 3 правки.

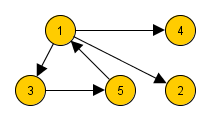
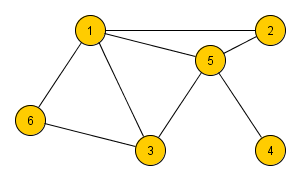
Рис. 1. Граф, на вершинах которого отмечены степени.
Степень (валентность) вершины графа — количество рёбер графа 

При подсчёте степени ребро-петля учитывается дважды.[1]
Степень вершины обычно обозначается как 

Максимальная и минимальная степень вершин графа G обозначаются соответственно Δ(G) и δ(G).
На рис. 1 максимальная степень равна 5, минимальная — 0.
В регулярном графе степени всех вершин одинаковы, поэтому в данном случае можно говорить о степени графа.
Лемма о рукопожатиях[править | править код]
По формуле суммы степеней для графа 
то есть сумма степеней вершин любого графа равна удвоенному числу его рёбер. Кроме того, из формулы следует, что в любом графе число вершин нечётной степени чётно. Данное утверждение (и сама формула) известны как лемма о рукопожатиях. Название происходит от известной математической задачи: необходимо доказать, что в любой группе число людей, пожавших руку нечётному числу других, чётно.
Последовательность степеней вершин[править | править код]

Рис. 2. Два неизоморфных графа с одинаковой последовательностью степеней (3, 2, 2, 2, 2, 1, 1, 1).
Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью.[2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристикой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.
Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.
Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность di (при i = 1,…,n) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство
Например, последовательность (3, 3, 3, 1) не может являться последовательностью простого графа; она удовлетворяет неравенству Эрдёша — Галлаи только при k равном 1, но не при k равном 2 или 3.
Согласно критерию Гавела — Хакими, если невозрастающая последовательность (d1, d2, …, dn) это последовательность степеней простого графа, то (d2 − 1, d3 − 1, …, dd1+1 − 1, dd1+2, dd1+3, …, dn) некоторая последовательность степеней простого графа. Этот факт позволяет построить полиномиальный алгоритм нахождения простого графа с заданной реализуемой последовательностью.
Сопоставим исходной последовательности чисел вершины графа без ребер с требуемыми степенями. Указанное преобразование последовательностей задает как минимум одну вершину графа, все инцидентные ей ребра и множество вершин с новыми требуемыми дополнениями степеней. Упорядочивая оставшиеся вершины по невозрастанию дополнений степеней, получим невозрастающую последовательность степеней простого графа. Повторяя преобразование и упорядочение не более n-1 раза, получаем весь граф.
Проблема нахождения или оценки числа графов по заданной последовательности относится к области перечисления графов.
Частные значения[править | править код]

Рис. 3. Концевыми вершинами являются 4, 5, 6, 7, 10, 11 и 12.
- Вершина степени 0 называется изолированной.
- Вершина степени 1 называется концевой (англ. end vertex), висячей (англ. pendant vertex) или листом графа (англ. leaf vertex). Ребро, инцидентное такой вершине называется висячим (англ. terminal (pendant) edge, end-edge). На рис. 3 висячим ребром является {3,5}. Подобная терминология используется в изучении деревьев в общем и как структур данных.
- Вершина степени n-1 графа порядка n называется доминирующей (англ. dominating vertex).
Общие свойства[править | править код]
- Если все вершины графа имеют одинаковую степень k, граф называют k-регулярным или регулярным графом степени k. В этом случае сам граф имеет степень k.
- Эйлеров путь существует в неориентированном, связном графе тогда и только тогда, когда граф имеет 0 или 2 вершины нечётной степени. Если граф содержит 0 вершин нечётной степени, Эйлеров путь является циклом.
- Орграф является псевдолесом[неизвестный термин] только если полустепень исхода каждой вершины не больше 1. Функциональный граф — частный случай псевдолеса, в котором полустепени исхода всех вершин равны 1.
- Согласно теореме Брукса, хроматическое число любого графа за исключением клики или нечётного цикла не превышает максимальной степени его вершин (Δ). Согласно теореме Визинга, хроматический индекс любого графа не превышает Δ + 1.
- k-вырожденным графом называется граф, в котором каждый подграф имеет вершину степенью не больше k.
См. также[править | править код]
- Полустепень захода и полустепень исхода вершин ориентированных графов
- Распределение степеней
Примечания[править | править код]
- ↑ Дистель, стр. 5
- ↑ Дистель, стр. 278
Источники[править | править код]
- Дистель, Рейнхард (2005), Graph Theory (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-26183-4, <http://diestel-graph-theory.com/index.html>.
- Эрдёш, П. & Галлаи, T. (1960), Gráfok előírt fokszámú pontokkal, Matematikai Lapok Т. 11: 264—274, <http://www.renyi.hu/~p_erdos/1961-05.pdf>.
- Хакими, С. Л. (1962), On realizability of a set of integers as degrees of the vertices of a linear graph. I, Journal of the Society for Industrial and Applied Mathematics Т. 10: 496–506.
- Сирксма, Хирард & Хоохефен, Хан (1991), Seven criteria for integer sequences being graphic, Journal of Graph Theory Т. 15 (2): 223–231, DOI 10.1002/jgt.3190150209.
Время на прочтение
4 мин
Количество просмотров 23K
“Графы являются одним из объединяющих понятий информатики – абстрактное представление, которое описывает организацию транспортных систем, взаимодействие между людьми и телекоммуникационные сети. То, что с помощью одного формального представления можно смоделировать так много различных структур, является источником огромной силы для образованного программиста”. Стивен С. Скиена
В этой статье:
-
Введение
-
Классификация графов
Введение
Сначала под землей города Москвы ничего не было. Потом была построена первая станция метро, а затем и вторая и третья. Образовалось множество станций метро. На карту было занесено множество точек. Позже между станциями стали прокладывать пути линии. И соединилась станция метро А со станцией метро Б. Все остальные станции также стали соединятся друг с другом и на карте появилось множество линий. В итоге мы имеем Московский метрополитен очень красивый, я там был проверял.
Посмотрите какая красота. У нас имеется множество точек (которые называются вершинами или узлами), а также множество линий (называемые рёбрами или дугами). Обозначим множество вершин буквой V от английского vertex−вершина и множество рёбер обозначим E от английского edge−ребро. Граф в формулах именуют буквой G. Все вершины обязательно должны быть идентифицированы.
Отмечу, что число вершин обозначается буквой n:

Число рёбер обозначается буквой m:

Таким образом граф задается и обозначается парой V,E:
Граф – это совокупность пары множеств. Конечного есть и бесконечные, однако мы их пока не рассматриваем непустого множества V и множества E заданного неупорядоченными парами множества V.
Также определение графа рассказывается в этой статье на Хабре (https://habr.com/ru/post/65367/)
Неформально граф является совокупностью точек и линий. Линии в котором задаются парой вершин, расположенных не важно в каком порядке.
Разберем определение графа подробней. Может ли в G быть пустым множество E? Да без проблем! Такой граф будет называться нулевым, а вершины в нем будут называться изолированными.

Только вот множество V вершины пустым быть не может. Ведь множество E рёбра задается парой неупорядоченных вершин множества V. Две вершины образующие ребро, называются концами этого ребра.
Множество E задается парой неупорядоченных вершин множества V.
Пример: Пусть множество V = {1,2,3,4,5}. Тогда множество E = {1,2, 2,3, 3,4, 1,5, 1,4, 3,1}
Граф будет выглядеть следующим образом:

Висячей вершиной называется вершина которая соединена только с одной соседней вершиной. В нашем случаи висячей вершиной будет вершина 5, так как она соединена только с вершиной 1.
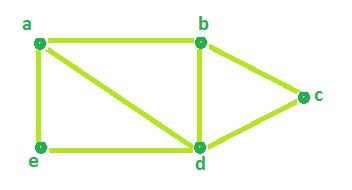
Степенью вершины – является количество рёбер исходящих выходящих из вершины и входящих в нее. Данное определение верно для ориентированных графов см. классификацию графов. Для неориентированных графов исходящая степень равна входящей. Степенью вершины 1 будет является число 4. Так как вершина 1 соединена с вершиной 2, 3, 4, 5.
Степень записывают, как:
Максимальная степень, то есть какое количество степеней вообще присутствуют в графе обозначаются, как:
Минимальную как:
Формула суммы степеней для G = V,E выглядит так:
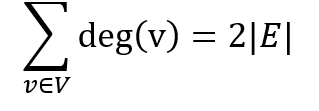
То есть сумма степеней всех вершин v графа равна удвоенному количеству его рёбер E. Считаем количество степеней в нашем примере. От этого никуда не денешься. Я насчитал 12. А теперь считаем, сколько у нас рёбер. Их 6! Умножаем на 2 и получаем 12. Совпадение? Не думаю!
А давайте представим наш граф в другом виде, но с сохранением данных пар. G теперь имеет следующий вид:

Заметьте я не изменил пары между собой. Вершина 4 также соединяется с вершиной 3, а у вершины 1 степень также осталась 4. Так почему граф имеет совершенно другой вид и законно ли это?
Самое главное в графе это вершины и проведенные между ними рёбра. В связи с этим граф является топологическим объектом, а не геометрическим . То есть объектом который не меняется при любых растяжениях и сжатиях. Нам все равно какой мы сделали отрезок. Кривой, прямой, самое главное это наличие связи между вершинами. По этой причине графы являются очень универсальными в плане практического применения. Мы можем обозначать ими дороги, компьютерную сеть, людей которые дружат друг с другом или даже влюблены друг в друга.
Классификации графов
-
Первым признаком классификации является отсутствие или наличие ориентации у ребер.
Ребро является неориентированным если у него нет понятия начала или конца. То есть оба его конца равноправны. Такой граф называется неориентированным, обыкновенным или неографом.
Ориентированное ребро обозначается стрелкой. И указывает ориентацию от вершины к вершине. То есть данный граф имеет начало и конец. И называется он ориентированным или орграфом.
Также существует граф со смешанными ребрами. Это когда в графе присутствуют, как ориентированные рёбра, так и неориентированные.

-
Вторым признаком является отсутствие или наличие кратных ребер.
Кратные ребра – это ребра которые встречаются между двумя вершинами сразу несколько раз. В примере ниже мы видим, что вершина a соединена с вершиной c несколько раз. То же самое происходит и a c b. Такой граф называется мультиграфом.
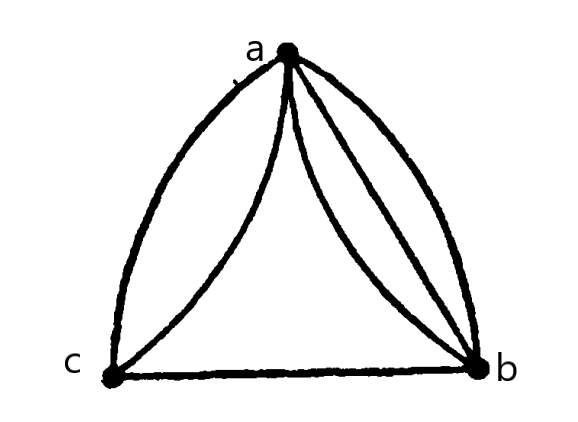
Граф в котором кратных ребер нет, является простым графом. В простом графе мы просто называем пару вершин для идентификации ребра, но в мультиграфе такое уже не сработает, так как одна и та же пара вершин будет указывать на два ребра и не понятно что к чему будет относится. Поэтому если вы повстречаете мультиграф, то вы должны обозначить каждое ребро отдельно.
Заключение
В данной стать я не рассмотрел, понятия смежности и инцидентности, однако я решил их рассмотреть в следующий раз. Также хочу отметить, что более подробно виды графов, я буду рассматривать в следующих статьях. Если у вас есть вопросы, предложения или я где-то допустил ошибки, то прошу написать их в комментариях.
Граф Г называется
полным, если каждые две его вершины
соединены одним и только одним ребром.
А
В
С
Д – не полный граф
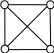
А В
С Д – полный граф
Только
для неориентированного графа существует
дополнение:
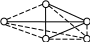
Г

![]()
– дополнение
Дополнением
графа Г называется новый граф
,
состоящий из всех тех же вершин, что и
граф Г и тех и только тех ребер, которые
надо добавить, чтобы граф Г стал полным.
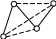

Степенью вершины
называется количество ребер ей
принадлежащих

В Д
Е
А С
Степень А=1, степень
В=2, степень С=2, степень Д=1, степень Е=0
Степень каждой
вершины полного графа на единицу меньше
числа вершин.
Теорема:
Сумма степеней всех вершин графа есть
число четное и равное удвоенному
количеству ребер
![]()
При
большом количестве вершин схема теряет
свою наглядность и поэтому используют
другой способ задания графов в виде
матрицы смежностей.
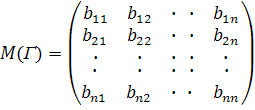
где
каждое 
М
– симметричная на главной диагонали –
0
М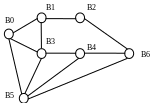
(Г)=

Лабораторная работа № 2.
Задание графа
матрицей смежности
Цель работы:
-
Изучить понятия
полный граф, дополнение графа. -
Рассмотреть способ
задания графа с помощью матрицы
смежности.
Литература:
-
“‘Графы и их
применение”. Березина Л.Ю.. М:
Просвещение. 1979г. -
“Теория графов.
Алгоритмический подход”, Кристофидес
Н. -
“Применение
теории графов в программировании”.
Евстигнеев В.А. – М.: Наука. 1985г.
Порядок
выполнения работы:
I
Разработать схему
алгоритмов основной программы и
подпрограмм.
II
Написать
и отладить программу на языке Turbo
Pascal.
Задача
Граф задан матрицей
смежности
М=
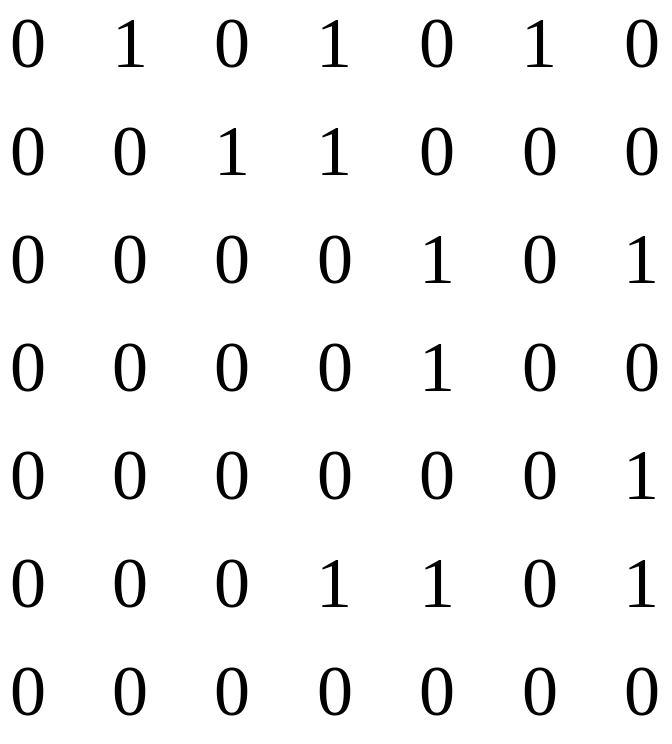
Изобразить
граф, исходя из внешнего вида данной
матрицы.
Краткие
теоретические сведения:
Матричный эквивалент
графа широко используется в работе с
графами на ЭВМ.
Граф называется
полным, если каждые две его вершины
соединены одним и только одним ребром.

-полный
граф
от граф не является
полным
Граф, не являющийся
полным, можно преобразовать в полный
граф с теми же вершинами, добавив
недостающие ребра.
Вершины
графа Г и ребра, которые добавлены, также
образуют граф, такой граф называется
дополнением и обозначается ![]()
.
Каждой
вершине графа ![]()
можно поставить в соответствие строку
и столбец с номером i,
причем
{
1, если ![]()
![]()
{
0, если ![]()
Тогда
матрица 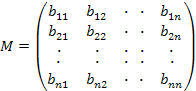
называется
матрицей смежностей графа Г и обозначается
М(Г).
Содержание
отчета:
-
Составление
алгоритмов. -
Написание
программы на языке Turbo
Pascal -
Отладка программы.
Контрольные
вопросы:
-
Что такое полный
граф? -
Дайте понятие
дополнение графа? -
Что такое матрица
смежностей графа? -
Как составить
матрицу смежностей?
Тема 7.3 Метрические характеристики графа.
П
усть
дан граф:
А3
Как от вершины А1
дойти до А5?
Существуют
следующие пути:
-
<A1,A4>,<A4,
A5> -
<A1, A2>,<A2,
A4>,<A4, A5> -
<A1, A3>,<A3,
A4>,<A4, A5> -
<A1,
A4>,<A4, A2>,<A2, A1>,<A1, A3>,<A3, A4>,<A4,
A5> -
<A1,
A4>,<A4,A2>,<A2, A1>,<A1, A4>,<A4, A5> –
не
является
путем,
т.к.
ребро
<A1, A4> встречается
дважды.
Путем
от вершина А1 до вершины Аn
называется такая последовательность
ребер, ведущая от А1 до Аn,
что любые два соседних ребра имеют общую
вершину и ни одного ребра не встречается
дважды.
Путь, в котором
начальные и конечные вершины совпадают
называют циклом.
Путь
от вершины А1 до Аn
называется простым, если он не проходит
ни через одну из вершин графа более
одного раза.
Цикл называется
простым, если он не проходит ни через
одну из вершин графа более одного раза.
Длиной пути (цикла)
называется количество ребер его
составляющих.
Дан граф. Найти
пути от А1 до А6 и определить их длину
-
<A1,A6>,
d=1 -
<A1,
A2>,<A2,
A6>,
d=2 -
<A1,
A2>,<A2, A5>,<A5, A4>,<A4, A3>,<A3, A2>,<A2,
A6>, d=6 -
<

A1,
A2>,<A2, A3>,<A3, A4>,<A4, A5>,<A5, A2>,<A2,
A6>, d=6
Р
асстоянием
от вершины А до вершины В называется
длина наименьшего пути, если не существует
пути от А до В, то считают что расстояние
равно бесконечности.
S(A1,A6)=1
S(A1, A7)=∞
В
ершины
А и В называются связными, если не
существует пути связывающего их.
Вершины:
-
A
и D
– несвязные -
A
и Е – несвязные -
А и В – связные
-
А
и С – связные
Соседние файлы в предмете Дискретная математика
- #
- #
- #
Содержание
- 1 Неориентированный граф
- 2 Ориентированный граф
- 3 Бесконечный граф
- 4 Регулярный граф
- 5 Источники информации
Неориентированный граф
| Лемма: |
|
Сумма степеней всех вершин графа (или мультиграфа без петель) — чётное число, равное удвоенному числу рёбер: |
| Доказательство: |
| Возьмем пустой граф. Сумма степеней вершин такого графа равна нулю. При добавлении ребра, связывающего любые две вершины, сумма всех степеней увеличивается на 2 единицы. Таким образом, сумма всех степеней вершин чётна и равна удвоенному числу рёбер. |
Например, для следующего графа выполнено:
Следствие 1. В любом графе число вершин нечётной степени чётно.
Следствие 2. Число рёбер в полном графе .
Ориентированный граф
| Лемма: |
|
Сумма входящих и исходящих степеней всех вершин ориентированного графа — чётное число, равное удвоенному числу рёбер: |
| Доказательство: |
|
Аналогично доказательству леммы о рукопожатиях неориентированном графе. То есть возьмем пустой граф и будем добавлять в него рёбра. При этом каждое добавление ребра увеличивает на единицу сумму входящих и на единицу сумму исходящих степеней. Таким образом, сумма входящих и исходящих степеней всех вершин ориентированного графа чётна и равна удвоенному числу рёбер. |
Бесконечный граф

Пример бесконечного графа, в котором не выполняется лемма
В бесконечном графе лемма не работает, даже в случае с конечным числом вершин нечётной степени. Покажем это на примере.
При выборе бесконечного пути из вершины (см. рисунок справа) имеем путь, в котором все вершины кроме стартовой имеют чётную степень, что противоречит следствию из леммы.
Регулярный граф
| Определение: |
| Граф называется регулярным, если степени всех его вершин равны. |
| Утверждение: |
|
В регулярном графе с вершинами ровно рёбер. |
| Утверждение: |
|
Если степень каждой вершины нечётна и равна , то количество рёбер кратно . |
|
Регулярный граф с рёбрами Действительно, так как степень каждой вершины нечётна, то число вершин в графе чётно(так сумма степеней всех вершин чётна). Пусть , то равенство принимает вид , то есть количество рёбер кратно . |
Источники информации
- Lecture Notes on Graph Theory By Tero Harju, Department of Mathematics University of Turku, 2011 — с. 7-8
- Handshaking lemma — Wikipedia