Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 марта 2018 года; проверки требуют 2 правки.
Мгнове́нный центр скоросте́й — при плоскопараллельном движении абсолютно твёрдого тела точка, связанная с этим телом, которая имеет следующие свойства: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело. Она существует в любой момент времени, но её положение меняется со временем за исключением одного случая — вращательного движения.
Положение мгновенного центра скоростей[править | править код]
Рис. 1. При качении колеса по горизонтальной дороге мгновенный центр скоростей находится в точке касания колеса и дороги — в точке А. 


Для того, чтобы определить положение мгновенного центра скоростей, необходимо знать направления скоростей любых двух различных точек тела, скорости которых не параллельны. Тогда для определения положения мгновенного центра скоростей необходимо провести перпендикуляры к прямым, параллельным линейным скоростям выбранных точек тела. В точке пересечения этих перпендикуляров и будет находиться мгновенный центр скоростей.
В том случае, если векторы линейных скоростей[1] двух различных точек тела параллельны друг другу, и отрезок, соединяющий эти точки, не перпендикулярен векторам этих скоростей, то перпендикуляры к этим векторам также параллельны. В этом случае говорят, что мгновенный центр скоростей находится в бесконечности, и тело движется мгновенно поступательно.
Если известны скорости двух точек, и эти скорости параллельны друг другу, и кроме того, указанные точки лежат на прямой, перпендикулярной скоростям, то положение мгновенного центра скоростей определяется так, как показано на рис. 2.
Положение мгновенного центра скоростей в общем случае не совпадает с положением мгновенного центра ускорений. Однако в некоторых случаях, например, при чисто вращательном движении, положения этих двух точек могут совпадать.

Рис. 2. Векторы скоростей точек колеса, лежащих на прямой РМ, образуют подобные треугольники; мгновенный центр скоростей находится в точке Р
Более общий случай сферического движения[править | править код]
Согласно теореме вращения Эйлера, любое вращающееся трёхмерное тело, имеющее неподвижную точку, также имеет и ось вращения. Таким образом, в более общем случае вращения трёхмерного тела говорят о мгновенной оси вращения.

Рис. 3. Чтобы определить положение мгновенного центра скоростей для шатуна в кривошипно-шатунном механизме, обычно необходимо провести перпендикуляры к векторам скоростей концов шатуна; мгновенный центр скоростей обозначен как CIR
Пример решения задачи[править | править код]
Найдём скорость точки K для колеса, показанного на рисунке 1, если задана скорость центра колеса (точки С), его радиус и угол АСК:



Решение
Найдём сначала угловую скорость колеса в данный момент времени при его вращении вокруг мгновенного центра скоростей (вокруг точки А):

Теперь, зная угловую скорость, найдём скорость точки К:

Чтобы найти численное значение 

или, учтя, что 

Вынесем R за знак корня:

Подставив заданые в условии численные значения, найдём:

Тогда, зная расстояние КА, можем найти численное значение скорости 

Ответ: 
Заметим, что для решения задачи знать численное значение R не обязательно.
Действительно, подставляя в формулу (*) выражения для 

Применение понятия мгновенного центра скоростей[править | править код]
Данное понятие используется при анализе движения звеньев кривошипно-шатунного механизма (рис. 3). Например, если известна постоянная угловая скорость вращающегося кривошипа (на рисунке 3 показан красным цветом), то скорость поршня не будет постоянной по модулю. Чтобы вычислить скорость поршня в разных положениях и построить соответствующий график, можно воспользоваться понятием мгновенного центра скоростей[2]. В свою очередь кривошипно-шатунные механизмы применяются в двигателях внутреннего сгорания, поршневых насосах, поворотных гидродвигателях и многих других устройствах. Таким образом, использование понятия мгновенного центра скоростей позволяет производить расчёты, необходимые для выбора оптимальной конструкции указанных механизмов.
Движения коленного, локтевого, плечевого и др. суставов биофизики также исследуют с помощью мгновенного центра скоростей.
Улучшения тормозных характеристик автомобилей можно добиться путём выбора оптимальной конструкции педалей тормоза и соответствующих кинематических расчётов, проведённых с помощью мгновенного центра скоростей.
Примечания[править | править код]
- ↑ Показанные на рис. 1 скорости являются линейными
- ↑ Скорости поршня в разных положениях можно также рассчитать графически с помощью плана скоростей
Литература[править | править код]
- Тарг С. М. Краткий курс теоретической механики. Учеб. для втузов.— 10-е изд., перераб. и доп. — М.: Высш. шк., 1986.— 416 с, ил.
- Основной курс теоретической механики (часть первая) Н. Н. Бухгольц, изд-во «Наука», Главная редакция физико-математической литературы, Москва, 1972, 468 стр.
В любой момент времени скорости
любых двух точек плоской фигуры
![]() и
и![]() связаны равенством
связаны равенством
|
|
|
Рис. 2.3 |
![]() (a)
(a)
Вектор
![]() представляет собой скорость, полученную
представляет собой скорость, полученную
точкой![]() при вращении плоской фигуры вокруг оси,
при вращении плоской фигуры вокруг оси,
проходящей через полюс![]() перпендикулярно плоской фигуре. Этот
перпендикулярно плоской фигуре. Этот
вектор направлен перпендикулярно
отрезку![]() (по касательной к окружности, которую
(по касательной к окружности, которую
описывает точка![]() при вращении тела вокруг оси
при вращении тела вокруг оси![]() ),
),
причем в сторону вращения тела (Рис.
2.3). В соответствии с формулой Эйлера
![]()
Пример 2.4
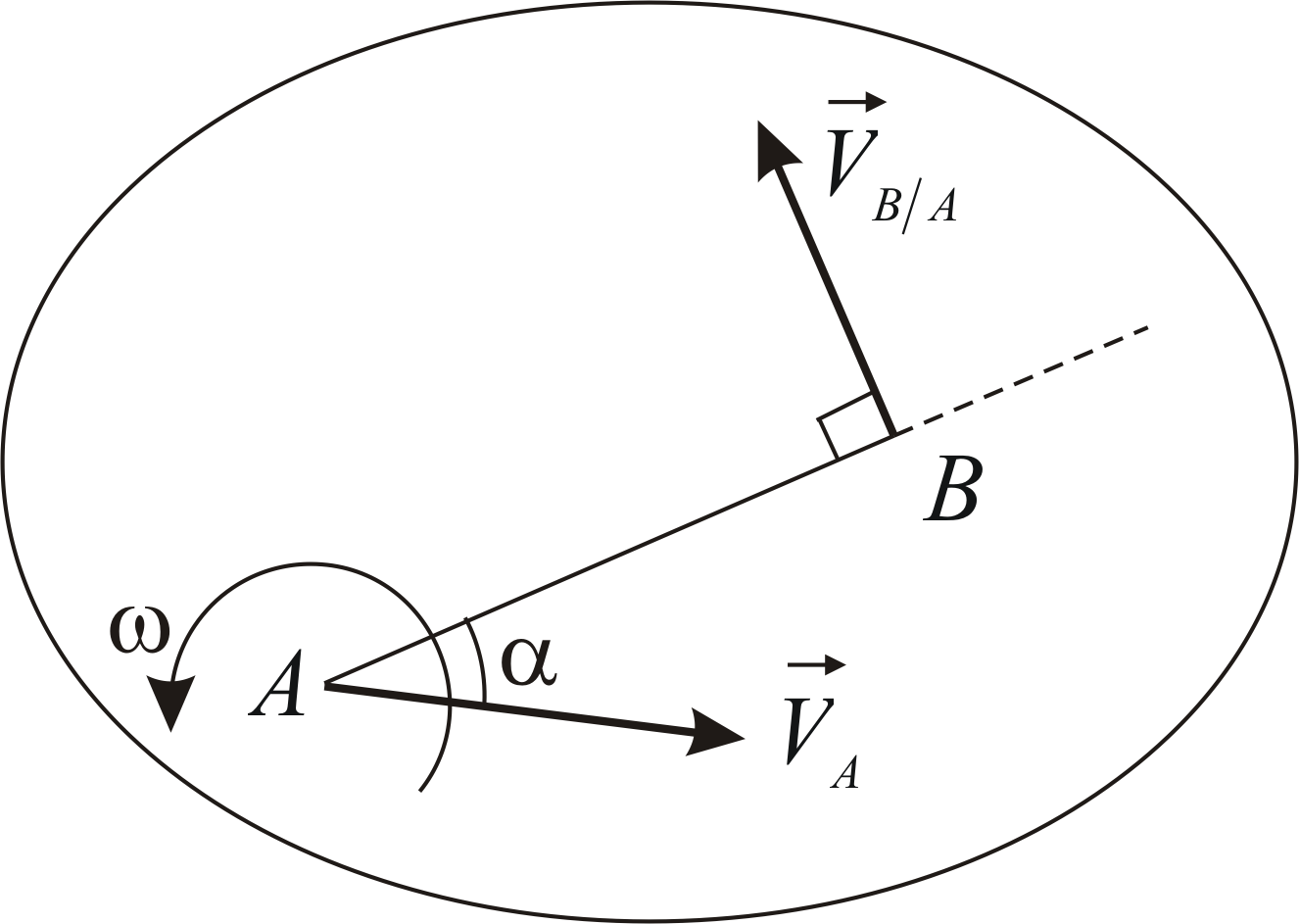
Пластина совершает плоскопараллельное
движение. В данный момент времени угловая
скорость пластины равна
![]() ,
,
проекция на ось![]() скорости точки
скорости точки![]() пластины равна
пластины равна![]() .
.
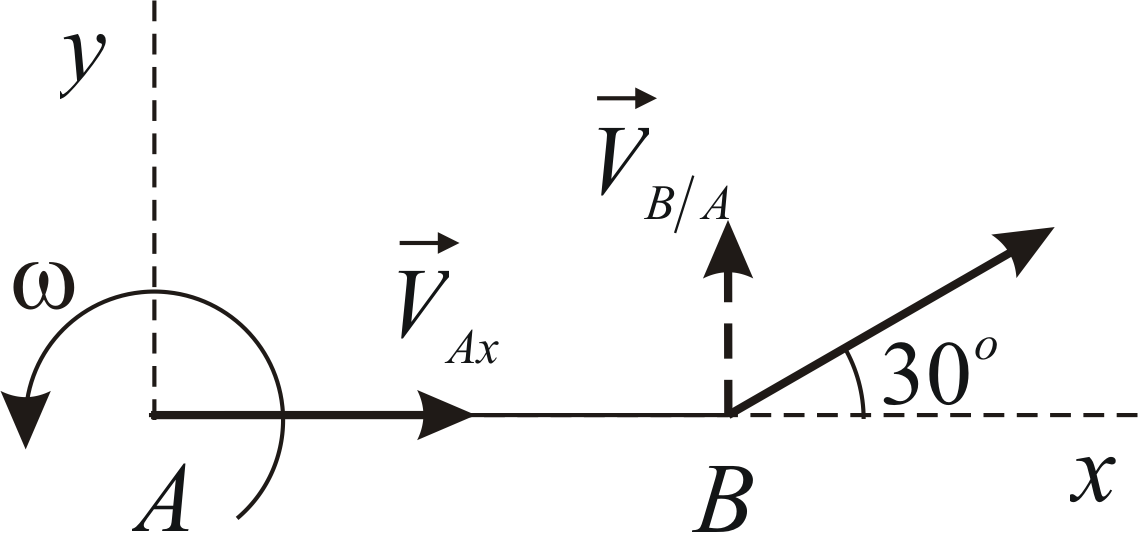
Скорость точки![]() образует с осью
образует с осью![]() угол
угол![]() (Рис. 2.4). Определить модули скоростей
(Рис. 2.4). Определить модули скоростей
точек![]() и
и![]() ,
,
если![]() .
.
|
|
|
Рис. 2.4 |
Запишем уравнение (a)
в проекциях на координатные оси:
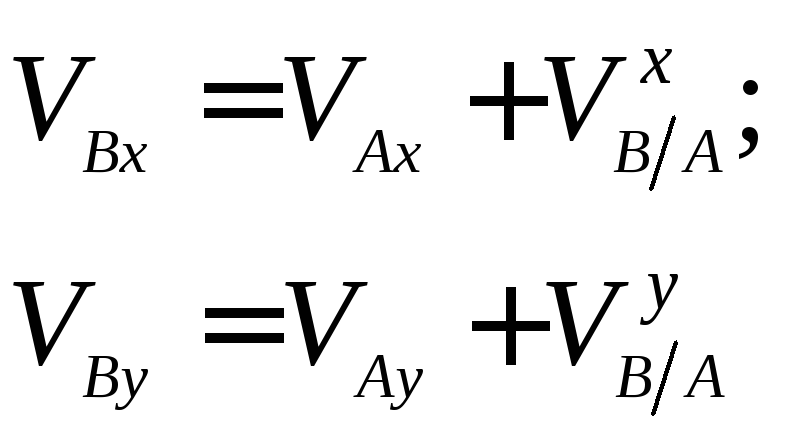 или
или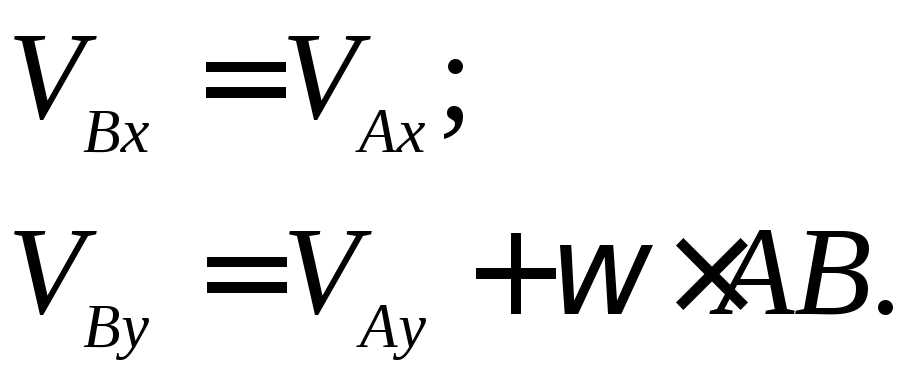
Учитывая данные задачи, получаем:
 или
или

Отсюда:
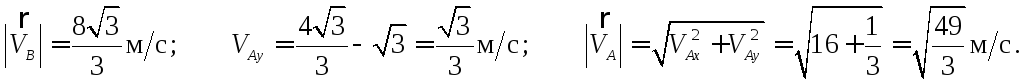
Следует заметить, что прямое
использование формулы (a)
целесообразно в довольно небольшом
числе случаев. В некоторых задачах имеет
смысл использовать так называемую
теорему о проекциях. Поскольку вектор![]() перпендикулярен отрезку
перпендикулярен отрезку![]() ,
,
из формулы (a) получаем
утверждение:
проекции скоростей концов отрезка,
соединяющего две точки абсолютно
твердого тела, на направление этого
отрезка равны.
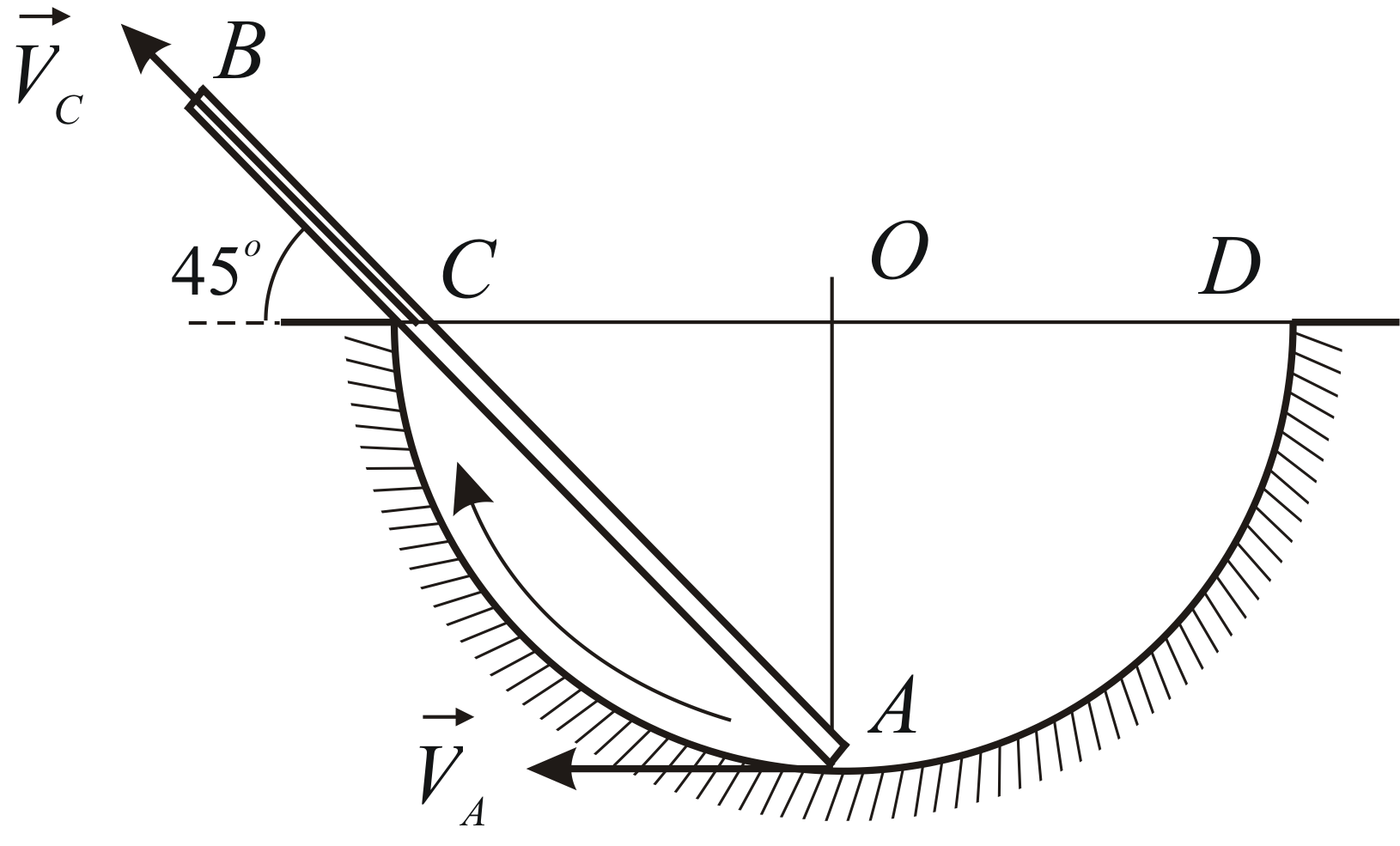
Пример 2.5
Стержень
![]() движется в плоскости рисунка, причём
движется в плоскости рисунка, причём
его конец![]() всё время находится на полуокружности
всё время находится на полуокружности![]() ,
,
а сам стержень всё время касается
неподвижного выступа![]() ,
,
расположенного на диаметре![]() (Рис. 2.5). Определить скорость
(Рис. 2.5). Определить скорость![]() точки стержня, касающейся выступа, в
точки стержня, касающейся выступа, в
тот момент времени, когда радиус![]() перпендикулярен
перпендикулярен![]() ,
,
если известно, что скорость точки![]() в этот момент
в этот момент![]() .
.
|
|
|
Рис. 2.5 |
Заметим, что направления скоростей
точек![]() и
и![]() в данный момент времени известны.
в данный момент времени известны.
Скорость точки![]() направлена по касательной к траектории,
направлена по касательной к траектории,
т.е. по касательной к окружности в нижней
точке. Скорость точки![]() направлена вдоль стержня, т.к. по условию
направлена вдоль стержня, т.к. по условию
задачи стержень не отрывается от выступа.
Таким образом, для заданного положения
стержня известны углы, которые образуют
векторы скоростей точек![]() и
и![]() с отрезком
с отрезком![]() .
.
В таком случае целесообразно использовать
теорему о проекциях скоростей:
![]()
Решение задач с помощью мгновенного
центра скоростей. Основной способ
определения поля скоростей при
плоскопараллельном движении твёрдого
тела основан на использовании мгновенного
центра скоростей.
Как уже говорилось, за полюс можно
принять любую точку плоской фигуры. В
данный момент времени различные точки
тела имеют разные скорости. За полюс
имеет смысл принимать точку, скорость
которой в данный момент времени равна
нулю.
Точка, принадлежащая плоской фигуре
или неизменно с ней связанная, скорость
которой в данный момент времени равна
нулю, называется мгновенным центром
скоростей.
|
|
|
Рис. 2.6 |
Скорость любой точки![]() плоской фигуры определяется так же, как
плоской фигуры определяется так же, как
если бы тело вращалось вокруг оси,
проходящей через мгновенный центр
скоростей перпендикулярно плоскости
движения плоской фигуры (Рис. 2.6):
![]()
![]()
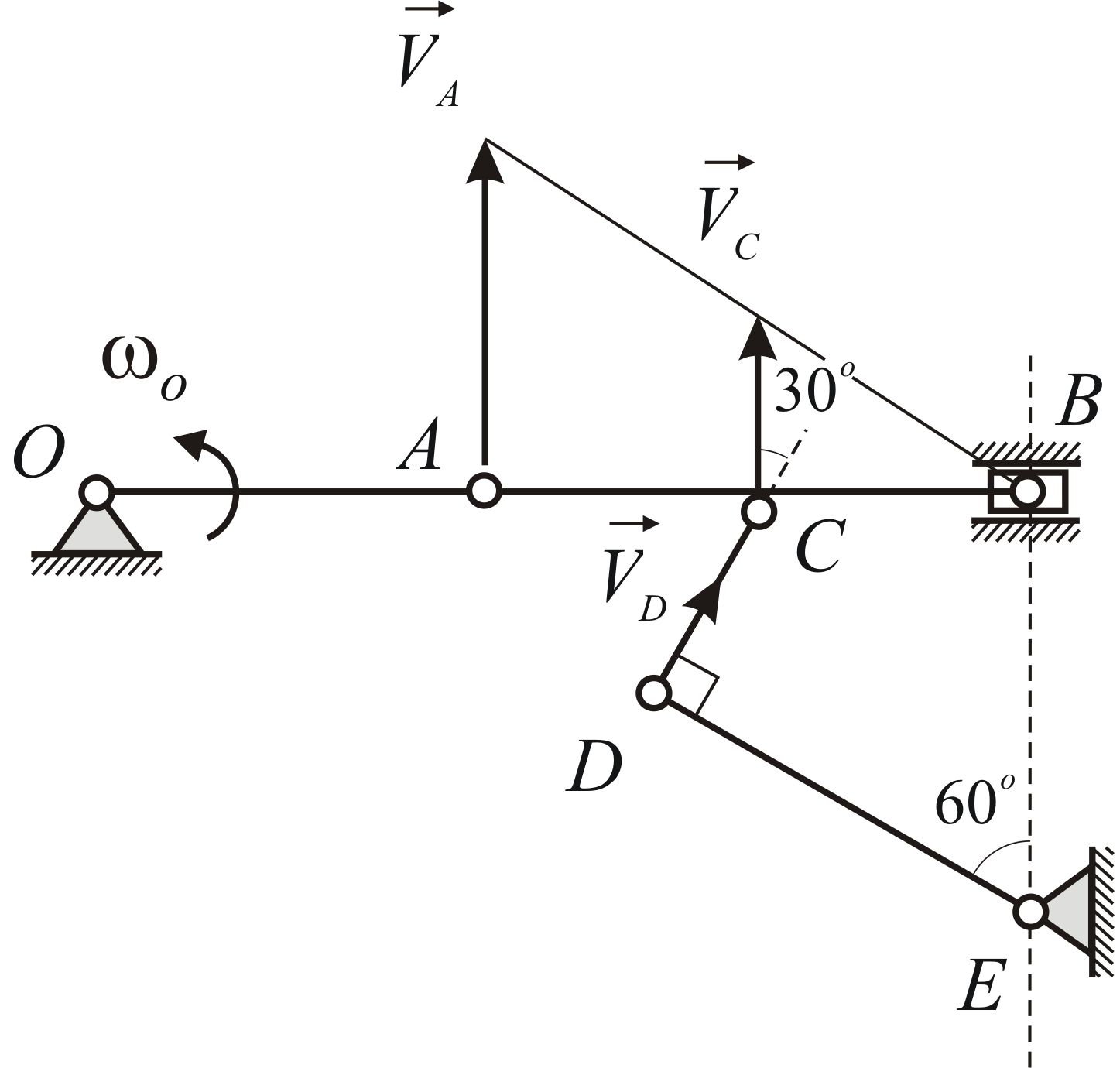
Пример 2.6
Кривошипн0-шатунный механизм связан
шарнирно в середине
![]() шатуна со стержнем
шатуна со стержнем![]() ,
,
а последний – со стержнем![]() ,
,
который может вращаться вокруг оси![]() .
.
Определить угловую скорость стержня![]() в указанном на Рис. 2.7 положении механизма,
в указанном на Рис. 2.7 положении механизма,
если точки![]() и
и![]() расположены на одной вертикали; угловая
расположены на одной вертикали; угловая
скорость![]() кривошипа
кривошипа![]() равна 8 рад/с,
равна 8 рад/с,![]()
![]()
|
|
|
Рис. 2.7 |
Стержень![]() вращается вокруг неподвижной оси.
вращается вокруг неподвижной оси.
Скорость точки![]() определяем по формуле Эйлера:
определяем по формуле Эйлера:
![]()
Движение стержня
![]() плоскопараллельное. Мгновенный центр
плоскопараллельное. Мгновенный центр
скоростей находится в точке![]() .
.
Учитывая, что скорости точек тела
пропорциональны расстояниям до
мгновенного центра скоростей, получаем:
![]() Отсюда:
Отсюда:![]()
Движение стержня
![]() плоскопараллельное. Скорость точки
плоскопараллельное. Скорость точки![]() направлена по касательной к окружности
направлена по касательной к окружности
радиуса![]() ,
,
которая является траекторией точки![]() .
.
При заданном положении механизма
направление скорости точки![]() совпадает с направлением стержня
совпадает с направлением стержня![]() .
.
Для определения скорости точки![]() имеет смысл использовать теорему о
имеет смысл использовать теорему о
проекциях скоростей:
![]()
Остаётся определить угловую скорость
стержня
![]() .
.
Поскольку движение этого стержня
вращательное, используем формулу Эйлера:
![]()
Пример 2.7
Колесо радиуса
![]() катится без скольжения по неподвижной
катится без скольжения по неподвижной
поверхности (Рис. 2.8). Скорость центра
колеса![]() .
.
Определить скорости точек![]() и
и![]()
|
|
|
Рис. 2.8 |
Мгновенный центр скоростей![]() находится в точке касания колеса и
находится в точке касания колеса и
дороги. Зная скорость центра, находим
угловую скорость колеса:
![]()
Скорости точек колеса определяем по
формуле Эйлера:

![]()
Качение колеса представляет интерес
еще и в том отношении, что позволяет
проиллюстрировать смысл формулы (a).
Пусть колесо, движение которого мы
рассматриваем, – ведущее колесо, т.е.
оно принудительно вращается некоторым
приводом. Рассмотрим возможные
режимы движения.
Может случиться так, что колесо
вращается, но автомобиль не перемещается
– буксует. В этом случае движение колеса
представляет собой вращение вокруг
неподвижной оси
![]() .
.
Все точки колеса будут описывать
окружности с центром в точке![]() ,
,
радиусы которых равны расстояниям от
этих точек до оси колеса. Скорость любой
точки направлена по касательной к этой
окружности и определяется по формуле
Эйлера.
Другое возможное движение колеса
представляет собой качение с
проскальзыванием. Автомобиль при этом
перемещается, но колеса вращаются
несоразмерно быстро. Скорость оси колеса
отлична от нуля и вступает в свои права
формула (a). Скорость,
например, точки![]() ,
,
которая в первом случае была ее полной
скоростью, становится скоростью,
полученной точкой![]() при вращении колеса вокруг оси
при вращении колеса вокруг оси![]() .
.
Полная же скорость точки![]() теперь геометрически складывается из
теперь геометрически складывается из
скорости точки![]() и скорости, полученной точкой
и скорости, полученной точкой![]() при вращении колеса вокруг оси
при вращении колеса вокруг оси![]()
![]()
Заметим, что в этом случае движение
оси (т.е. автомобиля) и вращение колеса
происходят независимо друг от друга и
каждое из них должно быть задано.
Последний режим движения колеса –
качение без скольжения. Именно этот
случай рассмотрен в примере 2.7. Движение
оси и вращение колеса оказываются
взаимосвязанными. В каждое мгновение
очевидно положение точки, скорость
которой равна нулю. В такой ситуации
при определении скоростей точек колеса
удобнее за полюс брать не точку
![]() ,
,
а мгновенный центр скоростей![]() .
.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 16.3;
16.10; 16.15; 16.16; 16.19; 16.24; 16.28; 16.29; 16.31;
16.32; 16.33; 16.34; 16.35; 16.36; 16.38; 16.39.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплект СР-20.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 6
Пример 2.8
Определить скорость и ускорение ползуна
![]() кривошипного механизма, а также угловую
кривошипного механизма, а также угловую
скорость и угловое ускорение шатуна![]() в положении, изображенном на Рис. 2.9.
в положении, изображенном на Рис. 2.9.
Кривошип![]() вращается замедленно, имея в данный
вращается замедленно, имея в данный
момент времени угловую скорость![]() и угловое ускорение
и угловое ускорение![]() .
.
Ползун движется по криволинейной
направляющей, имеющей в данном положении
механизма радиус кривизны![]() .
.
Дано:![]() .
.
Зная направления скоростей точек
![]() и
и![]() ,
,
построим мгновенный центр скоростей![]() стержня
стержня![]() ,
,
после чего определим угловую скорость
стержня![]()
![]()
и скорость точки
![]()
![]()
Попытка определить угловое ускорение
стержня
![]() ,
,
используя определение
![]()
закончится неудачей, поскольку зависимость
![]() неизвестна.
неизвестна.
Для определения ускорения точки
![]() принимаем за полюс точку
принимаем за полюс точку![]() .
.
Поскольку известны траектории всех
точек во всех их движениях, представим
ускорения точек их составляющими:
![]()
![]()
Вычислим векторы, входящие в уравнение
![]() .
.
|
|
|
Рис. 2.9 |
Точка
![]() принадлежит вращающемуся телу
принадлежит вращающемуся телу![]() .
.
Определяем модули составляющих ускорения
этой точки:
![]()
![]()
направления векторов показаны на
Рис. 2.9.
Точка
![]() движется по криволинейной направляющей.
движется по криволинейной направляющей.
Касательное и нормальное ускорения
точки![]() определяются по формулам:
определяются по формулам:
![]()
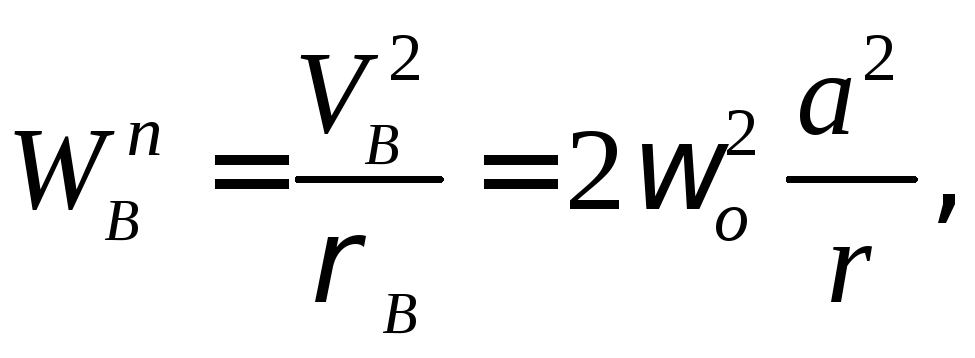
направления составляющих ускорения
показаны на Рис. 2.9. По приведенной
формуле не удается вычислить касательное
ускорение точки
![]() ,
,
поскольку неизвестны зависимости
расстояний![]() и
и![]() от времени.
от времени.
Находим составляющие ускорения,
полученного точкой
![]() при вращении шатуна
при вращении шатуна![]() вокруг оси
вокруг оси![]() .
.
Заметим, что вращательное ускорение
остается неизвестным по модулю, поскольку
неизвестно угловое ускорение шатуна:
![]()
![]()
Таким образом, из шести векторов,
входящих в равенство
![]() ,
,
только два неизвестны по модулю. Определим
эти неизвестные из уравнения![]() .
.
Это уравнение можно решить аналитически
или геометрически. Рассмотрим оба
способа решения.
Имеет смысл выбрать координатные
оси так, чтобы в каждое уравнение в
проекциях входила только одна неизвестная.
Направим ось
![]() вдоль
вдоль![]() (перпендикулярно
(перпендикулярно![]() ),
),
а ось![]() по направлению
по направлению![]() (перпендикулярно
(перпендикулярно![]() ).
).
Записывая уравнение![]() в проекциях на ось
в проекциях на ось![]() ,
,
получаем:
![]()
Отсюда

Отрицательный знак говорит о том,
что предполагаемое направление вектора
![]() было выбрано ошибочно; в действительности
было выбрано ошибочно; в действительности
этот вектор направлен в противоположную
сторону.
Записывая уравнение
![]() в проекциях на ось
в проекциях на ось![]() ,
,
получаем:
![]()
Отсюда
![]()
![]()
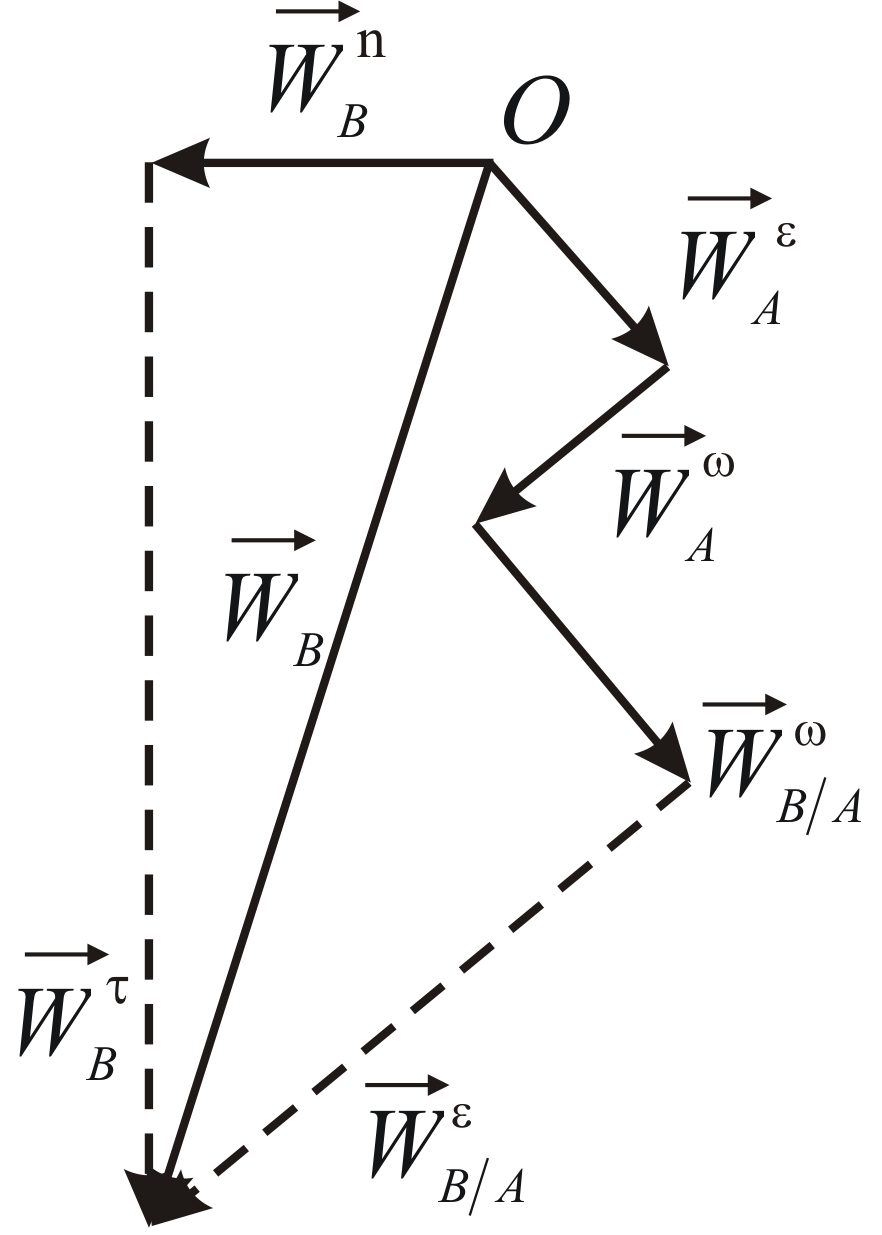
|
|
|
Рис. 2.10 |
Вычислив![]() ,
,
можем определить угловое ускорение
стержня![]() :
:
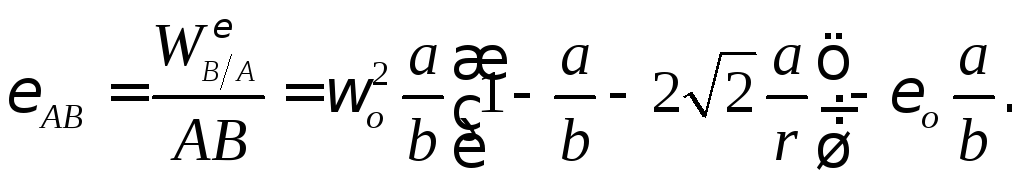
Рассмотрим геометрический способ
решения уравнения
![]() .
.
Построим в масштабе сумму векторов,
стоящих в правой части уравнения![]() .
.
От некоторой точки![]() отложим
отложим![]() ,
,
от его конца отложим![]() ,
,
а затем![]() (Рис. 2.10). Остается построить
(Рис. 2.10). Остается построить![]() ,
,
модуль которого неизвестен. Проведем
через конец![]() пунктирную прямую, параллельную
пунктирную прямую, параллельную![]() .
.
Конец суммы векторов, стоящих в правой
части уравнения![]() ,
,
лежит на этой прямой.
Обратимся к левой части уравнения
![]() .
.
Отложим от точки![]() известный вектор
известный вектор![]() .
.
Через его конец проведем пунктирную
прямую, параллельную вектору![]() .
.
Точка пересечения построенных прямых
определяет положение конца вектора
ускорения точки![]() .
.
Пример 2.9
Колесо радиуса
![]() катится без скольжения по прямолинейному
катится без скольжения по прямолинейному
пути (Рис. 2.11). Ось колеса движется
ускоренно, имея в данный момент времени
скорость![]() и ускорение
и ускорение![]() .
.
Определить проекции ускорение любой
точки![]() обода колеса на оси координат.
обода колеса на оси координат.
Принимая за полюс точку
![]() ,
,
получаем:
![]()
![]()
причем
![]()
где
![]() – угловая скорость колеса;
– угловая скорость колеса;![]() – его угловое ускорение.
– его угловое ускорение.
|
|
|
Рис. 2.11 |
Зная положение мгновенного
центра скоростей колеса – точка касания
колеса и дороги, определяем угловую
скорость колеса:
![]()
В рассматриваемой задаче расстояние
от точки
![]() ,
,
скорость которой известна, до мгновенного
центра скоростей![]() со временем не изменяется. Это
со временем не изменяется. Это
обстоятельство позволяет найти угловое
ускорение колеса в данный момент времени
по определению углового ускорения:
![]() ,
,
так как
![]() представляет собой проекцию вектора
представляет собой проекцию вектора
ускорения точки![]() на направление её вектора скорости,
на направление её вектора скорости,
которая в рассматриваемом случае равна![]() .
.
Записывая уравнение
![]() в проекциях на координатные оси, получаем
в проекциях на координатные оси, получаем
проекции вектора ускорения точки![]() :
:
![]()
![]()
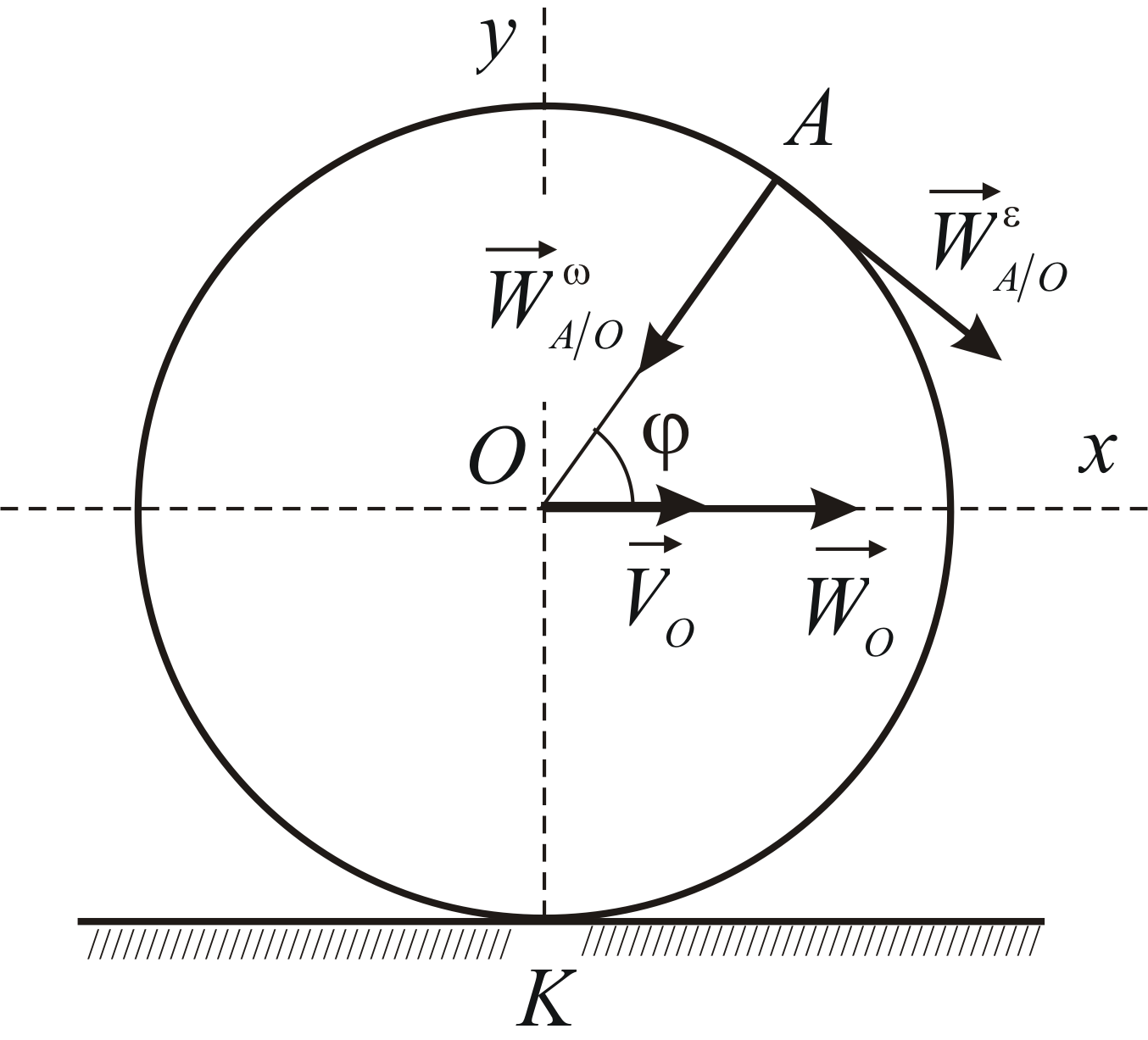
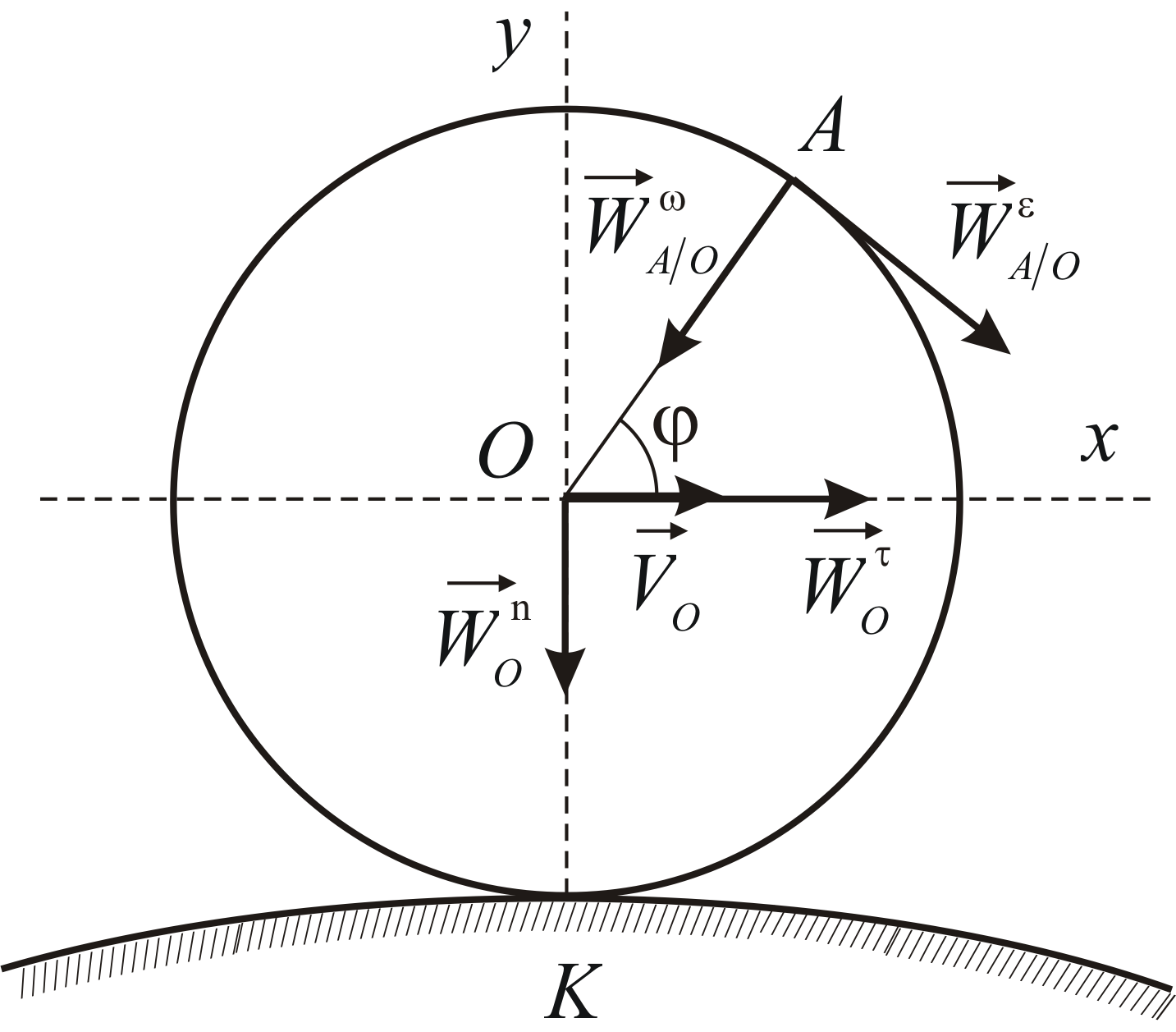
Пример 2.10
Колесо радиуса
![]() катится без скольжения по криволинейной
катится без скольжения по криволинейной
поверхности (Рис.2.12). Ось колеса движется
ускоренно, имея в данный момент времени
скорость![]() и касательное ускорение
и касательное ускорение![]() .
.
Определить проекции ускорения любой
точки![]() обода колеса на заданные координатные
обода колеса на заданные координатные
оси, если радиус кривизны в точке![]() равен
равен![]() .
.
|
|
|
Рис. 2.12 |
Задача решается так же, как в
примере 2.9, но в отличие от предыдущей
задачи, траектория точки![]() – кривая линия. У точки
– кривая линия. У точки![]() появляется вторая составляющая ускорения
появляется вторая составляющая ускорения
– нормальная:
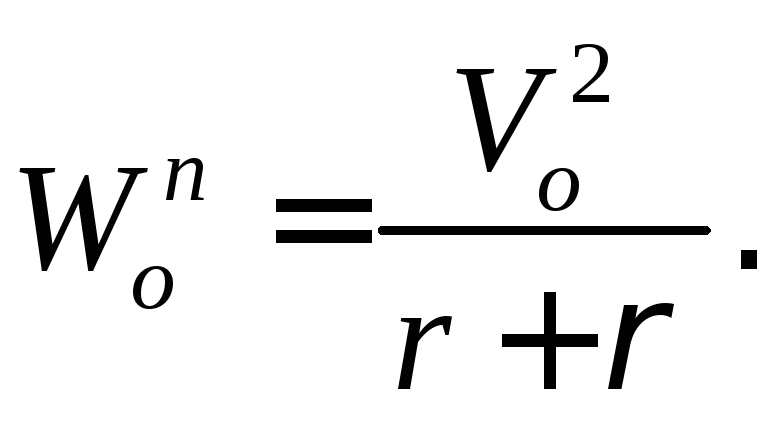
В результате получаем:
![]()
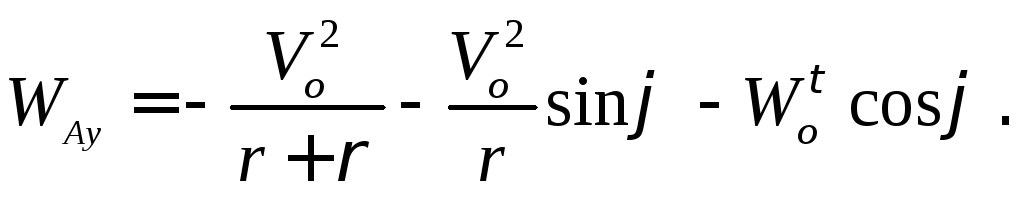
Пример 2.11
Колесо радиуса
![]() катится без проскальзывания по
катится без проскальзывания по
прямолинейному пути. Ось колеса движется
равномерно со скоростью![]() (Рис. 2.13). Определить ускорение любой
(Рис. 2.13). Определить ускорение любой
точки![]() колеса.
колеса.
|
|
|
Рис. 2.13 |
Ось колеса движется равномерно
и прямолинейно. Следовательно, точка![]() – мгновенный центр ускорений. Для любой
– мгновенный центр ускорений. Для любой
точки![]() колеса получаем:
колеса получаем:
![]()
Но угловая скорость колеса
![]() постоянна и, следовательно, угловое
постоянна и, следовательно, угловое
ускорение колеса равно нулю.
Тогда
![]()
![]()
Таким образом, ускорение любой точки
совпадает с осестремительным ускорением,
полученным этой точкой при вращении
колеса вокруг оси, проходящей через
центр колеса
![]() перпендикулярно плоскости движения.
перпендикулярно плоскости движения.
ЗАДАЧИ, РЕКОМЕНДУЕМЫЕ ДЛЯ РАЗБОРА В
АУДИТОРИИ И ДЛЯ ЗАДАНИЯ НА ДОМ:
Из сборника задач И.В.Мещерского: 18.11;
18.13; 18.16; 18.18; 18.22; 18.23; 18.25; 18.26;
18.28; 18.37; 18.38; 18.39; 18.40.
Из учебника «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА –
теория и практика»: комплекты СР-21;
СР-22.
ПРАКТИЧЕСКИЕ
ЗАНЯТИЯ № 7-8
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.2015560.03 Кб15PSY – recommendation.pdf
- #
- #
как найти угловую скорость точки обода колеса если известна скорость его центра?
Ученик
(95),
закрыт
10 лет назад
Viktor Weimert
Ученик
(186)
10 лет назад
Скорость центра и угловая, одна и та же скорость. Если центр колеса врощяется Например: со скоростью 1000,оборотов в минуту, то эта скорость распространяется на всё колесо! За исключением, передать скорость с одного колеса на другое с помощью ремня, с разными диаметроми колёс, То скорость меняется в ту или другую сторону! в зависимости от диаметра ведущего колеса. если в ведущем колесе диаметр больше ведомого, то в ведомом колесе скорость увеличивается.
Пунчик
Оракул
(99651)
10 лет назад
нужно еще знать какое движение совершает колесо – просто вращается или движется плоско парралельно, т. к. вы не уточнили какя скорость центра известна – линейная или угловая
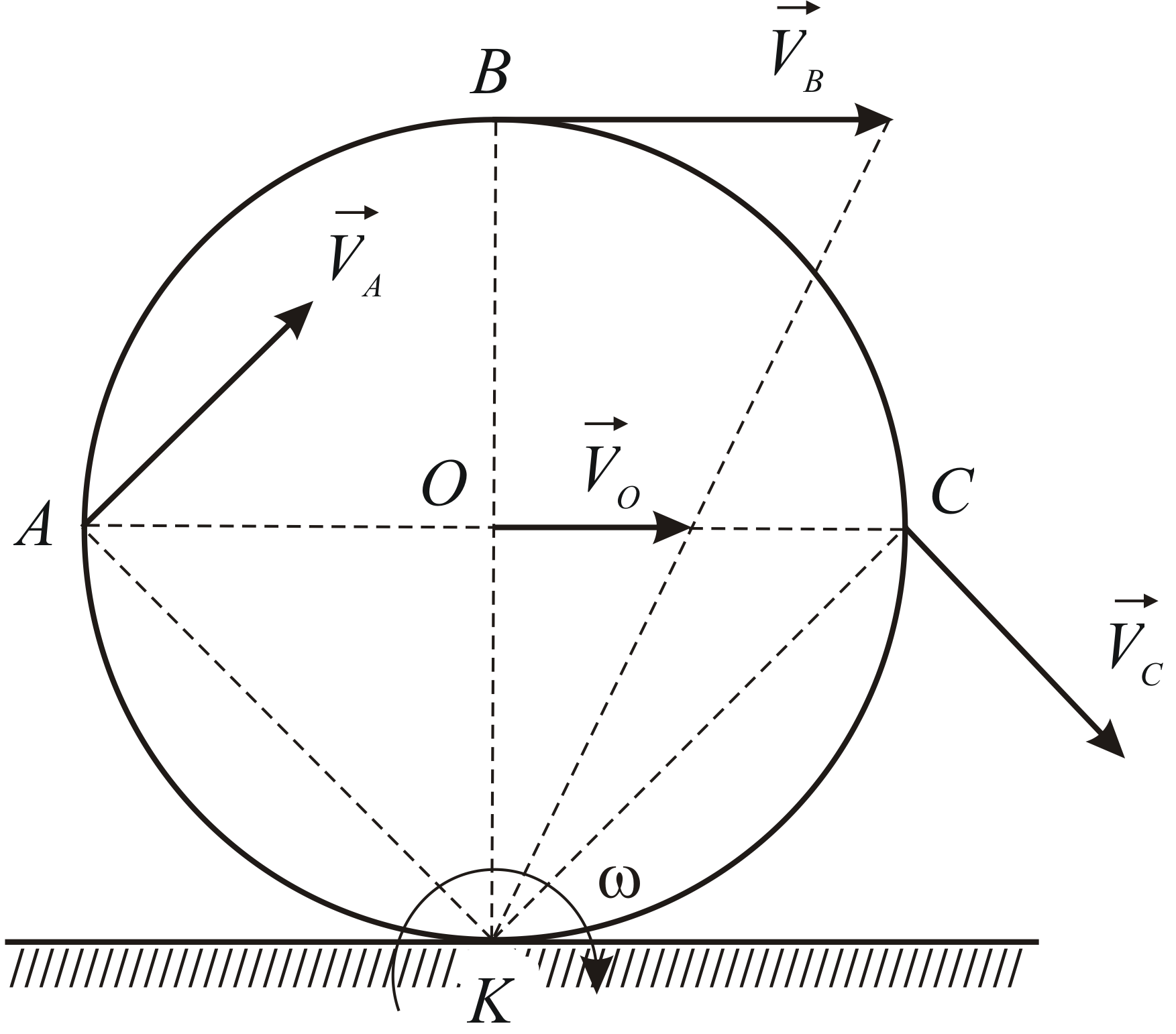
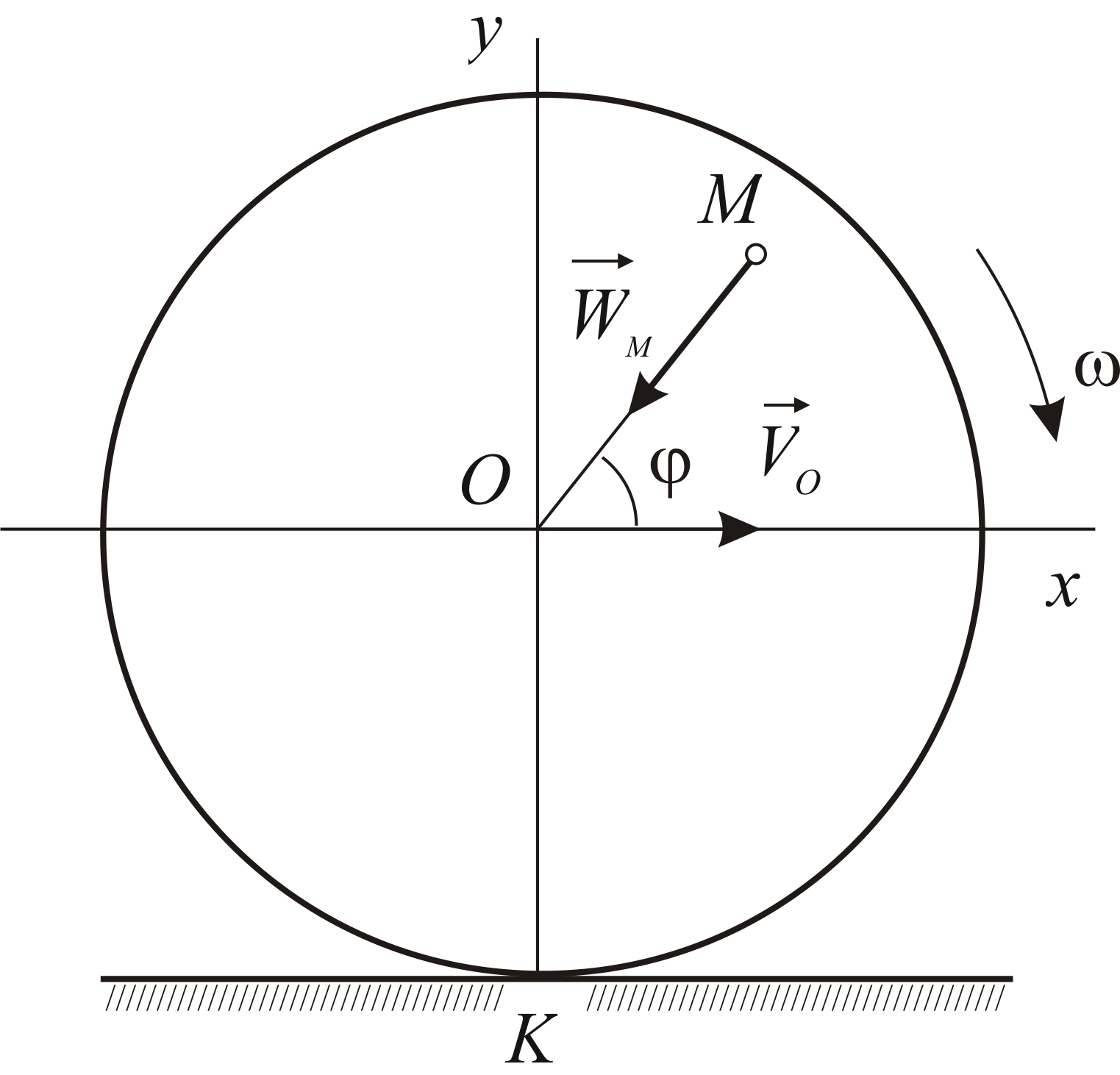
Пример решения задачи по определению величины и направления полной скорости и полного ускорения при сложном движении точки колеса кривошипа.
Теория по теме
Задача
Колесо I с радиусом R вращается вокруг оси, проходящей через центр колеса перпендикулярно плоскости чертежа с угловой скоростью ωI и угловым ускорением εI.
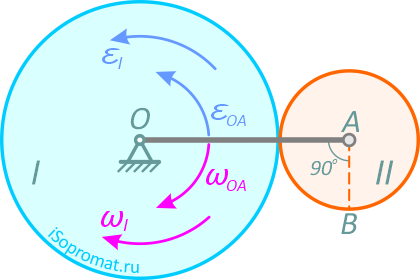
Рис. 2.7
Независимо от него на той же оси вращается кривошип ОА с угловой скоростью ωOA и угловым ускорением εOA. Кривошип приводит в движение колесо II с радиусом r, которое катится по колесу I (рис. 2.7).
Найти скорость VB и ускорение aB точки B, если R=20 см, r=10 см, ωI=5 с-1, εI=1 с-2, ωOA=3 с-1, εOA=2 с-2.
Другие примеры решений >
Помощь с решением задач >
Решение
Колесо I и кривошип совершают вращательное движение, а колесо II – плоскопараллельное движение.
Найдем скорость точки В, для этого определим положение мгновенного центра скоростей колеса II. Чтобы найти МЦС нужно, знать направление скоростей хотя бы двух точек тела.
Найдем скорость точки А, которая принадлежит колесу II и кривошипу ОА.
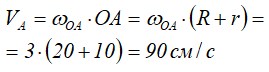
Вектор VA направлен перпендикулярно отрезку ОА в сторону вращения кривошипа (рис. 2.8).
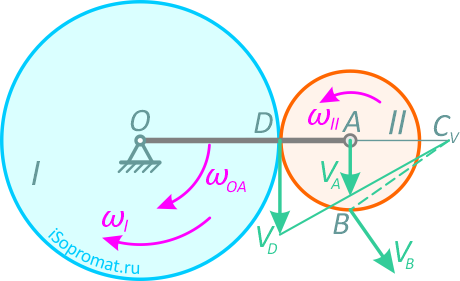
Рис. 2.8
В точке соприкосновения колес скорость точки колеса II должна равняться скорости точки колеса I. Обозначим эту точку буквой D. Эта точка не принадлежит кривошипу ОА. Так как движение колеса I известно, можно найти скорость точки D.
![]()
Вектор скорости точки D направлен перпендикулярно радиусу OD в сторону вращения колеса I. Таким образом, нам известны скорости двух точек колеса II. Проведем перпендикуляр к скоростям в точках А и D и прямую, проходящую через концы векторов скоростей VD и VA.
В точке пересечения этих линий и будет МЦС для колеса II. Обозначим его буквой CV.
Найдем расстояние ACV:
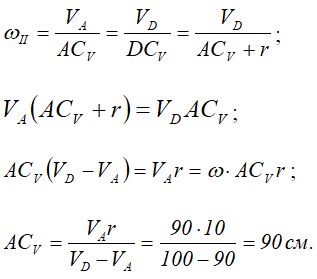
Тогда
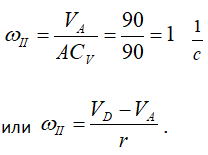
Зная угловую скорость колеса II и его МЦС, найдем скорость точки В.
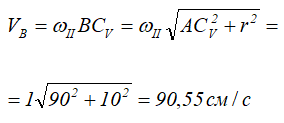
Вектор VB направлен перпендикулярно отрезку ВСV в сторону вращения колеса II.
Определим ускорение точки В.
Согласно теореме, ускорение точки В определятся по формуле
![]()
где aA — ускорение точки А, принятой за полюс;
aBA — ускорение точки В во вращательном движении, вокруг
полюса А.
Точка А принадлежит кривошипу ОА – движение которого известно, тогда
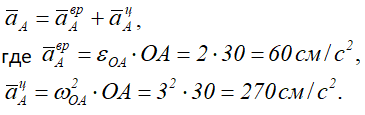
Вектор aτA — направлен перпендикулярно ОА, в сторону, обратную VA, т.к. вращение кривошипа по условию задачи замедленное.
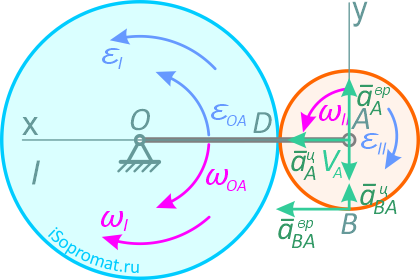
Рис. 2.9
Вектор anA — направлен от А к О.
Вектор
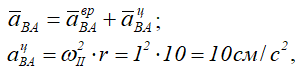
и направлен от точки В к полюсу А.
![]()
Для его вычисления найдем угловое ускорение εII:
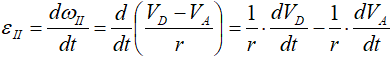
r – в задачах такого типа величина постоянная, выносится за знак производной:
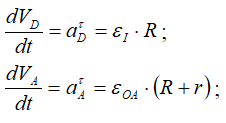
Отсюда
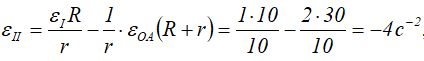
Знак «-» говорит о том, что колесо II вращается замедленно.
Величина
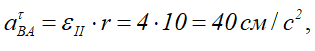
и направлена перпендикулярно anBA. Полное ускорение найдем, сложив все слагаемые:
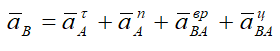
Направив ось АX вдоль АО, ось АY перпендикулярно АО, получим:
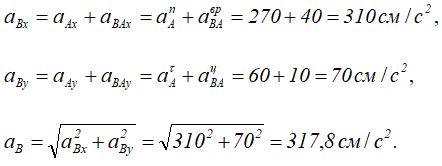
Вектор aB составляет с осью АХ угол α, косинус
которого
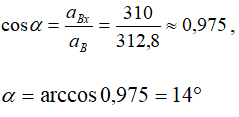
а с осью AY угол β, косинус которого:
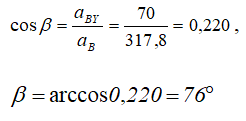
Другие примеры решения задач >
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности с постоянной по модулю скоростью
теория по физике 🧲 кинематика
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.
Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:
- Траектория движения тела есть окружность.
- Вектор скорости всегда направлен по касательной к окружности.
- Направление скорости постоянно меняется под действием центростремительного ускорения.
- Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.
Период, частота и количество оборотов
Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.
Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов
За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.
Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.
Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости
Линейная скорость
Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t
Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело
Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость
Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ
Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты
- У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v1 = v2.
- У вращающихся шестерен линейные скорости точек их поверхности также равны: v1 = v2.
- Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T1 = T2, ν1 = ν2, ω1 = ω2. Но v1 ≠ v2.
Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.
В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.
Центростремительное ускорение
Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.
Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.
Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алгоритм решения
- Записать исходные данные.
- Записать формулу для определения искомой величины.
- Подставить известные данные в формулу и произвести вычисления.
Решение
Записываем исходные данные:
- Радиус окружности, по которой движется автомобиль: R = 100 м.
- Скорость автомобиля во время движения по окружности: v = 20 м/с.
Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

pазбирался: Алиса Никитина | обсудить разбор | оценить
Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?
а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза
Алгоритм решения
- Записать исходные данные.
- Определить, что нужно найти.
- Записать формулу зависимости центростремительного ускорения от частоты.
- Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
- Приравнять правые части формул и найти искомую величину.
Решение
Запишем исходные данные:
Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:



Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».
pазбирался: Алиса Никитина | обсудить разбор | оценить
Движение по окружности
Движение по окружности – простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории – предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости – радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → – v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → – v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → – радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов – нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 – v 1 – изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/fizika/kinematika/dvizhenie-po-okruzhnosti/
[/spoiler]