The proper name for what many people call a diamond shape is actually a rhombus — a four-sided figure where every side is the same length and each opposite pair of angles is equal. Rhombuses show up in everything from kites to floor tiles and, depending on which information you have about the rhombus in question, you can calculate its area in the following three ways.
- Pencil
- Paper
- Scientific Calculator (optional)
-
It doesn’t matter which side you use for the “square the length of any side” method, because all sides of a rhombus are the same length. Similarly, which angle you use for that method doesn’t matter either because adjacent angles of a rhombus are always supplementary, which means every angle inside a rhombus has an identical sine value.
Multiply the altitude of the diamond times the length of one of its sides. The altitude is the distance between any two opposite sides of the diamond. So if the diamond has an altitude of 8 inches and its sides are each 10 inches long, its area is 8 * 10 = 80 inches squared.
Square the length of any side, and multiply the result by the sine of one of the angles inside the diamond. The sine of an angle can be determined using a scientific calculator or from a list of sines of common angles. So if the diamond has a side of length 6 inches and one of its angles measure 30 degrees with a sine of 0.5, the length of the side squared is 6 * 6 = 36, which multiplied by the sine gives you 36 * 0.5 = 18 inches squared as the area.
Multiply the lengths of the diagonals inside the diamond — that is, the two lines between opposite vertices — together. Divide the result by 2 to get the area. So for a diamond with diagonal lengths of 8 inches and 4 inches, its area would be (8 * 4)/2 = 16 inches squared.
Things You’ll Need
Tips
Ромб представляет собой четырехугольник, у которого есть противоположные параллельные и совпадающие стороны и две диагонали, которые пересекаются точно посередине друг друга и перпендикулярны. Каждый бриллиант – это тоже параллелограмм. Мы будем называть D большой диагональю, а d – малой диагональю.
Рассмотрим ромб диагоналей D и d.
Ваш район будет предоставлен:
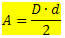
Где,
D → – наибольшая диагональ
d → – наименьшая диагональ
Обратите внимание, что площадь ромба составляет половину произведения его диагональных размеров.
Пример 1. Вычислите площадь диагоналей ромба 7 см и 4 см.
Решение: даны D = 7 см и d = 4 см. Таким образом, просто замените значения в формуле площади. Таким образом,

Пример 2. Вычислите площадь алмаза диаметром 5 см и меньшей диагональю 6 см.
Не останавливайся сейчас… После рекламы есть еще кое-что;)
Решение: чтобы вычислить площадь, нам нужно знать размеры двух диагоналей, но проблема дала нам только один для малой диагонали. Итак, нам нужно определить размер самой длинной диагонали.
Используя теорему Пифагора, мы должны:

Зная размеры двух диагоналей, просто используйте формулу площади. Таким образом,
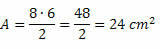
Пример 3. Рассмотрим бриллиант площадью 27 см.2 и большей диагональю 9 см. Какая мера на стороне этого алмаза?
Решение: чтобы определить размер на стороне алмаза, необходимо знать размеры двух диагоналей. Итак, нам нужно найти размер наименьшей диагонали. Поскольку мы знаем значение площади ромба и размер большой диагонали, отсюда следует, что:
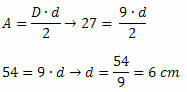
Зная размеры двух диагоналей, применим теорему Пифагора:
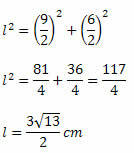
Ромб представляет собой четырехугольный параллелограмм с четырьмя равными сторонами. Для определения площади алмаза используются три формулы. Если вы хотите встретиться с ними, следуйте этим шагам.
шаги
Метод 1 из 3: использование диагоналей

Шаг 1. Найдите длину каждой диагонали
Диагонали ромба – это линии, соединяющие противоположные вершины (углы) фигуры. Они перпендикулярны и образуют четыре прямоугольных треугольника на своем пересечении.
Допустим, диагонали составляют 6 см и 8 см в длину

Шаг 2. Умножьте длину диагоналей
Просто запишите размеры, эквивалентные длине каждой диагонали, и умножьте их. В данном случае 6 см × 8 см = 48 см.2. Не забывайте квадратные единицы, поскольку мы работаем с квадратными единицами.

Шаг 3. Разделите результат на 2
Так как 6 см × 8 см = 48 см2, просто разделите результат на 2,48 см2 / 2 = 24 см2. Следовательно, площадь алмаза равна 24 см.2.
Метод 2 из 3: Использование базы и высоты

Шаг 1. Узнайте длину и высоту основания
Вы можете представить этот процесс как эквивалент умножения высоты на сторону алмаза. Допустим, эта высота равна 7 см, а основание – 10 см.

Шаг 2. Умножьте базу и высоту
Как только вы узнаете основание и высоту ромба, вам просто нужно умножить их, чтобы найти площадь формы. Таким образом, 10 см × 7 см = 70 см.2. В результате площадь ромба равна 70 см.2.
Метод 3 из 3: Использование тригонометрии

Шаг 1. Выровняйте размер с обеих сторон
У алмаза четыре равные стороны, поэтому не имеет значения, какую сторону вы выберете. Допустим, у стороны есть размер, равный 2 см. 2 см × 2 см = 4 см2.

Шаг 2. Умножьте результат на синус одного из углов
Независимо от того, какую сторону вы выберете, допустим, один из углов равен 33 градусам. Просто умножьте синус (33) на 4 см.2 чтобы получить алмазную площадку. (2 см)2 × синус (33) = 4 см2 × 1 = 4 см2. Площадь ромба равна 4 см.2.
Популярные по теме
Правильное название для того, что многие называют ромбом, на самом деле ромб – четырехсторонняя фигура, где каждая сторона имеет одинаковую длину, а каждая противоположная пара углов равна. Ромбы отображаются во всем, от воздушных змеев до плиток на полу, и, в зависимости от того, какая информация о ромбе у вас есть, вы можете рассчитать его площадь следующими тремя способами.
-
Неважно, какую сторону вы используете для метода «квадрат длины любой стороны», потому что все стороны ромба имеют одинаковую длину. Точно так же то, какой угол вы используете для этого метода, также не имеет значения, потому что смежные углы ромба всегда являются дополнительными, что означает, что каждый угол внутри ромба имеет одинаковое значение синуса.
Умножьте высоту алмаза на длину одной из его сторон. Высота – это расстояние между любыми двумя противоположными сторонами алмаза. Таким образом, если высота алмаза составляет 8 дюймов, а длина каждой стороны составляет 10 дюймов, его площадь составляет 8 * 10 = 80 дюймов в квадрате.
Выровняйте длину любой стороны и умножьте результат на синус одного из углов внутри алмаза. Синус угла можно определить с помощью научного калькулятора или из списка синусов общих углов. Так, если у алмаза есть сторона длины 6 дюймов, и один из его углов измеряет 30 градусов с синусом 0, 5, длина стороны в квадрате составляет 6 * 6 = 36, что умножено на синус дает 36 * 0, 5 = 18 дюймов в квадрате, как площадь.
Умножьте длины диагоналей внутри ромба – то есть две линии между противоположными вершинами – вместе. Разделите результат на 2, чтобы получить площадь. Таким образом, для алмаза с длиной диагонали 8 дюймов и 4 дюйма его площадь будет (8 * 4) / 2 = 16 дюймов в квадрате.
подсказки
Как убрать алмазную зону

В этой статье показано, как рассчитать площадь алмаза, имеющего форму с четырьмя равными сторонами. Квадрат – это ромб, но ромб не обязательно должен быть квадратом. Есть несколько способов получить площадь алмаза, в зависимости от того, что вы знаете о нем, и если вы продолжаете читать, вы можете изучить различные формулы, которые помогут вам получить площадь алмаза.
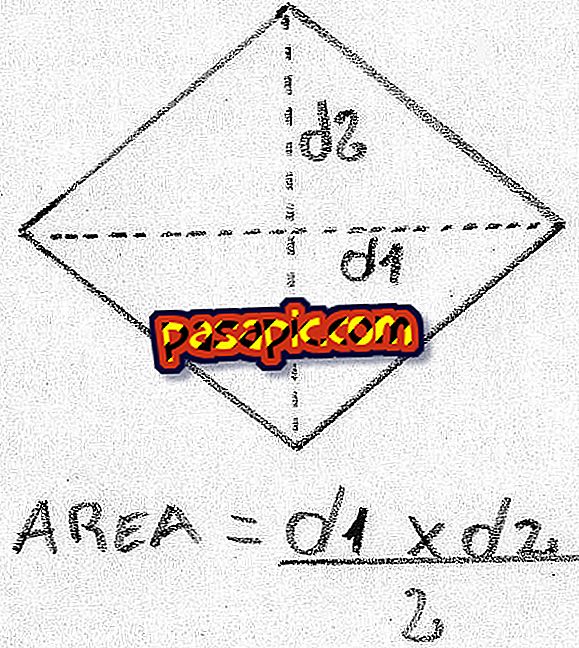
диагонали
Вы можете вычислить площадь алмаза, если знаете длину диагоналей, представляющих собой линии, соединяющие противоположные углы. Площадь алмаза – это диагональ, умноженная на другую диагональ, деленную на 2.
Пример. Если диагональ равна 3, а другая диагональ равна 4, 3 x 4 = 12 и 12/2 = 6.
Таким образом, площадь составляет 6.
База и высота
Если вы знаете длину любой стороны ромба и высоту, которая является кратчайшим расстоянием между любой из частей и противоположной стороной, вы можете рассчитать площадь ромба . Просто найдите длину одной стороны и умножьте ее на высоту.
Формула:
- A = L xh
Сторона и угол
Если вы знаете любую сторону и любой угол алмаза, вы можете использовать тригонометрический метод . Для этого метода необходимо использовать научный калькулятор с тригонометрическими функциями (синус, косинус, тангенс).
Площадь ромба является квадратом (или рядом), умноженным на синус угла. Независимо от того, под каким углом оба имеют одинаковый синус, потому что они оба составляют в целом 180.
Формула:
- A = L x L x sin (a)
