Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 27 человек из 18 регионов


- Сейчас обучается 126 человек из 41 региона




Описание презентации по отдельным слайдам:
-

1 слайд
График квадратичной функции, содержащей переменную под знаком абсолютной величины.
Знание только тогда знание, когда оно приобретено усилиями
своей мысли, а не памятью.Л. Н. Толстой.
Выполнила: Асламурзаева Белла,
ученица 9 «А» класса,
СОШ №46 им. И .ДзусоваРуководитель: Дряева М.Г.
Преподаватель математики СОШ №46 им. И .Дзусова -

2 слайд
Содержание:
1.Введение
2.Основные определения и свойства.
3.Построение графика квадратичной функции,
содержащей переменную под знаком модуля.
4.Выводы.
5. Используемая литература. -

3 слайд
Цель работы – рассмотреть построение графика квадратичной функции, содержащей переменную под знаком модуля.
Объект исследования: график квадратичной функции.
Предмет исследования: изменения графика квадратичной функции в зависимости от расположения знака абсолютной величины.
Задачи:
1) Изучить литературу о свойствах абсолютной величины и квадратичной функции.
2) Исследовать изменения графика квадратичной функции в зависимости от расположения знака абсолютной величины.
Практическая значимость моей работы заключается:
1) в использовании приобретенных знаний по данной теме, а также углубление их и применение к другим функциям и уравнениям;
2) в использовании навыков исследовательской работы в дальнейшей учебной деятельности. -

4 слайд
Основные определения и свойства
Функция, определяемая формулой у=ах²+вх+с, где х и у переменные, а параметры а, в и с – любые действительные числа, причём а≠0, называется квадратичной.Абсолютной величиной неотрицательного числа называется само это число, абсолютной величиной отрицательного числа называется противоположное ему положительное число.
Свойства:
1.|a| ≥0,
2. |a|²= a²,
3.|a∙b|=|a|∙|b|,
4. |a/b|=|a|/|b|, b≠0 -

5 слайд
Построение графика линейной функции, содержащей
переменную под знаком модуля.
1)f(x)= |x-1|.
x = 1- корень
подмодульного
выражения.
Возьмем x=0, (0<1) и
х=2, (2>1).
Вычисляя функции в
точках 1,0 и 2,получаем
график, состоящий из
двух отрезков. -

6 слайд
2) f(x)= |x-1|+|x-2|.
Вычисляя значение
функции в точках
1, 2, 0 и 3,
получаем график,
состоящий из трех
отрезков прямых. -

7 слайд
Построение графика квадратичной функции, содержащей переменную под знаком модуля
На примере функции у = x ²-6х +5 рассмотрим
всевозможные случаи расположения модуля.у = |x 2 – 6х +5|
у = | х | 2 – 6х +5
у = х² – 6|х| +5
у = |х|² – 6|х|+5
у = |х² – 6х| +5
у = |х² – 6|х| +5|
у = x 2 -|6х + 5|
|y|= x 2 – 6х +5 -

8 слайд
Построим график функции у = |x 2 – 6х +5|
Пользуясь определением модуля, рассмотрим два случая:
Пользуясь определением модуля, рассмотрим два случая:
Пользуясь определением модуля, рассмотрим два случая:
Пользуясь определением модуля, рассмотрим два случая:
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
. Выделим все точки параболы с неотрицательной ординатой.
Выделим все точки параболы с неотрицательной ординатой.
x ²– 6х +5≥ 0, тогда у= x² –
6х +5.Выделим все точки
параболы с неотрицательной ординатой.
2) x² – 6х +5<0, тогда у= -(x ²– 6х +5) или -x² + 6х -5>0, y= -x² + 6х -5. -

9 слайд
Рассмотрим график функции у = |х|²– 6х +5
Т.к. |x|²= x² , то функция у = |х|² – 6х +5
совпадает с функцией
у = x ²-6х +5 ,а , значит,
имеют один и тот же график. -

10 слайд
Рассмотрим график функции у = х² – 6|х| +5
Пользуясь определением модуля, рассмотрим два случая:
1)Пусть x≥0, тогда y= х² – 6х +5.
Построим параболу у = х² – 6х +5 и
обведём ту её часть, которая
соответствует неотрицательным
значениям х, т.е. часть, расположенную
правее оси Оу.
2)Пусть x<0, тогда y= x² + 6х +5.
В той же координатной плоскости построим параболу
у = х² +6х +5 и обведём ту её часть, которая соответствует
отрицательным значениям х, т.е. часть, расположенную
левее оси Оу. Обведённые части парабол вместе образуют График функции у = х² – 6|х| +5 -

11 слайд
Рассмотрим график функции
у = |х|² – 6|х|+5.
Т.к. |x|²= x² , то функция у = |х|² – 6|х| +5
совпадает с функцией у = x ²-6|х| +5
(см пред. пример) -

12 слайд
Построим график функции у = |х2 – 6х| +5
1)у = х² – 6х
2)у = |х² – 6х|
3)у = |х² – 6х| +5 -

13 слайд
Построим график функции у = |х2 – 6|х| +5|.
1) у =х²- 6|х| +5 (рассмотрено в 10 слайде)
2)у = |х² – 6|х| +5| -

14 слайд
Построим график функции у = x 2 -|6х + 5|.
1)Найдем нули функции: у =6х + 5 , 6х + 5=0, x= – ⅚.
2) Рассмотрим два случая:1)6х+5≥0, т.е. х ≥ -⅚, , тогда функция примет вид у =x² – 6х -5.
2) 6х+5<0, т.е. х < -⅚, тогда функция принимает вид у =x² + 6х +5.
3)Построили график функции у = x 2 -|6х + 5|. -

15 слайд
Равенство |y|= x 2 – 6х +5 не задает функции т. к. при
x 2 – 6х +5 >0 имеем 2 значения y, соответствующих данному значению
x, а при x 2 – 6х +5 <0, ни одного такого значения. График данного
уравнения строится так:
Отбрасываем ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отображаем
относительно оси Ох.1)При x²– 6х +5 >0, y= x² – 6х +5
2)при x² – 6х +5 <0, y= -(x² – 6х +5)
3) Построили график функции
|y|= x² – 6х +5 -

16 слайд
Выводы:
1)Для построения графика функции y = |f(x)| , надо сохранить ту часть графика функции y = f(x), точки которой находятся на оси Ох или выше оси Ох, и симметрично отразить относительно оси Ох ту часть графика функции y = f(x), которая расположена ниже оси Ох.
2) Для построения графика y = f(|x|) надо сохранить ту часть графика функции y = f(|x|), точки которой на оси Оу или справа от неё и симметрично отразить эту часть графика относительно оси Оу.
3) Чтобы построить график уравнения |y|= f(x) нужно:
Отбросить ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отобразить
относительно оси Ох -

17 слайд
1. y=(|x|-1)4 , где -3 ≤ x≤3
2. x=0, где 0 ≤ у≤81.
-

18 слайд
-2|x|²+8, где -2≤x≤2
y=4, где -2≤x≤2
1)y=2|x|²
2) y= -2|x|²
3) y= -2|x|²+8
-2≤x≤2
4)y=4, где
-1,4≤x≤1,4
2. -

19 слайд
y=-(|x|-1)4 +8 , где -3 ≤ x≤0
1)y=(|x|-1)4 , где -3 ≤ x≤0
2) y=-(|x|-1)4 , где -3 ≤ x≤0
3) y=-(|x|-1)4 +8 , где -3 ≤ x≤03.
-

20 слайд
y= x²+(|y-4|-2) ²=4,где0≤y≤8, x=0
x²+y²=4
1) y=± ², 0≤x≤2
2)y=± ²+6
3)y= ± ²+2
4)x=0, 0≤y≤8
4. -

21 слайд
5.
y=-(x-1.5)6 +4, 0,4≤x ≤ 2,6
y=(x-1.5)6 ,
0,35 ≤ x≤2,64
x=0,35, 2 ≤ y ≤ 8
y=8, 0,35 ≤ x≤2,5 -

22 слайд
1.y= x4+4, -2 ≤ x≤2
2. y=x6 ,-1 ≤ x≤26.
-

23 слайд
1) y=-2|x|2+8
2) y=0, -3 ≤ x≤3
3) y=-x2+9, -3,2 ≤ x≤-3
4) ) y=-x2+9, 3 ≤ x≤3,2
7. -

24 слайд
1.y= x4+4, -2 ≤ x≤2
2. y=x6 ,-1 ≤ x≤28.
-

25 слайд
9.
1) y=(|x|-1)4 ,-3≤x≤3
2)x=0, 0≤y≤8
3)y= x2+ 2,5x, 2≤х≤2,5 -

26 слайд
10.
1)y= – (x-5)6 +8, 0,4≤y≤2,6
2)y= (x-5)6 +4,4 , 0,4≤y≤2,6
3)y=(x-1,7)6 ,0,35≤x≤2,5 -

27 слайд
11.
1)y= – (x-5)6 +8, 0,4≤y≤2,6
2)y= (x-5)6 +4,4 , 0,4≤y≤2,6
3)y=(x-1,7)6 ,0,35≤x≤2,5 -

Краткое описание документа:
1)Для построения графика функции y = |f(x)| , надо сохранить ту часть графика функции y = f(x), точки которой находятся на оси Ох или выше оси Ох, и симметрично отразить относительно оси Ох ту часть графика функции y = f(x), которая расположена ниже оси Ох.
2) Для построения графика y = f(|x|) надо сохранить ту часть графика функции y = f(|x|), точки которой на оси Оу или справа от неё и симметрично отразить эту часть графика относительно оси Оу.
3) Чтобы построить график уравнения |y|= f(x) нужно:
Отбросить ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отобразить
относительно оси Ох
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 257 950 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 16.01.2015
- 1681
- 19
Рейтинг:
5 из 5
- 16.01.2015
- 6409
- 23
- 16.01.2015
- 1211
- 1
- 15.01.2015
- 3247
- 4
- 15.01.2015
- 1350
- 2
- 15.01.2015
- 701
- 1
Рейтинг:
3 из 5
- 15.01.2015
- 5372
- 9
График квадратичной функции, содержащей модуль.
Функция, определяемая формулой у=ах²+вх+с, где х и у переменные, а параметры а, в и с – любые действительные числа, причём а≠0, называется квадратичной.
График функции у=ах²+вх+с есть парабола; осью симметрии параболы является прямая . При а>0 «ветви» параболы направлены вверх, при а<0 – вниз.
Чтобы построить график квадратичной функции, нужно:
1) найти координаты вершины параболы и отметить её в координатной плоскости;
2) построить ещё несколько точек, принадлежащих параболе;
3) соединить отмеченные точки плавной линией.
Определение: абсолютной величиной неотрицательного числа называется само это число, абсолютной величиной отрицательного числа называется противоположное ему положительное число.
Свойства: 1 .|a| ≥0, 3 .|a∙b|=|a|∙|b|,
2. |a|²= a², 4. |a/b|=|a|/|b|, b≠0
2. Построение графика квадратичной функции, содержащей переменную под знаком модуля.
На примере функции у= x ^2– 6х +5 рассмотрены всевозможные случаи расположения модуля.
у = |x 2 – 6х +5|
у = | х | 2 – 6х +5
у = х² – 6|х| +5
у = |х|² – 6|х|+5
у = |х² – 6х| +5
у = |х² – 6|х| +5|
у = x 2 -|6х + 5|
|y|= x 2 – 6х +5
Пример 1:Построим график функции у = |x 2 – 6х +5|.
Пользуясь определением модуля, рассмотрим два случая:
1) x 2– 6х +5≥ 0, тогда у= x 2– 6х +5.
Построим данную параболу. Выделим все точки параболы с неотрицательной ординатой.
2) x 2– 6х +5<0, тогда у= -(x 2– 6х +5) или -x 2+ 6х -5>0, y= -x 2+ 6х -5.
Построим график данной функции, и выделим все точки параболы с положительной ординатой. Все выделенные в обоих случаях точки образуют график функции у = |x 2 – 6х +5|.
.
Итак ,можно сделать вывод: чтобы получить график функции у = |x 2 -6х + 5|, нужно часть параболы, расположенной ниже оси Ох, зеркально отобразить относительно оси Ох .
Пример 2:Рассмотрим график функции у = |х|²– 6х +5.
Т. к. |х|²= х², то график функции у =|х|² – 6х +5 совпадет с графиком функции у = х² – 6х +5, не содержащей знак абсолютной величины.
.
Пример 3: Рассмотрим график функции у = х² – 6|х| +5.
Воспользуемся определением модуля числа.
Пусть x≥0, тогда y= х² – 6х +5.
Построим параболу у = х² – 6х +5 и обведём ту её часть, которая соответствует неотрицательным значениям х , т.е. часть, расположенную правее оси Оу.
2)Пусть x<0, тогда y= x² + 6х +5.
В той же координатной плоскости построим параболу у = х² +6х +5 и обведём ту её часть, которая соответствует отрицательным значениям х, т.е. часть, расположенную левее оси Оу. Обведённые части парабол вместе образуют график функции у = х² – 6|х| +5
Итак, можно сделать вывод: для построения графика функции у = х² – 6|х| +5. надо сохранить ту часть графика , точки которой находятся на оси Oy или справа от нее, и симметрично отобразить ее относительно оси Оy.
Пример 4: Рассмотрим график функции у = |х|² – 6|х|+5.
Т.к. |х|²= х², то график функции у = |х|² – 6|х| +5 совпадает с графиком функции у = х² – 6|х| +5, рассмотренном в примере 3.
Пример 5. Построим график функции у = |х² – 6х| +5.
Для этого построим сначала график функции у = х² – 6х. Чтобы получить из него график функции у = |х² – 6х|, нужно часть параболы, расположенную ниже оси х, заменить линией ей симметричной относительно оси х. Т.к. нам
Нужно построить график функции у = |х² – 6х| +5, то график рассмотренной нами функции у = |х² – 6х| нужно просто поднять по оси у на 5 единиц вверх.
Пример 6: Построим график функции у = |х² – 6|х| +5|.
Для этого сначала построим график функции у =х²- 6|х| +5. (см. пример 3).
Т. к. наша функция полностью находится под знаком модуля, то для того, чтобы построить график функции
у = |х² – 6|х| +5|, нужно часть параболы, расположенную ниже оси Ох, заменить линией ей симметричной относительно оси Ох.
Пример 7:Построим график функции у = x 2 -|6х + 5|.
Пользуясь определением модуля, рассмотрим два случая:
6х+5≥0, т.е. х ≥ -5∕6, , тогда функция примет вид у=x² – 6х -5.
Построим параболу и обведем ту часть , где x≥-5∕6,
6х+5<0, т.е. х < -5∕6, тогда функция принимает вид у=x² + 6х +5.
Построим эту параболу и обведем ту её часть, которая расположена левее точки с абсциссой х =-5∕6,
Обведенные в обоих случаях части парабол являются графиком данной функции.
Пример 8. |y|= x 2 – 6х +5
Равенство |y|= x 2 – 6х +5 не задает функции, т. к. при
x 2 – 6х +5 >0 имеем 2 значения y, соответствующих
данному значению x, а при x 2 – 6х +5 <0, ни одного такого
значения. График данного уравнения строится так:
Отбрасываем ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отображаем
относительно оси Ох.
1)Для построения графика функции y = |f(x)| , надо сохранить ту часть графика функции y = f(x), точки которой находятся на оси Ох или выше оси Ох, и симметрично отразить относительно оси Ох ту часть графика функции y = f(x), которая расположена ниже оси Ох.
2) Для построения графика y = f(|x|) надо сохранить ту часть графика функции y = f(|x|), точки которой на оси Оу или справа от неё и симметрично отразить эту часть графика относительно оси Оу.
3) Чтобы построить график функции |y|= x 2 – 6х +5 нужно:
Отбросить ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отобразить
относительно оси Ох
Используемая литература:
1.Математика. Алгебра. Функции. Анализ данных. 9 кл.: М.: Учеб. для общеобразоват. учреждений / Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович, Л. В. Кузнецова, С. С. Минаева. 2. Курс высшей математики для техникумов. И. Ф. Суворов, Москва – 1967.
3. Математика. Алгебра и элементарные функции. М. И. Абрамович, М. Т. Стародубцев.
4. А.Г. Мордкович Книга для учителя. Беседы с учителями. Москва – «Оникс 21 век», «Мир и образование», 2005 г.
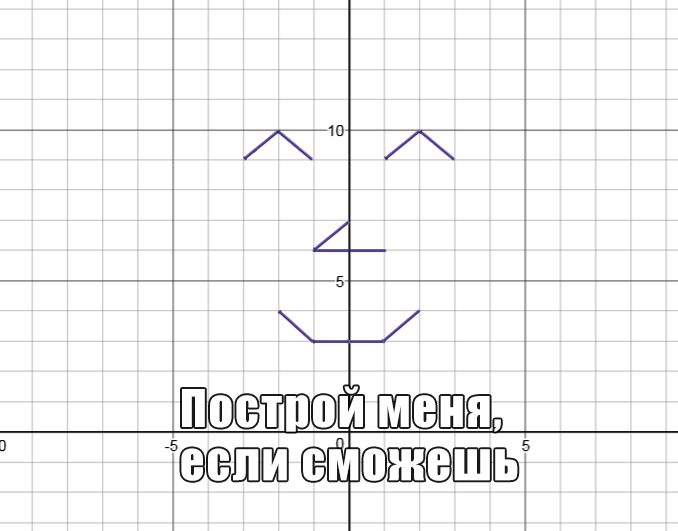
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:
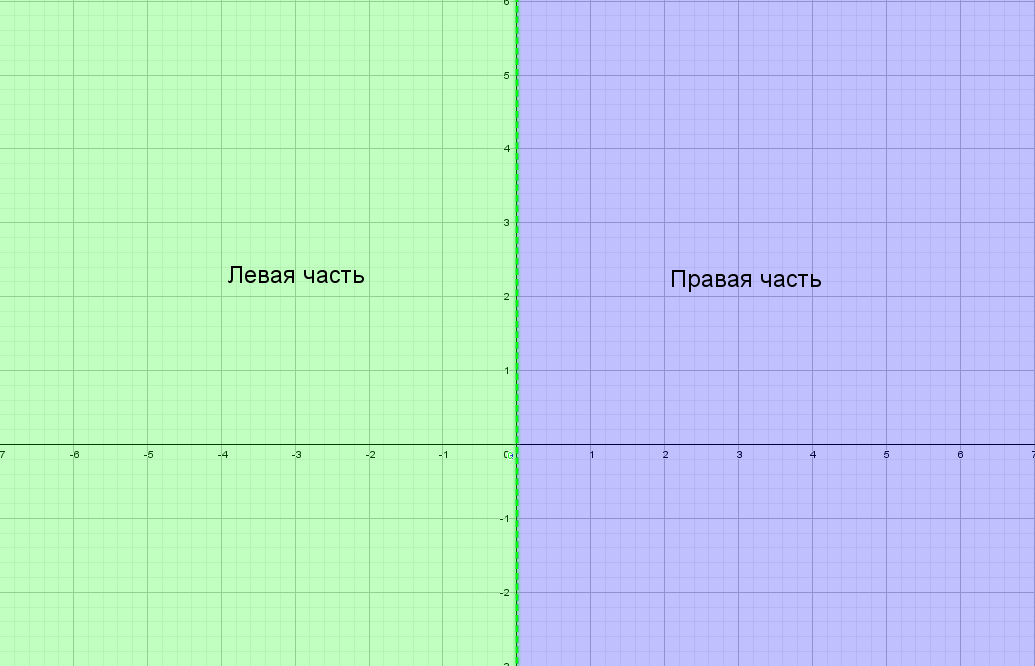
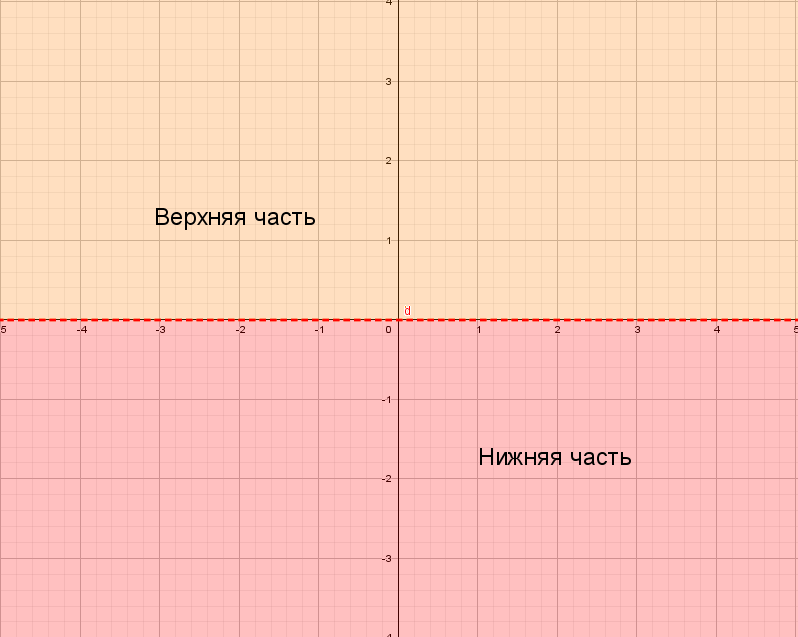
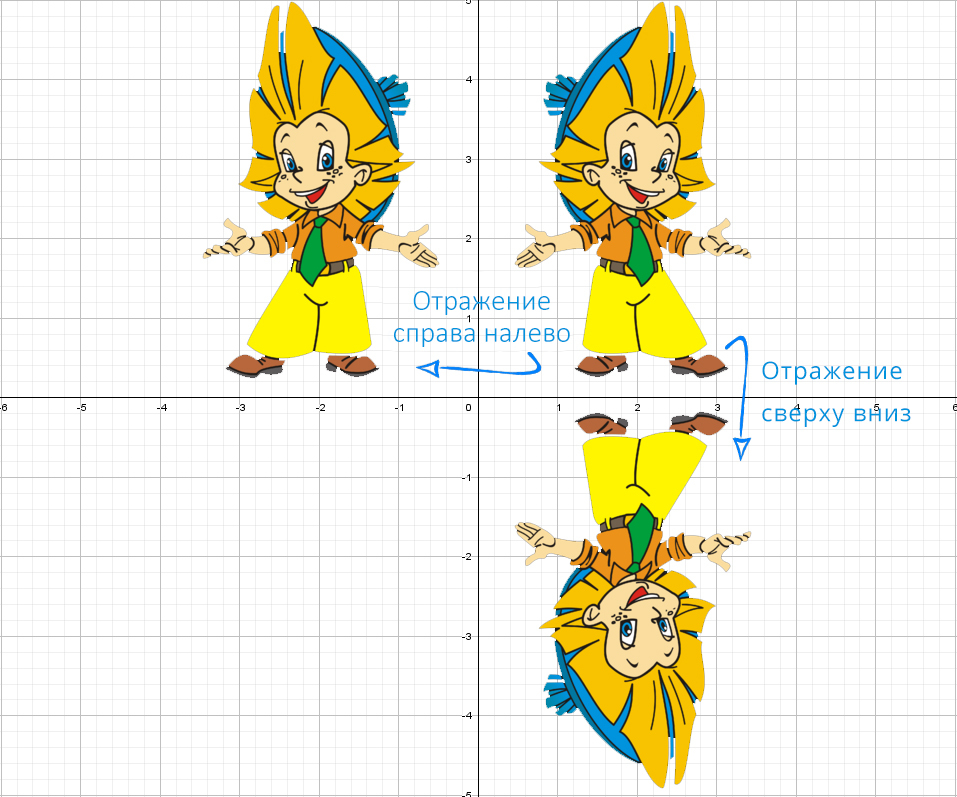
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
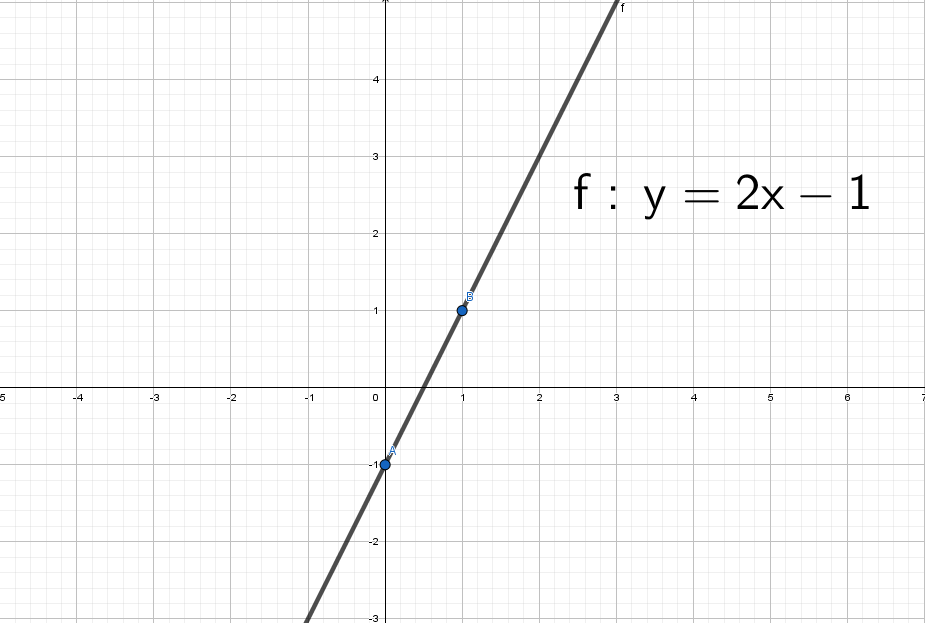
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
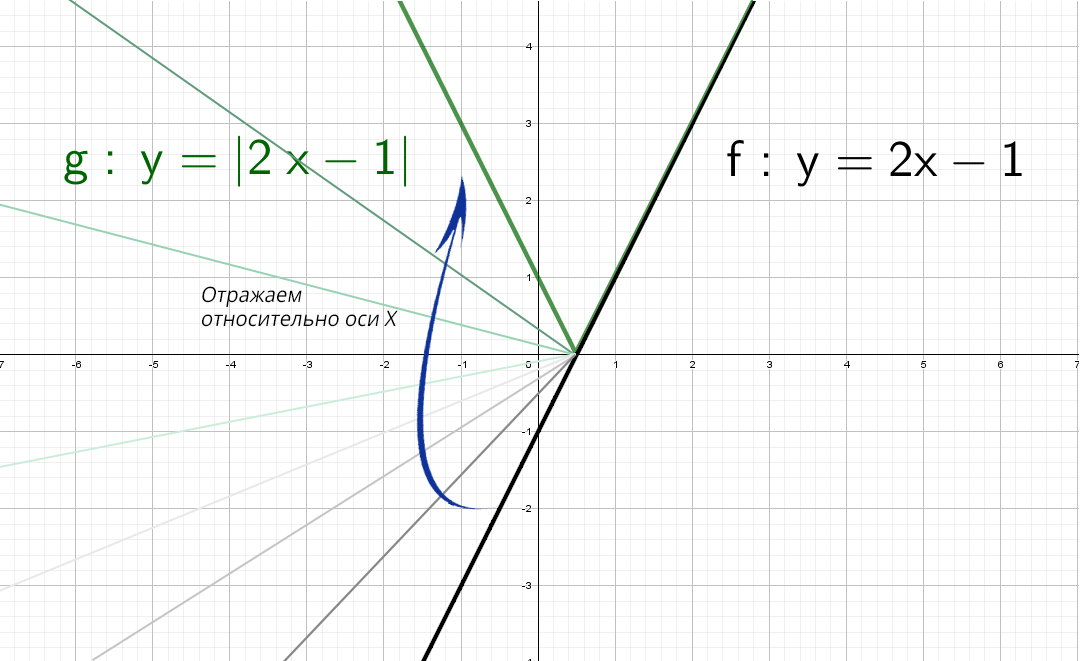 Получается такая зеленая “галочка”.
Получается такая зеленая “галочка”.
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
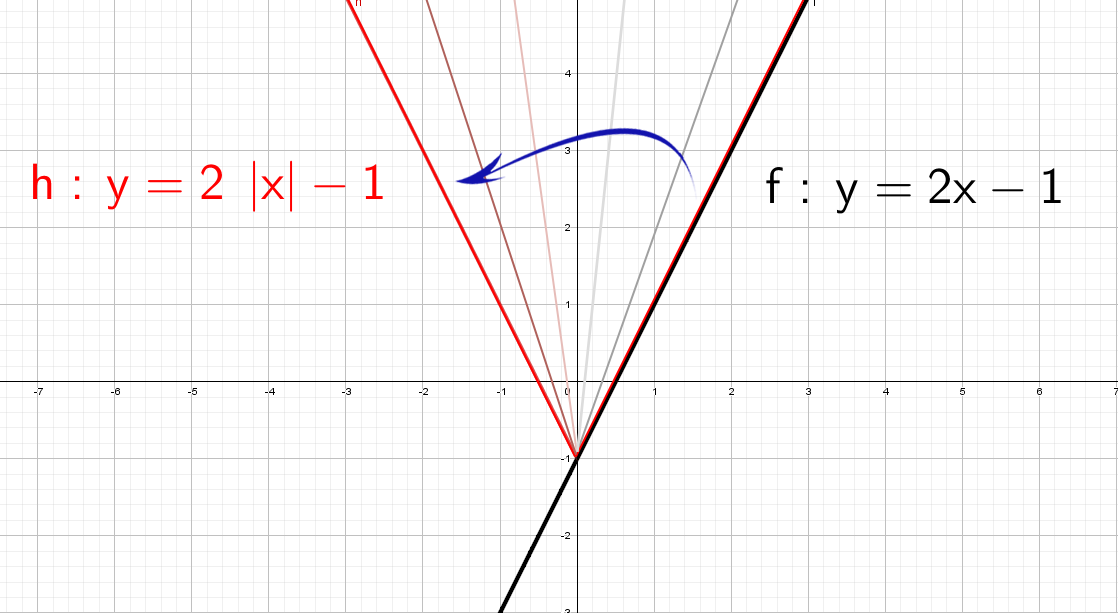
Здесь отражаем относительно оси «y». Такая же галочка, только теперь через другую ось.
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
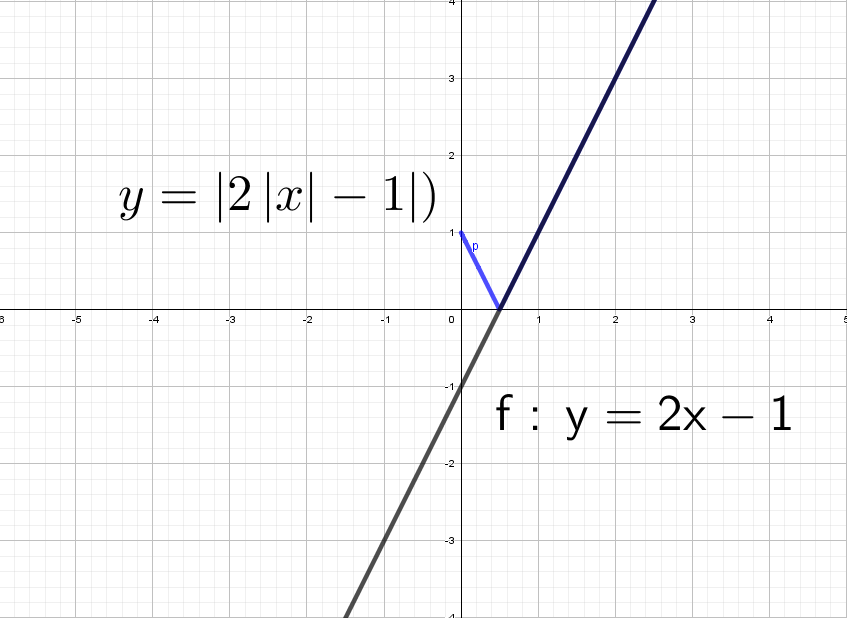
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
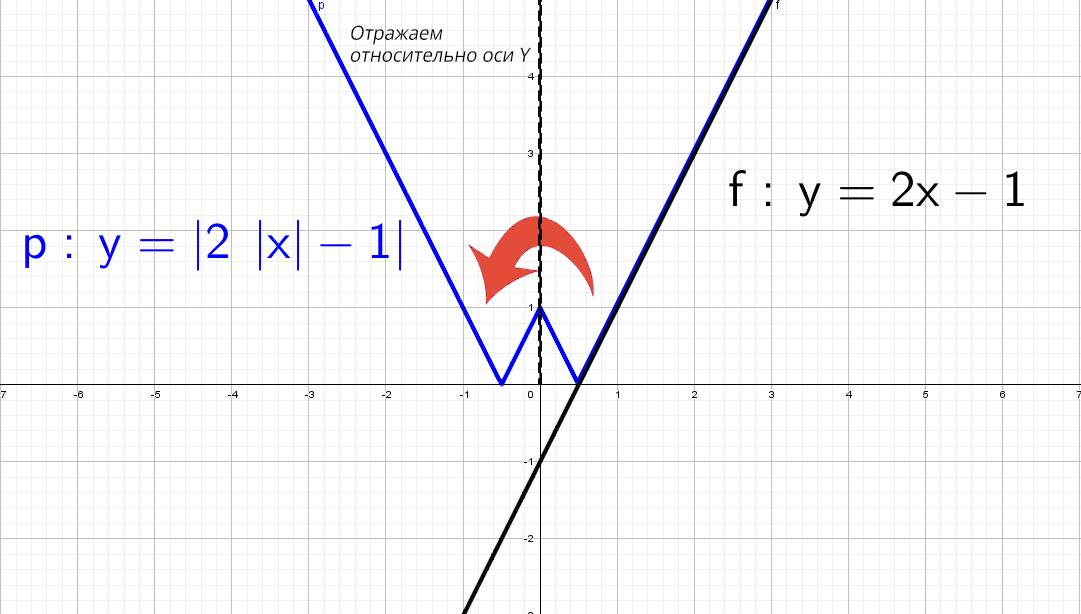
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x₁ = 1 и x₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.
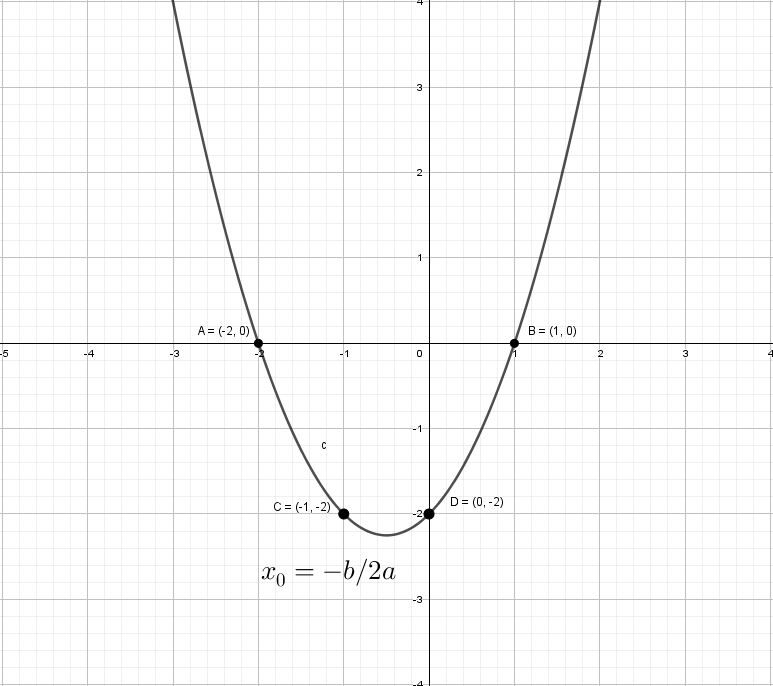
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
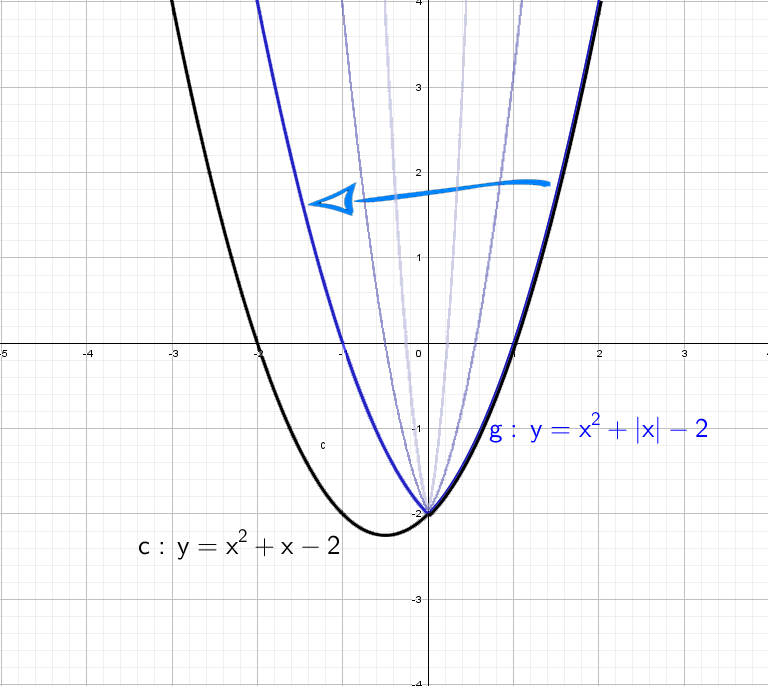
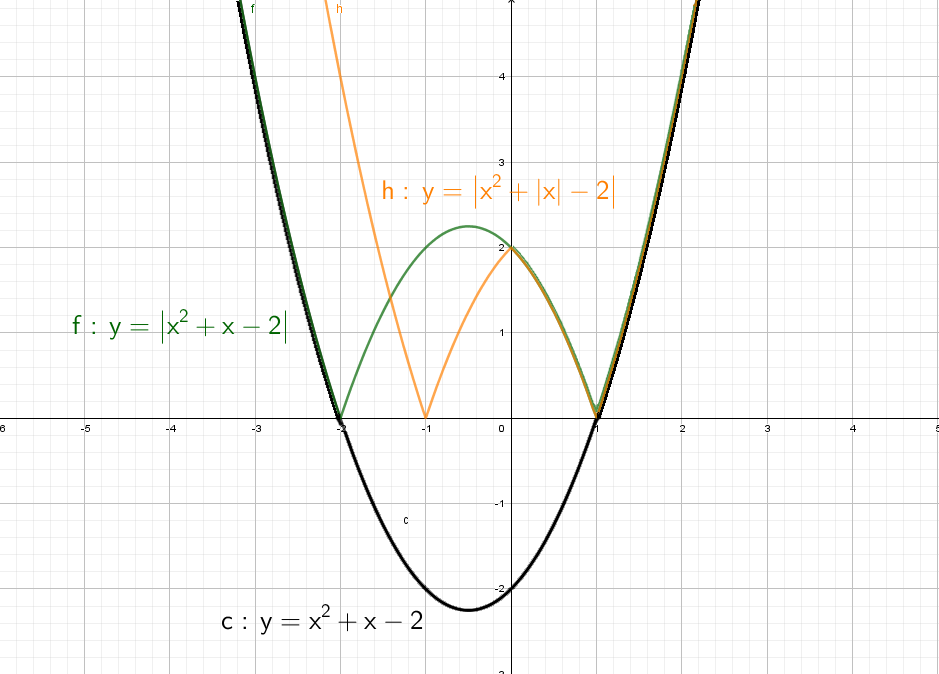
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
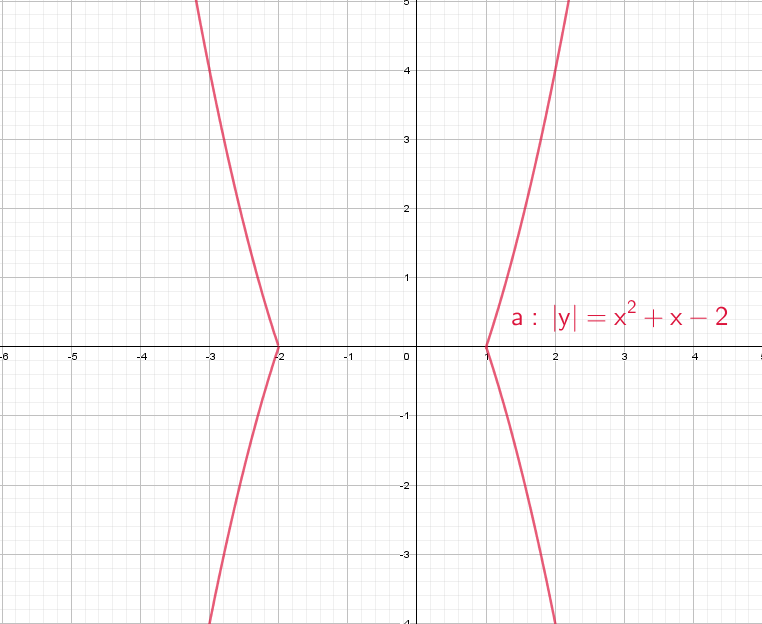
А теперь сразу комбо:
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет “шире”, расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.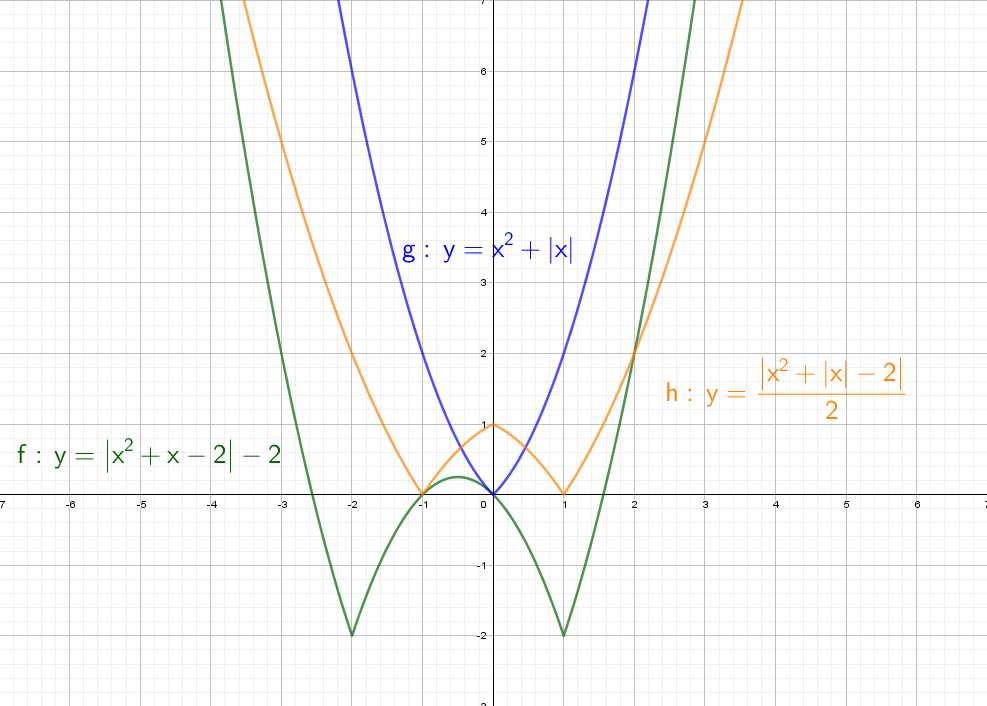
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
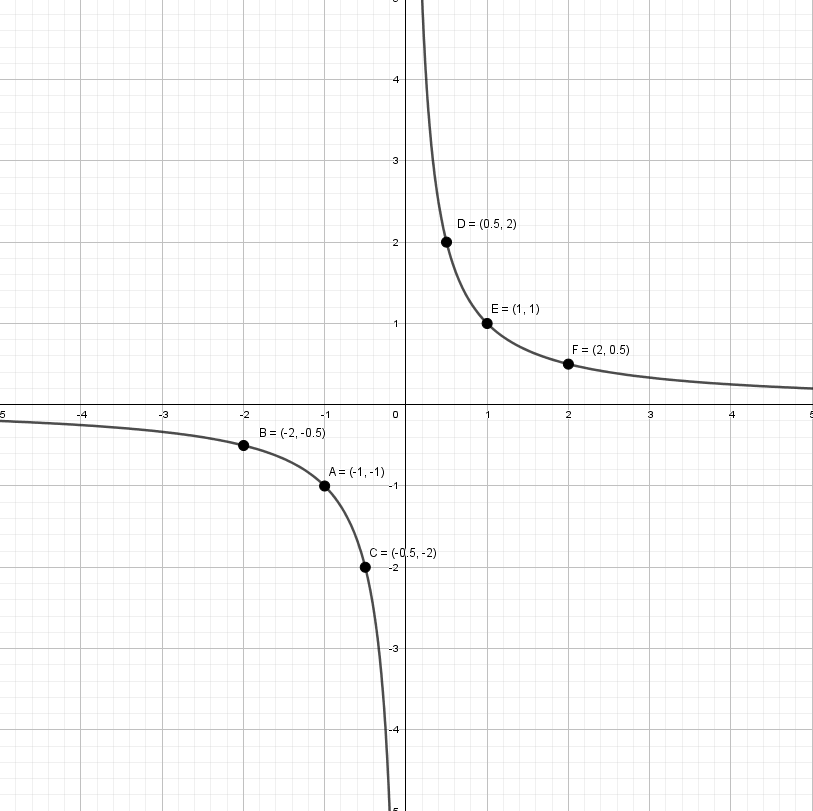
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
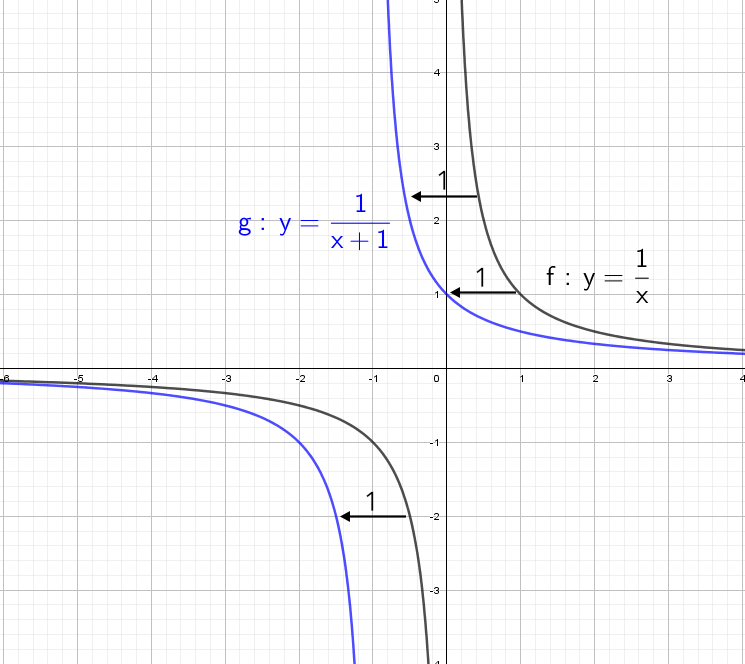
А что будет, если мы добавим в знаменателе «−1»? График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
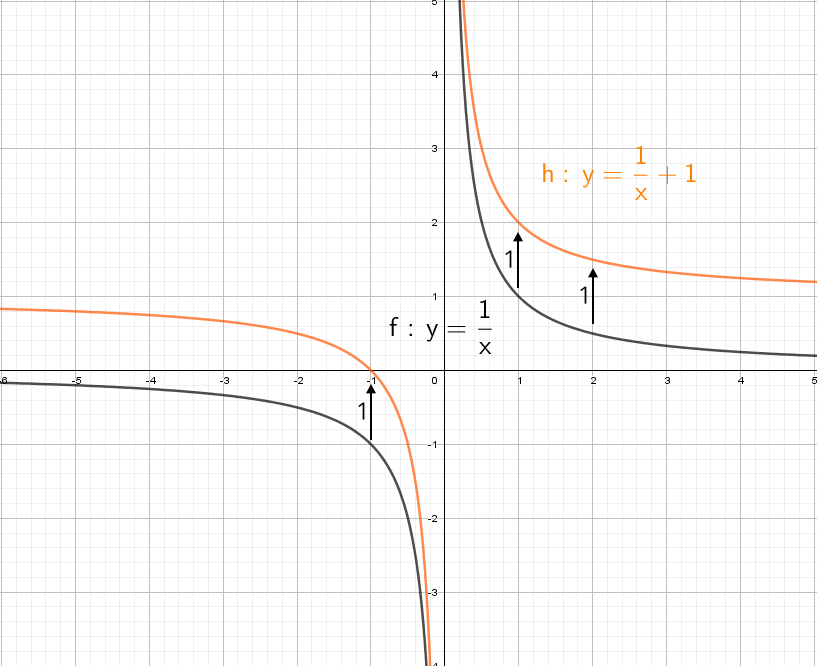 Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
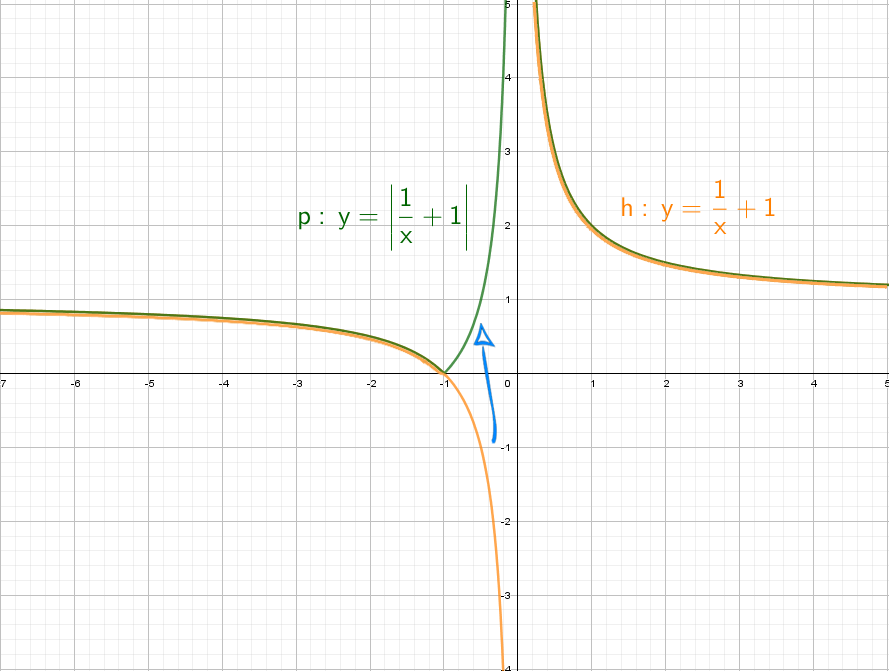
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
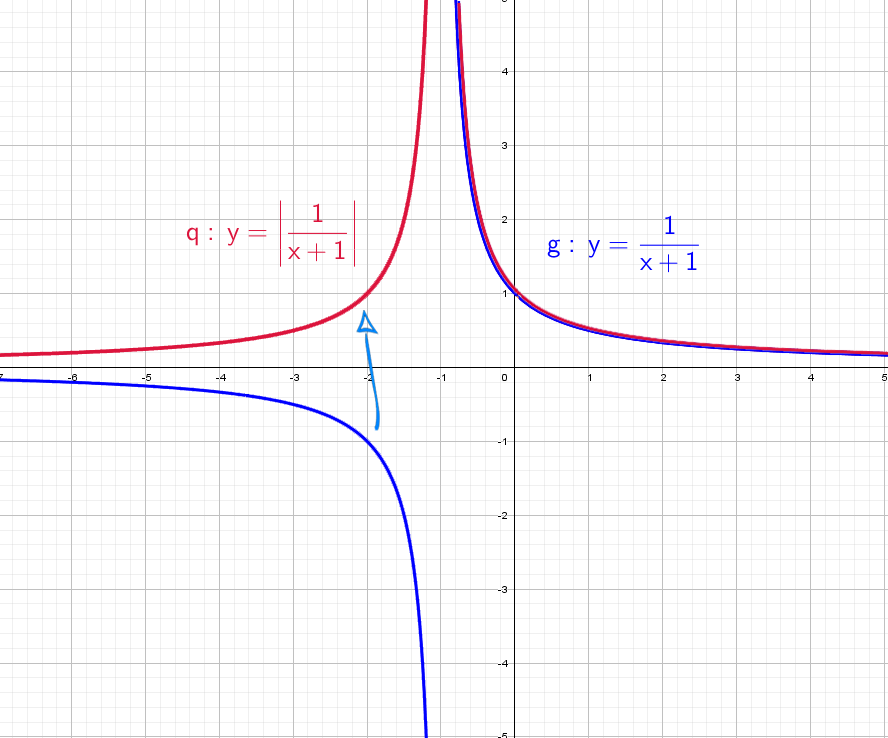
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
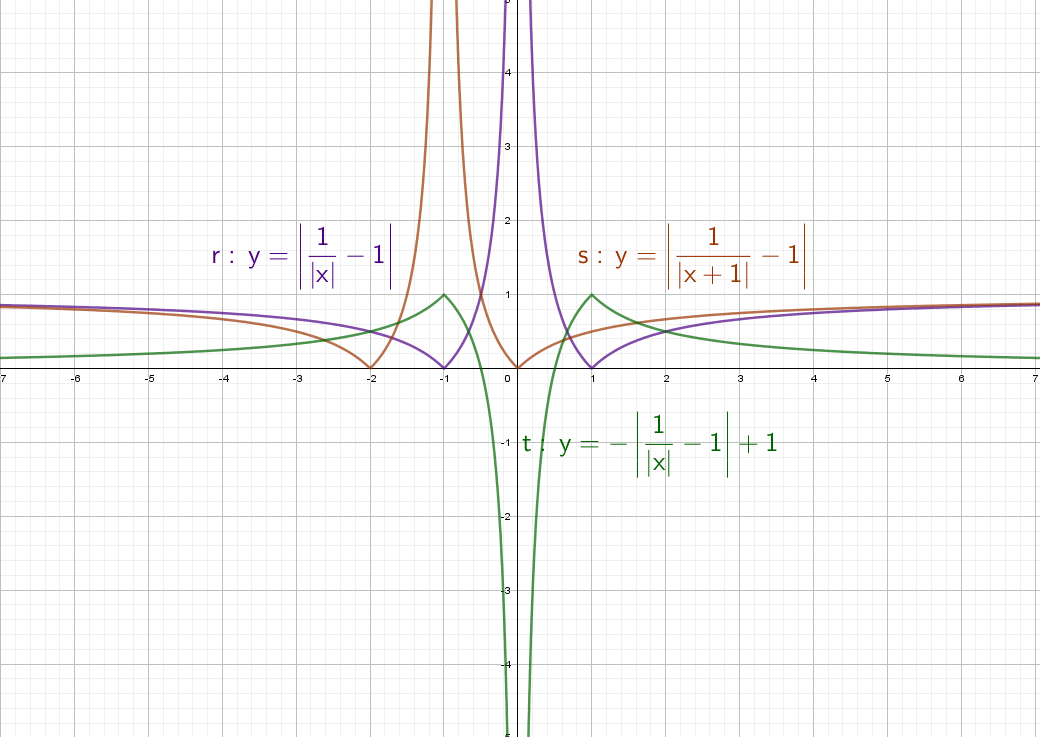
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
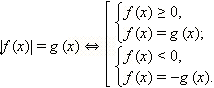
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
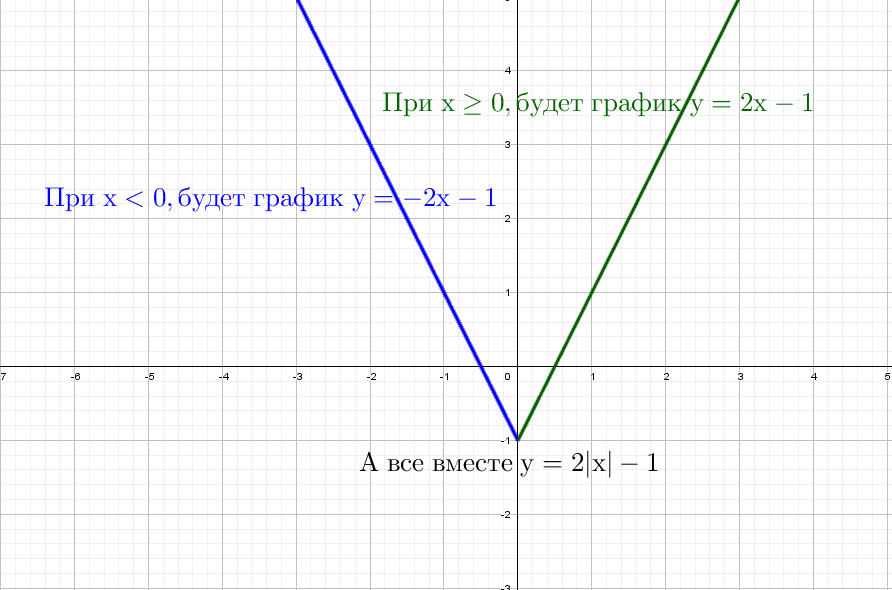
Для параболы с одним модулем будет два кусочно-заданных графика: 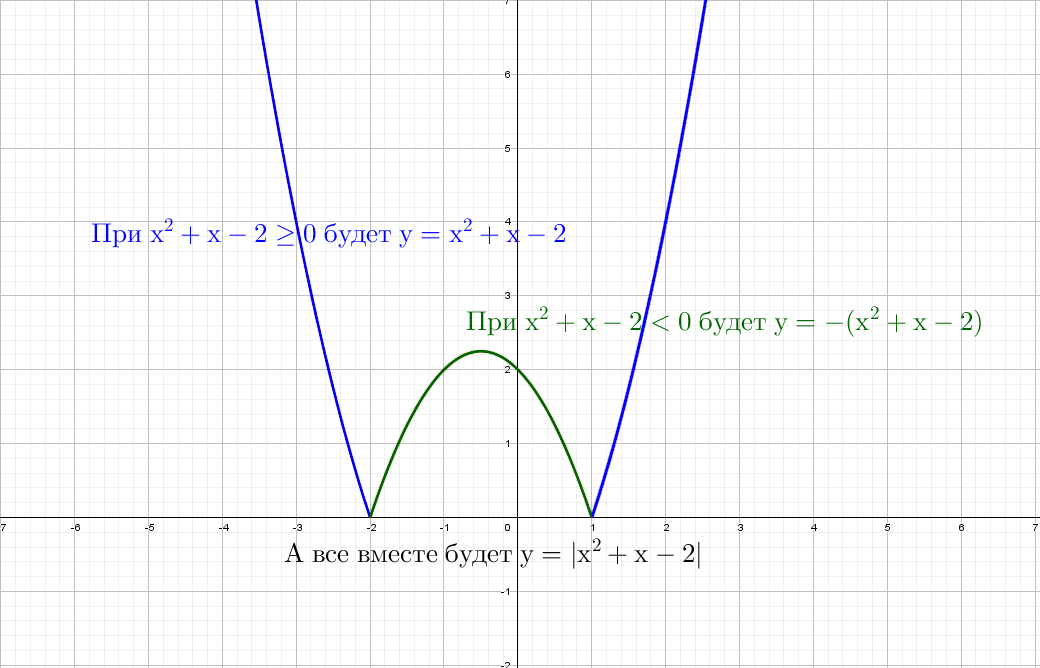
C двумя модулями кусочно-заданных графиков будет четыре:
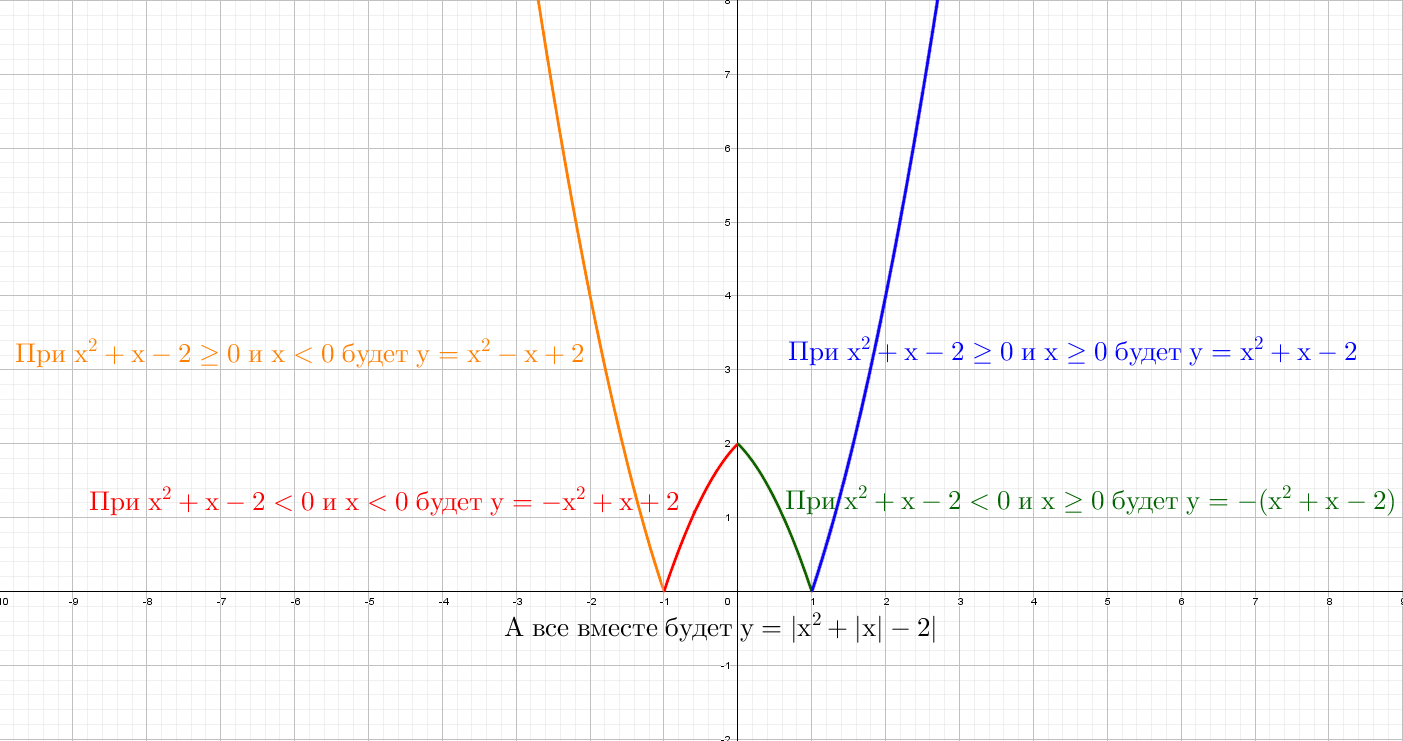 Таким способом, медленно и кропотливо можно построить любой график!
Таким способом, медленно и кропотливо можно построить любой график!
Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Будь в курсе новых статеек, видео и легкого математического юмора.
Построение графиков с модулем
путём преобразований
Модуль аргумента и модуль функции
Если Вы попали на эту страницу из поисковика, миновав предыдущие разделы темы “Графики функций и их преобразования”, то рекомендую сначала повторить графики основных элементарных функций и общие правила преобразования графиков функций.
В контексте построения графиков это означает использование преобразования симметрии относительно осей координат.


Пример 1.


В этом примере оба графика получены из графика функции y = x − 3.
Первый — преобразованием Гf(x) → Гf(|x|) , второй — преобразованием Гf(x) → Г|f(x)| .
Пример 2.


В этом примере оба графика получены из графика функции y = x 2 − 2x − 3.
Первый — преобразованием Гf(x) → Гf(|x|) , второй — преобразованием Гf(x) → Г|f(x)| .
Один из способов быстро и точно построить исходную параболу по характерным точкам показан в видео на канале Mathematichka.
III При построении из графика функции y = f(x) более сложных графиков, например, вида y = k·f (a|x| + b) + c или y = k·|f (ax + b)| + c тщательно соблюдайте последовательность преобразований.
Ниже показаны примеры графиков различных функций, содержащих модуль, которые получены из графика функции (y=sqrt.) y = √|x| __ .
| 1. (y=sqrt) √x _ –> | 2. (y=sqrt<|x|>) √|x| __ –> | 3. (y=sqrt<|x-1|>) y = √|x − 1| _____ | 4. (y=sqrt<|x|-1>) y = √|x| − 1 _____ | 5. (y=|sqrt-1|.) y = | √x − 1 _ | |
IV Равенство вида |y| = f (x) по определению не является функцией, так как допускает неоднозначность при вычислении значения y. Однако линию на координатной плоскости оно задает, и эту линию тоже можно построить, исходя из графика функции y = f(x) .
Для этого нужно:
- Построить график функции y = f(x) .
- Исключить его часть, расположенную ниже оси абсцисс, поскольку указанное равенство возможно только для положительных значений f(x).
- Построить нижнюю часть линии (при отрицательных y) симметричным отображением относительно оси Ox.
Эти кривые также получены из графика функции (y=sqrt). y = √x _ .
| 6. (|y|=sqrt) | 7. (|y|=|sqrt-1|) | 8. (|y|=sqrt<|x|>.) |
Пример 3.
Задан график функции y = x 2 .
Построить кривые, удовлетворяющие уравнению, |y| = x 2 − 2|x| − 5 .
Заметим, что x 2 = |x| 2 (значение четной степени, как и значение модуля, всегда неотрицательно). Поэтому, выделяя полный квадрат, преобразуем функцию к виду |y| = (|x| − 1) 2 − 6 и строим её график последовательными преобразованиями.
Строим график функции f(x) = (x − 1) 2 − 6 переносом на 1 вправо вдоль оси Ox, а затем переносом вниз на 6 единиц вдоль оси Oy.
Строим график функции f(|x|) = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Oy.
Строим линии, удовлетворяющие уравнению |y| = (|x| − 1) 2 − 6 с использованием преобразования симметрии относительно оси Ox.
| 1.y = x 2 | 2.y = (x − 1) 2 | 3.y = (x − 1) 2 − 6 | 4.y = (|x| − 1) 2 − 6 |
| 5.y = (|x| − 1) 2 − 6, y ≥ 0 | 6.|y| = (|x| − 1) 2 − 6 |
Следующий график постройте самостоятельно, чтобы убедиться, что вы правильно поняли материал.
Пример 4.
Задан график функции y = x 2 .
Построить график функции y = |x 2 − 2x − 5| .

Сумма модулей
Если формула функции включает сумму или разность несколько модулей, то следует разбить координатную плоскость на участки и построить каждую ветвь графика отдельно. Границы участков определяются приравниванием каждого модуля к нулю и решением соответствующего уравнения. Подробный пример такого подхода можно увидеть в задаче 1 на странице, посвященной решению уравнений с параметрами.
Однако, если подмодульные выражения простые и содержат элементарные функции, графики которых вам хорошо известны, то можно получить результат прямым сложением ординат этих графиков в характерных точках.
Пример 5.
Построить график функции y = |x + 2| + |x − 1| .

Эти два модуля содержат только линейные функции, графиками которых являются прямые линии. В результате сложения должна получиться ломаная линия, состоящая из трёх звеньев. (2 модуля, следовательно 2 уравнения, каждое из которых имеет одно решение, следовательно 2 границы, которыми плоскость разбита на 3 участка.) Трёхзвенную ломаную можно построить по 4-ём точкам.
На одних осях независимо друг от друга строим графики функций y = |x + 2| и y = |x − 1| , используя сдвиг и отражение. Складываем ординаты в точках излома x = −2 и x = 1 и в двух удобных точках на крайних участках, например, при x = −3 и x = 3 . На приведенном рисунке красным цветом представлен результирующий график, полученный по этим 4-ём точкам: (−3;5 ), (−2;3 ), (1; 3), (3;7).
Теперь проверьте себя.
Пример 6.
Построить график функции y = |x + 2| + |x − 1| − |x| .


Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Есть вопросы? пожелания? замечания?
Обращайтесь – mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте ссылки.
Графики прямой, параболы, гиперболы, с модулем

Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
Для понимания друг друга введу немного «обзываний» системы координат:



Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
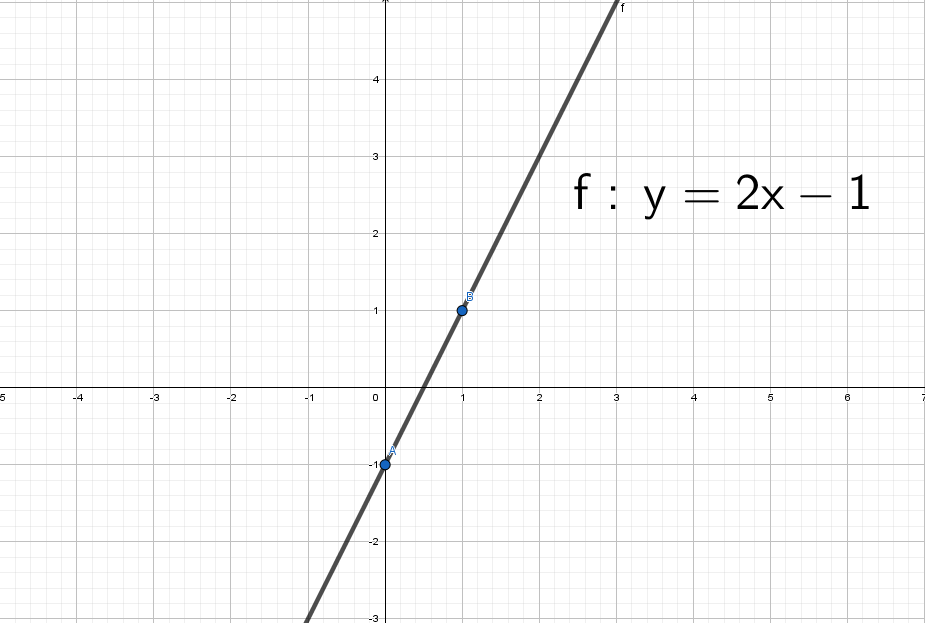
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение , получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
 Получается такая зеленая “галочка”.
Получается такая зеленая “галочка”.
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.

Здесь отражаем относительно оси «y» . Такая же галочка, только теперь через другую ось.
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!

А после этого отражаем относительно оси «y» то, что мы получили справа налево:

Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x ₁ = 1 и x ₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.

А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:

А дальше что мелочиться: рассмотри сразу остальные графики с модулем!

Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.

А теперь сразу комбо:
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет “шире”, расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум , потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:

А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:

А что будет, если мы добавим в знаменателе « − 1»? График сдвинется вправо на единицу.
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
 Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.

Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.

Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.

Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
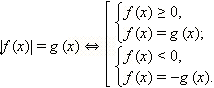
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:

Для параболы с одним модулем будет два кусочно-заданных графика: 
C двумя модулями кусочно-заданных графиков будет четыре:
 Таким способом, медленно и кропотливо можно построить любой график!
Таким способом, медленно и кропотливо можно построить любой график!
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль .
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Уравнения графиков функций с модулями
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
[spoiler title=”источники:”]
http://ik-study.ru/ege_math/grafiki_s_moduliem
http://yukhym.com/ru/matematika/uravneniya-s-modulyami-graficheskij-metod.html
[/spoiler]

Цели:
- Найти способ раскрытия модуля, при построении
графиков функции; - Развить умения и навыки построения графиков
квадратичной функции; - Вызвать интерес у учащихся к самостоятельному и
научному поиску.
Для достижения данной цели учащимся
предлагается решить следующие задачи:
- Изучить литературу по теме “модуль” и
“построения графиков квадратичной функции”; - Построить данные графики математическим
способом; - Построить графики с помощью компьютера,
используя программу EXCEL; - Сравнить результаты построения и сделать к
каждому типу задач выводы. - Оформить результаты, как научно
исследовательскую работу.
Учитель предлагает рассмотреть решение задач
типа:
Задача 1. Построить график функции у =? f(х)c , где
f(х)- квадратичная функция.
Задача 2. Построить график функции у =f(c хc ), где
f(х)- квадратичная функция.
Задача 3. Построить график функции у =f( -c хc ), где
f(х)- квадратичная функция.
Задача 4. Построить график функции у =c f(c хc )c ,
где f(х)- квадратичная функция.
Для решения данных задач необходимо
- Знать определение модуля и умение его
раскрывать; - Знать общие методы построение графика
квадратичной функции; - Рассмотреть 2-3 примера каждой задачи.
- Сравнить их с графиком функции у =f(х) , где f(х) –
квадратичная функция. - Сделать соответствующие выводы.
По решению данных задач рассмотреть следующие
примеры:
f(х) = c х2 -2х – 3c f(х) = х2 -2c хc
– 3f(х) = х2 +2c хc – 3
f(х) = c х2 -2c хc – 3 c
f(х) = х2 -2х – 3
f(х) = c -х2 + 6х – 5c f(х) = – х2 +6c
хc – 5f(х) = -х2 -6c хc – 5
f(х) = c -х2 +6c хc – 5 c
f(х) = -х2 +6х – 5
Занятие 1
Построить графики функций
математическим способом.
Цель занятия:
- Повторить теорию необходимую для построения
графиков функций, содержащих знак модуля. - Построить заданные графики функций.
Чтобы построить график функции необходимо
знать
1. что модуль числа не может быть отрицательным.
- Для положительного числа и нуля он равен самому
числу, а для отрицательного – противоположному.
2. общую схему построение графика квадратичной
функции:
- нахождение координат вершины параболы;
- составление таблицы значений;
- построение графика функции.
Учащиеся дают понятие модуль и как построить
график квадратичной функции (общую схему).
- Модулем числа называют расстояние от точки,
изображающей это число на координатной прямой,
до начала отсчета. Возьмем два противоположных
числа а и –а, точки изображающие их на
координатной прямой, расположены на одинаковом
расстоянии от начала отсчета. Для такого
расстояния придумано специальное название –
модуль числа а. Обозначают так:| а| . В самом деле
расстояние от точки А(5) до нуля равно 5, а
расстояние от точки В(-3) до нуля равно 3. Модули
противоположных чисел равны. Раз модуль – это
расстояние, он никогда не бывает отрицательным.
Поэтому для положительного числа и нуля он равен
самому числу, а для отрицательного –
противоположному. - Для построения графика квадратичной функции
вершина параболы находится по формулам:
Х= -В¤ 2а; у =ах2+вх +с, затем составляется
таблица и строится график.
I. Рассмотрим построение графиков функции вида
у = c f(х)c на примерах:
а)f(х) = c х2 -2х – 3c , б) f(х) = c -х2 + 6х – 5c .
А) Построим график функции f(х) = c х2 -2х – 3c .
1. Раскроем модуль:
c х2 -2х – 3c = х2 -2х – 3, если х2 -2х
– 3? 0 ,
c х2 -2х – 3c = – (х2 -2х – 3), если х2
-2х – 3< 0
Построим график квадратичной функции у = х2
-2х – 3.
Координатами вершины параболы у=х2 -2х – 3
будет точка с координатами (1;4).
Составим таблицу (*)значений для графика
функции у=х2 -2х – 3
Х -4 -3 -2 -1 0 1 2 3 4 у 21 12 5 0 -3 -4 -3 0 5
С учетом того, что при х2 -2х – 3< 0 функция
задана иным графиком у = – (х2 -2х – 3), таблица
будет следующей:
Х -4 -3 -2 -1 0 1 2 3 4 у 21 12 5 0 3 4 3 0 5
По данной таблице построю график функции.
Б) Построение графика функции f(х) = c -х2 + 6х
– 5c . При аналогичном рассуждении, получу график
функции .
Занятие 2
Построение графиков функции с помощью
компьютера.
Цель занятия:
- Изучить теорию построения графиков с помощью
компьютера. - Построить графики заданных функций с помощью
компьютера.
Используя компьютерную программу MS Excel. Эта
программа позволила мне еще изучить изменения
графиков в зависимости от значения тех или иных
параметров. Процесс разработки моделей и их
исследование на компьютере можно разделить на
несколько основных этапов.
- Описательная информационная модель (выделяем с
точки зрения целей проводимого исследования,
параметры объекта, а несущественными
параметрами пренебрегаем); - Формализованная модель (описание
информационной модели в программе MS Excel с помощью
формул); - Компьютерная модель (построение компьютерной
модели с использованием электронных таблиц MS
Excel); - Компьютерный эксперимент (построение графиков
функций); - Анализ полученных результатов и корректировка
исследуемой модели (в случае несоответствия
результатов, полученных при исследовании
информационной модели, измеряемым параметрам
реальных объектов можно сделать вывод, что на
предыдущих этапах построения модели были
допущены ошибки).
Исследуем графики функций y = f(x) и y=¦f(x) ¦, где f(x) =
x 2-2x-3 на промежутке [-2; 4]. Представим данные
функции в табличной форме
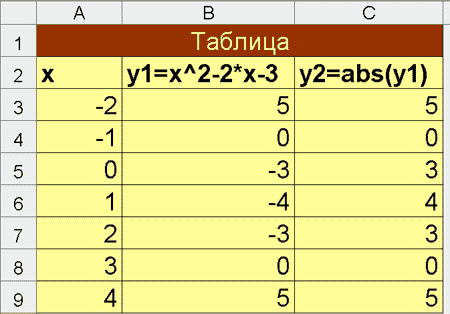
а) данные в представлены виде чисел

б) данные представлены в виде чисел и
формул
Используя мастер диаграмм, по полученным
данным строим точечную диаграмму со значениями,
соединенными сглаживающими линиями без
маркеров. Полученный результат не удовлетворяет
результатам нашего предварительного
исследования. Это хорошо видно на диаграмме.
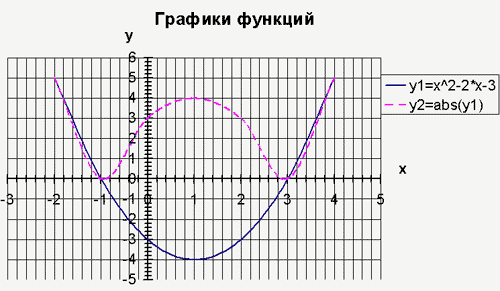
Для уменьшения погрешности исследований
при построении графиков функций, значения
аргумента изменяю на 0,1 (шаг), в формулах для
автоматизации расчетов использую относительную,
абсолютную и смешенные адресации ячеек. (Приложение 1).
Скорректированные параметры позволяют более
точно выполнить построения графиков функций в
программе MS Excel и подтвердить правильность моих
исследований математическим путем – “на
бумаге”.
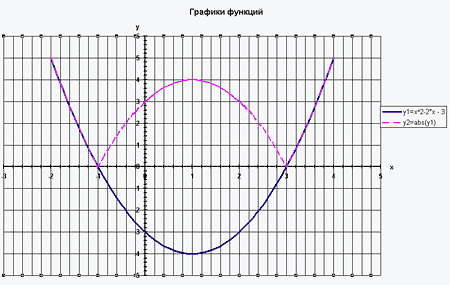
(Приложение 2)
График функции f(х) = c -х2 + 6х – 5c исследую
аналогичным образом. (Приложение
3).
Занятие 3
Построение графиков
(практическое занятие)
Цель занятия:
- Отработка навыков построения графиков
квадратичной функции двумя способами.
Решить задачи типа 2,3,4. на предложенных
примерах (аналогично занятиям 1и 2)
Приведу некоторые решения:
а)f(х) =х2 -2c хc – 3,
б)f(х) =-х2 + 6c х c – 5.
1. Если х? 0, то c хc =х, тогда получим f(х) =х2 -2х
– 3,
если х< 0, то c хc = – х, тогда получим
2. Построю графики функций f(х) =х2 -2х – 3, f(х)
=х2 +2х – 3 в одной системе координат. Точки с
координатами (1;-4) и (-1;-4) координаты вершин
парабол соответственно.
Составлю таблицу значений (**) для построение
графика функции
f(х) =х2 +2х– 3.
| Х | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| у | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | 21 |
Воспользовавшись таблицей (*) и (**) Искомый
график функции будет часть параболы f(х) =х2
-2х – 3 при х> 0 и часть параболы f(х) =х2
+2х – 3 при х< 0.
(Приложение 4)
б) Построение графика функции f(х) =-х2 + 6c хc
– 5. При аналогичном рассуждении, построю график
функции и проверю правильность построения
используя компьютер. (Приложение
5).
Решение третий тип задач , на примерах функций:
а) f(х) = х2 +2c хc – 3;
б) f(х) = -х2 -6c хc – 5.
Чтобы построить график функции f(х) = х2 +2c
хc – 3 опять использую:
1. Раскрытие знака модуль.
Если х>0,то получим f(х) =х2 +2х – 3,
Если х< 0,то получим f(х) =х2 -2х – 3.
2. Построю график функции, воспользовавщися
таблицами (*) и (**) и с учетом, что
f(х) =х2 +2х – 3, при х>0, а f (х) =х2 -2х
– 3. при х< 0. Получим график функции. Исследую
построение графика в компьютерной программе.
(приложение 4).
Рассмотрю построение графика функции f(х) = -х2
-6c хc – 5 аналогично. (Приложение
5).
Для решение последней задачи я использовала
также два примера.
А)f(х) =? х2 -2c хc – 3? , б) (х) = -? х2 + 6c х c –
5? .
Чтобы построить данные графики функции уже
использую известные мне преобразования, построю
графики функций f(х) =х2 -2c хc – 3 и f(х) =? х2
-2c хc – 3? . В результате получаю следующий график
функции. (Приложение 6).
При построении графика f(х) =-? х2 + 6c х c – 5?
также использую преобразования и построю
графики функций f(х) = – х2 +6c хc – 5 и f(х) =-? х2
+6c хc – 5? . (Приложение 7).
Занятия 4.
Итоговое занятие.
Цель занятия:
- Рассмотреть полученные графики функций каждого
типа задач на рассмотренных примерах и сделать
соответствующие выводы.
1. Результаты построенных графиков функций
первого типа позволили сделать следующий вывод:
График функции у = c f(х)c совпадает с графиком
функции у = f(х) на тех промежутках, где f(х)>0, а
на промежутках где f(х)< 0, график функции
у = c f(х)c получается из графика функции у = f(х) с
помощью симметрии относительно оси Ох.
2. Глядя, на построенные графики второго типа
замечаем:
Для построения графика функции у =f(c хc ), где f(х)-
квадратичная функция надо построить функцию у =
f(х), затем оставить только его часть, лежащую
справа от оси Оу, и отобразить эту часть
симметрично той же оси.
3. Рассматривая графики функций третьего вида
получаем следующий вывод:
Для построения графика функции у =f (- c хc ), где
f(х)- квадратичная функция надо построить функцию
у = f(х), затем оставить только его часть, лежащую
справа (слева) от оси Оу, и отобразить эту часть
симметрично той же оси.
4. Для построения графика функции у =c f(c хc )c , где
f(х)- квадратичная функция надо построить график
функции у = f(х). Тогда, используя известные
преобразования, построим у =f(c хc ) и у = c f(х)c .
Выводы:
При решении данных задач мне удалось оказать
помощь в построении графиков функций, содержащих
знак модуля, а главное убедить, что математика –
это содержательное, увлекательное и доступное
поле деятельности, дающее ученику богатую пищу
ума, связывающее его с общечеловеческой
культурой, формирующее важнейшие черты его
личности. РАССМАТРИВАЕМЫЕ ПРИЕМЫ ПОСТРОЕНИЯ
ГРАФИКОВ ФУНКЦИЙ МОЖНО ПРИМЕНИТЬ НЕ ТОЛЬКО К
КВАДРАТИЧНЫМ ФУНКЦИЯМ, НО И К ЛИНЕЙНЫМ,
ТРИГОНОМЕТРИЧЕСКИМ, ПОКАЗАТЕЛЬНЫМ И
ЛОГАРИФМИЧЕСКИМ.
Список литературы
- “Математика”. Учебник 6 класс Н.Я. Виленкин, В.И.
Жохов. – Изд.4 –е.- М. Издательство “Русское
слово”, 1997г. - “Алгебра”. Учебник 9 класс. Ю.Н. Макарычев, Н.Г.
Миндюк . М. Просвещение, 2004г. - “Математика” Еженедельная
учебно-методическая газета. Издательский дом
“Первое сентября”. №48, 2003г. - “Математика” Еженедельная
учебно-методическая газета. Издательский дом
“Первое сентября”. №7, 1998г. - Тесты и экзаменационные задания по математике.
Учебное пособие. Е.С.Баранова, Н.В. Васильева. –
Издательский дом “Питер”, 2005 г. - “Абсолютная величина”. Гайдуков И.И.. – М.:
Просвещение, 1968. - “Функции и построение графиков”. Гурский И.П..-
М.: Просвещение, 1968. - “Задачи повышенной трудности в курсе алгебры
для 7-9 классов”. Кострикина Н.П.. М.: Просвещение,
1991.
