Как найти градиент потенциала электрического поля

Вектор градиента потенциала поля

§7 Работа силы электростатического поля при перемещении заряда.

Потенциальный характер сил поля.

Циркуляция вектора напряженности

Рассмотрим электростатическое поле, создаваемое зарядом q . Пусть в нем перемещается пробный заряд q ₀ . В любой точке поля на заряд q ₀ действует сила

де – модуль силы, – орт радиус-вектора , определяющего положение заряда q ₀ относительно заряда q . Так как сила меняется от точки к точке, то работу силы электростатического поля запишем как работу переменной силы:

Ввиду того, что рассматривали перемещение заряда из точки 1 в точку 2 по произвольной траектории, можно сделать вывод, что работа по перемещению точечного заряда в электростатическом поле не зависит от формы пути, а определяется лишь начальным и конечным положением заряда. Это свидетельствует о том, что электростатическое поле является потенциальным, а сила Кулона – консервативной силой. Работа по перемещению заряда в таком поле по замкнутому пути всегда рвана нулю.

– проекция на направление контура ?.

Учтем, что работа по замкнутому пути равно нулю

– ЦИРКУЛЯЦИЯ вектора напряженности.

Циркуляция вектора напряженности электростатического поля, взятая по произвольному замкнутому контуру всегда равна нулю.

§7 Потенциал.

Связь между напряженностью и потенциалом.

Градиент потенциала.

Эквипотенциальные поверхности

Поскольку электростатическое поле является потенциальным работа по перемещению заряда в таком поле может быть представлена, как разность потенциальных энергий заряда в начальной и конечной точках пути. (Работа равна уменьшению потенциальной энергии, или изменению потенциальной энергии, взятому со знаком минус.)

Постоянную определяют из условия, что при удалении заряда q ₀ на бесконечность его потенциальная энергия должна быть равна нулю.

.

Различные пробные заряды q _{0 i} , помещенные в данную точку поля будут обладать в этой точке различными потенциальными энергиями:

…

Отношение W _{пот i} к величине пробного заряда q _{0 i} , помещенного в данную точку поля является величиной постоянной для данной точки поля для всех пробных зарядов. Это отношение называется ПОТЕНЦИАЛОМ.

ПОТЕНЦИАЛ – энергетическая характеристика электрического поля. ПОТЕНЦИАЛ численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

Работу по перемещению заряда можно представить в виде

.

Потенциал измеряется в Вольтах

ЭКВИПОТЕНЦИАЛЬНЫМИ ПОВЕРХНОСТЯМИ называются поверхности равного потенциала (φ = const ). Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Связь между напряженностью и потенциалом φ можно найти, исходя из того, что работу по перемещению заряда q на элементарном отрезке d ? можно представить как

С другой стороны

– градиент потенциала.

Напряженность поля равна градиенту потенциала, взятому со знаком минус.

Градиент потенциала показывает, как меняется потенциал на единицу длины. Градиент перпендикулярен функции и направлен в сторону возрастания функции. Следовательно, вектор напряженности перпендикулярен эквипотенциальной поверхности и направлен в сторону убывания потенциала.

Рассмотрим поле, создаваемое системой N точечных зарядов q ₁ , q ₂ , … q_N . Расстояния от зарядов до данной точки поля равны r ₁ , r ₂ , … r_N . Работа, совершаемая силами этого поля над зарядом q ₀ , будет равна алгебраической сумме работ сил, каждого заряда в отдельности.

гле

Потенциал поля, создаваемого системой зарядов, определяется как алгебраическая сумма потенциалов, создаваемых в этой же точке каждым зарядом в отдельности.

§9 Вычисление разности потенциалов плоскости, двух плоскостей, сферы, шара, цилиндра

Используя связь между φ и определим разность потенциалов между двумя произвольными точками

Разность потенциалов поля равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ.

2. Разность потенциалов поля двух бесконечных параллельных разноименно заряженных плоскостей с поверхностной плотностью заряда σ.

Если х₁ = 0; х₂ = d , то или

3. Разность потенциалов поля равномерно заряженной сферической поверхности радиуса R .

Внутри сферической поверхности потенциал всюду одинаков и равен

4. Разность потенциалов поля объемно заряженного шара радиуса R с общим зарядом Q.

Вне шара r ₁ , r ₂ > R ,

Внутри шара

5. Разность потенциалов поля равномерно заряженного цилиндра (или бесконечно длинной нити).

r > R :

Градиент потенциала

Градиент потенциала – это скорость возрастания потенциала в направлении кротчайшем между двумя точками.

Между двумя точками имеется некоторая разность потенциалов. Если эту разность разделить на кратчайшее расстояние между взятыми точками, то полученное значение будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками.

Градиент потенциала показывает направление наибольшего возрастания потенциала, численно равен модулю напряженности и отрицательно направлен по отношению к нему.

В определении градиента существенны два положения:

1) Направление, в котором берутся две близлежащие точки, должно быть таким, чтобы скорость изменения была максимальной.

2) Направление таково, что скалярная функция в этом направлении возрастает.

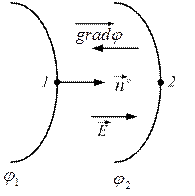
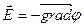
Для декартовой системы координат:

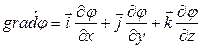
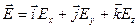
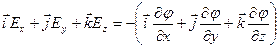
Скорость изменения потенциала в направлении оси Х, Y, Z:

; ;

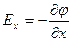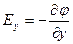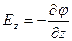
Два вектора равны только тогда, когда равны друг другу их проекции. Проекция вектора напряженности на ось Х равна проекции скорости изменения потенциала вдоль оси Х, взятой с обратным знаком. Аналогично для осей Y и Z.

; ; .

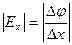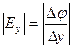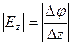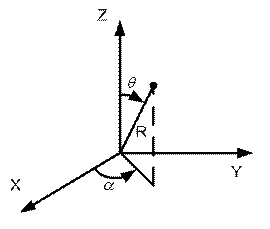
В цилиндрической системе координат выражение градиента потенциала будет иметь следующий вид:

.

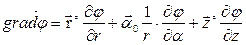А в сферической системе координат:

.

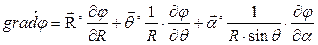Дифференциальный оператор Гамильтона (оператор Набла)

Для сокращения записи операций над скалярными и векторными величинами употребляют дифференциальный оператор Гамильтона или оператор Набла:

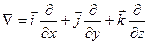
Под дифференциальным оператором Гамильтона понимают сумму частных производных по 3-м координатным осям, умноженных на соответствующие единичные векторы (орты).

Применим оператор Гамильтона к потенциалу:

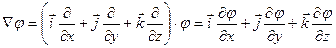
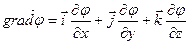
Правые части одинаковы, значит, будут одинаковы и левые части:

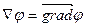
Оператор Гамильтона сочетает в себе как векторные, так и скалярные свойства и может быть применен к скалярным и векторным функциям.

Дата добавления: 2015-07-30 ; просмотров: 19538 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Градиент потенциальных характеристик, как его рассчитать и пример

градиент потенциала является вектором, который представляет отношение изменения электрического потенциала по отношению к расстоянию в каждой оси декартовой системы координат. Таким образом, вектор градиента потенциала указывает направление, в котором скорость изменения электрического потенциала больше, в зависимости от расстояния.

В свою очередь, модуль градиента потенциала отражает скорость изменения электрического потенциала в определенном направлении. Если значение этого известно в каждой точке пространственной области, то электрическое поле может быть получено из градиента потенциала.

Электрическое поле определяется как вектор, с которым оно имеет определенное направление и величину. Определяя направление, в котором электрический потенциал уменьшается быстрее, удаляясь от контрольной точки, и деля это значение на пройденное расстояние, получается величина электрического поля..

• 1 Характеристики
• 2 Как рассчитать?
• 3 Пример
  • 3.1 Упражнение
• 4 Ссылки

черты

Градиент потенциала представляет собой вектор, ограниченный конкретными пространственными координатами, который измеряет отношение изменения между электрическим потенциалом и расстоянием, пройденным этим потенциалом.

Наиболее выдающиеся характеристики градиента электрического потенциала подробно описаны ниже:

1- Потенциальный градиент – это вектор. Следовательно, он имеет определенную величину и направление.

2- Поскольку потенциальный градиент является вектором в пространстве, он имеет величины, адресованные по осям X (ширина), Y (высокая) и Z (глубина), если в качестве эталонной системы координат берется декартова система координат.

3- Этот вектор перпендикулярен эквипотенциальной поверхности в точке, в которой оценивается электрический потенциал.

4- Вектор градиента потенциала направлен в направлении максимального изменения функции электрического потенциала в любой точке..

5- Модуль градиента потенциала равен модулю, полученному из функции электрического потенциала по отношению к расстоянию, пройденному в направлении каждой из осей декартовой системы координат..

6- Потенциальный градиент имеет нулевое значение в стационарных точках (максимальная, минимальная и седловая точки).

7- В международной системе единиц (СИ) единицами измерения градиента потенциала являются вольт / метры.

8. Направление электрического поля такое же, в котором электрический потенциал уменьшает свою величину быстрее. В свою очередь, градиент потенциала указывает в направлении, в котором потенциал увеличивает свое значение по отношению к изменению положения. Тогда электрическое поле имеет то же значение градиента потенциала, но с противоположным знаком.

Как рассчитать?

Разность электрических потенциалов между двумя точками (точка 1 и точка 2) определяется следующим выражением:

V1: электрический потенциал в точке 1.

V2: электрический потенциал в точке 2.

E: величина электрического поля.

Ѳ: угол наклона вектора электрического поля, измеренного относительно системы координат.

Выражая указанную формулу дифференциальным способом, получаем следующее:

Коэффициент E * cos (Ѳ) относится к модулю компонента электрического поля в направлении dl. Пусть L – горизонтальная ось плоскости отсчета, тогда cos (Ѳ) = 1, вот так:

Далее, отношение между изменением электрического потенциала (dV) и изменением пройденного расстояния (ds) является модулем градиента потенциала для упомянутого компонента.

Из этого следует, что величина градиента электрического потенциала равна компоненте электрического поля в направлении исследования, но с противоположным знаком.

Однако, поскольку реальная среда является трехмерной, градиент потенциала в данной точке должен быть выражен как сумма трех пространственных компонентов на осях X, Y и Z декартовой системы..

Разбивая вектор электрического поля на три прямоугольных компонента, мы получаем следующее:

Если в плоскости имеется область, в которой электрический потенциал имеет одинаковое значение, частная производная этого параметра по каждой из декартовых координат будет равна нулю.

Таким образом, в точках, которые находятся на эквипотенциальных поверхностях, напряженность электрического поля будет иметь нулевую величину.

Наконец, вектор градиента потенциала может быть определен как точно такой же вектор электрического поля (по величине) с противоположным знаком. Таким образом, мы имеем следующее:

пример

Из приведенных выше расчетов необходимо:

Теперь, прежде чем определять электрическое поле как функцию градиента потенциала или наоборот, сначала необходимо определить направление, в котором разность электрических потенциалов растет..

После этого определяется коэффициент изменения электрического потенциала и изменения пройденного расстояния..

Таким образом, мы получаем величину соответствующего электрического поля, которая равна величине градиента потенциала в этой координате.

осуществление

Есть две параллельные пластины, как показано на следующем рисунке.

Шаг 1

Направление роста электрического поля на декартовой системе координат определяется.

Электрическое поле растет только в горизонтальном направлении, учитывая расположение параллельных пластин. Следовательно, можно сделать вывод, что компоненты градиента потенциала на оси Y и оси Z равны нулю..

Шаг 2

Данные, представляющие интерес различаются.

– Разность потенциалов: dV = V2 – V1 = 90 В – 0 В => dV = 90 В.

– Разница в расстоянии: дх = 10 сантиметров.

Чтобы обеспечить соответствие единиц измерения, используемых в соответствии с Международной системой единиц, величины, не выраженные в СИ, должны быть соответственно преобразованы. Таким образом, 10 сантиметров равны 0,1 метра, и, наконец, dx = 0,1 м.

Шаг 3

Величина вектора градиента потенциала рассчитывается соответствующим образом.

[spoiler title=”источники:”]

http://helpiks.org/4-37431.html

http://ru.thpanorama.com/articles/electrnica/gradiente-de-potencial-caractersticas-cmo-calcularlo-y-ejemplo.html

[/spoiler]

Связь между напряженностью и потенциалом электрического поля. Градиент потенциала. Теорема о циркуляции электрического поля.

Напряженность
и потенциал
– это две характеристики одного и того
же объекта – электрического поля,
поэтому между ними должна существовать
функциональная связь. Действительно,
работа сил поля по перемещению заряда
q
из одной точки пространства в другую
может быть представлена двояким образом:

Откуда
следует, что

Или

Это
и есть искомая связь
между напряженностью и потенциалом
электрического поля в дифференциальном
виде.

–
вектор, направленный из точки с меньшим
потенциалом в точку с большим потенциалом.

.

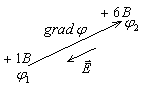
Из
свойства потенциальности электростатического
поля следует, что работа сил поля по
замкнутому контуру (φ₁=
φ₂)
равна нулю:

,

поэтому
можем написать
.

Последнее
равенство отражает суть второй
основной
теоремы
электростатики – теоремы
о циркуляции
электрического
поля,
согласно которой циркуляция
полявдоль
произвольного
замкнутого контура равна нулю.
Эта теорема является прямым следствием
потенциальности
электростатического
поля.

Эквипотенциальные
линии и поверхности и их свойства.

Линии
и поверхности, все точки которых имеют
одинаковый
потенциал,
называются эквипотенциальными.
Их свойства непосредственно вытекают
из представления работы сил поля и
иллюстрируются рисунке.

1)–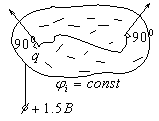
работа по перемещению заряда вдоль
эквипотенциальной линии (поверхности)
равна нулю, т. к..

2)– силовые линии поля в каждой точке
ортогональны к эквипотенциальной линии
(поверхности).

Потенциалы простейших электрических полей.

Из
соотношения
,
определяющего связь между напряженностью
и потенциалом электрического поля,
следует формула для вычисления потенциала
поля:

где
интегрирование производится вдоль
силовой линии поля; С
– произвольная постоянная, с точностью
до которой определяется потенциал
электрического поля.

Если
направление поля
совпадает с направлением радиус–вектора(),
то вычисления можно производить по
формуле:

.

Потенциал поля точечного заряда.

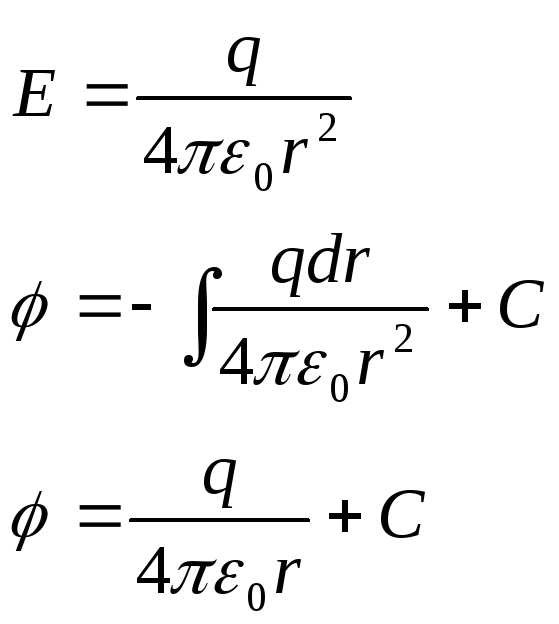
При
полагают, что,
тогда.

Таким
образом, потенциал поля
точечного
заряда
определяется по формуле:

.

Вопросы для самоконтроля

1. Что
   представляют собой электрические
   заряды? Какие виды зарядов вы знаете?

2. Сформулируйте
   закон сохранения электрического заряда.

3. Сформулируйте
   закон Кулона.

4. Что
   представляет собой электростатическое
   поле?

5. Каково
   числовое значение, единица и размерность
   электрической постоянной?

6. Что
   называется напряженностью электрического
   поля?

7. Сформулируйте
   принцип суперпозиции электрических
   полей.

8. Какое
   практическое применение имеет теорема
   Остроградского-Гаусса?

9. Сформулируйте
   определение потенциала точки
   электрического поля.

10. Что
    называется вольтом и какая его
    размерность?

11. Чему
    равна работа по перемещению заряда
    вдоль эквипотенциальной поверхности?

12. Каким
    соотношением связаны между собой
    потенциал и напряженность электрического
    поля?

СПИСОК
ЛИТЕРАТУРЫ

Основная

1. Детлаф,
   А.А. Курс
   физики учеб. пособие / А.А. Детлаф, Б.М.
   Яворский.-7-е изд. Стер.-М. : ИЦ
   «Академия».-2008.-720 с.

2. Савельев,
   И.В. Курс
   физики: в 3т.:учеб.пособие/И.В. Савельев.-4-е
   изд. стер. – СПб.; М. Краснодар: Лань.-2008

Т.2:
Электричество. Колебания и волны.
Волновая оптика. – 480 с.

1. Трофимова,
   Т.И. курс
   физики: учеб. пособие/ Т.И. Трофимова.-
   15-е изд., стер.- М.: ИЦ «Академия», 2007.-560
   с.

Дополнительная

1. Фейнман,
   Р. Фейнмановские
   лекции по физике / Р.
   Фейнман, Р. Лейтон, М. Сэндс.
   –
   М.: Мир.

Т.1.
Современная наука о природе. Законы
механики. – 1965. –232 с.

Т.
2. Пространство, время, движение. – 1965.
– 168 с.

Т.
3. Излучение. Волны. Кванты. – 1965. – 240 с.

1. Берклеевский
   курс физики. Т.1,2,3. – М.: Наука, 1984

Т.
1. Китель, Ч.
Механика / Ч. Китель, У. Найт, М. Рудерман.
– 480 с.

Т.
2. Парселл, Э.
Электричество и магнетизм / Э. Парселл.
– 448 с.

Т.
3. Крауфорд, Ф.
Волны / Ф. Крауфорд – 512 с.

1. Фриш,
   С.Э. Курс общей
   физики: в 3 т.: учеб. / С.Э. Фриш, А.В.
   Тиморева.- СПб.: М.; Краснодар: Лань.-2009.

Т.
1. Физические основы механики. Молекулярная
физика. Колебания и волны: учебник – 480
с.

Т.2:
Электрические и электромагнитные
явления: учебник. – 518 с.

Т.
3. Оптика. Атомная физика : учебник– 656
с.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

From Wikipedia, the free encyclopedia

In physics, chemistry and biology, a potential gradient is the local rate of change of the potential with respect to displacement, i.e. spatial derivative, or gradient. This quantity frequently occurs in equations of physical processes because it leads to some form of flux.

Definition[edit]

One dimension[edit]

The simplest definition for a potential gradient F in one dimension is the following:^[1]

where ϕ(x) is some type of scalar potential and x is displacement (not distance) in the x direction, the subscripts label two different positions x₁, x₂, and potentials at those points, ϕ₁ = ϕ(x₁), ϕ₂ = ϕ(x₂). In the limit of infinitesimal displacements, the ratio of differences becomes a ratio of differentials:

The direction of the electric potential gradient is from to .

Three dimensions[edit]

In three dimensions, Cartesian coordinates make it clear that the resultant potential gradient is the sum of the potential gradients in each direction:

where e_x, e_y, e_z are unit vectors in the x, y, z directions. This can be compactly written in terms of the gradient operator ∇,

although this final form holds in any curvilinear coordinate system, not just Cartesian.

This expression represents a significant feature of any conservative vector field F, namely F has a corresponding potential ϕ.^[2]

Using Stokes’ theorem, this is equivalently stated as

meaning the curl, denoted ∇×, of the vector field vanishes.

Physics[edit]

Newtonian gravitation[edit]

In the case of the gravitational field g, which can be shown to be conservative,^[3] it is equal to the gradient in gravitational potential Φ:

There are opposite signs between gravitational field and potential, because the potential gradient and field are opposite in direction: as the potential increases, the gravitational field strength decreases and vice versa.

Electromagnetism[edit]

In electrostatics, the electric field E is independent of time t, so there is no induction of a time-dependent magnetic field B by Faraday’s law of induction:

which implies E is the gradient of the electric potential V, identical to the classical gravitational field:^[4]

In electrodynamics, the E field is time dependent and induces a time-dependent B field also (again by Faraday’s law), so the curl of E is not zero like before, which implies the electric field is no longer the gradient of electric potential. A time-dependent term must be added:^[5]

where A is the electromagnetic vector potential. This last potential expression in fact reduces Faraday’s law to an identity.

Fluid mechanics[edit]

In fluid mechanics, the velocity field v describes the fluid motion. An irrotational flow means the velocity field is conservative, or equivalently the vorticity pseudovector field ω is zero:

This allows the velocity potential to be defined simply as:

Chemistry[edit]

In an electrochemical half-cell, at the interface between the electrolyte (an ionic solution) and the metal electrode, the standard electric potential difference is:^[6]

where R = gas constant, T = temperature of solution, z = valency of the metal, e = elementary charge, N_A = Avogadro constant, and a_M^+z is the activity of the ions in solution. Quantities with superscript ⊖ denote the measurement is taken under standard conditions. The potential gradient is relatively abrupt, since there is an almost definite boundary between the metal and solution, hence the interface term.^{[clarification needed]}

Biology[edit]

In biology, a potential gradient is the net difference in electric charge across a cell membrane.

Non-uniqueness of potentials[edit]

Since gradients in potentials correspond to physical fields, it makes no difference if a constant is added on (it is erased by the gradient operator ∇ which includes partial differentiation). This means there is no way to tell what the “absolute value” of the potential “is” – the zero value of potential is completely arbitrary and can be chosen anywhere by convenience (even “at infinity”). This idea also applies to vector potentials, and is exploited in classical field theory and also gauge field theory.

Absolute values of potentials are not physically observable, only gradients and path-dependent potential differences are. However, the Aharonov–Bohm effect is a quantum mechanical effect which illustrates that non-zero electromagnetic potentials along a closed loop (even when the E and B fields are zero everywhere in the region) lead to changes in the phase of the wave function of an electrically charged particle in the region, so the potentials appear to have measurable significance.

Potential theory[edit]

Field equations, such as Gauss’s laws for electricity, for magnetism, and for gravity, can be written in the form:

where ρ is the electric charge density, monopole density (should they exist), or mass density and X is a constant (in terms of physical constants G, ε₀, μ₀ and other numerical factors).

Scalar potential gradients lead to Poisson’s equation:

A general theory of potentials has been developed to solve this equation for the potential. The gradient of that solution gives the physical field, solving the field equation.

See also[edit]

• Tensors in curvilinear coordinates

References[edit]

1