Содержание:
- Необходимое условие экстремума
- Первое достаточное условие экстремума
- Второе достаточное условие экстремума
Определение
Точка $x_{0}$ называется точкой локального максимума
функции $f(x)$, если существует такая окрестность
этой точки, что для всех $x$ из этой окрестности
выполняется неравенство: $f(x) leq fleft(x_{0}right)$.
Точка $x_{0}$ называется точкой локального минимума
функции $f(x)$, если существует такая окрестность этой
точки, что для всех $x$ из этой окрестности
$f(x) geq fleft(x_{0}right)$.
Значение функции в точке максимума называется локальным максимумом, значение функции в точке минимума –
локальным минимумом данной функции. Локальные максимум и минимум функции называются локальными экстремумами.
Точка $x_{0}$ называется точкой строгого локального
максимума функции $y=f(x)$, если для всех
$x$ из окрестности этой точки будет справедливо
строгое неравенство $f(x) lt fleft(x_{0}right)$.
Точка $x_{0}$ называется точкой строгого локального
минимума функции $y=f(x)$, если для всех
$x$ из окрестности этой точки будет
справедливо строгое неравенство $f(x)>fleft(x_{0}right)$.
Наибольшее или наименьшее значение функции на промежутке называется глобальным экстремумом.
Замечание
Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка.
Необходимое условие экстремума
Теорема
(Необходимое условие экстремума)
Если функция $y=f(x)$ имеет экстремум в точке
$x_{0}$, то ее производная
$f^{prime}left(x_{0}right)$ либо равна нулю, либо не существует.
Точки, в которых производная равна нулю: $f^{prime}(x)=0$,
называются стационарными точками функции.
Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются
критическими точками этой функции. То есть критические точки – это либо стационарные точки (решения
уравнения $f^{prime}(x)=0$), либо это точки, в которых производная
$f^{prime}(x)$ не существует.
Замечание
Не в каждой своей критической точке функция обязательно имеет максимум или минимум.
Первое достаточное условие экстремума
Теорема
(Первое достаточное условие экстремума)
Пусть для функции $y=f(x)$ выполнены следующие условия:
- функция непрерывна в окрестности точки $x_{0}$;
- $f^{prime}left(x_{0}right)=0$ или $f^{prime}left(x_{0}right)$ не существует;
- производная $f^{prime}(x)$ при переходе через точку $x_{0}$ меняет свой знак.
Тогда в точке $x=x_{0}$ функция
$y=f(x)$ имеет экстремум, причем это минимум, если
при переходе через точку $x_{0}$ производная меняет свой
знак с минуса на плюс; максимум, если при переходе через точку $x_{0}$
производная меняет свой знак с плюса на минус.
Если производная $f^{prime}(x)$ при переходе через точку
$x_{0}$ не меняет знак, то экстремума в точке
$x=x_{0}$ нет.
Таким образом, для того чтобы исследовать функцию $y=f(x)$
на экстремум, необходимо:
- найти производную $f^{prime}(x)$;
- найти критические точки, то есть такие значения $x$,
в которых $f^{prime}(x)=0$ или
$f^{prime}(x)$ не существует; - исследовать знак производной слева и справа от каждой критической точки;
- найти значение функции в экстремальных точках.
Пример
Задание. Исследовать функцию $y(x)=x^{4}-1$ на экстремум.
Решение. Находим производную заданной функции:
$y^{prime}=left(x^{4}-1right)^{prime}=4 x^{3}$
Далее ищем критические точки функции, для этого решаем уравнение $y^{prime}(x)=0$:
$y^{prime}=4 x^{3}=0 Rightarrow x=0$
Первая производная определена во всех точках. Таким образом, имеем одну критическую точку
$x=0$. Наносим эту точку на координатную прямую и
исследуем знак производной слева и справа от этой точки (для этого из каждого промежутка берем произвольное
значение и находим значение производной в выбранной точке, определяем знак полученной величины):

Так как при переходе через точку $x=0$ производная
сменила свой знак с “-” на “+”, то в этой точке функция достигает минимума (или минимального значения), причем
$y_{min }=y(0)=0^{4}-1=-1$.
Замечание. Также можно определить интервалы
монотонности функции: так как на интервале
$(-infty ; 0)$ производная
$y^{prime}(x) lt 0$, то на этом интервале функция
$y(x)=x^{4}-1$ является убывающей; на интервале
$(0 ;+infty)$ производная
$y^{prime}(x)>0$, значит заданная функция возрастает на нем.
Ответ. $y_{min }=y(0)=-1$
Второе достаточное условие экстремума
Теорема
(Второе достаточное условие экстремума)
Пусть для функции $y=f(x)$ выполнены следующие условия:
- она непрерывна в окрестности точки $x_{0}$;
- первая производная $f^{prime}(x)=0$ в точке $x_{0}$;
- $f^{prime prime}(x) neq 0$ в точке $x_{0}$ .
Тогда в точке $x_{0}$ достигается экстремум,
причем, если $f^{prime prime}left(x_{0}right)>0$, то в точке
$x=x_{0}$ функция
$y=f(x)$ имеет минимум; если
$f^{prime prime}left(x_{0}right) lt 0$, то в точке
$x=x_{0}$ функция
$y=f(x)$ достигает максимум.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Исследовать функцию $y(x)=frac{x^{2}-1}{x^{2}+1}$ на экстремум с помощью второй производной.
Решение. Находим первую производную заданной функции:
$y^{prime}(x)=left(frac{x^{2}-1}{x^{2}+1}right)^{prime}=frac{2 xleft(x^{2}+1right)-left(x^{2}-1right) cdot 2 x}{left(x^{2}+1right)^{2}}=frac{4 x}{left(x^{2}+1right)^{2}}$
Находим точки, в которых первая производная равна нулю:
$y^{prime}(x)=0 Rightarrow frac{4 x}{left(x^{2}+1right)^{2}}=0 Rightarrow x=0$
Вторая производная заданной функции:
$y^{prime prime}(x)=left(frac{4 x}{left(x^{2}+1right)^{2}}right)^{prime}=frac{4left(x^{2}+1right)^{2}-4 x cdot 2left(x^{2}+1right) cdot 2 x}{left(x^{2}+1right)^{4}}=$
$=-frac{4left(3 x^{2}-1right)}{left(x^{2}+1right)^{3}}$
В стационарной точке $x=0$ вторая производная
$y^{prime prime}(0)=-frac{4 cdot(-1)}{1^{3}}=4>0$, а значит, в этой точке функция достигает
минимум, причем $y_{min }=y(0)=frac{0^{2}-1}{0^{2}+1}=-1$.
Ответ. $y_{min }=y(0)=-1$
Остались вопросы?
Здесь вы найдете ответы.
Что подразумевается под понятием «экстремум»?
Экстремум представляет собой значение функции на определенном интервале в
момент достижения им минимального или максимального показания. Под
понятием «экстремумы» или по-другому минимумы/максимумы подразумевается
значение функции (у).
Точка экстремума – что это такое?
Если в определенной точке достигается экстремум или, иными словами,
максимальное/минимальное значение функции на заданном интервале, то эта
точка носит название точки экстремума. Из этого следует, что при
достижении минимума, точка экстремума будет названа точкой минимума, и,
наоборот, при достижении максимума эта точка будет называться точкой
максимума. В случае, когда указываются точки экстремумов (или
минимумов/максимумов) подразумеваются иксы, в которых достигаются
минимальные или максимальные значения.
Что имеется в виду под понятием «точка минимума функции»?
Любая точка x₀ будет определена в качестве точки минимума функции y = f(x)
при соблюдении условия о том, что имеется такая V, представляющая собой
окрестность (x₀ – V; x₀+V) упомянутой ранее точки, из которой для каждого
значения x <> x₀ действительно следующее неравенство:
f(x)>f(x₀).
Как описать точку минимума функции?
Под понятием «минимум функции» имеется в виду та точка на ней, в которой
функция имеет значение, являющееся наименьшим среди всех значений,
приобретаемых ею в любой из других соседних точек. Другими словами, это
означает, что в случае, когда функция, достигнув определенной точки,
прекращает падать, а, наоборот, наблюдается ее рост, то данная точка и
представляет собой точку ее минимума.
Каким образом можно вычислить значение функции y=x⁴-4x³+6x²-4x, которого она
достигает в точке своего минимума?
Для ответа на поставленный вопрос нужно отыскать точку минимума указанной
функции, в которой ее значение перестает падать. Это можно сделать
следующим образом:
y’ = 4x³ – 12x² + 12x – 4
Предположив, что минимальное значение данной функции равно 0, можно
переписать равенство в следующем виде:
4x³ – 12x² + 12x – 4 = 0
Сократим данное уравнение на 4:
x³ – 3x² + 3x – 1 = 0
Получившееся равенство также может быть записано в следующем виде после
перемены местами слагаемых:
(x³ – 1) + (-3x² + 3x) = 0
Распишем слагаемые в ином виде, чтобы избавиться от третьей степени:
(x – 1)(x² + x + 1) -3x(x – 1) = 0
Это же уравнение может выглядеть так:
(x -1)(x² + x + 1- 3x) = 0
Произведем сложение слагаемых х и -3х:
(x – 1) (x² -2x + 1) = 0
Теперь для упрощения можно переписать уравнение в таком виде:
(x – 1)(x-1)² = 0
Получившееся равенство:
(x – 1)³ = 0
В этом случае х = 1
-∞ 1 +∞
Знаками «+» и «-» обозначены значения производной.
После проведенных вычислений было установлено, что х = 1, что является
точкой минимума функции:
у = 1⁴- 4*1³ + 6*1² – 4*1 = 1 – 4 +6 – 4 = -1
Какие расчеты нужно произвести, для того чтобы вычислить точку максимума для
функции y = -x/x²+484?
Точкой максимума называется то значение х, достигнув которого, производная
начинает менять свой знак с плюса на минус. Зная это, можно перейти к
поиску точки максимума для функции, указанной в задании.
Для этого нужно начать с поиска производной, используя следующую формулу:
(U/V)’ = (U’V – UV’)/V²
Подставляем приведенные в задании значения и получаем:
y’ = (-(x² + 484) – 2x)/(x² + 484)² = (-x²-484 -2x)/(x² +484)²
Теперь следует приравнять производную к 0 и начать решать получившееся
уравнение:
(-x²-484 -2x)/(x² +484)² = 0
Упростим уравнение и получим:
(-x²-484 -2x) = 0
(x² +484)² ≠ 0
-x²-484 -2x = 0
Избавимся от минусов в уравнении:
x² + 2x +484 = 0
D < 0
В результате вычислений стало ясно, что корней нет. Это значит, что
невозможно поставить их на числовой прямой, для того чтобы проверить знаки
производной по соседству с этими точками. На основании этого можно сделать
вывод о том, что указанная в задании функция не имеет точек экстремума.
Что представляет собой точка максимума функции?
Под точкой максимума функции понимается та точка, в которой она достигает
значения, являющегося наибольшим среди тех значений, что достигаются ею в
соседних точках. Это означает, что в точке, при пересечении которой
функция прекращает расти, и наблюдается ее падение, и достигается ее
максимум.
Имеется график производной функции. Каким образом можно вычислить точки ее
максимума и минимума?
В случае, если имеется график производной функции, и при этом требуется
определить ее экстремумы, то необходимо вычислить точки пересечения этого
графика производной с осью Ох. По-другому они называются «нулями»
производной. В случае, когда, пересекая конкретную точку, график
производной восходит из области со знаком «-» в область со знаком «+», и в
это время производная меняет свой знак на противоположный, функция также
изменяется с убывания на рост. В этом случае данная точка, которая
пересекается графиком производной, представляет собой точку минимума. Если
же при пересечении графиком производной какой-либо точки он идет из
положительной в отрицательную область, а функция из возрастания меняется
на убывание, то речь идет о точке ее максимума.
Как можно вычислить экстремумы и точки экстремума функции y=4x⁴+2x²+1?
Для того чтобы найти ответ на поставленный вопрос, сначала нужно
приравнять функцию к 0:
у = 0
Это же означает, что:
4X⁴ + 2X² + 1 = 0
Введем обозначения:
Х2 = А, при этом А больше 0.
С учетом введенных обозначений равенство будет иметь следующий вид:
4A² + 2A + 1 = 0
D = 4 – 4 = 0 ; √ D = 0
A = (- 2) : 4 = (- 0,5) (< 0) 1
Очевидно, что корней нет.
Ответ: х = 0, у = 1.
Дана функция y = x² -3x+2. Как можно вычислить экстремум этой функции?
Имеется функция y = x² -3x+2, которую также можно переписать в следующем
виде:
у = -0,25+ (x-1,5)²
Отсюда следует, что:
miny = – 0,25 при условии, что х-1,5 = 0
Можно сделать вывод о том, что х = 1,5.
Запишем производную данной функции:
y ‘= (x² -3x+2)’ =2x -3
А затем приравняем ее к 0:
y ‘ = 0, значит:
2x -3 = 0.
Это позволяет сделать вывод о том, что:
x = 3/2.
Получается, что, если x < 3/2, то производная y’ < 0, и при этом функция убывает.
Если же x >3/2, то производная y’ > 0, и в этом случае функция возрастает.
x =3/2=1,5 – это единственная точка экстремума, которая является точкой
минимума.
miny =(1,5)² -3*1,5+2 = -0,25.
Как раскрыть понятие «критическая точка функции»?
Критическая точка функции представляет собой ту точку, при пересечении с
которой производная данной функции становится равной 0, либо она вовсе не
существует.
Возможно ли привести доказательства того, что функция f(x) =2x – 3/x не
может иметь критической точки?
Для начала нужно определить, что под критической точкой функции
подразумевается та точка, при пересечении с которой производная
приобретает нулевое значение, либо же эта производная просто не существует
в этой точке, что означает, что функцию в данной точке невозможно
дифференцировать.
Проверим, применимо ли это утверждение к упомянутой в задании функции:
f ‘(x) =(sin2x – 3x)’ = 2sin2x-3
Приравняем производную функции к 0:
f ‘(x) = 0, это значит, что 2sin2x-3 = 0.
Следовательно:
sin2x= 3 2 не имеет решения
Ответ: заданная функция не имеет критических точек и существует при любых
х.
Каким способом можно определить критические точки функции y=|x|/1+x²?
Под критическими точками функции понимаются те точки, в которых ее
производная равна 0 или вовсе не существует.
В задании дана функция:
y=|x|/(1+x²)
Предположим, что x<0, тогда:
y=-x/(1+x²)
Запишем производную функции и приравняем ее к 0:
y`=(-1-x²+2x²)/(1+x²)²=(x²-1)/(1+x²)²=(x-1)(x+1)/(1+x²)²=0
х = 1 не соответствует условию, значит х = -1.
Теперь предположим, что x≥0.
Снова записываем производную имеющейся функции и приравниваем ее к 0:
y`=(1+x²-2x²)/(1+x²)²=(1-x²)/(1+x²)²=(1-x)(x+1)/(1+x²)²=0
х = – 1 не отвечает условию, значит х = 1.
Ответ: х = 1, х = -1.
Читать дальше: наибольшее и наименьшее значение функции.
-
Стационарные точки функции.
Необходимое условие локального
экстремума функции -
Первое достаточное условие локального
экстремума -
Второе и третье достаточные условия
локального экстремума -
Наименьшее и наибольшее
значения функции на сегменте -
Выпуклые функции и точки перегиба
1. Стационарные точки функции. Необходимое условие локального экстремума функции
Определение 1.
Пусть функция ![]()
определена на ![]() .
.
Точка ![]()
называется стационарной точкой функции
![]() ,
,
если ![]()
дифференцирована в точке ![]()
и ![]() .
.
Теорема 1 (необходимое
условие локального экстремума функции).
Пусть функция ![]()
определена на ![]()
и имеет в точке ![]()
локальный экстремум. Тогда выполняется
одно из условий:
-
функция

не имеет в точке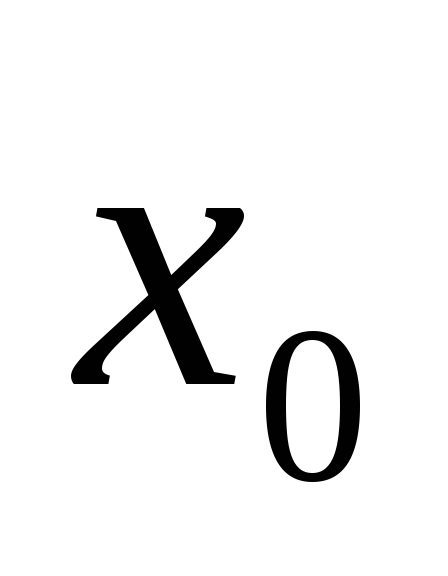
производной; -
функция
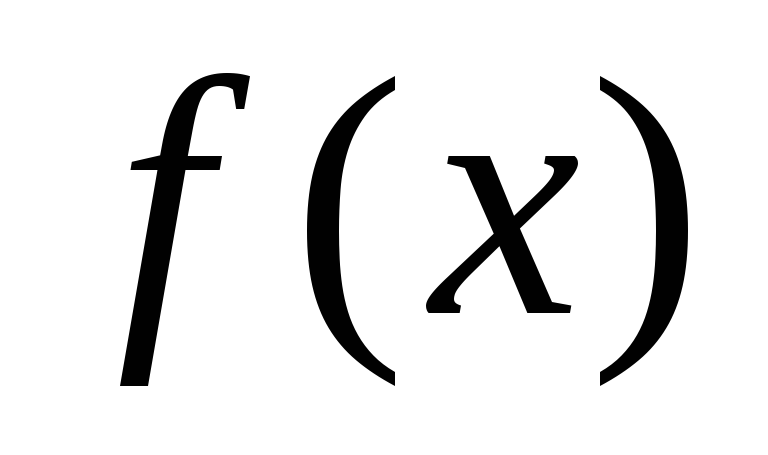
имеет в точке
производную и .
.
Таким образом, для того,
чтобы найти точки, которые являются
подозрительными на экстремум, надо
найти стационарные точки функции и
точки, в которых производная функции
не существует, но которые принадлежат
области определения функции.
Пример.
Пусть ![]() .
.
Найти для нее точки, которые являются
подозрительными на экстремум. Для
решения поставленной задачи, в первую
очередь, найдем область определения
функции: ![]() .
.
Найдем теперь производную функции:
![]() .
.
Точки, в которых производная
не существует: ![]() .
.
Стационарные точки функции:
![]() .
.
Поскольку и ![]() ,
,
и ![]()
принадлежат области определения функции,
то они обе будут подозрительными на
экстремум. Но для того, чтобы сделать
вывод, будет ли там действительно
экстремум, надо применять достаточные
условия экстремума.
2. Первое достаточное условие локального экстремума
Теорема 1 (первое достаточное
условие локального экстремума).
Пусть функция ![]()
определена на ![]()
и дифференцирована на этом интервале
везде за исключением, возможно, точки
![]() ,
,
но в этой точке ![]()
функция ![]() является
является
непрерывной. Если
существуют такие правая и левая
полуокрестности точки ![]() ,
,
в каждой из которых ![]()
сохраняет определенный знак, то
1) функция ![]()
имеет локальный экстремум в точке ![]() ,
,
если ![]()
принимает значения разных знаков в
соответствующих полуокрестностях;
2) функция ![]()
не имеет локальный экстремум в точке
![]() ,
,
если справа и слева от точки ![]()
![]()
имеет одинаковый знак.
Доказательство.
1) Предположим, что в полуокрестности ![]()
производная ![]() ,
,
а в ![]()
![]() .
.
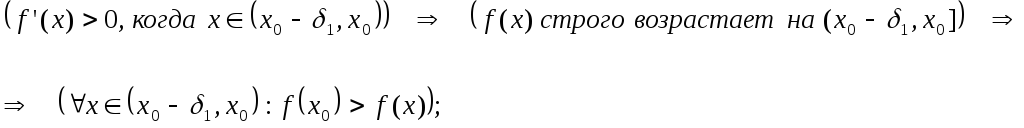
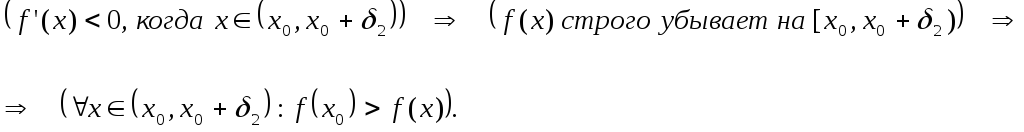
Таким образом в точке ![]()
функция ![]()
имеет локальный экстремум, а именно –
локальный максимум, что и нужно было
доказать.
2) Предположим, что слева
и справа от точки ![]()
производная сохраняет свой знак,
например, ![]() .
.
Тогда на ![]()
и ![]()
функция ![]()
строго монотонно возрастает, то есть:
![]() ,
,
![]() .
.
Таким образом экстремума
в точке ![]()
функция ![]()
не имеет, что и нужно было доказать.
Замечание 1.
Если производная ![]()
при прохождении через точку ![]()
меняет знак с «+» на «-», то в точке ![]()
функция ![]()
имеет локальный максимум, а если знак
меняется с «-» на «+», то локальный
минимум.
Замечание 2.
Важным является условие непрерывности
функции ![]()
в точке ![]() .
.
Если это условие не выполняется, то
теорема 1 может не иметь места.
Пример.
Рассматривается функция (рис.1):


Эта функция определена на ![]()
и непрерывна везде, кроме точки ![]() ,
,
где она имеет устранимый разрыв. При
прохождении через точку ![]()
![]()
меняет знак с «-» на «+», но локального
минимума в этой точке функция не имеет,
а имеет локальный максимум по определению.
Действительно, около точки ![]()
можно построить такую окрестность, что
для всех аргументов из этой окрестности
значения функции будут меньше, чем
значение ![]() .
.
Теорема 1 не сработала потому, что в
точке ![]()
функция имела разрыв.
Замечание 3.
Первое достаточное условие локального
экстремума не может быть использовано,
когда производная функции ![]()
меняет свой знак в каждой левой и каждой
правой полуокрестности точки ![]() .
.
Пример.
Рассматривается функция:

Поскольку ![]() ,
,
то ![]() ,
,
а потому ![]() ,
,
но ![]() .
.
Таким образом:
![]() ,
,
т.е. в точке ![]()
функция ![]()
имеет локальный минимум по определению.
Посмотрим, сработает ли здесь первое
достаточное условие локального
экстремума.
Для ![]() :
:
![]() .
.
Для первого слагаемого правой
части полученной формулы имеем:
![]() ,
,
а потому в малой окрестности
точки ![]()
знак производной определяется знаком
второго слагаемого, то есть:
![]() ,
,
а это означает, что в любой
окрестности точки ![]()
![]()
будет принимать как положительные, так
и отрицательные значения. Действительно,
рассмотрим произвольную окрестность
точки ![]() :
:
![]() .
.
Когда
![]() ,
,
то
![]()
(рис.2), а ![]()
меняет свой знак здесь бесконечно много
раз. Таким образом, нельзя использовать
в приведенном примере первое достаточное
условие локального экстремума.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Экстремум функции
- Необходимые условия экстремума
- Достаточные условия экстремума
- Аналогично доказывается достаточность условия существования максимума
- Общая постановка задачи оптимизации и основные положения
- Необходимые и достаточные условия безусловного экстремума
Экстремум функции
Понятие экстремума:
Будем рассматривать непрерывные функции, которые не меняются монотонно, то есть такие, которые на отдельных промежутках возрастают, а на других убывают. Графики таких функций схематически можно изобразить рисунком 9.
Тогда существуют такие значение функции f (x), которые по сравнению с другими соседними значения являются наибольшими или наименьшими. Такие значения называют соответственно максимумами и минимумами.

Рис. 9.
На рисунке 9 
 — максимумы,
— максимумы,  — минимумы.
— минимумы.
Определение 1. Максимумом функции f (x) называется такое значение f ( ), которое не меньше всех значений функции в точках, достаточно близких к
), которое не меньше всех значений функции в точках, достаточно близких к  . При этом выполняется неравенство
. При этом выполняется неравенство  для любых достаточно малых
для любых достаточно малых  .
.
Точка  , в которой функция f (x) достигает максимума f (
, в которой функция f (x) достигает максимума f ( ), называется точкой максимума.
), называется точкой максимума.
Определение 2. Минимумом функции f (x) называется такое значение f ( ), которое не больше всех значений функции в точках, достаточно близких к
), которое не больше всех значений функции в точках, достаточно близких к  . При этом имеем
. При этом имеем  для любых достаточно малых
для любых достаточно малых  .
.
Точка  , в которой функция f (x) достигает минимума f (
, в которой функция f (x) достигает минимума f ( ), называется точкой минимума.
), называется точкой минимума.
Максимумы и минимумы вместе называют экстремумами. Функция может иметь внутри интервала (a, b) несколько экстремумов.
Необходимые условия экстремума
Для отыскания экстремумов рассмотрим сначала необходимые условия экстремума.
ТЕОРЕМА (необходимое условие экстремума). Если функция f (x) имеет в точке  экстремум, то ее производная в этой точке равна нулю, или не существует.
экстремум, то ее производная в этой точке равна нулю, или не существует.
Доказательство. Пусть в точке  функция f (x) имеет производную и достигает максимума. Это означает, что при достаточно малом
функция f (x) имеет производную и достигает максимума. Это означает, что при достаточно малом  имеем
имеем  Из этого следует, что отношение
Из этого следует, что отношение  , если
, если  и
и  , если
, если  Переходя в неравенствах к пределам, получим
Переходя в неравенствах к пределам, получим
 и
и 
А это может одновременно выполняться только при 
Аналогично доказывается первая часть теоремы в случае, когда функция f (x) достигает в точке  минимума.
минимума.
Но непрерывная функция f (x) может иметь экстремум в точках, в которых производная не существует. Например, функция  в точке x = 0 не дифференцируема, но достигает в ней минимума, что видно из графика (рис. 3). Такие точки называют угловыми. Но эти условия не являются достаточными. Производная может быть равна нулю не только в точках экстремума.
в точке x = 0 не дифференцируема, но достигает в ней минимума, что видно из графика (рис. 3). Такие точки называют угловыми. Но эти условия не являются достаточными. Производная может быть равна нулю не только в точках экстремума.
Так производной функции  является
является  . В точке x = 0 y’= 0, но в этой точке функция не достигает экстремального значения.
. В точке x = 0 y’= 0, но в этой точке функция не достигает экстремального значения.
Точки, в которых производная функции равна нулю или не существует, называются стационарными или критическими точками первого рода.
Достаточные условия экстремума
ТЕОРЕМА (первое правило). Если производная функции f ‘(x) при переходе через критическую точку  слева направо изменяет знак с «+» на «-», то f (x) имеет максимум в точке
слева направо изменяет знак с «+» на «-», то f (x) имеет максимум в точке  , если изменение знака происходит с «-» на «+», то функция имеет минимум в этой точке. Отсутствие изменения знака указывает на отсутствие экстремума.
, если изменение знака происходит с «-» на «+», то функция имеет минимум в этой точке. Отсутствие изменения знака указывает на отсутствие экстремума.
Доказательство. Если производная f ‘(x) при переходе через точку  меняет знак с «+» на «-», то это означает, что при достаточно малом
меняет знак с «+» на «-», то это означает, что при достаточно малом  производная f’ (x) положительная на промежутке
производная f’ (x) положительная на промежутке  и отрицательная на промежутке
и отрицательная на промежутке  Следовательно, функция f (x) возрастает на промежутке
Следовательно, функция f (x) возрастает на промежутке  и убывает на промежутке
и убывает на промежутке  , то есть в точке
, то есть в точке  достигает максимума.
достигает максимума.
Аналогично доказывается утверждение теоремы относительно минимума функции.
ТЕОРЕМА (второе правило). Если в точке  первая производная f ‘(x) функции f (x) равна нулю, а ее вторая производная f “(x) непрерывна в окрестности этой точки и f “(x) ≠ 0, то функция f (x) имеет максимум в точке
первая производная f ‘(x) функции f (x) равна нулю, а ее вторая производная f “(x) непрерывна в окрестности этой точки и f “(x) ≠ 0, то функция f (x) имеет максимум в точке  , когда
, когда  и минимум, когда
и минимум, когда 
Доказательство. Пусть  и
и  . Тогда в результате непрерывности f ”(x) она положительная на малом интервале
. Тогда в результате непрерывности f ”(x) она положительная на малом интервале  Это означает, что f ‘(x), для которой f” (x) является производной, возрастает на этом интервале. Поскольку
Это означает, что f ‘(x), для которой f” (x) является производной, возрастает на этом интервале. Поскольку  то на промежутке
то на промежутке  производная
производная  а на промежутке
а на промежутке  производная f'(x) > 0.
производная f'(x) > 0.
Поэтому f (x) в интервале  убывает, а в интервале
убывает, а в интервале  возрастает. Значит, в точке
возрастает. Значит, в точке  функция f (x) имеет минимум.
функция f (x) имеет минимум.
Аналогично доказывается достаточность условия существования максимума
Замечание. Надо иметь в виду, что вторым правилом нельзя пользоваться в случае, когда критическая точка  получена от того, что в ней производная не существует, а также если
получена от того, что в ней производная не существует, а также если  Тогда пользуются первым правилом.
Тогда пользуются первым правилом.
Пример. Найти максимум и минимум функции 
Решение. Данная функция определена на промежутке ( ). Находим производную и приравниваем ее к нулю.
). Находим производную и приравниваем ее к нулю.

Корни данного уравнения 
Сначала используем первое правило 
Область определения функции критическими точками делится на промежутки  (рис. 10). Найдем знаки производной в каждом из этих промежутков, подставив конкретные числа из них в производную.
(рис. 10). Найдем знаки производной в каждом из этих промежутков, подставив конкретные числа из них в производную.

Рис. 10.
Например,

Итак, в точке x = 1 — максимум.

В точке x = 3 — минимум. 
При применении второго правила находим вторую производную
y” = 2x – 4.
Подставляем значение  и
и  во вторую производную:
во вторую производную:
В точке  — максимум, в точке
— максимум, в точке  — минимум.
— минимум.
Общая постановка задачи оптимизации и основные положения
Постановка задачи поиска минимума функций содержит:
Требуется найти такой вектор  из множества допустимых решений, которому соответствует минимальное значение целевой функции на этом множестве:
из множества допустимых решений, которому соответствует минимальное значение целевой функции на этом множестве: 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Замечания 1.1.
1. Задача поиска максимума функции  сводится к задаче поиска минимума путем замены знака перед функцией на противоположный (рис. 1.1):
сводится к задаче поиска минимума путем замены знака перед функцией на противоположный (рис. 1.1): 

2. Задача поиска минимума и максимума целевой функции  называется задачей поиска экстремума
называется задачей поиска экстремума

3. Если множество допустимых решений X задается ограничениями (условиями), накладываемыми на вектор  , то решается задача поиска условного экстремума. Если
, то решается задача поиска условного экстремума. Если  , т.е. ограничения (условия) на вектор х отсутствуют, решается задача поиска безусловного экстремума.
, т.е. ограничения (условия) на вектор х отсутствуют, решается задача поиска безусловного экстремума.
4. Решением задачи поиска экстремума является пара  , включающая точку
, включающая точку  и значение целевой функции в ней.
и значение целевой функции в ней.
5. Множество точек минимума (максимума) целевой функции  на множестве X обозначим
на множестве X обозначим  . Оно может содержать конечное число точек (в том числе одну), бесконечное число точек или быть пустым.
. Оно может содержать конечное число точек (в том числе одну), бесконечное число точек или быть пустым.
Возможно вам будут полезны данные страницы:
Определение 1.1. Точка  называется точкой глобального (абсолютного) минимума функции
называется точкой глобального (абсолютного) минимума функции  на множестве X, если функция достигает в этой точке своего наименьшего значения, т.е.
на множестве X, если функция достигает в этой точке своего наименьшего значения, т.е.

Определение 1.2. Точка  называется точкой локального (относительного) минимума функции
называется точкой локального (относительного) минимума функции  на множестве X, если существует
на множестве X, если существует  , такое, что если
, такое, что если  – евклидова норма вектора х.
– евклидова норма вектора х.
Замечания 1.2.
1. В определении 1.1 точка  сравнивается по величине функции со всеми точками из множества допустимых решений X, а в определении 1.2 – только с принадлежащими ее е – окрестности (рис. 1.2).
сравнивается по величине функции со всеми точками из множества допустимых решений X, а в определении 1.2 – только с принадлежащими ее е – окрестности (рис. 1.2).

2. Если в определениях 1.1 и 1.2 знак неравенства  заменить на
заменить на  , то получатся определения глобального (абсолютного) и локального (относительного) максимумов.
, то получатся определения глобального (абсолютного) и локального (относительного) максимумов.
3. Глобальный экстремум всегда является одновременно локальным, но не наоборот.
Определение 1.3. Поверхностью уровня функции  называется множество точек, в которых функция принимает постоянное значение, т.е.
называется множество точек, в которых функция принимает постоянное значение, т.е.  . Если
. Если  поверхность уровня изображается линией уровня на плоскости
поверхность уровня изображается линией уровня на плоскости  .
.
Пример с решением
Пример 1.1.
Построить линии уровня функций:
а)
В) 
Уравнения линий уровня имеют следующий вид:
а)  – уравнение окружностей с центром в точке
– уравнение окружностей с центром в точке  и радиусом, равным
и радиусом, равным  (рис. 1.3,
(рис. 1.3,  );
);


Пример 1.2.
На рис. 1.4 изображены линии уровня функции. Цифры указывают значение функции  на соответствующей линии. Точкам Л и 5 соответствуют значения функции
на соответствующей линии. Точкам Л и 5 соответствуют значения функции  . Требуется классифицировать точки экстремума.
. Требуется классифицировать точки экстремума.
Функция рассматривается на множестве
, т.е. решается задача поиска безусловного экстремума.
В точке А с координатами  достигается локальный минимум; в точке В с координатами
достигается локальный минимум; в точке В с координатами  достигается локальный и глобальный минимум одновременно; в точке С нет ни минимума, ни максимума, так как по одним направлениям функция убывает, а по другим возрастает. Заметим, что изображенная структура линий уровня типична для так называемых многоэкстремальных задач.
достигается локальный и глобальный минимум одновременно; в точке С нет ни минимума, ни максимума, так как по одним направлениям функция убывает, а по другим возрастает. Заметим, что изображенная структура линий уровня типична для так называемых многоэкстремальных задач.

Пример 1.3.
На рис. 1.5 изображен график функции  , определенной на множестве X = R. Требуется классифицировать точки экстремума.
, определенной на множестве X = R. Требуется классифицировать точки экстремума.
Решается задача поиска безусловного экстремума. На рис. 1.5 выделим  -окрестности точек A,B,…,F и проверим выполнение определений 1.1 и 1.2 с учетом пп. 1, 2 замечаний 1.1, 1.2. В результате получаем: точка А – точка локального минимума; точки В, Е – точки локального максимума; бесконечное множество точек из отрезка CD – точки локального минимума; точка F – точка локального и одновременно глобального минимума; глобальный максимум отсутствует.
-окрестности точек A,B,…,F и проверим выполнение определений 1.1 и 1.2 с учетом пп. 1, 2 замечаний 1.1, 1.2. В результате получаем: точка А – точка локального минимума; точки В, Е – точки локального максимума; бесконечное множество точек из отрезка CD – точки локального минимума; точка F – точка локального и одновременно глобального минимума; глобальный максимум отсутствует.

Пример 1.4.
Найти точки экстремума функций  и
и  на множестве
на множестве  . Обе целевые функции имеют в точке
. Обе целевые функции имеют в точке  локальный и одновременно глобальный минимум, а локальных и глобальных максимумов не имеют (см. рис. 1.3 а,6}.
локальный и одновременно глобальный минимум, а локальных и глобальных максимумов не имеют (см. рис. 1.3 а,6}.
Пример 1.5.
Найти точки экстремума функции  на множестве
на множестве  Решается задача поиска условного экстремума. Линии уровня функции
Решается задача поиска условного экстремума. Линии уровня функции  представляются окружностями (см. рис. 1.3, о), а множество допустимых решений X – параболой с уравнением
представляются окружностями (см. рис. 1.3, о), а множество допустимых решений X – параболой с уравнением  . В точке
. В точке  достигается глобальный минимум (рис. 1.6). Заметим, что эта точка является точкой касания линии уровня и кривой, описывающей множество X. Глобальный максимум на данном множестве не достигается. Если поменять знак перед функцией на противоположный, то в точке
достигается глобальный минимум (рис. 1.6). Заметим, что эта точка является точкой касания линии уровня и кривой, описывающей множество X. Глобальный максимум на данном множестве не достигается. Если поменять знак перед функцией на противоположный, то в точке  функция
функция  будет достигать глобального максимума на множестве X, что соответствует п. 1 замечаний 1.1.
будет достигать глобального максимума на множестве X, что соответствует п. 1 замечаний 1.1.

Пример 1.6.
Найти точки экстремума функции  на множестве
на множестве 
Решается задача поиска условного экстремума. Линии уровня функции  представляются окружностями (см. рис. 1.3, о), а множество допустимых решений X – графиком прямой. В точке
представляются окружностями (см. рис. 1.3, о), а множество допустимых решений X – графиком прямой. В точке  достигается глобальный минимум (рис. 1.7). Глобальный максимум на данном множестве не существует. Заметим, что, как и в, примере 1.5, в точке
достигается глобальный минимум (рис. 1.7). Глобальный максимум на данном множестве не существует. Заметим, что, как и в, примере 1.5, в точке  линии уровня касаются кривой, описывающей ограничения.
линии уровня касаются кривой, описывающей ограничения.

Пример 1.7.
Найти точки экстремума функции  на множестве
на множестве  Решается задача поиска условного экстремума. Линии уровня функции /(х) представляются окружностями (см. рис. 1.3, а), а множество X – гиперболой (рис. 1.8). Имеются две точки глобального минимума:
Решается задача поиска условного экстремума. Линии уровня функции /(х) представляются окружностями (см. рис. 1.3, а), а множество X – гиперболой (рис. 1.8). Имеются две точки глобального минимума:


В них выполняется свойство касания линий уровня и кривых, описывающих множество X, отмеченное при решении примеров 1.5, 1.6. Точки глобального и локального максимума отсутствуют.
Пример 1.8.
Найти точки экстремума функции  на множестве допустимых решений
на множестве допустимых решений 
Решается задача поиска условного экстремума. Линии уровня функции имеют уравнение  и представляются прямыми, параллельными оси
и представляются прямыми, параллельными оси  . Множество допустимых решений, где все ограничения выполняются одновременно, заштриховано на рис. 1.9. В точке
. Множество допустимых решений, где все ограничения выполняются одновременно, заштриховано на рис. 1.9. В точке  достигается глобальный максимум, на множестве точек отрезка АВ достигается глобальный минимум с значением целевой функции
достигается глобальный максимум, на множестве точек отрезка АВ достигается глобальный минимум с значением целевой функции 

Пример 1.9.
Найти точки экстремума функции  на множестве
на множестве 
Решается задача поиска условного экстремума. Глобальный максимум достигается в точке В при  . Локальный минимум достигается в точке С при
. Локальный минимум достигается в точке С при  , а глобальный минимум – в точке А при
, а глобальный минимум – в точке А при 
 (рис. 1.10).
(рис. 1.10).
Пример 1.10.
Найти точки экстремума функции  на множестве
на множестве 
Решается задача поиска условного экстремума. Функция не имеет точек локального и глобального экстремума, так как не выполняются определения 1.1 и 1.2 (рис 1.11). При приближении к левой границе значение функции стремится к  (функция является неограниченной снизу), а при приближении к правой границе функция возрастает, но не имеет максимума, так как точка
(функция является неограниченной снизу), а при приближении к правой границе функция возрастает, но не имеет максимума, так как точка  не принадлежит множеству X.
не принадлежит множеству X.

Необходимые и достаточные условия безусловного экстремума
Постановка задачи
Дана дважды непрерывно дифференцируемая функция  , определенная на множестве
, определенная на множестве  .
.
Требуется исследовать функцию  на экстремум, т.е. определить точки
на экстремум, т.е. определить точки  ее локальных минимумов и максимумов на
ее локальных минимумов и максимумов на  :
:

Стратегия решения задачи
Находятся точки  локальных экстремумов с помощью необходимых условий первого и второго порядка (порядок условий определяется порядком используемых производных), а также достаточных условий безусловного локального экстремума. Вычисляются значения
локальных экстремумов с помощью необходимых условий первого и второго порядка (порядок условий определяется порядком используемых производных), а также достаточных условий безусловного локального экстремума. Вычисляются значения  функции в найденных точках локальных экстремумов. Утверждение 2.1 (необходимые условия экстремума первого порядка).
функции в найденных точках локальных экстремумов. Утверждение 2.1 (необходимые условия экстремума первого порядка).
Пусть  есть точка локального минимума (максимума) функции
есть точка локального минимума (максимума) функции  на множестве
на множестве  и
и  дифференцируема в точке
дифференцируема в точке  . Тогда градиент функции
. Тогда градиент функции  в точке
в точке  равен нулю, т.е.
равен нулю, т.е.
 или
или

Определение 2.1. Точки  , удовлетворяющие условию (2.2) или (2.3), называются стационарными.
, удовлетворяющие условию (2.2) или (2.3), называются стационарными.
Утверждение 2.2 (необходимые условия экстремума второго порядка).
Пусть точка  есть точка локального минимума (максимума) функции
есть точка локального минимума (максимума) функции  на множестве
на множестве  и функция
и функция  дважды дифференцируема в этой точке. Тогда матрица Гессе
дважды дифференцируема в этой точке. Тогда матрица Гессе  функции
функции  , вычисленная в точке
, вычисленная в точке  , является положительно полуопределенной (отрицательно полуопределенной), т.е.
, является положительно полуопределенной (отрицательно полуопределенной), т.е.

Утверждение 2.3 (достаточные условия экстремума).
Пусть функция  в точке
в точке  дважды дифференцируема, ее градиент равен нулю, а матрица Гессе является положительно определенной (отрицательно определенной), т.е.
дважды дифференцируема, ее градиент равен нулю, а матрица Гессе является положительно определенной (отрицательно определенной), т.е.
Тогда точка  есть точка локального минимума (максимума) функции
есть точка локального минимума (максимума) функции  на множестве
на множестве  .
.
Определение 2.2. Рассмотрим определитель матрицы Гессе  , вычисленной в стационарной точке
, вычисленной в стационарной точке
 1. Определители
1. Определители  называются угловыми минорами.
называются угловыми минорами.
2. Определители  -го порядка
-го порядка  , получающиеся из определителя матрицы
, получающиеся из определителя матрицы  вычеркиванием каких-либо
вычеркиванием каких-либо  строк и
строк и  столбцов с одними и теми же номерами, называются главными минорами.
столбцов с одними и теми же номерами, называются главными минорами.
Для проверки выполнения достаточных условий экстремума и необходимых условий второго порядка используются два способа.
Первый способ (с помощью угловых и главных миноров).
А. Критерий проверки достаточных условий экстремума (критерий Сильвестра). 1. Для того чтобы матрица Гессе  была положительно определенной
была положительно определенной  и точка
и точка  являлась точкой локального минимума, необходимо и достаточно, чтобы знаки угловых миноров были строго положительны:
являлась точкой локального минимума, необходимо и достаточно, чтобы знаки угловых миноров были строго положительны:
2. Для того чтобы матрица Гессе  была отрицательно определенной
была отрицательно определенной  и точка
и точка  являлась точкой локального максимума, необходимо и достаточно, чтобы знаки угловых миноров чередовались, начиная с отрицательного:
являлась точкой локального максимума, необходимо и достаточно, чтобы знаки угловых миноров чередовались, начиная с отрицательного:
 Б. Критерий проверки необходимых условий экстремума второго порядка.
Б. Критерий проверки необходимых условий экстремума второго порядка.
1. Для того чтобы матрица Гессе  была положительно полуопределенной
была положительно полуопределенной  и точка
и точка  может быть являлась точкой локального минимума, необходимо и достаточно, чтобы все главные миноры определителя матрицы Гессе были неотрицательны.
может быть являлась точкой локального минимума, необходимо и достаточно, чтобы все главные миноры определителя матрицы Гессе были неотрицательны.
2. Для того чтобы матрица Гессе  была отрицательно полуопределенной
была отрицательно полуопределенной  и точка
и точка  может быть являлась точкой локального максимума, необходимо и достаточно, чтобы все главные миноры четного порядка были неотрицательны, а все главные миноры нечетного порядка – неположительны. Второй способ (с помощью собственных значений матрицы Гессе).
может быть являлась точкой локального максимума, необходимо и достаточно, чтобы все главные миноры четного порядка были неотрицательны, а все главные миноры нечетного порядка – неположительны. Второй способ (с помощью собственных значений матрицы Гессе).
Определение 2.3. Собственные значения  матрицы
матрицы  размера
размера  находятся как корни характеристического уравнения (алгебраического уравнения
находятся как корни характеристического уравнения (алгебраического уравнения  степени):
степени):

Замечание 2.1. Собственные значения вещественной симметрической матрицы  вещественны.
вещественны.
Оба способа проверки достаточных и необходимых условий экстремума второго порядка приведены в табл. 2.1.
Алгоритм решения задачи
Шаг 1. Записать необходимые условия экстремума первого порядка в форме (2.3) и найти стационарные точки  в результате решения системы
в результате решения системы  в общем случае нелинейных алгебраических уравнений с
в общем случае нелинейных алгебраических уравнений с  неизвестными. Для численного решения системы могут использоваться методы простой итерации, Зейделя, Ньютона. Имя Шаг 2. В найденных стационарных точках
неизвестными. Для численного решения системы могут использоваться методы простой итерации, Зейделя, Ньютона. Имя Шаг 2. В найденных стационарных точках  проверить выполнение достаточных, а если они не выполняются, то необходимых условий второго порядка с помощью одного из двух способов (см. табл. 2.1).
проверить выполнение достаточных, а если они не выполняются, то необходимых условий второго порядка с помощью одного из двух способов (см. табл. 2.1).
Шаг 3. Вычислить значения  в точках экстремума.
в точках экстремума.
Описанный алгоритм отображен на рис. 2.1, где показана последовательность действий в случаях выполнения и невыполнения соответствующих условий экстремума при применении первого способа.
Замечания 2.2.
1. Продолжение исследований, которое требуется в ряде случаев, разобранных в табл. 2.1, при решении практических задач, как правило, не проводится, за исключением небольшого числа модельных примеров. 2. Если требуется определить глобальные экстремумы, то они находятся результате сравнения значений функции в точках локальных минимумов и максимумов с учетом ограниченности функции на  .
.
3. Для случая функции  одной переменной
одной переменной  можно сформулировать правило, заменяющее п. 2 алгоритма:
можно сформулировать правило, заменяющее п. 2 алгоритма:
Если функция  и ее производные непрерывны, то точка
и ее производные непрерывны, то точка  является точкой экстремума тогда и только тогда, когда число
является точкой экстремума тогда и только тогда, когда число  – четное, где
– четное, где  – порядок первой не обращающейся в нуль в точке
– порядок первой не обращающейся в нуль в точке  производной. Если
производной. Если  , то в точке
, то в точке  – локальный минимум, а если
– локальный минимум, а если  , то в точке
, то в точке  – локальный максимум. Если число
– локальный максимум. Если число  нечетное, в точке
нечетное, в точке  нет экстремума.
нет экстремума.
4. Часто на практике, особенно при применении численных методов поиска экстремума, рассматриваемых в последующих разделах, требуется проверить, выполняются ли необходимые и достаточные условия экстремума в некоторой точке. Такой анализ необходим, так как многие численные методы позволяют найти лишь стационарную точку, тип которой требует уточнения.

Пример 2.1.
Найти экстремум функции  на множестве
на множестве  .
.
1. Запишем необходимые условия экстремума первого порядка:

В результате решения системы получаем стационарную точку  2. Проверим выполнение достаточных условий экстремума. Первый способ. Матрица Гессе имеет вид
2. Проверим выполнение достаточных условий экстремума. Первый способ. Матрица Гессе имеет вид  . Так как
. Так как  то в точке
то в точке  локальный минимум (строка 1 в табл. 2.1).
локальный минимум (строка 1 в табл. 2.1).
Второй способ. Найдем собственные значения матрицы Гессе, используя (2.10):
 Отсюда
Отсюда  Так как все собственные значения положительны, то в точке
Так как все собственные значения положительны, то в точке  локальный минимум (строка 1 в табл. 2.1). Из примера 1.19 следует, что функция является строго выпуклой на множестве
локальный минимум (строка 1 в табл. 2.1). Из примера 1.19 следует, что функция является строго выпуклой на множестве  . Поэтому точка локального минимума является и точкой глобального минимума (см. п. 3 утверждения 1.1).
. Поэтому точка локального минимума является и точкой глобального минимума (см. п. 3 утверждения 1.1).
3. Вычислим значение функции в точке глобального минимума:  .
.
Пример 2.2.
Найта экстремум функции  на множестве
на множестве  .
.
1. Запишем необходимые условия первого порядка:  В результате решения системы получаем стационарную точку
В результате решения системы получаем стационарную точку  .
.
2. Проверим выполнение достаточных условий экстремума и необходимых условий второго порядка. Первый способ. Матрица Гессе имеет вид  Так как
Так как  выполняются (строки 1 и 2 в табл. 2.1). Согласно схеме (рис. 2.1)?проверим выполнение необходимых условий второго порядка. Главные миноры первого порядка (
выполняются (строки 1 и 2 в табл. 2.1). Согласно схеме (рис. 2.1)?проверим выполнение необходимых условий второго порядка. Главные миноры первого порядка ( ) получаются из Д 2 в результате вычеркивания
) получаются из Д 2 в результате вычеркивания  строк и столбцов с одинаковыми номерами: -2, 2. Главный минор второго порядка (
строк и столбцов с одинаковыми номерами: -2, 2. Главный минор второго порядка ( ) получается из
) получается из  в результате вычеркивания
в результате вычеркивания  строк и столбцов, т.е. совпадает с
строк и столбцов, т.е. совпадает с  : -4. Отсюда следует, что необходимые условия экстремума второго порядка не выполняются (строки 3 и 4 в табл. 2.1). Так как матрица Гессе не является нулевой, то можно сделать вывод о том, что в точке
: -4. Отсюда следует, что необходимые условия экстремума второго порядка не выполняются (строки 3 и 4 в табл. 2.1). Так как матрица Гессе не является нулевой, то можно сделать вывод о том, что в точке  нет экстремума (строка 6 в табл. 2.1).
нет экстремума (строка 6 в табл. 2.1).
Второй способ. Найдем собственные значения матрицы Гессе, используя (2.10):

Отсюда  т.е. собственные значения имеют разные знаки. Поэтому точка
т.е. собственные значения имеют разные знаки. Поэтому точка  не является точкой минимума или максимума (строка 6 в табл. 2.1), а является седловой точкой (аналогична изображенной на рис. 1.3, в). 3. Так как экстремум не достигается ни в одной точке,
не является точкой минимума или максимума (строка 6 в табл. 2.1), а является седловой точкой (аналогична изображенной на рис. 1.3, в). 3. Так как экстремум не достигается ни в одной точке,  не вычисляется.
не вычисляется.
Пример 2.3.
Найти экстремум функции  на множестве
на множестве 
1. Запишем необходимые условия экстремума первого порядка: 
В результате решения системы получаем стационарную точку 
2. Проверим выполнение достаточных и необходимых условий второго по-Матрица Гессе имеет вид  Так как
Так как  , то достаточные условаия экстремума не выполняются (строки 1 и 2 в табл. 2.1). Согласно схеме (рис. 2.1) проверим выполнение необходимых условий экстремума второго порядка. Аналогично решению примера 2.2 получаем главные миноры первого порядка: 2, 0 и главный минор второго порядка: 0. Так как все главные миноры неотрицательные, то в точке х’ может быть минимум и требуется дополнительное исследование (строка 3 в табл. 2.1).
, то достаточные условаия экстремума не выполняются (строки 1 и 2 в табл. 2.1). Согласно схеме (рис. 2.1) проверим выполнение необходимых условий экстремума второго порядка. Аналогично решению примера 2.2 получаем главные миноры первого порядка: 2, 0 и главный минор второго порядка: 0. Так как все главные миноры неотрицательные, то в точке х’ может быть минимум и требуется дополнительное исследование (строка 3 в табл. 2.1).
3. Вычислим значение целевой функции в точке  и рассмотрим
и рассмотрим  -окрестность точки х’, а также поведение функции
-окрестность точки х’, а также поведение функции  на множестве
на множестве  При любых
При любых  имеем:
имеем:  (см. рис. 1.2), что соответствует не только определению 1.2, но и определению 1.1. Поэтому точка
(см. рис. 1.2), что соответствует не только определению 1.2, но и определению 1.1. Поэтому точка  является точкой глобального минимума.
является точкой глобального минимума.


Лекции:
- Параллельность прямой и плоскости
- Формулы комбинаторики
- Элементарные функции комплексного переменного. Дробно-рациональные функции
- Равномерная сходимость функционального ряда
- Критерий Сильвестра
- Функция распределения
- Рациональные числа
- Матричные уравнения: пример решения
- Разложение в ряд Тейлора
- Дифференциальные уравнения первого порядка

Функция (синяя) и её производная (красная). Глобальный максимум функции обозначен символом 
Экстре́мум (лат. extremum — крайнее) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Задачи нахождения экстремума возникают во всех областях человеческого знания: теория автоматического управления, проблемы экономики, биология, физика и т. д.[1]
Определения[править | править код]
Пусть дана функция 


Если неравенства выше строгие, то 
Значение функции 
Замечание[править | править код]
Функция 


Необходимые условия существования локальных экстремумов[править | править код]
- Из леммы Ферма вытекает следующее[2]:
- Пусть точка
является точкой экстремума функции
, определенной в некоторой окрестности точки
.
- Тогда либо производная
не существует, либо
.
Эти условия не являются достаточными, так, функция может иметь нуль производной в точке, но эта точка может не быть точкой экстремума, а являться, скажем, точкой перегиба, как точка (0,0) у функции 
Достаточные условия существования локальных экстремумов[править | править код]

то 
Заметим, что при этом функция не обязательно дифференцируема в точке 
и

и
то 
Если 


Если 


Если 
См. также[править | править код]
- Критическая точка (математика)
- Методы оптимизации
- Условный экстремум
Примечания[править | править код]
- ↑ Пшеничный, 1969, с. 7.
- ↑ Кудрявцев Л. Д. Математический анализ. — 2-е изд. — М.: Высшая школа, 1973. — Т. 1.
Литература[править | править код]
- Пшеничный Б.Н. Необходимые условия экстремума. — М.: Наука, 1969. — 150 с.
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Возрастание и убывание функции на интервале
Функция y=f(x) будет возрастать на интервале x, когда при любых x1∈X и x2∈X , x2>x1неравенство f(x2)>f(x1) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.
Функция y=f(x) считается убывающей на интервале x, когда при любых x1∈X, x2∈X, x2>x1 равенство f(x2)>f(x1) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.

Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть (a;b), где х=а, х=b, точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x.
Основные свойства элементарных функций типа y=sinx – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале -π2; π2, тогда возрастание на отрезке имеет вид -π2; π2.
Точки экстремума, экстремумы функции
Точка х0 называется точкой максимума для функции y=f(x), когда для всех значений x неравенство f(x0)≥f(x) является справедливым. Максимум функции – это значение функции в точке, причем обозначается ymax.
Точка х0 называется точкой минимума для функции y=f(x), когда для всех значений x неравенство f(x0)≤f(x) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида ymin.
Окрестностями точки х0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [a;b]. Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х=b.
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Пусть задана функция y=f(x), которая дифференцируема в ε окрестности точки x0, причем имеет непрерывность в заданной точке x0. Отсюда получаем, что
- когда f'(x)>0 с x∈(x0-ε; x0) и f'(x)<0 при x∈(x0; x0+ε), тогда x0 является точкой максимума;
- когда f'(x)<0 с x∈(x0-ε; x0) и f'(x)>0 при x∈(x0; x0+ε), тогда x0 является точкой минимума.
Иначе говоря, получим их условия постановки знака:
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком, то есть с + на -, значит, точка называется максимумом;
- когда функция непрерывна в точке x0, тогда имеет производную с меняющимся знаком с – на +, значит, точка называется минимумом.
Алгоритм для нахождения точек экстремума
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
- найти область определения;
- найти производную функции на этой области;
- определить нули и точки, где функция не существует;
- определение знака производной на интервалах;
- выбрать точки, где функция меняет знак.
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Найти точки максимума и минимума заданной функции y=2(x+1)2x-2.
Решение
Область определения данной функции – это все действительные числа кроме х=2. Для начала найдем производную функции и получим:
y’=2x+12x-2’=2·x+12’·(x-2)-(x+1)2·(x-2)'(x-2)2==2·2·(x+1)·(x+1)’·(x-2)-(x+1)2·1(x-2)2=2·2·(x+1)·(x-2)-(x+2)2(x-2)2==2·(x+1)·(x-5)(x-2)2
Отсюда видим, что нули функции – это х=-1, х=5, х=2, то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:

Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х=-2, х=0, х=3, х=6.
Получаем, что
y'(-2)=2·(x+1)·(x-5)(x-2)2x=-2=2·(-2+1)·(-2-5)(-2-2)2=2·716=78>0, значит, интервал -∞; -1 имеет положительную производную. Аналогичным образом получаем, что
y'(0)=2·(0+1)·0-50-22=2·-54=-52<0y'(3)=2·(3+1)·(3-5)(3-2)2=2·-81=-16<0y'(6)=2·(6+1)·(6-5)(6-2)2=2·716=78>0
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Получим, что в точке х=-1 функция будет непрерывна, значит, производная изменит знак с + на -. По первому признаку имеем, что х=-1 является точкой максимума, значит получаем
ymax=y(-1)=2·(x+1)2x-2x=-1=2·(-1+1)2-1-2=0
Точка х=5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
ymin=y(5)=2·(x+1)2x-2x=5=2·(5+1)25-2=24
Графическое изображение

Ответ: ymax=y(-1)=0, ymin=y(5)=24.
Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x0, этим и упрощает вычисление.
Найти точки максимума и минимума функции y=16×3=2×2+223x-8.
Решение.
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
-16×3-2×2-223x-8, x<016×3-2×2+223x-8, x≥0
После чего необходимо найти производную:
y’=16×3-2×2-223x-8′, x<016×3-2×2+223x-8′, x>0y’=-12×2-4x-223, x<012×2-4x+223, x>0
Точка х=0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
lim y’x→0-0=lim yx→0-0-12×2-4x-223=-12·(0-0)2-4·(0-0)-223=-223lim y’x→0+0=lim yx→0-012×2-4x+223=12·(0+0)2-4·(0+0)+223=+223
Отсюда следует, что функция непрерывна в точке х=0, тогда вычисляем
lim yx→0-0=limx→0-0-16×3-2×2-223x-8==-16·(0-0)3-2·(0-0)2-223·(0-0)-8=-8lim yx→0+0=limx→0-016×3-2×2+223x-8==16·(0+0)3-2·(0+0)2+223·(0+0)-8=-8y(0)=16×3-2×2+223x-8x=0=16·03-2·02+223·0-8=-8
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
-12×2-4x-223, x<0D=(-4)2-4·-12·-223=43×1=4+432·-12=-4-233<0x2=4-432·-12=-4+233<0
12×2-4x+223, x>0D=(-4)2-4·12·223=43×3=4+432·12=4+233>0x4=4-432·12=4-233>0
Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x=-6, x=-4, x=-1, x=1, x=4, x=6. Получим, что
y'(-6)=-12×2-4x-223x=-6=-12·-62-4·(-6)-223=-43<0y'(-4)=-12×2-4x-223x=-4=-12·(-4)2-4·(-4)-223=23>0y'(-1)=-12×2-4x-223x=-1=-12·(-1)2-4·(-1)-223=236<0y'(1)=12×2-4x+223x=1=12·12-4·1+223=236>0y'(4)=12×2-4x+223x=4=12·42-4·4+223=-23<0y'(6)=12×2-4x+223x=6=12·62-4·6+223=43>0
Изображение на прямой имеет вид

Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
x=-4-233, x=0, x=4+233, тогда отсюда точки максимума имеют значениx=-4+233, x=4-233
Перейдем к вычислению минимумов:
ymin=y-4-233=16×3-22+223x-8x=-4-233=-8273ymin=y(0)=16×3-22+223x-8x=0=-8ymin=y4+233=16×3-22+223x-8x=4+233=-8273
Произведем вычисления максимумов функции. Получим, что
ymax=y-4+233=16×3-22+223x-8x=-4+233=8273ymax=y4-233=16×3-22+223x-8x=4-233=8273
Графическое изображение

Ответ:
ymin=y-4-233=-8273ymin=y(0)=-8ymin=y4+233=-8273ymax=y-4+233=8273ymax=y4-233=8273
Второй признак экстремума функции
Если задана функция f'(x0)=0, тогда при ее f”(x0)>0 получаем, что x0 является точкой минимума, если f”(x0)<0, то точкой максимума. Признак связан с нахождением производной в точке x0.
Найти максимумы и минимумы функции y=8xx+1.
Решение
Для начала находим область определения. Получаем, что
D(y): x≥0x≠-1⇔x≥0
Необходимо продифференцировать функцию, после чего получим
y’=8xx+1’=8·x’·(x+1)-x·(x+1)'(x+1)2==8·12x·(x+1)-x·1(x+1)2=4·x+1-2x(x+1)2·x=4·-x+1(x+1)2·x
При х=1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х=1. Получаем:
y”=4·-x+1(x+1)2·x’==4·(-x+1)’·(x+1)2·x-(-x+1)·x+12·x'(x+1)4·x==4·(-1)·(x+1)2·x-(-x+1)·x+12’·x+(x+1)2·x'(x+1)4·x==4·-(x+1)2x-(-x+1)·2x+1(x+1)’x+(x+1)22x(x+1)4·x==-(x+1)2x-(-x+1)·x+1·2x+x+12x(x+1)4·x==2·3×2-6x-1x+13·x3⇒y”(1)=2·3·12-6·1-1(1+1)3·(1)3=2·-48=-1<0
Значит, использовав 2 достаточное условие экстремума, получаем, что х=1 является точкой максимума. Иначе запись имеет вид ymax=y(1)=811+1=4.
Графическое изображение

Ответ: ymax=y(1)=4..
Третье достаточное условие экстремума
Функция y=f(x) имеет ее производную до n-го порядка в ε окрестности заданной точки x0 и производную до n+1-го порядка в точке x0. Тогда f'(x0)=f”(x0)=f”'(x0)=…=fn(x0)=0.
Отсюда следует, что когда n является четным числом, то x0 считается точкой перегиба, когда n является нечетным числом, то x0 точка экстремума, причем f(n+1)(x0)>0, тогда x0 является точкой минимума, f(n+1)(x0)<0, тогда x0 является точкой максимума.
Найти точки максимума и минимума функции yy=116(x+1)3(x-3)4.
Решение
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
y’=116x+13′(x-3)4+(x+1)3x-34’==116(3(x+1)2(x-3)4+(x+1)34(x-3)3)==116(x+1)2(x-3)3(3x-9+4x+4)=116(x+1)2(x-3)3(7x-5)
Данная производная обратится в ноль при x1=-1, x2=57, x3=3. То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что
y”=116x+12(x-3)3(7x-5)’=18(x+1)(x-3)2(21×2-30x-3)y”(-1)=0y”57=-368642401<0y”(3)=0
Значит, что x2=57 является точкой максимума. Применив 3 достаточный признак, получаем, что при n=1 и f(n+1)57<0.
Необходимо определить характер точек x1=-1, x3=3. Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что
y”’=18(x+1)(x-3)2(21×2-30x-3)’==18(x-3)(105×3-225×2-45x+93)y”'(-1)=96≠0y”'(3)=0
Значит, x1=-1 является точкой перегиба функции, так как при n=2 и f(n+1)(-1)≠0. Необходимо исследовать точку x3=3. Для этого находим 4 производную и производим вычисления в этой точке:
y(4)=18(x-3)(105×3-225×2-45x+93)’==12(105×3-405×2+315x+57)y(4)(3)=96>0
Из выше решенного делаем вывод, что x3=3 является точкой минимума функции.
Графическое изображение

Ответ: x2=57 является точкой максимума, x3=3 – точкой минимума заданной функции.




