Как найти погрешность выборки – Сайт, где вы сможете решить свои вопросы

погрешность выборки
Чаще всего именно системную ошибку измерения называют погрешностью выборки. Значит, для определения погрешности выборки надо определить системную ошибку измерения. Последние годы я применяю достаточно простую методику для того, чтобы определить систематическую ошибку измерения, полученную в ходе социологического опроса.

На самом деле определение погрешности выборки — дело нетривиальное. Для того, чтобы определить погрешность выборки, надо какое-то значение генеральной совокупности (к примеру, рейтинг) сравнить с этим же значением в выборке. Но мы же проводим выборочное исследование для того, чтобы по данным выборке судить о данных всей генеральной совокупности и в данном случае погрешность должна сказать, насколько сильно значение во всей генеральной совокупности может отличаться от выборочного. Получаем уравнение с двумя неизвестными.

Давайте разбираться в ситуации.

Говорить об ошибке выборки для всего опроса не совсем корректно. Под ошибкой понимают разницу между показателем какого-либо признака в генеральной совокупности и в выборке. Таким образом, для каждого признака надо говорить о своей погрешности. Высказывание «погрешность опроса» чаще всего бывает бессмысленным, лучше говорить о «погрешности вопроса». Но моя методика как раз подходит для практически всего исследования.

В политических исследованиях, да и в коммерческих тоже, мы чаще всего имеем дело с бинарными вопросами, то есть вопросами, на который дается ответ «да» или «нет». Классический рейтинговый вопрос «За кого бы Вы проголосовали, если бы выборы состоялись в ближайшие выходные?» — частный случай бинарного вопроса. Его можно представить как несколько вопросов о поддержке каждого кандидата или партии: «Если бы выборы проходили в ближайшие выходные, проголосовали бы вы за кандидата N***?» и два варианта «Да, проголосовал» и «Нет, не проголосовал».

В статистике для оценки погрешности биноминального распределения используется следующая формула:

Формула расчета погрешности для биноминального распределения

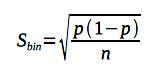
где S_bin — ошибка биноминального распределения

p — процент наблюдений (рейтинг)

n — размер выборки.

Максимального значения ошибка достигается, когда p=50%, то есть пополам ответили «да, проголосовал бы» и «нет, нет не проголосовал бы». Во всех остальных случаях ошибка меньше. Мы можем оценить ошибку взяв максимальное значение.

На следующем шаге мы воспользуемся правилом «Двух сигм» (или, по желанию, правилом «Трех сигм»). Правило говорит, что 95% всех значений распределения укладываются в интервал

В этом случае ошибку, согласно правилу «двух сигма» при 95%-ном доверительном интервале равна ±2*S_bin. В итоге мы получаем формулу, с помощью которой можно оценить ошибку выборки при 95%-ном доверительном интервале и ошибка будет зависеть только от размера выборки:

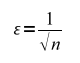
Где ε — погрешность выборки, n — размер выборки.

Получаем, что для выборки в 1000 человек погрешность измерения составит 3% при 95%-ном доверительном интервале.

Источник

Один из первых шагов при планировании количественного маркетингового исследования – определение объема выборки.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних

1. Формула (даже две)

Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).

Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.

На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

пример неправильного размера выборки, как опеределить размер выборки

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).

В таких случаях для расчета объема выборки используется следующая формула:

где

n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.

Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.

Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.

Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.

Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне

Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.

ШПАРГАЛКА (скопируйте ссылку или текст)

Подходы к решению проблемы:

Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,

N – объем генеральной совокупности,

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,

p – доля респондентов с наличием исследуемого признака,

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)

∆ – предельная ошибка выборки.

Например,

рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:

Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%

При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.

2. Причины «раздувать» выборку

Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).

Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок

Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра

При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).

Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:

увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).

Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ

Доверительный уровень:

Ошибка выборки (?):
%

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

РЕЗУЛЬТАТ

Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.

Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.

Объем выборки рассчитывается по следующим формулам

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.

Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.

ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:

Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:

n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек

Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Доля признака (p):
%

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для доли признака рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

Δ– предельная ошибка выборки.

Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p – ∆; p + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:

Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%

Рассчитаем доверительный интервал:

(p – ∆; p + ∆) = (20% – 2,48%; 20% + 2,48%) = (17,52%; 22,48%)

Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).

Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Среднее значение (x̄):

Стандартное отклонение (s):

РЕЗУЛЬТАТ

Ошибка выборки для среднего значения рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

s – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Δ– предельная ошибка выборки.

Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ – ∆; x ̅ + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:

Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44

Рассчитаем доверительный интервал:

(x ̅ – ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)

Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ

Доверительный уровень:

	Измерение 1	Измерение 2
Доля признака (p):	%	%
Объём выборки (n):

РЕЗУЛЬТАТ

Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ

Доверительный уровень:

	Измерение 1	Измерение 2
Среднее значение (x̄):
Стандартное отклонение (s):
Объём выборки (n):

РЕЗУЛЬТАТ

Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?

В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Распределения значений в выборках близки к нормальному распределению.

В калькуляторе используются следующие вводные данные:

Среднее значение ( ̅x) – среднее арифметическое показателя.

Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

Вы можете подписаться на уведомления о новых материалах СканМаркет

Источник

Как определить размер выборки?

Время на прочтение
4 мин

Количество просмотров 55K

Статистика знает все. И Ильф и Е. Петров, «12 Стульев»

Представьте себе, что вы строите крупный торговый центр и желаете оценить автомобильный поток въезда на территорию парковки. Нет, давайте другой пример… они все равно этого никогда не будут делать. Вам необходимо оценить вкусовые предпочтения посетителей вашего портала, для чего необходимо провести среди них опрос. Как увязать количество данных и возможную погрешность? Ничего сложного — чем больше ваша выборка, тем меньше погрешность. Однако и здесь есть нюансы.

Графики

Теоретический минимум

Не будет лишним освежить память, эти термины нам пригодятся далее.

Популяция – Множество всех объектов, среди которых проводится исследования.
Выборка – Подмножество, часть объектов из всей популяции, которая непосредственно участвует в исследовании.
Ошибка первого рода — (α) Вероятность отвергнуть нулевую гипотезу, в то время как она верна.
Ошибка второго рода — (β) Вероятность не отвергнуть нулевую гипотезу, в то время как она ложна.
1 — β — Статистическая мощность критерия.
μ₀ и μ₁ — Средние значения при нулевой и альтернативной гипотезе.

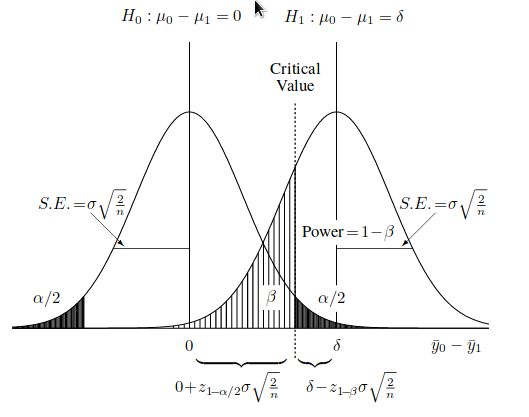
Сравнение двух альтернативных средних значений

Уже в самих определениях ошибки первого и второго рода имеется простор для дебатов и толкований. Как с ними определиться и какую выбрать в качестве нулевой? Если вы исследуете уровень загрязнения почвы или вод, то как сформулируете нулевую гипотезу: загрязнение присутствует, или нет загрязнения? А ведь от этого зависит объем выборки из общей популяции объектов.

Характеристики распределения и стандартное отклонение

Исходная популяция, также как и выборка может иметь любое распределение, однако среднее значение имеет нормальное или гауссово распределение благодаря Центральной Предельной Теореме.

Относительно параметров распределения и среднего значения в частности возможно несколько типов умозаключений. Первое из них называется доверительным интервалом. Он указывает на интервал возможных значений параметра, с указанным коэффициентом доверия. Так например 100(1-α)% доверительный интервал для μ будет таким (Ур. 1).

$hat{mu} pm t_{{alpha/2};df}sqrt{frac{hatsigma^2}{n}}$

df — Степень свободы = n — 1, от английского «degrees of freedom».
$t_{{alpha/2};df}$ — Двусторонняя критическая величина, t-критерий Стьюдента.

Второе из умозаключений — проверка гипотезы. Оно может быть примерно таким.

H₀: μ = h
H₁: μ > h
H₂: μ < h

С доверительным интервалом 100(1-α) для μ можно сделать выбор в пользу H₁ и H₂ :

Если нижний предел доверительного интервала 100(1-α) < h, то тогда отвергаем H₀ в пользу H₂.
Если верхний предел доверительного интервала 100(1-α) > h, то тогда отвергаем H₀ в пользу H₁.
Если доверительного интервала 100(1-α) включает в себя h, то тогда мы не может отвергнуть H₀ и такой результат считается неопределенным.

Если нам нужно проверить значение μ для одной выборки из общей совокупности, то критерий обретет вид.

Где $t = (hat{mu} - h)/sqrtfrac{hatsigma^2}{n}$ .

Доверительный интервал, погрешность и размер выборки

Возьмем самое первое уравнение и выразим оттуда ширину доверительного интервала (Ур. 2).

$w = 2t_{{alpha/2};df}sqrt{frac{hatsigma^2}{n}}$

В некоторых случаях мы можем заменить t-статистику Стьюдента на z стандартного нормального распределения. Еще одним упрощением заменим половину от w на погрешность измерения E. Тогда наше уравнения примет вид (Ур. 3).

$E = z_{alpha/2}sqrt{frac{hatsigma^2}{n}}$

Как видим погрешность действительно уменьшается вместе с ростом количества входных данных. Откуда легко вывести искомое (Ур. 4).

$n = left[frac{z_{alpha/2}*sigma}{E}right]^2$

Практика — считаем с R

Проверим гипотезу о том, что среднее значение данной выборки количества насекомых в ловушке равно 1.

H₀: μ = 1
H₁: μ > 1

Насекомые	0	1	2	3	4	5	6
Ловушки	10	9	5	5	1	2	1

> x <- read.table("/tmp/tcounts.txt")
> y = unlist(x, use.names="false")
> mean(z);sd(z)
[1] 1.636364
[1] 1.654883

Обратите внимание, что среднее и стандартное отклонение практически равны, что естественно для распределения Пуассона. Доверительный интервал 95% для t-статистики Стьюдента и df=32.

> qt(.975, 32)
[1] 2.036933

и наконец получаем критический интервал для среднего значения: 1.05 — 2.22.

> μ=mean(z)
> st = qt(.975, 32)
> μ + st * sd(z)/sqrt(33)
[1] 2.223159
> μ - st * sd(z)/sqrt(33)
[1] 1.049568

В итоге, следует отбраковать H₀ и принять H₁ так как с вероятностью 95%, μ > 1.

В том же самом примере, если принять, что нам известно действительное стандартное отклонение — σ, а не ее оценка полученная с помощью случайной выборки, можно рассчитать необходимое n для данной погрешности. Посчитаем для E=0.5.

> za2 = qnorm(.975)
> (za2*sd(z)/.5)^2
[1] 42.08144

Поправка на ветер

На самом деле нет никаких причин, полагать, что нам будет известна σ (дисперсия), в то время как μ (среднее) нам еще только предстоит оценить. Из-за этого уравнение 4 имеет мало практической пользы, кроме особо рафинированных примеров из области комбинаторики, а реалистичное уравнение для n несколько сложнее при неизвестной σ (Ур. 5).

$n = 4tildesigma^2 (z_{alpha/2}/w)^2 + z^2_{alpha/2}/2$

Обратите внимание, что σ в последнем уравнении не с шапкой (^), а тильдой (~). Это следствие того, что в самом начале у нас нет даже оценочного стандартного отклонения случайной выборки — $hatsigma$ , и вместо нее мы используем запланированное — $tildesigma$ . Откуда же мы берем последнее? Можно сказать, что с потолка: экспертная оценка, грубые прикидки, прошлый опыт и т. д.

А что на счет второго слагаемого правой стороны 5-го уравнения, откуда оно взялось? Так как $z_{alpha/2} < t_{{alpha/2};df}$ , необходима поправка Гюнтера.

Помимо уравнений 4 и 5 есть еще несколько приблизительно-оценочных формул, но это уже заслуживает отдельного поста.

Использованные материалы

Sample sizes
Hypothesis testing

Источник

Как интерпретировать предел погрешности (с примерами)

17 авг. 2022 г.
читать 2 мин

В статистике предел погрешности используется для оценки того, насколько точна некоторая оценка доли населения или среднего значения населения.

Обычно мы используем предел погрешности при расчете доверительных интервалов для параметров совокупности .

В следующих примерах показано, как рассчитать и интерпретировать предел погрешности для доли населения и среднего значения населения.

Пример 1. Интерпретация предела погрешности для доли населения

Мы используем следующую формулу для расчета доверительного интервала для доли населения:

Доверительный интервал = p +/- z * (√ p (1-p) / n )

куда:

p: доля выборки
z: выбранное значение z
n: размер выборки

Часть уравнения, которая следует за знаком +/-, представляет собой погрешность:

Погрешность = z * (√ p (1-p) / n )

Например, предположим, что мы хотим оценить долю жителей округа, поддерживающих определенный закон. Мы выбираем случайную выборку из 100 жителей и спрашиваем их об их отношении к закону.

Вот результаты:

Размер выборки n = 100
Доля в пользу закона p = 0,56

Предположим, мы хотим рассчитать 95-процентный доверительный интервал для истинной доли жителей округа, поддерживающих закон.

Используя приведенную выше формулу, мы вычисляем погрешность:

Погрешность = z * (√ p (1-p) / n )
Погрешность = 1,96 * (√ 0,56 (1-0,56) / 100 )
Погрешность = 0,0973

Затем мы можем рассчитать 95% доверительный интервал следующим образом:

Доверительный интервал = p +/- z * (√ p (1-p) / n )
Доверительный интервал = 0,56 +/- 0,0973
Доверительный интервал = [0,4627, 0,6573]

Доверительный интервал 95% для доли жителей округа, поддерживающих закон, оказывается равным [0,4627, 0,6573] .

Это означает, что мы на 95% уверены, что истинная доля жителей, поддерживающих закон, составляет от 46,27% до 65,73%.

Доля жителей в выборке, поддержавших закон, составила 56%, но, вычитая и добавляя погрешность к этой доле выборки, мы можем построить доверительный интервал.

Этот доверительный интервал представляет собой диапазон значений, которые, скорее всего, содержат истинную долю жителей округа, поддерживающих закон.

Пример 2. Интерпретация предела погрешности для среднего значения генеральной совокупности

Мы используем следующую формулу для расчета доверительного интервала для среднего значения генеральной совокупности:

Доверительный интервал = x +/- z*(s/ √n )

куда:

x : выборочное среднее
z: z-критическое значение
s: стандартное отклонение выборки
n: размер выборки

Часть уравнения, которая следует за знаком +/-, представляет собой погрешность:

Погрешность = z*(s/ √n )

Например, предположим, что мы хотим оценить средний вес популяции дельфинов. Мы собираем случайную выборку дельфинов со следующей информацией:

Размер выборки n = 40
Средний вес выборки x = 300
Стандартное отклонение выборки s = 18,5

Используя приведенную выше формулу, мы вычисляем погрешность:

Погрешность = z*(s/ √n )
Погрешность = 1,96*(18,5/ √40 )
Погрешность = 5,733

Затем мы можем рассчитать 95% доверительный интервал следующим образом:

Доверительный интервал = x +/- z*(s/ √n )
Доверительный интервал = 300 +/- 5,733
Доверительный интервал = [294,267, 305,733]

95% доверительный интервал для среднего веса дельфинов в этой популяции оказывается равным [294,267, 305,733] .

Это означает, что мы на 95% уверены, что истинный средний вес дельфинов в этой популяции составляет от 294,267 до 305,733 фунтов.

Средний вес дельфинов в выборке составлял 300 фунтов, но, вычитая и добавляя погрешность к этой выборке, мы можем построить доверительный интервал.

Этот доверительный интервал представляет собой диапазон значений, которые, скорее всего, содержат истинный средний вес дельфинов в этой популяции.

Дополнительные ресурсы

В следующих руководствах представлена дополнительная информация о допустимой погрешности:

Погрешность и стандартная ошибка: в чем разница?
Как найти погрешность в Excel
Как найти погрешность на калькуляторе TI-84

Источник

Часто политические опросы и другие статистические данные показывают свои результаты с точностью до ошибки. Нередко можно увидеть, что в ходе опроса общественного мнения утверждается, что определенный процент респондентов пользуется поддержкой той или иной проблемы или кандидата, плюс-минус определенный процент. Именно этот термин «плюс» и «минус» является пределом погрешности. Но как рассчитать погрешность? Для простой случайной выборки из достаточно большой совокупности погрешность или погрешность – это просто повторное определение размера выборки и используемого уровня достоверности.

Содержание

Формула погрешности
Уровень уверенности
Критическое значение
Размер выборки
Несколько примеров

Формула погрешности

Далее мы будем использовать формулу погрешности. Мы будем планировать наихудший случай, когда мы понятия не имеем, какой истинный уровень поддержки представляют проблемы в нашем опросе. Если бы мы имели некоторое представление об этом числе, возможно, из предыдущих данных опроса, мы бы получили меньшую погрешность.

Формула, которую мы будем использовать это: E = z _α/2/(2√ n)

Уровень уверенности

Первая часть информации, которая нам нужна для расчета погрешности, – это определить, какой уровень уверенности мы желаем. Это число может быть меньше 100%, но наиболее распространенные уровни достоверности – 90%, 95% и 99%. Из этих трех наиболее часто используется уровень 95%.

Если мы вычтем уровень достоверности из единицы, то мы получим значение альфа, записанное как α, необходимого для формулы.

Критическое значение

Следующим шагом в вычислении запаса или ошибки является поиск соответствующее критическое значение. На это указывает термин z _α/2 в приведенной выше формуле. Поскольку мы приняли простую случайную выборку из большой совокупности, мы можем использовать стандартное нормальное распределение z– баллов .

Предположим, что мы работаем с доверием 95%. Мы хотим найти z -счет z * , для которого область между -z * и z * составляет 0,95. Из таблицы видно, что это критическое значение составляет 1,96.

Мы также могли найти критическое значение следующим образом. Если мы будем думать в терминах α/2, поскольку α = 1 – 0,95 = 0,05, мы увидим, что α/2 = 0,025. Теперь мы ищем в таблице оценку z с площадью 0,025 справа от нее. В итоге мы получим такое же критическое значение 1,96.

Другие уровни уверенности дадут нам другие критические значения. Чем выше уровень уверенности, тем выше будет критическое значение. Критическое значение для уровня уверенности 90% при соответствующем значении α, равном 0,10, составляет 1,64. Критическое значение для уровня достоверности 99% при соответствующем значении α, равном 0,01, составляет 2,54.

Размер выборки

Единственное другое число, которое нам нужно, чтобы использовать формулу для расчета погрешности, – это размер выборки. , обозначается в формуле n . Затем мы извлекаем квадратный корень из этого числа.

Из-за расположения этого числа в приведенной выше формуле, чем больше размер выборки, которую мы используем, тем будет меньше погрешность. Поэтому большие образцы предпочтительнее меньших. Однако, поскольку статистическая выборка требует ресурсов времени и денег, существуют ограничения на то, насколько мы можем увеличить размер выборки. Наличие квадратного корня в формуле означает, что четырехкратное увеличение размера выборки даст только половину погрешности.

Несколько примеров

Чтобы понять формулу, давайте рассмотрим пару примеров.

Каков предел погрешности для простого случайная выборка из 900 человек с доверительной вероятностью 95%?
Используя таблицу, мы получаем критическое значение 1,96, поэтому предел погрешности составляет 1,96/(2 √ 900 = 0,03267, или около 3,3%.
Каков предел погрешности для простой случайной выборки из 1600 человек при уровне достоверности 95%?
В то же время Уровень уверенности в качестве первого примера, увеличение размера выборки до 1600 дает нам погрешность 0,0245 или около 2,5%.

Источник

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

Как определить размер выборки?

Теоретический минимум

Доверительный интервал, погрешность и размер выборки

Практика — считаем с R

Поправка на ветер

Использованные материалы

Как интерпретировать предел погрешности (с примерами)

Пример 1. Интерпретация предела погрешности для доли населения

Пример 2. Интерпретация предела погрешности для среднего значения генеральной совокупности

Дополнительные ресурсы

Формула погрешности

Уровень уверенности

Критическое значение

Размер выборки

Несколько примеров

Вам также может понравиться

Как найти мастеров в салон на работу

Что такое слишком велик для конечной файловой системы как исправить

Как найти тиктокера в тик токе

Добавить комментарий Отменить ответ