Удельное сопротивление ρ зависит от температуры.
Как найти формулу для длины проводника
Проверка непрерывности тока и падения напряжения
Подробнее.
Определить длину проводника очень просто – достаточно измерить ее. Однако, если проводника нет или он очень длинный, измерить его напрямую может быть очень сложно.
– Строительная рулетка;
– амперметр (тестер);
– тормозной суппорт;
– График электропроводности металлов.
Чтобы определить длину проводника, измерьте длину каждого участка рулеткой и сложите их. Этот метод подходит для открытой проводки и измерительных проводов во временных кабельных соединениях.
Если проводка скрытая, используйте подходящую схему проводки, чтобы определить точную длину проводов. Если это невозможно, попытайтесь восстановить расположение проводов косвенным образом, основываясь на расположении розеток, выключателей, распределительных коробок и т.д.
Важным правилом для электриков является то, что все провода должны быть проложены либо горизонтально, либо вертикально. Кроме того, горизонтальные участки проводов обычно проходят вдоль верхнего края стены (под потолком). Однако определить фактическое положение проводов может только специальный прибор или опытный электрик.
Если нет возможности проследить скрытую проводку, необходимо измерить электрическое сопротивление отдельных участков кабеля. Сечение провода и материал, из которого он изготовлен, также должны быть включены в расчет. Обычно это медь или алюминий. Поскольку формула для расчета сопротивления – R = ? * L * s, длина проводника может быть рассчитана по формуле:
Где:
L – длина проводника,
R – сопротивление проводника,
? – удельное сопротивление материала, из которого изготовлен проводник,
s – площадь поперечного сечения проводника.
При расчете длины проводника необходимо учитывать следующие параметры и коэффициенты.
Удельное сопротивление медного проводника составляет 0,0154 – 0,0174 Ω, а алюминиевого – 0,0174 Ω: 0,0262 – 0,0278 Ω.
(Если проводник имеет длину 1 метр и поперечное сечение 1 мм)?
Площадь поперечного сечения проводника равна:
Где:
? – pi составляет приблизительно 3,14,
D – диаметр проволоки (который можно легко измерить штангенциркулем).
Если проволока намотана, определите длину одного витка и умножьте на количество витков.
Если катушка имеет круглое сечение, измерьте диаметр катушки (средний диаметр катушки, если это многослойная катушка). Затем умножьте диаметр на число “пи” и количество витков:
d – диаметр катушки,
n – число витков провода.
Специфическое сопротивление является свойством материала, из которого изготовлен проводник.
Электрическое сопротивление проводника прямо пропорционально произведению удельное сопротивление материала проводника по его длине и обратно пропорциональна площади его поперечного сечения.
| электрическое сопротивление проводника, | ом |
| удельное сопротивление материала проводника, | ом-м |
| длина проводника, | счетчик |
| поперечное сечение проводника | метр2 |
Единица удельного сопротивления в СИ
Удельное сопротивление ρ зависит от температуры.
Можно предположить, что FA = Ftj. FA = BIlsinα, где sin α = 1; длина F = mg
Таблица весов кабелей
Ниже приведена таблица сечений ВВГ.
| Сечение кабеля ВВГ | Расчетный вес продукта на 1 км цепи, 660 В (кг) | Вес продукта на 1 км цепи, 1000 В (кг) |
| 1×1,5 | 39 | 44 |
| 1×2,5 | 50 | 55 |
| 1×4 | 70 | 78 |
| 1×6 | 91 | 99 |
| 1×10 | 140 | 143 |
| 1×16 | 224 | 229 |
| 1×25 | 321 | 327 |
| 1×35 | 418 | 423 |
| 1×50 | 550 | 556 |
| 1×70 | 765 | |
| 1×95 | 1028 | |
| 1×120 | 1279 | |
| 1×150 | 1595 | |
| 1×185 | 1993 | |
| 1×240 | 2573 | |
| 1×300 | 3218 | |
| 2×1,5 | 72 | 81 |
| 2×2,5 | 94 | 117 |
| 2×4 | 147 | 165 |
| 2×6 | 191 | 210 |
| 2×10 | 293 | 300 |
| 2×16 | 442 | 449 |
| 2×25 | 657 | 667 |
| 2×35 | 854 | 865 |
| 2×50 | 1146 | 1160 |
| 2×70 | 1587 | |
| 2×95 | 2127 | |
| 2×120 | 2638 | |
| 2×150 | 3288 | |
| 2×2,5+1×1,5 | 128 | 141 |
| 3×1,5 | 93 | 117 |
| 3×2,5 | 137 | 151 |
| 3×4 | 194 | 218 |
| 3×6 | 257 | 282 |
| 3×10 | 403 | 413 |
| 3×16 | 619 | 628 |
| 3×25 | 926 | 941 |
| 3×35 | 1203 | 1232 |
| 3×50 | 1635 | 1653 |
| 3×1,5+1×1 | 123 | 138 |
| 3×2,5+1×1,5 | 161 | 178 |
| 3×4+1×2,5 | 229 | 253 |
| 3×6+1×4 | 308 | 339 |
| 3×10+1×6 | 471 | 490 |
| 3×16+1×10 | 749 | 761 |
| 3×25+1×16 | 1112 | 1130 |
| 3×35+1×16 | 1418 | 1438 |
| 3×50+1×25 | 1985 | |
| 3×70+1×35 | 2687 | |
| 3×95+1×50 | 3638 | |
| 3×120+1×70 | 4568 | |
| 3×150+1×70 | 5426 | |
| 3×185+1×95 | 6789 | |
| 3×240+1×120 | 8740 | |
| 4×1,5 | 128 | 143 |
| 4×2,5 | 170 | 187 |
| 4×4 | 244 | 274 |
| 4×6 | 326 | 358 |
| 4×10 | 518 | 530 |
| 4×16 | 818 | 835 |
| 4×25 | 1203 | 1222 |
| 4×35 | 1607 | 1629 |
| 4×50 | 2133 | 2157 |
| 4×70 | 3035 | |
| 4×95 | 4114 | |
| 4×120 | 5077 | |
| 4×150 | 6214 | |
| 4×185 | 7667 | |
| 4×240 | 9952 | |
| 5×1,5 | 156 | 175 |
| 5×2,5 | 208 | 229 |
| 5×4 | 302 | 340 |
| 5×6 | 406 | 445 |
| 5×10 | 646 | 661 |
| 5×16 | 1024 | 1041 |
| 5×25 | 1535 | 1559 |
| 5×35 | 2019 | 2045 |
| 5×50 | 2692 | 2722 |
| 5×70 | 3812 | |
| 5×95 | 5154 | |
| 5×120 | 6389 | |
| 5×150 | 8056 |
Для определения направления магнитной силы Ампера используется правило левой руки: если левая рука расположена так, что линии магнитного поля входят в ладонь, а четыре вытянутых пальца направлены в сторону тока в проводнике, то большой палец, согнутый под углом 90°, укажет направление силы Ампера.
Свойства электрических кабелей
При всем разнообразии кабельной продукции и огромном выборе проводов для электроустановок существуют правила выбора. Вам не нужно заучивать наизусть все марки кабелей и проводов, вам нужно уметь читать и расшифровывать их маркировку. Для начала полезно знать разницу между проводом и кабелем.
Провод – это проводник, используемый для соединения двух участков цепи. Он может иметь один или несколько токопроводящих проводников. Проводники могут быть:
Оголенные линии используются там, где невозможно установить контакт с проводами под напряжением. В большинстве случаев они используются на воздушных линиях.
Изоляционное покрытие наносится в один или два слоя. Провода с двумя или тремя жилами в двойной изоляции ошибочно принимают за кабель. Путаница возникает из-за того, что изоляция покрывает каждый проводник, а снаружи имеется общее полимерное или иное покрытие. Такие провода нашли применение внутри электроприборов, распределительных щитов или шкафов. Дома их прячут в стены или прокладывают в специальных каналах.
Изолированные изделия используются повсеместно. В зависимости от электробезопасности помещения и места установки выбирается класс изоляции.
Многопроводниковые кабели используются там, где требуются небольшие изгибы в сложных трассах, где не могут пройти однопроводниковые аналоги. Этот тип кабеля подходит для прокладки в кабельных каналах. Одножильные кабели труднее сгибать в таких условиях, требуется усилие и существует опасность повреждения жилы.
Для информации. Маркировка АППВ 3*2,5 обозначает кабель с алюминиевыми жилами, с изоляцией из ПВХ, плоский, с разделительным основанием. Расшифровка знаков указана в справочниках.
Конструктивно кабель представляет собой несколько индивидуально изолированных жил, заключенных во внешний защитный слой из диэлектрического материала. Пространство между жилами и оболочкой заполняется бумажными или пластиковыми лентами или кабельными нитями для предотвращения залипания. Кроме того, изделие может быть усилено бронированной лентой или стальной оплеткой для защиты от механических повреждений.
Существуют сложные формулы, которые рассчитывают тепловой баланс, используя температуру плавления и коэффициент термического сопротивления проводника для определения площади поперечного сечения проводника.
Расчет электрического проводника
Электрические свойства проводника во многом зависят от вещества, из которого он изготовлен. Наиболее важными из них являются:
- Удельное сопротивление проводящего вещества [ρ].измеряется в Ом-м в Международной системе единиц (СИ). Это означает, что единица СИ удельного сопротивления равна удельному сопротивлению вещества, при котором однородный проводник длиной 1 м и площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Также довольно часто используется внесистемное устройство Ом-м²/м. 1 Ом-м²/м = 10 -6 Ом-м
- Температурный коэффициент электрического сопротивления [α]указывает на температурную зависимость электрического сопротивления и измеряется в градусах Кельвина минус один градус K -1 . Она равна относительному изменению удельного сопротивления ⁄ электрического сопротивления вещества при изменении температуры на единицу. Расчет удельного сопротивления ρt при любой температуре t рассчитывается по классической формуле (1):
ρt – удельное сопротивление при температуре t t – температура ρ20 – удельное сопротивление при 20°C α – Температурный коэффициент сопротивления Формула применима в небольшом диапазоне температур от 0 до 100 °C. За пределами этого температурного диапазона или для получения более точных результатов можно использовать более сложные расчеты.
Ниже приведена таблица наиболее распространенных металлов для проводников, а также их удельное сопротивление и температурные коэффициенты электрического сопротивления. Эти таблицы взяты из различных источников. Следует отметить, что как удельное сопротивление проводника, так и его температурный коэффициент электрического сопротивления зависят от чистоты металла, а в случае сплавов (сталей) могут значительно отличаться от одной марки к другой.
| Таблица 1 | ||
| Металл | Значение сопротивления [ρ] при t = 20 °C, Ом-м²/м | Температурный коэффициент электрического сопротивления [α], K -1 |
| Медь | 0.0175 | 0.0043 |
| Алюминий | 0.0271 | 0.0039 |
| Сталь | 0.125 | 0.006 |
| Серебро | 0.016 | 0.0041 |
| Золото | 0.023 | 0.004 |
| Платина | 0.107 | 0.0039 |
| Магний | 0.044 | 0.0039 |
| Цинк | 0.059 | 0.0042 |
| Олово | 0.12 | 0.0044 |
| Вольфрам | 0.055 | 0.005 |
| Никель | 0.087 | 0.0065 |
| Никель | 0.42 | 0.0001 |
| Нихром | 1.1 | 0.0001 |
| Фехраль | 1.25 | 0.0002 |
| Хромала | 1.4 | 0.0001 |
Программное обеспечение I&C Программа использует следующие входные и выходные параметры и их единицы измерения для расчета свойств электрического проводника:
- Вещество, из которого изготовлен проводник (см. таблицу 1)
- Длина проводника. мм, см, м, км, дюймы, футы, ярды
- Температура проводника. °C, °F
- Диаметр проводника. мм
- Площадь поперечного сечения проводника. мм², кКмлkcmil – одна тысяча окружных миль = 0,5067 мм².
- Сопротивление проводника. Ом, кОм, МОм.
На следующих рисунках показаны снимки экрана модулей Программные модули I&C программные модули для расчета параметров проводника.
Рисунок 1 Рисунок 2 Рисунок 3
Ответ: два параллельных проводника с токами, текущими в одном направлении, фактически притягиваются друг к другу.
Как найти длину проводника
Автор Ольга Громышева задал вопрос в категории Естественные науки Какая формула для нахождения длины проводника? и получил лучший ответ
Ответ от Crabochka и формула – R=p*L /S. Отсюда мы вычисляем L
Детально проверьте непрерывность тока и падения напряжения.
Найти длину проводника очень просто – достаточно измерить ее. Однако, если проводник недоступен или очень длинный, измерить его напрямую может быть очень сложно.
– строительная рулетка; – амперметр (тестер); – штангенциркуль; – таблица проводимости металла.
Чтобы определить длину проводника, измерьте длину каждой секции с помощью измерительной ленты и сложите их. Этот метод подходит для открытой проводки и для измерения проводников во временных кабельных соединениях.
Если проводка скрыта, используйте подходящую схему проводки, чтобы найти точную длину проводов. Если схема проводки отсутствует, попытайтесь косвенно восстановить расположение проводки по расположению розеток, выключателей, распределительных коробок и т.д.
Важным правилом для электриков является то, что все провода должны быть проложены горизонтально или вертикально. Однако горизонтальные участки проводки обычно проходят вдоль верхнего края стены (под потолком).
Однако определить фактическое положение проводов может только специальный прибор или опытный электрик.
Если невозможно проследить трассу скрытого электрического кабеля, необходимо измерить электрическое сопротивление отдельных участков кабеля. Сечение провода и материал, из которого он изготовлен, также должны быть включены в расчет. Обычно это медь или алюминий. Поскольку формула для расчета сопротивления – R = ? * L * s, длина проводника может быть рассчитана по формуле:
Где: L – длина проводника, R – сопротивление проводника, ? – удельное сопротивление материала проводника, s – площадь поперечного сечения проводника.
При расчете длины проводника необходимо учитывать следующие параметры и коэффициенты.
Удельное сопротивление медного провода составляет 0,0154 – 0,0174 Ом, алюминиевого провода – 0,0174 Ом: 0,0262 – 0,0278 Ом. (Если длина проволоки 1 метр, а поперечное сечение 1 мм)?
Площадь поперечного сечения проводника равна:
Где: ? – pi приблизительно равен 3,14, а D – диаметр проволоки (который легко измерить штангенциркулем).
Если проволока намотана, определите длину одного витка и умножьте на количество витков.
Если катушка имеет круглое сечение, измерьте диаметр катушки (средний диаметр катушки, если это многослойная катушка). Затем умножьте диаметр на число “пи” и на количество витков:
d – диаметр катушки, n – число витков провода.
Удельное сопротивление – это свойство материала, из которого изготовлен проводник.
Электрическое сопротивление проводника прямо пропорционально произведению сопротивления материала проводника и его длины и обратно пропорционально площади его поперечного сечения.
| электрическое сопротивление проводника, | ом |
| удельное сопротивление материала проводника, | ом-м |
| длина проводника, | счетчик |
| поперечное сечение проводника | метр2 |
Единица удельного сопротивления в СИ
Удельное сопротивление ρ зависит от температуры.




Расчет площади поперечного сечения кабельной продукции в зависимости от токовой нагрузки необходим для дальнейшей защиты от перегрева. Когда через кабели проходит слишком большой электрический ток по отношению к их площади поперечного сечения, изоляционный слой может быть поврежден и расплавиться.
Приводные устройства
Преобразование ватт в амперы и наоборот является относительным, поскольку это разные единицы измерения. Амперы – это физическая мера электрического тока, т.е. скорость, с которой ток течет по кабелю. Ватты – это мера электрической мощности, т.е. скорости потребления электроэнергии. Однако этот перевод необходим для расчета соответствия значения тока значению его силы.
Отношение к другим единицам СИ
Что такое амперы с точки зрения соотношения между электрическими единицами, можно увидеть на примерах:
- При силе тока в 1 ампер (A) через поперечное сечение проводника за одну секунду проходит заряд в 1 кулон (Cl);
- Если к пластинам конденсатора с емкостью 1 Ф приложить ток силой 1 ампер, напряжение на пластинах увеличится на 1 В в секунду;
- Мощность гальванических источников и батарей измеряется в ампер-часах (А*ч, или A*h), 1 А*ч = 3660 К, это количество электричества, которое проходит через проводник за 1 час;
- Максимальная кажущаяся мощность (в ваттах) выпрямителей или источников питания, вторая по важности характеристика этих источников, обозначается B*A;
- Количество электричества в ударе молнии составляет около 500 килоампер (1 кА = 10³ A);
- Лампочка мощностью 0,1 киловатт (кВт) потребляет ток 0,5 А.
Число ампер обозначено на корпусах автоматических выключателей и предохранителей.
Преобразование ампер в ватты и киловатты
Знание того, как рассчитать соотношение ампер и ватт, необходимо для того, чтобы определить, какой прибор способен выдержать мощность подключаемых потребителей. К таким устройствам относятся защитные устройства или распределительные устройства.
Перед выбором автоматического выключателя или устройства защитного отключения (УЗО) необходимо рассчитать потребляемую мощность всех подключаемых электроприборов (утюг, лампа, стиральная машина, компьютер и т.д.). Кроме того, зная, о каком предохранителе или автоматическом выключателе идет речь, можно определить, какие устройства могут справиться с нагрузкой, а какие нет.
Чтобы перевести амперы в киловатты и наоборот, существует формула: I=P/U, где I – амперы, P – ватты и U – вольты. Вольт – это напряжение в сети. В бытовых помещениях используется однофазное сетевое напряжение 220 вольт. На заводе для подключения промышленного оборудования используется трехфазное сетевое напряжение 380 вольт. Исходя из этой формулы, зная амперы, можно рассчитать их соответствие ваттам и наоборот – перевести ватты в амперы.
Ситуация: имеется автоматический выключатель. Технические параметры: номинальный ток 25 A, 1-полюсный. Необходимо рассчитать мощность устройств, которые может обслуживать автоматический выключатель.
Самый простой способ – ввести технические данные в калькулятор и рассчитать мощность. Можно также использовать формулу I=P/U, получим: 25A=xW/220V.
Для перевода из ватт в киловатты необходимы следующие показатели мощности в ваттах:
- 1000 Вт = 1 кВт,
- 1 000 000 ватт = 1 000 кВт = 1 000 мегаватт,
- 1000 000 000 ватт = 1000 МВт = 1000000 кВт и т.д.
Таким образом, 5500 Вт = 5,5 кВт. Ответ: Автоматический выключатель, рассчитанный на 25 А, может выдержать нагрузку всех электроприборов общей мощностью 5,5 кВт, не более.
На основе формулы с данными напряжения и тока выберите тип кабеля в соответствии с мощностью и током. В таблице показана зависимость тока от сечения кабеля:
Медные провода и кабелиСечение жил, мм²Медные провода, кабели
| Напряжение 220 В | Напряжение 380 В | |||
| Ток, A | Мощность, кВт | Ток, A | Мощность, кВт | |
| 1,5 | 19 | 4,1 | 16 | 10,5 |
| 2,5 | 27 | 5,9 | 25 | 16,5 |
| 4 | 38 | 8,3 | 30 | 19,8 |
| 6 | 46 | 10,1 | 40 | 26,4 |
| 10 | 70 | 15,4 | 50 | 33 |
| 16 | 85 | 18,7 | 75 | 49,5 |
| 25 | 115 | 25,3 | 90 | 59,4 |
| 35 | 135 | 29,7 | 115 | 75,9 |
| 50 | 175 | 38,5 | 145 | 95,7 |
| 70 | 215 | 47,3 | 180 | 118,8 |
| 95 | 260 | 57,2 | 220 | 145,2 |
| 120 | 300 | 66 | 260 | 171,6 |
Преобразование из ватт в амперы
Преобразование ватт-ампер необходимо, если нужно установить защитное устройство и выбрать, на какой ток оно должно быть настроено. В инструкции по эксплуатации указано, сколько ватт потребляет бытовой прибор, подключенный к однофазной сети.
Задача – рассчитать, сколько ампер в ваттах или какая электрическая розетка подходит для подключения, если микроволновая печь потребляет 1,5 кВт. Для упрощения расчетов лучше перевести киловатты в ватты: 1,5 кВт = 1500 Вт. Подставьте значения в формулу и получите: 1500 ВТ / 220 В = 6,81 А. Округлив значения в большую сторону, получаем 1500 Вт в пересчете на амперы – ток потребления УВЧ составляет не менее 7 А.
Если к одному защитному устройству одновременно подключено несколько устройств, сложите все значения потребляемого тока, чтобы подсчитать, сколько ампер в ваттах. Например, в комнате имеется освещение с 10 светодиодными лампами по 6 Вт каждая, утюг мощностью 2 кВт и телевизор мощностью 30 Вт. Во-первых, все значения нужно перевести в ватты, получится:
- 6*10= 60 ватт,
- утюг мощностью 2 кВт = 2000 Вт,
- телевизор 30 Вт.
Теперь мы можем преобразовать амперы в ватты, для этого подставим значения в формулу 2090/220 В = 9,5 А
10 A. Ответ: Потребляемый ток составляет около 10 А.
Вы должны знать, как перевести амперы в ватты без калькулятора. В таблице показано количество потребляемой электроэнергии для однофазной и трехфазной сети.
- Расчет электрической печи: важные моменты проектирования. Методика расчета печи с формулами и допусками.
- Конструкция и оболочка кабеля из сшитого полиэтилена. Секторные или круглые проводники, в зависимости от того, что лучше.
- Электричество. Сила электричества.
- Температурная зависимость сопротивления проводника – Основы электроники.
- Электрическое сопротивление в зависимости от сечения, длины и материала проводника – Основы электроники.
- Сечение кабеля – как выбрать в зависимости от силы тока или мощности.
- Намотка индукторов.
Как определить длину проводника если известно напряжение силы тока, удельные сопротивления, и сечение проводника
Егор Фёдоров
Знаток
(400),
закрыт
9 лет назад
Как определить длину проводника если известно напряжение силы тока, удельные сопротивления, и сечение проводника
Алексей Бараев
Гений
(69534)
11 лет назад
Такой физической величины, как “напряжение силы тока” в природе не существует.
Зная силу тока (I), текущего по проводнику и напряжение (U) на концах проводника можем определить его общее сопротивление по закону Ома: I=U/R –> R=U/I
Общее сопротивление проводника связано с его удельным сопротивлением, длиной и сечением формулой:
R= r*l / S, отсюда длина l = RS / r, где S – сечение, r – удельное сопротивление (обычно обозначается греч. буковой “ро”), l – длинна
In electrical engineering, electrical length is a dimensionless parameter equal to the physical length of an electrical conductor such as a cable or wire, divided by the wavelength of alternating current at a given frequency traveling through the conductor.[1][2][3] In other words, it is the length of the conductor measured in wavelengths. It can alternately be expressed as an angle, in radians or degrees, equal to the phase shift the alternating current experiences traveling through the conductor.[1][3]
Electrical length is defined for a conductor operating at a specific frequency or narrow band of frequencies. It is determined by the construction of the cable, so different cables of the same length operating at the same frequency can have different electrical lengths. A conductor is called electrically long if it has an electrical length much greater than one; that is it is much longer than the wavelength of the alternating current passing through it, and electrically short if it is much shorter than a wavelength. Electrical lengthening and electrical shortening means adding reactance (capacitance or inductance) to an antenna or conductor to increase or decrease the electrical length,[1] usually for the purpose of making it resonant at a different resonant frequency.
This concept is used throughout electronics, and particularly in radio frequency circuit design, transmission line and antenna theory and design. Electrical length determines when wave effects become important in a circuit. Ordinary lumped element electric circuits only work well for alternating currents at frequencies for which the circuit is electrically small (electrical length much less than one). For frequencies high enough that the wavelength approaches the size of the circuit (the electrical length approaches one) the lumped element model on which circuit theory is based becomes inaccurate, and transmission line techniques must be used.[4]: p.12–14
Definition[edit]
Electrical length is defined for conductors carrying alternating current (AC) at a single frequency or narrow band of frequencies. An alternating electric current of a single frequency 



so 
The electrical length 



The phase velocity 

Phase shift definition[edit]
In radio frequency applications, when a delay is introduced due to a conductor, it is often the phase shift 
Significance[edit]
The electrical length of a conductor determines when wave effects (phase shift along the conductor) are important.[4]: p.12–14 If the electrical length 

Velocity factor[edit]
In a vacuum an electromagnetic wave (radio wave) travels at the speed of light 


wavelengths.
In the SI system of units, empty space has a permittivity of 


Equivalent circuit of a lossless transmission line. 

In cables and transmission lines an electrical signal travels at a rate determined by the effective shunt capacitance 

Each cycle of the alternating current takes time to charge the capacitance between the conductors, and the rate of change of the current is slowed by the series inductance of the wires; this determines the phase velocity at which the wave moves along the line. Some transmission lines consist only of bare metal conductors, if they are far away from other high permittivity materials their signals propagate at very close to the speed of light, 
where 
Most transmission lines contain a dielectric material (insulator) filling some or all of the space in between the conductors. The permittivity 






The effective permittivity 





so the phase velocity is
So the velocity factor of the line is
In many lines only a fraction of the space surrounding the line is occupied by a solid dielectric. With only part of the electromagnetic field effected by the dielectric, there is less reduction of the wave velocity. In this case an effective permittivity 
where the fill factor F expresses the effective proportion of space around the line occupied by dielectric.
In most transmission lines there are no materials with high magnetic permeability, so 


Since the electromagnetic waves travel slower in the line than in free space, the wavelength of the wave in the transmission line 



Transmission lines[edit]
| Type of line | Velocity factor κ[10] |
Velocity of signal in cm per ns |
|
|---|---|---|---|
| Parallel line, air dielectric |
.95 | 29 | |
| Parallel line, polyethylene dielectric (Twin lead) |
.85 | 28 | |
| Coaxial cable, polyethylene dielectric |
.66 | 20 | |
| Twisted pair, CAT-5 | .64 | 19 | |
| Stripline | .50 | 15 | |
| Microstrip | .50 | 15 |
Ordinary electrical cable suffices to carry alternating current when the cable is electrically short; the electrical length of the cable is small compared to one, that is when the physical length of the cable is small compared to a wavelength, say 
As frequency gets high enough that the length of the cable becomes a significant fraction of a wavelength, 
To mitigate these problems, at these frequencies transmission line is used instead. A transmission line is a specialized cable designed for carrying electric current of radio frequency. The distinguishing feature of a transmission line is that it is constructed to have a constant characteristic impedance along its length and through connectors and switches, to prevent reflections. This also means AC current travels at a constant phase velocity along its length, while in ordinary cable phase velocity may vary. The velocity factor 
Electrical length is widely used with a graphical aid called the Smith chart to solve transmission line calculations. A Smith chart has a scale around the circumference of the circular chart graduated in wavelengths and degrees, which represents the electrical length of the transmission line.
The equation for the voltage as a function of time along a transmission line with a matched load, so there is no reflected power, is
where
is the peak voltage along the line
is the angular frequency of the alternating current in radians per second
is the wavenumber, equal to the number of radians of the wave in one meter
is the distance along the line
is time
In a matched transmission line, the current is in phase with the voltage, and their ratio is the characteristic impedance 
Antennas[edit]
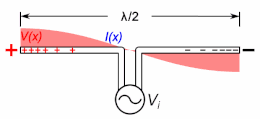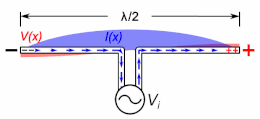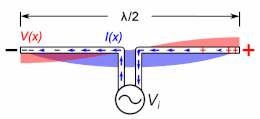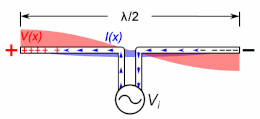
A half-wave dipole antenna showing the standing waves of voltage (red) and current (blue) on the antenna. The antenna is resonant at the frequency at which the electrical length is equal to
An important class of radio antenna is the thin element antenna in which the radiating elements are conductive wires or rods. These include monopole antennas and dipole antennas, as well as antennas based on them such as the whip antenna, T antenna, mast radiator, Yagi, log periodic, and turnstile antennas. These are resonant antennas, in which the radio frequency electric currents travel back and forth in the antenna conductors, reflecting from the ends.
If the antenna rods are not too thick (have a large enough length to diameter ratio), the current along them is close to a sine wave, so the concept of electrical length also applies to these.[3] The current is in the form of two oppositely directed sinusoidal traveling waves which reflect from the ends, which interfere to form standing waves. The electrical length of an antenna, like a transmission line, is its length in wavelengths of the current on the antenna at the operating frequency.[1][12][13][4]: p.91–104 An antenna’s resonant frequency, radiation pattern, and driving point impedance depend not on its physical length but on its electrical length.[14] A thin antenna element is resonant at frequencies at which the standing current wave has a node (zero) at the ends (and in monopoles an antinode (maximum) at the ground plane). A dipole antenna is resonant at frequencies at which it’s electrical length is a half wavelength (

Resonant frequency is important because at frequencies at which the antenna is resonant the input impedance it presents to its feedline is purely resistive. If the resistance of the antenna is matched to the characteristic resistance of the feedline, it absorbs all the power supplied to it, while at other frequencies it has reactance and reflects some power back down the line toward the transmitter, causing standing waves (high SWR) on the feedline. Since only a portion of the power is radiated this causes inefficiency, and can possibly overheat the line or transmitter. Therefore, transmitting antennas are usually designed to be resonant at the transmitting frequency; and if they cannot be made the right length they are electrically lengthened or shortened to be resonant (see below).
End effects[edit]

Reduction factor of physical length of a resonant dipole from a half-wavelength electrical length as a function of element thickness
A thin-element antenna can be thought of as a transmission line with the conductors separated,[15] so the near-field electric and magnetic fields extend further into space than in a transmission line, in which the fields are mainly confined to the vicinity of the conductors. Near the ends of the antenna elements the electric field is not perpendicular to the conductor axis as in a transmission line but spreads out in a fan shape (fringing field).[16] As a result, the end sections of the antenna have increased capacitance, storing more charge, so the current waveform departs from a sine wave there, decreasing faster toward the ends.[17] When approximated as a sine wave, the current does not quite go to zero at the ends; the nodes of the current standing wave, instead of being at the ends of the element, occur somewhat beyond the ends.[18] Thus the electrical length of the antenna is longer than its physical length.
The electrical length of an antenna element also depends on the length-to-diameter ratio of the conductor.[19][15][20][21] As the ratio of the diameter to wavelength increases, the capacitance increases, so the node occurs farther beyond the end, and the electrical length of the element increases.[19][20] When the elements get too thick, the current waveform becomes significantly different from a sine wave, so the entire concept of electrical length is no longer applicable, and the behavior of the antenna must be calculated by electromagnetic simulation computer programs like NEC.
As with a transmission line, an antenna’s electrical length is increased by anything that adds shunt capacitance or series inductance to it, such as the presence of high permittivity dielectric material around it. In microstrip antennas which are fabricated as metal strips on printed circuit boards, the dielectric constant of the substrate board increases the electrical length of the antenna. Proximity to the Earth or a ground plane, nearby grounded towers, metal structural members, guy lines and the capacitance of insulators supporting the antenna also increase the electrical length.[20]
These factors, called “end effects”, cause the electrical length of an antenna element to be somewhat longer than the length of the same wave in free space. In other words, the physical length of the antenna at resonance will be somewhat shorter than the resonant length in free space (one-half wavelength for a dipole, one-quarter wavelength for a monopole).[19][20] As a rough generalization, for a typical dipole antenna, the physical resonant length is about 5% shorter than the free space resonant length.[19][20]
Electrical lengthening and shortening[edit]
In many circumstances for practical reasons it is inconvenient or impossible to use an antenna of resonant length. An antenna of nonresonant length at the operating frequency can be made resonant by adding a reactance, a capacitance or inductance, either in the antenna itself or in a matching network between the antenna and its feedline.[20] A nonresonant antenna appears at its feedpoint electrically equivalent to a resistance in series with a reactance. Adding an equal but opposite type of reactance in series with the feedline will cancel the antenna’s reactance; the combination of the antenna and reactance will act as a series resonant circuit, so at its operating frequency its input impedance will be purely resistive, allowing it to be fed power efficiently at a low SWR without reflections.
In a common application, a monopole antenna with an electrical length shorter than a quarter-wavelength (

Conversely, an antenna longer than resonant length at its operating frequency, such as a monopole longer than a quarter wavelength but shorter than a half wavelength, will have inductive reactance. This can be cancelled by adding a capacitor of equal but opposite reactance at the feed point to make the antenna resonant. This is called electrically shortening the antenna.
Scaling properties of antennas[edit]
Two antennas that are similar (scaled copies of each other), fed with different frequencies, will have the same radiation resistance and radiation pattern and fed with equal power will radiate the same power density in any direction if they have the same electrical length at the operating frequency; that is, if their lengths are in the same proportion as the wavelengths.[22][4]: p.12–14
This means the length of antenna required for a given antenna gain scales with the wavelength (inversely with the frequency), or equivalently the aperture scales with the square of the wavelength.
Electrically short antennas[edit]
An electrically short conductor, much shorter than one wavelength, makes an inefficient radiator of electromagnetic waves. As the length of an antenna is made shorter than its fundamental resonant length (a half-wavelength for a dipole antenna and a quarter-wavelength for a monopole), the radiation resistance the antenna presents to the feedline decreases with the square of the electrical length, that is the ratio of physical length to wavelength, 

A second disadvantage is that since the capacitive reactance of the antenna and inductive reactance of the required loading coil do not decrease, the Q factor of the antenna increases; it acts electrically like a high Q tuned circuit. As a result, the bandwidth of the antenna decreases with the square of electrical length, reducing the data rate that can be transmitted. At VLF frequencies even the huge toploaded wire antennas that must be used have bandwidths of only ~10 hertz, limiting the data rate that can be transmitted.
Regimes of electromagnetics[edit]
The field of electromagnetics is the study of electric fields, magnetic fields, electric charge, electric currents and electromagnetic waves. Classic electromagnetism is based on the solution of Maxwell’s equations. These equations are mathematically difficult to solve in all generality, so approximate methods have been developed that apply to situations in which the electrical length of the apparatus is very short (



Circuit theory: When the wavelength of the electrical oscillations is much larger than the physical size of the circuit (
), say
,[26] the action occurs in the near field. The phase of the oscillations and therefore the current and voltage can be approximated as constant along the length of connecting wires. Also little energy is radiated in the form of electromagnetic waves, the power radiated by a conductor as an antenna is proportional to the electrical length squared
. So the electrical energy remains in the wires and components as quasistatic near-field electric and magnetic fields. Therefore, the approximation of the lumped element model can be used, and electric currents oscillating at these frequencies can be processed by electric circuits consisting of lumped circuit elements such as resistors, capacitors, inductors, transformers, transistors, and integrated circuits linked by ordinary wires. Mathematically Maxwell’s equations reduce to circuit theory (Kirchhoff’s circuit laws).
, Distributed-element model (microwave theory): When the wavelength of the waves is of the same order of magnitude as the size of the equipment (
), as it is in the microwave part of the spectrum, full solutions of Maxwell’s equations must be used. At these frequencies, wires are replaced by transmission lines and waveguide and lumped elements are replaced by resonant stubs, irises, and cavity resonators. Often only a single mode (wave pattern) is propagating through the apparatus, which simplifies the mathematics. A modification of circuit theory called the distributed-element model can often be used, in which extended objects are regarded as electrical circuits with capacitance, inductance and resistance distributed along their length. A graphical aid called the Smith chart is often used to analyze transmission lines.
, Optics: When the wavelength of the electromagnetic wave is much smaller than the physical size of the equipment that manipulates it (
), say
, most of the path of the waves is in the far field. In the far field, the electric and magnetic fields cannot be separated but propagate together as an electromagnetic wave. Unlike in the case of microwaves, the number of modes propagating is usually large. Since little of the energy is stored in the quasistatic (induction) electric or magnetic fields at the surface boundaries between media (called evanescent fields in optics), the concepts of voltage, current, capacitance, and inductance have little meaning and are not used, and the medium is characterized by its index of refraction
, absorption, permittivity
, permeability
, and dispersion. At these frequencies electromagnetic waves are manipulated by optical elements such as lenses, mirrors, prisms, optical filters and diffraction gratings. Maxwell’s equations can be approximated by the equations of geometrical optics.
Historically, electric circuit theory and optics developed as separate branches of physics until at the end of the 19th century James Clerk Maxwell’s electromagnetic theory and Heinrich Hertz’s discovery that light was electromagnetic waves unified these fields as branches of electromagnetism.
Definition of variables[edit]
| Symbol | Unit | Definition |
|---|---|---|
 |
meter−1 | Wavenumber of wave in conductor 
|
 |
farads / meter | Permittivity per meter of the dielectric in cable |
 |
farads / meter | Permittivity of free space, a fundamental constant |
 |
farads / meter | Effective relative permittivity per meter of cable |
 |
none | Relative permittivity of the dielectric in cable |
 |
none | Velocity factor of current in conductor 
|
 |
meter | Wavelength of radio waves in conductor |
 |
meter | Wavelength of radio waves in free space |
 |
henries / meter | Effective magnetic permeability per meter of cable |
 |
henries / meter | Permeability of free space, a fundamental constant |
 |
none | Relative permeability of dielectric in cable |
 |
none | Index of refraction of dielectric material |
 |
none | Constant = 3.14159 |
 |
radians or degrees | Phase shift of current between the ends of the conductor |
 |
radians / second | Angular frequency of alternating current 
|
 |
meters / second | Speed of light in vacuum |
 |
farads / meter | Shunt capacitance per unit length of the conductor |
 |
hertz | Frequency of radio waves |
 |
none | Fill factor of a transmission line, the fraction of space filled with dielectric |
 |
none | Electrical length of conductor |
 |
none | Electrical length of electromagnetic wave of length l in free space |
 |
meter | Length of the conductor |
 |
henrys / meter | Inductance per unit length of the conductor |
 |
second | Period of radio waves |
 |
second | time |
 |
meters / second | phase velocity of current in conductor |
 |
meter | distance along conductor |
References[edit]
- ^ a b c d e f
“Electrical length”. ATIS Telecom Glossary. Alliance for Telecommunications Industry Solutions website. 2019. Retrieved 24 December 2022. ANSI (American National Standards Institute) accredited definition - ^ a b Kaiser, Kenneth L. (2004). Electromagnetic Compatibility Handbook. CRC Press. pp. 3.1–3.2. ISBN 9780849320873.
- ^ a b c d Weik, Martin (2012). Communications Standard Dictionary. Springer. p. 283. ISBN 9781461304296.
- ^ a b c d e f g Schmitt, Ron (2002). Electromagnetics Explained: A Handbook for Wireless RF, EMC, and High-Speed Electronics. Newnes. ISBN 9780750674034.
- ^ a b c d e f g h i Paul, Clayton R. (2011). Transmission Lines in Digital and Analog Electronic Systems. Wiley. pp. 6–11. ISBN 9781118058244.
- ^ a b Drollinger, Francis J. (1980). Ground Radio Communications Specialist: Vol. 7 – Auxiliary circuits and systems. US Air Force Technical Training School. pp. 16–18.
- ^ Rao, R. S. (2012). Electromagnetic Waves and Transmission Lines. PHI Learning. p. 445. ISBN 9788120345157.
- ^ Carr, Joseph J. (1997). Microwave & Wireless Communications Technology. Newnes. p. 51. ISBN 0750697075.
- ^ Amlaner, Charles J. Jr. (March 1979). “The design of antennas for use in radio telemetry”. A Handbook on Biotelemetry and Radio Tracking: Proceedings of an International Conference on Telemetry and Radio Tracking in Biology and Medicine, Oxford, 20–22 March 1979. Elsevier. p. 260. Retrieved 23 November 2013.
- ^ Keller, Reto B. (2022). Design for Electromagnetic Compatibility-In a Nutshell. Springer International. p. 39. ISBN 9783031141867.
- ^ Keller, Reto (2018). “Chapter 5: Transmission lines”. Electromagnetic compatibility knowledge base. Academy of EMC website. Retrieved 24 December 2022.
- ^ a b Radioman 3 & 2, US Navy Training Course NAVPERS 10228-E. Bureau of Naval Personnel, US Navy. 1967. p. 131.
- ^ Singh, Yaduvir (2011). Electro Magnetic Field Theory. Dorling Kindersley. p. 451. ISBN 9788131760611.
- ^ Griffith, B. Whitfield (2000). Radio-electronic Transmission Fundamentals. Noble Publishing. pp. 335–337. ISBN 9781884932137.
- ^ a b US Air Force Manual 52-19: Antenna Systems. US Air Force. 1953. pp. 104–105.
- ^ Schelkunoff, Sergei A.; Friis, Harold T. (1952). Antennas: Theory and Practice. John Wiley and Sons. p. 245.
- ^ Rudge, Alan W.; Milne, K. (1982). The Handbook of Antenna Design, Vol. 2. IET. p. 564. ISBN 9780906048870.
- ^ The effect of this on the antenna is equivalent to the current wave moving along the antenna at a phase velocity
lower than the speed of light
, as in a transmission line, and some sources explain it this way. However, this is not a physically correct description
- ^ a b c d Lewis, Geoff (2013). Newnes Communications Technology Handbook. Elsevier. p. 46. ISBN 9781483101026.
- ^ a b c d e f The A.R.R.L. Antenna Book, 5th Ed. American Radio Relay League. 1949. pp. 27–28.
- ^ Carr, Joseph (2001). Antenna Toolkit, 2nd Ed. Elsevier. pp. 52–54. ISBN 9780080493886.
- ^ Levin, Boris (2019). Wide-Range Antennas. CRC Press. p. 26. ISBN 9781351043229.
- ^ Azadeh, Mohammad (2009). Fiber Optics Engineering. Springer Science and Business Media. p. 11. ISBN 9781441903044.
- ^ Pozar, David M. (2011). Microwave Engineering, 4th Ed. Wiley Global Education. pp. 1–2. ISBN 9781118213636.
- ^ Karmel, Paul R.; Colef, Gabriel D.; Camisa, Raymond L. (1998). Introduction to Electromagnetic and Microwave Engineering. John Wiley and Sons. pp. 1–2. ISBN 9780471177814.
- ^ Clark, Alan Robert; Fourie, Andre P. C. (2001). Antennas in Practice (PDF). Poynting Innovations. p. 3. ISBN 0620276193.
Длина проводника по сопротивлению
Определить длину проводника если известно, материал, сопротивление и сечение проводника.
Общее сопротивление проводника связано с его удельным сопротивлением, длиной и сечением формулой:
R= r*l / S
отсюда длина l = RS / r,
Где:
- S – сечение проводника в мм2
- R – сопротивление проводника в Ом,
- r – удельное сопротивление (обозначается буковой “ро”)
- l – расчетная длина проводника (в метрах)
Расчет производить исходя из температуры проводника +20 °C
Поделиться в соц сетях:

Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Электрический проводник
Расчет параметров
Электрические свойства проводника в большой степени зависят от вещества из которого он сделан. Важнейшими являются:
- Удельное сопротивление вещества проводника [ρ], измеряется в Ом·м в международной системе единиц (СИ). Это означает, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом.
Также довольно часто применяется внесистемная единица Ом·мм²/м.
1 Ом·мм²/м = 10 −6 Ом·м - Температурный коэффициент электрического сопротивления [α], характеризует зависимость электрического сопротивления от температуры и измеряется в Кельвин в минус первой степени K −1 . Это величина, равная относительному изменению удельного ⁄ электрического сопротивления вещества при изменении температуры на единицу. Расчет удельного сопротивления ρt при произвольной температуре t производится по классической формуле (1):
ρt — удельное сопротивление при температуре t
t — температура
ρ20 — удельное сопротивление при температуре 20°C
α — температурный коэффициент сопротивления
Формула применима в небольшом диапазоне температур: от 0 до 100 °C. Вне этого диапазона или для точных результатов применяют более сложные вычисления.
Ниже приведена таблица наиболее популярных металлов для изготовления проводников, с их удельными сопротивлениями и температурными коэффициентами электрического сопротивления. Данные таблицы взяты из различных источников. Следует обратить внимание на то, что и удельное сопротивление проводника, и его температурный коэффициент электрического сопротивления зависят от чистоты металла, а в случае сплавов (сталь) могут существенно отличаться от марки к марке.
| Таблица 1 | ||
| Металл | Удельное сопротив ление [ρ] при t = 20 °C, Ом·мм²/м |
Температурный коэффициент электрического сопротивления [α], K −1 |
| Медь | 0.0175 | 0.0043 |
| Алюминий | 0.0271 | 0.0039 |
| Сталь | 0.125 | 0.006 |
| Серебро | 0.016 | 0.0041 |
| Золото | 0.023 | 0.004 |
| Платина | 0.107 | 0.0039 |
| Магний | 0.044 | 0.0039 |
| Цинк | 0.059 | 0.0042 |
| Олово | 0.12 | 0.0044 |
| Вольфрам | 0.055 | 0.005 |
| Никель | 0.087 | 0.0065 |
| Никелин | 0.42 | 0.0001 |
| Нихром | 1.1 | 0.0001 |
| Фехраль | 1.25 | 0.0002 |
| Хромаль | 1.4 | 0.0001 |
Программа КИП и А при вычислении свойств электрического проводника оперирует со следующими входными ⁄ выходными параметрами и их единицами измерения:
- Вещество, из которого изготовлен проводник (Смотрите таблицу 1)
- Длина проводника. мм, см, м, км, дюймы, футы, ярды
- Температура проводника. °C, °F
- Диаметр проводника. мм
- Сечение проводника. мм², kcmil
kcmil — тысяча круговых мил = 0.5067 мм² - Сопротивление проводника. Ом, кОм, МОм
Ниже, на рисунках представлены скриншоты модулей программы КИП и А по расчету параметров проводника.
Расчет сопротивления электрического проводника
Сопротивление электрического проводника рассчитываем по формуле:
- R — сопротивление электрического проводника
- ρ — удельное сопротивление проводника
вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)]- ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
- L — длина электрического проводника
- S — сечение электрического проводника
Расчет длины электрического проводника
Длину электрического проводника рассчитываем по формуле:
- L — длина электрического проводника
- R — сопротивление электрического проводника
- S — сечение электрического проводника
- ρ — удельное сопротивление проводника
вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)]- ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
Расчет сечения электрического проводника
Минимальное сечение электрического проводника при допустимых потерях напряжения рассчитываем по формуле:
S = I * ρ * L / ΔU
- S — сечение электрического проводника
- I — сила тока в электрической цепи
- L — длина электрического проводника
при двухпроводной линии, длина проводника (значение L) удваивается - ΔU — допустимые потери напряжения
- ρ — удельное сопротивление проводника
вычисляется по формуле (1): ρ = ρ20[1 + α(t — 20)]- ρ20 — удельное сопротивление проводника при температуре t = 20°C (Таблица 1)
- t — температура проводника
- α — температурный коэффициент электрического сопротивления (Таблица 1)
Источник
Как найти длину проводника формула через силу тока
Как найти длину провода зная плотность
Как найти длину проводника
Найти длину проводника очень просто – достаточно его измерить. Однако, если проводник недоступен или имеет очень большую длину, то его непосредственное измерение может оказаться весьма затруднительным. Статьи по теме:
Инструкция 1 Чтобы найти длину проводника, измерьте рулеткой длины его отдельных участков и сложите их. Этот метод подходит для открытой электропроводки и замеров провода во временных кабельных соединениях. 2 Если электропроводка скрытая, то для нахождения точной длины проводника воспользуйтесь соответствующей электромонтажной схемой. Если таковой схемы нет, то попробуйте косвенно восстановить размещение проводов по положению розеток, выключателей, распределительных коробок и т.п. признакам. 3 Учтите важное правило электромонтажников: все провода должны прокладываться строго горизонтально или вертикально. Причем, горизонтальные участки провода, как правило, проходят вдоль верхнего края стены (под потолком). Однако, действительное расположение проводов сможет определить только специальный прибор или опытный электрик. 4 Если восстановить траекторию скрытой электропроводки невозможно, то измерьте электрическое сопротивление отдельных участков проводника. Для расчетов уточните также сечение проволоки и материал, из которого она состоит. Как правило, это – медь или алюминий. Так как формула для расчета сопротивления: R = ρ * L * s, то длину проводника можно рассчитать по формуле:L = R / ρs,где: L – длина проводника,R – сопротивление проводника,ρ – удельное сопротивление материала из которого сделан проводник,s – площадь поперечного сечения проводника. 5 При расчете длины проводника учтите следующие параметры и соотношения.Удельное сопротивление медного провода составляет 0,0154 — 0,0174 ом, алюминиевого: 0,0262 — 0,0278 ом.(Если длина проводника равна 1 метру, а сечение – 1 мм²).Сечение проводника равняется:s = π/4 * D²,где: π — число «пи», приблизительно равное 3,14,D – диаметр проволоки (который легко замерить штангенциркулем). 6 Если провод смотан в катушку, то определите длину одного витка и умножьте на количество витков. Если катушка имеет круглое сечение, то измерьте диаметр катушки (средний диаметр обмотки, если она многослойная). Затем умножьте диаметр на число «пи» и на количество витков:L = d * π * n,где:d –диаметр катушки,n – количество витков провода. Статьи по теме:





Примеры
Покажем на простых примерах, как решать задачи на вычисление силы тока по формуле.

Решение: При параллельном соединении нагрузочных элементов U = const, то есть, напряжение одинаково на всех резисторах и составляет 100 В. Тогда, по закону Ома I = U/R
Для вычисления искомого параметра на всем участке цепи, нам необходимо знать общее сопротивление этого участка. Учитывая тот факт, что при параллельном соединении нагрузочных элементов в цепи их общее сопротивление равно:
Имеем: 1/R= 1/5 + 1/25 + 1/50 = 13/50; R = 50/13 ≈ 3.85 (Ом)
Тогда: I = U/R = 100 В/3,85 Ом ≈26 А.
- Сила тока на сопротивлениях: I1 =20 А; I2 = 4А; I3 = 2 А.
- Сила тока, поступающего на рассматриваемый участок цепи равна 26 А.
Воспользуемся формулой для нахождения силы тока, включающей напряжение и мощность: I = P/U.
- 2 кВт преобразим в ватты: 2 кВт = 2000 Вт.
- Подставляем данные: I = 2 000 Вт/ 220 В ≈ 9 А
- Ответ: Нагревательный элемент электрочайника рассчитан на 9 А.
Применяя закон Ома для полной цепи, запишем: I = ε / (R+r′)
Ответ: сила тока 1 А.
За время t электричество выполнит работу A = U*I*t.
Напряжение сети известно – оно составляет 220 В.Силу тока находим по формуле: I = U/R, тогда A = (U 2 /R)*t или
A = ((220 В) 2 / 40 Ом) * 2 ч = 2420 Втч = 2,42 кВтч
Ответ: За 2 часа работы электроплита потребляет 2,42 кВт часов электроэнергии.
Применяя формулы для вычисления параметров электричества, пользуясь фундаментальными законами физики можно находить неизвестные данные для составных элементов цепей и электроприборов с целью оценки их состояния. В каждом отдельном случае необходимо определить известные параметры тока, которые можно использовать в дальнейших вычислениях. Обычно, это напряжение, мощность или сопротивление нагрузки.
«Протоптанные» пути вычислений
Все существующие расчетные способы опираются на выведенный Омом закон, согласно которому сила тока, помноженная на напряжение, равняется мощности. Бытовое напряжение – величина постоянная, равная в однофазной сети стандартным 220 В. Значит, в легендарной формуле остаются лишь две переменные: это ток с мощностью. «Плясать» в расчетах можно и нужно от одной из них. Через расчетные значения тока и предполагаемой нагрузки в таблицах ПУЭ найдем требующийся размер сечения.
Обратите внимание, что сечение кабеля рассчитывают для силовых линий, т.е. для проводов к розеткам. Линии освещения априори прокладывают кабелем с традиционной величиной площади сечения 1,5 мм².

Если в обустраиваемом помещении нет мощного диско-прожектора или люстры, требующей питания в 3,3кВт и больше, то увеличивать площадь сечения жилы осветительного кабеля не имеет смысла. А вот розеточный вопрос – дело сугубо индивидуальное, т.к. подключать к одной линии могут такие неравнозначные тандемы, как фен с водонагревателем или электрочайник с микроволновкой.
Тем, кто планирует нагрузить силовую линию электрической варочной поверхностью, бойлером, стиральной машиной и подобной «прожорливой» техникой, желательно распределить всю нагрузку на несколько розеточных групп.

Если технической возможности разбить нагрузку на группы нет, бывалые электрики рекомендуют без затей прокладывать кабель с медной жилой сечением 4-6 мм². Почему с медной токоведущей сердцевиной? Потому что строгим кодексом ПУЭ прокладка кабеля с алюминиевой «начинкой» в жилье и в активно используемых бытовых помещениях запрещена. Сопротивление у электротехнической меди гораздо меньше, тока она пропускает больше и не греется при этом, как алюминий. Алюминиевые провода используются при устройстве наружных воздушных сетей, кое-где они еще остались в старых домах.
Обратите внимание! Площадь сечения и диаметр жилы кабеля – вещи разные. Первая обозначается в квадратных мм, второй просто в мм. Главное не перепутать!
Для поиска табличных значений мощности и допустимой силы тока можно пользоваться обоими показателями. Если в таблице указан размер площади сечения в мм², а нам известен только диаметр в мм, площадь нужно найти по следующей формуле:
Физический смысл сопротивления
Протекание электрического тока через проводник приводит к направленному движению свободных электронов. Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева , а именно из электронной конфигурации элемента. Электроны начинают ударяться о кристаллическую решетку элемента и передают энергию последней. В этом случае возникает тепловой эффект при действии тока на проводник.
При этом взаимодействии они замедляются, но затем под действием электрического поля, которое их ускоряет, начинают двигаться с той же скоростью. Электроны сталкиваются огромное количество раз. Этот процесс и называется сопротивлением проводника.
Следовательно, электрическим сопротивлением проводника считается физическая величина, характеризующая отношение напряжения к силе тока.
Что такое электрическое сопротивление: величина, указывающая на свойство физического тела преобразовывать энергию электрическую в тепловую, благодаря взаимодействию энергии электронов с кристаллической решеткой вещества. По характеру проводимости различаются:
- Проводники (способны проводить электрический ток, так как присутствуют свободные электроны).
- Полупроводники (могут проводить электрический ток, но при определенных условиях).
- Диэлектрики или изоляторы (обладают огромным сопротивлением, отсутствуют свободные электроны, что делает их неспособными проводить ток).
Обозначается эта характеристика буквой R и измеряется в Омах (Ом). Применение этих групп веществ является очень значимым для разработки электрических принципиальных схем приборов.
Для полного понимания зависимости R от чего-либо нужно обратить особое внимание на расчет этой величины.
Расчет размера сечения по нагрузке
Простейший способ подбора кабеля с нужным размером — расчет сечения провода по суммарной мощности всех подключаемых к линии агрегатов.
Алгоритм расчетных действий следующий:
- для начала определимся с агрегатами, которые предположительно могут использоваться нами одновременно. Например, в период работы бойлера нам вдруг захочется включить кофемолку, фен и стиралку;
- затем согласно данным техпаспортов или согласно приблизительным сведениям из приведенной ниже таблицы банально суммируем мощность одновременно работающих по нашим планам бытовых агрегатов;
- предположим, что в сумме у нас вышло 9,2 кВт, но конкретно этого значения в таблицах ПУЭ нет. Значит, придется округлить в безопасную большую сторону – т.е. взять ближайшее значение с некоторым превышением мощности. Это будет 10,1 кВт и соответствующее ему значение сечения 6 мм².
Все округления «направляем» в сторону увеличения. В принципе суммировать можно и силу тока, указанную в техпаспортах. Расчеты и округления по току производятся аналогичным образом.

Как рассчитать сечение по току?
Табличные значения не могут учесть индивидуальных особенностей устройства и эксплуатации сети. Специфика у таблиц среднестатистическая. Не приведены в них параметры максимально допустимых для конкретного кабеля токов, а ведь они отличаются у продукции с разными марками. Весьма поверхностно затронут в таблицах тип прокладки. Дотошным мастерам, отвергающим легкий путь поиска по таблицам, лучше воспользоваться способом расчета размера сечения провода по току. Точнее по его плотности.
Допустимая и рабочая плотность тока
Начнем с освоения азов: запомним на практике выведенный интервал 6 — 10. Это значения, полученные электриками многолетним «опытным путем». В указанных пределах варьирует сила тока, протекающего по 1 мм² медной жилы. Т.е. кабель с медной сердцевиной сечением 1 мм² без перегрева и оплавления изоляции предоставляет возможность току от 6 до 10 А спокойно достигать ожидающего его агрегата-потребителя. Разберемся, откуда взялась и что означает обозначенная интервальная вилка.
Согласно кодексу электрических законов ПУЭ 40% отводится кабелю на неопасный для его оболочки перегрев, значит:
- 6 А, распределенные на 1 мм² токоведущей сердцевины, являются нормальной рабочей плотностью тока. В данных условиях проводник работать может бесконечно долго без каких-либо ограничений по времени;
- 10 А, распределенные на 1 мм² медной жилы, протекать по проводнику могут краткосрочно. Например, при включении прибора.
Потоку энергии 12 А в медном миллиметровом канале будет изначально «тесно». От тесноты и толкучки электронов увеличится плотность тока. Следом повысится температура медной составляющей, что неизменно отразиться на состоянии изоляционной оболочки.

Обратите внимание, что для кабеля с алюминиевой токоведущей жилой плотность тока отображает интервал 4 – 6 Ампер, приходящийся на 1 мм² проводника.
Выяснили, что предельная величина плотности тока для проводника из электротехнической меди 10 А на площадь сечения 1 мм², а нормальные 6 А. Следовательно:
- кабель с жилой сечением 2,5 мм² сможет транспортировать ток в 25 А всего лишь несколько десятых секунды во время включения техники;
- он же бесконечно долго сможет передавать ток в 15А.
Общие сведения
Электрический ток — это направленное движение носителей зарядов под действием электромагнитной силы. Природа его появления связана со структурой тела. При комнатной температуре энергетическое состояние вещества можно описать как равновесное. Тела состоят из молекул и атомов. В свою очередь, в состав последних входят протоны, нейтроны. Они образуют ядро, вокруг которого по орбитали вращаются отрицательно заряженные частицы — электроны.
Молекула или атом имеют нейтральный заряд. Это связано с тем, что количество электронов равняется числу протонов. Если же к телу приложена внешняя сила, например, электромагнитное поле, деформирование, нагрев, то отрицательные частицы могут получит дополнительную энергию. В результате межатомные связи нарушатся, а электроны покинут орбитали, став свободными. Под действием силы их движение станет упорядоченным — возникнет ток.

Кроме этого, в структуре тела могут существовать и несвязанные электроны. Их происхождение связано с примесями в веществах, дефектами структуры. По сути, они также являются свободными. В равновесном состоянии их движение беспорядочное и обусловлено тепловыми колебанием. В зависимости от числа свободных частиц, которые могут участвовать в переносе заряда, все тела делятся на два больших класса:
- Диэлектрики — непроводники электрического тока, характеризуются способностью к поляризации. Межатомные связи довольно прочны. В структуре практически нет свободных электронов. Например, чистая вода, полимеры, резина.
- Проводники — вещества, содержащие большое количество зарядов, способных перемещаться, образовывая ток. Например, металлы, углерод.
Существует ещё класс, расположенный между диэлектриками и проводниками, называют его полупроводники. Главное его отличие — это высокая зависимость степени электропроводности от температуры и числа примесей. Причём полупроводнику свойственны характеристики и диэлектрика, и проводника.
С точки зрения электричества, тела характеризуются двумя свойствами: величиной электропроводности и сопротивлением. Эти два параметра обратно пропорциональны друг другу. Так, вычисление их значений позволяет определить, к какому типу относится то или иное вещество. Проводники характеризуются малым значением сопротивления и высокой электропроводностью, а диэлектрики — наоборот.
Какой кабель лучше купить?
Следуя жестким рекомендациям ПУЭ, покупать для обустройства личной собственности будем кабельную продукцию с «литерными группами» NYM и ВВГ в маркировке. Именно они не вызывают нареканий и придирок со стороны электриков и пожарников. Вариант NYM – аналог отечественных изделий ВВГ.

Лучше всего, если отечественный кабель будет сопровождать индекс НГ, это означает, что проводка будет пожароустойчивой. Если предполагается прокладывать линию за перегородкой, между лагами или над подвесным потолком, купите изделия с низким дымовыделением. У них будет индекс LS.

Вот таким нехитрым способом рассчитывается сечение токопроводящей жилы кабеля. Сведения о принципах вычислений помогут рационально подобрать данный важный элемент электросети. Необходимый и достаточный размер токоведущей сердцевины обеспечит питанием домашнюю технику и не станет причиной возгорания проводки.
Источник















