От двух до пяти, Или о равных отрезках в трапеции
Наш разговор посвящен равным отрезкам в трапеции. Некоторые из этих отрезков весьма знамениты, с другими мы где-то (возможно, на олимпиадах) встречались. Третьи и вовсе могут нам показаться незнакомыми. Но все вместе они являют любопытную коллекцию важных, полезных, подчас непростых задач. В основном нас ожидают встречи с двумя и тремя равными отрезками, но в целом их насчитывается от двух до пяти. Итак, начинаем!..
Задача 1. Докажите, что x = y, где EF ![]() AD (рис. 1).
AD (рис. 1).
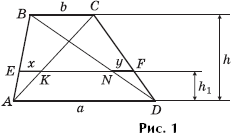
Доказательство. Треугольники AEK и ABC подобны и
![]() (1)
(1)
Аналогично, треугольники DFN и DCB подобны и
![]() (2)
(2)
Сравнив (1) и (2), получаем: x = y.
Задача 2. Покажите, что x = y, где EF ![]() AD (L — точка пересечения продолжений боковых сторон трапеции ABCD и лежит на EF (рис. 2)).
AD (L — точка пересечения продолжений боковых сторон трапеции ABCD и лежит на EF (рис. 2)).
При помощи одной линейки постройте отрезок, равный ![]()
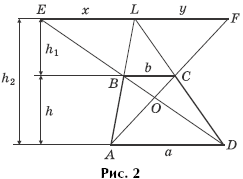
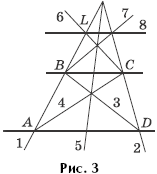
Решение. Поскольку треугольники BLE и BAD, CLF и CDA подобны, то после составления пропорций, как и в задаче 1, получим: x = y. Далее:
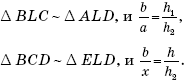 |
(3) (4) |
Сложим левые и правые части равенств (3) и (4). С учетом того, что h1 + h = h2, получим:![]() или bx + ab = ax, откуда
или bx + ab = ax, откуда ![]() Значит, отрезок EF и есть тот отрезок, который необходимо построить при помощи одной линейки. Остается показать, как через данную точку L построить прямую, параллельную двум данным
Значит, отрезок EF и есть тот отрезок, который необходимо построить при помощи одной линейки. Остается показать, как через данную точку L построить прямую, параллельную двум данным
( BC и AD), пользуясь только линейкой.
Такое построение предложено на рисунке 3 с указанием порядка проведения линий. Дополнительные комментарии представляются излишними.
Задача 3. Найдите отношение оснований трапеции ABCD, если x = y, где x = LO, y = OM (рис. 4).
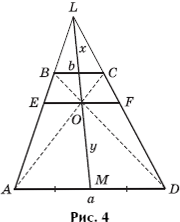
Решение. Поскольку LO = OM, то ![]() (средняя линия в треугольнике ALD). С другой стороны, EF — один из самых знаменитых отрезков в трапеции ABCD, и
(средняя линия в треугольнике ALD). С другой стороны, EF — один из самых знаменитых отрезков в трапеции ABCD, и ![]() (покажите!). Тогда имеем:
(покажите!). Тогда имеем: ![]() или 4b = a + b, откуда
или 4b = a + b, откуда ![]()
Задача 4. Под каким углом пересекаются боковые стороны трапеции, если x = y (рис. 5), где x — отрезок, соединяющий середины диагоналей, y — отрезок, соединяющий середины оснований.
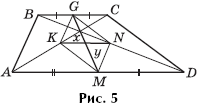
Решение. KG ![]() NM и KG = NM — они параллельны и равны
NM и KG = NM — они параллельны и равны ![]() AB как средние линии соответственно в треугольниках ABC и ABD. Значит, KGNM — параллелограмм. Но поскольку x = y, то это параллелограмм с равными диагоналями, то есть прямоугольник. Следовательно, ∠ KGN = 90°. Тогда и угол между прямыми AB и CD также равен 90°.
AB как средние линии соответственно в треугольниках ABC и ABD. Значит, KGNM — параллелограмм. Но поскольку x = y, то это параллелограмм с равными диагоналями, то есть прямоугольник. Следовательно, ∠ KGN = 90°. Тогда и угол между прямыми AB и CD также равен 90°.
Задача 5. Для оснований трапеции ABCD справедливо равенство a2 = b2 + ab. Докажите, что x = y, или BO = DN, где CK ![]() AB (рис. 6).
AB (рис. 6).
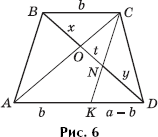
Доказательство. Равенство a2 = b2 + ab равносильно пропорции ![]() Треугольники BOC и DOA подобны, и
Треугольники BOC и DOA подобны, и ![]() Треугольники DNK и BNC подобны, и
Треугольники DNK и BNC подобны, и ![]() Поскольку
Поскольку ![]() то
то ![]() Имеем:
Имеем:
x2 + xt = y2 + yt,
или
(x – y)(x + y + t) = 0.
Однако x + y + t > 0, поэтому x = y.
Задача 6. В трапеции ABCD x = y = z, ∠ACD = 90°(рис. 7). Найдите углы трапеции.
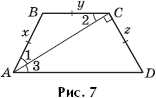
Решение. Пусть ∠1 = ∠2 = α. Тогда ∠2 = ∠3 = α
(внутренние накрест лежащие при BC ![]() AD). Значит, ∠A = ∠D = 2α. Из треугольника ACD
AD). Значит, ∠A = ∠D = 2α. Из треугольника ACD
α + 2α = 90°, откуда α = 30°.
Ответ: 60° и 120°.
Статья опубликована при поддержке интернет-сайта “ЕГЭ по математике ОНЛАЙН”. Электронный онлайн курс ЕГЭ по математике 2016 – базовый и профильный уровень, расширенный доступ бесплатно, индивидуальные рекомендации, демонстрационный вариант ЕГЭ 2015 года. Пройти тест Вы сможете на сайте, который располагается по адресу: егэ-по-математике.онлайн.
Задача 7. Пересеките трапецию ABCD прямой, параллельной основаниям так, чтобы ее отрезок, лежащий внутри трапеции, делился диагоналями на три равные части.
Решение. Пусть M — середина основания AD, AC и BD — диагонали (рис. 8). Пусть также
K = BM ∩ AC. Проведем через K прямую EF параллельно AD. При этом EK = KN = NF, или
x = y = z. Действительно, x = y, так как AM = MD,
а x = z — по задаче 1.
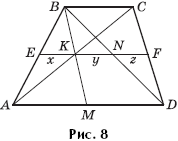
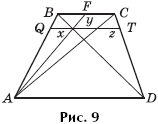
Замечание. Существуют два отрезка, отвечающих требованиям задачи. Кроме отрезка EF, это будет еще и отрезок QT (рис. 9). Он строится так же, как и отрезок EF, но берется F — середина основания BC.
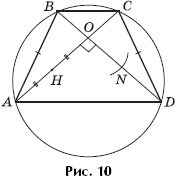
Задача 8. ABCD — равнобокая трапеция с перпендикулярными диагоналями AC и BD. Известно, что ортоцентр треугольника ABD делит пополам его высоту AO. Проведя не более одной линии, разделите диагональ BD на три равные части (рис. 10).
Решение. Поскольку трапеция равнобокая, то около нее можно описать окружность. Пусть H — ортоцентр треугольника ABD и AH = HO. C — точка, симметричная ортоцентру H относительно BD (так как она лежит на описанной окружности треугольника ABD). Тогда OC = OH = AH. Диагонали AC и BD равны. Остается из точки O раствором циркуля, равным BO, сделать засечку на диагонали BD — получим точку N. При этом BO = ON = ND.
Задача 9. Существует ли трапеция ABCD, в которой EF — средняя линия и x = y = z = t (рис. 11)?
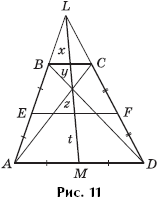
Решение. Так как EF — средняя линия трапеции ABCD, то она делит любой отрезок между основаниями трапеции пополам, то есть y + z = t. Но, согласно условию, y + z = 2t. Противоречие. Такой трапеции, где x = y = z = t, как на рисунке 11, не существует.
Задача 10. При каком отношении оснований трапеции x = y = z = t = q (рис. 12)?
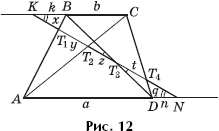
Решение. Пусть BK = k и DN = n. Равные по условию отрезки обозначим через x. Треугольники KT3B и NT3D подобны, (по двум углам). Тогда ![]()
Треугольники KT1B и NT1A подобны, и
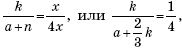
откуда ![]()
Далее, треугольники KT2C и NT2A подобны и ![]()
Имеем: ![]()
откуда ![]() Стало быть,
Стало быть, 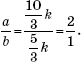
Еще несколько задач на равные отрезки в трапециях предложим вниманию читателей для самостоятельного решения.
Задача 11. Покажите, что ![]() (рис. 13).
(рис. 13).
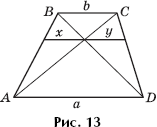
Задача 12. Диагонали трапеции делят ее среднюю линию на три равные части. Найдите отношение оснований. Ответ: 2 : 1.
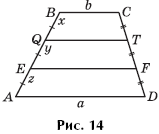
Задача 13. Основания трапеции ABCD равны a и b. EF и QT параллельны основаниям, при этом x = y = z (рис. 14). Найдите EF и QT.
Ответ: ![]()
Задача 14. При помощи одной линейки на основании AD трапеции ABCD постройте точки K и N такие, что AK = KN = ND.
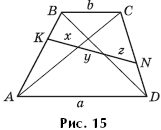
Задача 15. (Санкт-Петербургские олимпиады.) На боковых сторонах трапеции ABCD нашлись точки K и N такие, что KN не параллелен основаниям и при этом x = y = z (рис. 15).
Найдите отношение оснований.
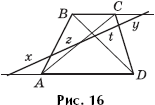
Задача 16. Дано: x = y. Докажите, что z = t (рис. 16).
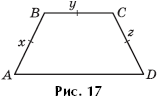
Задача 17. В трапеции ABCD x = y = z (рис. 17). При каком отношении оснований площадь трапеции будет наибольшей?
Филипповский Г.
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m – b
b = 2m – a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 – 2ad·cos β
d2 = √a2 + c2 – 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab – | a(d 2 – c2) |
| a – b |
| d2 = | √ | c2 + ab – | a(c2 – d 2) |
| a – b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a – h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a – h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab – d22
d2 = √c2 + d 2 + 2ab – d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 – | ( | (a – b)2 + c2 – d 2 | ) | 2 |
| 2 | 2(a – b) |
5. Формула Герона для трапеции
| S = | a + b | √(p – a)(p – b)(p – a – c)(p – a – d) |
| |a – b| |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p – a)(p – c)(p – d1) |
где
a – большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
25
Июл 2013
Категория: Справочные материалы
Трапеция. Свойства трапеции
2013-07-25
2016-06-15
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .

4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то

Площадь
или
где
– средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Автор: egeMax |
комментарий 431
Печать страницы
Виды трапеции
- Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
- Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне
Свойства трапеции
-
Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме
$$
FE = {AB + DC over 2}
$$ -
Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD - Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
- Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
-
Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е.
$$
KL = {DC – AB over 2}
$$ - Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности
Свойства и признаки равнобедренной трапеции

- В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
- В равнобедренной трапеции длины диагоналей равны (AC = BD)
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная
- Около равнобедренной трапеции можно описать окружность
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований
Формулы площади произвольной трапеции

Площадь трапеции через основания и высоту
$$
S = {AB + DC over 2} * AG
$$
Площадь трапеции через среднюю линию и высоту
$$
S = FE * AG
$$
Площадь трапеции через диагонали и угол между ними
$$
S = {AC * BD over 2} * sin(∠AOD) = {AC * BD over 2} * sin(∠AOB)
$$
Площадь трапеции через четыре стороны
$$
S = {DC + AB over 2} * sqrt{AD^2 – ({(DC – AB)^2 + AD^2 – BC^2 over 2 * (DC – AB)})^2}
$$
Формулы площади равнобедренной трапеции


Площадь трапеции через стороны
$$
S = {DC + AB over 2} * sqrt{AD^2 – {(DC – AB)^2 over 4}}
$$
Площадь трапеции через стороны и угол
$$
S = AD * sin(∠ADC) * (DC – AD * cos(∠ADC))
$$
$$
S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC))
$$
Площадь трапеции через диагонали и угол между ними
$$
S = {AC^2 over 2} * sin(∠AOD) = {AC^2 over 2} * sin(∠BOC)
$$
Площадь трапеции через среднюю линию, боковую сторону и угол при основании
$$
S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB)
$$
Площадь трапеции если в нее вписана окружность
$$
S = {4 * R_В^2 over sin(∠ADC)} = {4 * R_В^2 over sin(∠DAB)}
$$
$$
S = {AB * DC over sin(∠ADC)} = {AB * DC over sin(∠DAB)}
$$
Формулы сторон произвольной трапеции

Основание через другое основание и среднюю линию
$$
AB = 2 * FE – DC
$$
$$
DC = 2 * FE – AB
$$
Основание через другое основание, диагонали и угол между ними
$$
DC = {AC * BD over AG} * sin(∠AOD) – AB
$$
$$
AB = {AC * BD over AG} * sin(∠AOD) – DC
$$
Длины сторон
$$
DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
AB = DC – AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD)
$$
$$
AB = DC – AD * cos(∠ADC) – BC * cos(∠BCD)
$$
$$
AD = {AG over sin(∠ADC)}
$$
$$
BC = {AG over sin(∠BCD)}
$$
Формулы сторон равнобедренной трапеции


Длины сторон
$$
AD = {AG over sin(∠ADC)}
$$
$$
AD = {DC – AB over 2 * cos(∠ADC)}
$$
$$
DC = AB + 2 * AG * ctg(∠ADC)
$$
$$
AB = DC – 2 * AG * ctg(∠ADC)
$$
$$
DC = AB + 2 * AB * cos(∠ADC)
$$
$$
AB = DC – 2 * AB * cos(∠ADC)
$$
Длина основания через диагональ, боковую сторону и другое основание
$$
DC = {AC^2 – DA^2 over AB}
$$
$$
AB = {AC^2 – DA^2 over DC}
$$
Длина боковой стороны через диагональ и основания
$$
AD = sqrt{AC^2 – AB * DC}
$$
Длина основания через высоту, другое основание, диагонали и угол между ними
$$
DC = {AC^2 over AG} * sin(∠AOD) – AB
$$
$$
AB = {AC^2 over AG} * sin(∠AOD) – DC
$$
Длина основания через высоту, другое основание и площадь трапеции
$$
DC = {2 * S over AG} – AB
$$
$$
AB = {2 * S over AG} – DC
$$
Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
$$
AD = {S over FE * sin(∠ADC)} = {S over FE * sin(∠DAB)}
$$
Длина боковой стороны через площадь трапеции, основания и угол при основании
$$
AD = {2 * S over (AB + DC) * sin(∠ADC)}
$$
$$
AD = {2 * S over (AB + DC) * sin(∠DAB)}
$$
Формулы сторон прямоугольной трапеции

Длины оснований
$$
DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD)
$$
$$
AB = DC – BC * cos(∠BCD) = DC – AD * ctg(∠BCD)
$$
$$
DC = AB + sqrt{BC^2 – AD^2}
$$
$$
AB = DC – sqrt{BC^2 – AD^2}
$$
Длина основания через боковую сторону, другое основание, диагонали и угол между ними
$$
DC = {AC * BD over AD} * sin(∠AOD) – AB
$$
$$
AB = {AC * BD over AD} * sin(∠AOD) – DC
$$
Длина основания через площадь трапеции, другое основание и высоту
Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG)
$$
DC = {2 * S over AD} – AB
$$
$$
AB = {2 * S over AD} – DC
$$
Формулы диагоналей произвольной трапеции

Длина диагоналей через четыре стороны
$$
BD = sqrt{BC^2 + DC * AB – {DC * (BC^2 – AD^2) over DC – AB}}
$$
$$
AC = sqrt{AD^2 + DC * AB – {DC * (AD^2 – BC^2) over DC – AB}}
$$
Длина диагоналей по теореме косинусов
$$
BD = sqrt{DC^2 + BC^2 – 2 * DC * BC * cos(∠BCD)}
$$
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * AD * cos(∠ADC)}
$$
Длина диагоналей через высоту
$$
BD = sqrt{AG^2 + (DC – AG * ctg(∠BCD))^2}
$$
$$
BD = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$
$$
BD = sqrt{DC^2 + BC^2 – 2 * DC * sqrt{BC^2 – AG^2}}
$$
$$
AC = sqrt{AG^2 + (DC – AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠BCD))^2}
$$
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * sqrt{AD^2 – AG^2}}
$$
Длина диагоналей через стороны и другую диагональ
$$
BD = sqrt{AD^2 + BC^2 + 2 * DC * AB – AC^2}
$$
$$
AC = sqrt{AD^2 + BC^2 + 2 * DC * AB – BD^2}
$$
Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
$$
BD = {AG * (DC + AB) over AC * sin(∠AOD)}
$$
$$
AC = {AG * (DC + AB) over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
$$
BD = {2 * S over AC * sin(∠AOD)}
$$
$$
AC = {2 * S over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
$$
BD = {2 * FE * AG over AC * sin(∠AOD)}
$$
$$
AC = {2 * FE * AG over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Формулы диагоналей равнобедренной трапеции


Длина диагоналей через стороны
$$
AC = sqrt{AD^2 + AB * DC}
$$
Длина диагоналей по теореме косинусов
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * AD * cos(∠ADC)}
$$
$$
AC = sqrt{DC^2 + AD^2 + 2 * DC * AD * cos(∠DAB)}
$$
$$
AC = sqrt{AB^2 + AD^2 – 2 * AB * AD * cos(∠DAB)}
$$
$$
AC = sqrt{AB^2 + AD^2 + 2 * AB * AD * cos(∠ADC)}
$$
Длина диагоналей
$$
AC = sqrt{AG^2 + FE^2}
$$
$$
AC = sqrt{AG^2 + {(DC + AB)^2 over 4 }}
$$
$$
AC = sqrt{{AG * (AB + DC) over sin(∠AOD)}} = sqrt{{2 * S over sin(∠AOD)}} = sqrt{{2 * FE * AG over sin(∠AOD)}}
$$
Длина диагоналей через высоту основание и угол при основании
$$
AC = sqrt{AG^2 + (DC – AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$
Длина диагоналей через сторону и высоту
$$
AC = sqrt{DC^2 + AD^2 – 2 * DC * sqrt{AD^2 – AG^2}}
$$
Формулы диагоналей прямоугольной трапеции

$$
BD = sqrt{AD^2 + AB^2}
$$
$$
AC = sqrt{AC^2 + DC^2}
$$
Формулы средней линии произвольной трапеции

Длина средней линии через основания
$$
FE = {DC + AB over2}
$$
Длина средней линии через основание, высоту и углы при нижнем основании
$$
FE = DC – AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$
Длина средней линии через площадь и высоту
$$
FE = {S over AG}
$$
Формулы средней линии равнобедренной трапеции


Длина средней линии через основания
$$
FE = {DC + AB over2}
$$
Длина средней линии через основание, высоту и углы при нижнем основании
$$
FE = DC – AG * ctg(∠ADC) = AB + AG * ctg(∠ADC)
$$
Длина средней линии через основания, боковую сторону и высоту
$$
FE = DC – sqrt{AD^2 – AG^2} = AB + sqrt{AD^2 – AG^2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC^2 over 2 * AG} * sin(∠AOD) = {AC^2 over 2 * AG} * sin(∠AOB)
$$
Длина средней линии через площадь и боковую сторону
$$
FE = {S over AD * sin(∠ADC)}
$$
Формулы средней линии прямоугольной трапеции

Длина средней линии через основания, высоту и угол при нижнем основании
$$
FE = DC – AG * {ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠BCD) over 2}
$$
Длина средней линии через основания, боковую сторону и угол при нижнем основании
$$
FE = DC – BC * {cos(∠BCD) over 2}
$$
$$
FE = AB + BC * {cos(∠BCD) over 2}
$$
Длина средней линии через основания и боковые стороны
$$
FE = DC – {sqrt{BC^2 – AD^2} over 2}
$$
$$
FE = AB + {sqrt{BC^2 – AD^2} over 2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$
Формулы высоты произвольной трапеции

Длина высоты через четыре стороны
$$
AG = sqrt{AD^2 – ({(DC – AB)^2 + AD^2 – BC^2 over 2 * (DC – AB)})^2}
$$
Длина высоты через боковую сторону и прилегающий угол к основанию
$$
AG = AD * sin(∠ADC) = BC * sin(∠BCD)
$$
Длина высоты через диагонали и углы между ними
$$
AG = {AC * BD over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC * BD over AB + DC} * sin(∠AOB)
$$
Длина высоты через среднюю линию, диагонали и углы между ними
$$
AG = {AC * BD over 2 * FE} * sin(∠AOD)
$$
$$
AG = {AC * BD over 2 * FE} * sin(∠AOB)
$$
Длина высоты через площадь и основания
$$
AG = {2 * S over AB + DC}
$$
Длина высоты через площадь и среднюю линию
$$
AG = {S over FE}
$$
Формулы высоты равнобедренной трапеции


Длина высоты через по сторонам
$$
AG = sqrt{AD^2 – {(DC – AB)^2 over 4}}
$$
Длина высоты через боковую сторону и прилегающий угол к основанию
$$
AG = AD * sin(∠ADC)
$$
Длина высоты через основания и прилегающий угол к основанию
$$
AG = {DC – AB over 2} * tg(∠ADC)
$$
Длина высоты через диагонали и углы между ними
$$
AG = {AC^2 over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC^2 over AB + DC} * sin(∠AOB)
$$
Длина высоты через площадь и основания
$$
AG = {2 * S over AB + DC}
$$
Длина высоты через площадь и среднюю линию
$$
AG = {S over FE}
$$
Формулы боковых сторон прямоугольной трапеции

Сторона AD
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.
Сторона BC по трём сторонам
$$
BC = sqrt{AD^2 + (DC – AB)^2}
$$
Сторона BC через основания и угол ∠BCD
$$
BC = {DC – AB over cos(∠BCD)}
$$
Сторона BC через Сторону AD
$$
BC = {AD over sin(∠BCD)}
$$
Сторона BC через площадь, среднюю линию и угол ∠BCD
$$
BC = {S over FE * sin(∠BCD)}
$$
Сторона BC через площадь, основания и угол ∠BCD
$$
BC = {2 * S over (AB + DC) * sin(∠BCD)}
$$
Трапеция, ее свойства, формулы площади, высоты, сторон.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция (понятие, определение)
Видеоурок “Трапеция”
Виды трапеций
Элементы трапеции: основания, боковые стороны, средняя линия и высота
Свойства трапеции
Свойства равнобедренной трапеции
Формулы трапеции
Трапеция (понятие, определение):
Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.

Рис. 1. Трапеция
Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
@ https://youtu.be/Q4EpXexoMrM
Виды трапеций:
Равнобедренная трапеция или равнобокая трапеция – это трапеция, у которой боковые стороны равны.

Рис. 2. Равнобедренная трапеция
Прямоугольная трапеция – это трапеция, один из углов при боковой стороне которой прямой.
Прямоугольная трапеция – это трапеция, имеющая прямые углы при боковой стороне.

Рис. 3. Прямоугольная трапеция
Элементы трапеции: основания, боковые стороны, средняя линия и высота:
Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.

Рис. 4. Трапеция
AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.
AD – большее основание трапеции, BC – меньшее основание трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, называется средняя линия.

Рис. 5. Трапеция и срединная линия
Расстояние между основаниями трапеции называется высотой трапеции.

Рис. 6. Трапеция
Высота трапеции (h) определяется формулой:

где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
Свойства трапеции:
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Рис. 7. Трапеция и срединная линия
MN || BC, MN || AD,
l = (a + b) / 2
2. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.

Рис. 8. Трапеция
MN = (b – a) / 2
3. Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360° .
Сумма углов, прилежащих к боковой стороне трапеции, равна 180° .

Рис. 9. Трапеция
4. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

Рис. 9. Трапеция
5. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
 Рис. 10. Трапеция
Рис. 10. Трапеция
AB = BK
6. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Рис. 11. Трапеция
∠BAD + ∠CDA = 90°, MN = (AD – DC) / 2
7. В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.

Рис. 12. Трапеция
AB + CD = AD + BC
В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

Рис. 13. Трапеция
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).

Рис. 14. Трапеция
MN = (AB + CD) / 2,
MN = (AD + BC) / 2
8. Диагонали трапеции делят ее на 4 треугольника.
Два из них, прилежащие к основаниям, подобны.
Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.

Рис. 15. Трапеция
Треугольники BCO и AOD подобны. Коэффициент подобия треугольников (k) находится как отношение оснований трапеции. k = AD / BC. Отношение площадей этих подобных треугольников есть k2.
Треугольники ABO и CDO имеют одинаковую площадь.
9. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями.

Рис. 16. Трапеция
BC : AD = OC : AO = OB : DO
10. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c 2 + d 2
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
11. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основания трапеции, так же делит диагонали пополам.

Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия

Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия, UV – отрезок, который соединяет основания трапеции
12. Средняя линия разбивает трапецию на две трапеции, площади которых соотносятся как:

где b – большее основание трапеции, a – меньшее основание трапеции, S1 и S2 – площади образованных трапеций, в результате разделения средней линией.

Рис. 18. Трапеция
S1 – площадь трапеции MBCN,
S2 – площадь трапеции AMND
Свойства равнобедренной трапеции:
1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.
2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
3. Углы при любом основании равнобедренной трапеции равны.
4. Сумма противоположных углов равнобедренной трапеции равна 180°.
5. Длины диагоналей равнобедренной трапеции равны.
6. Вокруг равнобедренной трапеции можно описать окружность.
7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.
Формулы трапеции:
Пусть a – большее основание трапеции, b – меньшее основание трапеции, c – левая сторона трапеции, d – правая сторона трапеции, α и β – углы при нижнем основании трапеции, d1 и d2 – диагонали трапеции, m – средняя линия трапеции, h – высота трапеции, γ и δ – углы между диагоналями трапеции, S – площадь трапеции, P – периметр трапеции.
Формулы для определения сторон трапеции:
Через среднюю линию и одно из оснований трапеции:
a = 2m – b
b = 2m – a
Через высоту и углы при нижнем основании трапеции:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
Через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
Через высоту и углы при нижнем основании трапеции:

Формулы для определения средней линии трапеции:
Через длины оснований трапеции:

Через площадь и высоту трапеции:

Формулы для определения высоты трапеции:
Через сторону и прилегающий угол при нижнем основании трапеции:
h = c·sin α = d·sin β
Через диагонали трапеции и углы между ними:

Через диагонали трапеции, углы между ними и среднюю линию трапеции:

Через площадь и длины оснований трапеции:

Через площадь и длину средней линии трапеции:

Формула для определения периметра трапеции:
P = a + b + c + d
Формулы для определения площади трапеции:
Через основания и высоту трапеции:

Через среднюю линию и высоту трапеции:
S = m · h
Через диагонали трапеции и угол между ними:

Через все стороны трапеции:

С помощью формулы Герона для трапеции:

Как называется объемная трапеция?
Если трапецию изобразить в объеме, то такая фигура будет напоминать усеченную пирамиду.
В правильной усеченной пирамиде боковые грани являются равнобокими трапециями.
Квадрат
Овал
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Трапеция
Тупой угол
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Видео https://youtu.be/Q4EpXexoMrM
Коэффициент востребованности
6 463
