|
Сколько будет 10 в минус 2, 3, 4, 5, 6, 7, 8, 9 степени?
Для определения степени числа 10 нам для начала нужно разобраться с понятием степени.Например вместо записи шести одинаковх множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 (6)-где цифра 6 находится в верхнем правом углу.В нашем случае ответы будут следующими.
Zolotynka 6 лет назад Как верно было сказано, 10 в минусовой степени представляет собой единицу, которую следует разделить на 10 в искомой степени (в нашем случае во 2, 3, 4… и так до 9). Для наглядности прошу обратить внимание на следующий пример:
Здесь четко видно, что существует возможность мгновенно ответить на вопрос: сколько будет 10 в любой минусовой степени – для этого нужно просто сдвигать десятичную точку: так, 10 в минус 1 степени – один ноль перед единицей, в минус 3 – три нуля перед единицей, в минус 9 – 9 и так далее… Кстати, глядя на эту табличку, сразу понятно, сколько будет 10, например, в нулевой степени.
HotMilk 6 лет назад В минусовой степени число 10, это уже будет не целое число, а десятичное и количество знаков после запятой соответствует значению срепени. Вторая орицательная срепень – 0,01 Третья отрицательная степень – 0,001 Четвертая отричарельная степень – 0,0001 Пятая отрицательная степень – 0,00001 Шестая отрицательная степень – 0, 000001 Седьмая отрицательная степень – 0,0000001 Восьмая отрицарельная степень – 0,00000001 Девятая отрицательная степень – 0, 000000001
88SkyWalker88 6 лет назад Итак, 10 в минус второй степени будет 0,01; 10 в минус третьей степени будет 0,001; 10 в минус четвертой степени будет 0,0001; 10 в минус пятой степени будет 0,00001; 10 в минус шестой степени будет 0,000001; 10 в минус седьмой степени будет 0,0000001; 10 в минус восьмой степени будет 0,00000001; 10 в минус девятой степени будет 0,000000001. Минус перед показателем степени означает, что число равно единица деленная на заданное число в заданной степени без минуса. Т.е. в общем виде число А в степени минус n равно 1/А^n (единица деленная на А в степени n). Следовательно, 10 в минус 2; 3; 4 и т.д.степени равно 1/10^2 = 1/100 = 0,01; 1/10^3 = 1/1000 = 0,001; 1/10^4 = 1/10000 = 0,0001 и т.д. Т.е. 10^ -n = 1/10^n
Помощни к 6 лет назад С каждым последующим числом в минусовой степени единицы все дальше отодвигается от запятой и нуля. То есть 10 в минус первой степени – это одна десятая. А минус второй – это уже одна сотая. Потом идет одна тысячная, десяти-, стотысячная, миллионная и т. д. Такую степень придумали, чтобы можно было записывать целыми числами значения, которые значительно ниже 1.
Лолочка611 6 лет назад Интересующее вас число десять в минус второй, третьей, четвертой, пятой, шестой, седьмой, восьмой и девятой степенях имеет следующие значения: -2 степень будет 0,01 -3 степень будет 0,001 -4 степень будет 0,0001 -5 степень будет 0,00001 -6 степень будет 0, 000001 -7 степень будет 0,0000001 -8 степень будет 0,00000001 -9 степень будет 0, 000000001
Leona-100 7 лет назад Из школьного курса математики мы знаем, что число десять в минусовой степени будет равняться: 0,01 (минус 2), 0,001 (-3), 0,0001(-4), 0,00001 (-5), 0,000001 (-6), 0,0000001 (- 7-й), 0,00000001 (-8) и 0,000000001 ( в минус 9 степени). Это и будет правильными ответами на ваш вопрос из школьного учебника.
moreljuba 6 лет назад Число в минусовой степени наверняка у многих вызывает затруднения и сразу же в голое возникает куча закономерных вопросов, о том как же рассчитать и получить это число без минусовой степени. А на самом-то деле всего-то нужно единцу разделить на данное число в положительной степени, вот и получаем: Марлена 6 лет назад Если число имеет отрицательную степень, то число степени показывает нам насколько чисел после запятой мы должны отойти. Вот указанные значения: 0,01 – десять минус второй степени 0,001 – десять минус третьей степени Знаете ответ? |
Лучший ответ
Spathi
Искусственный Интеллект
(224376)
11 лет назад
Отрицательная степень равна единице, деленной на такую же положительную.
10^-2 = 1/(10^2) = 1/100 = 0,01
Остальные ответы
Julia
Гуру
(2502)
11 лет назад
10 деленное на 10 в квадрате, т. е. 10 / 100
SpathiИскусственный Интеллект (224376)
11 лет назад
Неверно.
Александр Зиновьев
Знаток
(273)
11 лет назад
10 в -2 степени, это значит 10 надо разделить на 10. в -3 это 10:10:10.
А 10 во 2 степени наоборот 10*10 и т. д.
Источник: Свой мозг)))
SpathiИскусственный Интеллект (224376)
11 лет назад
Бред собачий. Почитайте учебник по алгебре.
rafael ahmetov
Высший разум
(122431)
11 лет назад
Это означает обратную величину к 10 во второй степени, т. е. 10^(-2)=1/(10^2)=1/100=0,01.
Анатолий Саламатов
Гуру
(4164)
11 лет назад
Это значит: единица деленная на 10 во второй степени.
То есть: 1/100=0,01
Саша Русанов
Высший разум
(209180)
11 лет назад
10 в – n это 1 деленная на 10 в n.
Kris Korvin
Просветленный
(24475)
11 лет назад
Это будет 1/10 во 2- степени=1/100=0,01
Сергей Айкин
Мудрец
(12925)
11 лет назад
В горах живёшь ?! Гуль – читай !
фирдавс мамбетов
Ученик
(245)
6 лет назад
E
наталья букина
Ученик
(130)
4 года назад
спасибо
Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно
прочитать урок
«Степень»
и «Свойства степеней».
Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении
примеров.
Как возвести число в отрицательную степень
Запомните!
![]()
Чтобы возвести число в отрицательную степень нужно:
- «перевернуть» число. Записать его в виде дроби с единицой наверху (в
числителе) и с
исходным числом в степени внизу; - заменить отрицательную степень на
положительную; - возвести число в положительную степень.
Общая формула возведения в отрицательную степень выглядит следующим образом.
a−n =
,где a ≠ 0, n ∈ z (n принадлежит целым числам).
Примеры возведения в отрицательную степень.
- 6−2 = =
- (−3)−3 = = = −
- 0,2−2 = =
Запомните!
![]()
Любое число в нулевой степени — единица.
a0 = 1
,где a ≠ 0
Примеры возведения в нулевую степень.
- ()0 = 1
- (−5)0 = 1
- d0 = 1
Как найти 10 в минус 1 степени
В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:
10−1 = 0,1
Теперь, зная определение отрицательной степени, давайте разберемся, почему «10» в минус первой степени равно
«0,1».
Возведем «10−1» по правилам отрицательной степени.
Перевернем «10» и запишем её в виде дроби
«
»
и заменим отрицательную степень
«−1» на
положительную степень «1».
Возведем «10» в «1» степень. Помним, что любое число в первой степени равно самому числу.
Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.
По такому же принципу можно найти «10» в минус второй, третьей и т.д.
10−2 = 0,01
10−3 = 0,001
10−4 = 0,0001
Запомните!
![]()
Для упрощения перевода «10» в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один».
Проверим правило выше для «10−2».
Т.к. у нас степень «−2», значит, будет всего один ноль (положительное
значение степени «2 − 1 = 1». Сразу после запятой ставим один ноль и за ним «1».
Рассмотрим «10−1».
Т.к. у нас степень «−1», значит, нулей после запятой не будет (положительное
значение степени «1 − 1 = 0». Сразу после запятой ставим «1».
То же самое правило работает и для «10−12». При переводе в десятичную дробь будет
«12 − 1 = 11 » нулей и «1» в конце.
10−12 = 0,000 000 000 001
Как возвести в отрицательную степень дробь
Запомните!
![]()
Чтобы возвести дробь в отрицательную степень нужно:
- «перевернуть» дробь;
- заменить отрицательную степень на
положительную; - возвести дробь в положительную степень.
Пример. Требуется возвести в отрицательную степень дробь.
Перевернем дробь «
»
и заменим отрицательную степень «−3» на положительную «3».
Возведем дробь в положительную степень по правилу возведения дроби в положительную степень.
Т.е. возведем и числитель «3», и знаменатель «10» в третью степень.
()−3 = ()3 =
=
Для более грамотного ответа запишем полученный результат в виде десятичной дроби.
()−3 = ()3 =
= = 0,027
Как возвести отрицательное число в отрицательную степень
Как и при возведении отрицательного числа в положительную степень, в первую
очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.
Запомните!
![]()
Отрицательное число, возведённое в
чётную степень, — число
положительное.
Отрицательное число, возведённое в
нечётную степень, — число
отрицательное.
Пример.
(−5) −2 =
Перевернем число «−5» и заменим отрицательную степень
«−2»
на положительную
«2».
Так как степень «2» — четная, значит, результат возведения в степень будет
положительный. Поэтому
убираем знак минуса при раскрытии скобок.
Далее откроем скобки
и возведем во вторую степень и числитель «1»,
и знаменатель «5».
Как возвести отрицательную дробь в отрицательную степень
Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.
Запомните!
![]()
Отрицательная дробь, возведённая в
чётную степень, — дробь
положительная.
Отрицательная дробь, возведённая в
нечётную степень, — дробь
отрицательная.
Разберемся на примере. Задание: возвести отрицательную дробь
«(− )»
в «−3» степень.
По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень «−3» на положительную
«3».
Теперь определим конечный знак результата возведения в «3» степень.
Степень «3» — нечетная, значит, по правилу возведения отрицательного числа в степень дробь
останется отрицательной.
Нам остается только раскрыть скобки и возвести в степень и числитель «3», и знаменатель
«2» в третью степень.
Для окончательного ответа выделим целую часть из дроби.
(−
) −3 = (−
) 3 = −
= −
= − 3
Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.
Правило возведения отрицательного числа в степень гласит: если степень четная, значит, результат возведения
будет положительным.
Свойства отрицательной степени
Все свойства степени, которые используются для положительной степени,
точно также применяются и для отрицательной степени.
В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени
и покажем примеры их использования.
Запомните!
![]()
- am · an = am + n
- =
am − n - (an)m = an · m
- (a · b)n = an · bn
Примеры решений заданий с отрицательной
степенью
Разбор примера
Представить в виде степени.
2) a6 · b6 = (ab)6
4) (c5)2 = c10
Разбор примера
Записать в виде степени с отрицательным числом.
Разбор примера
Вычислить.
3) (
) −12 : (
) 2 =
(
) 12 · (
) 2 =
(
) 12 · (
) 2 =
·
=
=
=
=
·
= 1312 − 2 · 22 − 12
= 1310 · 2−10 = 1310 ·
=
=
=
= (
) 10
Разбор примера
Выполнить действия.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
20 ноября 2016 в 12:53
Виктор Помаранов

Профиль
Благодарили: 0
Сообщений: 1

Виктор Помаранов
Профиль
Благодарили: 0
Сообщений: 1
0,4•(-10)3-7•(-10)2+64
0
Спасибо
Ответить
21 ноября 2016 в 13:13
Ответ для Виктор Помаранов
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Нечетная стпень-не меняет знак, четная — меняет.
0,4 · (-1000) ? 7 · 100 +64 = ?400 ?700 +64 = ?1036
Ответ: ?1036
0
Спасибо
Ответить
23 августа 2016 в 11:52
Мария Кузьменко

Профиль
Благодарили: 0
Сообщений: 1

Мария Кузьменко
Профиль
Благодарили: 0
Сообщений: 1
Помогите решить, пожалуйста подробно))
4 в 6 степени минус 3 в 6 степени
0
Спасибо
Ответить
30 августа 2016 в 15:01
Ответ для Мария Кузьменко
Наталия Зимарина

Профиль
Благодарили: 0
Сообщений: 1

Наталия Зимарина
Профиль
Благодарили: 0
Сообщений: 1
46 -36=(43)2-(33)2=(43-33)(43+33)=(64-27)(64+27)=37 · 81=2997
0
Спасибо
Ответить
|
Запись an означает что число a должно быть умножено n раз: |
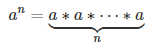 |
Пример 1. 53=5*5*5=125
Деление это обратная операция умножению. Отрицательная степень означает сколько раз нужно разделить число.
|
Число в отрицательной степени a-n может быть записано в виде: |
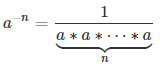 |
Пример 2. 5-3=1÷5÷5÷5=0,008
| Пример 2 может быть записан в виде. | 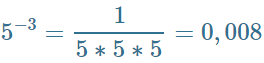 |
| Определение. Если a≠0 и n – целое отрицательное число, то | 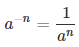 |
Для вычисления числа a-n в отрицательной степени нужно:
1.Вычислить an
|
2.Затем разделить 1 на полученный результат, т.е. |
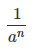 |
Предлагаем попробовать наш калькулятор степеней, который поможет возвести в степень онлайн любое число.
Использовать калькулятор очень просто — введите число, которое вы хотите возвести в степень, а затем число — степень и нажмите на кнопку «Посчитать».
Примечательно то, что наш онлайн калькулятор степеней может возвести в степень как положительную, так и отрицательную. А для извлечения корней на сайте есть другой калькулятор.
Как возвести число в степень.
Давайте рассмотрим процесс возведения в степень на примере. Пусть нам необходимо возвести число 5 в 3-ю степень. На языке математики 5 — это основание, а 3 — показатель (или просто степень). И записать это можно кратко в таком виде:
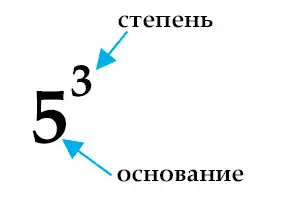
Возведение в степень
А чтобы найти значение, нам будет необходимо число 5 умножить на себя 3 раза, т. е.
53 = 5 x 5 x 5 = 125
Соответственно, если мы хотим найти значение числа 7 в 5 степени, мы должны число 7 умножить на себя 5 раз, т. е. 7 x 7 x 7 x 7 x 7. Другое дело когда требуется возвести число в отрицательную степень.
Как возводить в отрицательную степень.
При возведении в отрицательную степень необходимо использовать простое правило:
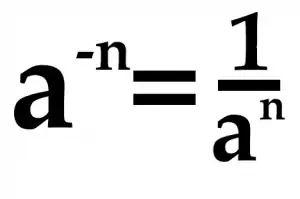
как возводить в отрицательную степень
Все очень просто — при возведении в отрицательную степень мы должны поделить единицу на основание в степени без знака минус — т. е. в положительной степени. Таким образом, чтобы найти значение
2-3
мы должны поступить следующим образом:
2-3 =1 / (23)
А так как 23 =8, то мы получим
2-3 =1 / 8 = 0,125
Ваша оценка
[Оценок: 18286 Средняя: 3.8]
Калькулятор степеней Автор admin средний рейтинг 3.8/5 – 18286 рейтинги пользователей





