Получил просьбу разобрать, как вычислять арксинус и другие функции сложнее экспоненты, если аргумент комплексный. Давайте разберем.
Начнем с общих вопросов. Аналитическая функция (заданная хоть где-нибудь сходящимся степенным рядом) может быть продолжена на всю свою область определения (которая ей присуща, а не задается извне), и, соответственно, представлена в данной точке из области определения некоторым сходящимся степенным рядом. Возможно, не одним. Подставив туда данное комплексное число, найдем значение функции. Их может быть несколько, если рядов больше одного.
Впрочем, не все функции во всех точках аналитические, даже среди элементарных. Корень, например, не аналитичен в нуле, хотя определен там…
Если функция задана через четыре действия арифметики (конечное число операций), то проблем с вычислением нет: арифметика определена полностью и однозначно.
Это многочлены и дробно-рациональные функции, то есть отношение двух многочленов. Довольно обширный и хороший класс функций. В него входят, в частности, все целые степени.
Если приходится делить на нуль, то либо получится полюс, если предел бесконечен, либо устранимая особая точка, если предел конечен. Других вариантов в данном случае не будет, хотя в общем случае бывают еще существенно особые точки, в которых предел по разным кривым может быть вообще любой, и в любой окрестности такой точки функция принимает все значения, или все кроме одного. Про особые точки я рассказывал.
Пример устранимой точки: нуль для z/z или sin(z)/z. Пример полюса: нуль для 1/z или (z+1)/z².
Примером функции с существенно особой точкой является exp(1/z): нуль именно такая точка, причем экспонента принимает в любой окрестности нуля все значения, кроме нулевого. А sin(1/z) тоже имеет существенно особую точку в нуле, но принимает в окрестности вообще все значения, без исключений.
Если мы добавим рациональные или вещественные степени, то тоже все делается, только теперь значений может быть много, и может теряться аналитичность: функция может быть определена в точке, но не быть аналитичной.
Комплексные степени вводятся через формулу Эйлера, которую я уже много раз приводил:
Что делает формула Эйлера — вопрос, кстати, очень тонкий. Я планирую скоро выпустить материал на эту тему. Можно сказать, что она задает функцию “экспонента”, особенно если записать формулу так:
Хотя обычно определение экспоненты другое, через ряд, например. Экспонента однозначна, так что все в порядке. Еще можно сказать, что формула Эйлера задает одно из значений (главное значение) степени числа е с показателем ix. Как найти остальные значения, я рассказывал.
Наконец, можно сказать, что формула Эйлера позволяет выразить комплексное число, записанное в тригонометрической форме, в форме экспоненциальной. Аналог: теорема Лагранжа о том, что любое натуральное представимо в виде суммы четырех квадратов. Ну а здесь любое комплексное с модулем единица представимо в виде числа е в некоторой мнимой степени (которая есть аргумент числа, умноженный на i).
В любом случае, формула Эйлера дает правило, как возводить число e в мнимую степень. По обычным правилам степени можно научиться возводить е в любую комплексную степень (получая, впрочем, только одно из значений), что вторая из приведенных формул и описывает.
Теперь мы можем любое комплексное число записать в экспоненциальной форме через модуль и аргумент:
Традиционно с большой буквы пишут многозначные функции, а они же с малой означают “главное значение” или одну из “ветвей”.
После этого легко определить логарифм (который всегда бесконечнозначен) для всех ненулевых чисел:
А умея вычислять логарифм, можно вычислить любую степень любого числа (кроме нуля):
Нет только степеней нуля, кроме положительных. Причем все степени, кроме целых, всегда многозначны.
Теперь тригонометрия. Из формулы Эйлера для x и –x получаем формулы для синуса и косинуса, которые распространяем на любые комплексные x:
Поделив одну на другую, получим тангенс:
Теперь обратные тригонометрические функции. Арксинус x=arcsin(z) определяется уравнением z=sin(x) относительно x. Решаем:
Записываем корни квадратного уравнения (в комплексных числах всё так же, через дискриминант, как в школе учили):
Ну, и логарифмируем (с учетом, что 1/i=-i):
Аналогично с арккосинусом:
С тангенсом еще проще. Уравнение tg(x)=z; подставляем, преобразуем, выражаем x:
У арктангенса есть особые точки в ±i. Именно поэтому разложение в ряд в окрестности нуля сходится в круге радиуса 1. Так что тангенс не может равняться i или -i.
Вычислим арктангенс числа 1. Для этого поделим i+1 на i-1, домножив на i+1 сверху и снизу. Снизу получим квадрат модуля, это 2, а сверху, по формуле квадрата суммы, 2i. Под логарифмом стоит i, число с модулем 1 и аргументом π/2. Получаем π/4, как и положено.
Замечу, что никто не мешает использовать эти формулы без всякой ТФКП, если у вас в программной библиотеке (или калькуляторе) логарифм есть, а арккосинуса нету. Главное, аккуратно обработать все вхождения i, чтобы они самоистребились, а не выдали ошибку.
Путеводитель по каналу
Тригонометрические функции комплексного числа
| Расчетное комплексное число(радианы или градусы) |
| Точность вычисления от 1 до 14 |
| Синус числа |
| Косинус числа |
| Тангенс числа |
| Котангенс числа |
| Если исходное число было в градусах, то |
| Синус числа (если заданное число было в градусах) |
| Косинус числа (если заданное число было в градусах) |
| Тангенс числа (если заданное число было в градусах) |
| Котангенс числа (если заданное число было в градусах) |
В статье рассматривается способы расчета и выдача значений основных тригонометрических функций
Синус комплексного числа
Если представить комплексное число как (z=x+iy)
То синус числа, выраженный через гиперболические функции
(sin(z)=sin(x)ch(y)+icos(x)sh(y))
Косинус комплексного числа
Если представить (z=x+iy)
То косинус числа, выраженный через гиперболические функции
(cos(z)=cos(x)ch(y)-isin(x)sh(y))
Введите в поле число, комплексное или вещественное и программа выдаст результат
Тангенс комплексного числа
Если представить (z=x+iy)
То тангенс числа, выраженный через синус и косинус
(operatorname{tg}z{}=cfrac{sin(z)}{cos(x)})
или
(operatorname{tg},z{}=cfrac{sin(2x)}{cos(2x)+ch(2y)}+icfrac{sh(2y)}{cos(2x)+ch(2y)})
Котангенс комплексного числа
Котангенс комплексного числа также легко решается
(operatorname{ctg},z{}=cfrac{cos(z)}{sin(x)})
Тригонометрическая форма комплексных чисел
29 ноября 2021
Второй урок по комплексным числам. Если вы только начинаете изучать эту тему (что такое комплексная единица, модуль, сопряжённые), см. первый урок: «Что такое комплексное число».
Сегодня мы узнаем:
- Что такое тригонометрическая форма
- Умножение и деление комплексных чисел в тригонометрической форме
- Формула Муавра (возведение в степень)
- Дополнение 1. Геометрический подход, чтобы не путать, где синус, а где косинус
- Дополнение 2. Как быстро и надёжно искать аргумент комплексного числа?
Начнём с ключевого определения.
1. Тригонометрическая форма
Определение. Тригонометрическая форма комплексного числа — это выражение вида
[z=left| z right|cdot left( cos text{ }!!varphi!!text{ }+isin text{ }!!varphi!!text{ } right)]
где $left| z right|$ — модуль комплексного числа, $text{ }!!varphi!!text{ }$ — некоторый угол, который называется аргумент комплексного числа (пишут $text{ }!!varphi!!text{ }=arg left( z right)$).
Любое число $z=a+bi$, отличное от нуля, можно записать с тригонометрической форме. Для этого нужно вычислить модуль и аргумент. Например:
Записать в тригонометрической форме число $z=sqrt{3}+i$.
Переписываем исходное число в виде $z=sqrt{3}+1cdot i$ и считаем модуль:
[left| z right|=sqrt{{{left( sqrt{3} right)}^{2}}+{{1}^{2}}}=2]
Выносим модуль за скобки:
[z=sqrt{3}+1cdot i=2cdot left( frac{sqrt{3}}{2}+frac{1}{2}cdot i right)]
Вспоминаем тригонометрию, 10-й класс:
[frac{sqrt{3}}{2}=cos frac{text{ }!!pi!!text{ }}{6};quad frac{1}{2}=sin frac{text{ }!!pi!!text{ }}{6}]
Окончательный ответ:
[z=2cdot left( cos frac{text{ }!!pi!!text{ }}{6}+icdot sin frac{text{ }!!pi!!text{ }}{6} right)]
Понятно, что вместо $frac{text{ }!!pi!!text{ }}{6}$ с тем же успехом можно взять аргумент $frac{13text{ }!!pi!!text{ }}{6}$. Синус и косинус не поменяется. Главное — выбрать такой аргумент, чтобы в тригонометрической форме не осталось никаких минусов. Все минусы должны уйти внутрь синуса и косинуса. Сравните:
Записать в тригонометрической форме число $z=-1-i$.
Правильно:
[z=sqrt{2}cdot left( cos frac{5text{ }!!pi!!text{ }}{4}+isin frac{5text{ }!!pi!!text{ }}{4} right)]
Неправильно:
[begin{align} & z=-sqrt{2}cdot left( cos frac{text{ }!!pi!!text{ }}{4}+isin frac{text{ }!!pi!!text{ }}{4} right) \ & z=sqrt{2}cdot left( -cos frac{text{ }!!pi!!text{ }}{4}-isin frac{text{ }!!pi!!text{ }}{4} right) \ & z=sqrt{2}cdot left( cos frac{3text{ }!!pi!!text{ }}{4}-isin frac{3text{ }!!pi!!text{ }}{4} right) \ end{align}]
2. Умножение и деление комплексных чисел
Комплексные числа, записанные в тригонометрической форме, очень удобно умножать и делить.
Теорема. Пусть даны два комплексных числа:
[begin{align} & {{z}_{1}}=left| {{z}_{1}} right|cdot left( cos alpha +isin alpha right) \ & {{z}_{2}}=left| {{z}_{2}} right|cdot left( cos beta +isin beta right) \ end{align}]
Тогда их произведение равно
[{{z}_{1}}cdot {{z}_{2}}=left| {{z}_{1}} right|cdot left| {{z}_{2}} right|cdot left( cos left( alpha +beta right)+isin left( alpha +beta right) right)]
А если ещё и $left| {{z}_{2}} right|ne 0$, то их частное равно
[frac{{{z}_{1}}}{{{z}_{2}}}=frac{left| {{z}_{1}} right|}{left| {{z}_{2}} right|}cdot left( cos left( alpha -beta right)+isin left( alpha -beta right) right)]
Получается, что при умножении комплексных чисел мы просто умножаем их модули, а аргументы складываем. При делении — делим модули и вычитаем аргументы. И всё!
Найти произведение и частное двух комплексных чисел:
[begin{align} & {{z}_{1}}=2cdot left( cos frac{pi }{3}+isin frac{pi }{3} right) \ & {{z}_{2}}=5cdot left( cos frac{pi }{6}+isin frac{pi }{6} right) \ end{align}]
Считаем произведение:
[begin{align} {{z}_{1}}cdot {{z}_{2}} & =2cdot 5cdot left( cos left( frac{pi }{3}+frac{pi }{6} right)+isin left( frac{pi }{3}+frac{pi }{6} right) right)= \ & =10cdot left( cos frac{pi }{2}+isin frac{pi }{2} right) \ end{align}]
Считаем частное:
[begin{align} frac{{{z}_{1}}}{{{z}_{2}}} & =frac{2}{5}cdot left( cos left( frac{pi }{3}-frac{pi }{6} right)+isin left( frac{pi }{3}-frac{pi }{6} right) right)= \ & =0,4cdot left( cos frac{pi }{6}+isin frac{pi }{6} right) \ end{align}]
По сравнению со стандартной (алгебраической) формой записи комплексных чисел экономия сил и времени налицо.:)
3. Формула Муавра
Пусть дано комплексное число в тригонометрической форме:
[z=left| z right|cdot left( cos text{ }!!varphi!!text{ }+isin text{ }!!varphi!!text{ } right)]
Возведём его в квадрат, умножив на само себя:
[begin{align} {{z}^{2}} & =zcdot z = \ & =left| z right|left| z right|cdot left( cos left( text{ }!!varphi!!text{ + }!!varphi!!text{ } right)+isin left( text{ }!!varphi!!text{ + }!!varphi!!text{ } right) right)= \ & ={{left| z right|}^{2}}cdot left( cos 2text{ }!!varphi!!text{ }+isin 2text{ }!!varphi!!text{ } right) \ end{align}]
Затем возведём в куб, умножив на себя ещё раз:
[{{z}^{3}}={{left| z right|}^{3}}cdot left( cos 3varphi +isin 3varphi right)]
Несложно догадаться, что будет дальше — при возведении в степень $n$. Это называется формула Муавра.
Формула Муавра. При возведении всякого комплексного числа
[z=left| z right|cdot left( cos varphi +isin varphi right)]
в степень $nin mathbb{N}$ получим
[{{z}^{n}}={{left| z right|}^{n}}cdot left( cos left( nvarphi right)+isin left( nvarphi right) right)]
Простая формула, которая ускоряет вычисления раз в десять! И кстати: эта формула работает при любом $nin mathbb{R}$, а не только натуральном. Но об этом позже. Сейчас примеры:
Вычислить:
[{{left( sqrt{3}-i right)}^{16}}]
Представим первое число в тригонометрической форме:
[begin{align} sqrt{3}-i & = 2cdot left( frac{sqrt{3}}{2}+icdot left( -frac{1}{2} right) right)= \ & =2cdot left( cos left( -frac{pi }{6} right)+isin left( -frac{pi }{6} right) right) \ end{align}]
По формуле Муавра:
[begin{align} & {{left( 2cdot left( cos frac{11pi }{6}+isin frac{11pi }{6} right) right)}^{16}}= \ & ={{2}^{16}}cdot left( cos frac{88pi }{3}+isin frac{88pi }{3} right)= \ & ={{2}^{16}}cdot left( cos frac{4pi }{3}+isin frac{4pi }{3} right) \ end{align}]
Последним шагом мы воспользовались периодичностью синуса и косинуса, уменьшив аргумент сразу на 28π.
Следующую задачу в разных вариациях любят давать на контрольных работах и экзаменах:
Вычислить:
[{{left( left( -frac{sqrt{2}}{2} right)+left( -frac{sqrt{2}}{2} right)i right)}^{2022}}]
Теперь второе число запишем в комплексной форме:
[begin{align} & left( -frac{sqrt{2}}{2} right)+left( -frac{sqrt{2}}{2} right)i= \ & =1cdot left( cos frac{5pi }{4}+isin frac{5pi }{4} right) \ end{align}]
По формуле Муавра:
[begin{align} & {{left( 1cdot left( cos frac{5pi }{4}+isin frac{5pi }{4} right) right)}^{2022}}= \ & ={{1}^{2022}}cdot left( cos frac{5055pi }{2}+isin frac{5055pi }{2} right)= \ & =1cdot left( cos frac{3pi }{2}+isin frac{3pi }{2} right)=-i \ end{align}]
Вот так всё просто! Следующие два раздела предназначены для углублённого изучения. Для тех, кто хочет действительно разобраться в комплексных числах.
4. Дополнение 1. Геометрический подход
Многие путают местами косинус и синус. Почему комплексная единица стоит именно у синуса? Вспомним, что есть декартова система координат, где точки задаются отступами по осям $x$ и $y$:
А есть полярная система координат, где точки задаются поворотом на угол $varphi $ и расстоянием до центра $r$:
А теперь объединим эти картинки и попробуем перейти из декартовой системы координат в полярную:
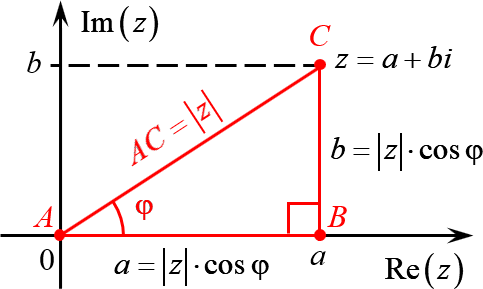
Комплексное число $z=a+bi$ задаёт на плоскости точку $C$, удалённую от начала координат на расстояние
[AC=sqrt{{{a}^{2}}+{{b}^{2}}}=left| z right|]
Треугольник $ABC$ — прямоугольный. Пусть $angle BAC=varphi $. Тогда:
[begin{align} & AB=ACcdot cos varphi =left| z right|cdot cos varphi \ & BC=ACcdot sin varphi =left| z right|cdot sin varphi \ end{align}]
С другой стороны, длины катетов $AB$ и $BC$ — это те самые отступы $a$ и $b$, с помощью которых мы задаём комплексное число. Поэтому:
[begin{align} a+bi & =left| z right|cos varphi +icdot left| z right|sin varphi = \ & =left| z right|left( cos varphi +isin varphi right) \ end{align}]
Итак, мы перешли от пары $left( a;b right)$ к паре $left( left| z right|;varphi right)$, где $left| z right|$ — модуль комплексного числа, $varphi $ — его аргумент (проще говоря, угол поворота).
Важное замечание. А кто сказал, что такой угол $varphi $ существует? Возьмём число $z=a+bi$ и вынесем модуль за скобку:
[begin{align} z & =a+bi= \ & =sqrt{{{a}^{2}}+{{b}^{2}}}cdot left( frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}}+icdot frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)= \ & =left| z right|cdot left( cos text{ }!!varphi!!text{ }+isin text{ }!!varphi!!text{ } right) \ end{align}]
Осталось подобрать такой угол $varphi $, чтобы выполнялось два равенства:
[begin{align} & frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}}=cos text{ }!!varphi!!text{ } \ & frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}}=sin text{ }!!varphi!!text{ } \ end{align}]
Такой угол обязательно найдётся, поскольку выполняется основное тригонометрическое тождество:
[begin{align} {{sin }^{2}}text{ }!!varphi!!text{ } & +{{cos }^{2}}text{ }!!varphi!!text{ }= \ & ={{left( frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)}^{2}}+{{left( frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)}^{2}}= \ & =frac{{{a}^{2}}}{{{a}^{2}}+{{b}^{2}}}+frac{{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}=frac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}}=1 \ end{align}]
На практике основная трудность заключается именно в поиске подходящего аргумента.
5. Дополнение 2. Как найти аргумент?
В учебниках пишут много разной дичи, типа вот этой:
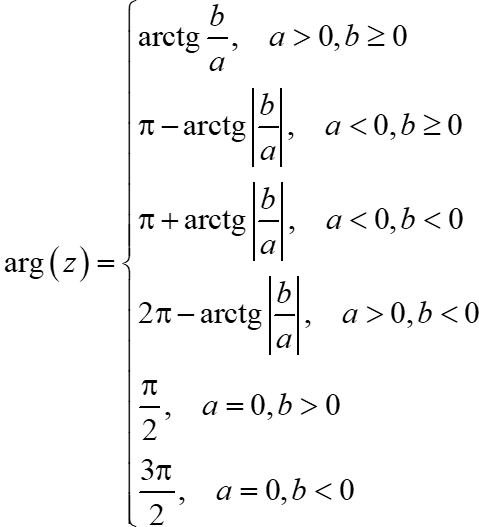
Формула правильная, но пользы от неё — ноль. Запомнить сложно, а применять и вовсе невозможно. Мы пойдём другим путём.
5.1. Точки на координатных осях
Для начала рассмотрим точки, лежащие осях координат.
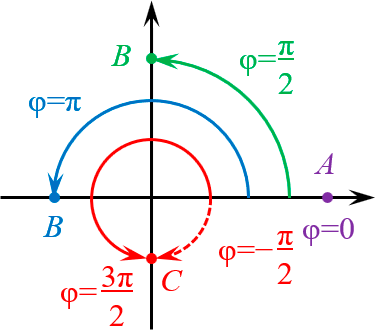
Тут всё очевидно:
- На положительной полуоси абсцисс $varphi =0$ (фиолетовая точка $A$).
- На отрицательной — $varphi =pi $ (синяя точка $B$).
- На положительной полуоси ординат $varphi =frac{pi }{2}$ (зелёная точка $B$).
- На отрицательной — $varphi =frac{3pi }{2}$ (красная точка $C$). Однако ничто не мешает рассмотреть $varphi =-frac{pi }{2}$ — результат будет тем же самым.:)
5.2. Точки с арктангенсом
А если точки не лежат на осях, то в записи комплексного числа $a+bi$ числа $ane 0$ и $bne 0$. Рассмотрим вспомогательный угол
[{{varphi }_{1}}=operatorname{arctg}left| frac{b}{a} right|]
Очевидно, это острый угол:
[0 lt operatorname{arctg}left| frac{a}{b} right| lt frac{pi }{2}]
Зная знаки чисел $a$ и $b$, мы немедленно определим координатную четверть, в которой располагается искомая точка. И нам останется лишь отложить вспомогательный угол ${{varphi }_{1}}$ от горизонтальной оси в эту четверть.
В правой полуплоскости мы откладываем от «нулевого» луча:
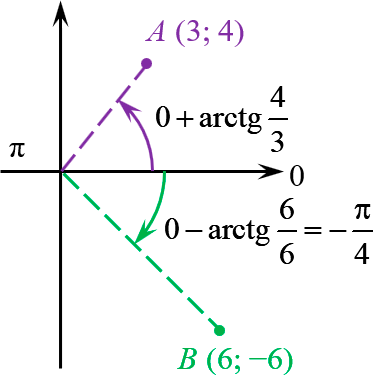
Точка $Aleft( 3;4 right)$ удалена от начала координат на расстояние 5:
[begin{align} 3+4i & =5cdot left( cos varphi +isin varphi right) \ varphi & =operatorname{arctg}frac{4}{3} end{align}]
Для точки $Bleft( 6;-6 right)$ арктангенс оказался табличным:
[6-6i=6sqrt{2}cdot left( cos left( -frac{pi }{4} right)+isin left( -frac{pi }{4} right) right)]
В левой полуплоскости откладываем от луча, соответствующего углу $pi $:
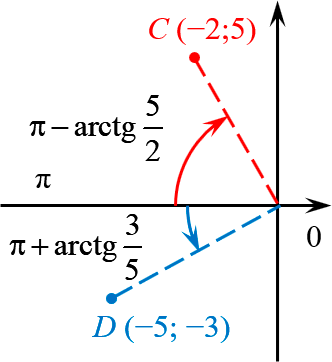
Итого для точки $Cleft( -2;5 right)$ имеем:
[begin{align} -2+5i & =sqrt{29}cdot left( cos varphi +isin varphi right) \ varphi & =pi -operatorname{arctg}frac{5}{2} end{align}]
И, наконец, для точки $Dleft( -5;-3 right)$:
[begin{align} -5-3i & =sqrt{34}cdot left( cos varphi +isin varphi right) \ varphi & =pi +operatorname{arctg}frac{3}{5} end{align}]
Звучит просто, выглядит красиво, работает идеально! Но требует небольшой практики. Пробуйте, тренируйтесь и берите на вооружение.
А в следующем уроке мы научимся извлекать корни из комплексных чисел.:)
Смотрите также:
- Как извлекать корни из комплексных чисел

- Комплексные числа — первый и самый важный уок

- Тест к параграфу «Что такое логарифм» (легкий)

- Тест к уроку «Площади многоугольников без координатной сетки» (средний)

- Четырехугольная пирамида: как найти координаты вершин

- Задача C1: тригонометрические уравнения и формула двойного угла

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 октября 2022 года; проверки требует 1 правка.

Геометрический смысл формулы Эйлера
Формула Эйлера связывает комплексную экспоненту с тригонометрическими функциями. Названа в честь Леонарда Эйлера, который её ввёл.
Формула Эйлера утверждает, что для любого вещественного числа 
,
где 

— мнимая единица.
История[править | править код]
Формула Эйлера впервые была приведена в статье английского математика Роджера Котса (помощника Ньютона) «Логометрия» (лат. Logometria), опубликованной в журнале «Философские труды Королевского общества» в 1714 году[1] и перепечатана в книге «Гармония мер» (лат. Harmonia mensurarum), которая была издана в 1722 году, уже после смерти автора[2]. Котс привёл её как небольшое предложение среди множества геометрических построений, которое после перевода на современный математический язык и исправления ошибки в знаке, имеет вид[3]:
.
Эйлер опубликовал формулу в её привычном виде в статье 1740 года и в книге «Введение в анализ бесконечно малых» (лат. Introductio in analysin infinitorum) (1748)[4], построив доказательство на равенстве бесконечных разложений в степенные ряды правой и левой частей. Ни Эйлер, ни Котс не представляли себе геометрической интерпретации формулы: представление о комплексных числах как точках на комплексной плоскости появилось примерно 50 лет спустя у К. Весселя.
Производные формулы[править | править код]
При помощи формулы Эйлера можно определить функции 

,
.
Далее можно ввести понятие тригонометрических функций комплексной переменной. Пусть 
,
.
Известное тождество Эйлера, связывающее пять фундаментальных математических констант:
является частным случаем формулы Эйлера при 
Применение в теории чисел[править | править код]
В аналитической теории чисел часто рассматриваются специальные суммы вида 


Для теории чисел, изучающей целые числа, имеют значение прежде всего выводимые из формулы Эйлера индикаторные тождества, касающиеся произвольного целого числа 
Применение в комплексном анализе[править | править код]
Благодаря формуле Эйлера появилась так называемая тригонометрическая и показательная запись комплексного числа: 
Также значительным следствием можно считать формулы возведения комплексного числа в произвольную степень: 






Формула возведения в степень верна не только для целых 
Взаимосвязь с тригонометрией[править | править код]
Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:
Вышеуказанные уравнения могут быть получены путём сложения или вычитания формул Эйлера:
с последующим решением относительно синуса или косинуса.
Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:
Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения результат выражения остается вещественным. Например:
Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением. Например:
Данная формула используется для рекурсивного вычисления значений cos(nx) для целых значений n и произвольных значений x (в радианах).
Доказательство[править | править код]
Доказательство формулы Эйлера можно провести с использованием ряда Маклорена. Разложим функцию 


Но


Поэтому 
Наглядная демонстрация[править | править код]
Известно, что 
Нижеследующие изображения иллюстрируют, что предел 


-

n=1
-

n=2
-

n=3
-
n=4
-
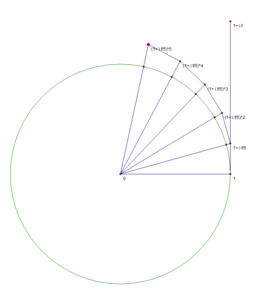
n=5
-
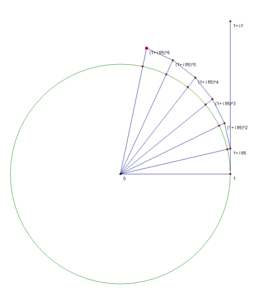
n=6
-

n=8
-
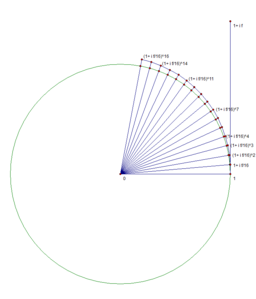
n=16
Процесс изменения 

Общеизвестно, что 





Показательная форма комплексного числа[править | править код]
Показательная и тригонометрические формы комплексных чисел связаны между собой формулой Эйлера.
Пусть комплексное число 

Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь 

Примечания[править | править код]
- ↑ Cotes R. Logometria (англ.) // Philosophical Transactions of the Royal Society of London : journal. — 1714-1716. — Vol. 29. — P. 32. — doi:10.1098/rstl.1714.0002. Архивировано 6 июля 2017 года.
- ↑ Cotes R. Harmonia mensurarum (неопр.). — 1722. — С. 28. Архивная копия от 7 июня 2020 на Wayback Machine
- ↑ González-Velasco Enrique A. Journey through Mathematics: Creative Episodes in Its History (англ.). — 2011. — P. 182. Архивная копия от 19 октября 2014 на Wayback Machine
- ↑ Euler L. Cap.VIII. De quantitatibus transcendentibus ex Circulo ortis // Introductio in analysin infinitorum (неопр.). — 1748. — Т. 1. — С. 104.
Литература[править | править код]
- Гутов А. З. Аналог формулы Эйлера для обобщённых синуса и косинуса // Современные методы физико-математических наук. Труды международной конференции. Орёл, 2006. С. 35—37. Архивная копия от 25 сентября 2020 на Wayback Machine
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973.
- Стиллвелл Д. Математика и её история. — Москва-Ижевск: Институт компьютерных исследований, 2004. — 530 с. Архивная копия от 7 июня 2015 на Wayback Machine
Содержание
Комплексные числа
Алгебра — это наука о решении уравнений. Но в каких числах? Если принимать в рассмотрение только множество натуральных чисел $ mathbb N_{} $, то уравнение $ 5+x=3 $ решений не имеет. Дополнив множество $ mathbb N_{} $ нулем и отрицательными числами, мы добиваемся того, что во множестве $ mathbb Z_{} $
целых чисел любое уравнение $ a+x=b $ получает решение, причем единственное. Но вот уравнение $ 2cdot x=3 $ решений снова не имеет… Снова дополняем множество $ mathbb Z_{} $ дробными числами до множества $ mathbb Q_{} $ рациональных чисел. В этом множестве будет существовать единственное решение уравнения
$ acdot x=b $ если только $ a_{}ne 0 $. Но вот уравнение $ x^2-2=0 $ решений в $ mathbb Q_{} $ не
имеет. Пополнив множество рациональных чисел числами иррациональными, мы получаем решение — в вещественных числах $ mathbb R_{} $ — и этого уравнения, но, однако же, не любого квадратного! Так, не существует вещественного числа, удовлетворяющего уравнению $ x^2+1=0 $.
Задача. Расширить множество вещественных чисел так, чтобы в этом расширении уравнение $ x^2+1=0 $ имело решение.
Такое расширение должно «наследовать» все свойства вещественных чисел, т.е. в этом множестве операции должны подчиняться аксиомам коммутативности, ассоциативности и дистрибутивности:
1.
$ {mathfrak a}_1+{mathfrak a}_2={mathfrak a}_2+{mathfrak a}_1 $;
2.
$ ({mathfrak a}_1+{mathfrak a}_2)+{mathfrak a}_3={mathfrak a}_1+({mathfrak a}_2
+{mathfrak a}_3) $;
3.
$ {mathfrak a}_1cdot {mathfrak a}_2={mathfrak a}_2cdot {mathfrak a}_1 $;
4.
$ ({mathfrak a}_1cdot {mathfrak a}_2)cdot {mathfrak a}_3={mathfrak a}_1cdot ({mathfrak a}_2cdot
{mathfrak a}_3) $;
5.
$ ({mathfrak a}_1+{mathfrak a}_2)cdot {mathfrak a}_3={mathfrak a}_1cdot {mathfrak a}_3+
{mathfrak a}_2cdot {mathfrak a}_3 $;
6.
существует нейтральный элемент $ {mathfrak o} $ относительно сложения:
$ {mathfrak a}+{mathfrak o}={mathfrak a} $;
7.
существует нейтральный элемент $ {mathfrak e} $ относительно умножения:
$ {mathfrak a}cdot {mathfrak e}={mathfrak a} $.
Все указанные равенства должны выполняться для произвольных чисел $ {mathfrak a},
{mathfrak a}_1,{mathfrak a}_2,{mathfrak a}_3 $.
Определение
Комплéксным1) числом
называется упорядоченная пара вещественных чисел $ z=(a,b) $. Аксиоматически вводятся понятие равенства
комплексных чисел, а также правила действий над ними.
Два комплексных числа $ z_1=(a,b) $ и $ z_2=(c,d) $ называются равными: $ z_1=z_2 $ тогда и только тогда, когда $ a=c $ и $ b=d $. В противном случае они называюся неравными.
?
Доказать, что
$$left(2,, sqrt{12} right)=left(frac{1}{2} sqrt{7+4sqrt{3}}+
frac{1}{2} sqrt{7-4sqrt{3}},, 2sqrt{3} right) .$$
Суммой комплексных чисел $ z_1=(a,b) $ и $ z_2=(c,d) $ называется комплексное число
$$ z_3=z_1+z_2 = (a+c,b+d) . $$
П
Пример. $ (1,-1)+(2,1)=(3,0) $, $ (0,1)+(1,0)=qquad qquad $ , $ (3,2)+(-3,-2)=qquad $ .
Произведением комплексных чисел $ z_1=(a,b) $ и $ z_2=(c,d) $ называется комплексное число
$$ z_4=z_1cdot z_2 = (ac-bd, ad+bc) . $$
§
Так же как и в случае вещественных чисел, для знака умножения используют $ times_{} $; часто его вовсе опускают: $ z_1cdot z_2 = z_1times z_2 = z_1z_2 $.
П
Пример. $ (2,3)cdot (1,2)=(-4,7) $, $ (1,-1)cdot(1,1)= qquad $ ,
$ (0,1)cdot(0,1)=qquad $ .
В отличие от суммы комплексных чисел, определение произведения кажется довольно
искусственным. Ответ на вопрос
Что послужило основанием для такого правила умножения?
будет дан
☟
НИЖЕ. А пока убедимся, что даже введенное таким «неестественным» способом, оно,
тем не менее, сохранит те свойства операций над числами вещественными, которые
упомянуты выше. Имеем, например:
$$z_1cdot z_2=(ac-bd, ad+bc), z_2cdot z_1=(ca-db,, da+cb) Rightarrow
z_1cdot z_2=z_2cdot z_1 . $$
Остальные свойства проверяются аналогично.
Теперь осталось определить операции, противоположные сложению и умножению, т.е. вычитание и деление.
Разностью комплексных чисел $ z_1 $ и $ z_2 $ называется число $ z_5 $ такое, что $ z_2+z_5=z_1 $. Этот факт записывают:
$ z_5 = z_1-z_2 $.
Вопрос о существовании и единственности такого числа решается конструктивно:
его построением. Пусть $ z_1=(a,b) $, $ z_2=(c,d) $, $ z_5=(x,y) $, тогда
$$(c,d)+(x,y)=(a,b) iff c+x=a, d+y=b iff x=a-c, y=b-d ,
$$
т.е. $ (a,b)-(c,d)=(a-c,, b-d) $. В частности,
$$(a,b)-(a,b)=(0,0) quad mbox{ или }quad (a,b)+(0,0)=(a,b)$$
для любого комплексного числа. Таким образом, комплексное
число $ (0,0) $ играет для сложения ту же роль, что для вещественных чисел играл нуль $ 0 $.
Частным комплексных чисел $ z_1 $ и $ z_2 $ называется число $ z_6 $ такое, что $ z_2cdot z_6=z_1 $. Этот факт записывают:
$$ z_6= z_1colon z_2 quad mbox{ или } z_6 = z_1big/ z_2 . $$
Вопрос о существовании и единственности такого числа решается конструктивно:
его построением. Пусть $ z_1=(a,b) $, $ z_2=(c,d) $, $ z_6=(x,y) $, тогда
$$(c,d)cdot (x,y)=(a,b) iff
left{begin{array}{c}
cx-dy=a, \
dx+cy=b
end{array} right.
iff
left{begin{array}{c}
(c^2+d^2)x=(ac+bd), \
(c^2+d^2)y=(bc-ad).
end{array} right.
$$
Таким образом, необходимым условием существования частного является
$ c^2+d^2ne 0 $ т.е. $ z_2ne (0,0) $. При выполнении этого условия, частное
будет единственно и определяется формулой:
$$(a,b) colon (c,d) =left( frac{ac+bd}{c^2+d^2} , ,
frac{bc-ad}{c^2+d^2} right) . $$
Запомнить и применять эту формулу довольно сложно, но, как мы вскоре увидим,
в этом и нет необходимости.
А пока что заметим, что введенные на множестве комплексных чисел операции
полностью подчиняются указанной в начале раздела
системе аксиом
1
–
7
чисел вещественных.
Нейтральный элемент относительно сложения совпадает с числом $ (0,0) $, а относительно умножения — с числом $ (1,0) $:
$$
(a,b)cdot (x,y)=(a,b) iff
left{
begin{array}{l}
a,x-b,y=a, \
b,x+a,y=b,
end{array}
right.
iff
left{
begin{array}{l}
left(a^2+b^2 right)x=left(a^2+b^2 right), \
left(a^2+b^2 right)y=0
end{array}
right. qquad Rightarrow y=0,, x=1 .
$$
Каждое комплексное число может быть представлено в виде
$$z=(a,b)=(a,0)+(0,b)=(a,0)+(b,0)(0,1) , $$
т.е. в виде комбинации комплексных чисел вида $ (a,0) $ — с нулевой второй
компонентой, и одного специального числа $ (0,1) $. За последним закрепляется
обозначение2)
$$ mathbf i = (0,1) . $$
Следует заметить, что множество комплексных чисел, имеющих нулевую вторую компоненту
$$ left{ (a,0) mid ain mathbb R right} $$
обладает
свойством замкнутости относительно операций сложения и умножения.
Замкнутость понимается в том смысле, что сумма и произведение чисел с нулевой второй компонентой
снова будет числом с нулевой второй компонентой; то же справедливо и
для разности и произведения:
$$(a,0)+(b,0)=(a+b,0), (a,0)-(b,0)=(a-b,0), $$
$$ (a,0)cdot(b,0)=(ab,0) , (a,0)colon (b,0)= left( frac{a}{b} ,0 right) ( npu bne 0) . $$
Как легко видеть, первые компоненты под действием таких операций ведут себя
в точности как обычные вещественные числа (с сохранением
системы аксиом
1
–
7
). Исходя из этого обстоятельства,
производится отождествление комплексного числа $ (a,0) $ с вещественным
числом $ a_{} $. Результатом этого является следующая нормальная форма
записи комплексного числа
$$ (a,b)=a+ b mathbf i = a+ mathbf i b npu quad {a,b } subset mathbb R .$$
Для числа $ mathbf i $ получаем одно определяющее равенство:
$$
mathbf i^2=(0,1)cdot (0,1)=(-1,0)=-1 .
$$
Из соображений упрощения записи, договорились число $ 0+mathbf i b $
записывать просто в виде $ mathbf i b $, а числа $ a+mathbf i 1 $ и $ a-mathbf i 1 $
записывать в виде $ a+mathbf i $ и $ a-mathbf i $.
Польза от нормальной формы записи состоит в том, что она упрощает действия с комплексными числами. В самом деле, перемножение двух комплексных чисел, представленных в нормальной форме,
можно начать производить по обычным правилам перемножения вещественных
чисел:
$$(a+mathbf i , b)(c+ mathbf i , d)=ac + mathbf i, ad+ mathbf i, bc+ mathbf i^2 bd , $$
а затем воспользоваться равенством $ mathbf i^2 = -1 $:
$$= (ac-bd)+mathbf i , (ad+bc) . $$
Мы получили тот же результат, что формально определен аксиомой.
Если $ n_{} $ — целое число, то число
$$
z^n =
left{
begin{array}{cl}
overbrace{ztimes dots times z}^{n} & npu n>0, \
1 & npu n=0, zne 0, \
1/z^{-n} & npu n<0, zne 0
end{array} right.
$$
называется $ mathbf n $-й степенью числа $ z_{} $.
Для вычисления $ z^n $ при $ n>1 $ и $ z=a+ mathbf i, b $ можно применить формулу бинома Ньютона:
$$
left(a+ mathbf i, b right)^n =
$$
$$
=a^n+C_n^1 a^{n-1}bmathbf i+C_n^2 a^{n-2}b^2mathbf i^2
+C_n^3 a^{n-3}b^3mathbf i^3+C_n^4 a^{n-4}b^4mathbf i^4+dots+b^n mathbf i^n
$$
(здесь $ C_n^k $ означает биномиальный коэффициент );
и для приведения этого числа к нормальной форме, нам потребуется вычислить
степени $ mathbf i $. Получаем последовательно:
$$mathbf i^2=-1, mathbf i^3=mathbf i^2mathbf i=-mathbf i, mathbf i^4=1, mathbf i^5=mathbf i, dots $$
и понятно, что последовательность оказывается циклической с периодом $ 4_{} $.
Окончательно:
$$left(a+ mathbf i, b right)^n
=left(a^n- C_n^2 a^{n-2}b^2 +C_n^4 a^{n-4}b^4 – dots right)
+ mathbf i left(C_n^1 a^{n-1}b-C_n^3 a^{n-3}b^3+ dots right) .
$$
П
Пример. Найти нормальную форму числа $ (1+mathbf i )^3 $.
Решение. Разложение по формуле бинома дает
$ (1+mathbf i)^3= (1-3) +mathbf i (3-1) =-2+2mathbf i $.
♦
П
Пример. Найти нормальную форму числа
$$ frac{(3+2mathbf i )^2(1-3mathbf i )}{(3+mathbf i )^2(1+2mathbf i )}+frac{1+mathbf i }{1-mathbf i } .
$$
Решение.
$$(3+2mathbf i)^2=5+12 mathbf i ,
(5+12 mathbf i)(1-3mathbf i)=5-15mathbf i+12mathbf i-36mathbf i^2=41-3mathbf i ,$$
$$(3+mathbf i)^2=8+6mathbf i ,
(8+6mathbf i)(1+2mathbf i)=8+16mathbf i +6mathbf i +12mathbf i^2=-4+22 mathbf i .$$
Для вычисления частного $ (41-3mathbf i)/(-4+22mathbf i) $
воспользуемся следующим приемом: домножим и числитель и знаменатель дроби
на число $ (-4-22 mathbf i) $. Получим
$$
frac{(41-3mathbf i)(-4-22 mathbf i)}{(-4+22 mathbf i)(-4-22 mathbf i)}=
frac{-164-902 mathbf i +12 mathbf i +66 mathbf i^2}{16+88mathbf i – 88 mathbf i – 484 mathbf i^2}=
frac{-230-890 mathbf i}{500}
=-frac{23}{50}
-frac{89}{50} mathbf i .
$$
Аналогично:
$$
frac{1+mathbf i}{1-mathbf i}=frac{(1+mathbf i)^2}{(1-mathbf i)(1+mathbf i)}=frac{2mathbf i}{2}=mathbf i .
$$
Ответ. $ -frac{23}{50} -frac{39}{50} mathbf i $.
Прием, использованный нами при решении последнего примера, можно сделать универсальным.
Число $ a-mathbf i b $ называется числом, комплексно-сопряженным (или просто сопряженным) числу $ z=a+mathbf i b $.
Оно обозначается $ overline{z} $. Сама операция нахождения $ overline{z} $ называется комплексным сопряжением.
П
Пример. $ overline{-2-2mathbf i}=-2+2mathbf i, overline{3mathbf i}=-3mathbf i, overline{4}=4 $.
?
Доказать, что
а) $ overline{overline{z}}=z $;
б) $ overline{z_1+z_2}=overline{z_1}+overline{z_2} $;
в) $ overline{z_1cdot z_2}=overline{z_1} cdot overline{z_2} $.
Легко установить, что сумма и произведение двух комплексно-сопряженных
чисел будет числом вещественным:
$$ {.}_{} mbox{ при } z= a+ mathbf i b mbox{ имеем: } z+overline{z}=2a, z cdot overline{z}=a^2+b^2 . $$
На последнем свойстве и основан прием вычисления частного двух чисел $ z_1/z_2 $.
Именно, эта дробь домножается на число, сопряженное к знаменателю:
$$
frac{z_1}{z_2}=frac{z_1 overline{z_2}}{z_2 overline{z_2}} ;
$$
при перемножении в знаменателе образуется вещественное число:
$$
=frac{(a+mathbf i b)(c-mathbf i d)}{c^2+d^2} ,
$$
и, таким образом, операцию деления сводим к операции умножения:
$$
=frac{(ac+bd)+ mathbf i (bc-ad)}{c^2+d^2}=frac{ac+bd}{c^2+d^2} +
mathbf i frac{bc-ad}{c^2+d^2} .
$$
Для комплексного числа, представленного в нормальной форме $ z=a+mathbf i b $, число $ a $ называется вещественной частью и
обозначается $ mathfrak{Re}(z) $, число $ b_{} $ называется мнимой частью и
обозначается $ mathfrak{Im} (z) $. Таким образом, $ z=mathfrak{Re}(z) +mathbf i mathfrak{Im}(z) $.
Число $ mathbf i $ называется мнимой единицей. Число $ zne 0 $, имеющее ненулевую мнимую часть:
$ mathfrak{Im}(z) ne 0 $, называется мнимым числом, а число $ z $, имеющее нулевую вещественную часть: $ mathfrak{Re}(z)=0 $, называется чисто мнимым.
В некоторых учебниках (см., к примеру, [5]) мнимая часть числа $ a+mathbf i b $ определяется как число $ mathbf i b $; но всё же чаще я встречал это определение именно в приводимом здесь (и в дальнейшем используемом) варианте.
Аксиому равенства комплексных чисел можно записать теперь в виде:
$$z_1=z_2 quad iff quad mathfrak{Re}(z_1)=mathfrak{Re} (z_2), mathfrak{Im} (z_1)=mathfrak{Im} (z_2) .$$
?
Найти вещественное число $ x_{} $, удовлетворяющее уравнению
$$ (1+ mathbf i)x^3+(1+2, mathbf i)x^2- (1+4,mathbf i)x – 1+ mathbf i = 0 . $$
?
Верно ли равенство $ mathfrak{Re}(z_1z_2)= mathfrak{Re}(z_1) mathfrak{Re}(z_2) $?
Множество всех комплексных чисел с определенными выше операциями обозначается $ mathbb C_{} $ . Отождествление комплексного числа
$ z_{} $, у которого
$ mathfrak{Im} (z)=0 $, с вещественным числом $ mathfrak{Re}(z) $ позволяет говорить, что множество
$ mathbb C_{} $ включает в себя множество вещественных чисел $ mathbb R_{} $: $ mathbb R_{} subset mathbb C_{} $.
Комплексные числа «наследуют» все привычные нам свойства чисел вещественных, кроме одного: их нельзя сравнивать в смысле отношений $ >_{} $ или $ < $:
неравенство $ 1+7mathbf i>3-2mathbf i $ так же бессмысленно, как и $ 1+7mathbf i<3-2mathbf i $.
Геометрическая интерпретация
Определение комплексного числа как упорядоченной пары вещественных чисел
напоминает определение вектора на плоскости. Если на плоскости $ (x,y) $
задана декартова прямоугольная система координат, то задание точки $ {mathbf A} $
ее координатами $ x=a,y=b $ однозначно определяет вектор, имеющий начало в начале координат $ {mathbf O} $ ($ x=0,y=0 $), а конец — в точке $ {mathbf A} $. Такое соответствие

$$
vec{mathbf OA} longleftrightarrow (a,b) longleftrightarrow
z=a+mathbf i , b $$
позволяет дать интерпретацию комплексного числа как вектора на плоскости.
Сама эта плоскость называется комплексной плоскостью, ось абсцисс на ней — вещественной осью (на ней располагаются вещественные числа), ось ординат — мнимой осью
(на ней располагаются чисто мнимые числа).
?
Изобразить на комплексной плоскости а) число $ (-z) $; б) число $ overline{z} $.
Определения равенства и суммы (разности) векторов и комплексных чисел

оказываются идентичными: сумма комплексных чисел определяет вектор на
плоскости, равный сумме векторов, соответствующих слагаемым (по какому бы
способу — параллелограмма или треугольника — она ни вычислялась).
Подмеченная аналогия между алгебраическим объектом и геометрическим
прекращается как только мы попытаемся установить соответствие между
операциями умножения. В самом деле, согласно
введенному в предыдущем пункте определению, произведение комплексных чисел есть снова
комплексное число, т.е. — в нашей геометрической интерпретации
— вектор. Вспомним, что скалярное произведение векторов определяется
как число вещественное, т.е. является скаляром3).
Однако, несмотря на то, что не всегда удается установить параллель между
свойствами двух объектов, хотя бы некоторые результаты, а также приемы
исследования, могут допускать распространение. Один из таких приемов
лежит на виду. Вспомним, что вектор на плоскости может быть задан не
только в декартовых координатах, но и в полярных, т.е. своей длиной
и углом, образованным с полярной осью.
Тригонометрическая форма комплексного числа
Для числа $ z=a+mathbf i , b $ его модулем (или абсолютной величиной) называется неотрицательное вещественное число обозначаемое $ |z| $, определяемое как
$$|z|=sqrt{a^2+b^2}= sqrt{z, overline{z}} ; $$
при этом корень квадратный в правой части понимается как корень арифметический, т.е. как единственное неотрицательное вещественное число, квадрат которого равен $ a^2+b^2 $.
Геометрическая интерпретация модуля комплексного числа очевидна: это длина
вектора, этим числом порождаемого. В случае когда $ mathfrak{Im} (z) =0 $ введенное определение модуля соответствует определению модуля вещественного числа: $ |z|=|a| $.
Аргументом комплексного числа $ z=a+mathbf i , bne 0 $

называется величина угла4),
образованного на комплексной плоскости вектором $ vec{mathbf OA} $
с вещественной осью. При этом, для однозначности определения, договоримся,
что угол будет отсчитываться от вещественной оси в положительном направлении,
т.е. против часовой стрелки, и что он будет находиться в интервале $ [0,2, pi[ $
если вычисляется в радианах. Аргумент комплексного числа $ 0_{} $ не определяется.
Будем обозначать аргумент числа $ z_{} $ через $ operatorname{arg}, (z) $.
Для определения $ operatorname{arg}, (z) $ мы имеем две формулы:
$$
cos left( operatorname{arg}, (z) right) = frac{a}{sqrt{a^2+b^2}} ,
sin left( operatorname{arg}, (z) right) = frac{b}{sqrt{a^2+b^2}} ,
$$
которые позволяют однозначно восстановить5)
угол в интервале $ [0, 2, pi[ $.
Итак, ненулевое комплексное число $ zne 0 $, наряду со своей нормальной формой
$ z=a+mathbf i , b $, может быть представлено еще и в форме
$$
z= rho left(cos varphi + mathbf i sin varphi right) quad npu
rhoge 0, 0 le varphi < 2, pi .
$$
Последняя называется тригонометрической формой комплексного числа. Формулы, связывающие две формы:
$$ rho=|z|=sqrt{a^2+b^2}, cos varphi = a / rho, sin varphi = b / rho , . $$
П
Пример. Найти тригонометрическую форму комплексных чисел
а) $ -4 $ ; б) $ mathbf i $ ; в) $ -6,mathbf i $ ; г) $ -1+mathbf i $;
д) $ frac{1}{2}-mathbf i frac{sqrt{3}}{2} $;
е) $ -2+mathbf i $ .
Решение.
$$
begin{array}{c|c|c|c|c}
z & |z| & cos &operatorname{sign} (sin ) & operatorname{arg}(z) \
hline
-4=-4+0mathbf i & 4 & -1 & & pi \
mathbf i=0+1mathbf i & sqrt{0+1}=1 & 0 & >0 & pi/2 \
-6,mathbf i=0-6,mathbf i & sqrt{0+36}=6 &
0 &<0 & 3pi/2\
-1+mathbf i=-1+1mathbf i & sqrt{1+1}=sqrt{2}&
-frac{scriptstyle 1}{scriptstyle{sqrt{2}}}=-frac{scriptstyle{sqrt{2}}}{scriptstyle 2} &
>0 & 3pi/4 \
frac{1}{2}-mathbf i frac{scriptstyle{sqrt{3}}}{scriptstyle 2} &
sqrt{frac{1}{4}+frac{3}{4}}=1 & frac{1}{2} & <0 & 5pi/3 \
-2+mathbf i & sqrt{4+1}=sqrt{5} & scriptstyle{-2}/{scriptstyle sqrt{5}}&
>0 & arccos left(-scriptstyle{2}/scriptstyle{sqrt{5}} right) approx \
& & & & approx 2.67794
end{array}
$$
Ответ. а) $ 4left(cos pi + mathbf i , sin pi right) $;
б) $ cos pi/2 + mathbf i , sin pi/2 $;
в) $ 6left(cos 3pi/2 + mathbf i , sin 3pi/2 right) $;
г) $ sqrt{2} left(cos 3pi/4 + mathbf i , sin 3pi/4 right) $;
д) $ cos 5pi/3 + mathbf i , sin 5pi/3 $;
е)
$ sqrt{5} left{cos left( arccos left(
-scriptstyle{2}/scriptstyle{sqrt{5}} right) right) +mathbf i
sin left( arccos left(-scriptstyle{2}/scriptstyle{sqrt{5}} right) right) right}
approx 2.23606 left( cos 2.67794 + mathbf i sin 2.67794 right) $.
?
Пусть $ z=a+mathbf i , b $.
Выразить а) $ operatorname{arg} (-z) $ ; б) $ operatorname{arg} (overline{z}) $
в) $ operatorname{arg} (1/z) $; г) $ operatorname{arg} (b+mathbf i, a) $ через
$ operatorname{arg} (z) $.
В дальнейшем я иногда буду пренебрегать требованием, чтобы в тригонометрической форме аргумент
соответствовал интервалу $ [0, 2, pi[ $, т.е. буду допускать
неоднозначность в определении $ operatorname{arg} (z) $.
С учетом этого допущения, сформулируем следующий критерий равенства чисел $ z_{1} $ и $ z_{2} $, представленных в тригонометрической форме.
Т
Теорема. Комплексные числа равны тогда и только тогда, когда их модули равны, а их аргументы различаются на целое кратное числа $ 2, pi $ или, если использовать терминологию из теории чисел, сравнимы по модулю $ 2, pi $:
$$
rho_1 left(cos varphi_1 + mathbf i , sin varphi_1 right)=
rho_2 left(cos varphi_2 + mathbf i , sin varphi_2 right) iff
$$
$$
iff rho_1=rho_2 , varphi_1 equiv varphi_2 pmod{2, pi} .
$$
Доказательство следует из аксиомы равенства комплексных чисел.
♦
В каждом разделе математики имеется исторически сложившаяся система названий
и обозначений, при этом иногда одни и те же слова или символы в разных разделах
обозначают совершенно не связанные по смыслу объекты. В частности, это
относится к слову «модуль»: если в разделе МОДУЛЯРНАЯ АРИФМЕТИКА оно означает натуральное число $ M_{} $, по отношению к которому сравниваются два других целых числа (одинаковы ли у них остатки при делении на $ M_{} $), то в теории комплексных чисел оно закреплено за другим понятием. К сожалению,![]() в настоящем разделе приходится использовать оба этих определения; хорошо хоть обозначения у них разные…
в настоящем разделе приходится использовать оба этих определения; хорошо хоть обозначения у них разные…
В противоположность предыдущему замечанию — удобное обозначение почему бы не тиражировать?![]() В разделе МОДУЛЯРНАЯ АРИФМЕТИКА сравнимость понималась по отношению к натуральному числу и формально вводилось через операцию деления на модуль; мы же использовали в только что приведенной теореме обобщение этого понятия: $ varphi_1 equiv varphi_2 pmod{2, pi} $, основанное на свойстве разности двух чисел $ varphi_1 – varphi_2 $ быть целым кратным (иррационального!) числа $ 2, pi $. В дальнейшем мы заимствуем и другое полезное обозначение из теории чисел: $ varphi_1 = varphi pmod{2, pi} $ означает, что угол $ varphi_1 $ — это «загнанный в интервал» $ [0, 2, pi[ $ угол $ varphi $, т.е. $ varphi_1 $ отличается от $ varphi_{} $ на целое кратное числа $ 2, pi $ и, при этом, $ varphi_1 in [0, 2, pi[ $.
В разделе МОДУЛЯРНАЯ АРИФМЕТИКА сравнимость понималась по отношению к натуральному числу и формально вводилось через операцию деления на модуль; мы же использовали в только что приведенной теореме обобщение этого понятия: $ varphi_1 equiv varphi_2 pmod{2, pi} $, основанное на свойстве разности двух чисел $ varphi_1 – varphi_2 $ быть целым кратным (иррационального!) числа $ 2, pi $. В дальнейшем мы заимствуем и другое полезное обозначение из теории чисел: $ varphi_1 = varphi pmod{2, pi} $ означает, что угол $ varphi_1 $ — это «загнанный в интервал» $ [0, 2, pi[ $ угол $ varphi $, т.е. $ varphi_1 $ отличается от $ varphi_{} $ на целое кратное числа $ 2, pi $ и, при этом, $ varphi_1 in [0, 2, pi[ $.
Тригонометрическая форма комплексных чисел позволяет дать геометрическую интерпретацию
правилам их умножения и деления.
Т
Теорема. Имеет место равенство:
$$rho_1 left(cos varphi_1 + mathbf i , sin varphi_1 right) cdot
rho_2 left(cos varphi_2 + mathbf i , sin varphi_2 right)=
$$
$$
= rho_1 rho_2 left(cos (varphi_1+varphi_2) + mathbf i ,
sin (varphi_1+varphi_2) right) ;
$$
иными словами: при перемножении комплексных чисел перемножаются их модули и
складываются аргументы (по модулю $ 2, pi $):
$$
left| z_1cdot z_2 right| = left| z_1 right| cdot left| z_2 right| ,
operatorname{arg} (z_1 cdot z_2)= operatorname{arg} (z_1) + operatorname{arg} (z_2) pmod{2, pi} .
$$
Доказательство.
$$ z_1z_2=rho_1 rho_2big(left[cos varphi_1cos varphi_2 –
sin varphi_1sin varphi_2 right] + mathbf i ,
left[cos varphi_1sin varphi_2 +
sin varphi_1cos varphi_2 right] big) =
$$
$$
=rho_1 rho_2left(cos (varphi_1+varphi_2) + mathbf i ,
sin (varphi_1+varphi_2) right) .
$$
♦
Настоящее замечание может быть пропущено без ущерба для понимания оставшейся части раздела.
Переписав равенство для модуля произведения из последней теоремы для нормальной формы записи комплексных чисел, получаем совершенно вещественное равенство (фактически, если рассматривать входящие в это равенство параметры как переменные величины — тождество для полиномов от нескольких переменных ):
$$(a^2+b^2)(c^2+d^2)=(ac-bd)^2+(ad+bc)^2 , $$
иными словами: произведение суммы квадратов на сумму квадратов есть снова сумма двух квадратов. Существуют ли подобные тождества с большим, чем $ 2_{} $ числом квадратов? Ответ оказывается положительным: подобные тождества для $ 4_{} $-х квадратов были получены Эйлером (см.
☞
ЗДЕСЬ ), а для $ 8_{} $-ми квадратов — Кэли. Доказано, что других случаев быть не может. Эта задача тесно связана с понятием гиперкомплексных чисел, т.е. многомерных аналогов комплексных чисел (см.
☞
ЗДЕСЬ ).
=>
Справедлива формула
$$
frac{z_1}{z_2}=frac{rho_1}{rho_2 }left(cos (varphi_1-varphi_2) + mathbf i ,
sin (varphi_1-varphi_2) right) quad npu z_2 ne 0
.
$$
=>
Индукцией по числу сомножителей показывается справедливость общей формулы:
$$
prod_{j=1}^n z_j= prod_{j=1}^n rho_j
left(cos sum_{j=1}^n varphi_j + mathbf i ,
sin sum_{j=1}^n varphi_j right) .
$$
В частном случае, когда все сомножители одинаковы, приходим к
одной замечательной формуле —
Формула Муавра
Т
Теорема. Для любого целого $ n $ справедлива формула Муавра:
$$
left(cos varphi + mathbf i , sin varphi right)^n = cos nvarphi + mathbf i , sin nvarphi
.
$$
Доказательство для положительных $ n $ следует из результата предыдущего пункта. При $ n=0 $ формула
фактически является формальным определением нулевой степени комплексного числа.
Для отрицательного показателя $ n=-m, min mathbb N $ справедливость формулы доказывается
сведением к уже рассмотренному случаю положительного показателя:
$$
left(cos varphi + mathbf i , sin varphi right)^{n}=
left(cos varphi + mathbf i , sin varphi right)^{-m}=
$$
$$
=frac{1}{left(cos varphi + mathbf i , sin varphi right)^{m}}
=
frac{1}{cos mvarphi + mathbf i , sin mvarphi}= frac{cos mvarphi – mathbf i , sin mvarphi }{cos^2 mvarphi + sin^2 mvarphi }
=
$$
$$
=cos mvarphi – mathbf i , sin mvarphi=
cos (- mvarphi) + mathbf i , sin (- mvarphi)=cos nvarphi + mathbf i , sin nvarphi .
$$
♦
=>
Справедлива формула возведения в степень комплексного числа, представленного в тригонометрической форме:
$$
left[ rho left(cos varphi + mathbf i , sin varphi right) right]^n
= rho^n left( cos nvarphi + mathbf i , sin n varphi right)
npu forall rho ne 0 u nin mathbb Z
.
$$
П
Пример. Вычислить
$$
left[frac{1}{2 sqrt{2}}left(sqrt{3} – mathbf i , sqrt{5} right) right]^{117}
.
$$
Решение. С одной стороны, можно воспользоваться формулой бинома Ньютона —
мы получим точный ответ, хотя и дорогой ценой… Если же нас интересует
приближенное значение, то его можно получить по формуле Муавра, предварительно представив число
в тригонометрической форме:
$$
left| z right| = 1,
cos (operatorname{arg} (z)) = frac{1}{2}sqrt{frac{3}{2}} approx 0.61237,
sin (operatorname{arg} (z)) <0 qquad Rightarrow
$$
$$
Rightarrow qquad operatorname{arg} (z) = 2pi – arccos left( frac{1}{2}sqrt{frac{3}{2}} right) approx
5.37144 .
$$
Применяем формулу Муавра:
$$z^{117}approx cos left( 117 times operatorname{arg} (z) right) +
mathbf i , sin left( 117 times operatorname{arg} (z) right)
$$
и отбрасываем целое кратное $ 2 pi_{ } $:
$$ 117 times operatorname{arg} (z) approx 0.14077
+ 200 pi quad Rightarrow quad
z^{117}approx cos 0.14077 + mathbf i , sin 0.14077 .$$
Ответ.
$$frac{sqrt{2}}{2^{60}} left[466022392183308159, sqrt{3}+
mathbf i , 51153470739918917, sqrt{5} right] approx
0.99010 + mathbf i , 0.14030 .
$$
?
Вычислить
а) $ left(sqrt{3}+ mathbf i , right)^n $ ; б)
$ left[ sin varphi_1 – sin varphi_2 + mathbf i , left( cos varphi_1 –
cos varphi_2 right) right]^n $.
И
Биографические заметки о Муавре
☞
ЗДЕСЬ
Неравенства для модуля
Т
Теорема. Справедливо неравенство треугольника:
$$
left| z_1 + z_2 right| le left| z_1right| + left| z_2right| .
$$
Доказательство. Имеем:
$$left| z_1 + z_2 right|^2=left( z_1 + z_2 right)overline{left( z_1 + z_2 right)}=
left( z_1 + z_2 right)left( overline{z_1} + overline{z_2} right)=
z_1overline{z_1} + z_1overline{z_2}+ overline{z_1}z_2+ z_2 overline{z_2}=
$$
$$
=rho_1^2 + rho_2^2 +rho_1 rho_2 left( cos varphi_1 + mathbf i sin varphi_1
right)left( cos varphi_2 – mathbf i sin varphi_2
right) +
$$
$$
+ rho_1 rho_2 left( cos varphi_1 – mathbf i sin varphi_1
right)left( cos varphi_2 + mathbf i sin varphi_2 right)=
$$
$$
=rho_1^2 + rho_2^2 +2,rho_1 rho_2 left(cos varphi_1 cos varphi_2+
sin varphi_1 sin varphi_2 right)=
$$
$$
=rho_1^2 + rho_2^2 +2,rho_1 rho_2 cos left( varphi_1 – varphi_2 right) le
rho_1^2 + rho_2^2 +2,rho_1 rho_2 = left( rho_1 +rho_2 right)^2
$$
поскольку $ left| cos left( varphi_1 – varphi_2 right) right|le 1 $.
Извлекая корень (арифметический), получаем доказываемое неравенство.
♦
?
При каких условиях на $ z_{1} $ и $ z_{2} $ неравенство треугольника
превращается в равенство?
=>
$ displaystyle left| sum_{j=1}^n z_j right| le sum_{j=1}^n |z_j | $.
=>
$ displaystyle left| z_1 + z_2 right| ge big| | z_1 | – | z_2 | big| ,
left| z_1 – z_2 right| ge big| | z_1 | – | z_2 | big| $.
?
Доказать «равенство параллелограмма»:
$$ |z_1+z_2|^2+|z_1-z_2|^2=2|z_1|^2 + 2|z_2|^2 quad mbox{ при }
{z_1, z_2 } subset mathbb C . $$
Выведение тригонометрических формул
Сумма синусов (косинусов)
Задача. Найти компактное выражение для
$$
B= sin varphi + sin 2, varphi + dots + sin n, varphi .
$$
Для пояснения такой постановки сошлемся на известные выпускнику школы формулы, выражающие
суммы арифметической и геометрической прогрессий:
$$
a+(a+d)+dots+(a+(n-1)d)=frac{(2a+(n-1)d)n}{2} ,
$$
$$
a+aq+dots+aq^{n-1}
=afrac{q^n-1}{q-1} quad npu qne 1 .
$$
О подобных формулах говорят, что соответствующие суммы «свернулись».
Поставленную задачу будем решать путем ее усложнения. Попробуем одновременно
с указанной суммой свернуть и сумму
$$
A= cos varphi + cos 2, varphi + dots + cos n, varphi .
$$
Для этого составим выражение
$$
A+ mathbf i B= left( cos varphi + mathbf i sin varphi right) +
left( cos 2, varphi + mathbf i sin 2,varphi right) + dots +
left( cos n, varphi + mathbf i sin n, varphi right)=
$$
на основании формулы Муавра:
$$
=left( cos varphi + mathbf i sin varphi right) +
left( cos varphi + mathbf i sin varphi right)^2 + dots +
left( cos varphi + mathbf i sin varphi right)^n .
$$
Введем новую переменную: $ z= cos varphi + mathbf i sin varphi $. Тогда
последняя сумма оказывается суммой геометрической прогрессии:
$$ A+ mathbf i B =z+z^2+dots +z^n =frac{z^{n+1} – z}{z-1} quad npu zne 1
. $$
Возвращаемся к исходной переменной $ varphi $:
$$
A+ mathbf i, B =frac{left(cos varphi + mathbf i, sin varphi right)^{n+1} –
left(cos varphi + mathbf i, sin varphi right)}
{cos varphi + mathbf i, sin varphi-1}
npu varphi ne 2, pi k , kin mathbb Z .
$$
(последнее условие можно записать в виде $ varphi notequiv 0 pmod{2, pi} $)
и снова применяем формулу Муавра, только теперь уже «в обратном направлении»:
$$
A+ mathbf i, B =
frac{left(cos (n+1), varphi + mathbf i, sin (n+1), varphi right) –
left(cos varphi + mathbf i, sin varphi right)}
{cos varphi + mathbf i, sin varphi-1}
$$
при $ varphi notequiv 0 pmod{2, pi} $.
Искомое выражение для $ B $ получится если мы вычислим мнимую часть дроби, стоящей в правой части.
Мы сейчас сделаем это, только предварительно слегка преобразуем числитель и знаменатель
с использованием известных тригонометрических формул:
$$
cos alpha – cos beta = 2 sin frac{alpha + beta }{2} ,
sin frac{beta – alpha}{2} quad , quad
sin alpha – sin beta = 2 cos frac{alpha + beta }{2} ,
sin frac{ alpha – beta}{2} .
$$
Итак, числитель правой части формулы равен
$$
left(cos (n+1), varphi – cos , varphi right) +
mathbf i , left(sin (n+1), varphi – sin , varphi right)=
$$
$$
=-2, sin frac{(n+2), varphi}{2} , sin frac{n, varphi}{2} +
2, mathbf i, cos frac{(n+2), varphi}{2} , sin frac{n, varphi}{2}=
$$
$$
=2, mathbf i, sin frac{n, varphi}{2}
left(cos frac{(n+2), varphi}{2} + mathbf i, sin frac{(n+2), varphi}{2} right)
;
$$
а знаменатель:
$$
(cos varphi -1) + mathbf i, sin varphi =-2, sin^2 frac{varphi}{2} +
2, mathbf i, sin frac{varphi}{2} , cos frac{varphi}{2}
=2, mathbf i, sin frac{varphi}{2}
left(cos frac{varphi}{2} + mathbf i, sin frac{varphi}{2} right) .
$$
Следовательно,
$$
A+ mathbf i, B =
frac{sin displaystyle frac{n, varphi}{2} }{sin displaystyle frac{varphi}{2} }
cdot
frac{displaystyle cos frac{(n+2), varphi}{2} + mathbf i, sin frac{(n+2), varphi}{2}}
{displaystyle cos frac{varphi}{2} + mathbf i, sin frac{varphi}{2}}=
$$
ко второй дроби применяем формулу деления чисел, представленных в тригонометрической форме:
$$
=
frac{sin displaystyle frac{n, varphi}{2} }{sin displaystyle frac{varphi}{2} }
left(cos frac{(n+1), varphi}{2} + mathbf i, sin frac{(n+1), varphi}{2} right)
,
$$
и вычислить мнимую часть этого выражения не составляет труда.
Окончательно имеем:
$$
sin varphi + sin 2, varphi + dots + sin n, varphi =
frac{sin displaystyle frac{n}{2} , varphi , sin displaystyle frac{n+1}{2} , varphi }
{sin displaystyle frac{1}{2} , varphi}
npu varphi notequiv 0 pmod{2, pi} .
$$
В качестве «бонуса» мы получили и аналогичную формулу для косинусов:
$$
cos varphi + cos 2, varphi + dots + cos n, varphi =
frac{sin displaystyle frac{2,n+1}{2} , varphi}{2 sin displaystyle frac{1}{2} ,
varphi} – frac{1}{2} .
$$
После того, как искомая формула выведена,
не составляет труда доказать ее другим способом —
без применения аппарата комплексных чисел. В самом
деле, домножим левую ее часть на $ sin varphi/2 $:
$$
sin varphi cdot sin frac{1}{2} , varphi +
sin 2, varphi cdot sin frac{1}{2} , varphi + dots +
sin n, varphi cdot sin frac{1}{2} , varphi =
$$
и преобразуем каждое произведение в разность косинусов:
$$
=frac{1}{2} bigg(cos frac{3}{2} , varphi – cos frac{1}{2} , varphi
+ cos frac{5}{2} , varphi – cos frac{3}{2} , varphi + dots +
$$
$$
+ cos left( n + frac{1}{2} right) , varphi –
cos left( n – frac{1}{2} right) , varphi
bigg) =
$$
все слагаемые, кроме двух, сокращаются:
$$
=frac{1}{2} left(cos left( n + frac{1}{2} right) , varphi –
cos frac{1}{2} , varphi right) =
sin displaystyle frac{n}{2} , varphi ,
sin displaystyle frac{n+1}{2} , varphi ,
$$
и мы получили числитель дроби, стоящей в правой части выведенной формулы.
В чем же заключалась польза от комплексных чисел, если доказать
формулу можно и без их использования? — Да в том, что эти числа позволили
нам вывести эту формулу, т.е. дали возможность угадать неизвестный путь к истине.
?
Свернуть сумму
$$cos varphi + cos 3, varphi + dots + cos (2n-1)varphi . $$
Ответ
☞
ЗДЕСЬ
§
Применение формулы суммы косинусов см. в разделе
☞
ТРИГОНОМЕТРИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ
Синус и косинус кратного угла
Задача. Найти общую формулу, выражающую $ cos n varphi $ через
$ cos varphi $ и $ sin varphi $.
Из школьного курса алгебры известна такая формула для $ n_{}=2 $: $ cos 2 varphi =
cos^2 varphi – sin^2 varphi $.
Для выведения же общей формулы воспользуемся двумя формулами разложения
$ left(cos varphi + mathbf i , sin varphi right)^n $: формулой бинома Ньютона
$$
left(cos varphi + mathbf i , sin varphi right)^n =
$$
$$
=cos^{n} varphi+C_n^1 cos^{n-1} varphi sin varphi mathbf i+C_n^2 cos^{n-2} varphi sin^2 varphi mathbf i^2
+C_n^3 cos^{n-3} varphi sin^3 varphi mathbf i^3+
$$
$$
+C_n^4 cos^{n-4} varphi sin^4 varphi mathbf i^4+dots+sin^n varphi mathbf i^n
$$
и формулой Муавра. Получаем:
$$ cos nvarphi + mathbf i , sin nvarphi =left(cos varphi + mathbf i , sin varphi right)^n= $$
$$
=left(cos^n varphi – C_n^2 cos^{n-2}varphi sin^2 varphi +
C_n^4 cos^{n-4}varphi sin^4 varphi – dots right) +
$$
$$
+ mathbf i , left(C_n^1 cos^{n-1}varphi sin varphi –
C_n^3 cos^{n-3}varphi sin^3 varphi- dots right) .
$$
На основании аксиомы равенства комплексных чисел:
$$
begin{array}{cl}
cos nvarphi = & cos^n varphi – displaystyle frac{n(n-1)}{2} cos^{n-2}varphi sin^2 varphi +
C_n^4 cos^{n-4}varphi sin^4 varphi – dots \
= & displaystyle sum_{j=0}^{lfloor n/2 rfloor} (-1)^j
C_n^{2, j} sin^{2, j} varphi cos^{n-2,j} varphi ; \
sin nvarphi = & sin varphi left(n cos^{n-1}varphi
-C_n^3 cos^{n-3}varphi sin^2 varphi +C_n^5 cos^{n-5}varphi sin^4 varphi-dots right) = \
= &displaystyle
sum_{j=0}^{lfloor (n-1)/2 rfloor} (-1)^j
C_n^{2, j+1} sin^{2, j+1} varphi cos^{n-2,j-1} varphi
.
end{array}
$$
Здесь $ C_n^k $ означает биномиальный коэффициент,
а $ lfloor quad rfloor $ — целую часть числа.
Таким образом, снова комплексные числа позволили нам вывести два совершенно
вещественных равенства.
П
Пример.
$$
begin{array}{ll}
cos , 4varphi &= cos^4 varphi – 6, cos^2 varphi sin^2 varphi + sin^4 varphi ,\
sin , 5varphi &= 5 , cos^4 varphi sin varphi – 10 , cos^2 varphi sin^3 varphi+ sin^5 varphi .
end{array}
$$
?
Найти выражения $ sin , n varphi $ через $ sin varphi $ и $ cos , n varphi $ через $ cos varphi $.
Решение
☞
ЗДЕСЬ.
?
Найти выражение $ operatorname{tg}, n varphi $ через $ operatorname{tg} , varphi $.
§
Решение обратной задачи: выражение $ cos^n varphi $ и $ sin^n varphi $ через косинусы и
синусы кратных углов, т.е. через $ cos varphi,sin varphi,cos 2varphi ,
sin 2varphi ,dots, cos nvarphi , sin nvarphi $
☞
ЗДЕСЬ.
Извлечение корня из комплексного числа
Пусть $ n_{} $ означает натуральное число. Корнем $ n_{} $-й степени из комплексного числа $ z_{} $
называется такое комплексное число $ w_{} $, что $ w^n=z $. Очевидно, что корень первой степени из $ z_{} $ совпадает с самим числом $ z_{} $ и корень любой степени из $ 0_{} $ равен $ 0_{} $ (в дальнейшем эти случаи рассматривать не будем). Обозначение корня при $ nge 2 $ такое же как и в случае вещественных чисел:
$$ w = sqrt[n]{z}, mbox{ а при } n=2 mbox{ показатель обычно не указывают: } w=sqrt{z} . $$
Задача. Вычислить $ displaystyle sqrt[n]{z} $.
Квадратный корень
Пусть $ z_{} $ представлено в каноническом виде: $ z=a+mathbf i b $ при
$ { a,b }subset mathbb R $. Будем искать число $ w $ также в каноническом виде:
$ w=x+ mathbf i y $, где $ x_{} $ и $ y_{} $ неизвестные вещественные величины. По определению квадратного корня, должно быть выполнено:
$$w^2=z iff (x+ mathbf i y)^2 = a+mathbf i b
iff (x^2-y^2) + 2,mathbf i xy = a+mathbf i b iff
$$
$$
iff x^2-y^2 = a, 2, xy = b .
$$
(на основании аксиомы равенства комплексных чисел). Возведем оба получившихся уравнения в квадрат и сложим:
$$left(x^2+y^2 right)^2 = a^2+ b^2 iff x^2+y^2 = sqrt{a^2+ b^2}
mbox{(поскольку } {x,y }subset mathbb R mbox{ )} . $$
Вместе с первым уравнением получаем линейную систему
относительно $ x_{}^2 $ и $ y_{}^2 $. Решаем ее относительно $ x_{}^2 $:
$$x^2=frac{1}{2} left(a+sqrt{a^2+ b^2} right)
Rightarrow
x=pm frac{1}{sqrt{2}} sqrt{a+sqrt{a^2+ b^2}}
.
$$
Имеем: $ x=0 iff b=0, ale 0 $. В этом случае $ y=pm sqrt{-a} $.
Таким образом:
$$
sqrt{a}= pm mathbf i sqrt{-a} quad npu a<0 .
$$
Если $ b ne 0 $, то
$$
y=frac{b}{2,x}= pm
frac{b}{sqrt{2}, sqrt{a+sqrt{a^2+ b^2}}}=
pm frac{1}{sqrt{2}} sqrt{- a+sqrt{a^2+ b^2} } , operatorname{sign}, (b)
;
$$
здесь $ operatorname{sign} $ означает знак числа.
Таким образом:
$$
sqrt{z} =pm frac{1}{sqrt{2}} left(sqrt{a+sqrt{a^2+ b^2}}
+mathbf i sqrt{-a+sqrt{a^2+ b^2}} ,
, operatorname{sign} , (b) right) .
$$
?
Вычислить а) $ sqrt{2, mathbf i} $; б) $ sqrt{-3} $ ; в) $ sqrt{2-3, mathbf i} $.
Формулы для вычисления квадратного корня позволят теперь решить любое
квадратное уравнение
$$z^2+p, z+q=0, quad npu {p,q }subset mathbb C .$$
В самом деле, преобразуем левую часть, выделив полный квадрат:
$$
z^2+p, z+q=z^2+p, z+left(frac{p}{2}right)^2 +left(q-frac{p^2}{4} right)=
left( z + frac{p}{2} right)^2 – frac{mathcal D}{4}
$$
при
$$ mathcal D= p^2-4, q ,$$
т.е. известному нам по вещественному случаю дискриминанте квадратного трехчлена.
Итак, квадратное уравнение преобразовано к виду:
$$left( z + frac{p}{2} right)^2 = frac{mathcal D}{4} ,$$
их которого получаем привычную форму записи его корней
$$
z_{1,2}=frac{1}{2} left(-ppm sqrt{mathcal D} right) ,
$$
с той только оговоркой, что теперь под $ sqrt{mathcal D} $ понимается
два значения корня квадратного из комплексного числа.
П
Пример. Решить уравнение $ z^2-2, z+3=0 $.
Решение. Здесь $ mathcal D=-8 $ и $ sqrt{mathcal D}= pm mathbf i 2 sqrt{2} $.
Ответ. $ 1pm mathbf i sqrt{2} $.
П
Пример. Решить уравнение $ z^2-(3+2, mathbf i ), z +(5+5, mathbf i ) =0 $.
Решение. Здесь $ mathcal D=(3+2, mathbf i )^2-4, (5+5, mathbf i )=-15 – 8, mathbf i $. По
формуле извлечения корня: $ sqrt{mathcal D}=pm (1-4, mathbf i ) $.
Ответ. $ 2- mathbf i , 1+3, mathbf i $.
П
Пример. Решить уравнение $ (3- mathbf i ), z^2+(1+ mathbf i ), z + 6, mathbf i =0 $.
Решение. Можно сначала поделить все уравнение на коэффициент при $ z^2 $,
но можно действовать и напрямую, обобщив понятие дискриминанта:
$$ mathcal D=(1+ mathbf i )^2- 4, (3- mathbf i ), 6, mathbf i=-24-70, mathbf i ,
sqrt{mathcal D}=pm ( 5 – 7, mathbf i ) ,$$
а также формулу вычисления корней:
$$
z_{1,2}=frac{-(1+ mathbf i) pm ( 5 – 7, mathbf i )}{2 (3- mathbf i)}
.
$$
Ответ. $ 1-mathbf i , -frac{6}{5} + frac{3}{5} mathbf i $.
Общий случай
Алгоритм предыдущего пункта может быть очевидным образом обобщен для нахождения корней степеней $ 2^m $ из комплексных чисел. Понятно также, что количество корней возрастает вдвое при переходе от $ 2^m $ к $ 2^{m+1} $. Вопрос о том будут ли все эти корни различными пока открыт.
Попробуем найти приемом, задействованным в предыдущем пункте, величину $ sqrt[3]{z} $.
$$ w^3=z iff (x+ mathbf i y)^3 = a+mathbf i b
iff
left(x^3-3, x y^2 right) + mathbf i , (3, x^2 y-y^3) = a+mathbf i b
$$
$$
iff
left{ begin{array}{c}
x^3-3, x y^2 = a, \
3, x^2 y-y^3 = b .
end{array} right.
$$
Возведем оба получившихся уравнения в квадрат и сложим:
$$x^6+3, x^4y^2+3, x^2y^4+y^6=a^2+b^2 iff (x^2+y^2)^3=a^2+b^2
$$
$$
iff x^2+y^2 = sqrt[3]{a^2+b^2} . $$
Выразим отсюда $ y^2 $ и подставим в первое уравнение:
$$
4, x^3 – 3, x sqrt[3]{a^2+b^2} -a =0 .
$$
Получилось кубическое уравнение относительно неизвестной вещественной величины $ x_{} $. Существует общий метод решения подобного уравнения (см.
☞
ЗДЕСЬ); однако его применение к настоящему случаю отягощается серьезной проблемой.
Настоящее замечание может быть пропущено без ущерба для понимания оставшейся части раздела.
Речь идет о формуле Кардано представления корней кубического уравнения в радикалах относительно коэффициентов этого уравнения. Однако в данном конкретном примере мы сталкиваемся с так называемым неприводимым случаем формулы Кардано: заведомо вещественные корни могут быть выражены только посредством мнимых чисел! Получаем порочный круг6): искомые комплексные величины $ sqrt[3]{z} $ ищутся через посредство кубического уравнения с вещественными корнями, для которых, в свою очередь, имеется только комплексные представления.
Попробуем решить получившееся кубическое уравнение хотя бы при частных значениях $ a_{} $ и $ b_{} $. Пусть, например,
$ b=0 $, тогда
$$4, x^3 – 3, x sqrt[3]{a^2} -a=(x- sqrt[3]{a})
left(4, x^2 +4,sqrt[3]{a} x +left( sqrt[3]{a} right)^2 right)=
(x- sqrt[3]{a})left( 2, x + sqrt[3]{a} right)^2 ,$$
т.е. решениями уравнения являются
$$x_1=sqrt[3]{a}, x_{2,3}=- frac{1}{2} sqrt[3]{a} . $$
Подставляя в первое из уравнений, получим соответствующие значения для $ y_{} $:
$$y_1=0, y_{2,3}=pm frac{sqrt{3}}2 sqrt[3]{a} . $$
Таким образом, кубический корень из вещественного числа $ z=a $
имеет три значения:
$$
left{ sqrt[3]{a}, sqrt[3]{a} left(-frac{1}{2} pm mathbf i
frac{sqrt{3}}2 right) right} .
$$
Рассмотрим теперь случай $ a_{}=0 $. Уравнение принимает вид
$$4, x^3 – 3, x sqrt[3]{b^2}=0 ,$$
из которого сразу же находятся значения $ x_{} $:
$$x_1=0, x_{2,3}= pm frac{sqrt{3}}{2} sqrt[3]{b} . $$
Соответствующие значения для $ y $:
$$
y_1=- sqrt[3]{b}, y_{2,3}= frac{1}{2} sqrt[3]{b} . $$
Таким образом, кубический корень из чисто мнимого числа $ z=mathbf i b $
имеет три значения:
$$
left{ -mathbf i sqrt[3]{b}, sqrt[3]{b} left( pm
frac{sqrt{3}}2 + frac{1}{2}, mathbf i right) right} .
$$
Теперь приведем другой способ вычисления $ w=sqrt[n]{z} $, основанный на
тригонометрической форме записи чисел $ w_{} $ и $ z_{} $. Пусть
$$z=a+mathbf i b= rho left( cos varphi + mathbf i sin varphi right) ,
w=x+mathbf i y = r left( cos vartheta + mathbf i sin vartheta right) .$$
Применяя формулу Муавра, получаем
$$w^n=r^n left( cos nvartheta + mathbf i sin nvartheta right)=
rho left( cos varphi + mathbf i sin varphi right)$$
и на основании правила равенства комплексных чисел, представленных в тригонометрической форме, получаем:
$$r^n = rho , nvartheta equiv varphi pmod{2 pi}$$
Первое из этих равенств мы получали в явном виде для квадратных и
кубических корней, оно равносильно
$$r= sqrt[n]{rho} , $$
т.е. модуль корня $ n_{} $-й степени из комплексного числа равен (арифметическому)
корню $ n_{} $-й степени из модуля этого числа.
Т
Теорема. Существует $ n_{} $ различных значений корня
$ n_{} $-й степени из комплексного числа $ z=rho (cos varphi + mathbf i sin varphi ) $.
Все они даются формулой
$$
w_k= sqrt[n]{rho} left(cos frac{varphi+2 pi k}{n} + mathbf i
sin frac{varphi+2 pi k}{n}right) npu kin {0,1,dots, n-1} .
$$
Доказательство того, что при любом целом числе $ k_{} $ числа $ w_k $ являются корнями $ n $-й
степени из $ z_{} $ уже проведено. Далее, из периодичности $ sin $ и $ cos $ следует, что
$$w_{0}=w_{nk}, w_{1}=w_{nk+1},dots , w_{n-1}=w_{nk+n-1} quad npu kin mathbb Z
,
$$
т.е. все эти корни содержатся в объявленном множестве. Осталось показать,
что все числа $ w_0,w_1,dots, w_{n-1} $ различны. Но это так и есть, поскольку
их аргументы не подчиняются правилу равенства комплексных чисел.
♦
П
Пример. Вычислить $ sqrt[3]{mathbf i} $ .
Решение. $ mathbf i= cos {pi}/2 + mathbf i sin {pi}/2 $
$$sqrt[3]{mathbf i} = sqrt[3]{cos frac{pi}2 + mathbf i sin frac{pi}{2}}=
cos frac{{pi}/2 + 2pi k}{3} + mathbf i
sin frac{{pi}/2 + 2pi k}{3} npu k in {0,1,2}.$$
Видим, что значения
$$w_0=cos frac{pi}6 + mathbf i sin frac{pi}6=frac{sqrt{3}}2 + frac{1}{2} {mathbf i}
, quad
w_1= cos frac{5pi}6 + mathbf i sin frac{5pi}6=-frac{sqrt{3}}2 + frac{1}{2} {mathbf i}
, quad
w_2=cos frac{3pi}2 + mathbf i sin frac{3pi}2=-mathbf i $$
совпадают с выведенной выше формулой для $ sqrt[3]{mathbf i b} $.
♦
П
Пример. Вычислить $ sqrt[7]{1+9, mathbf i} $.
Решение.
$$ 1+9, mathbf i =sqrt{82}left(cos varphi + mathbf i sin varphi right) quad
npu varphi=arccos frac{1}{sqrt{82}} approx 1.460139106 .
$$
Значения корней получаются по формуле
$$
{w_k}_{k=0}^6=left{ sqrt[14]{82}
left(cos frac{varphi+2 pi k}{7} + mathbf i
sin frac{varphi+2 pi k}{7}right) right}_{k=0}^6
approx
$$
$$
approx big{1.34024 + 0.28368, mathbf i,
0.61383 + 1.22472 , mathbf i, -0.57480 + 1.24351, mathbf i,
-1.33060 + 0.32591, mathbf i, -1.08442 – 0.83710 , mathbf i,
$$
$$
-0.02165 – 1.36976 , mathbf i,
1.05742 – 0.87096 , mathbf i big} .
$$
Изобразим корни на комплексной плоскости:
видим, что они располагаются на окружности с центром в $ 0_{} $ и радиусом $ sqrt[14]{82} approx 1.36993 $; и делят эту окружность на $ 7_{} $ дуг одинаковой длины.


Аналитика подтвержает геометрию: число $ w_k $ может быть получено домножением $ w_0 $ на число $ cos 2 pi k/7 + mathbf i
sin 2 pi k/7 $, что соответствует повороту вектора $ vec{Ow_0} $ на угол кратный $ 2pi/7 $.
♦
Корни из единицы
Обобщим соображения из последнего примера: корень $ n_{} $-й степени из комплексного числа $ z_{} $ можно представить в виде произведения
$$
sqrt[n]{rho} left(cos frac{varphi+2 pi k}{n} + mathbf i
sin frac{varphi+2 pi k}{n}right) =
$$
$$
=sqrt[n]{rho} left(
cos frac{varphi}{n} + mathbf i
sin frac{varphi}{n} right)
left(
cos frac{2 pi k}{n} + mathbf i
sin frac{2 pi k}{n} right)=
w_0
left(
cos frac{2 pi k}{n} + mathbf i
sin frac{2 pi k}{n} right)
$$
двух сомножителей, первый из которых не зависит от $ k_{} $. Числа
$$
varepsilon_k = cos frac{2 pi k}{n} + mathbf i
sin frac{2 pi k}{n}
$$
при $ kin {0,1,dots,n-1} $ имеют очевидный смысл — они являются
корнями $ n $-й степени из единицы:
$$
varepsilon_k^n=1 quad npu quad kin {0,1,dots,n-1 } .
$$
Также очевидно, что $ varepsilon_0=1 $.
Т
Теорема. Множество всех корней $ n_{} $-й степени из комплексного
числа $ z_{} $ можно представить в виде произведения какого-то фиксированного корня
на множество всех корней $ n_{} $-й степени из $ 1_{} $:
$${w_k }_{k=0}^{n-1} = {w_j varepsilon_k }_{k=0}^{n-1} .$$
Доказательство. Для $ j=0 $ справедливость утверждения уже показана. Для $ j>0 $
она очевидно следует из равенства $ w_j varepsilon_k=w_0 varepsilon_{k+j} $
и цикличности последовательности $ {varepsilon_{k}}_{k=0,1,2,dots} $.
♦
П
Пример. Множества корней $ n_{} $-й степени из $ 1_{} $:
$$begin{array}{l|l}
n=1& 1 \
& \
n=2& 1,, -1 \
& \
n=3& 1,, -frac{1}{2} + mathbf i frac{sqrt{3}}{2},,
-frac{1}{2} – mathbf i frac{sqrt{3}}2 \
& \
n=4& 1,, mathbf i,, -1,, -mathbf i \
& \
n=5& 1,, frac{1}{4} left( scriptstyle{(sqrt{5}-1)} +displaystyle{mathbf i} scriptstyle{sqrt{2 (5+sqrt{5})}} right),,
frac{1}{4} left( -scriptstyle{(sqrt{5}+1)} +displaystyle{mathbf i} scriptstyle{sqrt{2 (5-sqrt{5})}} right),,
frac{1}{4} left( -scriptstyle{(sqrt{5}+1)} – displaystyle{mathbf i} scriptstyle{sqrt{2 (5-sqrt{5})}} right),,
frac{1}{4} left( scriptstyle{(sqrt{5}-1)} – displaystyle{mathbf i} scriptstyle{sqrt{2 (5+sqrt{5})}} right) \
& \
n=6& 1, frac{1}{2} + mathbf i frac{sqrt{3}}{2} , -frac{1}{2} + mathbf i frac{sqrt{3}}{2},
-1, – frac{1}{2} – mathbf i frac{sqrt{3}}{2}, frac{1}{2} – mathbf i frac{sqrt{3}}{2}
end{array}
$$
Как были получены эти выражения? — Мы ведь не выводили в предыдущем пункте алгебраического представления для, скажем $ sqrt[5]{z} $, но, тем не менее, какие-то значения в таблице привели. Ответ на этот вопрос заключается в том, что уравнение $ z^n-1=0 $, определяющее корни $ n_{} $-й степени из $ 1_{} $, иногда удается решить в «хороших» выражениях (см.
☞
ВОЗВРАТНЫЙ ПОЛИНОМ ). Так, к примеру, уравнение $ z^9-1=0 $ можно переписать в виде:

$$ (z^9-1)equiv (z-1)(z^2+z+1)(z^6+z^3+1)=0 , $$
и выражения для, по крайней мере, трех его корней угадываются сразу:
$$ left{ 1,, -frac{1}{2} + mathbf i frac{sqrt{3}}{2},,
-frac{1}{2} – mathbf i frac{sqrt{3}}2 right} . $$
Разумеется, они совпадают с уже встречавшимися в таблице корнями кубическими из $ 1_{} $. Оставшееся уравнение $ z^6+z^3+1=0 $ можно свести к квадартному заменой переменной. Но дальше пройти не удается: алгебраические выражения для корней этого уравнения не получить.
♦
Уравнение $ z^n-1=0 $ называется уравнением деления круга — с очевидным геометрическим смыслом 7).
Т
Теорема. Для любых $ {k,ell}subset {0,1,dots,n-1} $ справедливы
равенства
$$ varepsilon_{k}=varepsilon_{1}^k , overline{varepsilon_{k}}= frac{1}{varepsilon_{k}}=varepsilon_{n-k},
varepsilon_{k}varepsilon_{ell}= varepsilon_{k+ell pmod{n}}=
left{
begin{array}{lc}
varepsilon_{k+ell} & npu k+ell<n \
varepsilon_{k+ell-n} & npu k+ellge n
end{array}
right.
.
$$
?
Вычислить сумму всех корней $ n_{} $-й степени из $ 1_{} $.
Решение
☞
ЗДЕСЬ
Пусть $ varepsilon_{} $ — корень $ n_{} $-й степени из $ 1_{} $.
Говорят, что он является первообразным корнем n-й степени из 1 или что он принадлежит показателю n если $ varepsilon_{} $ не является корнем меньшей степени из $ 1_{} $:
$$ varepsilon^j ne 1 quad npu jin {1,dots,n-1},quad varepsilon^n = 1 . $$
Образно говоря: если мы построим таблицу подобную той, что построена в предыдущем примере, для всех корней степеней $ 2,3,dots, n $, то первообразным корнем $ n_{} $-й степени из $ 1_{} $ будет тот, который нигде раньше в этой таблице не встречался.
П
Пример. В приведенном выше примере, корень $ displaystyle -frac{1}{2} + mathbf i frac{sqrt{3}}{2} $ не является первообразным корней $ 6_{} $-й степени из $ 1_{} $, но является
первообразным корнем $ 3_{} $-й степени из $ 1_{} $.
Т
Теорема. Корень
$$ varepsilon_k = cos frac{2 pi k}{n} + mathbf i
sin frac{2 pi k}{n}
$$
будет первообразным степени $ n_{} $ тогда и только тогда, когда $ operatorname{HOD} (k,n)=1 $ ( $ operatorname{HOD} $ означает наибольший общий делитель ).
?
Указать индексы $ kin{0,dots, 15} $, которые соответствуют первообразным корням $ displaystyle cos frac{2 pi k}{16} + mathbf i sin frac{2 pi k}{16} $ степени $ 16 $ из $ 1_{} $.
?
Будет ли произведение двух первообразных корней степени $ n_{} $ первообразным корнем степени $ n_{} $ ?
=>
При любом $ nin mathbb N $ корень
$$ varepsilon_1 = cos frac{2 pi }{n} + mathbf i
sin frac{2 pi }{n}
$$
будет первообразным степени $ n_{} $.
?
Будет ли $ varepsilon_{n-1} $ первообразным корнем?
=>
Число первообразных корней $ n_{} $-й степени из $ 1_{} $ равно $ phi (n) $, где $ phi $ — функция Эйлера.
?
[2]. Пусть $ varepsilon_{k} $ — первообразный корень. Доказать, что
$ varepsilon_{k}^{k^{^{phi(n)-1}}} = varepsilon_{1} $.
=>
Произвольный корень $ n_{} $-й степени из $ 1_{} $ может быть получен как некоторая степень произвольного первообразного корня $ n_{} $-й степени из $ 1_{} $.
В самом деле, если $ varepsilon^n=1 $ и $ varepsilon^jne 1 $ при $ jin {1,2,dots,n-1} $, то все числа $ varepsilon, varepsilon^2,dots,varepsilon^{n-1} $ будут корнями $ n_{} $-й степени из $ 1_{} $, все они будут различны между собой и отличны от $ 1_{} $. Следовательно, эти степени представляют собой перестановку корней $ varepsilon_1, varepsilon_2,dots, varepsilon_{n-1} $.
?
В каком случае степень первообразного корня будет первообразным корнем?
§
Подробнее об уравнении деления круга
☞
ЗДЕСЬ
§
Использование корней из единицы
☞
ДИСКРЕТНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ
Экспоненциальное представление комплексного числа
Материал настоящего раздела довольно сложен и может быть пропущен при первом чтении.
Еще одно представление комплексного числа может быть организовано на основании важной функции комплексного аргумента.
В курсе математического анализа доказывается существование следующего предела
$$
lim_{nto+infty} left(1+frac{1}{n}right)^n ,
$$
он имеет специальное обозначение8):
$$
e approx 2.7182818284590452353602874713526624977572470936999595ldots
$$
и исключительно важен в приложениях. Также доказывается, что показательная функция $ e^x $ (экспонента) может быть представлена рядом Тейлора
$$
e^x=1+x+ frac{x^2}{2!}+dots + frac{x^n}{n!}+dots = sum_{j=0}^{infty} frac{x^j}{j!}
$$
сходящимся при всех $ xin mathbb R $. Аналогичным рядом по комплексной переменной $ z=x+ mathbf i y $ определяется комплексная экспонента:
$$
e^z=1+z+ frac{z^2}{2!}+dots + frac{z^n}{n!}+dots = sum_{j=0}^{infty} frac{z^j}{j!} ;
$$
и в курсе теории функций комплексной переменной доказывается, что этот ряд сходится при всех $ zin mathbb C $.
По аналогии с рядами Тейлора для функций
$$
sin x = x – frac{x^3}{3!}+frac{x^5}{5!}-frac{x^7}{7!}+dots = sum_{j=0}^{infty} frac{(-1)^jx^{2j+1}}{(2j+1)!}
$$
и
$$
cos x = 1- frac{x^2}{2!}+frac{x^4}{4!}-frac{x^6}{6!}+dots = sum_{j=0}^{infty} frac{(-1)^jx^{2j}}{(2j)!}
$$
определяются тригонометрические функции
$$
sin z = z – frac{z^3}{3!}+frac{z^5}{5!}-frac{z^7}{7!}+dots = sum_{j=0}^{infty} frac{(-1)^jz^{2j+1}}{(2j+1)!}
$$
и
$$
cos z = 1- frac{z^2}{2!}+frac{z^4}{4!}-frac{z^6}{6!}+dots = sum_{j=0}^{infty} frac{(-1)^jz^{2j}}{(2j)!} ;
$$
оба ряда сходятся при всех $ zin mathbb C $.
В комплексной плоскости (как и на вещественной оси) справедливы тождества
$$ sin (-z) equiv – sin z,quad cos (-z) equiv cos z , $$
т.е. функция $ sin $ является нечетной, а функция $ cos $ — четной.
Т
Теорема [Эйлер]. Формула
$$ e^{mathbf i z} equiv cos z + mathbf i sin z $$
имеет место при всех $ z in mathbb C $.
Доказательство.
$$
begin{array}{ccl}
e^{mathbf i z}&=& displaystyle 1+mathbf i z+ frac{mathbf i^2 z^2}{2!}+frac{mathbf i^3 z^3}{3!}+frac{mathbf i^4 z^4}{4!}+ dots = 1+mathbf i z- frac{z^2}{2!}-frac{mathbf i z^3}{3!}+frac{z^4}{4!}+ dots \
& = & displaystyle left(1- frac{z^2}{2!}+frac{z^4}{4!}-dots right) + mathbf ileft(z-frac{z^3}{3!}+frac{z^5}{5!}- dots right) = \
& = & cos z + mathbf i sin z .
end{array}
$$
♦
=>
Для вещественного числа $ varphi $ имеем
$$ e^{{mathbf i}varphi }= cos varphi + mathbf i sin varphi ; $$
сравнивая это выражение с тригонометрической формой комплексного числа $ z_{} $ получаем его экспоненциальное представление
$$ z= rho e^{{mathbf i}varphi } . $$
=>
Следующая формула Эйлера связывает между собой четыре знаменитые математические величины:
$$ e^{mathbf i pi}= – 1 . $$
И
См. по поводу этой формулы
☞
цитату А.Н.Крылова.
=>
Тригонометрические функции комплексного аргумента могут быть выражены как линейные комбинации экспонент:
$$ cos z= frac{1}{2} left( e^{{mathbf i} z}+e^{-{mathbf i} z} right),quad sin z= frac{1}{2{mathbf i}} left( e^{{mathbf i} z}-e^{-{mathbf i} z} right) .
$$
?
Угадайте первые три цифры числа $ 1001^{1000} $. ![]()
А зачем они всё же нужны?
Этот вопрос — о полезности комплексных чисел, о необходимости их введения — остается открытым. Проанализируем все полученные в настоящем разделе результаты на предмет ответа на вопрос: «стоила ли овчинка выделки?», т.е. оправдано ли введение новой (и подозрительно мнимой) сущности получением новых ивещественных результатов?
1.
Применение комплексных чисел для выведения тригонометрических формул. Действительно, использование аппарата мнимых чисел позволило упростить вывод вещественных равенств. Однако, после получения ответа в задаче о суммировании $ sin varphi + sin 2,varphi+dots + sin n, varphi $ был сразу же показан альтернативный способ получения того же ответа без использования комплексных чисел. Можно ожидать, что и остальные результаты того пункта — как то выражение синусов и косинусов кратных углов как степеней косинусов и синусов исходного угла, а также решение обратной задачи — тоже допускают принципиально вещественное решение9). Таким образом, польза от введения комплексных чисел не очень оправдана применением их для решения подобных задач.
2.
Геометрические приложения. Проанализируем их на примерах трех введенных операций. Пусть $ w=x+ mathbf i y $ — переменная величина, т.е. числа $ { x,y } subset mathbb R $ могут принимать произольные значения, а $ z=a+ mathbf i b $ — фиксированное комплексное число. Геометрический смысл операции суммирования $ w+z $ заключается в преобразовании комплексной плоскости, а именно — в сдвиге ее точек
$$ (x,y) mapsto (x+a,y+b) $$
на фиксированную величину.
Вторая из введенных операций — комплексное сопряжение — также имеет простое геометрическое содержание:
$$ w mapsto overline{w} quad iff quad (x,y) mapsto (x,-y) ; $$
каждая точка комплексной плоскости зеркально отражается относительно вещественной оси.
Наконец, операция умножения комплексных чисел: $ w mapsto wcdot z $. Геометрию этой операции мы анализировали ВЫШЕ переходом к тригонометрической форме записи комплексного числа. Проведем более подробый анализ. Рассмотрим сначала частный случай числа $ z_{} $: пусть его модуль равен $ 1_{} $, т.е. $ z = cos varphi + mathbf i sin varphi $. Умножение числа $ w_{} $ на такое число $ z_{} $ равносильно повороту точек комплексной плоскости на угол $ varphi $ вокруг начала координат. Так, к примеру, умножению на мнимую единицу $ mathbf i $ соответствует поворот точек плоскости на угол $ pi/2 $; а если еще раз повернем на тот же угол — то результатом будет преобразование
$$ (x,y) mapsto (-x,-y) ; $$
и результат снова полностью соответствует основополагающему правилу комплексных чисел: $ mathbf i^2=-1 $.
Рассмотрим теперь другой частный случай выбора числа $ z_{} $. Пусть оно будет вещественно: $ z=a in mathbb R $ и отлично от $ 0_{} $. Тогда
$$ w mapsto a cdot w quad iff quad (x,y) mapsto (ax,ay) ; $$
и мы имеем дело с растяжением каждого отрезка комплексной плоскости, имеющего одним концом начало координат, на величину10) $ a_{} $.
Теперь понятно, что умножение $ w_{} $ на произвольное число $ z = rho (cos varphi + mathbf i sin varphi) $ (отличное от $ 0_{} $) сводится к комбинации рассмотренных выше преобразований: т.е. к одновременному повороту вокруг начала координат на угол $ varphi $ и растяжению с коэффициентом $ rho $.
Подводим итоги: комплексные числа позволяют дать аналитические выражения (формулы) для ряда важных операций на плоскости, как то — сдвига, зеркального отражения, поворота, растяжения. Сразу же возникают соображения о возможности комбинирования этих операций ($ w mapsto z_1cdot w + z_2 $, $ w mapsto z_1cdot (overline{w} + z_2) $ и т.п.) для покрытия возможно большего разнообразия мыслимых геометрических преобразований. В этом месте происходит зарождение отдельного раздела комплексного анализа — теории функций комплексной переменной11). Пока не устремляясь к этим красочным горизонтам, охладим наш пыл одним критическим замечанием.
Дело в том, что все указанные геометрические преобразования могут быть аналитически представлены и без введения комплексной переменной. Формулы
$$ X=x+a, Y=y+b ; $$
$$X=x,Y=-y ; $$
$$X= x cos varphi – y sin varphi, quad Y=x sin varphi + y cos varphi ; $$
$$ X=ax, Y=ay $$
полностью описывают все обсужденные операции на вещественной плоскости $ (x,y) $. Никакой мнимой единицы вводить не нужно… ![]() И мы вынуждены повторить приведенный выше вывод: польза от введения комплексных чисел не очень оправдана применением их для решения подобных задач.
И мы вынуждены повторить приведенный выше вывод: польза от введения комплексных чисел не очень оправдана применением их для решения подобных задач.
Это мнение следует считать моим личным и весьма субъективным. В книге [3] можно найти ряд приложений комплексных чисел к задачам геометрии. Моих знаний не достаточно для оценки этих задач как представляющих исключительно только исторический интерес.
3.
Решение уравнений. Да, задача, поставленная в начале раздела, решена: мы придали смысл словам «решить уравнение $ x^2+1 = 0 $»; более того, на основе разработанного аппарата, мы смогли решить любое уравнение второго порядка. А зачем это нужно? Какой смысл имеют мнимые корни такого уравнения, какую реальность они отражают? — Ответа на этот вопрос пока не даем. Отметим только два обстоятельства. Первое: если полагать, что реальную смысловую нагрузку несут хотя бы вещественные решения уравнения, то, оказывается, что без комплексных чисел не обойтись.
П
Пример. Решить уравнение $ x^3-3,x+1=0 $.
Ответом будут три вещественных корня:
$$ 2 cos ({2pi}/9) approx 1.53208, 2 cos ({4pi}/9) approx 0.34729, 2 cos ({8pi}/9) approx -1.87938 , . $$
Истинность можно проверить подстановкой в уравнение (с применением формулы приведения для степени косинуса, выведенной
☞
ЗДЕСЬ ). Как был получен этот ответ?
Решение этого примера на основе формулы Кардано изложено
☞
ЗДЕСЬ. Это решение существенно использует комплексные числа в промежуточных выкладках, хотя они и не участвуют в конечном результате. В данном конкретном примере можно было бы обойтись без них — например, каким-то чудесным способом угадав ответ. Но попробуйте угадать ответ для, скажем, уравнения $ x^3-17,x+2=0 $ (которое также имеет три вещественных корня). Ответ можно выразить в виде определенной комбинации
коэффициентов уравнения, но эта комбинация будет явным образом содержать $ mathbf i $. Попытки избавиться от мнимой единицы не приводят к результату. Именно эта задача — решения кубического уравнения с вещественными коэффициентами и заведомо вещественными решениями — привела к первому появлению комплексных чисел на математическом горизонте в XVI веке; иными словами, для получения правильного вещественного ответа пришлось вводить число с парадоксальным правилом возведения в квадрат: $ mathbf i^2=-1 $. См. свидетельство «психологического шока» первооткрывателя
☞
слова Кардано.
♦
Второе обстоятельство, оправдывающее введение комплексных чисел, заключается в их достаточности для решения произвольного уравнения вида $ a_0x^n+a_1x^{n-1}+dots+a_n=0 $; здесь $ n_{} $ — натуральное число, $ a_0,a_1,dots,a_n $ — произвольные фиксированные числа, а $ x_{} $ — неизвестная, относительно которой разыскивается решение уравнения. Оказывается, что все решения этого уравнения можно найти в комплексных числах — при любых коэффициентах (будь они вещественные или даже мнимые).
Иными словами, введения других, «сверхкомплексных», чисел не требуется. Этот результат носит название “Основной теоремы высшей алгебры”; это название объясняется тем, что вплоть до конца XIX века основной задачей алгебры считалась задача решения уравнений и систем уравнений.
4.
Наконец, исключительно важное значение мнимые числа имеют в экономической науке. К примеру, вручение престижной премии ![]() в номинации «Экономика» за 2002 г. см.
в номинации «Экономика» за 2002 г. см.
☞
ЗДЕСЬ.
.
Задачи
Источники
[1]. Uspensky J.V. Theory of Equations. New York. McGraw-Hill. 1948
[2]. Задача № E 1899 из журнала American Mathematical Monthly, v. 74, N 8, 1967, c. 1010
[3]. Яглом И.М. Комплексные числа и их применение в геометрии. М.Едиториал УРСС, 2004
[4]. Фаддеев Д.К. Лекции по алгебре. М.Наука. 1984
[5]. Курош А.Г. Курс высшей алгебры. М. Наука. 1965

![{displaystyle sum limits _{k=1}^{p}{e^{2pi {frac {nk}{p}}i}}=p[p|n]=left{{begin{matrix}p,&nequiv 0{pmod {p}}\0,&nnot equiv 0{pmod {p}}end{matrix}}right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e2a4b8961a3cdf92a2ff179b54fc1df45c7be42)
![{displaystyle int limits _{0}^{1}{e^{2pi nalpha i}}=[n=0]=left{{begin{matrix}1,&n=0\0,&nnot =0end{matrix}}right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/011f42c7e795bc201a0098186b95948feebd1ff7)






![{begin{aligned}cos xcdot cos y&={frac {(e^{{ix}}+e^{{-ix}})}{2}}cdot {frac {(e^{{iy}}+e^{{-iy}})}{2}}\&={frac {1}{2}}cdot {frac {e^{{i(x+y)}}+e^{{i(x-y)}}+e^{{i(-x+y)}}+e^{{i(-x-y)}}}{2}}\&={frac {1}{2}}left[underbrace {{frac {e^{{i(x+y)}}+e^{{-i(x+y)}}}{2}}}_{{cos(x+y)}}+underbrace {{frac {e^{{i(x-y)}}+e^{{-i(x-y)}}}{2}}}_{{cos(x-y)}}right].end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d953d6ec5434efb1934f3f4d1fdae6fedc9f4093)
![{begin{aligned}cos(nx)&={mathrm {Re}}{ e^{{inx}} }={mathrm {Re}}{ e^{{i(n-1)x}}cdot e^{{ix}} }\&={mathrm {Re}}{ e^{{i(n-1)x}}cdot (e^{{ix}}+e^{{-ix}}-e^{{-ix}}) }\&={mathrm {Re}}{ e^{{i(n-1)x}}cdot underbrace {(e^{{ix}}+e^{{-ix}})}_{{2cos(x)}}-e^{{i(n-2)x}} }\&=cos[(n-1)x]cdot 2cos(x)-cos[(n-2)x].end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7733a7cfc3712263a53993cd6eacf6f4a26811a7)

