Как найти максимальное напряжение балки

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x

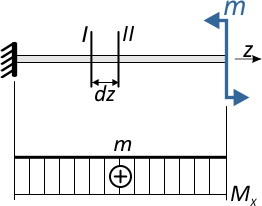
представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.

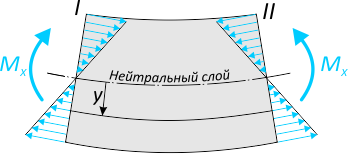
Закон распределения нормальных напряжений по высоте сечения выражается формулой:

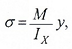
где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2:

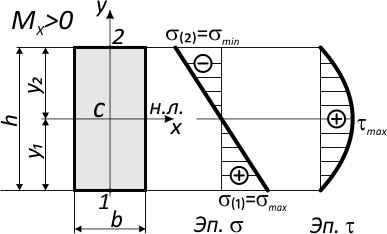
Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.

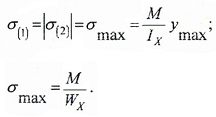
Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2:

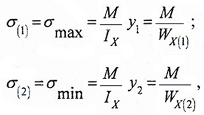
где:

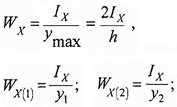
W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.

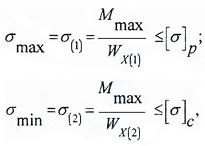
Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[σ], [σ]_р, [σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]_с>[σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
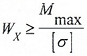
3. Определение максимально допустимой нагрузки
   

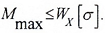
Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского

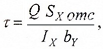
где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Другие видео

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max:

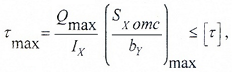
где [τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

1. По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
2. По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
3. По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда M_max и Q_max действуют в одном и том же сечении балки).

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид:

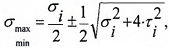
так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Другие видео

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

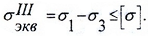
Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >

Для
подбора поперечного сечения балки
необходимо сначала определить в ней
максимальный изгибающий момент (М)
и по нему для конкретных размеров сечения
балки (ширины и высоты) определяется
максимальное напряжение ().
Сечение подбирается так, чтобы это
напряжение ()
не превышало расчетного сопротивления
материала балки (в данном случае
древесины) R_u
. Для
обеспечения экономичности выбора
сечения необходимо, чтобы разница между

и
R_u
была как
можно меньшей. Такой расчет относится
«расчетам по несущей способности»
(иначе «расчетам по I
группе предельных состояний»).

После
подбора сечения по несущей способности
производится «расчет по деформациям»
(иначе «расчет по II
группе предельных состояний»), т.е.
определяется прогиб балки и оценивается
его допустимость. Если при сечении
балки, выбранном по несущей способности,
прогиб оказывается больше допустимого,
сечение дополнительно увеличивают,
если меньше – оставляют без изменения.

2.5. Расчет по несущей способности

Максимальный
изгибающий момент М
в балке определяется по правилам механики
(сопротивления материалов) по формуле

,
(1)

где
q_I
–
погонная нагрузка на балку (кН/м)

l
– пролет
балки (м).

Напряжение
в балке 
определяется
по формуле

,
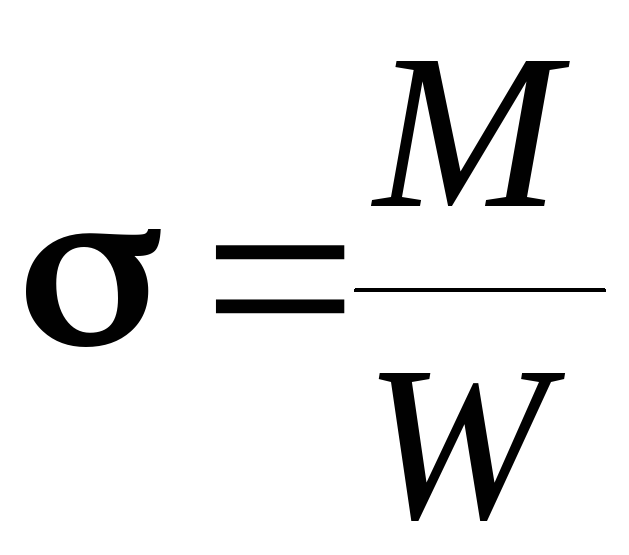(2)

где
М – изгибающий
момент (кНм),
определяемый по формуле (1),

W
– момент сопротивления сечения (м³).

,
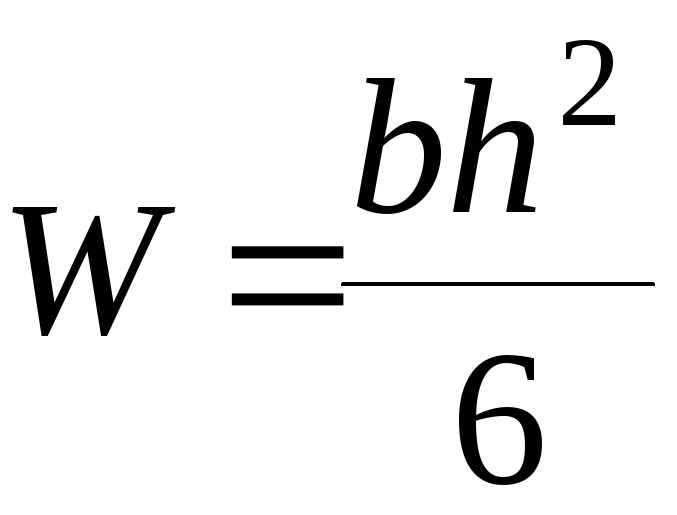(3)

где
b,
h
– соответственно ширина и высота
сечения балки.

Пример.
Пролет балки l
= 3.6м,
погонная нагрузка q_I
= 2.56
кН/м.
Проверить сечение балки 0.10.2м
(большая
сторона – высота).

=
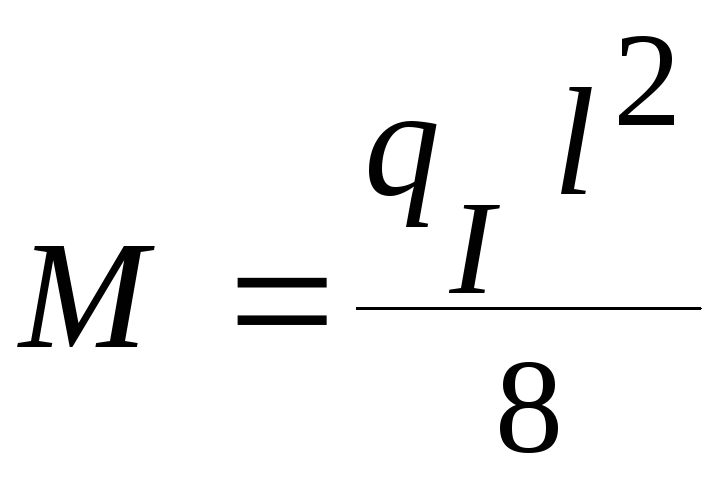
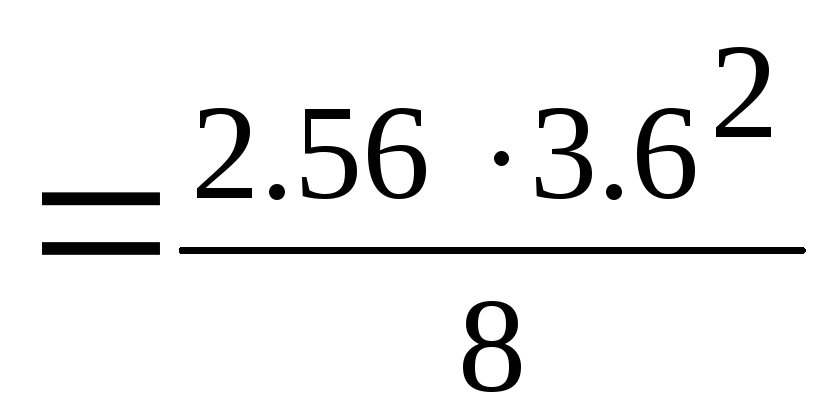4.15 кНм

=
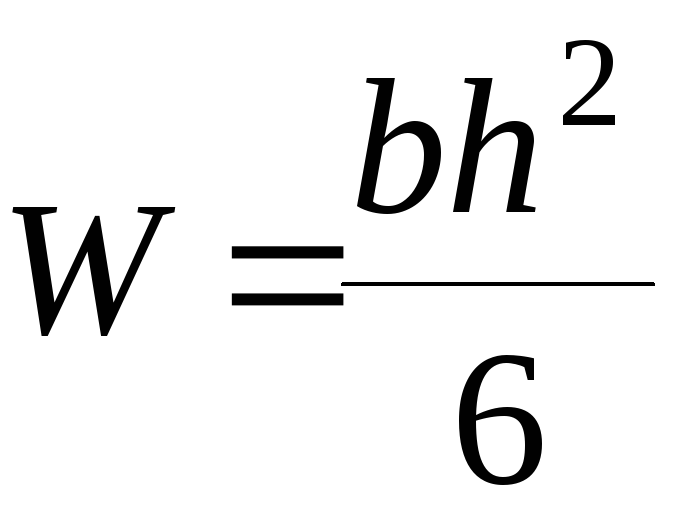
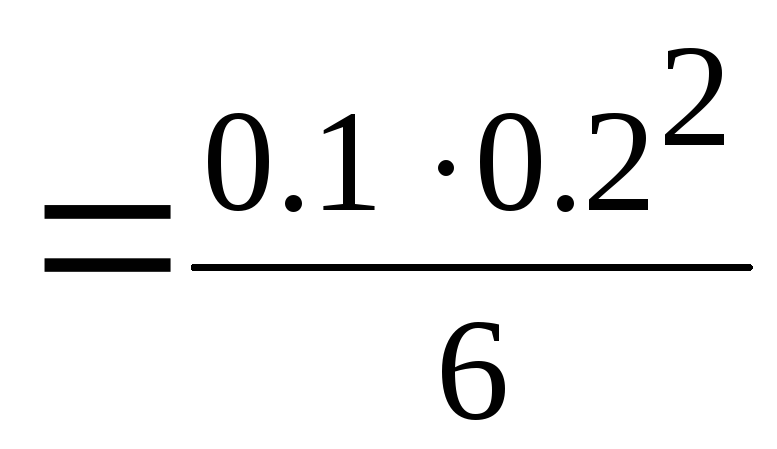0.00056 м³

=
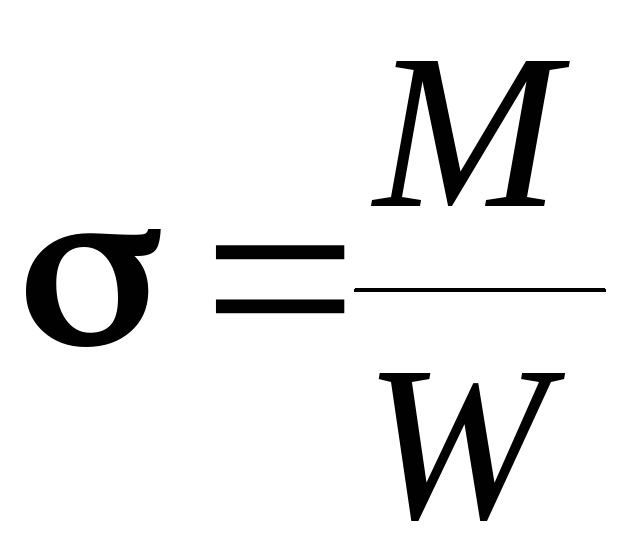
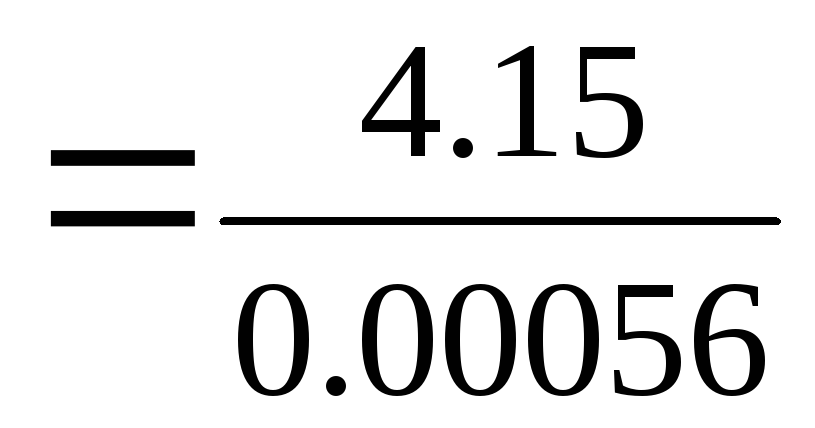6 200 кН/м²
(кПа)
=6.2 МПа < R_u
=13 МПа

Таким
образом сечение 0.10.14м
удовлетворяет требованиям прочности
(несущей способности), однако полученное
максимальное напряжение 
примерно
вдвое ниже
расчетного сопротивления древесины R_u
, т.е. «запас
прочности» неоправданно велик. Уменьшим
сечение до 0.10.14
м
и проверим возможность его приеменения.

W=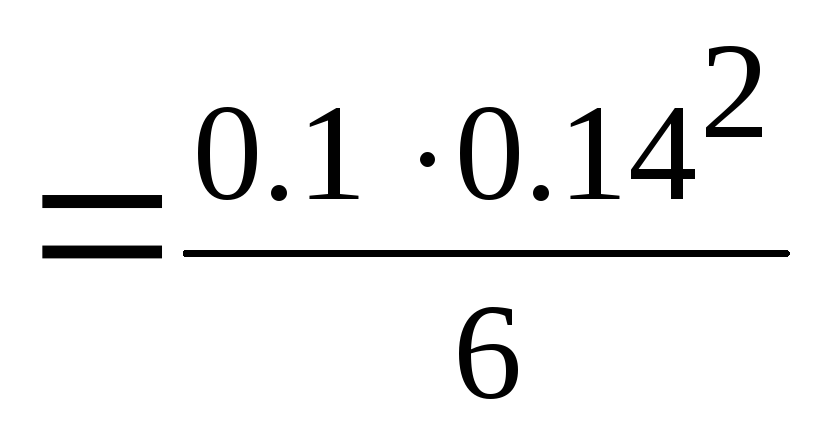
0.000327м³

=
12 691кПа
= 12.7 МПа <
13 МПа

«Запас»
при сечении 0.1
0.14 м
менее 5%, что вполне удовлетворяет
требованиям экономичности. Таким образом
принимаем (на данном этапе) сечение 0.1
0.14 м .

2.6.
Расчет по деформациям

Прогиб
балки f
определяется
по формуле (сопротивление материалов)

,
(4)

где
q_II
– погонная нагрузка на балку (кН/м)
применительно к расчетам по деформациям
(см. таблицу 4);

l
– пролет
балки (м);

Е
– модуль упругости материала балки,
т.е. древесины (кПа);

I
– момент
инерции сечения балки (м⁴)

,
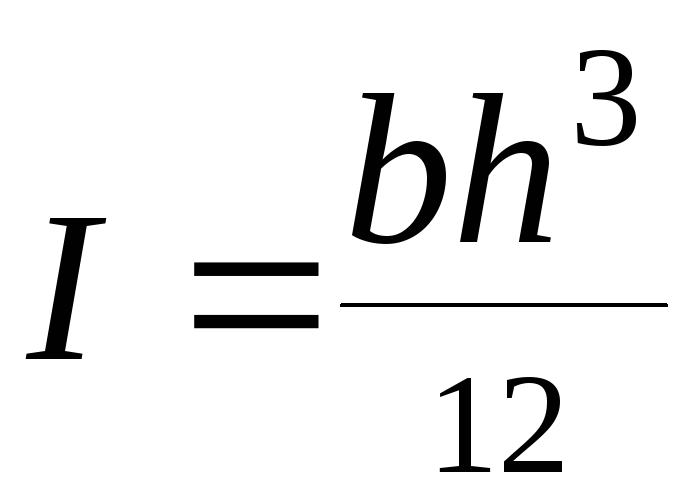(5)

где обозначения
те же, что и в формуле (2).

Пример.
Погонная нагрузка q_II
=1.8 кН/м
, Е =10 000МПа
= 10 ⁷
кПа (см. раздел 3.1), пролет балки l
= 3.6м
.Проверить
сечение балки 0.10.14м.

=
0.0000228 м⁴
= 2.28
10^-5 м⁴

=
0.0173м =
1.73 см

Относительный
прогиб балки, т.е. отношение прогиба f
к пролету l,
составляет в данном случае

=
<

Полученный
относительный прогиб меньше допустимого
(1/200). В связи с этим принимаем сечение
балки 0.10.14м
как окончательное, удовлетворяющее
требованиям не только несущей способности,
но и деформативности.

Очевидно,
что любая другая строительная конструкция
также должна удовлетворять требованиям
как по несущей способности, так и по
деформативности. Проверка соответствия
ее параметров обоим требованиям не
проводиться лишь в случаях, когда ясно
без расчета, что одно из требований
заведомо удовлетворяется.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

На двутавровую балку (№ 20)длиной l=9м, свободно лежащую на двух жестких опорах , с высоты h=5 см падает груз Q=1200Н.

Требуется: найти наибольшее нормальное напряжение в балке и определить прогиб балки в месте падения груза.

1)     Рассчитываем балку на действие статической нагрузки. Прикладываем силу Q и строим эпюру изгибающих моментов М_F. Для этого определяем реакции:

Максимальный момент будет равен: 

2)     В место падения груза прикладываем единичную силу   и строим единичную эпюру (эпюру моментов от единичной нагрузки).

Максимальный момент будет равен: 

3)     Определяем максимальный прогиб балки в месте падения груза при  статическом действии нагрузки по любому изученному методу определения перемещений. Например, по правилу Верещагина:

4)     Определяем динамический коэффициент:

5)     Наибольшее нормальное напряжение в балке при ударе

6) Наибольший прогиб при ударе:

Консольная балка из двутавра №22 подверглась удару при падении груза F=10кН в сечении С. Высота падения Н=2см.

Найти прогиб свободного конца балки.

Решение:

Здесь придется дважды определить прогибы от статического действия силы веса падающего груза: прогиб в точке С для определения динамического коэффициентаи прогиб конца консоли для ответа на поставленный в задаче вопрос:

«Перемножением» эпюр находим:

Динамический коэффициент при ударе

Тогда динамический прогиб конца консоли будет:

Пусть груз F=10кН падает с высоты H=10см на двутавровую стойку длиной ℓ=4м.

Определить:

1)  максимальное нормальное напряжение

2)  наибольшее укорочение стойки при ударе.

Считать, что стойка не теряет устойчивости.

Решение.

Расчетными формулами при ударе являются:

где динамический коэффициент при ударе

— эти параметры соответствуют статическому способу приложения силы веса падающего груза, то есть:

На двутавровой балке установлен электродвигатель весом G=5кН, при работе которого из-за дисбаланса вращающихся частей возникает вертикальная центробежная сила  при скорости вращения n=300 об/мин.

Определить наибольшие нормальные напряжения и прогиб.

Решение:

Балка находится под действием двух нагрузок: под действием статической нагрузки – веса двигателя G и под действием динамической (вибрационной) нагрузки F. Поэтому все параметры складываются из статической и динамической составляющих:

Статические составляющие от силы G найдем как обычно при статическом расчете:

Наибольшее статическое напряжение в среднем сечении балки будет:

Для определения статического прогиба среднего сечения выберем вспомогательное состояние и построим эпюру  :

Прогиб от статической нагрузки G будет:

Динамические значения параметров от действия вибрационной нагрузки определяются с помощью динамического коэффициента следующим образом:

В формулу динамического коэффициента вибрационной нагрузки входит величина ω – круговая частота собственных (свободных) колебаний, определяемая по формуле:

где: g=9,81м/сек² –ускорение свободного падения,

 Δ_ст – перемещение точки расположения колеблющейся массы (в данном случае двигателя) от собственного веса.

Тогда значение динамического коэффициента вибрационной нагрузки будет:

Здесь круговая частота действия самой вибрационной нагрузки

Далее находим   , для чего к балке прикладывается наибольшая величина вибрационной нагрузки статическим образом:

Прогиб середины пролета в балке на двух опорах можно вычислить и по известной формуле:

Тогда динамические значения искомых параметров будут:

представляет собой амплитуду колебаний массы (двигателя), то есть наибольшее отклонение от положения статического равновесия. Поэтому наибольшее значение прогиба складывается из статического смещения и амплитуды колебаний 

Наибольшее нормальное напряжение

Содержание

Цель работы.. 3

Расчетная схема. 3

Исходные данные. 3

Часть 1. Расчет максимального
напряжения балки с бесконечным числом степеней свободы путем приведения к
эквивалентной с одной степенью свободы. 4

1.1       Записываем
уравнение упругой линии балки (функция статического прогиба) 4

1.2       Из
условия на промежуточной опоре и граничном условии на правом конце балки
определяем неизвестные параметры, входящие в уравнение упругой линии. 4

1.3       По
формуле Релея определяем приближенное значение частоты собственных колебаний
балки, соответствующих собственной нагрузки. 4

1.4       Определяем
показатель затухания и значение собственной частоты, учитывающее демпфирование. 4

1.5       Запишем
общее выражение для прогиба балки как системы с одной степенью свободы для
ударного воздействия. 5

1.6       Определяем
коэффициент динамичности. 5

1.7       Определяем
координату точки и момента времени в которые был достигнут максимальный прогиб
балки по модулю.. 5

1.8       Записываем
выражение для изгибающего момента. 7

1.9       Максимальное
значение изгибных напряжений. 8

Часть 2. Расчет максимального
напряжения балки с бесконечным числом степеней свободы методом разложения на
собственные формы балки, с использованием первых четырех форм. 9

2.1 Записываем функции Крылова: 9

2.2  Записываем общее выражение для
функции формы с учетом закрепления на левом краю балки. 9

2.3  Из условия на промежуточной
опоре и граничном условии на правом конце балки определяем неизвестные
параметры, входящие в уравнение упругой линии. 9

2.4 Выражаем
коэффициенты. 9

2.5  Подставим данные соотношения в
выражение для функции формы. 9

2.6   Составляем уравнение частот. 10

2.7. Используя пакет mathematica
определяем 4 наименьших положительных корня уравнения. 10

2.8  Записываем общее выражение для
прогиба балки. 13

2.9 Выражение для изгибающего момента. 15

2. 10 Определяем максимальные
напряжения. 16

Выводы.. 17

Цель работы: Рассчитать
максимальные напряжения в балке, возникающие в результате ударного нагружения
распределенной нагрузкой . Построить
графики прогиба балки и изгибающего момента в зависимости от координаты и
времени.

Курсовая работа состоит из 2
частей:

1. Расчет максимального
напряжения методом приведения балки к системе с одной степенью свободы.

2.  Расчет максимального напряжения
методом разложения на собственные формы балки, с использованием первых трех
форм.

Расчетная
схема.

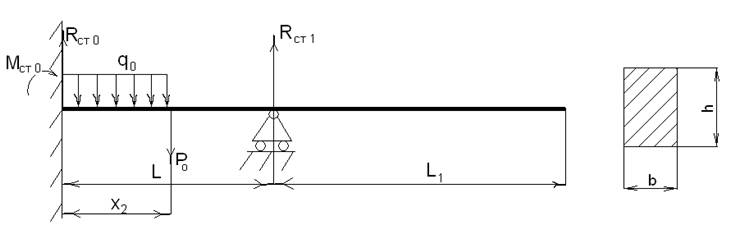Рис.1 Расчетная
схема.

Исходные данные.

Воздействие на балку		ударное.
Нагрузка	Р0	400     Н/м
Распределенная нагрузка		320     Н/м
Длина пролетов балки	L L1	2.5       м 3          м
Координаты начала и конца приложения распределенной нагрузки q		0        м 1.25   м
Поперечное сечение балки	b h	15        мм 35        мм
Безразмерный коэффициент демпфирования	γ	0.012
Модуль упругости стали	Е	2∙1011    Па
Плотность стали	ρ	7800     кг/м3

Момент инерции балки:

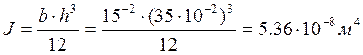
Погонная масса балки:

=
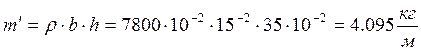
2.5 + 3 = 5.5 м –длина балки

Часть 1. Расчет максимального напряжения балки с
бесконечным числом степеней свободы путем приведения к эквивалентной с одной
степенью свободы.

1.1  Записываем
уравнение упругой линии балки (функция статического прогиба).

 

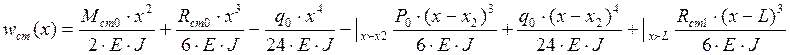
, -статические реакции при жесткой
заделке и на опоре

– статический момент при
жесткой заделке.

1.2  Из условия на
промежуточной опоре и граничном условии на правом конце балки определяем
неизвестные параметры, входящие в уравнение упругой линии.

Условие, что прогиб на опоре равен нулю.

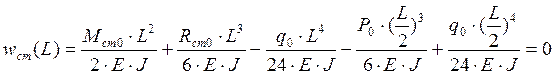
Условие, что изгибающий момент на свободном краю равен нулю.

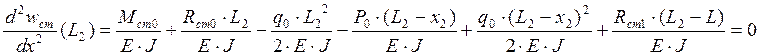
Условие, что перерезывающая сила на свободном краю равна
нулю.

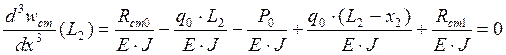
Решая систему уравнений определяем :

=  -328.125  Н*м

=    631.25 Н

=    168.75  Н

1.3  По формуле
Релея определяем приближенное значение частоты собственных колебаний балки,
соответствующих собственной нагрузки.

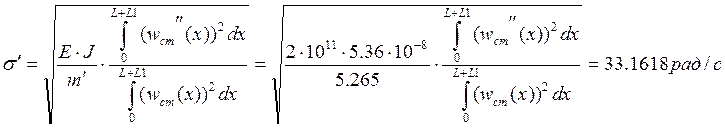
1.4  Определяем
показатель затухания и значение собственной частоты, учитывающее демпфирование.        

           

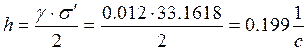
1.5  Запишем общее выражение для прогиба балки как системы с одной степенью
свободы для ударного воздействия.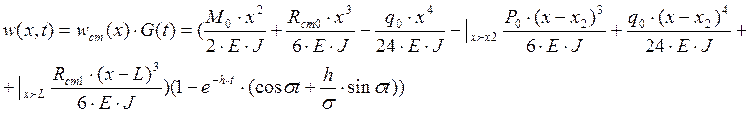    

Где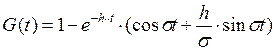

1.6  Определяем коэффициент динамичности.

1.7  Определяем координату точки и момента времени в которые был достигнут
максимальный прогиб балки по модулю.

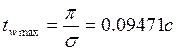
Строим график зависимости

   

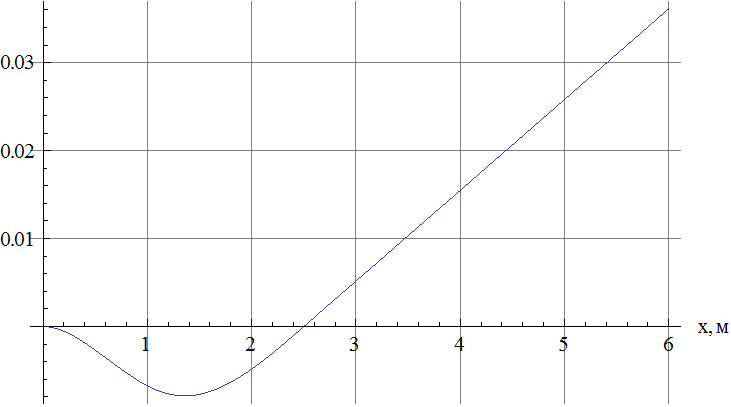
Рис.2 Изменение статического прогиба по длине балки.

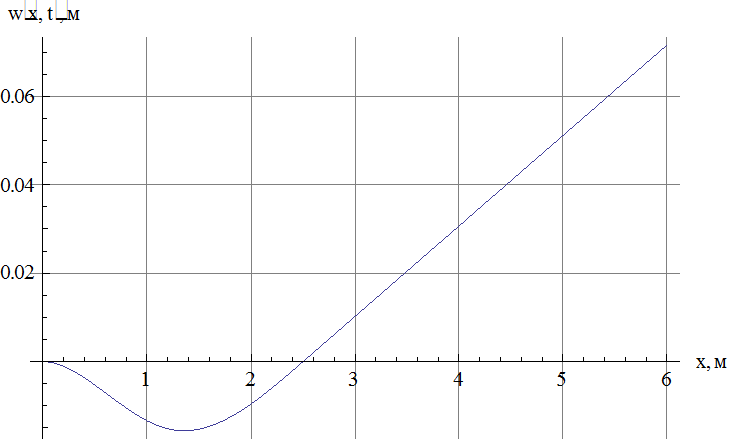
Рис.3. Зависимость прогиба от координаты в
момент достижения максимального по модулю прогиба.

из рис 3 видно:

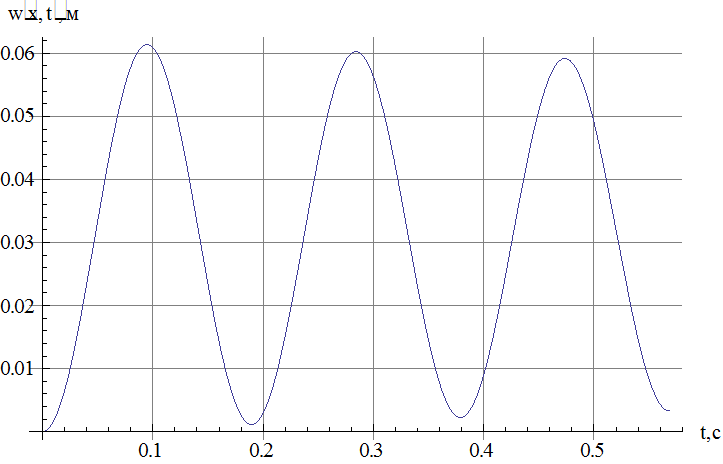
Рис.4 Зависимость прогиба от
времени в сечении, в котором достигается максимальный по модулю прогиб.

1.8  Записываем выражение для изгибающего момента.

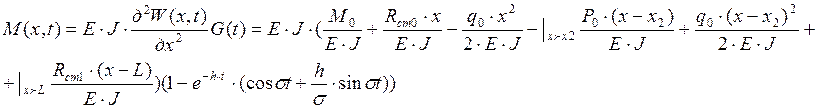 Строим
график зависимости

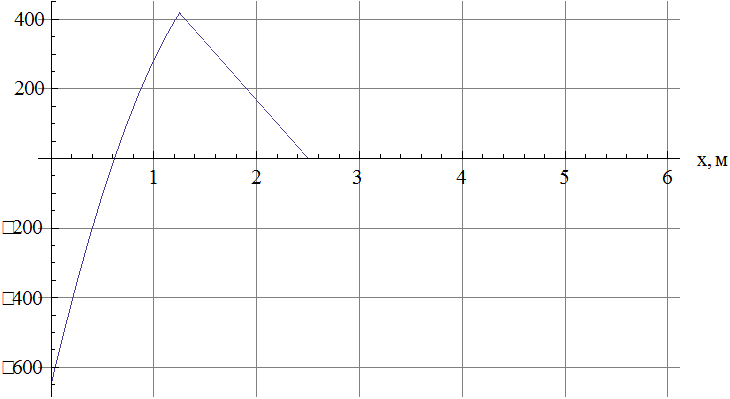
Рис.5 Зависимость изгибающего
момента от координаты в момент достижения максимального по модулю изгибающего
момента.

из рис 5 видно:

    

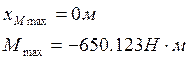
Строим график зависимости  – рис.6

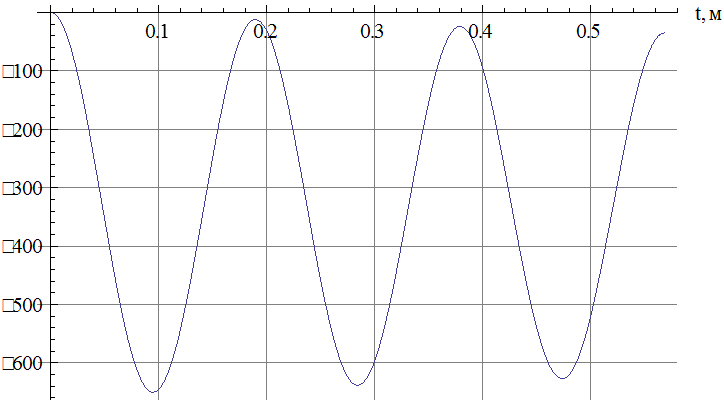
                   Рис.6 Зависимость изгибающего момента от
времени в сечении, в котором достигается его максимальное по модулю значение

1.9  Максимальное значение изгибных напряжений.

W-момент сопротивления сечения балки

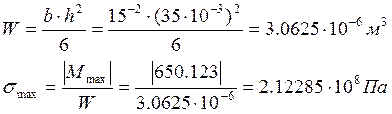
Часть 2. Расчет максимального напряжения балки с
бесконечным числом степеней свободы методом разложения на собственные формы
балки, с использованием первых четырех форм.

2.1 Записываем функции Крылова:

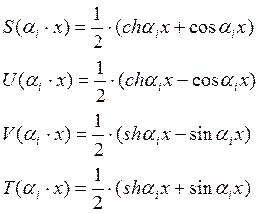
-волновое
число i-ой формы

2.2  Записываем общее выражение для функции формы с
учетом закрепления на левом краю балки.

С_3i, С_4i, -константы .

i-номер
формы

  2.3  Из условия на промежуточной опоре и
граничном условии на правом конце балки определяем неизвестные параметры,
входящие в уравнение упругой линии.

Условие, что прогиб на опоре равен нулю.

Условие, что изгибающий момент на свободном краю равен нулю.

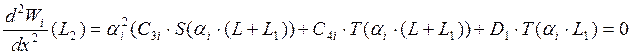
Условие, что перерезывающая сила на свободном краю равна
нулю.

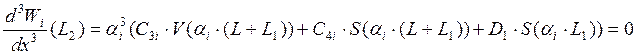
поскольку идет поиск  ненулевого
решения, то  принимаем С_3i=1

2.4 Выражаем
коэффициенты.

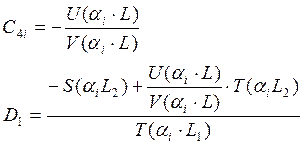
 2.5  Подставим данные соотношения в выражение
для функции формы.

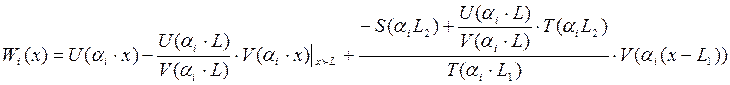
2.6   Составляем уравнение частот

 

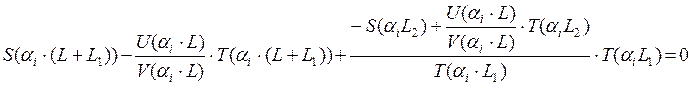
Введем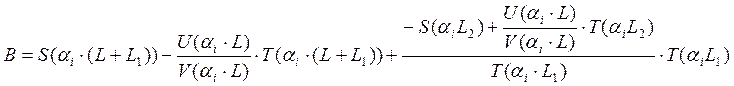

Зависимость прогиба
от координаты в момент достижения максимального по модулю прогиба.

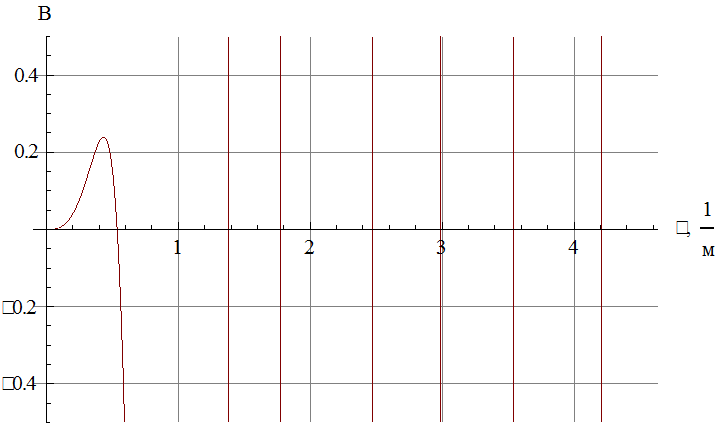
Рис. 7 График левой
части уравнения.

2.7. Используя пакет mathematica определяем 4
наименьших положительных корня уравнения

 

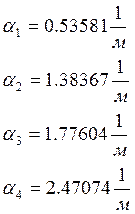
Строим график
собственных форм.

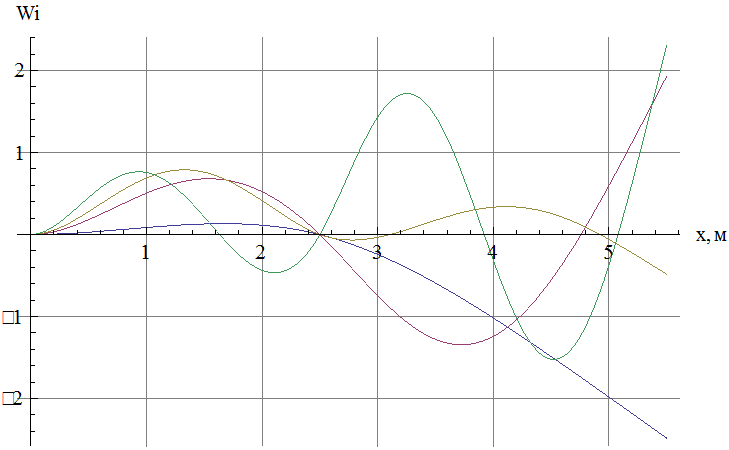Рис.8 График собственных форм.

а) 1-я форма

Определяем коэффициенты С_i для первой формы

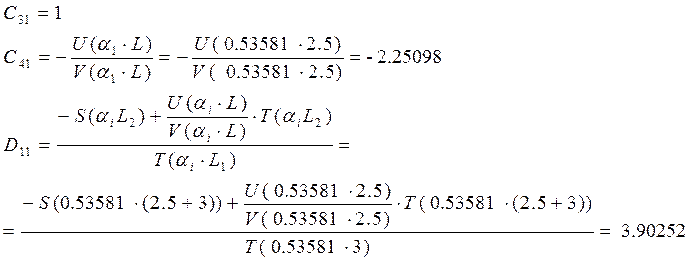
функция формы

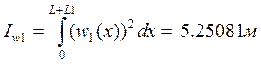
Эквивалентная масса по первой форме

Эквивалентная жесткость по первой форме

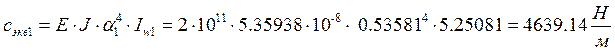
Эквивалентная сила по первой форме

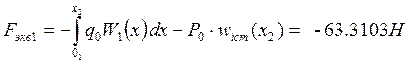
Приближенное значение первой собственной частоты

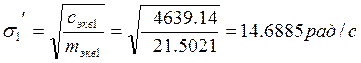
Эквивалентный коэффициент демпфирования

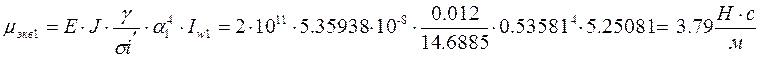
Коэффициент затухания по первой форме

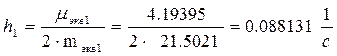
Точное значение первой собственной частоты

Временная функция

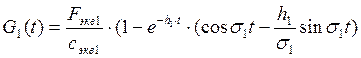
Аналогично рассчитываем для 3-х оставшихся форм и получаем
следующие значения:

б) 2-я форма

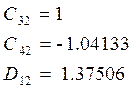
функция формы

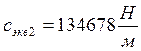
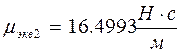
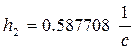
Временная функция

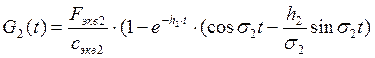
в) 3-я форма

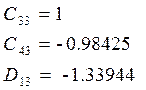
функция формы

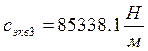
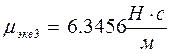
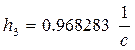
Временная функция

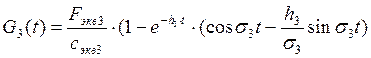
г) 4-я форма

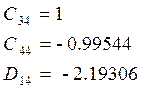
функция формы

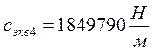
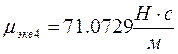
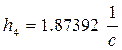
Временная функция

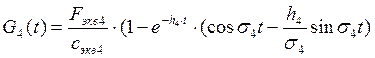
 2.8  Записываем общее выражение для прогиба балки

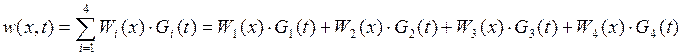
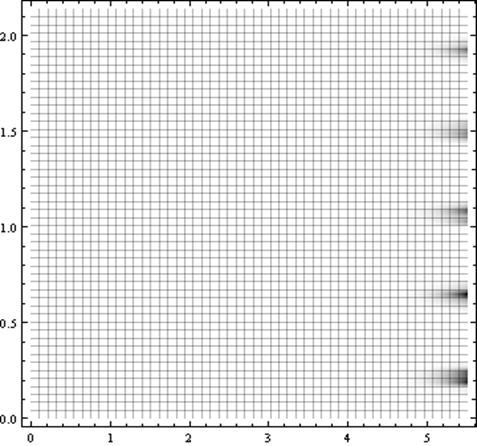
Для определения максимального по
модулю значения функции строим график.

       t, с

x, м

Рис.9.  График функции

Из рис.9. видно, что глобальный
экстремум находится в области, ограниченной следующими значениями аргумента 5 м<
x<5.5 м , 0.5 с< t<0.8
с

    

Строим график зависимости – рис.10   

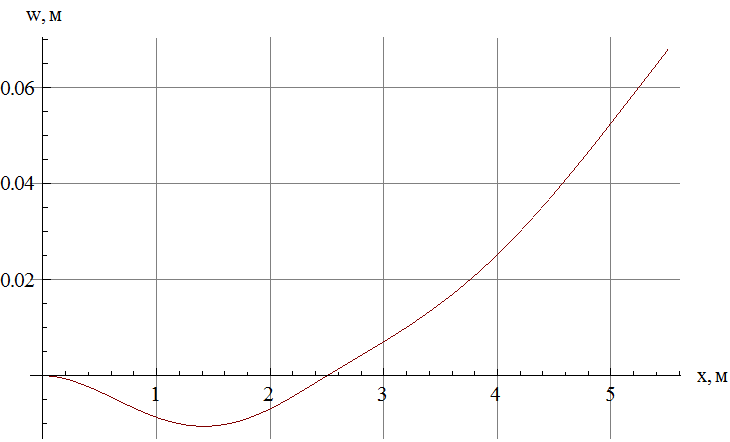
Рис.10. Зависимость прогиба от координаты в момент
достижения максимального по модулю прогиба.

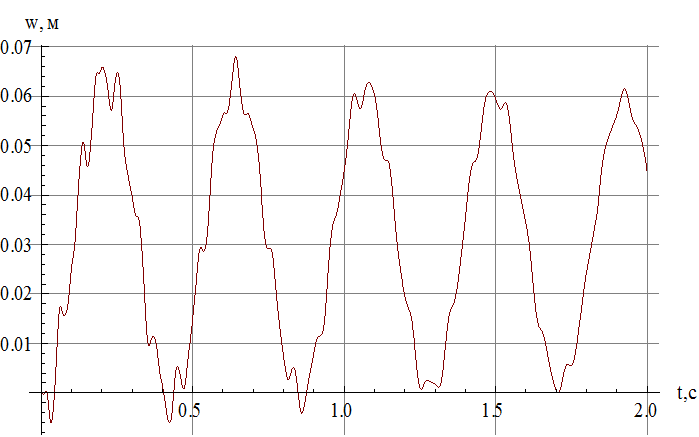
Рис.11 Зависимость прогиба от времени в сечении, в котором
достигается максимальный по модулю прогиб.

2.9 Выражение для изгибающего момента

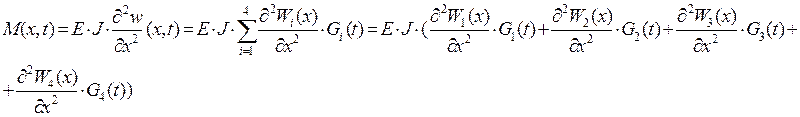
 Строим график зависимости –
рис.12

  t, с

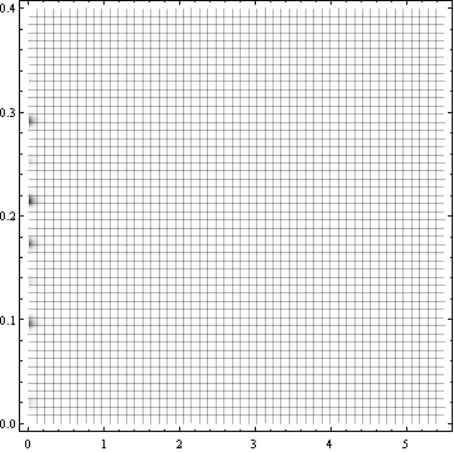x,м

Рис. 12 График зависимости

Из рис.12 видно, что глобальный
экстремум находится в области, ограниченной следующими значениями аргумента 0 м<
x<0.5 м , 0 с< t<0.5 с

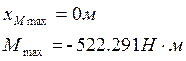
Строим график зависимости

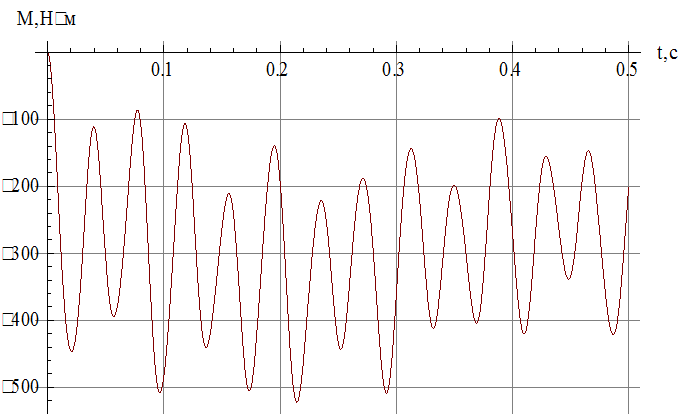
Рис.13  Зависимость изгибающего момента от времени в
сечении, в котором достигается его максимальное по модулю значение

Строим график зависимости –
рис.14

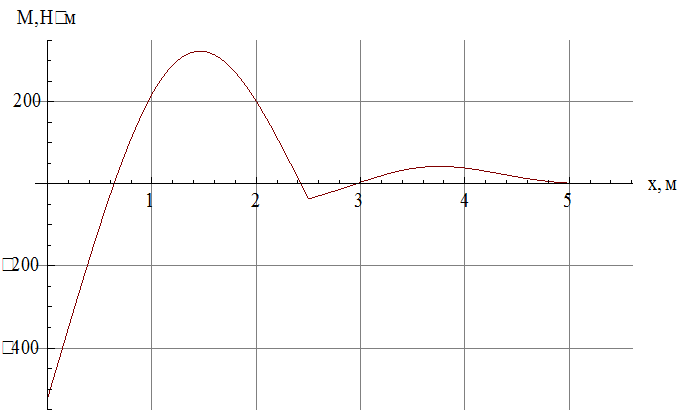
Рис.14 Зависимость изгибающего
момента от координаты в момент достижения максимального по модулю изгибающего
момента.

2. 10 Определяем максимальные напряжения.

Выводы

Максимальные напряжения в балке:

Из первой части:

Из второй части:

В обоих
случаях напряжения меньше предела прочности стали.

Во второй части курсовой работы был получен более точный результат
максимальных напряжений в балке, т.к. в первой части мы сделали грубое
допущение, что балка является системой с одной степенью свободы.

Во  второй части для расчета балки были использованы 4 собственных
формы. Каждую форму можно рассматривать как степень свободы.