| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
lim_{(x,y)to (3,3)}(frac{x-y}{sqrt{x}-sqrt{y}})
-
lim_{(x,y)to (0,0)}(frac{x^2+y^2}{sqrt{x^2+y^2+1}-1})
-
lim_{(x,y)to (0,0)}(frac{3x^{3}y}{x^{4}+y^{4}})
-
lim_{(x,y)to (0,0)}(frac{xy}{x^{2}+y^{2}})
- Показать больше
Описание
Пошаговое решение ограничений для нескольких переменных
multi-var-calculus-limit-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Advanced Math Solutions – Limits Calculator, Infinite limits
In the previous post we covered substitution, where the limit is simply the function value at the point. But what…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Examples for
Limits are the underlying tool used in calculus, appearing in the definitions of continuity, derivatives and integrals. Wolfram|Alpha has the power to compute bidirectional limits, one-sided limits, supremum and infimum limits, discrete limits and multivariable limits. More information, such as plots and series expansions, is provided to enhance mathematical intuition about a limit.
Limits
Compute limits numerically and symbolically.
Compute a limit:
lim (sin x – x)/x^3 as x->0
Start Limit, Start variable, n , variable End,Start target value, ∞ , target value End,Start expression, Start Power, Start base, 1+ Start Fraction, Start numerator, 1 , numerator End,Start denominator, n , denominator End , Fraction End , base End,Start exponent, n , exponent End , Power End , expression End , Limit Endlimnmm-template-arrow-right-8∞1+1n n
Take the limit of a difference quotient:
lim ((x+h)^5 – x^5)/h as h->0
Compute a limit involving abstract functions:
lim (f(x+h) – 2f(x) + f(x-h)) / h^2 as h->0
Multivariable Limits
Explore limits of expressions in two or more dimensions.
Compute a multidimensional limit:
lim sin(x^2 y)/(x^2+y^2) as (x,y)->(0,0)
lim(x,y) -> (0,0) (x^2-xy+y^2)/(x^2+y^2)
limit x/(x+y^5) as (x,y)->(0,0)
Find the value of a nested limit:
limit arctan(x^2/y^2) as x -> 0 as y -> 0
Discrete Limits
Evaluate limiting behavior of sequences.
Compute discrete limits:
discrete limit of (3 n)/(1 + 6 n) as n -> infinity
discrete lim n/(n + 1)
Compute discrete supremum or infimum limits:
discrete lim inf of (-1)^n as n -> infinity
discrete limsup of sin(pi/3 n) * cos(pi/4 m) as {m, n} -> {infinity, infinity}
One-Sided Limits
Compute one-sided limits from a specified direction.
Compute one-sided limits at a point of discontinuity:
lim (x^2 + 2x + 3)/(x^2 – 2x – 3) as x->3
Start Limit, Start variable, x , variable End,Start target value, 2 , target value End,Start expression, Start Piecewise, Start first value, Start Power, Start base, x , base End,Start exponent, 2 , exponent End , Power End , first value End,Start first condition, x≤2 , first condition End,Start second value, 5x-7 , second value End,Start second condition, x > 2 , second condition End , Piecewise End , expression End , Limit Endlimxmm-template-arrow-right-82 x2x≤25x–7x > 2
Specify the direction of approach:
Start Limit from the Right, Start variable, x , variable End,Start target value, 0 , target value End,Start expression, Start Fraction, Start numerator, x , numerator End,Start denominator, Start Absolute, Start argument, x , argument End , Absolute End , denominator End , Fraction End , expression End , Limit from the Right Endlimxmm-template-arrow-right-80+xx
limit tan(t) as t->pi/2 from the left
Limit Representations
Express functions in terms of limits.
Find limit representations for a function:
exp(z) limit representation
Si(x) limit rep
Поделиться калькулятором пределов
Добавить в закладки
Добавьте калькулятор пределов в закладки вашего браузера
1. Для Windows или Linux – нажмите Ctrl + D .
2. Для MacOS – нажмите Cmd + D .
3. Для iPhone (Safari) – нажмите и удерживайте , затем нажмите Добавить закладку
4. Для Google Chrome : нажмите 3 точки в правом верхнем углу, затем нажмите знак звездочки
Как использовать?
Калькулятор лимита с шагами
онлайн калькулятор пределов поможет вам найти предел функции по отношению к переменной. Это онлайн-инструмент, который помогает вам вычислять значение функции, когда вход приближается к определенному значению.
Калькулятор пределов с шагами показывает пошаговое решение пределов вместе с графиком и расширением ряда. Он использует все предельные правила, такие как сумма, произведение, частное и правило Лопиталя, для расчета точного значения.
Вы можете оценить пределы относительно (text{x, y, z, v, u, t}) и (w) с помощью этого калькулятора пределов.
Это не то. С помощью этого инструмента вы также можете найти,
- Правый предел (+)
- Левый предел (-)
- двусторонний предел
Как работает калькулятор лимитов?
Чтобы оценить предел с помощью этого решателя пределов, выполните следующие шаги.
- Введите функцию в данное поле ввода.
- Выберите соответствующую переменную.
- Введите предельное значение.
- Выберите сторону ограничения. т. е. левое, правое или двустороннее.
- Нажмите кнопку «Рассчитать», чтобы получить результат.
- Используйте кнопку «Сброс», чтобы ввести новые значения, и значок клавиатуры , чтобы ввести дополнительные значения.
Вы найдете ответ под инструментом. Нажмите «Показать шаги», чтобы просмотреть пошаговое решение.
Что такое предел в исчислении?
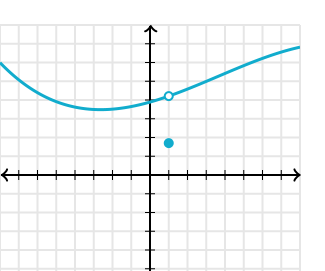
Предел функции — это значение, к которому f(x) приближается по мере приближения x к некоторому числу. Пределы можно использовать для определения производных, интегралов и непрерывности, находя предел данной функции. Это написано как:
Если f – функция с действительным знаком, а a – действительное число, то приведенное выше выражение читается как
предел f x, когда x приближается к a, равен L.
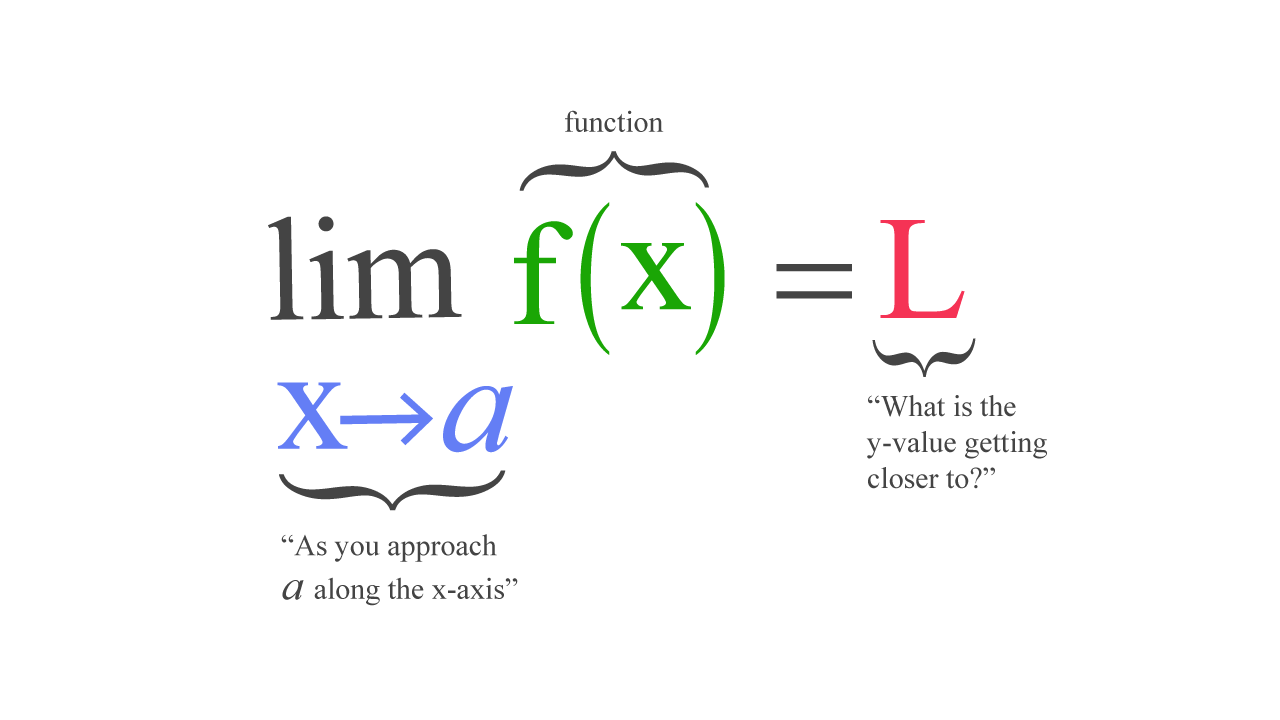
Как найти предел? – со ступеньками
Пределы могут применяться в виде чисел, постоянных значений (π, G, k), бесконечности и т. д. Давайте рассмотрим несколько примеров, чтобы узнать, как оценивать пределы.
Пример — правый предел
(lim _{xto :2^+}frac{left(x^2+2right)}{left(x-1right)})
Решение:
Правый предел – это предел функции по мере ее приближения с правой стороны.
Шаг 1: Примените ограничение x➜2 к приведенной выше функции. Поместите предельное значение вместо x.
(lim :_{xto 2^+}frac{left(x^2+2right)}{left(x-1right)})
(=frac{left(2^2+2right)}{left(2-1right)})
Шаг 2: Решите уравнение, чтобы получить результат.
(=frac{left(4+2right)}{left(2-1right)} =frac{6}{1} =6 )
Шаг 3: Запишите выражение с его ответом.
(lim :_{xto ::2^+}frac{left(x^2+2right)}{left(x-1right)}=6)
График
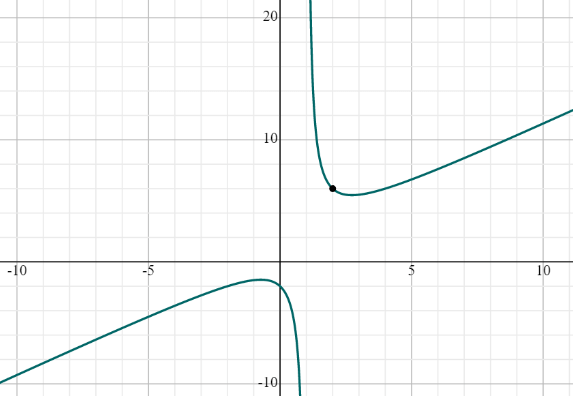
Пример — левосторонний предел
(lim _{xto 3^-}left(frac{x^2-3x+4}{5-3x}right))
Решение:
Левый предел означает предел функции по мере ее приближения с левой стороны.
Шаг 1: Поместите предельное значение в функцию.
(lim _{xto 3^-}left(frac{x^2-3x+4}{5-3x}right))
(=frac{left(3^2-3left(3right)+4right)}{left(5-3left(3right)right)})
Шаг 2: Решите уравнение дальше.
(=frac{left(9-9+4right)}{left(5-9right)})
(=frac{left(0+4right)}{left(-4right)} =frac{4}{-4} =-1 )
Шаг 3: Запишите функцию, как написано ниже.
(lim :_{xto :3^-}left(frac{x^2-3x+4}{5-3x}right)=-1)
График
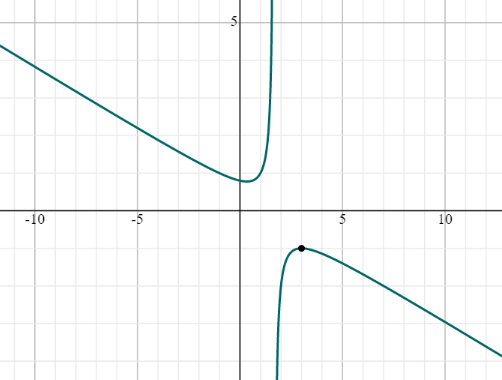
Пример — двусторонний лимит
( lim _{xto 5}left(cos^3left(xright)cdot sinleft(xright)right) )
Решение:
Двусторонний предел существует, если предел, идущий с обоих направлений (положительного и отрицательного), одинаков. Это то же самое, что лимит.
Шаг 1: Подставьте значение limit в функцию.
(lim _{xto 5}left(cos^3left(xright)cdot sinleft(xright)right))
(=cos^3left(5right)cdot :sinleft(5right))
Шаг 2: Упростите уравнение, как мы это делали в предыдущих примерах.
( lim _{xto 5}left(cos^3left(xright)cdot sinleft(xright)right) )
( =cos^3left(5right):sinleft(5right))
Шаг 3: Приведенное выше уравнение можно рассматривать как окончательный ответ. Однако, если вы хотите решить его дальше, решите тригонометрические значения в уравнении.
(=frac{1141}{50000}cdot :-frac{23973}{25000} =-frac{10941}{500000} )
(lim ::_{xto ::5}left(cos^3left(xright)cdot ::sinleft(xright)right))
(=-0.021882 )
График
Часто задаваемые вопросы
Есть ли у sin x предел?
Грех x не имеет предела. Это связано с тем, что по мере приближения x к бесконечности значение y колеблется между 1 и −1.
Каков предел e до бесконечности?
Предел e до бесконечности (∞) равен e.
Каков предел, когда e^x приближается к 0?
Предел, когда e^x приближается к 0, равен 1.
Каков предел, когда x приближается к бесконечности ln(x)?
Предел ln(x) при стремлении x к бесконечности равен +∞. Предел этого натурального логарифма может быть доказан доведением до абсурда.
- Если x >1ln(x) > 0, предел должен быть положительным.
- Поскольку ln(x2) − ln(x1) = ln(x2/x1). Если x2>x1, разность положительна, поэтому ln(x) всегда возрастает.
- Если lim x→∞ ln(x) = M ∈ R, мы имеем ln(x) < M ⇒ x < eM, но x→∞, поэтому M не может находиться в R, и предел должен быть +∞.
Онлайн калькуляторы пределов, производных и их приложений
Данный раздел содержит
онлайн калькуляторы
для вычисления пределов и производных различных порядков для функций одной или многих переменных, заданных в обычной, неявной или параметрической форме. Для каждого калькулятора предусмотренно подробное решение.
Пределы, производные и их приложения
9
Вычисление пределов
Калькулятор вычисляет предел выражения с описанием подробного хода решения на русском языке
Вычисление производной
Калькулятор позволяет вычислить производную обычной функции с пошаговым решением на русском языке.
Вычисление частных производных
Калькулятор находит частную производную функции нескольких переменных с описанием подробного хода решения на русском языке.

