Why would you use a list comprehension? A list comprehension only knows about any one member of a list at a time, so that would be an odd approach. Instead:
def findMiddle(input_list):
middle = float(len(input_list))/2
if middle % 2 != 0:
return input_list[int(middle - .5)]
else:
return (input_list[int(middle)], input_list[int(middle-1)])
This one should return the middle item in the list if it’s an odd number list, or a tuple containing the middle two items if it’s an even numbered list.
Edit:
Thinking some more about how one could do this with a list comprehension, just for fun. Came up with this:
[lis[i] for i in
range((len(lis)/2) - (1 if float(len(lis)) % 2 == 0 else 0), len(lis)/2+1)]
read as:
“Return an array containing the ith digit(s) of array lis, where i is/are the members of a range, which starts at the length of lis, divided by 2, from which we then subtract either 1 if the length of the list is even, or 0 if it is odd, and which ends at the length of lis, divided by 2, to which we add 1.”
The start/end of range correspond to the index(es) we want to extract from lis, keeping in mind which arguments are inclusive/exclusive from the range() function in python.
If you know it’s going to be an odd length list every time, you can tack on a [0] to the end there to get the actual single value (instead of an array containing a single value), but if it can or will be an even length list, and you want to return an array containing the two middle values OR an array of the single value, leave as is. 🙂
Почему вы используете понимание списка? Понимание списка знает только об одном члене списка за раз, так что это будет странный подход. Вместо:
def findMiddle(input_list):
middle = float(len(input_list))/2
if middle % 2 != 0:
return input_list[int(middle - .5)]
else:
return (input_list[int(middle)], input_list[int(middle-1)])
Это должно возвращать средний элемент в списке, если он представляет собой список нечетных номеров, или кортеж, содержащий два элемента, если он является четным списком.
Редактировать:
Еще раз подумав о том, как можно сделать это с пониманием списка, просто для удовольствия. Пришел к следующему:
[lis[i] for i in
range((len(lis)/2) - (1 if float(len(lis)) % 2 == 0 else 0), len(lis)/2+1)]
читать как:
“Возвращает массив, содержащий i й разряд массива lis, где я – члены диапазона, начинающийся the length of lis, divided by 2, from which we then subtract either 1 if the length of the list is even, or 0 if it is odd и заканчивается the length of lis, divided by 2, to which we add 1 “
Начало/конец диапазона соответствуют индексу (es), который мы хотим извлечь из lis, имея в виду, какие аргументы включены/исключены из функции range() в python.
Если вы знаете, что каждый раз он будет списком нечетной длины, вы можете сделать ставку на [0] до конца, чтобы получить фактическое одиночное значение (вместо массива, содержащего одно значение), но если оно может или будет список длины, и вы хотите вернуть массив, содержащий два средних значения или массив из одного значения, оставить как есть. 🙂
Зачем вам использовать понимание списка? Понимание списка знает только о любом члене списка за раз, так что это был бы странный подход. Вместо:
def findMiddle(input_list):
middle = float(len(input_list))/2
if middle % 2 != 0:
return input_list[int(middle - .5)]
else:
return (input_list[int(middle)], input_list[int(middle-1)])
Этот должен возвращать средний элемент в списке, если это список нечетных чисел, или кортеж, содержащий два средних элемента, если это список с четным номером.
Редактировать:
Подумайте еще о том, как можно сделать это с помощью понимания списка, просто для удовольствия. Придумали это:
[lis[i] for i in
range((len(lis)/2) - (1 if float(len(lis)) % 2 == 0 else 0), len(lis)/2+1)]
читать как:
“Вернуть массив, содержащий ith цифра (ы) массива lisгде я есть / являются членами диапазона, который начинается в the length of lis, divided by 2, from which we then subtract either 1 if the length of the list is even, or 0 if it is oddи который заканчивается в the length of lis, divided by 2, to which we add 1“.
Начало / конец диапазона соответствуют индексу (ам), из которых мы хотим извлечь lisучитывая, какие аргументы являются включающими / исключающими из range() функция в питоне.
Если вы знаете, что каждый раз это будет нечетный список длины, вы можете [0] до конца, чтобы получить фактическое единственное значение (вместо массива, содержащего единственное значение), но если это может или будет список четной длины, и вы хотите вернуть массив, содержащий два средних значения ИЛИ массив из одно значение, оставить как есть.:)
Массивы
Массивы – одна из самых фундаментальных структур данных в информатике. Они встроены во все языки программирования, даже такие низкоуровневые, как C или Assembler. Массивы представляют собой группу элементов одного типа, которые расположены на непрерывном участке памяти компьютера. Например, [5, 8, -1] или ['a', 'b', 'c'].
Поскольку элементы массива стоят рядом друг с другом, мы можем получить доступ к любому их индексу. Например, к первому, третьему или последнему элементу за время O(1).
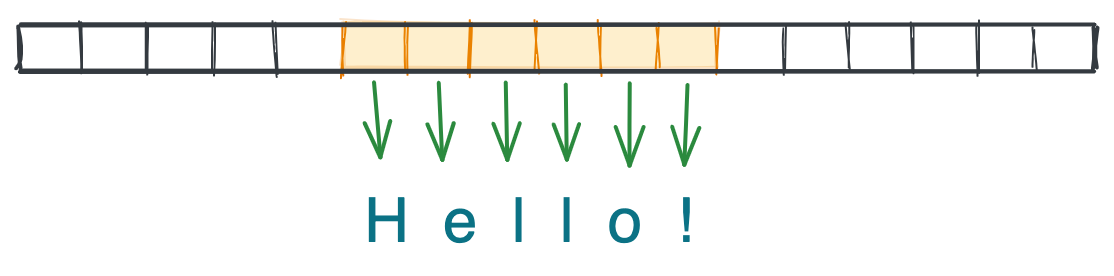
В таких языках, как C и Java, требуется заранее указывать размер массива и тип данных. Структура списка в Python позволяет обойти эти требования, сохраняя данные в виде указателей на местоположение элементов в памяти, автоматически изменяя размер массива, когда место заканчивается. Элементам памяти не обязательно находиться рядом друг с другом.
Реализация
Основные ограничения, с которыми мы сталкиваемся при создании массивов на языке Python:
- После выделения места для массива мы не можем получить больше, не создав новый массив.
- Все значения в массиве должны быть одного типа.
Мы можем реализовать в Python очень простой класс Array, который имитирует основную функциональность массивов в языках более низкого уровня.
from typing import Any
class Array:
def __init__(self, n: int, dtype: Any):
self.vals = [None] * n
self.dtype = dtype
def get(self, i: int) -> Any:
"""
Возвращает значение как индекс i
"""
return self.vals[i]
def put(self, i: int, val: Any) -> None:
"""
Обновляем массив как индекс i с val. Val должно быть одного типа с self.dtype
"""
if not isinstance(val, self.dtype):
raise ValueError(f"val явл {type(val)}; должно быть {self.dtype}")
self.vals[i] = val
Давайте рассмотрим, какие способы реализации класса Array мы можем использовать. Создадим экземпляр. Подтвердим, что первый индекс пустой. Заполним слот символом char, а затем вернем его. Наши предыдущие действия подтвердили, что массив отвергает non-char (несимвольные) значения. Код не самый лучший, но рабочий:
arr = Array(10, str)
arr.get(0) # None
arr.put(0, 'a') # None
arr.get(0) # 'a'
arr.put(1, 5)
# ValueError: val is <class 'int'>; must be <class 'str'>
Пример
В процессе работы с массивами вы, скорее всего, захотите использовать встроенный список Python, или массив NumPy, а не созданный нами класс Array. Однако, в целях использования массива, который не меняет размер, необходимо разобраться с Leetcode LC 1089: Duplicate Zeros (Дублирование нулей). Цель данных действий – продублировать все нули в массиве, изменяя его на месте таким образом, чтобы элементы двигались вниз и исчезали, а не увеличивали размер массива или создавали новый.
def duplicate_zeros(arr: list) -> None:
"""
Дублируем все нули в массиве, оставляя его первоначальную длину. Например, [1, 0, 2, 3] -> [1, 0, 0, 2]
"""
i = 0
while i < len(arr):
if arr[i] == 0:
arr.insert(i, 0) # Вставляем 0 как индекс i
arr.pop() # Убираем последний элемент
i += 1
i += 1
В итоге мы итеративно перемещаемся по списку, пока не найдем ноль. Затем вставляем еще один ноль и исключаем последний элемент для сохранения размера массива.
Обратите внимание: в данном случае важно использовать цикла while, а не for, так как мы изменяем массив по мере его прохождения. Тщательный контроль над индексом i позволяет нам пропустить вставленный ноль, чтобы избежать двойного счета.
Связанные списки
Связанные списки – еще одна ключевая структура данных в информатике. Как и массивы, связный список – это группа значений. Однако, в отличие от массивов, значения в связанном списке не обязательно должны быть одного типа, и нам не нужно заранее определять размер списка.
Основным элементом связанного списка является узел, который содержит некоторые данные и указатель на любое место в памяти.
Ниже представлен связанный список со значениями [1, 'a', 0.3]. Обратите внимание на различие размеров элементов. Мы видим четыре байта для целых и плавающих чисел, один байт для символов. Каждый узел имеет четырехбайтовый указатель, расстояние между узлами различно, последний из них содержит нулевой указатель, который указывает в пространство.
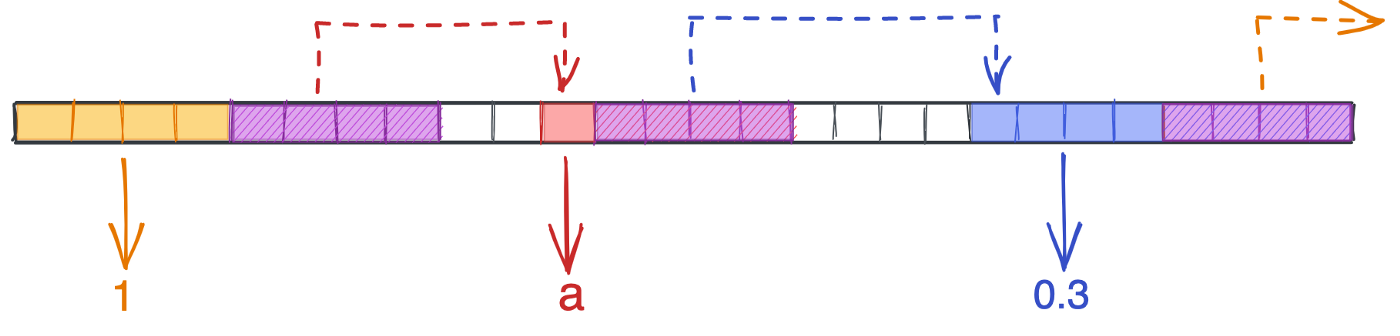
Отсутствие ограничений на типы данных и длину делает связанные списки привлекательными. Однако эта гибкость создает некоторые проблемы. Программе доступен только верх списка, а это значит, что для поиска любого другого узла нам придется пройти весь список. Другими словами, мы лишаемся O(1) поиска для любого элемента, кроме первого узла. Если вы запрашиваете 100-й элемент, то для его получения потребуется 100 шагов: схема O(n).
Можно сделать связанные списки более универсальными. Для этого необходимо добавить указатели на предыдущие узлы и раскрыть конец списка, или сделать его кольцевым. В целом, выбор связанных списков вместо массивов является платой за удобство.
Реализация
Чтобы создать связанный список в Python, начнем с определения узла. Необходимы только две части: данные, которые хранит узел и указатель на следующий узел в списке. Добавим метод __repr__ для того, чтобы было легче увидеть содержание узла.
class ListNode:
def __init__(self, val=None, next=None):
self.val = val
self.next = next
def __repr__(self):
return f"ListNode со значением {self.val}"
Далее попробуем использовать класс ListNode. Важно отметить, что вершина списка – это наша переменная head. Необходимо итеративно добавлять .next для доступа к более глубоким узлам, поскольку мы не можем ввести индекс типа [1] или [2], чтобы добраться до них.
head = ListNode(5)
head.next = ListNode('abc')
head.next.next = ListNode(4.815162342)
print(head) # ListNode со значением 5
print(head.next) # ListNode со значением abc
print(head.next.next) # ListNode со значением 4.815162342
Для того чтобы было легче добавить узел как в конец, так и в начало списка, напишем функции:
def add_to_end(head: ListNode, val: Any) -> None:
ptr = head
while ptr.next:
ptr = ptr.next
ptr.next = ListNode(val)
def add_to_front(head: ListNode, val: Any) -> ListNode:
node = ListNode(val)
node.next = head
return node
В add_to_end создаем переменную ptr (указатель). Она начинается с head и обходит список, пока не достигнет последнего узла, атрибутом .next которого является нулевой указатель. Далее, устанавливаем значение .next этого узла в новый ListNode. Внутри функции не нужно ничего возвращать, чтобы изменение вступило в силу.
В add_to_front мы создаем новый head, устанавливаем указатель .next в вершину существующего связанного списка. Вручную обновляем head вне данной функции с помощью нового узла. В противном случае, head по-прежнему будет указывать на старый head.
# Создает и расширяет список
head = ListNode(5)
add_to_end(head, 'abc')
add_to_end(head, 4.815162342)
# Вывод
print(head) # ListNode со значением 5
print(head.next) # ListNode со значением abc
print(head.next.next) # ListNode со значением 4.815162342
# Пытаемся обновить head
add_to_front(head, 0)
print(head) # ListNode со значением 5
# Корректное обновление head
head = add_to_front(head, 0)
print(head) # ListNode со значением 0
Пример
Один из частых вопросов, который возникает во время работы со связными списками – возврат среднего узла. Так как обычно существует только начало списка, нет возможности заранее узнать его длину. Исходя из этого, может показаться, что нам придется обойти список дважды: один раз, чтобы узнать его длину, а второй, чтобы пройти половину пути.
Ранее мы использовали указатель, чтобы обойти список по одному узлу за раз, пока не дойдем конца.
На самом деле существует способ найти середину списка за один проход.
Что если у нас будет два указателя? Первый из них будет перемещаться по одному узлу за подход, а второй – по два. В тот момент, когда быстрый указатель достигнет конца списка, наш первоначальный указатель окажется только в середине.
Исходя из написанного выше, мы ответим на LC 876: Середина связанного списка (Middle of the Linked List) следующим образом:
def find_middle(head: ListNode) -> ListNode:
"""
Return middle node of linked list. If even number of nodes,
returns the second middle node.
"""
# Смотрим на медленную и быструю точки
slow = head
fast = head.next
# Прогоняем список через цикл
while fast and fast.next:
slow = slow.next
fast = fast.next.next
return slow
В данном случае при работе с Leetcode, мы убеждаемся, что head.next – правильный вариант.
# Список: A -> B -> C -> D -> E
# Середина: C
# Начало с head: неправильно
# Slow: A -> B -> C -> D ==> Середина: D
# Fast: A -> C -> E -> null
# Начало с head.next: правильно
# Slow: A -> B -> C ==> Середина: C
# Fast: B -> D -> null
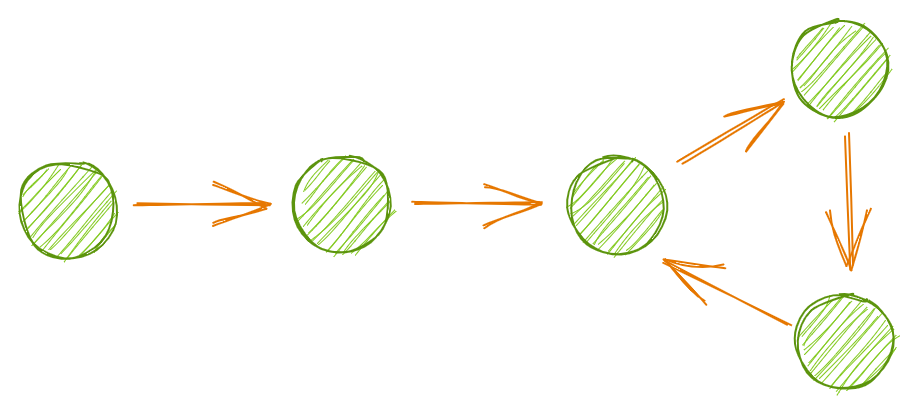
LC 141. Linked List Cycle: Цикл связанного списка – пример использования медленных и быстрых указателей. Наша цель определить, есть ли в списке цикл, который возникает, когда следующий указатель узла показывает на более ранний узел в списке.
Проблема в том, что проход списка через цикл будет бесконечным.
Один из вариантов решения заключается в том, что нам нужно установить ограничение на продолжительность выполнения обхода, или решить проблему повторяющихся паттернов за некоторый период времени.
Более простой подход заключается в использовании двух указателей.
В данном случае невозможно использование while fast и fast.next, так как эти методы имеют значение False только при достижении конца списка. Вместо этого, подставим slow и fast на первый и второй узлы. Будем перемещать их по списку с разной скоростью, пока они не совпадут. В конце списка вернем False. Если два указателя будут показывать на один и тот же узел, вернем True.
def has_cycle(head: ListNode) -> bool:
"""
Определяем где связанный список имеет цикл
"""
slow = head
fast = head.next
while slow != fast:
# Находим конец списка
if not (fast or fast.next):
return False
slow = slow.next
fast = fast.next.next
return True
***
Мы узнали, что такое массивы и связанные списки. Это важная составляющая структур данных, которая используется во всех языках программирования.
В следующей части материала приступим к изучению деревьев и графов.
Материалы по теме
- 📈 Big O нотация: что это такое и почему ее обязательно нужно знать каждому программисту
- Какие алгоритмы нужно знать, чтобы стать хорошим программистом?
- Изучаем алгоритмы: полезные книги, веб-сайты, онлайн-курсы и видеоматериалы
В этой статье будут рассмотрены популярные алгоритмы, принципы их работы и реализация на Python. А ещё сравним, как быстро они сортируют элементы в списке.
В качестве общего примера возьмём сортировку чисел в порядке возрастания. Но эти методы можно легко адаптировать под ваши потребности.
Пузырьковая сортировка
Этот простой алгоритм выполняет итерации по списку, сравнивая элементы попарно и меняя их местами, пока более крупные элементы не «всплывут» в начало списка, а более мелкие не останутся на «дне».
Алгоритм
Сначала сравниваются первые два элемента списка. Если первый элемент больше, они меняются местами. Если они уже в нужном порядке, оставляем их как есть. Затем переходим к следующей паре элементов, сравниваем их значения и меняем местами при необходимости. Этот процесс продолжается до последней пары элементов в списке.
При достижении конца списка процесс повторяется заново для каждого элемента. Это крайне неэффективно, если в массиве нужно сделать, например, только один обмен. Алгоритм повторяется n² раз, даже если список уже отсортирован.
Для оптимизации алгоритма нужно знать, когда его остановить, то есть когда список отсортирован.
Чтобы остановить алгоритм по окончании сортировки, нужно ввести переменную-флаг. Когда значения меняются местами, устанавливаем флаг в значение True, чтобы повторить процесс сортировки. Если перестановок не произошло, флаг остаётся False и алгоритм останавливается.
Реализация
def bubble_sort(nums):
# Устанавливаем swapped в True, чтобы цикл запустился хотя бы один раз
swapped = True
while swapped:
swapped = False
for i in range(len(nums) - 1):
if nums[i] > nums[i + 1]:
# Меняем элементы
nums[i], nums[i + 1] = nums[i + 1], nums[i]
# Устанавливаем swapped в True для следующей итерации
swapped = True
# Проверяем, что оно работает
random_list_of_nums = [5, 2, 1, 8, 4]
bubble_sort(random_list_of_nums)
print(random_list_of_nums)Алгоритм работает в цикле while и прерывается, когда элементы ни разу не меняются местами. Вначале присваиваем swapped значение True, чтобы алгоритм запустился хотя бы один раз.
Время сортировки
Если взять самый худший случай (изначально список отсортирован по убыванию), затраты времени будут равны O(n²), где n — количество элементов списка.
Сортировка выборкой
Этот алгоритм сегментирует список на две части: отсортированную и неотсортированную. Наименьший элемент удаляется из второго списка и добавляется в первый.
Алгоритм
На практике не нужно создавать новый список для отсортированных элементов. В качестве него используется крайняя левая часть списка. Находится наименьший элемент и меняется с первым местами.
Теперь, когда нам известно, что первый элемент списка отсортирован, находим наименьший элемент из оставшихся и меняем местами со вторым. Повторяем это до тех пор, пока не останется последний элемент в списке.
Реализация
def selection_sort(nums):
# Значение i соответствует кол-ву отсортированных значений
for i in range(len(nums)):
# Исходно считаем наименьшим первый элемент
lowest_value_index = i
# Этот цикл перебирает несортированные элементы
for j in range(i + 1, len(nums)):
if nums[j] < nums[lowest_value_index]:
lowest_value_index = j
# Самый маленький элемент меняем с первым в списке
nums[i], nums[lowest_value_index] = nums[lowest_value_index], nums[i]
# Проверяем, что оно работает
random_list_of_nums = [12, 8, 3, 20, 11]
selection_sort(random_list_of_nums)
print(random_list_of_nums) По мере увеличения значения i нужно проверять меньше элементов.
Время сортировки
Затраты времени на сортировку выборкой в среднем составляют O(n²), где n — количество элементов списка.
Сортировка вставками
Как и сортировка выборкой, этот алгоритм сегментирует список на две части: отсортированную и неотсортированную. Алгоритм перебирает второй сегмент и вставляет текущий элемент в правильную позицию первого сегмента.
Алгоритм
Предполагается, что первый элемент списка отсортирован. Переходим к следующему элементу, обозначим его х. Если х больше первого, оставляем его на своём месте. Если он меньше, копируем его на вторую позицию, а х устанавливаем как первый элемент.
Переходя к другим элементам несортированного сегмента, перемещаем более крупные элементы в отсортированном сегменте вверх по списку, пока не встретим элемент меньше x или не дойдём до конца списка. В первом случае x помещается на правильную позицию.
Реализация
def insertion_sort(nums):
# Сортировку начинаем со второго элемента, т.к. считается, что первый элемент уже отсортирован
for i in range(1, len(nums)):
item_to_insert = nums[i]
# Сохраняем ссылку на индекс предыдущего элемента
j = i - 1
# Элементы отсортированного сегмента перемещаем вперёд, если они больше
# элемента для вставки
while j >= 0 and nums[j] > item_to_insert:
nums[j + 1] = nums[j]
j -= 1
# Вставляем элемент
nums[j + 1] = item_to_insert
# Проверяем, что оно работает
random_list_of_nums = [9, 1, 15, 28, 6]
insertion_sort(random_list_of_nums)
print(random_list_of_nums)Время сортировки
Время сортировки вставками в среднем равно O(n²), где n — количество элементов списка.
Пирамидальная сортировка
Также известна как сортировка кучей. Этот популярный алгоритм, как и сортировки вставками или выборкой, сегментирует список на две части: отсортированную и неотсортированную. Алгоритм преобразует второй сегмент списка в структуру данных «куча» (heap), чтобы можно было эффективно определить самый большой элемент.
Алгоритм
Сначала преобразуем список в Max Heap — бинарное дерево, где самый большой элемент является вершиной дерева. Затем помещаем этот элемент в конец списка. После перестраиваем Max Heap и снова помещаем новый наибольший элемент уже перед последним элементом в списке.
Этот процесс построения кучи повторяется, пока все вершины дерева не будут удалены.
Реализация
Создадим вспомогательную функцию heapify() для реализации этого алгоритма:
def heapify(nums, heap_size, root_index):
# Индекс наибольшего элемента считаем корневым индексом
largest = root_index
left_child = (2 * root_index) + 1
right_child = (2 * root_index) + 2
# Если левый потомок корня — допустимый индекс, а элемент больше,
# чем текущий наибольший, обновляем наибольший элемент
if left_child < heap_size and nums[left_child] > nums[largest]:
largest = left_child
# То же самое для правого потомка корня
if right_child < heap_size and nums[right_child] > nums[largest]:
largest = right_child
# Если наибольший элемент больше не корневой, они меняются местами
if largest != root_index:
nums[root_index], nums[largest] = nums[largest], nums[root_index]
# Heapify the new root element to ensure it's the largest
heapify(nums, heap_size, largest)
def heap_sort(nums):
n = len(nums)
# Создаём Max Heap из списка
# Второй аргумент означает остановку алгоритма перед элементом -1, т.е.
# перед первым элементом списка
# 3-й аргумент означает повторный проход по списку в обратном направлении,
# уменьшая счётчик i на 1
for i in range(n, -1, -1):
heapify(nums, n, i)
# Перемещаем корень Max Heap в конец списка
for i in range(n - 1, 0, -1):
nums[i], nums[0] = nums[0], nums[i]
heapify(nums, i, 0)
# Проверяем, что оно работает
random_list_of_nums = [35, 12, 43, 8, 51]
heap_sort(random_list_of_nums)
print(random_list_of_nums)Время сортировки
В среднем время сортировки кучей составляет O(n log n), что уже значительно быстрее предыдущих алгоритмов.
Сортировка слиянием
Этот алгоритм относится к алгоритмам «разделяй и властвуй». Он разбивает список на две части, каждую из них он разбивает ещё на две и т. д. Список разбивается пополам, пока не останутся единичные элементы.
Соседние элементы становятся отсортированными парами. Затем эти пары объединяются и сортируются с другими парами. Этот процесс продолжается до тех пор, пока не отсортируются все элементы.
Алгоритм
Список рекурсивно разделяется пополам, пока в итоге не получатся списки размером в один элемент. Массив из одного элемента считается упорядоченным. Соседние элементы сравниваются и соединяются вместе. Это происходит до тех пор, пока не получится полный отсортированный список.
Сортировка осуществляется путём сравнения наименьших элементов каждого подмассива. Первые элементы каждого подмассива сравниваются первыми. Наименьший элемент перемещается в результирующий массив. Счётчики результирующего массива и подмассива, откуда был взят элемент, увеличиваются на 1.
Реализация
def merge(left_list, right_list):
sorted_list = []
left_list_index = right_list_index = 0
# Длина списков часто используется, поэтому создадим переменные для удобства
left_list_length, right_list_length = len(left_list), len(right_list)
for _ in range(left_list_length + right_list_length):
if left_list_index < left_list_length and right_list_index < right_list_length:
# Сравниваем первые элементы в начале каждого списка
# Если первый элемент левого подсписка меньше, добавляем его
# в отсортированный массив
if left_list[left_list_index] <= right_list[right_list_index]:
sorted_list.append(left_list[left_list_index])
left_list_index += 1
# Если первый элемент правого подсписка меньше, добавляем его
# в отсортированный массив
else:
sorted_list.append(right_list[right_list_index])
right_list_index += 1
# Если достигнут конец левого списка, элементы правого списка
# добавляем в конец результирующего списка
elif left_list_index == left_list_length:
sorted_list.append(right_list[right_list_index])
right_list_index += 1
# Если достигнут конец правого списка, элементы левого списка
# добавляем в отсортированный массив
elif right_list_index == right_list_length:
sorted_list.append(left_list[left_list_index])
left_list_index += 1
return sorted_list
def merge_sort(nums):
# Возвращаем список, если он состоит из одного элемента
if len(nums) <= 1:
return nums
# Для того чтобы найти середину списка, используем деление без остатка
# Индексы должны быть integer
mid = len(nums) // 2
# Сортируем и объединяем подсписки
left_list = merge_sort(nums[:mid])
right_list = merge_sort(nums[mid:])
# Объединяем отсортированные списки в результирующий
return merge(left_list, right_list)
# Проверяем, что оно работает
random_list_of_nums = [120, 45, 68, 250, 176]
random_list_of_nums = merge_sort(random_list_of_nums)
print(random_list_of_nums)Обратите внимание, что функция merge_sort(), в отличие от предыдущих алгоритмов, возвращает новый список, а не сортирует существующий. Поэтому такая сортировка требует больше памяти для создания нового списка того же размера, что и входной список.
Время сортировки
В среднем время сортировки слиянием составляет O(n log n).
Быстрая сортировка
Этот алгоритм также относится к алгоритмам «разделяй и властвуй». Его используют чаще других алгоритмов, описанных в этой статье. При правильной конфигурации он чрезвычайно эффективен и не требует дополнительной памяти, в отличие от сортировки слиянием. Массив разделяется на две части по разные стороны от опорного элемента. В процессе сортировки элементы меньше опорного помещаются перед ним, а равные или большие —позади.
Алгоритм
Быстрая сортировка начинается с разбиения списка и выбора одного из элементов в качестве опорного. А всё остальное передвигаем так, чтобы этот элемент встал на своё место. Все элементы меньше него перемещаются влево, а равные и большие элементы перемещаются вправо.
Реализация
Существует много вариаций данного метода. Способ разбиения массива, рассмотренный здесь, соответствует схеме Хоара (создателя данного алгоритма).
def partition(nums, low, high):
# Выбираем средний элемент в качестве опорного
# Также возможен выбор первого, последнего
# или произвольного элементов в качестве опорного
pivot = nums[(low + high) // 2]
i = low - 1
j = high + 1
while True:
i += 1
while nums[i] < pivot:
i += 1
j -= 1
while nums[j] > pivot:
j -= 1
if i >= j:
return j
# Если элемент с индексом i (слева от опорного) больше, чем
# элемент с индексом j (справа от опорного), меняем их местами
nums[i], nums[j] = nums[j], nums[i]
def quick_sort(nums):
# Создадим вспомогательную функцию, которая вызывается рекурсивно
def _quick_sort(items, low, high):
if low < high:
# This is the index after the pivot, where our lists are split
split_index = partition(items, low, high)
_quick_sort(items, low, split_index)
_quick_sort(items, split_index + 1, high)
_quick_sort(nums, 0, len(nums) - 1)
# Проверяем, что оно работает
random_list_of_nums = [22, 5, 1, 18, 99]
quick_sort(random_list_of_nums)
print(random_list_of_nums) Время выполнения
В среднем время выполнения быстрой сортировки составляет O(n log n).
Обратите внимание, что алгоритм быстрой сортировки будет работать медленно, если опорный элемент равен наименьшему или наибольшему элементам списка. При таких условиях, в отличие от сортировок кучей и слиянием, обе из которых имеют в худшем случае время сортировки O(n log n), быстрая сортировка в худшем случае будет выполняться O(n²).
Иногда полезно знать перечисленные выше алгоритмы, но в большинстве случаев разработчик, скорее всего, будет использовать функции сортировки, уже предоставленные в языке программирования.
Отсортировать содержимое списка можно с помощью стандартного метода sort():
>>> apples_eaten_a_day = [2, 1, 1, 3, 1, 2, 2]
>>> apples_eaten_a_day.sort()
>>> apples_eaten_a_day
[1, 1, 1, 2, 2, 2, 3]Или можно использовать функцию sorted() для создания нового отсортированного списка, оставив входной список нетронутым:
>>> apples_eaten_a_day_2 = [2, 1, 1, 3, 1, 2, 2]
>>> sorted_apples = sorted(apples_eaten_a_day_2)
>>> sorted_apples
[1, 1, 1, 2, 2, 2, 3]Оба эти метода сортируют в порядке возрастания, но можно изменить порядок, установив для флага reverse значение True:
# Обратная сортировка списка на месте
>>> apples_eaten_a_day.sort(reverse=True)
>>> apples_eaten_a_day
[3, 2, 2, 2, 1, 1, 1]
# Обратная сортировка, чтобы получить новый список
>>> sorted_apples_desc = sorted(apples_eaten_a_day_2, reverse=True)
>>> sorted_apples_desc
[3, 2, 2, 2, 1, 1, 1]В отличие от других алгоритмов, обе функции в Python могут сортировать также списки кортежей и классов. Функция sorted() может сортировать любую последовательность, которая включает списки, строки, кортежи, словари, наборы и пользовательские итераторы, которые вы можете создать.
Функции в Python реализуют алгоритм Tim Sort, основанный на сортировке слиянием и сортировке вставкой.
Сравнение скоростей сортировок
Для сравнения сгенерируем массив из 5000 чисел от 0 до 1000. Затем определим время, необходимое для завершения каждого алгоритма. Повторим каждый метод 10 раз, чтобы можно было более точно установить, насколько каждый из них производителен.
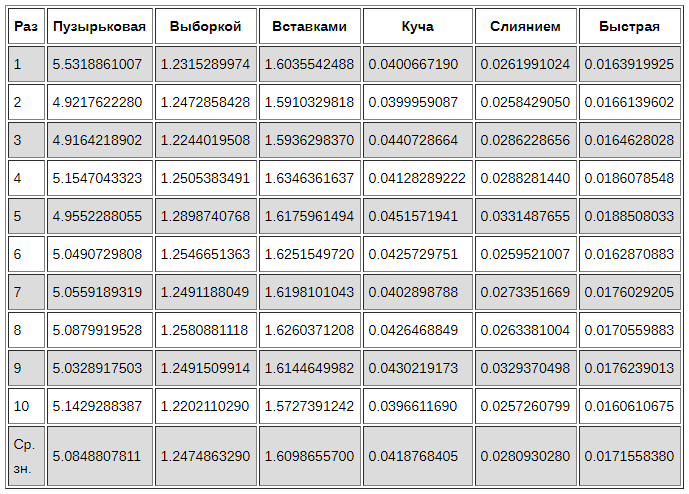
Пузырьковая сортировка — самый медленный из всех алгоритмов. Возможно, он будет полезен как введение в тему алгоритмов сортировки, но не подходит для практического использования.
Быстрая сортировка хорошо оправдывает своё название, почти в два раза быстрее, чем сортировка слиянием, и не требуется дополнительное место для результирующего массива.
Сортировка вставками выполняет меньше сравнений, чем сортировка выборкой и в реальности должна быть производительнее, но в данном эксперименте она выполняется немного медленней. Сортировка вставками делает гораздо больше обменов элементами. Если эти обмены занимают намного больше времени, чем сравнение самих элементов, то такой результат вполне закономерен.
Вы познакомились с шестью различными алгоритмами сортировок и их реализациями на Python. Масштаб сравнения и количество перестановок, которые выполняет алгоритм вместе со средой выполнения кода, будут определяющими факторами в производительности. В реальных приложениях Python рекомендуется использовать встроенные функции сортировки, поскольку они реализованы именно для удобства разработчика.
Предлагаем также ознакомиться с алгоритмами сортировки на Java.
Перевод статьи «Sorting Algorithms in Python»
