Составь графическую модель и реши уравнения:
21 : x = 3
x : 8 = 3
9 * x = 27

reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Урок 40. Уравнения. Номер №4
Решение
![]() Получай решения и ответы с помощью нашего бота
Получай решения и ответы с помощью нашего бота
![]() Посмотреть калькулятор Вычисления в столбик
Посмотреть калькулятор Вычисления в столбик

21 : x = 3
x = 21 : 3
x = 7

x : 8 = 3
x = 3 * 8
x = 24
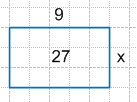
9 * x = 27
x = 27 : 9
x = 3
Пушкин сделал!
Разбор домашних заданий 1-4 класс
Home » Петерсон Математика » Урок 40. Уравнения. Л.Г. Петерсон Математика 2 класс Ответы
Урок 40. Уравнения. Л.Г. Петерсон Математика 2 класс Ответы
1. Составь 4 равенства из чисел 3, 9 и 27. Построй графическую модель и отметь на ней данные числа.

9 ∙ 3 = 27 27 : 9 = 3
3 ∙ 9 = 27 27 : 3 = 9
2. Найди неизвестное число:

х = 5 ∙ 3 х = 24 : 8 х = 12 : 2
х = 15 х = 3 х = 6
3. Подбери для каждого уравнения подходящий рисунок. Как найти х? Сделай вывод.


Чтобы найти неизвестную сторону прямоугольника, надо площадь разделить на вторую сторону.
Чтобы найти площадь прямоугольника, надо перемножить его длину на ширину.

4. Составь графическую модель и реши уравнения:
21 : х = 3 х : 8 = 3 9 ∙ х = 27

21 : х = 3 х : 8 = 3 9 ∙ х = 27
х = 21: 3 х = 3 ∙ 8 х = 27 : 9
х = 7 х = 24 х = 3
Проверка: Проверка: Проверка:
21 : 7 = 3 24 : 8 = 3 9 ∙ 3 = 27
3 = 3 3 = 3 27 = 27
5. Реши уравнения. Как можно проверить своё решение?
х ∙ 2 = 18 12 : х = 4 х : 4 = 2
х ∙ 2 = 18 12 : х = 4 х : 4 = 2
х = 18 : 2 х = 12 : 4 х = 2 ∙ 4
Проверка: Проверка: Проверка:
9 ∙ 2 = 18 12 : 3 = 4 8 : 4 = 2
18 = 18 4 = 4 2 = 2
6. Реши уравнения с комментированием:
х : 3 = 9 х ∙ 2 = 10 12 : х = 6
Целое : часть = часть (1)
Часть ∙ часть = целое (2)
х : 3 = 9 х ∙ 2 = 10 12 : х = 6
Ц : 3 = 9 ч ∙2 = 10 12 : ч = 6
х = 9 ∙3 (2) х = 10 : 2 (1) х = 12 : 6 (1)
х = 27 х = 5 х = 2
Проверка: Проверка: Проверка:
27 : 3 = 9 5 ∙ 2 = 10 12 : 2 = 6
9 = 9 10 = 10 6 = 6
7. БЛИЦтурнир

а) а — b (р.) – во втором аквариуме
a — b + a (р.) в двух аквариумах
б) а) а + b (р.) – во втором аквариуме
a + b + a (р.) — в двух аквариумах
в) m + n (ягод) — на двух кустах
m + n – a (ягод) – зелёных на кустах
г) b + c (яб.) — съел Миша
d – (b + c) (яб.) – осталось
д) a + b (д.) – солнечных
a + b + a + b = 2 ∙ (a + b) (д.) – длились каникулы
е) b + c (м.) – уехало
a – (b + c) (м.) — осталось в гараже
8. Выполни действия:

0 ∙6 + 94 ∙ 1 = 0 + 94 = 94 24 – 24 : 1 = 24 -24 = 0
1 ∙ 38 – 2 ∙ 0 = 38 – 0 =38 58 ∙ 1 – 58 = 58 – 58 = 0
35 : 35 + 0 : 47 = 1 + 0 = 1
42 : 1 – 5 ∙ 1 = 42 – 5 = 37
9. Какие числа надо вставить вместо пропусков?

10. Составь выражения и найди их значения:
а) Из суммы чисел 216 и 347 вычесть разность чисел 540 и 458.
б) К разности чисел 829 и 734 прибавить сумму чисел 593 и 17.
(216 + 347) – (540 — 458) = 563 – 82 = 471
(829 – 734) + (593 + 17) = 95 + 610 = 705
11. Перечерти в тетрадь рисунок по клеточкам. Отметь на луче ОА точки В и С. Сколько лучей стало на чертеже? Пересекает ли луч ОА прямая m? Пересекает ли эта прямая лучи ВА и СА?


На рисунке стало 3 луча:ОА, ВА, СА. Прямая m пересекает луч ОА, так как у прямой нет начала, нет конца. Пересекает луч ВА (пересекает отрезок ВС), но не пересекает луч СА.
12. Что изменилось на рисунках?


2. Рисунок на рамке картины
3. Положение солнца на картине
4. Изменилось дерево на картине
5. Перекладины на стуле
6. Ручка лежала справа от тетради
7. – 8. Полоса на вазе стала широкой с кружками
9. Осталось 1 яблоко и груша
10. Подставка у вазы стала широкой
11. Мышка повернута в другую сторону
12. Мяч лежит по – другому
13. Хвост кота был слегка поднят, здесь лежит прямо
14. Изменился бант у кота
13*. Продолжи числовой ряд на три числа, сохрани закономерность:
а) 129, 138, 147 … б) 4, 12, 21, 31, 42 …

14*. Составь слова и найди лишнее слово:
ТРБА НАВКЧУ ААММ ТЕСАРС УРДГ ППАА
БРАТ ВНУЧКА МАМА СЕСТРА ДРУГ ПАПА
Лишнее слово ДРУГ, потому что не относится к членам семьи.
Здравствуйте! Меня зовут Мария, я автор сайта Пушкин сделал. Надеюсь, что мой сайт вам помогает, в свою очередь прошу помощи у вас. Моему сыну поставили диагноз аутизм. Ему необходимы ежедневные коррекционные занятия, если вы можете помочь, буду вам благодарна. Каждые ваши 10 рублей – еще один шанс для моего ребенка жить полноценной жизнью. Страница для сбора здесь
Графическое решение уравнений
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти

На этом видеоуроке к изучению предлагается тема «Функция y=x 2 . Графическое решение уравнений». В ходе этого занятия учащиеся смогут познакомиться с новым способом решения уравнений – графическим, который основан на знании свойств графиков функций. Учитель покажет, как можно решить графическим способом функцию y=x 2 .
Методика организации решения уравнений графическим способом как средство формирования графических умений у учащихся
Разделы: Математика
Графический метод обладает рядом преимуществ:
- он часто проще аналитического;
- обладает наглядностью. Особенно когда нет решений или требуется установить количество корней.
- он красив и доставляет эстетическое наслаждение. Выполнять графики нужно в цвете. Это помогает в выборе ответа.
Умение строить графики функций не является самоцелью. Часто построение графиков связано с исследованием поведения функций. Однако необходимость построения графиков облегчают нахождение решений уравнений и неравенств, сокращая или упрощая аналитические выкладки и часто при этом являются единственным методом решения таких задач. Графический метод решения способствует лучшему усвоению ряда понятий: функции, корней уравнения и неравенства, систем уравнений. При этом целесообразно при графическом решении уравнений устанавливать связи с такими свойствами функций как возрастание и убывание, знакопостоянство, обращение функции в ноль и т.д., что помогает глубже понять функциональную зависимость между величинами. Изучение поведения функций и построение их графиков является важным разделом математики. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством их решения. Кроме того, умение строить график представляет большой самостоятельный интерес. Материал, связанный с построением графиков функций, в средней школе изучается недостаточно полно с точки зрения требований, предъявляемых на экзаменах. Поэтому задачи на построение графиков нередко вызывают затруднения у учащихся.
Для того, чтобы по графикам можно было получать достаточно приемлемые числовые ответы, графики должны быть особенно тщательно построены. Решается задача организации работы таким образом, чтобы выработать навыки быстрого построения графиков элементарных функций и их преобразований. Работа над формированием графических умений начинается с 5-го класса.
Изящно выполненная работа способствует развитию чувства красоты, удовлетворения от проделанной работы.
Изучение поведения функций и построение их графиков являются важным разделом школьного курса. Свободное владение техникой построения графиков часто помогает решать сложные задачи, а порой является единственным средством их решения. Кроме того, умение строить графики функций представляет большой интерес для самих учащихся. Однако на базе основной школы материал, связанный с этим вопросом, представлен несколько хаотично, изучается недостаточно полно, многие важные моменты не входят в программу.
Цель – прояснить и дополнить школьный материал, связанный с функциями и построение их графиков, применением их к решению уравнений, их систем.
В требованиях к уровню подготовки выпускников по разделу «Функции и графики» прописано:
- решать уравнения, системы уравнений, используя свойства функций и их графические представления;
- находить приближённые решения уравнений и их систем, используя графический метод.
В преподавание алгебры по учебнику под редакцией А.С.Теляковского. Линейная функция и функции у=х 2 , у=х 3 изучаются в 7 классе. Практически не вырабатываются навыки в применении графиков этих функций. Единственное упражнение: найти координаты точек пересечения графиков функций у=8,5х и у=0,5х-19,5. графики линейных функций только иллюстрируют решение систем линейных уравнений.
Автор вводит некоторые упражнения, необходимые в дальнейшем при решении уравнений и их систем:
– постройте в одной и той же координатной плоскости а) у=х 2 ; у=4; б) у=х 2 ; у=2х.
– изобразите схематически графики функций у = -0,9х + 4; у = 2,3х; у = х/10 . Но упражнения вводятся как дополнительные. И в «Задачах повышенной трудности» (в конце учебника) есть уравнения, которые тоже можно решать графическим способом: |х -3| = 7; |х+2| = 9; |4 – х| = 1,5.
В 8 классе изучаются функции у = к/х; у =. Представлены функции у = 4/|х|, у = -6/|х|.
– Могут ли графики функций у=к/х и у = ах +в пересекаться
а) в одной точке;
б) в двух точках;
в) в трёх точках.
– Могут ли графики функций у = к/х и у = ах +в пересекаться в двух точках, лежащих
а) в одной четверти;
б) в первой и второй четвертях;
в) в первой и третьей четвертях.
Опять же эти упражнения в дополнительных.
В 8 классе обучающихся знакомят с графическим способом решения уравнений (8/х = -х+6; (8/х = х 2 ). Появляются уравнения третьей степени, которые не решаются аналитическим способом. (х 3 – х + 1 = 0; х 3 + 2х – 4=0) На изучение этой темы отводится 1 час.
В 9 классе подробно изучается квадратичная функция и её график. Получены обучающимися представления о преобразовании графического объекта относительно осей координат. Именно в это время отрабатываются навыки в построении параболы. Но данные преобразования почти не переносятся на преобразования других графических объектов. Хотя есть два упражнения, которые соотносятся с заданиями, встречающимися в материалах ЕГЭ.
На рисунке изображён график одной их функций . Какой именно?
– Какой из трёх графиков, изображённых на рисунке, является графиком функции у = |х -2|
Сделаны попытки преобразования графических объектов.
– Какие преобразования надо выполнить, чтобы
а) из графика функции у=х 3 получить графики функций у = – х 3 ; у = (х-3) 3 ; у = х 3 + 4.
б) из графика функции у = получить графики функций у = – ;
– Постройте в одной координатной плоскости графики функций у = | х|; у =|х -4| ; у = |х -4|-3.
В учебнике 9 класса в главе «Целое уравнение и его корни» упоминается графический способ уравнений третьей и более высокой степени как один из способов наряду с разложением на множители.
Поэтому: уже в 7 классе строим графики функций у = | х| – 3, у = 4 – | х|; у =|х +4|; у = | х – 3|.
При построении параболы вводим первые преобразования:
– построить графики функций у = х 2 +3; у=х 2 -5, где смещение по оси ординат. А затем у = (х+2) 2 ; у = (х-1) 2 . Конечно, не все ученики усваивают, впрочем, как и всё содержание материала. Для успешных учеников это не сложно. Тем более это только пропедевтика.
В 8-м классе: Урок-практикум.
Тема: «График функции у = . Графический способ решения иррациональных уравнений»
Цель: отработать навыки в преобразовании графика функции у = , закрепить умения графически решать иррациональные уравнения.
I. Фронтально
1). Схематически в одной системе координат изобразить графики функций
2). Решить уравнения
II. Построить графики функций
III. Решение уравнений
X 2 -3 =
В 8 классе строим преобразования гиперболы и графика функции у = .
Упражнения взяты из «Сборника задач по алгебре 8-9 класса» М.Л.Галицкого, А.И.Звавича. Уже на факультативных занятиях или занятиях кружка решаем уравнения с параметром |х 2 -2х-3| = а. Определить, при каком а уравнение имеет три корня. Строим графики функций у = |х 2 -2х-3|; у = а. Получаем ответ а = 4.
В 9 классе больше занимаемся исследованием квадратного трёхчлена. Формулы функций усложняю. Рассматриваем графики вида у = (х 2 -2) 2 – (х 2 -1) 2 ;
Необычность конструкций, разрыв графиков, удаление точек вызывает некоторую удивлённость. Тем самым преодолевается стандартность мышления, развивается воображение, повышается интерес: а что ещё может получиться? В каких случаях?
Уравнения, решаемые графическим способом.
I. Решение уравнений Р(х) = 0, где Р(х) – многочлен степени большей 2.
[spoiler title=”источники:”]
http://interneturok.ru/lesson/algebra/7-klass/funkciya-yx2/graficheskoe-reshenie-uravneniy
http://urok.1sept.ru/articles/672912
[/spoiler]
1. Составь 4 равенства из чисел 3, 9 и 27. Построй графическую модель и отметь на ней данные числа.

9 ∙ 3 = 27 27 : 9 = 3
3 ∙ 9 = 27 27 : 3 = 9
2. Найди неизвестное число:

Решение:
х = 5 ∙ 3 х = 24 : 8 х = 12 : 2
х = 15 х = 3 х = 6
3. Подбери для каждого уравнения подходящий рисунок. Как найти х? Сделай вывод.

Решение:

Чтобы найти
неизвестную сторону прямоугольника, надо площадь разделить на вторую сторону.
Чтобы найти площадь прямоугольника, надо перемножить его длину на ширину.

4. Составь
графическую модель и реши уравнения:
21 : х =
3 х : 8 = 3 9 ∙ х = 27
Решение:

21 : х = 3 х : 8 = 3 9 ∙ х = 27
х = 21: 3 х = 3 ∙ 8 х = 27 : 9
х = 7 х = 24 х = 3
Проверка: Проверка: Проверка:
21 : 7 = 3 24 : 8 = 3 9 ∙ 3 = 27
3 = 3 3 = 3 27 = 27
5. Реши
уравнения. Как можно проверить своё решение?
х ∙ 2 =
18 12 : х = 4 х
: 4 = 2
Решение:
х ∙ 2 = 18 12 : х = 4 х : 4 = 2
х = 18 : 2
х = 12 : 4 х
= 2 ∙ 4
х = 9 х = 3 х = 8
Проверка:
Проверка: Проверка:
9 ∙ 2 = 18 12 : 3 = 4 8 : 4 = 2
18 = 18 4 = 4 2 = 2
6. Реши
уравнения с комментированием:
х : 3 =
9 х ∙ 2 = 10 12 : х = 6
Решение:
Целое : часть = часть (1)
Часть ∙ часть = целое
(2)
х : 3 =
9 х ∙ 2 =
10 12 : х = 6
Ц : 3 = 9 ч
∙2 = 10 12 : ч = 6
х = 9 ∙3 (2) х = 10
: 2 (1) х = 12 : 6 (1)
х = 27
х = 5 х = 2
Проверка:
Проверка: Проверка:
27 : 3 = 9
5 ∙ 2 = 10 12 : 2 = 6
9 = 9 10 = 10 6 = 6
7. БЛИЦтурнир

Решение:
а) а — b (р.) – во
втором аквариуме
a — b + a (р.) в
двух аквариумах
б) а) а + b (р.) – во
втором аквариуме
a + b + a (р.) — в двух аквариумах
в) m + n (ягод) — на
двух кустах
m + n – a (ягод) –
зелёных на кустах
г) b + c (яб.) — съел
Миша
d – (b + c) (яб.) –
осталось
д) a + b (д.) – солнечных
a + b + a + b = 2 ∙ (a + b) (д.) – длились каникулы
е) b + c (м.) – уехало
a – (b + c) (м.) — осталось в гараже
8. Выполни действия:

Решение:
0 ∙6 + 94 ∙ 1 = 0 + 94
= 94 24 – 24 : 1 =
24 -24 = 0
1 ∙ 38 – 2 ∙ 0 = 38 – 0 =38 58 ∙ 1 – 58 = 58 – 58 =
0
35 : 35 + 0 : 47 = 1 + 0 = 1
42 : 1 – 5
∙ 1 = 42 – 5 = 37
9. Какие числа надо вставить вместо пропусков?

10. Составь
выражения и найди их значения:
а) Из суммы
чисел 216 и 347 вычесть разность чисел 540 и 458.
б) К
разности чисел 829 и 734 прибавить сумму чисел 593 и 17.
Решение:
(216 + 347) – (540 — 458) = 563 – 82 = 471
(829 – 734) + (593 + 17) = 95 + 610 = 705
11. Перечерти в тетрадь рисунок по клеточкам. Отметь на луче ОА точки В и С. Сколько лучей стало на чертеже? Пересекает ли луч ОА прямая m? Пересекает ли эта прямая лучи ВА и СА?

Решение:

На рисунке стало 3 луча:ОА, ВА, СА. Прямая m пересекает луч
ОА, так как у прямой нет начала, нет конца. Пересекает луч ВА (пересекает
отрезок ВС), но не пересекает луч СА.
12. Что изменилось на рисунках?

Решение:

1. Обои
2. Рисунок на рамке картины
3. Положение солнца на картине
4. Изменилось дерево на картине
5. Перекладины на стуле
6. Ручка лежала справа от тетради
7. – 8. Полоса на вазе стала широкой с кружками
9. Осталось 1 яблоко и груша
10. Подставка у вазы стала широкой
11. Мышка повернута в другую сторону
12. Мяч лежит по – другому
13. Хвост кота был слегка поднят, здесь лежит прямо
14. Изменился бант у кота
13*.
Продолжи числовой ряд на три числа, сохрани закономерность:
а) 129,
138, 147 … б) 4, 12, 21, 31,
42 …
Решение:

14*.
Составь слова и найди лишнее слово:
ТРБА НАВКЧУ ААММ
ТЕСАРС УРДГ ППАА
Решение:
БРАТ ВНУЧКА МАМА
СЕСТРА ДРУГ ПАПА
Лишнее слово ДРУГ, потому что не относится к членам семьи.
Назад к содержанию
Презентация на тему “Решение уравнений с использованием графической модели”
-
Скачать презентацию (0.37 Мб)
-
34 загрузки -
2.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Смотреть презентацию онлайн с анимацией на тему “Решение уравнений с использованием графической модели” по математике. Презентация состоит из 17 слайдов. Материал добавлен в 2017 году. Средняя оценка: 2.0 балла из 5.. Возможность скчачать презентацию powerpoint бесплатно и без регистрации. Размер файла 0.37 Мб.
-
Формат
pptx (powerpoint)
-
Количество слайдов
17
-
Слова
-
Конспект
Отсутствует
Содержание
-

Слайд 1
АВТОР: Руденко Наталья Николаевна ,учитель математики МОУ «СОШ №15 имени В.Л. Гриневича» города Прокопьевска
Решение уравнений
с использованием
графической модели. -

Слайд 2
1. х + а = в (или а + х = в)
Решение:а (часть)
х (часть)
в (целое)
х= в-а
-

Слайд 3
Например: х + 345 = 532
Решение:345 (часть)
х (часть)
532 (целое)
х= 532- 345, х = 187 -

Слайд 4
2. х – а = в
Решение:а (часть)
в (часть)
х (целое)
х = а + в -

Слайд 5
Например: х – 345 = 532
Решение:345 (часть)
532 (часть)
х (целое)
х = 532 + 345, х = 877 -

Слайд 6
3. а – х = в
Решение:в (часть)
х (часть)
а (целое)
х = а – в -

Слайд 7
Например: 532 – х = 345
Решение:345 (часть)
х (часть)
532 (целое)
х = 532 – 345, х = 187 -

Слайд 8
4. х · а = в (или а · х = в)
Решение:
х х х х х х х х х ха раз
в (целое)
х = в : а -

Слайд 9
Например: х · 17 = 425 Решение:
х х х х х х х х х х х х х х х х
17 раз
425 (целое)
х = 425 : 17, х = 25 -

Слайд 10
5. х : а = в
Решение:х (целое)
а раз
в
х = в · а -

Слайд 11
Например: х : 4 = 2096
Решение:4 раза
2096
х (целое)
х = 2096 · 4, х = 8384 -

Слайд 12
6. а : х = в
Решение:а (целое)
х разв
х = а: в -

Слайд 13
Например: 405 : х = 81
Решение:х раз
405 (целое)
81
х = 405 : 81, х = 5 -

Слайд 14
Используя примеры №1-№6
Решим уравнение: 5х +47 = 297
Решение:5 раз
Х
47
297
х = (297 – 47) : 5, х = 50 -

Слайд 15
Используя примеры №1-№6
Решим уравнение: х : 4 – 24 = 16
Решение:Х (целое)
24
16
х = (24+16) · 4, х = 160 -

Слайд 16
Используя примеры №1-№6
Решим уравнение: (х – 56 ) : 7=15
Решение:Х (целое)
56
7 раз
15
х = 15 · 7 + 56, х = 161 -

Слайд 17
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Александрова Э. И. Методика обучение математики в начальной школе ( 2 класс, 3 класс, 4 класс ) , [Текст]: методическое пособие/ Э. И. Александрова- М: ВИТА- ПРЕСС, 2010 г.
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации









Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте
Подведём итоги наших знаний о графиках функций.
Нами были изучены методы построения таких функций, как:
(y =b) (график — прямая, параллельная оси (x));
(y = kx) (график — прямая, которая проходит через начало координат);
(y = kx + m) (график — прямая);
(график — парабола).
При необходимости мы сможем преобразовать аналитическую модель на графическую. Допустим, аналитическую модель
y=x2
трансформировать в графическую модель в виде параболы, расположенной в прямоугольной системе координат.
Этот приём полезен при решении уравнений. Продемонстрируем это на примерах.
Пример:
решить уравнение
x2=2x+8
.
Рассмотрим две функции:
y=x2
, (y = 2x + 8) — выполним построение графиков этих функций в одной системе координат, чтобы найти их точки пересечения.

Парабола
y=x2
и прямая (y = 2x + 8) пересекаются в точках (A (- 2; 4)) и (B (4; 16)).
Корни уравнения
x2=2x+8
— значения (x), при которых выражения
x2
и (2x + 16) принимают одинаковые значения. Это первые координаты точек (A) и (B) пересечения графиков:
x1=−2;x2=4
.
Алгоритм графического решения уравнений
1. Преобразовать уравнение так, чтобы в левой и правой части стояли известные функции.



2. В одной системе координат начертить графики этих функций.
3. Определить точки пересечения полученных графиков.
4. Взять из них значения абсцисс.



